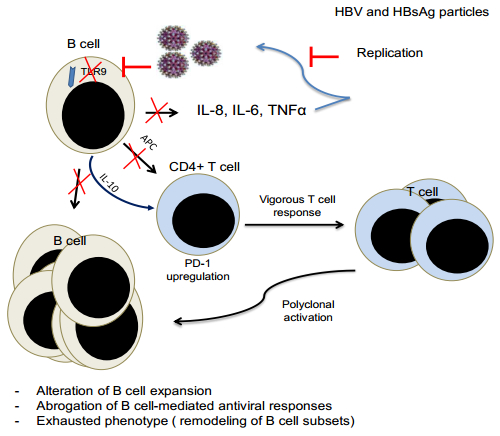
Chronic HBV infection affects more than 240 million people worldwide and is a major risk factor for developing cancer in which 10–30% of cases will progress towards liver cirrhosis and hepatocellular carcinoma. Infection outcome relies on the immune system maturity. Toll-like receptor 9 (TLR9) is a sensor of viral and bacterial DNA motifs and activates plasmacytoid dendritic cells (pDCs) and B cells to generate effective immune responses against infection. B cells, especially CD38hi plasma cells play a major role in mediating humoral immune responses to clear HBV infection. Many studies have shown that TLR9 function is abrogated by HBV in pDCs. We aim to discuss the importance of B cell function in CHB patients and summarize concisely studies that describe the effect of HBV on TLR9 mediated B cell function. The effect of HBV on TLR9 activity in B cells should give insights into oncoviral immune escape strategies providing knowledge that will be essential to develop novel immunotherapeutic approaches.
1.
Introduction
This paper concerns inverse problems for differential equations on quantum graphs. Under quantum graphs or differential equation networks (DENs) we understand differential operators on geometric graphs coupled by certain vertex matching conditions. Network-like structures play a fundamental role in many problems of science and engineering. The range for the applications of DENs is enormous. Here is a list of a few.
–Structural Health Monitoring. {DENs, classically, arise in the study of stability, health, and oscillations of flexible structures that are made of strings, beams, cables}, and struts. Analysis of these networks involve DENs associated with heat, wave, or beam equations whose parameters inform the state of the structure, see, e.g., [44].
–Water, Electricity, Gas, and Traffic Networks. An important example of DENs is the Saint-Venant system of equations, which model hydraulic networks for water supply and irrigation, see, e.g., [33]. Other important examples of DENs include the telegrapher equation for modeling electric networks, see, e.g., [3], the isothermal Euler equations for describing the gas flow through pipelines, see, e.g., [21], and the Aw-Rascle equations for describing road traffic dynamics, see e.g., [29].
–Nanoelectronics and Quantum Computing. Mesoscopic quasi-one-dimensional structures such as quantum, atomic, and molecular wires are the subject of extensive experimental and theoretical studies, see, e.g., [37], the collection of papers in [38,39,40]. The simplest model describing conduction in quantum wires is the Schrödinger operator on a planar graph. For similar models appear in nanoelectronics, high-temperature superconductors, quantum computing, and studies of quantum chaos, see, e.g., [42,41,45].
–Material Science. DENs arise in analyzing hierarchical materials like ceramic and metallic foams, percolation networks, carbon and graphene nano-tubes, and gra-phene ribbons, see, e.g., [1,46,47].
–Biology. Challenging problems involving ordinary and partial differential equations on graphs arise in signal propagation in dendritic trees, particle dispersal in respiratory systems, species persistence, and biochemical diffusion in delta river systems, see, e.g., [7,24,48].
Quantum graph theory gives rise to numerous challenging problems related to many areas of mathematics from combinatoric graph theory to PDE and spectral theories. A number of surveys and collections of papers on quantum graphs appeared in previous years; we refer to the monograph by Berkolaiko and Kuchment, [25], for a complete reference list. The inverse theory of network-like structures is an important part of a rapidly developing area of applied mathematics---analysis on graphs. Being tremendously important for all aforementioned applications these theories have not been, however, sufficiently developed. To date, there are relatively few results related to inverse problems on graphs, and almost exclusively they concern trees, i.e. graphs without cycles.
The first question to be asked when studying inverse problems is how to establish the uniqueness result, i.e. to characterize spectral, or scattering, or dynamical data ensuring uniques solution of the inverse problem. It was shown that inverse boundary spectral and scattering problems for differential equations on graphs with cycles do not have in general a unique solution [41,34,43]. The results on stable identification are known only for trees, and only for the case of boundary inputs (controls) and observations. It was proved that a DEN is identifiable if the actuators and sensors are placed at all or all but one boundary vertices.
There are two groups of uniqueness results in this direction: for trees with a priori known topology and lengths of the edges [28,49,32] and for trees with unknown topology [22,23,11,13]. The most significant result of the last two cited papers is developing a constructive and robust procedure for the recovery tree's parameters, which became known as the leaf peeling method. This method was extended to boundary inverse problems for various types of PDEs on trees in a series of our subsequent papers [7,15,20].
The boundary control method in inverse theory demonstrates [11,23] that inverse (identification) problems for DENs are closely related to control and observation problems for PDEs on graphs. The latter problems were studied in numerous papers, see, e.g. [5,16,30,35,44,50] and references therein.
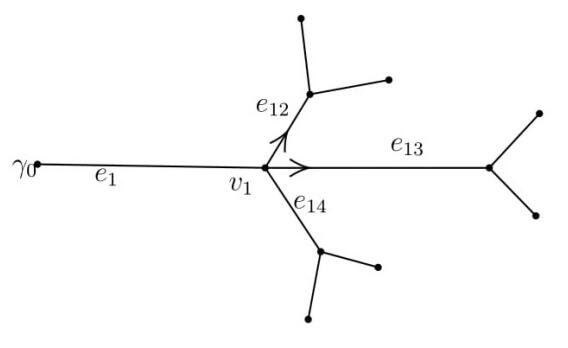
In this paper, we solve a non-standard dynamical inverse problem for the wave equation on a metric tree graph. Let Ω={V,E} be a finite compact and connected metric tree (i.e. graph without cycles), where V is a set of vertices and E is a set of edges. We recall that a graph is called a metric graph if every edge ej∈E,j=1,…,N, is identified with an interval (a2j−1,a2j) of the real line with a positive length ℓj. We denote the set of boundary vertices (i.e. vertices of degree one) by Γ={γ0,...,γm}, and the set of interior vertices (whose degree is at least two) by {vm+1,....,vN}. The vertices can be regarded as equivalence classes of the edge end points aj. For each vertex vk, denote its degree by Υk. We write j∈J(v) if ej∈E(v), where E(v) is the set of edges incident to v.
The graph Ω determines naturally the Hilbert space of square integrable functions H=L2(Ω). We define its subspace H1 as the space of continuous functions y on Ω such that y|e∈H1(e) for every e∈E and y|Γ=0, and let H−1 be the dual space to H1. When convenient, we will denote the restriction of a function y on Ω to ej by yj. For any vertex vk and function y(x) on the graph, we denote by ∂yj(vk) the derivative of yj at vk in the direction pointing away from the vertex.
We will assume that for each internal vertex vk, a mass Mk≥0 is placed at vk. Our system is described by the following initial boundary value problem (IBVP):
Here T is an arbitrary positive number, qj∈CN([a2j−1,a2j]) for all j, and f∈L2(0,T). In what follows, we will refer to γ0 as the root of Ω and f as the control. The well-posedness of this system is discussed in Section 2, see Theorem 2.8, where it is proved that uf∈C([0,T];H)∩C([0,T];H−1). In the absence of any masses, and for sufficiently regular q, it was discussed in several papers, see, e.g. [44,19,15,16]. In the presence of masses, the function u will have more regularity properties, see Section 2 and [2,36].
Inverse Problem 1. Assume an observer knows the topology of the tree, i.e. the number of boundary vertices and interior vertices, the adjacency relations for this tree, i.e. for each pair of vertices, whether or not there is an edge joining them. Assume the observer also knows the boundary condition (5), and that (6) holds at the other boundary vertices. The unknowns are the lengths {ℓj}, the masses Mk, and the function q. We wish to determine these quantities with a set of measurements that we describe now.
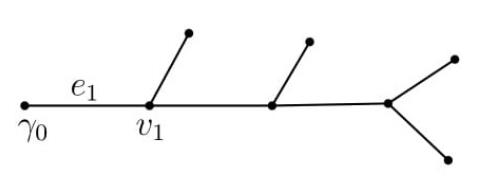
Let v1 be the interior vertex adjacent to γ0 and let e1 be the edge joining the two, see Figure 1. Our first measurement is then the following measurement at γ0:
Physically, this corresponds to applying a Dirichlet control and placing a tension sensor, both at γ0. In what follows, we will refer to R01 as the "root response operator".
Theorem 1.1. From operator R01 one can recover the following data: ℓ1,q1, Υ1, and M1.
The proof of this, appearing in Section 2, is an adaptation of an argument well known for the massless case, M1=0, see [11].
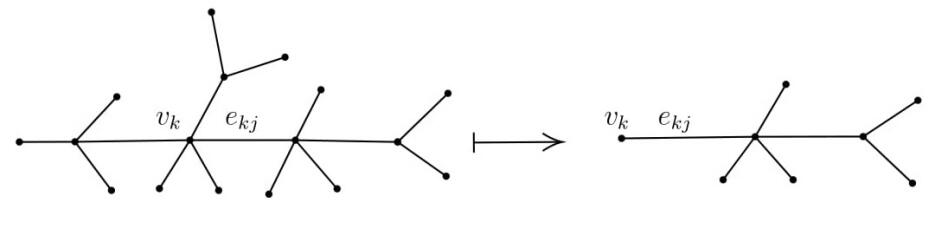
We now define the other measurements required for the inverse problem. For interior vertex vk we list the incident edges by {ekj: j=1,...,Υk}. Here ek1 is chosen to be the edge lying on the unique path from γ0 to vk, and the remaining edges are labeled randomly, see Figure 2. Then the tension sensors, represented by arrows in Figure 2, measure
We remark in passing that because the control and sensors are at different places, Theorem 1.1 does not apply. We will show that it is not required to measure ∂ufj(vk,t) for j=1 or Υk. Thus for the whole graph, the total number of sensors needed is 1+∑N−m−1k=1(Υk−2). It is easy to check that this number is equal to |Γ|−1. We denote by RT, which we call the "total response operator", the (|Γ|−1)-tuple (R01,R12,R13,....) acting on L2(0,T).
Let ℓ be equal to the maximum distance between γ0 and any other boundary vertex. In our first main result, we solve Inverse Problem 1.
Theorem 1.2. Assume qj∈CN([a2j−1,a2j]) for all j. Suppose T>2ℓ. Then from RT one can determine q, the point masses and the lengths of the edges.
Placement of internal sensors has been considered in the engineering and computer science literature, see, e.g. [26,27]. We are unaware of any mathematical works treating the inverse problem on general tree graphs with measurements at the internal vertices, except for [8] where the interior vertices are assumed to satisfy delta-prime matching conditions instead of (3), (4). Internal measurements might have advantages in situations where some boundary vertices are inaccessible. In future work, we will study inverse problems of graphs with cycles, in which case both boundary and internal observations appear to be necessary. For a discussion on inverse problems for graphs with cycles see [4] and references therein.
We briefly mention some of the ideas used in the proof of Theorem 1.2. Denote by Ωkj the unique subtree of Ω having vk as root with incident edge ekj, see Figure 3. In Section 3, we will define the operator ˜Rkj, analogously to our definition of R01, as the root response operator associated to Ωkj. Assume for now k=1 and fix j>1. We will show that ˜R1j can be determined by using our knowledge of R01 and R1j. This will be achieved using two ingredients. The first ingredient is an identity relating the Schwartz kernels of ˜R1j and R1j, using general properties of wave propagation on graphs. The second is our knowledge of the data associated with the edge e1. Having determined ˜R1j, we apply Theorem 1.1 to determine the data associated to e1j. Similarly we will determine the data associated to all edges incident to v1. Then using this newly determined data together with the appropriate components of RT, we then determine the data for all edges incident to the neighbors of v1. The argument can then be iterated until the data associated with each edge are determined.
The iterative nature of our solution actually allows us to solve what at first glance seems to be a much harder inverse problem.
Inverse Problem 2. Assume an observer knows Ω is a tree, that the boundary condition (5) holds, and that (6) holds at the other boundary vertices. All other data are unknowns. The problem then is to use RT to determine the topology, the lengths {ℓj}, the masses Mk, and the function q.
To solve this inverse problem, for P∈N, define ΩP to be the subgraph of Ω covered by paths in Ω starting at γ0 and containing (P+1) vertices. Define RTP to be the vector consisting of elements Rkj of RT such that vk∈ΩP. Then we have the following refinement of Theorem 1.2.
Theorem 1.3. Assume qj∈CN([a2j−1,a2j]) for all j. Suppose T>2ℓ. Then for any P∈N, one can determine from RT(P−1) the following: a) the topology of ΩP, b) Mk, Υk for all vk∈ΩP, and c) for each ej∈ΩP, the length of ej and qj.
We remark that in the theorem, Υk should be interpreted as the degree of vk as an element of Ω. Evidently, this theorem will allow one to solve Inverse Problem 2 by choosing P large enough. It will be clear that the proof of Theorem 1.2 actually proves Theorem 1.3.
In an engineering setting, Inverse Problem 2 could be solved using the following process. One begins with only the control and sensor at γ0. Once these are used to determine Υ1, one transports (Υ1−2) sensors to edges incident to v1, perhaps by robots along e1. Then the arguments of this paper allow one to determine ˜R1j, and thus the data associated with those edges including the degrees of the vertices adjacent to v1. Mathematically, this will be equivalent to having derived the conclusions of Theorem 1.3 for Ω1. Then more sensors would be transported to those vertices, enabling the next steps in our iterative process to proceed to solve for Ω2. Clearly this process could be continued until the graph is exhausted. It will be clear that our proof of Theorem 1.2 actually tracks this process.
We now compare our paper with the literature. All papers referred to in this paragraph assume all controls and measurements take place at boundary vertices. In [11], the authors consider trees with no masses, and assume that controls and measurements are placed at (|Γ|−1) boundary vertices. The authors use an iterative method called "leaf peeling'', where the response operator on Ω is used first to determine the data on the edges adjacent to the boundary, and then to determine the response operator associated to a proper subgraph. The leaf peeling argument includes spectral methods that require knowing RT for all T. The tools used in our paper mostly closely resemble those in [20,17], where an iterative dynamical argument, called "dynamical leaf peeling", is developed for a tree with no masses and with response operators at all but one boundary vertices, allowing for the solution of the inverse problem for finite T sufficiently large. The arguments in the present paper differ from those papers in two main ways: (a) the presence of masses in our paper complicates the underlying analysis, and (b) our use of interior measurements makes the proofs somewhat simpler. In [2], the methods of [11] are extended to the case where masses are placed at internal vertices, see also [6]; however these methods still require knowledge of RT for all T. Also in [2], it is proven that that for a single string of length ℓ with N attached masses and T>2ℓ, RT01 is sufficient to solve the inverse problem.
In the present paper we develop a new version of the dynamical leaf peeling method. A special feature of our paper is that we use only one control together internal observations. This may be useful in some physical settings where some or most boundary points are inaccessible, or where use of more than one control might be difficult. The extension of dynamical leafing peeling to systems with attached masses, for which the underlying analysis is more complicated than in the mass-free setting, should also be of interest. Another potential advantage of the method presented here is that we recover all parameters of the graphs, including its topology, from the (|Γ|−1)-tuple response operator acting on L2(0,T). In previous papers, the authors recovered the graph topology from a larger number of measurements: the (|Γ|−1)×(|Γ|−1) matrix (boundary) response operator or, equivalently, from (|Γ|−1)×(|Γ|−1) Titchmarsh–Weyl matrix function. In [12], the inverse problems on a star graph for the wave equation with general self-adjoint matching conditions was solved by the (|Γ|−1)×(|Γ|−1) matrix boundary response operator.
2.
Representation of solution and the response function for star graph
In this section, we prove well-posedness of our IBVP for a star shape graph. We also derive representations of both the solution and the Schwartz kernel of the components of the response operator. The representations will be used in Section 3 to solve the inverse problem. We then indicate how these results can be extended from star graphs to arbitrary trees.
2.1. Preliminaries
In what follows, it will convenient to denote
where Hn(R) are the standard Sobolev spaces. We define the Heaviside function by H(t)=1 for t>0, and H(t)=0 for t<0. Then define Hn∈Fn as the unique solution to
at times we will use H−1(t), resp. H−2(t) for δ(t), resp. δ′(t). In this section and those that follow, we will drop the superscript T from RT when convenient.
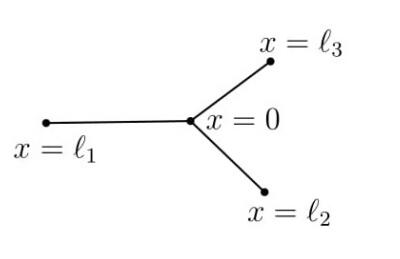
Consider a star shaped graph with edges e1,...,eN. For each j, we identify ej with the interval (0,ℓj) and the central vertex with x=0, see Figure 4.
Recall the notation qj=q|ej, and uj(⋅,t)=u(⋅,t)|ej. We consider the case where a point mass M≥0 is attached at the central vertex. Thus we consider the system
Let uf solve (9)-(14), and set
For (10), it is standard that the waves have unit speed of propagation on the interval, so g(t)=0 for t<ℓ1. It will be useful first to consider the vibrating string on an interval.
2.2. Representation of solution on an interval and reduced response operator
We will use a representation of uf(x,t) developed in [16]. For the reader's convenience, we recall facts proven in that work. Fix j∈{1,...,N}. We extend qj to (0,∞) as follows: first evenly with respect to x=ℓj, and then periodically. Thus qj(2nℓj±x)=qj(x) for all positive integers n.
Define wj to be the solution to the Goursat problem
A proof of solvability of the Goursat problem can be found in [14].
Consider the IBVP on the interval (0,ℓj):
Then the solution to (16)-(17) on ej can be written as
Setting h(t)=g(t), with g given by (15), we get a representation of the solution uf to (9)-(14) on e2,...,eN.
Define the "reduced response operator" on ej, with j≥2, by
associated to the IBVP (16)-(17). From (18) we immediately obtain:
Lemma 2.1. For j=2,...,N, and any h∈C∞0(R+), we have
with
and ˜r0j=∂wj(0,s)+2∑n≥1H(s−2nℓj)∂wj(2nℓj,s). If T is finite, the sums above are finite.
In what follows we will refer to ˜R0j(s) as the "response function".
It will be useful also to represent the solution of a wave equation on an interval when the control is on the right end. Thus consider the IBVP:
Set ˜q1(x)=q1(ℓ1−x), and extend ˜q1 to [0,∞) by ˜q1(2nℓ1±x)=˜q1(x). Define ωj to be the solution to the Goursat problem
By changing coordinates in (18), we get
2.3. Representation of R01 for M>0 for star graph
We begin section by proving an analog of Lemma 2.1 for R01(t), and also R1j(t) in the case of a positive mass at the central vertex. As a corollary, we recover the data associated to the edge e1. The case of a massless central vertex requires a modified analysis, and will be covered in the next subsection.
Lemma 2.2. The response function for RT01 has the form
Here r01 is a piecewise continuous function, an and bn are real constants,
If T is finite, then the sum is finite.
Proof. We see that on e1, the solution to (9)-(14) is given by
Thus by (18) with h=g and (20),
Next, we study the structure of g. Using the equation uf(0,t)=g(t), along with (12), (18) with h=g, and (20), we have
In what follows, we will assume t<T for some positive T, so the sums above are all finite. Adapting the argument in [11], we let f(t)=δ(t). In what follows, it will be useful to note that by the uniqueness of the solution of the wave equation, we have for p=p(t)
As a consequence, (R01p)(t)=(p∗uδx)(ℓ1,t), so R01(s)=uδx(ℓ1,s).
For g(t)=uδ(0,t), we claim g will have the structure:
Here ˜a∈F2, {βn} is a discrete, increasing set of positive constants with β0=ℓ1, and cn and tn are constants. In what follows, we will solve for these various unknowns, thereby justifying the claim. Assuming the claim for the moment and inserting f(t)=δ(t) and (25) into (23), the lemma follows except (21) which we will prove below.
We will now justify the claim. Substituting (25) into (24), and matching the δ′ terms, we get
We conclude that cm=2/M for all m. This equation together with (25) and (23) imply the equalities in (21). In what follows we denote cm as c. Matching the δ terms in (25) and (24),
We can solve for {βm} by matching β0<β1<β2<... with the set
Next, for any given m, we solve for tm as follows. First, inspection of (27) gives
For larger m, inspection of (27) gives three cases.
Case 1. βm=(2n+1)ℓ1 and βm≠2n0ℓj+(2m0+1)ℓ1 for any m0,n0,j∈N. Then tm=1M(−Nc+2ω1((2n+1)ℓ1,(2n+1)ℓ1)).
Case 2. For some positive integer L and any l=1,...,L, we have βm≠(2n+1)ℓ1 and βm=2nlℓjl+(2ml+1)ℓ1. Then tm=1M(−2Lc).
Case 3. For some positive integer L and any l=1,...,L, we have βm=(2n+1)ℓ1=2nlℓjl+(2ml+1)ℓ1. Then
Accounting for these cases, we thus solve for tm of each m.
Next, we solve for ˜a, which by (24) and (25) satisfies:
where ˜b0∈L2. We will assume ˜a∈F2 (an assumption later justified). Since ˜a′(0)=0, integrating the equation above gives
with ˜b1∈F1. We solve for ˜a by an iterative argument. For simplicity of presentation, assume β1=ℓ1+2ℓ2, β2=ℓ1+2ℓ3, and ℓ3<min(ℓ1,ℓj: j>3); the other cases can be treated similarly. Then for t<β1 we have ˜a(t−2nℓj−ℓ1)=0 for all j, so (29) simplifies to an equation that we can integrate to
with ˜b2∈F2. It is not hard to show that this is a Volterra equation of the second kind, and we can thus uniquely solve for ˜a(t)∈F1 for for t<2ℓ2. Next, we consider the interval t∈[β1,β2]=[ℓ1+2ℓ2,ℓ1+2ℓ3], so ˜a(t−2ℓj−ℓ1)=0 for j≠2. We claim the term ˜a(t−2ℓ2−ℓ1) has already been determined. To see this, note that by the construction of the set {βn} together with our assumption for β2, we have 2ℓ3<4ℓ2. Hence for t<2ℓ3+ℓ1, we have t−2ℓ2−ℓ1<2ℓ2, so ˜a(t−2ℓ2−ℓ1) has been determined as claimed. We can absorb this known term into ˜b2 in the right hand side of (29). We then integrate (29) to get
Again we solve this Volterra equation to determine ˜a(t)∈F1 for t<2ℓ3. Iterating this procedure, we can solve for ˜a(t) for any large t. Since the right hand side of (29) is in F1, it follows that ˜a∈F2. This completes the proof of the lemma.
Lemma 2.3. Let g(t) be given by (24). Then
where
Furthermore, ˜a∈F2, am=2/M for all m, and ν0=ℓ1, and am,tm are constants.
Proof. Since g(t)=uf(0,t)=(f∗uδ)(0,t), we have a(t)=uδ(0,t). The formula (31) follows from (25).
Proposition 1. Let T>2ℓ1 and M>0. From RT01 one can determine M,N,q1, and ℓ1.
Proof. One can determine ℓ1 immediately from Lemma 2.2 because α1≠0. Then a well known argument (see, eg. [11]) shows that one can recover q1 from RT01. Having determined q1 one can solve the Goursat problem to determine ω1, and then one gets M from (21). To find N we observe that near t=2ℓ1, setting f(t)=δ(t), we can extract from (23)
where c1,c2 are constants, F(t) is a function that has been explicitly determined, and G(t) is continuous. Thus we can distinguish the coefficient (t0+w1(ℓ1,ℓ1)ψ). Also, w1 can be determined from q1, and so we solve for t0 hence N (see (28)).
Lemma 2.4. Label the central vertex v1, and let ej be an incident edge other than e1. Assume M1>0. Let T>0, and let RT1j be associated with (9)-(14), defined by (RT1jf)(t)=∂ufj(v1,t). The response function for RT1j has the form
Here r1j∈F1, and the sequence {βn} is positive and strictly increasing, and bn,rn are constants.. If T is finite then the sums are finite.
Proof. the lemma follows immediately from Lemmas 2.2 and 2.3; the details are left to the reader.
2.4. Adaptation when M=0
We can adapt the methods of the previous subsection to the case the internal vertex is massless (also see [11] for a proof of the results below). Here we will only mention the modifications necessary. In Subsection 2.3, the argument carries through word for word until (24), which becomes a first order integral-differential equation, since M=0. As a consequence, the function g(t)=uδ(0,t) will be less regular, because its singularities are not mollified when transmitted across vertices. Instead of(25) and Lemma 2.3 we have:
Lemma 2.5. Let g(t) be given by (24) with M=0. Then
where
Here {ξk} is a increasing positive sequence, and ak,bk are constants. Furthermore, ˜a∈F1, and ξ0=ℓ1.
Inserting f(t)=δ(t) and (32) into (23), we obtain the following analog of Lemma 2.2:
Lemma 2.6. The response function for RT01 has the form
Here {ζn} is a increasing positive sequence with ζ0=0, ζ1=2ℓ1, and zn,yn are constants. Function r01 is piecewise continuous. If T is finite, then the sum is finite.
Proposition 2. Let T>2ℓ1. From RT01 one can determine M=0,N,q1, and ℓ1.
The reader is referred to [11] for a proof of this.
We conclude this section with the following lemma, whose proof is similar to that of Lemma 2.4 and is left to the reader.
Lemma 2.7. Label the central vertex v1, and let ej be an incident edge other than e1. Assume M1=0. Let T>0, and let RT1j be associated with (9)-(14), The response function for RT1j has the form
Here r1j∈L2, and the sequence {βn} is positive and strictly increasing, and an,bn are constants. If T is finite then the sums are finite.
This lemma should be compared with Lemma 2.4. For this lemma, the lead singularity is of the form δ′, compared with δ in the case M1>0; this reflects the mollifying effect of the mass.
2.5. Extension to trees
In this subsection, we extend some of the previous results to trees. The extensions will be used in Section 3 in solving the inverse problem on trees.
We begin by discussing the wellposed of the system (1)-(6). Let dj be the minimum number of nonzero masses on the path from edge ej to the boundary vertex γ0.
Theorem 2.8. If f∈L2(0,T) then uf∈C([0,T];H)∩C1([0,T];H−1). Furthermore, for each ej∈Ω, uf|ej∈C([0,T];Hdj(ej)).
The proof of the theorem is based on the analysis of the waves incoming to, transmitted through and reflected from an interior vertex, and the waves reflected from the boundary vertices. The details are left to the reader; also see [6].
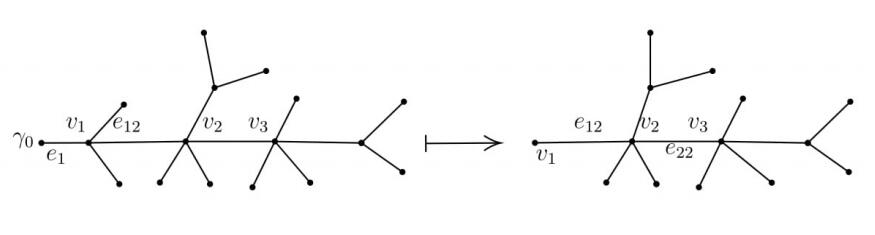
Theorem 2.9. Let u solve the system (1)-(6), and define R01 by (7). Let v1 be the vertex adjacent to γ0, with connecting edge labeled e1, as in Figure 5. Then
a) The response function for RT01 has the form
Here r01∈L2, and the sequence {ζn} is positive and strictly increasing, and an,bn are constants. If T is finite then the sums are finite, and
b) from R01 one can determine M1,Υ1,q1, and ℓ1.
Proof. We sketch this proof, leaving the details to the reader. The key point is the waves propagate at unit speed. Hence for T>2ℓ1+ϵ and ϵ>0 sufficiently small, the response operator R01 will not "feel'' the vertices vm for m>1, regardless of whether they are boundary or interior vertices. Thus by Propositions 1 and 2, l1, Υ1 and M1 can be determined. Having established l1, one determines q1 as in the proof of 1.
For an internal vertex vk, let K=K(k) be the number of positive masses on the path from γ0 to vk, including vk. We have the following generalization to a tree of Lemmas 2.4 and 2.7.
Lemma 2.10. Let T>0, and let RTkj be defined by (3)-(6) and (8). The response function for RTkj has the form
Here rkj∈FK, and the sequence {βn} is positive and strictly increasing, and bn,rn are constants. If T is finite then the sums are finite.
Proof. The proof follows from the proof of Lemma 2.2, together with the transmission and reflection properties of waves at interior vertices, and reflection properties at boundary vertices. The details are left to the reader; see also [11]- where, however, the formula analogous to Lemma 2.2 should have the terms of the form ρnδ(s−βn).
3.
Solving the inverse problem for the tree
In this section we prove Theorem 1.2. In the first subsection, we establish some notation, and give an outline of the solution method, Steps 1-3. Then in Subsection 3.2, we present the technical heart of our argument, using the equation
and the expansions for ˜R12(s), A(s) and R12(s) derived in the previous section to solve for ˜R12(s). Then, in Subsection 3.3, we show how to compute ˜R22(s). From the proof there, it will be evident that we can compute ˜Rkj(s) for general k,j.
3.1. Reduced response operators
We begin by establishing some notation. Let vk be some fixed interior vertex. We list the incident edges by {ekj: j=1,...,Υk}. Denote ℓkj:=|ekj|. Let j satisfy 1<j≤Υk. Denote by Ωkj as in the introduction, see Figure 3, and let the vertices of Ωkj be denoted Vkj.
We will define an associated response operator as follows. Suppose w=wp solves the following IBVP: for t∈[0,T],
and initial conditions
Then we define an associated reduced response operator
with associated response function ˜Rkj(s).
We have the following important result is essentially a restatement of Theorem 2.9.
Theorem 3.1. For vertex vk and incident edge ekj, suppose vk′ is the other vertex on ekj. Then from ˜Rkj one can determine the data: qkj,ℓkj,Mk′, and Υk′.
In this section we will present an iterative method to determine the operator ˜Rkj from the (|Γ|−1)-tuple of operators, RT, for arbitrary k,j. By Theorem 3.1, this allows us to solve the inverse problem. We now sketch our method for solving for ˜Rkj. Fix T>2ℓ. In what follows, we will repeatedly refer to Figure 6.
Step 1. Let v1 be the vertex adjacent to the root γ0, with connecting edge labeled e1. By Theorem 3.1, we can use RT01 to recover Υ1, ℓ1, q1, and M1.
Step 2. Consider e12. In the next subsection, we will show how to solve for ˜R12 given our knowledge of R01 and R12. Thus applying Theorem 3.1, we can solve for the data Υ2, |e12|, q2, and M2. Because R1j for j=2,...,Υ1−1 are known by assumption, the data associated to these edges can be solved for in the same way. We now consider the edge e1,Υ1. In the next subsection, we will also show that ∂uf1(v1,t) is also determined. Furthermore, by assumption we know ∂ufj(v1,t) for j=2,...,Υ1−1. Hence by (4), R1Υ1=∂ufΥ1(v1,t) is also determined, with it the data associated to that edge.
Step 3. In Subsection 3.3, we will solve for determine ˜R2j for all j. It will be clear at that point that the same argument can be used to solve for all ˜Rkj.
3.2. Solving for ˜R12
Proposition 3. The function ˜R12(s) can be determined from R01(s) and R12(s).
The rest of this subsection will be devoted to proving this proposition.
Let f∈L2(0,T), and let uf be the solution of (1)-(6). Since we know ℓ1 and q1, we can solve the wave equation on e1 with known boundary data. We identify e1 as the interval (0,ℓ1) with vk1 corresponding to x=0. Then uf, restricted to e1, solves the following Cauchy problem, where we view x as the "time" variable:
Since the operator R01 is known, we can thus uniquely determine uf(0,t)=uf(v1,t) and ∂uf1(v1,t). Since uf(0,t)=(uδ(0,⋅)∗f)(t), it follows that A(t)=uδ(v1,t) is a known quantity. We now show how A and R12 can be used to determine ˜R12(s). A key ingredient is the following equation, which relates R12(s) with ˜R12(s).
This follows from the definition of the response operators for any f∈L2, in particular (R12∗f)(t)=∂uf2(v1,t). We rewrite this equation:
Below, we will use (40) to determine ˜R12(s). To this end, we now insert representations of ˜R12(s), R12(s), and A that were derived in the previous section.
Since v1 is the root of Ω12, the following equation is essentially an restatement Theorem 3.1.
Here 0=ζ0<ζ1<..., and 0=η0<η1<..., and ˜r12(s) is piecewise continuous and vanishes for s<0. In what follows, we will for readability rewrite ˜r12 as ˜r.
We now must separately consider the cases M1>0 and M1=0.
Case A. M1>0
In what follows, it will be convenient to extend f(t)∈L2(0,T) as zero for t<0. By Lemma 2.10 and by an adaptation of Lemma 2.3 to general trees, we have the following expansions:
Here r12∈F1 and ˜a(s)∈F2, and {αk} and {βn} are positive and increasing. Clearly ˜a(s),r12(s),{ak}, {tk}, {αk}, {νk}, {bn}, {βn},{rn} are known because we assume knowledge of R01 and R12, whereas for now ˜r and the sets {ζp},{zp}, {yj}, {ηj} are unknown. In what follows, we mimick an iterative argument in [20]. Both sides of (40) are a linear combination of δ, Heavyside, and continuous functions. We will split the rather intricate argument solving for the unknowns in (40) into three lemmas. In the first, we match the delta functions on each side of (40).
Lemma 3.2. The sets {ζp},{zp}, can be determined by R01 and R12.
Proof. By (40), (41), (42), and (43), we get by matching delta functions:
Step 1. We solve for z1,ζ1. Since the sequences {βn},{ζp},{αk} are all strictly increasing, clearly we have β1=ζ1+α1, so that b1=z1a1, and so ζ1=β1−α1 and z1=b1/a1. We represent that the set {b1,β1}, {a1,α1} determines the set {z1,ζ1} by
Step 2. We solve for z2,ζ2. We match the term δ(t−β2) with its counterpart on the right hand side of (44). There are three possible cases.
Case 1. β2≠ζ1+α2.
In this case, we must have β2=ζ2+α1, hence
Case 2a. β2=ζ1+α2 and b2≠a2z1. Note that the last inequality can be verified by an observer at this stage, because we have determined b2,a2,z1. We conclude β2=ζ2+α1 and b2=a1z2+a2z1, and hence
Case 2b. β2=ζ1+α2 and b2=a2z1. Then β2<ζ2+α1. Note we have not yet solved for {ζ2,z2}. In this case, we now repeat the matching coefficient argument just used with δ(t−β3).
Again there are three cases:
Case 2bⅰ. β3≠ζ1+α3. Note all of these terms are known, so this inequality can be verified. In this case, β3=ζ2+α1, so ζ2=β3−α1 and z2=b3/a1.
Case 2bⅱ. β3=ζ1+α3 and b3≠z1a3. Then β3=ζ2+α1, and b3=z1a3+z2a1. Thus ζ2=β3−α1 and z2=(b3−z1a3)/a1.
Case 2bⅲ. β3=ζ1+α3 and b3=z1a3. Then β3<ζ2+α1, and we will need to continue our procedure with β4.
Repeating this procedure as necessary, say for a total of N2 times, we solve for {ζ2,z2}. We represent this process as
We must have N2 finite by (44) and the finiteness of the graph.
Step (p+1). we solve for zp+1,ζp+1
Iterating the procedure above, suppose for p∈N we have
Here Np is chosen to be minimal, and so βNp=ζp+α1. We wish to solve for {zp+1,ζp+1}.
We can again distinguish three cases:
Case 1. β(Np+1)≠ζj+αk, ∀j≤p, ∀k. Note that we know {ζj}p1 and {αk}, so these inequalities are verifiable. In this case, we must have β(Np+1)=ζp+1+α1 and a1zp+1=b(Np+1), so we have determined zp+1 and ζp+1 in this case.
Case 2. There exists an integer Q and pairs {ζjn,αjn}Qn=1, with jn≤p, such that
Note that all the numbers {ζjn,αjn} have been determined, so these equations can be all verified. In this case, we have either
Case 2ⅰ. b(Np+1)≠zj1aj1+...+zjQajQ. It follows then that β(Np+1)=ζp+1+α1, and
We thus solve for zp+1,ζp+1.
Case 2ⅱ. b(Np+1)=zj1aj1+...+zjQajQ. It follows then that β(Np+1)≠ζp+1+α1, and we have to repeat this process with β(Np+2).
Repeating the reasoning in Case 2ii as often as necessary, we will eventually solve for {zp+1,ζp+1}. Thus,
Hence we can solve for {ζp:p≤L},{zp:p≤L} for any positive integer L given knowledge of RT01,RT12 for T=T(L) sufficiently large.
Lemma 3.3. The sets {χj}, {yj} can be determined by R01 and R12.
Proof. We identify the Heavyside functions in (40). By (41), (42), and (43), we get
Since the left hand side is known, we can argue as in Lemma 3.2 to solve for {yj, ηj}. The details are left to the reader.
Lemma 3.4. The function ˜r can be determined by R01 and R12.
Proof. We solve for ˜r with an iterative integral equation argument. By (40), we have
Hence by (41), (42), and (43), we calculate
We set z:=t−α1=t−ν1=t−ℓ1 and use that ˜a(s)=0 for s<0 to obtain
Setting α0=ν0=0 for convenience, we introduce the number
Since we will be choosing finite T and t<T, we have α>0. The integral equation for ˜r can be solved by an iterative argument with a finite number of steps.
1) For z<0, we have ˜r(z)=0.
2) Suppose we have solved for ˜r(z) for z<(n−1)α, n≥1. We will now suppose
and identify terms in (45) that we already know. We have for k≥2
For s≥(n−1)α and z<nα we have
so
Similarly, for k≥2 we have z+α1−αk<(n−1)α, so
Combining (46) and (47) with (45), we get
This is a Volterra equation of the second kind, and thus we solve for ˜r(z) for z in
Iterating this argument finitely many times, we will have solved for ˜r=˜r12, and hence ˜RT12, on the interval [0,T] for any T>0.
Case B: M1=0.
In this case, we must replace (42), (43) by
with piecewise continuous r12 and continuous, piecewise C1 function ˜a. The argument is then a straightforward adaptation of Case A; the details are left to the reader.
Careful reading of Steps 2, 3 shows that we can choose any T>2(ℓ1+ℓ1j).
3.3. Solving for ˜R22
The purpose of this subsection is to determine ˜R22. Mimicking the previous subsection, let uδ solve (1)-(6), let B(t)=uδ(v2,t) and let f∈L2(0,T). We have the following formula holding by the definition of response operators:
Of course R22(s) is assumed to be known. We determine B as follows. We have from Step 2 that A(t)=uδ(v1,t) is known. We identify e12 as the interval (0,ℓ2) with v2 corresponding to x=0. Then B(t)=uf(v2,t) arises as a solution to the following Cauchy problem on e2, where we view x as the "time" variable:
Since q2,ℓ2, and R12 are all known, we can thus determine B(t)=y(0,t).
The rest of the argument here is a straightforward adaptation of the previous subsection. The details are left to the reader.
Acknowledgments
We would like to thank the referee for his many suggestions that improved the exposition in this paper.









 DownLoad:
DownLoad: