1. Introduction
Fluid flow through deformable porous media is relevant for many applications in
biology, medicine and bioengineering. Some important examples include blood flow through tissues in the human body [9, 11] and fluid flow inside cartilages, bones and engineered tissue scaffolds [10, 13, 21, 31, 37].
The mechanics of biological tissues typically exhibits both elastic and viscoelastic behaviors resulting from the combined action of various components, including elastin, collagen and extracellular
matrix [22, 23, 26, 30].
Thus, from the mathematical viewpoint, the study of fluid flows through deformable porous biological structures requires the coupling of poro-elasticity with structural viscoelasticity, leading to poro-visco-elastic models.
The theoretical study of fluid flow through deformable porous media has attracted a lot of attention since the beginning of the last century, initially motivated by applications in geophysics and petroleum engineering. The development of the field started with the work of Terzaghi in 1925 [38], which focused on finding an analytic solution for a one-dimensional (1D) model. However, it was Biot's work in 1941 [5] that set up the framework and ignited the mathematical development for fluid flow through poro-elastic media. To date, several books and articles have been devoted to the mathematical analysis and numerical investigation of poro-elastic models, such as [8, 12, 14, 15, 16, 25, 27, 28, 29, 34, 35, 36, 37, 40],
with applications ranging from engineering and geophysics to medicine and biology.
Recently, our team has developed a theoretical and numerical framework to study both poro-elastic and poro-visco-elastic models, as
motivated by biological applications [6]. The study showed that structural viscoelasticity plays a crucial role in determining the regularity requirements for volumetric and boundary forcing terms, as well as for the corresponding solutions. Moreover, in [2] it has been shown that the solution of the fluid-solid mixture (elastic displacement, fluid pressure, and Darcy velocity) is more sensitive to the boundary traction in the elastic case than in the visco-elastic scenario. These theoretical findings are
also supported by experimental and clinical evidences showing that changes in tissue viscoelasticity are associated with various pathological conditions, including atherosclerosis [24], osteoporosis [1], renal disease [20] and glaucoma [17].
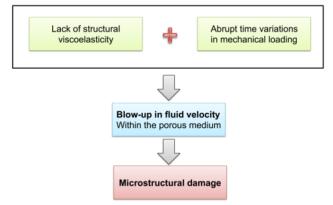
Interestingly, the study in [6] provided numerical clues that sudden changes in body forces and/or stress boundary conditions may lead to uncontrolled fluid-dynamical responses within the medium in the absence of structural viscoelasticity. This finding led us to formulate a novel hypothesis concerning the causes of damage in biological tissues, namely
that abrupt time variations in stress conditions combined with lack of structural viscoelasticity could lead to microstructural damage due to local fluid-dynamical alterations, as illustrated in Fig. 1.
The importance of the coupling between structural mechanics and fluid dynamics in the damage of deformable porous media has been investigated by several authors [39, 23, 33]. In the present study, we focus on a particular aspect of this coupling and we aim at characterizing and quantifying the influence of structural viscoelasticity on the biomechanical and fluid-dynamical responses to sudden changes in stress conditions.
Biomechanical applications are characterized by the fact that tissues
have a mass density that is similar to that of water.
For this reason, we consider in these pages
the case of deformable porous media constituted by incompressible solid and fluid components.
To mathematically define this concept, we introduce the following
relation between fluid pressure p, variation of fluid content ζ and volumetric dilation
∇⋅u, u denoting the solid displacement
where c0 is the storage coefficient and α is the Biot coefficient (see [16]).
In the case of incompressible solid and fluid components, we have c0=0 and α=1
(see [16]) so that (1a) becomes
Notice that unlike in standard elasticity theory, incompressibility of each component of a deformable
porous medium does not mean that both solid displacement and fluid velocity are divergence-free, rather,
that the volumetric deformation of the solid constituent corresponds to the
variation of fluid volume per unit volume of porous material, with the convention that
∇⋅u is positive for extension while ζ is positive for a
"gain" of fluid by the porous solid.
Building upon our theoretical and numerical results presented in [6], we devise a 1D problem for which
we exhibit an explicit solution where the discharge velocity goes to infinity if the stress boundary condition is not sufficiently smooth in time and the solid component is not viscoelastic. Interestingly, this blow-up in the velocity occurs even in the simple case where the permeability of the medium is assumed to be constant, in comparison to the general case of nonlinear permeability depending on dilation [6, 8] or pressure [36]. In addition, we perform a dimensional analysis that allows us to identify the parameters influencing the solution blow-up, thereby opening the path to sensitivity analysis on the system, and providing practical directions on how to control the biomechanical and fluid-dynamical response of the fluid-solid mixture, prevent microstructural damage and, in perspective, aid the experimental design of bioengineered tissues [18].
The article is organized as follows. Poro-visco-elastic models are described in Section 2, along with a summary of the related theoretical results. Section 3
focuses on a special 1D case, for which an explicit solution is derived and its well-posedness is studied in
the presence or absence of viscoelasticity. The dimensional analysis of the 1D problem is carried out in Section 4. Solution properties are explored in detail for the particular case of boundary traction with a discontinuity in time, see Section 5, and with a trapezoidal time profile, see Section 6. The application of this analysis to the case of confined compression of biological tissues is discussed in Section 7. Conclusions and perspectives are summarized in Section 8.
2. Poro-visco-elastic models: Description and theoretical results
Following the same notation as in [6], let Ω⊂Rd, with d=1,2 or 3, be the region of space occupied by a deformable porous medium and let (0,T) be the observational time interval.
In the assumptions of small deformations, full saturation of the mixture, incompressibility of the mixture
constituents and negligible inertia, we can write the balance of linear momentum for the mixture and the balance of mass for the fluid component as
respectively, where σ is the total stress tensor, ζ is the fluid content, v is the discharge velocity and F and S are volumetric sources of linear momentum and fluid mass, respectively.
The system must be completed by constitutive equations for σ, ζ and v. In line with the literature for poro-visco-elastic models in biological applications, we will adopt the following constitutive equations:
|
σe=λe(∇⋅u) I+2μeϵ(u)
|
(2d)
|
|
σv=λv(∇⋅∂u∂t) I+2μvϵ(∂u∂t)
|
(2e)
|
where
u is the displacement of the solid component, p is the Darcy pressure,
I is the identity tensor and ϵ(w)=(∇w+(∇w)T)/2 is the symmetric part of the gradient of the vector field w. The elastic parameters λe and μe and the viscoelastic parameters λv and μv are assumed to be given positive constants.
We remark that structural viscoelasticity is embodied in the term σv defined in (2e). If structural viscoelasticity is not present, then σv=0 and the set of equations (2a)-(2g) defines a poro-elastic medium.
In addition, the permeability K may be a positive constant, as in [5], or may depend nonlinearly on the solution, for example on the structural dilation, namely K=K(∇⋅u), as in [6, 8].
Finally, notice that (2f) corresponds to (1b)
consistently with the assumption of incompressibility of mixture constituents.
Most of the theoretical studies focused on the poro-elastic case without accounting for structural viscoelasticity. In the case of constant permeability, the coupling between the elastic and fluid subproblems is linear and the well-posedness and regularity of solutions have been studied by several authors [25, 35, 40].
In the case of non-constant permeability, the coupling between the two subproblems becomes nonlinear and only few theoretical results have been obtained. In [36], Showalter utilized monotone operator theory techniques in order to provide well-posedness of solutions in the case where the permeability is a nonlinear function of pressure.
To the best of our knowledge, Cao et al in [8] were the first to consider the permeability as a nonlinear function of dilation and provide existence of weak solutions for this nonlinear poro-elastic case. However, the analysis in [8] is performed upon assuming
homogeneous boundary conditions for both pressure and elastic displacement, which is often not the case from the viewpoint of applications.
Our recent paper in [6] extends the works mentioned above by considering
poro-elastic and poro-visco-elastic models with dilation-dependent permeability, non-zero volumetric sources of mass and momentum and non-homogeneous, mixed Dirichlet-Neumann boundary conditions. More precisely, in [6] we assumed that the boundary of Ω can be decomposed as ∂Ω=ΓN∪ΓD, with ΓD=ΓD,p∪ΓD,v, where the following boundary conditions are imposed:
|
σ⋅n=g,v⋅n=0onΓN×(0,T)
|
(3)
|
|
u=0,v⋅n=ψonΓDv×(0,T).
|
(5)
|
Our analysis showed that the data time regularity requirements and the smoothness of solutions significantly differ depending on whether the model is poro-elastic or poro-visco-elastic. In particular, in the visco-elastic case, if the source of linear momentum F is L2 in time and space, namely F∈L2(0,T;(L2(Ω))d), and the source of boundary traction g is L2 in time and H1/2 on the boundary, namely g∈L2(0,T;(H1/2(ΓN))d),
then there exists a weak solution to the system, with elastic displacement u∈H1 in time and space, namely u∈H1(0,T;(H1(Ω))d), and pressure p∈L2(0,T;H1(Ω)).
In comparison, in the poro-elastic case, one needs both F and g to be H1 in time in order to obtain a solution where both u and p are L2 in time and H1 in space. This proves that the system dynamics fundamentally changes as visco-elastic effects fade away. Moreover, the numerical simulations performed in [6] hinted at blow-up of fluid energy functional in the poro-elastic case with non-smooth sources F and g. In the following sections, we are going to further elaborate these concepts by means of a 1D poro-visco-elastic model for which we can obtain an explicit solution and assess the effect of structural viscoelasticity on the response of the deformable porous medium to sudden changes in mechanical load. The 1D model is described next.
3. 1D poro-visco-elastic model: Description and formulation
Let the space domain Ω be given by the
interval (0,L) and the volumetric sources of linear momentum and fluid
mass be zero. In this case, the balance of linear momentum for the mixture
and the balance of mass for the fluid component simplify to
|
∂2u∂t∂x+∂v∂x=0in(0,L)×(0,T).
|
(6b)
|
The associated constitutive equations are given by
|
σ0=μ∂u∂x+η∂2u∂t∂xin(0,L)×(0,T)
|
(7a)
|
|
v=−K∂p∂xin(0,L)×(0,T)
|
(7c)
|
where we have set μ=λe+2μe, η=λv+2μv and we have introduced the symbol σ0 to denote the contribution of the solid component to the total stress tensor σ. We emphasize that the permeability may be a function of space and dilation, namely
We complete the system with the
following boundary and initial conditions:
|
u(0,t)=v(0,t)=0for0<t<T
|
(8a)
|
|
p(L,t)=0 ; σ(L,t)=−P(t)for0<t<T
|
(8b)
|
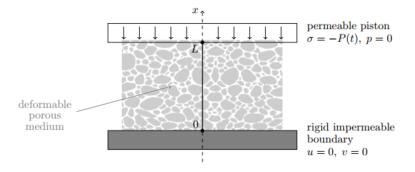
where g(t)=−P(t) is the boundary traction. For the ease of reference, the boundary conditions are schematized in Fig. 2.
If η=0 (i.e., no viscoelasticity is present) and under the assumption
that the permeability K and the boundary forcing term P are given positive constants, system (6)
degenerates into the poro-elastic model studied experimentally and
analytically in [37]. Specifically, the boundary and initial
conditions (8a)-(8c) correspond to the
creep experimental test performed in confined compression, where the boundary condition (8a)
represents an impermeable interface at the bottom of the specimen whereas
the boundary condition (8b) represents a free-draining permeable piston
at the top of the specimen.
System (6a)-(8c) can be rewritten solely in
terms of the displacement. Indeed, integration of (6b
) with respect to x yields
where A(t) is arbitrary. Thus, taking (8a) into
account, we obtain that A(t)=0. From (7c), we then have that
|
∂u∂t−K∂p∂x=0 in (0,L)×(0,T) .
|
On the other hand, using (7b) and (6a),
we derive that
Therefore the system (6a)-(8c) reduces to the following
initial boundary value problem in terms of the sole elastic displacement u:
|
∂u∂t−Kμ∂2u∂x2−Kη∂3u∂t∂x2=0in (0,L)×(0,T)
|
(9a)
|
|
μ∂u∂x(L,t)+η∂2u∂t∂x(L,t)=−P(t)for0<t<T
|
(9b)
|
Subsequently, we can recover the solid part of the stress tensor, discharge velocity,
pressure and total stress tensor on (0,L)×(0,T), respectively, as
Remark 1. For later reference, we write below the explicit form of the purely elastic problem which corresponds to setting η=0 in (9):
|
∂u∂t−Kμ∂2u∂x2=0in (0,L)×(0,T)
|
(11a)
|
|
μ∂u∂x(L,t)=−P(t)for0<t<T
|
(11b)
|
Remark 2. An important quantity associated with the fluid-solid mixture is the fluid
power density P(t), defined as
|
P(t)=∫L01K|v(x,t)|2dx.
|
(12)
|
From its definition, it follows that P(t) depends on both discharge velocity and permeability.
3.1. Formal derivation of the solution
Let us further assume that the permeability is constant, i.e.
|
K=K(x,∂u∂x)≡K0=constant>0.
|
In this case, system (9) is a linear
initial boundary value problem,
whose solution can be obtained by Fourier series expansion as described below.
Case 1. (η>0). First of all, we homogenize the boundary condition by
setting
having introduced the auxiliary function
|
U(t)=μη∫t0exp(−μη(t−s))P(s)ds=μηexp(−μηt)∗P(t)
|
where the star symbol denotes convolution. Thus, w(x,t) satisfies the problem
|
∂w∂t−K0μ∂2w∂x2−K0η∂3w∂t∂x2=xμU′(t)in (0,L)×(0,T)μ∂w∂x(L,t)+η∂2w∂t∂x(L,t)=0for0<t<Tw(0,t)=0for0<t<Tw(x,0)=0for0<x<L
|
(13)
|
where the prime symbol denotes differentiation for functions of a single variable.
The associated eigenvalue
problem is
|
Find y=y(x), 0<x< L, such that
|
The eigenvalues and the corresponding eigenfunctions are given by
|
λn=(2n+1)2π24L2andyn(x)=sin(2n+1)πx2Lforn=0,1,…
|
(14)
|
We seek a
solution of the form
where the coefficients cn(t) of the above series are determined
by the differential equation and the initial condition in (13
). Using the Fourier Sine series expansion
|
x=2L∞∑n=0(−1)nλnyn(x),0≤x≤L
|
the uniqueness of the Fourier expansion leads to the family of ordinary differential equations
|
(1+K0ηλn)c′n(t)+K0μλncn(t)=2(−1)nμLλnU′(t),cn(0)=0
|
whose solution is given by
|
cn(t)=2(−1)nμLλn(1+K0ηλn)exp(−K0μλn1+K0ηλnt)∗U′(t) .
|
Therefore, we get
|
u(x,t)=−U(t)μx+2μL∞∑n=0(−1)nyn(x)λn(1+K0ηλn)exp(−K0μλn1+K0ηλnt)∗U′(t).
|
In conclusion, after performing integration by parts in the convolution term and using the
identity ηU′(t)+μU(t)=μP(t), the formal solution to problem (9) is given by
|
u(x,t)=−2K0L∞∑n=0(−1)nyn(x)1+K0ηλnexp(−K0μλn1+K0ηλnt)∗P(t) .
|
(15)
|
Case 2. (η=0).
A direct substitution of expression (15) (with η=0)
into problem (11) shows that
|
u(x,t)=−2K0L∞∑n=0(−1)nyn(x)exp(−K0μλnt)∗P(t)
|
(16)
|
is the formal solution of the purely elastic problem.
In particular, in the case P(t)=constant,
expression (16) coincides with Eq. (8) of [37].
3.2. Weak solutions and well-posedness
In this section we prove that the
formal solutions (15) and (16) indeed solve the visco-elastic problem (9) and the purely elastic problem (11), respectively, in well-defined functional spaces. Let us begin by introducing the
functional framework. We consider the real Hilbert
space H=L2(0,L) equipped with the scalar product
|
(f,g)H=∫L0f(x)g(x) dx∀f,g∈H,
|
and endowed with the induced norm
The orthonormal sequence of eigenfunctions {√2Lyn(x)} forms a Hilbert space basis for H. A
distribution v in (0,L) belongs to H if and only if it
has a series expansion (converging in D′(0,L))
with coefficients cn satisfying
If this is the case, the series expansion of v converges in the mean.
Next, let
be the real Hilbert space equipped with the scalar product
and endowed with the induced norm (due to Poincaré's inequality)
Sobolev's Embedding Theorem ensures that V⊂C0([0,L]), so that the boundary value v(0)=0 for v∈V is assumed in a strong sense. The sequence of functions {√2Lλnyn(x)} forms a
Hilbert space basis for V. A function v∈H belongs to V if and only
if the Fourier coefficients of the series expansion (17) satisfy
More generally, the eigenfunction expansion (17) enables us to define a
one-parameter family Vs (s∈R) of spaces: the
distribution (17) belongs to Vs if and only if its coefficients cn
satisfy
In particular, we have that V−1≡V′ (the dual of V).
Case 1. (η>0).
Now we introduce the definition of weak solution for the poro-visco-elastic case.
Definition 3.1. A function u:[0,T]→V is a weak
solution to problem (9) if:
(ⅰ) u∈H1(0,T;V), implying that u,u′∈L2(0,T;V);
(ⅱ) for every v∈V and for t pointwise a.e. in [0,T],
|
(u′(t),v)H+K0(μu(t)+ηu′(t),v)V=−K0P(t)v(L);
|
(18)
|
(ⅲ) u(0)=0,
where we used the notation u(t)=u(⋅,t) and u′(t)=∂u∂t(⋅,t).
Remark 3. The initial condition (9d) is satisfied by u(t)∈V in the pointwise sense of condition (ⅲ), since it is well known that
condition (ⅰ) implies that u∈C0([0,T];V).
The Dirichlet boundary condition (9c) at x=0 is included in the requirement
that u(t)∈V, whereas the boundary condition (9b) at x=L is
taken into account in the linear form on the right hand side of (18), where v(L) is the pointwise value of the (continuous)
test function v∈V.
Theorem 3.2. Suppose P(t)∈L2(0,T). Then there is a unique weak solution u to problem (9), in the sense of Definition 3.1. Moreover, u is represented by the series expansion (15).
Proof. For sake of exposition, we rewrite u(x,t), given by (15), as
|
u(x,t)=∞∑n=0un(t)yn(x)
|
(19)
|
where
|
un(t)=−2K0L(−1)n1+K0ηλnexp(−K0μλn1+K0ηλnt)∗P(t)
|
(20)
|
so that
|
∂u∂t(x,t)=∞∑n=0u′n(t)yn(x)
|
(21)
|
where
|
u′n(t)=−2K0L(−1)n1+K0ηλnP(t)−K0μλn1+K0ηλnun(t).
|
(22)
|
[Regularity]. Firstly, we show that u(x,t) has the desired
regularity, namely u∈H1(0,T;V) and u(0)=0
. With this goal in mind, we study the convergence of the series expansions
in (19) and (21). For any a>0 Schwarz inequality implies that
|
|e−at∗P(t)|≤1√2a‖P‖L2(0,T).
|
Upon applying this estimate to (20) and (22) we see that there are
positive constants, generically denoted by C,
that are independent on n and t and for which it holds that
|
|un(t)|≤Cλn‖P‖L2(0,T)
|
(23)
|
and
|
|u′n(t)|≤Cλn(|P(t)|+‖P‖L2(0,T)).
|
(24)
|
Thus, u,u′∈L2(0,T;Vs) for every s<3/2,
thereby implying that conditions (ⅰ) and (ⅲ) of Def. 3.1 are satisfied.
[Existence]. In order to show that u satisfies condition (ⅱ), it
suffices to consider v=yn as test function, since {√2Lλnyn(x)} are a basis of V. Each
term on the left hand side of (18) can be computed as
|
(u(t),yn)V=(∂u∂x(⋅,t),dyndx(⋅))H=L2λnun(t)
|
|
(u′(t),yn)V=(∂2u∂t∂x(⋅,t),dyndx(⋅))H=L2λnu′n(t) .
|
Adding the above three terms, we obtain that
|
(u′(t),yn)H+K0(μu(t)+ηu′(t),yn)V=L2[(1+K0ηλn)u′n(t)+K0μλnun(t)] .
|
Thus, from (22) and the fact that
yn(L)=(−1)n, it follows that
the right hand side is equal to −K0P(t)yn(L), and this completes the proof of existence.
[Uniqueness] From the linearity of the equation, it suffices to
show that P=0 implies u=0. Let P=0 and let u∈H1(0,T;V) be a solution of
|
(u′(t),v)H+K0(μu(t)+ηu′(t),v)V=0,v∈V .
|
If we choose v=u(t) as a test function, then we obtain that
|
(u′(t),u(t))H+K0μ‖u(t)‖2V+K0η(u′(t),u(t))V=0
|
implying that
|
12ddt(‖u(t)‖2H+K0η‖u(t)‖2V)=−K0μ‖u(t)‖2V≤0 .
|
Integrating with respect to time and using the initial condition u(0)=0, we get
Hence u(t)=0 for every t in [0,T].
Remark 4. From (23), the fact that |yn(x)|≤1, and the
standard Weierstrass Test, it follows that the series (19) converges absolutely
and uniformly in the space-time rectangle Q=[0,L]×[0,T]
and its sum is continuous, i.e. u(x,t)∈C0(Q). In a similar way, under the stronger assumption P(t)∈L∞(0,T), estimate (24) implies |u′n(t)|≤Cλ−1n‖P‖L∞(0,T) so that ∂u∂t(x,t)∈C0(Q) also holds. Thus,
in the physically realistic case of bounded boundary traction P(t), discharge velocity and fluid power density are continuous and
bounded both in space and time, and this is true even though the
traction has jump discontinuities (e.g., it is a step pulse).
Case 2. (η=0). In the purely elastic problem, the formal solution (16) is again
written as given in (19) where now
|
un(t)=−2K0L(−1)nexp(−K0μλnt)∗P(t).
|
Then, estimates (23) and (24) become, respectively,
and
|
|u′n(t)|≤C√λn(|P(t)|+‖P‖L2(0,T)).
|
As a consequence, it can only be asserted that u∈L2(0,T;Vs)
for every s<1/2 and u′∈L2(0,T;Vs) for
every s<−3/2. On the other hand, if one assumes P(t)∈L∞(0,T), we find that
and
Hence, in this case, u∈L2(0,T;Vs) for every s<3/2
and u′∈L2(0,T;Vs) for every s<−1/2. In
particular, when the boundary traction is bounded, we have u(x,t)∈C0(Q) whereas the discharge velocity is a
distribution. In conclusion, we state the following definition and theorem (without proof):
Definition 3.3. A function u:[0,T]→V is a weak
solution to problem (11) if:
(ⅰ) u∈L2(0,T;V), u′∈L2(0,T;V′);
(ⅱ) for every v∈V and for t pointwise a.e. in [0,T],
|
⟨u′(t),v⟩+K0μ(u(t),v)V=−K0P(t)v(L)
|
(25)
|
where the brackets ⟨⋅,⋅⟩ denote pairing between V′ and V;
(ⅲ) u(0)=0.
Theorem 3.4. Suppose P(t)∈L∞(0,T). Then there exists a unique weak solution u
to problem (11), in the sense of Definition 3.3. Moreover, u
is represented by the series expansion (16).
4. Dimensionless problem
The goal of this section is to rewrite problem (9) in dimensionless form so that we can identify combinations of geometrical and physical parameters that most influence the solution properties. Dimensional analysis relies on the choice of a set of characteristic values that can be used to scale all the problem variables. Let us use the hat symbol to indicate dimensionless (or scaled) variables and the square brackets to indicate the characteristic value of that quantity. Then, for the problem at hand we would write:
|
ˆx=x[x],ˆt=t[t],ˆη=η[η],ˆλn=λn[λn],ˆP=P[P],ˆu=u[u],ˆv=v[v],ˆP=P[P] .
|
(26)
|
It is important to emphasize that there is no trivial choice for the characteristic values and, in general, this choice is not unique. In this particular case, though, we will leverage our knowledge of the forcing terms and the explicit formulas we obtained for the solution to guide us in the choice of some of these values. Since the problem is driven by the boundary condition on the traction with the given function P(t), we set
where Pref is a reference value, for example the mean value, of the given function P(t).
The expression for λn in (14) suggests to choose
and, consequently, the expression for u(x,t) in (15) suggests
to choose
|
[η]=1K0[λn]=L2K0,[t]=1K0μ[λn]=L2K0μ,[u]=K0L[P][t]=PrefLμ ,
|
(29)
|
whereas the expressions for v(x,t) in (10b) and P(t) in (12) suggest to choose
and
|
[P]=LK0[v]2=K0LP2ref
|
(31)
|
respectively. Using the above scalings, we obtain the following dimensionless problem:
|
∂ˆu∂ˆt−∂2ˆu∂ˆx2−ˆη∂3ˆu∂ˆt∂ˆx2=0in (0,1)×(0,ˆT)
|
(32a)
|
|
∂ˆu∂ˆx(1,ˆt)+ˆη∂2ˆu∂ˆt∂ˆx(1,ˆt)=−ˆP(ˆt)for0<ˆt<ˆT
|
(32b)
|
|
ˆu(0,ˆt)=0for0<ˆt<ˆT
|
(32c)
|
|
ˆu(ˆx,0)=0for0<ˆx<1
|
(32d)
|
where ˆT=T/[t] and ˆη≥0. Recalling again the expressions (15), (10b) and (12), we can now write solid displacement, discharge velocity and power density in dimensionless form as
|
ˆu(ˆx,ˆt)=−2∞∑n=0(−1)nyn(ˆx)1+ˆηˆλnexp(−ˆλn1+ˆηˆλnˆt)∗ˆP(ˆt)
|
(33)
|
|
ˆv(ˆx,ˆt )=2∞∑n=0(−1)nyn(ˆx)1+ˆηˆλn{ˆP(ˆt )−ˆλn1+ˆηˆλnexp(−ˆλn1+ˆηˆλnˆt)∗ˆP(ˆt)}
|
(34)
|
|
ˆP(ˆt)=2∞∑n=01(1+ˆηˆλn)2{ˆP(ˆt )−ˆλn1+ˆηˆλnexp(−ˆλn1+ˆηˆλnˆt)∗ˆP(ˆt)}2 .
|
(35)
|
Remark 5. As already mentioned above, the choice for the characteristic values is not unique. In this regard, it is worth noticing that our choice for [v], namely K0Pref/L, differs from that utilized in [37], which was K0μ/L instead. This difference actually follows from a different choice for the pressure scaling, namely Pref in our case, as opposed to μ in [37]. Indeed, the two scalings are equivalent if Pref and μ are of the same order of magnitude. In general, though, the scaling K0μ/L represents the characteristic velocity of wave propagation within the medium, whereas the scaling K0Pref/L represents the characteristic velocity induced by an external load of magnitude Pref. Since our analysis aims at assessing the influence of the external load on the biomechanical response of the medium, we chose [P]=Pref. However, the analysis could be easily adapted to other choices, should the scope of the investigation differ from that of this paper.
5. The case ˆP(ˆt )=step pulse
Let the boundary traction ˆP(ˆt ) be the dimensionless unit step starting at
ˆt=0 defined as
|
ˆP(ˆt )=H(ˆt )={0ifˆt<01ifˆt≥0 .
|
(36)
|
In this case, the dimensionless solid displacement (33), discharge velocity (34) and
power density (35) (hereon denoted with the subscript ˆη for later reference) become,
respectively,
|
ˆuˆη(ˆx,ˆt )=−2∞∑n=0(−1)nˆλn{1−exp(−ˆλnˆt1+ˆηˆλn)}yn(ˆx)=−ˆx+2∞∑n=0(−1)nˆλnexp(−ˆλnˆt1+ˆηˆλn)yn(ˆx)
|
(37a)
|
|
ˆvˆη(ˆx,ˆt)=2∞∑n=0(−1)n1+ˆηˆλnexp(−ˆλnˆt1+ˆηˆλn)yn(ˆx)
|
(37b)
|
|
ˆPˆη(ˆt)=2∞∑n=01(1+ˆηˆλn)2exp(−2ˆλnˆt1+ˆηˆλn) .
|
(37c)
|
The solution in the purely elastic case can be obtained by setting
ˆη=0 in (37).
Remark 6. If the unit step is shifted at ˆt=α>0, i.e. ˆP(ˆt)=H(ˆt−α), then the solution (33) is
|
ˆu(ˆx,ˆt)=ˆuˆη(ˆx,ˆt−α)H(ˆt−α)={0if0≤ˆt<αˆuˆη(ˆx,ˆt−α)ifˆt≥α.
|
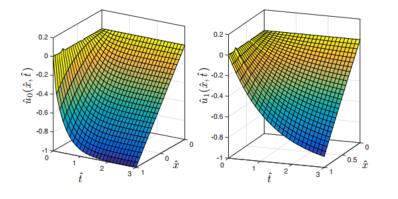
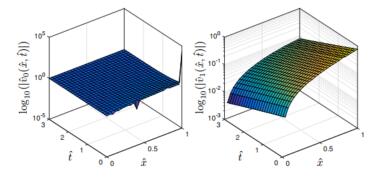
The space-time behavior of ˆuˆη, ˆvˆη and ˆPˆη is reported in Figures 4, 5
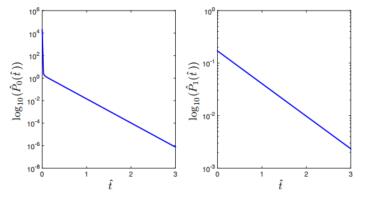
and 6, respectively, in the case of ˆη=0 and ˆη=1.
We remark that ˆvˆη and
ˆPˆη are reported in logarithmic scale to highlight
the presence of a blow-up at ˆx=1 and ˆt=0 in the purely elastic case ˆη=0.
Indeed, by setting
ˆη=ˆt=0 in (37c), we can verify that the power density satisfies
Proceeding analogously in the case of the discharge velocity, the Fourier expansion
in the purely elastic case is given by
|
ˆv0(ˆx,0)=2∞∑n=0(−1)nyn(ˆx)
|
which clearly lacks pointwise convergence for any ˆx≠0.
From the physical viewpoint, this means that,
at the switch on time of the driving term, here set at ˆt=0, the discharge velocity contains high-frequency
components whose superposition exhibits the following behaviors depending on ˆx:
(ⅰ) it relaxes
towards zero as ˆx→0; (ⅱ) it tends to infinity as ˆx→1, thereby exhibiting a blow-up; (ⅲ) it looks like an
amorphous blob for 0<ˆx<1.
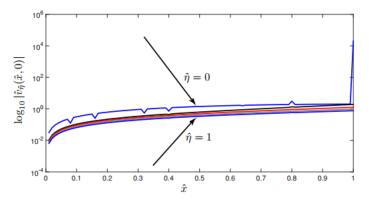
On the other hand, if viscoelastic effects are present, then the dimensionless discharge velocity at ˆt=0 is given by
|
ˆvˆη(ˆx,0)=2∞∑n=0(−1)n1+ˆηˆλnyn(ˆx) .
|
Here, the n−th coefficient is decreasing as 1/n2 and the discharge
velocity is continuous at ˆt=0. These concepts are illustrated in Fig. 7, which shows the spatial distribution of ˆvˆη at ˆt=0 for several values of ˆη
in the interval [0,1]. The log10 plot of ˆvˆη is reported in the figure to highlight
the blow-up of the discharge velocity in the purely elastic case at ˆx=1.
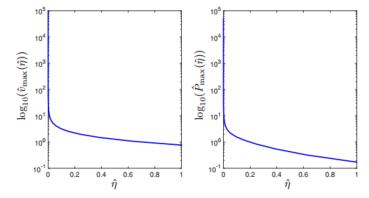
In order to further investigate this blow-up and its dependence on the structural viscoelasticity, we observe that the maximum value of ˆvˆη is attained at ˆx=1 and ˆt=0 and can be written as a function of ˆη as follows:
|
ˆvmax(ˆη)=max0≤ˆx≤1ˆt≥0|ˆvˆη(ˆx,ˆt)|=ˆvˆη(1,0)=2∞∑n=011+ˆηˆλn .
|
The above series may be summed ([19], formula no. 1.4212) and the final result is
|
ˆvmax(ˆη)=1√ˆηtanh(1√ˆη) .
|
(38)
|
Similarly, the dimensionless power density (37c) is decreasing in time and its
maximum is attained at ˆt=0:
|
ˆPmax(ˆη)=maxˆt≥0ˆPˆη(ˆt)=ˆPˆη(0)=2∞∑n=01(1+ˆηˆλn)2=12ˆη(tanh21√ˆη+√ˆηtanh1√ˆη−1) .
|
The behaviors of ˆvmax(ˆη) and ˆPmax(ˆη) with respect to ˆη are visualized in Fig. 8.
Clearly, the dimensionless parameter ˆη is the sole determinant of the blow-up in ˆvmax(ˆη) and ˆPmax(ˆη), with smaller values of ˆη leading to higher values of ˆvmax(ˆη) and ˆPmax(ˆη).
However, it is important to recall that ˆη does not depend solely on the viscoelasticity coefficient. The definition ˆη=ηK0/L2 implies that also small values of the permeability K0 and/or large values of the domain dimension L would reduce the value of ˆη. Precisely,
going back to dimensional units, we can use (30) and (31)
to obtain the following expressions:
|
vmax(ˆη)=PrefK0Lˆvmax(ˆη)
|
(39)
|
|
Pmax(ˆη)=P2refK0LˆPmax(ˆη).
|
(40)
|
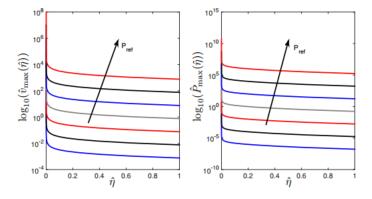
We can see that the magnitude Pref of the driving term appears as a multiplying constant in the expressions above, meaning that larger values of Pref will lead to larger values of vmax and Pmax. However, the factor that controls the blow-up still remains the dimensionless parameter
ˆη=ηK0/L2.
These concepts are illustrated in Fig. 9,
where we set K0/L=1 m2s Kg−1 and we consider increasing values of Pref
in the range [10−3,103] Nm−2.
6. The case ˆP(ˆt) = trapezoidal pulse
Let us now consider the case of a driving term given by a trapezoidal pulse, where the signal switch on and switch off are characterized by linear ramps. Thus,
let ˆP(ˆt)
be the dimensionless trapezoidal pulse of unit amplitude and let
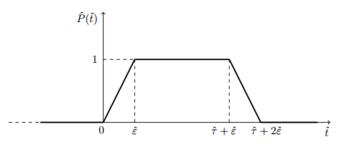
ˆε, ˆτ>0. Here we consider the following expression for ˆP(ˆt):
|
ˆP(ˆt)={0ifˆt<0ˆtˆεif0≤ˆt<ˆε1ifˆε≤ˆt<ˆε+ˆτˆτ−ˆtˆε+2ifˆε+ˆτ≤ˆt<2ˆε+ˆτ0ifˆt≥2ˆε+ˆτ
|
(41)
|
where ˆε is the pulse rise/fall time and ˆτ is
the pulse duration, as depicted in Fig. 10. Thus, the trapezoidal pulse defined in (41) reduces to a rectangular step pulse
as ˆε→0.
Let us now compute the dimensionless
discharge velocity resulting from the application of the trapezoidal pulse at the boundary, henceforth denoted by ˆVˆη(ˆx,ˆt) to distinguish it from the discharge velocity ˆvˆη(ˆx,ˆt) obtained for the step pulse. To this end, we observe that the trapezoidal pulse is actually the linear combination of four
ramp pulses of unit slope starting at times ˆt=0, ˆε
, ˆε+ˆτ, 2ˆε+ˆτ:
|
ˆP(ˆt)=1ˆε{ˆtH(ˆt)−(ˆt−ˆε)H(ˆt−ˆε)
|
(42)
|
|
−(ˆt−ˆτ−ˆε)H(ˆt−ˆτ−ˆε)+(ˆt−ˆτ−2ˆε)H(ˆt−ˆτ−2ˆε)}
|
where the function H(ˆt) was defined in (36).
In addition, we can see that
|
ˆu(ˆx,ˆt)=∫ˆt0ˆuˆη(ˆx,s)ds
|
solves problem (32) with ˆP(ˆt)=ˆtH(ˆt)
(the ramp pulse of unit slope starting at time ˆt=0), where ˆuˆη(ˆx,ˆt) is given by (37a).
Thus, using (10b), we have that the discharge velocity is given by
−ˆuˆη(ˆx,ˆt), so that, applying the linear superposition principle, ˆVˆη(ˆx,ˆt) is the linear combination of the
velocities corresponding to the various components of the pulse, namely:
|
ˆVˆη(ˆx,ˆt)=1ˆε{−ˆuˆη(ˆx,ˆt)H(ˆt)+ˆuˆη(ˆx,ˆt−ˆε)H(ˆt−ˆε)+ˆuˆη(ˆx,ˆt−ˆτ−ˆε)H(ˆt−ˆτ−ˆε)−ˆuˆη(ˆx,ˆt−ˆτ−2ˆε)H(ˆt−ˆτ−2ˆε)} .
|
(43)
|
An illustration of the typical form of
ˆVˆη(ˆx,ˆt) for ˆη≥0 and ˆε>0 is reported
in Fig. 11.
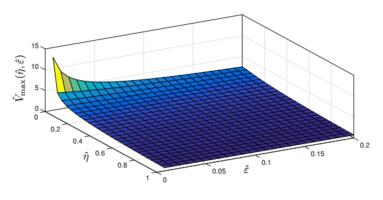
The maximum possible discharge velocity occurs at ˆx=1, ˆt=ˆε and can be written as
|
ˆVmax(ˆη,ˆε)=max0≤ˆx≤1ˆt≥0|ˆVˆη(ˆx,ˆt)|=ˆVˆη(1,ˆε)=2ˆε∞∑n=01ˆλn{1−exp(−ˆλnˆε1+ˆηˆλn)}.
|
(44)
|
The behavior of ˆVmax with respect to ˆη and ˆε is reported in Fig. 12. Interestingly, for all ˆη>0 and ˆε≥0 we have
and
since the trapezoidal pulse reduces to a rectangular pulse as ˆε→0. Thus, no blow-up takes place in the
viscoelastic case when the pulse is rectangular. Similarly, for all ˆη≥0 and ˆε>0 we have
|
ˆVmax(ˆη,ˆε)≤ˆVmax(0,ˆε)=2ˆε∞∑n=01−exp(−ˆλnˆε)ˆλn,
|
hence no blow-up takes place even in the purely elastic case when the pulse
is trapezoidal.
7. Application in biomechanics: Role of structural viscoelasticity in confined compression tests for biological tissues
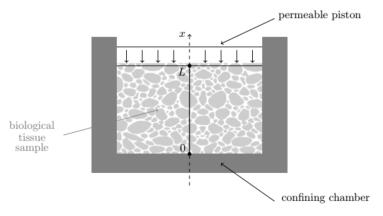
In this section, we utilize the mathematical analysis developed above to study some interesting features of confined compression tests, which are often utilized in biomechanics to characterize the properties of biological tissues.
A schematic of the confined compression experimental setting is depicted in Fig. 13, where a compressive load
is applied at the chamber top surface while
the bottom surface is maintained fixed.
Due to confinement,
deformation occurs only in the x direction. The analogy with the 1D setting depicted in Fig. 2 is straightforward, with a note of caution that 1D solutions are most representative of the biomechanical status of the material along vertical lines towards the center of the chamber.
The 1D model described in Section 3 allows us to generalize the mathematical analysis carried out in [37] by quantifying the effect of structural viscoelasticity on the tissue response to sudden changes in external pressure during confined compression experiments.
In this perspective, L represents the thickness of the undeformed tissue
sample and Pref represents the magnitude of the total compressive stress
applied at x=L. It is important to notice that the
confined compression creep experiment described in [37] is characterized by the same initial and boundary conditions as those given in (8).
However, the mathematical description adopted in [37] (based on the theory developed
in [22]), does not account for structural viscoelasticity, which amounts to setting
η=0 in (7a).
Table 1 summarizes the parameter values corresponding to the experiments on articular cartilage reported in [37].
Table 1. Numerical values of model parameters in the confined compression experiment for articular cartilage
reported in [37].
| symbol |
value |
units |
|
L |
0.81⋅10−3 |
m |
|
μ |
0.97⋅106 |
Nm−2 |
|
η |
0 |
N s m−2 |
|
K0 |
2.9⋅10−16 |
m4N−1s−1 |
|
Pref |
6⋅104 |
Nm−2 |
Characteristic velocities for the confined compression experiments reported in [37] are of the order of 0.35 μm/s.
However, our analysis showed that velocities in the sample may attain much higher values, particularly near the permeable piston, should viscoelasticity be too low and/or the time profile of the load protocol be too sharp. In order to make these concepts more specific, let us assume that: (ⅰ) the load protocol for the confined compression experiment corresponds to the trapezoidal pulse described in Section 6; and that (ⅱ) we should ensure that discharge velocities always remain below the threshold value Vth=0.35 μm/s in order to preserve the sample from microstructural damage. This means that ˆη and ˆε should be chosen as to guarantee that
|
ˆVmax(ˆη,ˆε)<ˆVth=LPrefK0 Vth=16.3 ,
|
(45)
|
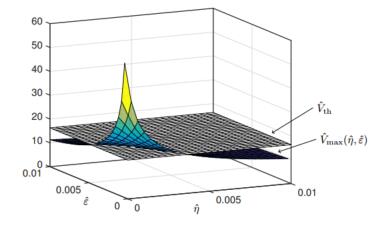
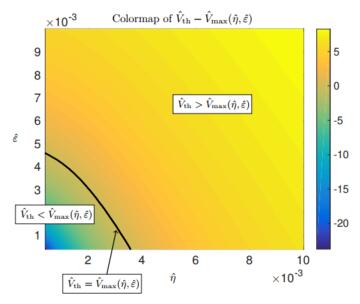
where ˆVmax(ˆη,ˆε) can be computed using the expression (44). Fig. 14 compares ˆVth with the values of ˆVmax obtained for different values of ˆη and ˆε. Indeed, we can identify a whole region in the (ˆη,ˆε)−plane for which ˆVmax(ˆη,ˆε)<ˆVth.
To better visualize the various regions of interest in the (ˆη,ˆϵ)−plane, we reported the colormap of the difference ˆVth−ˆVmax as a function of ˆη and ˆε in Fig. 15, where we clearly marked the curve in the parameter space for which ˆVth=ˆVmax. These results show that, for example, choosing ˆε≥5⋅10−3 would lead to fluid velocities below the recommended threshold regardless of the presence of structural viscoelasticity. On the other hand, should
the particular experimental conditions constrain us to enforce a rectangular pulse corresponding to ˆε=0, we can still maintain the maximum velocity below the threshold by modifying the structural properties of the sample to have, for example, ˆη≥4⋅10−3.
Interestingly, expression (29) defines ˆη=(K0/L2)η, meaning that ˆη can be increased by increasing the viscoelastic parameter η, increasing the permeability parameter K0, or decreasing the sample thickness L. In the same spirit as [7], a typical value of the viscoelastic parameter η for biological tissues can be estimated by setting
where
is the characteristic elastic time constant of the porous material under compression and ρ is the mass density of the fluid component of the mixture. Since the densities of most of the biological fluids are very similar to that of water, let us set
ρ=1000 Kg m−3.
Substituting (46a) and (46b) in (29) we obtain
Replacing the parameter values of Table 1 into (46c)
we obtain ˆη=1.15⋅10−8, which is 5 orders of magnitude smaller than what is needed to attain fluid velocities below the recommended threshold in the case of a rectangular pulse in the pressure load. Thus, in order to control the maximum fluid velocity within the tissue sample, one may decide to:
(ⅰ) vary the properties of the biological sample by manipulating ρ, μ, η, K0 or L; and/or
(ⅱ) vary the time profile of the load experimental protocol. The choice will depend on the particular conditions and constraints of the experiment at hand.
8. Conclusions and future perspectives
The exact solutions obtained for the 1D models considered in this article allowed us to clearly identify a blow-up in the solution of certain poroelastic problems.
Compared to the analysis carried out in [6], in which
singularities in the solution were demonstrated by numerical evidences when the hypotheses of the existence
theorem were not satisfied, the 1D study conducted here allowed us, via analytical solution,
to prove that singularities may arise even in the simple case of constant permeability.
The analysis allowed us to identify the main factors that give rise to the blow-up, namely the absence of structural viscoelasticity and the time-discontinuity of the boundary source of traction. It is very important to emphasize that even a small viscoelastic contribution, namely ˆη≪1, will prevent the blow-up. Similarly, a continuous time profile of the applied boundary load will prevent blow-up even if the structure is purely elastic.
These findings actually provide an evidence of a blow-up that was hypothesized by the theoretical work presented in [6]. Interestingly, the a priori estimates derived in [6] were not sufficient to bound the power density if the data were not regular enough. The 1D examples considered in this article show that indeed it is not possible to bound the power density if the structure is purely elastic and the boundary forcing term is discontinuous in time. Moreover, we have shown that this blow-up occurs even in the simple case of constant permeability.
We expect that similar results can be obtained for the 3D fluid-solid mixture described in (2a)-(2g) with boundary conditions (3)-(5). In particular, if one considers the coupling driven by a source of linear momentum and a source of boundary traction that are not time differentiable, then one can only obtain local in time existence of weak solutions for the system (in comparison to [6]), and prove blow-up of solutions in finite time (in the norm of the fluid energy).
We plan to provide this analysis in a subsequent paper.
In real situations, we will never see the fluid velocity spiking to infinity as predicted by the mathematical blow-up, since something will break first! For example, if the poroelastic model represents a biological tissue perfused by blood flowing in capillaries, as the maximum velocity becomes too high, capillaries will break letting blood out. Thus, from a practical perspective, it is crucial to identify parameters that can control the maximum value of the fluid velocity within a deformable porous medium in order to avoid microstructure damage. Our analysis showed that the maximum fluid velocity can be limited by:
(ⅰ) decreasing Pref, thereby reducing the load on the medium;
(ⅱ) increasing ˆε, thereby smoothing the load action on the medium;
(ⅲ) increasing η, thereby changing the structural properties of the solid component of the medium;
(ⅳ) decreasing K0, thereby changing the pore size, geometry and/or fluid viscosity;
(ⅴ) decreasing L, thereby changing the domain geometry. We have explored these concepts more concretely by applying them to the confined compression tests for biological tissues.
It is worth noting that
the extreme sensitivity of biological tissues to the active role of viscoelasticity
predicted by our theoretical analysis seems to agree with the conclusions of [32]
where experimental data based on magnetic resonance elastography show that viscoelasticity of
the brain is a result of structural alteration occurring in the course of physiological aging,
this suggesting that cerebral viscoelasticity may provide a sensitive marker
for a variety of neurological diseases such as normal pressure hydrocephalus,
Alzheimer's disease, or Multiple Sclerosis.
Further extensions of the current work may include:
(1) the study of porous deformable media with compressible components. This case mathematically
corresponds to considering (1a) instead of (1b),
and is of interest
in the wider context of applications of the poro-visco-elastic model to problems in geomechanics
(cf. the original contribution by Biot in [5] and the more recent
works [27, 28, 29] and [3, 4],
devoted to computational analysis and theoretical investigations, respectively); (2)
the investigation of time discontinuities in the volumetric sources of linear momentum, which were identified by the analysis in [6] as additional possible causes of blow-up. This case is actually extremely relevant in situations where the gravitational acceleration varies abruptly, such as during space flight take off and landing.
Finally, it is worth emphasizing that the 1D analysis presented in this article has made available a series of testable conditions leading to blow-up, and consequent microstructural damage, that could indeed be verified in laboratory experiments. We see the design and implementation of such experiments as the most interesting development of the present work.
Acknowledgments
Dr. Bociu has been partially supported by NSF CAREER DMS-1555062. Dr. Guidoboni has been partially supported by the award NSF DMS-1224195, the Chair Gutenberg funds of the
Cercle Gutenberg (France) and the LabEx IRMIA (University of Strasbourg, France).
Dr. Sacco has been partially supported by Micron Semiconductor Italia S.r.l., SOW nr. 4505462139.









 DownLoad:
DownLoad: