Figure 1.
Study area map.
Accurate flood forecasting is a crucial process for predicting the timing, occurrence, duration, and magnitude of floods in specific zones. This prediction often involves analyzing various hydrological, meteorological, and environmental parameters. In recent years, several soft computing techniques have been widely used for flood forecasting. In this study, flood forecasting for the Narmada River at the Hoshangabad gauging site in Madhya Pradesh, India, was conducted using an Artificial Neural Network (ANN) model, a Fuzzy Logic (FL) model, and an Adaptive Neuro-Fuzzy Inference System (ANFIS) model. To assess their capacity to handle different levels of information, three separate input data sets were used. Our objective was to compare the performance and evaluate the suitability of soft computing data-driven models for flood forecasting. For the development of these models, monthly discharge data spanning 33 years from six gauging sites were selected. Various performance measures, such as regression, root mean square error (RMSE), and percentage deviation, were used to compare and evaluate the performances of the different models. The results indicated that the ANN and ANFIS models performed similarly in some cases. However, the ANFIS model generally predicted much better than the ANN model in most cases. The ANFIS model, developed using the hybrid method, delivered the best performance with an RMSE of 211.97 and a coefficient of regression of 0.96, demonstrating the potential of using these models for flood forecasting. This research highlighted the effectiveness of soft computing techniques in flood forecasting and established useful suitability criteria that can be employed by flood control departments in various countries, regions, and states for accurate flood prognosis.
Citation: Ronak P. Chaudhari, Shantanu R. Thorat, Darshan J. Mehta, Sahita I. Waikhom, Vipinkumar G. Yadav, Vijendra Kumar. Comparison of soft-computing techniques: Data-driven models for flood forecasting[J]. AIMS Environmental Science, 2024, 11(5): 741-758. doi: 10.3934/environsci.2024037
| [1] | Vijendra Kumar, Kul Vaibhav Sharma, Nikunj K. Mangukiya, Deepak Kumar Tiwari, Preeti Vijay Ramkar, Upaka Rathnayake . Machine learning applications in flood forecasting and predictions, challenges, and way-out in the perspective of changing environment. AIMS Environmental Science, 2025, 12(1): 72-105. doi: 10.3934/environsci.2025004 |
| [2] | Kitipol Nualtong, Ronnason Chinram, Piyawan Khwanmuang, Sukrit Kirtsaeng, Thammarat Panityakul . An efficiency dynamic seasonal regression forecasting technique for high variation of water level in Yom River Basin of Thailand. AIMS Environmental Science, 2021, 8(4): 283-303. doi: 10.3934/environsci.2021019 |
| [3] | Adrian Schmid-Breton . Transboundary flood risk management in the Rhine river basin. AIMS Environmental Science, 2016, 3(4): 871-888. doi: 10.3934/environsci.2016.4.871 |
| [4] | G Mathias Kondolf, Pilar Lopez-Llompart . National-local land-use conflicts in floodways of the Mississippi River system. AIMS Environmental Science, 2018, 5(1): 47-63. doi: 10.3934/environsci.2018.1.47 |
| [5] | Seiran Haghgoo, Jamil Amanollahi, Barzan Bahrami Kamangar, Shahryar Sorooshian . Decision models enhancing environmental flow sustainability: A strategic approach to water resource management. AIMS Environmental Science, 2024, 11(6): 900-917. doi: 10.3934/environsci.2024045 |
| [6] | Said Qasim, Mohammad Qasim, Rajendra Prasad Shrestha, Amir Nawaz Khan . An assessment of flood vulnerability in Khyber Pukhtunkhwa province of Pakistan. AIMS Environmental Science, 2017, 4(2): 206-216. doi: 10.3934/environsci.2017.2.206 |
| [7] | Gene T. Señeris . Nabaoy River Watershed potential impact to flooding using Geographic Information System remote sensing. AIMS Environmental Science, 2022, 9(3): 381-402. doi: 10.3934/environsci.2022024 |
| [8] | Leon J. van Ruiten, Thomas Hartmann . The spatial turn and the scenario approach in flood risk management—Implementing the European Floods Directive in the Netherlands. AIMS Environmental Science, 2016, 3(4): 697-713. doi: 10.3934/environsci.2016.4.697 |
| [9] | Moven Manjowe, Terence Darlington Mushore, Juliet Gwenzi, Collen Mutasa, Electdom Matandirotya, Emmanuel Mashonjowa . Circulation mechanisms responsible for wet or dry summers over Zimbabwe. AIMS Environmental Science, 2018, 5(3): 154-172. doi: 10.3934/environsci.2018.3.154 |
| [10] | Flor Quispe, Eddy Salcedo, Hasnain Iftikhar, Aimel Zafar, Murad Khan, Josué E. Turpo-Chaparro, Paulo Canas Rodrigues, Javier Linkolk López-Gonzales . Multi-step ahead ozone level forecasting using a component-based technique: A case study in Lima, Peru. AIMS Environmental Science, 2024, 11(3): 401-425. doi: 10.3934/environsci.2024020 |
Accurate flood forecasting is a crucial process for predicting the timing, occurrence, duration, and magnitude of floods in specific zones. This prediction often involves analyzing various hydrological, meteorological, and environmental parameters. In recent years, several soft computing techniques have been widely used for flood forecasting. In this study, flood forecasting for the Narmada River at the Hoshangabad gauging site in Madhya Pradesh, India, was conducted using an Artificial Neural Network (ANN) model, a Fuzzy Logic (FL) model, and an Adaptive Neuro-Fuzzy Inference System (ANFIS) model. To assess their capacity to handle different levels of information, three separate input data sets were used. Our objective was to compare the performance and evaluate the suitability of soft computing data-driven models for flood forecasting. For the development of these models, monthly discharge data spanning 33 years from six gauging sites were selected. Various performance measures, such as regression, root mean square error (RMSE), and percentage deviation, were used to compare and evaluate the performances of the different models. The results indicated that the ANN and ANFIS models performed similarly in some cases. However, the ANFIS model generally predicted much better than the ANN model in most cases. The ANFIS model, developed using the hybrid method, delivered the best performance with an RMSE of 211.97 and a coefficient of regression of 0.96, demonstrating the potential of using these models for flood forecasting. This research highlighted the effectiveness of soft computing techniques in flood forecasting and established useful suitability criteria that can be employed by flood control departments in various countries, regions, and states for accurate flood prognosis.
Hydrological forecasting, particularly flood prediction, is a critical concern in hydrology, playing a pivotal role in water resource planning and development. It serves as an essential tool for managing reservoir outflows during upper river flows, contributing to effective water resource management [1]. Traditionally, flood forecasting models have been developed using either a physical understanding of the involved processes or a systems theoretic approach [2]. The physical approach emphasizes studying and understanding physical phenomena, while the systems theoretic approach focuses on the system's operation rather than its inherent nature or governing physical laws [3]. While conceptual (physics-based) models offer reasonable accuracy, their implementation and calibration pose significant challenges, requiring advanced mathematical tools and substantial expertise [4]. Due to the complexity of the physical approach, a systems theoretic perspective is often adopted. This approach approximates major physical factors and allows the neglect of minor features [5]. In such cases, data-driven models, which do not require complete physical understanding, become preferable. This is especially true in river flow forecasting, where the primary objective is to make accurate predictions at specific watershed locations.
In recent years, there has been an increased reliance on data-driven models for flood forecasting. Artificial Neural Networks (ANN) [2,6,7,8] and fuzzy logic have been successfully employed independently [9,10]. However, integrating their strengths has given rise to powerful intelligent systems known as neuro-fuzzy systems. For example, Nayak et al. [11] applied adaptive neuro-fuzzy inference systems (ANFIS) for hydrologic time series modeling of river flow, demonstrating superiority over traditional models in terms of computational speed, forecast errors, efficiency, and peak flow estimation. Similar results were also reported by Nayak et al. [12], where the performance of the ANFIS model was found to better capture the inherent nonlinearity in the rainfall-runoff process compared to independent fuzzy and ANN models. Advancements in computing power have facilitated the development of effective modeling tools. Emulating the human brain's low level mechanisms through ANN [13] and the fuzzy rule-based approach introduced by Zadeh [14], have led to significant breakthroughs [11,15]. Both ANN and fuzzy logic exhibit intrinsic generality, flexibility, and global performance, making them valuable building blocks in today's computational landscape [16].
ANNs, as semi-parametric regression estimators, are well-suited for hydrologic modeling [17,18,19], offering the ability to approximate virtually any measurable function with a high degree of accuracy [20]. The emergence of neural network technology has yielded many promising results in hydrology and water resource simulation [6]. Fuzzy rule-based modeling describes system behavior using natural language [21], finding applications in water resource forecasting [22,23,24,25,26,27,28]. The integration of these approaches into neuro-fuzzy systems capitalizes on the advantages of both fields, combining the learning capabilities of ANN with the fuzzy reasoning mechanism, thereby enhancing overall modeling capabilities [29,30,31,32]. The integration of neural networks and fuzzy logic in neuro-fuzzy systems represents a promising advancement in computational hydrology. This synergistic approach leverages the strengths of each technique, proving advantageous in handling large amounts of noisy data from dynamic and nonlinear systems, particularly when the underlying physical relationships are not well understood. Neuro-fuzzy systems, with their unique combination of neural network learning and fuzzy reasoning, hold great potential across various applications, from signal processing to database management [33].
Our objective is to compare the performance and evaluate the suitability of three soft computing technique-based models for flood forecasting. The flood problem faced by India is unique due to the varied climate and rainfall patterns across different regions of the country. It is often observed that one part of the country experiences floods while another part suffers from severe drought. Heavy and intense rainfall is a significant factor contributing to floods. However, floods may also be caused by various other factors, including the failure of flood control structures, drainage congestion, sudden release of water due to removing ice jams or landslides in mountainous streams, and coastal flooding due to high tides. Despite implementing various short and long-term measures to prevent and mitigate the consequences of floods, significant damages and losses persist due to increased human interference in natural processes and the encroachment of floodplain zones and riverbeds. Flood forecasting serves as a crucial tool for providing warnings to people residing in floodplains, helping to alleviate distress and minimize damage.
Atiya et al. [34] assessed the application of brain organizations to the issue of determining the progression of the Stream Nile in Egypt and used the time series as a benchmark to look at brain network estimating techniques. They compared four distinct strategies with preprocessing the information sources and results, including an original strategy proposed here in light of the discrete Fourier series. Khan et al. [35] combined three methods to reduce uncertainty in an FNN model for predicting the peak flow rate in Calgary's Bow River. The methods included an ANPSFS method, a search algorithm for network architecture selection. This approach demonstrates data-driven modeling's suitability for urban watershed flood modeling. Patel and Parekh [36] investigate the use of Artificial Intelligence Techniques (ANFIS) in flood forecasting for the Dharoi Dam in Gujarat, India. The technique combines neural network learning with fuzzy system representation. ANFIS models are trained and tested using statistical indices like RMSE, R2, and D. The results show that ANFIS can accurately and reliably forecast floods. Mistry and Parekh [37] used artificial neural networks (ANN) to predict river flow in the Deo River in Gujarat, India. The model considers rainfall and discharge parameters. Six alternative flood prediction models were developed using ANN, using different training algorithms. The best performance was achieved with an ANN model using the Cascade forward back-propagation training algorithm. The model's performance was evaluated using statistical parameters, showing its effectiveness in predicting floods and being used by flood control departments for forecasting. Ahmadia and Moradinia [38] used the Adaptive Neuro-Fuzzy Inference System (ANFIS) model and Harris Hawks Optimization (HHO) and Arithmetic Optimization Algorithm (AOA) to predict floods in Iran's Shahrchay River. Data from 2016 and 2017 was used for training and testing. The ANFIS-AOA model showed promising results, with NSE, RMSE, and Mapei values of 0.93, 1.34, and 0.69, respectively.
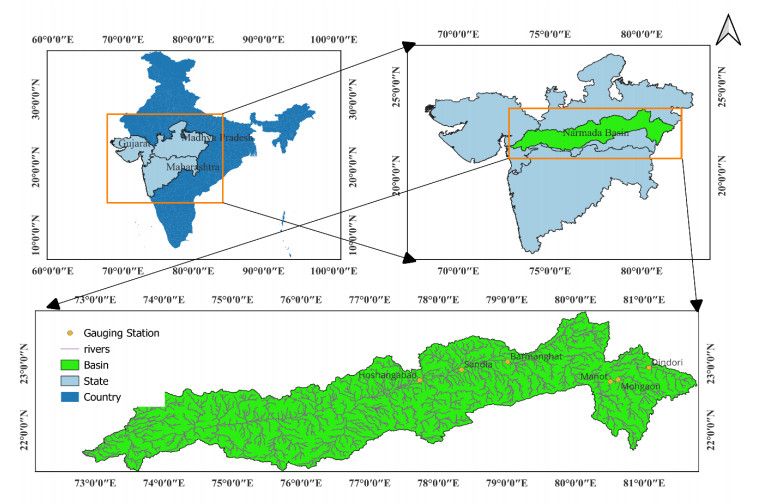
The Narmada River originates in Amarkantak, Madhya Pradesh, India, at an altitude of 1057 meters. It spans a length of 1,312 kilometers, emptying into the Gulf of Khambhat in the Arabian Sea near Bharuch, Gujarat. The Narmada Basin covers an area of 98,796 square kilometers and is between 72°32' E, 81°45' E, 21°20' N, and 23°45' N. The study area encompasses the upper basin of the Narmada River. The Narmada Basin survey G & D Hoshangabad site and flood forecast selected 13,120 square kilometers of drainage area. Emission data from Dindori, Manot, Barmanghat, Mohgaon, and Sandia is accessible from 1989 to 2021. To develop a flood forecasting model at the Hoshangabad site, discharge measurements from Dindori, Manot, Barmanghat, Mohgaon, and Sandia have been utilized. To validate the model, discharge data from the Hoshangabad gauge site has been employed (see Figure 1).
The Narmada's 75% reliable flow is characterized by a flow coefficient of 0.29. Annual precipitation in the upper basin of the Narmada exceeds 1400 mm, with some areas surpassing 1650 mm. In 1999, the Narmada River Basin, particularly Hoshangabad, experienced unprecedented rainfall, prompting the construction of three major dams in the former catchment area: Bharji Dam, Barna Dam, and Tawa Dam. Consequently, large parts of Hoshangabad city were inundated for an extended period, resulting in significant damage to the local economy. Monthly discharge data from the Narmada River Basin's six gauging sites for 33 years has been collected from the India Water Resources Information System (IWRIS).
Artificial neural networks, as their name implies, are built to imitate biological neural networks of living organisms. Neural network models are a particularly potent computer tool for modeling complex nonlinear interactions, especially when the explicit form of the link between the variables involved is unknown. The model inputs and architecture of an ANN are thus defined in terms of the number of layers, the nodes in each layer, the activation functions in each layer, and the connections between the layers. An ANN normally has three layers: An input layer, which brings data into the network; one or more hidden layers, which process the data; and an output layer, which generates a result for a specific output (Figure 2). Weights act as connections between the neurons in each layer. To produce the output, the input data is processed by a hidden layer and a nonlinear function of the output layer. A popular training algorithm with the benefit of being simple to learn and effective in many applications is the backpropagation method [13,39], having the advantage of easy understanding and can be successfully used in many applications. In this research, the Levenberg-Marquardt (LM) [22,40,41], which helps to train many neural networks with just a few thousand instances and a few hundred parameters, the gradient descent algorithm with variable learning and momentum factor (GDX) [27,42], and the conjugate descent algorithm (CGF) backpropagation algorithm [11,43,44] were used to train the ANN models in order to save the memory and check their performance.
General steps for flood forecasting using ANN:
(1) Data collection: Gather historical data on rainfall, river discharge, soil moisture, and other relevant variables.
(2) Preprocessing: Clean and preprocess the data to remove noise and inconsistencies.
(3) Model training: Train the ANN using historical data to learn the complex relationships between input variables and flood events.
(4) Model validation: Validate the ANN's performance using independent datasets or cross-validation techniques.
(5) Forecasting: Utilize the trained ANN to predict future flood events based on current and forecasted meteorological conditions.
Natural, continuous logic, known as fuzzy logic, is based somewhat on how people think. Theoretical mathematics responds to variables that are continually changing, challenging conventional reasoning by not being constrained to the dual computer values of zero (0) and one (1). Alternately, partial truths and multivalued truths are supported by fuzzy logic. It is especially helpful for issues where mathematical modeling is difficult or impossible due to missing, imperfect, or complicated data. Engineers can integrate ambiguous reasoning that is similar to human logic into computers by employing linguistic modeling rather than mathematical modeling when using real language in fuzzy control, which makes designing and modifying fuzzy logic systems more relevant.
To consider situations where decision-makers must accurately interpret and process information that is intrinsically imperfect, the fuzzy set theory was established. Fuzzy sets offer an analytical tool and a conceptual framework (Figure 3) for dealing with practical issues that lack precise information.
On the other hand, the meaning of ambiguity and comparison is infused with human semantics. The discrepancy in raters can be eliminated using linguistic data at various granularities. Machines might be able to understand and react to hazy human ideas like hot, cold, huge, and little with the help of fuzzy logic algorithms. They could also offer a reasonably straightforward method for obtaining firm conclusions from false information.
General steps for flood forecasting using fuzzy logic:
(1) Linguistic variable definition: Define linguistic variables representing input and output parameters, such as rainfall intensity, river flow rate, and flood severity.
(2) Fuzzy rule base construction: Develop a set of fuzzy rules that capture expert knowledge or historical relationships between input and output variables.
(3) Fuzzy inference: Apply fuzzy logic inference techniques, such as Mamdani or Sugeno methods, to determine the degree of membership for each fuzzy rule.
(4) Defuzzification: Convert the fuzzy output into crisp values representing forecasted flood conditions.
When creating an ANFIS to simulate a certain target system, choosing a FIS is crucial. In the literature, various FIS types are discussed [39,45,46] and each is distinguished only by the characteristics that come from it. A Takagi Sugeno Kang (TSK) fuzzy logic system [39,47,48,49] was utilized in the current work because fuzzy rules can be inferred using a related linear combination, and their factors may be evaluated using regression analysis. Do not forget that the FIS has one output (z) and two inputs (x, y). Figures show the design of the appropriate ANFIS for a TSK fuzzy inference system with two membership functions allocated to each input (x and y).
Neuro-fuzzy adopts IF-THEN fuzzy rules to relate the connection between the input data and output data sets of a modeling problem. The basic structure of the ANFIS model is demonstrated in Figure 4. In this model, the Takagi Sugeno inference method is essential in constructing the IF-THEN rules from input to end.
Rule1: If x is D1 and y is C1, so g1 = α1x+β1y+γ1,
Rule2: If x is D2 and y is C2, so g2 = α2x+β2y+γ2,
where α1, β1, γ1, and α2, β2, γ2 denote the consequence parameters, and D1, D2, C1, and C2 are considered to be membership functions. The ANFIS comprises five levels with a greater amount of inputs and only one output. This structure is structured as follows:
General steps for flood forecasting using ANFIS:
(1) Hybrid model structure: Design the ANFIS architecture, which typically consists of a fuzzy inference system followed by a neural network.
(2) Parameter initialization: Initialize the parameters of the ANFIS model, including fuzzy membership functions and neural network weights.
(3) Hybrid learning algorithm: Train the ANFIS model using a hybrid learning algorithm, such as backpropagation or least squares estimation, to optimize both fuzzy and neural components.
(4) Model evaluation: Evaluate the performance of the trained ANFIS model using validation datasets and performance metrics.
(5) Forecast generation: Generate flood forecasts using the trained ANFIS model, incorporating current and forecasted meteorological inputs
A crucial phase in the model development process involves identifying significant input parameters, a task that requires careful consideration due to potential correlations, noise, or lack of substantial relationships with the output variable [44,50]. Typically, initial sets of candidate inputs are specified using some degree of a priori knowledge [45,51]. While widely used, a priori identification is subjective and dependent on expert knowledge, making it case-specific. An ideal approach for determining suitable inputs involves a blend of a priori knowledge and analytical methods [47,52,53,54].
As mentioned in the previous section, three different types of models were constructed in this study, which were ANN, fuzzy logic, and ANFIS. To develop models for monthly flood forecasting at the Hoshangabad gauging station in the Narmada River, 33 years of monthly discharge data were used to model development and validation. Discharge at Dindori, Mohgaon, Manot, Barmanghat, and Sandia, which are located at the Upper Narmada Basin, is selected as an input parameter, and discharge at Hoshangabad, which is located at the Middle Narmada Basin, is selected as an output parameter. The function representing the relationship between the parameters is shown in Eq 1.
| QHoshangabad =f(QBamni ,QMohgaon ,QManot ,QBarmanghat ,QSandia ) | (1) |
The performance of the data-driven models was data-dependent, requiring the collection of sufficient amounts of data. The quality of the data should be carefully analyzed before application. This is important to improve the generalization capacity of the model. A detailed data analysis was performed to obtain the final data sets. Data sets with one or more of the input variables missing were excluded from further consideration. The training can be performed with 70% of overall datasets using. The testing and validation can be performed with 15% and 15%, respectively. To assess the model's ability to process a distinct number of databases, three separate datasets are selected, as shown in Table 1.
| Sr. No. | Model name | Data (%) | Data (Number) |
| 1 | ANN-1 | 100 | 326 |
| 2 | FUZZY-1 | 100 | 326 |
| 3 | ANFIS-1 | 100 | 326 |
| 4 | ANN-2 | 66 | Latest 217 |
| 5 | ANFIS-2 | 66 | Latest 217 |
| 6 | ANN-3 | 33 | Latest 109 |
| 7 | ANFIS-3 | 33 | Latest 109 |
DownLoad:
CSV
To measure the effectiveness of model predictions, quantitative assessments comparing model simulations with observed data serve as a crucial evaluation of predictive capabilities. Assessments commonly employ a range of statistics and techniques, often called 'goodness of fit' statistics. While principal measurements in hydrological literature have been extensively reviewed by Legates and McCabe [48,55,56,57], the use of global goodness of fit statistics for forecasting flood hydrographs exhibits diversity. Given the absence of a single evaluation measure [49,58,59,60,61], we adopt a multi-criteria assessment, employing various goodness of fit statistics. The parameters used to evaluate the performance of all models were the root mean square error (RMSE), coefficient of regression (R2), and percentage deviation (PD). RMSE assesses the overall accuracy of predictions, with lower values indicating better performance. R2 evaluates how well the model explains the variability in the data, where higher values indicate better fit. PD provides a measure of relative accuracy, highlighting how close predicted values are to actual observations.
Root mean square error is calculated as
| RMSE=[∑Ni=1(Oi−Pi)2N]1╱2 | (2) |
where, N = total number of measurements, Oi = measured discharge, and Pi = calculated discharge.
Coefficient of Regression is calculated as
| R2=[∑Ni=1(Oi−Oavg)∗(Pi−Pavg)√∑Ni=1(Oi−Oavg)2∗√∑Ni=1(Pi−Pavg)2]2 | (3) |
where, Oavg = average of measured discharge and Pavg = average of calculated discharge.
Percentage deviation is defined as
| PD=(Pp−Op)OpX 100 | (4) |
where Op and Pp = average measured and average calculated discharge values.
We use data driven models for developing a model for monthly flood forecasting over the Hoshangabad site of the Narmada River. The ANN, FL, and ANFIS models were used for the development of the model for the study area. Through the appropriate model, results are shown in this section using a graphical representation of the data. The overall performance of this model in the Narmada basin for the different data sets in terms of Regression, RMSE, and Percentage Deviation.
The performance graphs for the different soft-computing models (i.e., ANN, Fuzzy Logic, and ANFIS) for flood forecasting in the Narmada basin for the data set are shown in Figure 5. Results evidenced regression values of 0.9582, 0.7769, and 0.9665 for the ANN, the Fuzzy Logic, and the ANFIS model, respectively. Differently from the ANN and the ANFIS models, the performance of the Fuzzy Logic model is so poor that it has not been used in further procedures.
The performance graphs for the different soft-computing models (i.e., ANN and ANFIS) for flood forecasting in the Narmada basin for the latest 66% of data sets are shown in Figure 6. Results evidenced regression values of 0.966 and 0.9746 for the ANN and the ANFIS models, respectively, thus evidencing a good performance of both models.
Finally, the performance graphs for the different soft-computing models (i.e., ANN and ANFIS) for flood forecasting in the Narmada basin for the latest 33% of data sets are shown in Figure 7. Results evidenced regression values of 0.848 and 0.9837 for the ANN and the ANFIS model, respectively.
Table 2 shows the overall performance of the different soft-computing models (i.e., ANN, Fuzzy Logic, and ANFIS) for flood forecasting in the Narmada basin for the different data sets in Regression, RMSE, and Percentage Deviation. As a result, the performance of the Fuzzy Logic model compared to the ANN and ANFIS models is very poor, and thus it is possible to conclude that the Fuzzy Logic model is not suitable for flood forecasting on the Upper Narmada Basin. In fact, the performance measures for the Fuzzy Logic model evidenced a regression value of 0.7769, a RMSE of 960.88, and a Percentage Deviation of 135.051. On the contrary, the ANN model performance is very good, presenting a high regression value, equal to 0.9582, and low values of RMSE and of the Percentage Deviation, equal to 237.24 and 0.087, respectively. It is noteworthy that the performance of the ANN model decreases when the number of data sets decreases. Moreover, the ANFIS model's performance is higher than that of the ANN model for the same data sets, and, unlike the ANN model, the performance of the ANFIS model increases when the number of data sets decreases.
| Sr. No. | Model Name | R2 | RMSE | Percentage Deviation |
| 1 | ANN-1 | 0.9582 | 237.24 | –0.0870 |
| 2 | FUZZY-1 | 0.7769 | 960.88 | +135.0510 |
| 3 | ANFIS-1 | 0.9665 | 211.97 | –0.0013 |
| 4 | ANN-2 | 0.9188 | 219.03 | +1.1341 |
| 5 | ANFIS-2 | 0.9788 | 110.27 | +0.0006 |
| 6 | ANN-3 | 0.9154 | 262.62 | +59.7005 |
| 7 | ANFIS-3 | 0.9855 | 54.23 | +0.0001 |
DownLoad:
CSV
Overall, the results of the data-driven models show that the ANN and ANFIS models are accurate for monthly flood forecasting for the Narmada River. However, its accuracy depends on the quantity of data. Additionally, ANN model accuracy can improve by expanding the data, and for ANFIS, it can be done by reducing the data up to a specific point.
In this study, the ANFIS model performs better than the ANN model, and the same results have been found by Chatterjee et al. [62]. The ANN model of Chang et al. [2] had R2 values ranging from 0.8 to 0.95, which are generally comparable with other ANN and ANFIS model results. The Fuzzy Logic model of Nayak et al. [9] had R2 values ranging from 0.8 to 0.95, which is better than our fuzzy Logic model results. The ANN and ANFIS model of Nayak et al. [11] had R2 values ranging from 0.8 to 0.95, similar to our ANN and ANFIS results. Folorunsho et al. [63] evaluated different data driven models for flood prediction in urban areas. They reported that while ANN showed promising results, ANFIS provided more robust predictions with lower error rates, especially during extreme floods. A study by He et al. [64] compared ANN, ANFIS, and SVM for flood forecasting in river basins of a certain region. They found that ANFIS consistently outperformed ANN and SVM models in terms of accuracy and reliability.
Overall, the ANN and ANFIS models in this study generally perform well, with R2 values ranging from 0.9154 to 0.9855, which are comparable with other the studies related to flood forecasting. However, the fuzzy logic model seems to have slightly lower R2 values compared to some of the referenced studies. This could be due to various factors, such as differences in data, model architecture, or training methodologies.
We aimed to assess the performance of various data-driven models, including ANN, Fuzzy Logic, and ANFIS, for flood forecasting in the Narmada Basin. The following conclusions were drawn from the results:
a) The ANFIS model consistently outperformed the ANN and Fuzzy Logic models regarding flood forecasting accuracy, especially when the same number of data points was used. Additionally, the accuracy of the ANFIS model increased as the number of data points decreased.
b) The ANN model provided accurate flood forecasts, but its performance was slightly inferior to the ANFIS model when considering the same dataset size. Moreover, the accuracy of the ANN model decreased as the number of data points decreased.
c) In contrast, the Fuzzy Logic model exhibited lower accuracy than the ANN and ANFIS models when applied to the same dataset. The poor performance of the Fuzzy Logic model suggests its unsuitability for monthly flood forecasting in the studied area.
d) The study highlights that both ANN and ANFIS models are effective for flood forecasting. However, ANFIS is more suitable when the dataset size is smaller, whereas ANN is preferable for larger dataset sizes.
Additionally, we found that the models used in this study can accurately predict the near future within the next 30 years. This prediction limitation is attributed to the temporal relevance of rainfall, influenced by environmental variability and anthropogenic factors.
From the previous discussion, it is seen that various researchers have studied the applicability of ANN, ANFIS, and adaptive neuro-GA integrated system (ANGIS) models in flood forecasting. Also, comparative studies have been carried out to compare the performances of ANN, ANFIS, and ANGIS models for flood forecasting [62] and for the performances of ANN and ANGIS models for rainfall-runoff modeling [65]. However, a comprehensive study to compare the performances of ANN, Fuzzy, and ANFIS models in forecasting floods is missing. In this study, flood forecasting at the Hoshangabad gauging site of the Narmada River Basin in Madhya Pradesh, India is carried out using ANN, Fuzzy, and ANFIS models. The relative performances of these models are also compared.
Future research should extend the techniques to other catchments and forecasting with various lead time and lag time factors. Researchers can use other parameters like rainfall, temperature, soil moisture, etc. Several researchers have used ANN models for hydrology-related studies. Therefore, we suggest examining the performance of advanced ML architecture, such as deep neural networks, generative adversarial networks (GAN), and artificial neural networks (ANN), for the proposed work.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
We acknowledge Civil Engineering Department of Dr. S. & S. S. Ghandhy Government Engineering College for supporting this research.
The authors declare no conflict of interest.
| [1] | Brown M, Harris C (1994) Neurofuzzy adaptive modelling and control, Hertfordshire: Prentice Hall International (UK) Ltd. |
| [2] |
Chang FJ, Chiang YM, Chang LC, et al. (2007) Multi-step-ahead neural networks for flood forecasting. Hydrolog Sci J 52: 114–130. http://dx.doi.org/10.1623/hysj.52.1.114 doi: 10.1623/hysj.52.1.114
|
| [3] |
Chiu SL (1994) Fuzzy model identification based on cluster estimation. J Intell Fuzzy Syst 2: 267–278. http://dx.doi.org/10.3233/IFS-1994-2306 doi: 10.3233/IFS-1994-2306
|
| [4] |
Duan Q, Sorooshian S, Gupta VK, et al. (1992) Effective and efficient global optimization for conceptual Rainfall-Runoff models. Water Resour Res 28: 1015–1031. https://doi.org/10.1029/91WR02985 doi: 10.1029/91WR02985
|
| [5] | Sudheer KP (2000) Modeling hydrological processes using neural computing technique, Ph.D. thesis, Indian Institution of Technology Delhi, India. |
| [6] |
Dawson C, Wilby R (1998) An artificial neural network approach to rainfall-runoff modeling. Hydrolog Sci J 43: 47–66. https://doi.org/10.1080/02626669809492102 doi: 10.1080/02626669809492102
|
| [7] |
Sudheer KP, Gosain AK, Ramasastri KS, et al. (2002) A data driven algorithm for constructing artificial neural network rainfall-runoff models. Hydrol Process 16: 1325–1330. https://doi.org/10.1002/hyp.554 doi: 10.1002/hyp.554
|
| [8] |
Sudheer KP (2005) Knowledge extraction from Trained neural network river flow models. J Hydrol Eng 10: 264–269. https://doi.org/10.1061/(ASCE)1084-0699(2005)10:4(264) doi: 10.1061/(ASCE)1084-0699(2005)10:4(264)
|
| [9] |
Nayak PC, Sudheer KP, Ramasastri KS, et al. (2005) Fuzzy computing based rainfall-runoff model for real time flood forecasting. Hydrol Process 19: 955–968. https://doi.org/10.1002/hyp.5553 doi: 10.1002/hyp.5553
|
| [10] |
Singh SR (2007) A robust method of forecasting based on fuzzy time series. Appl Math.Comput 188: 472–484. https://doi.org/10.1016/j.amc.2006.09.140 doi: 10.1016/j.amc.2006.09.140
|
| [11] |
Nayak PC, Sudheer KP, Rangan DM, et al. (2004) A neuro-fuzzy computing technique for modeling hydrological time series. J Hydrol 291: 52–66. https://doi.org/10.1016/j.jhydrol.2003.12.010 doi: 10.1016/j.jhydrol.2003.12.010
|
| [12] |
Nayak PC, Sudheer KP, Rangan DM, et al. (2005) Short-term flood forecasting with a neurofuzzy model. Water Resour Res 41. https://doi.org/10.1029/2004WR003562 doi: 10.1029/2004WR003562
|
| [13] | Haykin S (1999) Neural networks: A comprehensive foundation, Hoboken: Prentice Hall. |
| [14] |
Zadeh LA (1965) Fuzzy sets. Inf Control 8: 338–353. https://doi.org/10.1016/S0019-9958(65)90241-X doi: 10.1016/S0019-9958(65)90241-X
|
| [15] |
Chang L, Chang F (2001) Intelligent control for modelling of real-time reservoir operation. Hydrol Process 15: 1621–1634. https://doi.org/10.1002/hyp.226 doi: 10.1002/hyp.226
|
| [16] |
Shamseldin AY, Nasr AE, O'Connor KM, et al. (2002) Comparison of different forms of the multi-layer feed-forward neural network method used for river flow forecasting. Hydrol Earth Syst Sc 6: 671–684. https://doi.org/10.5194/hess-6-671-2002 doi: 10.5194/hess-6-671-2002
|
| [17] |
Connor JT, Martin RD, Atlas LE, et al. (1994) Recurrent neural networks and robust time series prediction. IEEE T Neural Networ 5: 240–254. https://doi.org/10.1109/72.279188 doi: 10.1109/72.279188
|
| [18] |
Gohil M, Mehta D, Shaikh M, et al. (2024) An integration of geospatial and fuzzy-logic techniques for flood-hazard mapping. J Earth Syst Sc 133: 80. https://doi.org/10.1007/s12040-024-02288-1 doi: 10.1007/s12040-024-02288-1
|
| [19] | Babovic V, Keijzer M (2000) Forecasting of river discharges in the presence of chaos and noise, In: J. Marsalek, W. E. Watt, E. Zeman, F. Sieker, Eds., Flood Issues in Contemporary Water Management, Dordrecht: Springer, 71: 405–419. https://doi.org/10.1007/978-94-011-4140-6_42 |
| [20] |
Hornik K, Stinchcombe M, White H, et al. (1989) Multilayer feed forward networks are universal approximators. Neural Networks 2: 359–366. https://doi.org/10.1016/0893-6080(89)90020-8 doi: 10.1016/0893-6080(89)90020-8
|
| [21] |
Sugeno M, Yasukawa TA (1993) fuzzy-logic based approach to qualitative modeling. IEEE T Fuzzy Syst 1: 7–31. https://doi.org/10.1109/TFUZZ.1993.390281 doi: 10.1109/TFUZZ.1993.390281
|
| [22] | Fujita M, Zhu ML, Nakoa T, et al. (1992) An application of fuzzy set theory to runoff prediction, paper presented at Sixth IAHR International Symposium on Stochastic Hydraulics. Int Assoc for Hydraul Res. |
| [23] | Zhu ML, Fujita M (1994) Comparison between fuzzy reasoning and neural network method to forecast runoff discharge. J Hydrosci Hydraul Eng 12: 131–141. |
| [24] |
Zhu ML, Fujita M, Hashimoto N, et al. (1994) Long lead time forecast of runoff using fuzzy reasoning method. J Jpn Soc Hydrol Water Resour 7: 83–89. https://doi.org/10.3178/jjshwr.7.2_83 doi: 10.3178/jjshwr.7.2_83
|
| [25] | Stuber M, Gemmar P, Greving M, et al. (2000) Machine supported development of fuzzy-flood forecast systems, In Proceedings of European Conference on Advances in Flood Research, 504–515. |
| [26] |
See L, Openshaw S (1999) Applying soft computing approaches to river level forecasting. Hydrol Sci J 44: 763–778. https://doi.org/10.1080/02626669909492272 doi: 10.1080/02626669909492272
|
| [27] |
Hundecha Y, Bardossy A, Werner HW, et al. (2001) Development of a fuzzy logic-based rainfall-runoff model. Hydrol Sci J 46: 363–376. https://doi.org/10.1080/02626660109492832 doi: 10.1080/02626660109492832
|
| [28] |
Xiong L, Shamseldin AY, O'Connor KM, et al. (2001) A non-linear combination of the forecasts of rainfall-runoff models by the first-order Takagi-Sugeno fuzzy system. J Hydrol 245: 196–217. https://doi.org/10.1016/S0022-1694(01)00349-3 doi: 10.1016/S0022-1694(01)00349-3
|
| [29] |
Minns W, Hall MJ (1996) Artificial neural networks as rainfall-runoff models. Hydrol Sci J 41: 399–417. https://doi.org/10.1080/02626669609491511 doi: 10.1080/02626669609491511
|
| [30] | Khondker M, Wilson G, Klinting, et al. (1998) Application of neural networks in real time flash flood forecasting. 777–781. |
| [31] | Solomatine DP, Rojas CJ, Velickov S, et al. (2000) Chaos theory in predicting surge water levels in the North Sea, In Proceedings of the 4th International Conference on Hydroinformatics, Babovic V, Larsen CL, Eds., Rotterdam: Balkema, 1–8. |
| [32] |
Sudheer KP, Jain A (2004) Explaining the internal behaviour of artificial neural network river flow models. Hydrol Process 18: 833–844. https://doi.org/10.1002/hyp.5517 doi: 10.1002/hyp.5517
|
| [33] |
Jang JSR (1993) ANFIS: Adaptive-network based fuzzy inference system. IEEE T Syst Man Cybern 23: 665–685. https://doi.org/10.1109/21.256541 doi: 10.1109/21.256541
|
| [34] |
Atiya AF, El-Shoura SM, Shaheen SI, et al. (1999) A comparison between neural-network forecasting techniques—Case study: River flow forecasting, IEEE T Neural Netwo 10: 402–409. https://doi.org/10.1109/72.750569 doi: 10.1109/72.750569
|
| [35] |
Khan UT, Jianxun H, Valeo C, et al. (2018) River flood prediction using fuzzy neural networks: An investigation on automated network architecture, Water Sci Technol 238–247. https://doi.org/10.2166/wst.2018.107 doi: 10.2166/wst.2018.107
|
| [36] |
Patel D, Parekh F (2014) Flood forecasting using adaptive neuro-fuzzy inference system (ANFIS). Int J Eng Trends Technol 12: 510–514. https://doi.org/10.14445/22315381/IJETT-V12P295 doi: 10.14445/22315381/IJETT-V12P295
|
| [37] | Mistry S, Parekh F (2022) Flood forecasting using artificial neural network, In IOP Conference Series: Earth and Environmental Science, Bristol: IOP Publishing. https://doi.org/10.1088/1755-1315/1086/1/012036 |
| [38] |
Ahmadia N, Moradinia SF (2024) An approach for flood flow prediction utilizing new hybrids of ANFIS with several optimization techniques: A case study. Hydrol Res 55: 561–575. https://doi.org/10.2166/nh.2024.191 doi: 10.2166/nh.2024.191
|
| [39] | Takagi T, Sugeno M (1985) Fuzzy identification of systems and its application to modeling and control. IEEE T Syst Man Cybern 15: 116–132. https://doi.org/10.1109/TSMC.1985.6313399 |
| [40] |
Setnes M (2000) Supervised fuzzy clustering for rule extraction. IEEE T Fuzzy Syst 8: 416–424. https://doi.org/10.1109/91.868948 doi: 10.1109/91.868948
|
| [41] |
Guru N, Jha R (2019) Application of soft computing techniques for river flow prediction in the downstream catchment of Mahanadi River Basin using partial duration series, India. Iran J Sci Technol 44: 279–297. https://doi.org/10.1007/s40996-019-00272-0 doi: 10.1007/s40996-019-00272-0
|
| [42] |
Mamdani EH, Assilian S (1975) An experiment in linguistic synthesis with a fuzzy logic controller. Int J Man Mach Stud 7: 1–13. https://doi.org/10.1016/S0020-7373(75)80002-2 doi: 10.1016/S0020-7373(75)80002-2
|
| [43] | Tsukamoto Y (1979) An approach to fuzzy reasoning method. Adv Fuzzy Set Theor Appl 137–149. |
| [44] |
Maier HR, Dandy GC (2000) Neural networks for the prediction and forecasting of water resources variables: A review of modeling issues and application. Environ Modell Softw 15: 101–124. https://doi.org/10.1016/S1364-8152(99)00007-9 doi: 10.1016/S1364-8152(99)00007-9
|
| [45] |
Campolo M, Andreussi P, Soldati A, et al. (1999) River flood forecasting with neural network model. Water Resour Res 35: 1191–1197. https://doi.org/10.1029/1998WR900086 doi: 10.1029/1998WR900086
|
| [46] |
Thirumalaiah KC, Deo M (2000) Hydrological forecasting using neural networks. J Hydrol Eng 5: 180–189. https://doi.org/10.1061/(ASCE)1084-0699(2000)5:2(180) doi: 10.1061/(ASCE)1084-0699(2000)5:2(180)
|
| [47] |
Maier HR, Dandy GC (1997) Determining inputs for neural network models of multivariate time series. Comput-Aided Civ Inf 12: 353–368. https://doi.org/10.1111/0885-9507.00069 doi: 10.1111/0885-9507.00069
|
| [48] |
Legates DR, McCabe GJ (1999) Evaluating the use of "goodness-of-Fit" measures in hydrologic and hydroclimatic model validation. Water Resour Res 35: 233–241. https://doi.org/10.1029/1998WR900018 doi: 10.1029/1998WR900018
|
| [49] |
Sudheer KP, Jain SK, et al. (2003) Radial basis function neural networks for modeling stage discharge relationship. J Hydrol Eng 8: 161–164. https://doi.org/10.1061/(ASCE)1084-0699(2003)8:3(161) doi: 10.1061/(ASCE)1084-0699(2003)8:3(161)
|
| [50] |
Sajikumar N, Thandaveswara B (1999) A non-linear rainfall-runoff model using an artificial neural network. J Hydrol 216: 32–55. https://doi.org/10.1016/S0022-1694(98)00273-X doi: 10.1016/S0022-1694(98)00273-X
|
| [51] |
Luk K, Ball J, Sharma A, et al. (2000) A study of optimal model lag and spatial inputs to artificial neural network for rainfall forecasting. J Hydrol 227: 56–65. https://doi.org/10.1016/S0022-1694(99)00165-1 doi: 10.1016/S0022-1694(99)00165-1
|
| [52] |
Silverman D, Dracup JA (2000) Artificial neural networks and long-range precipitation in California. J Appl Meteorol 39: 57–66. https://doi.org/10.1175/1520-0450(2000)039<0057:ANNALR>2.0.CO;2 doi: 10.1175/1520-0450(2000)039<0057:ANNALR>2.0.CO;2
|
| [53] |
Coulibaly P, Anctil F, Bobee B, et al. (2000) Daily reservoir inflow forecasting using artificial neural networks with stopped training approach. J Hydrol 230: 244–257. https://doi.org/10.1016/S0022-1694(00)00214-6 doi: 10.1016/S0022-1694(00)00214-6
|
| [54] |
Coulibaly P, Anctil F, Bobée B, et al. (2001) Multivariate reservoir inflow forecasting using temporal neural networks. J Hydrol Eng 6: 367–376. https://doi.org/10.1061/(ASCE)1084-0699(2001)6:5(367) doi: 10.1061/(ASCE)1084-0699(2001)6:5(367)
|
| [55] |
Bowden GJ, Dandy GC, Maier HR, et al. (2005) Input determination for neural network models in water resources applications. Part 1—Background and methodology. J Hydrol 301: 75–92. https://doi.org/10.1016/j.jhydrol.2004.06.021 doi: 10.1016/j.jhydrol.2004.06.021
|
| [56] |
Nash JE, Sutcliffe JV (1970) River flow forecasting through conceptual models part Ⅰ—A discussion of principles. J Hydrol 10: 282–290. https://doi.org/10.1016/0022-1694(70)90255-6 doi: 10.1016/0022-1694(70)90255-6
|
| [57] |
Mangukiya NK, Mehta DJ, Jariwala R, et al. (2022) Flood frequency analysis and inundation mapping for lower Narmada basin, India. Water Pract Technol 17: 612–622. https://doi.org/10.2166/wpt.2022.009 doi: 10.2166/wpt.2022.009
|
| [58] |
Alyousifi Y, Othman M, Husin A, et al. (2021) A new hybrid fuzzy time series model with an application to predict PM10 concentration. Ecotox Environ Safe 227: 112875. https://doi.org/10.1016/j.ecoenv.2021.112875 doi: 10.1016/j.ecoenv.2021.112875
|
| [59] |
Mampitiya L, Rathnayake N, Leon LP, et al. (2023) Machine learning techniques to predict the air quality using meteorological data in two urban areas in Sri Lanka. Environments 10: 141. https://doi.org/10.3390/environments10080141 doi: 10.3390/environments10080141
|
| [60] |
Pawar U, Suppawimut W, Muttil N, et al. (2022) A GIS-based comparative analysis of frequency ratio and statistical index models for flood susceptibility mapping in the Upper Krishna Basin, India. Water 14: 3771. https://doi.org/10.3390/w14223771 doi: 10.3390/w14223771
|
| [61] |
Herath M, Jayathilaka T, Hoshino Y, et al. (2023) Deep machine learning-based water level prediction model for Colombo flood detention area. Appl Sci 13: 2194. https://doi.org/10.3390/app13042194 doi: 10.3390/app13042194
|
| [62] |
Mukherjee A, Chatterjee C, Raghuwanshi NS, et al. (2009) Flood forecasting using ANN, neuro-fuzzy, and neuro-GA models. J Hydrol Eng 14: 647–652. https://doi.org/10.1061/(ASCE)HE.1943-5584.0000040 doi: 10.1061/(ASCE)HE.1943-5584.0000040
|
| [63] | Folorunsho J, Obiniyi A (2014) A comparison of ANFIS and ANN-based models in river discharge forecasting. New Ground Res J Phys Sci 1: 1–16. |
| [64] |
He ZB, Wen XH, Liu H, et al. (2014) A comparative study of artificial neural network, adaptive neuro fuzzy inference system and support vector machine for forecasting river flow in the semiarid mountain region. J Hydrol 509: 379–386. https://doi.org/10.1016/j.jhydrol.2013.11.054 doi: 10.1016/j.jhydrol.2013.11.054
|
| [65] |
Jain A, Srinivasulu S (2004) Development of effective and efficient rainfall-runoff models using integration of deterministic, real-coded genetic algorithms and artificial neural network techniques. Water Resour Res 40. https://doi.org/10.1029/2003WR002355 doi: 10.1029/2003WR002355
|
Figures(7) / Tables(2)
Ronak P. Chaudhari, Shantanu R. Thorat, Darshan J. Mehta, Sahita I. Waikhom, Vipinkumar G. Yadav, Vijendra Kumar. Comparison of soft-computing techniques: Data-driven models for flood forecasting[J]. AIMS Environmental Science, 2024, 11(5): 741-758. doi: 10.3934/environsci.2024037
| Sr. No. | Model name | Data (%) | Data (Number) |
| 1 | ANN-1 | 100 | 326 |
| 2 | FUZZY-1 | 100 | 326 |
| 3 | ANFIS-1 | 100 | 326 |
| 4 | ANN-2 | 66 | Latest 217 |
| 5 | ANFIS-2 | 66 | Latest 217 |
| 6 | ANN-3 | 33 | Latest 109 |
| 7 | ANFIS-3 | 33 | Latest 109 |
DownLoad:
CSV
| Sr. No. | Model Name | R2 | RMSE | Percentage Deviation |
| 1 | ANN-1 | 0.9582 | 237.24 | –0.0870 |
| 2 | FUZZY-1 | 0.7769 | 960.88 | +135.0510 |
| 3 | ANFIS-1 | 0.9665 | 211.97 | –0.0013 |
| 4 | ANN-2 | 0.9188 | 219.03 | +1.1341 |
| 5 | ANFIS-2 | 0.9788 | 110.27 | +0.0006 |
| 6 | ANN-3 | 0.9154 | 262.62 | +59.7005 |
| 7 | ANFIS-3 | 0.9855 | 54.23 | +0.0001 |
DownLoad:
CSV
| Sr. No. | Model name | Data (%) | Data (Number) |
| 1 | ANN-1 | 100 | 326 |
| 2 | FUZZY-1 | 100 | 326 |
| 3 | ANFIS-1 | 100 | 326 |
| 4 | ANN-2 | 66 | Latest 217 |
| 5 | ANFIS-2 | 66 | Latest 217 |
| 6 | ANN-3 | 33 | Latest 109 |
| 7 | ANFIS-3 | 33 | Latest 109 |
| Sr. No. | Model Name | R2 | RMSE | Percentage Deviation |
| 1 | ANN-1 | 0.9582 | 237.24 | –0.0870 |
| 2 | FUZZY-1 | 0.7769 | 960.88 | +135.0510 |
| 3 | ANFIS-1 | 0.9665 | 211.97 | –0.0013 |
| 4 | ANN-2 | 0.9188 | 219.03 | +1.1341 |
| 5 | ANFIS-2 | 0.9788 | 110.27 | +0.0006 |
| 6 | ANN-3 | 0.9154 | 262.62 | +59.7005 |
| 7 | ANFIS-3 | 0.9855 | 54.23 | +0.0001 |
