Multi-modal feature fusion with multi-head self-attention for epileptic EEG signals

1.   Introduction

Epilepsy is a chronic brain dysfunction disease caused by a variety of causes, which is typically characterized by repeated and sudden excessive discharge of local neurons in the brain, resulting in central nervous system dysfunction ^[1]. Patients with epilepsy clinically exhibit symptoms such as muscle convulsions and loss of consciousness. Repeated seizures result in brain cell death, impairment of brain function, and life-threatening situations in severe cases. Furthermore, epilepsy imposes a significant burden on the patients' families and society. EEG plays an irreplaceable role in the diagnosis and treatment of epilepsy ^[2]. It has served as a crucial tool for clinical monitoring and diagnosis of epilepsy, offering a swift, reliable, cost-effective, and non-invasive technique to observe cerebral cortex brain activity ^[3]. Therefore, it is of great significance to study the prevention and treatment of epilepsy with EEG.

Traditional feature extraction for EEG signals was inefficient due to the differences in the subjective experience of experts. Consequently, the automatic detection of epileptic EEG signals is one of the hot issues in biomedical research ^[4]. Boashash et al. ^[5] classified and recognized neonatal epileptic EEG signals by comprehensively analyzing the statistical, image, and signal features in the time-frequency domain. On the other hand, nonlinear dynamic analysis methods mostly included signal sample entropy (SEn), approximate entropy, information entropy, and Lempel-Ziv complexity metric analysis ^[6], which are often combined with time-frequency domain features in classification. Sabeti et al. ^[7] classified epileptic EEG signals from patients and normal subjects by feature vectors comprising SEn, approximate entropy, and Lempel-Ziv complexity. The method of automatic detection of epilepsy not only helps doctors to improve the accuracy of epilepsy diagnosis but also greatly saves the diagnosis time, which was of great significance for the prevention, diagnosis, and treatment of epilepsy.

In recent years, machine learning has become popular with advances in computing and has been widely used in epilepsy recognition ^[8]. Researchers have tried to diagnose EEG signal features by machine learning. Extracting relevant features from the signals is the key to successfully diagnosing epilepsy. Whether it is manual extraction of a single-modal feature, manual extraction of multiple features, or automatic extraction of features by deep learning, their common purpose is to obtain more information about EEG signals ^[9], and the richness of such information is very important for in-depth understanding and analysis of EEG signals. Sharmila et al. ^[10] converted EEG signals into spectral images, but the experimental results were not satisfactory. The main reason was that a single convolutional neural network model extracts only the frequency domain and spatial domain features of EEG signals, ignoring the time domain features of EEG signals, resulting in poor classification performance. Brain activity is a time-dynamic process, and learning temporal evolution from EEG time series is important. Seal et al. ^[11] presented a deep mixing model with a convolutional neural network and a bidirectional short-duration memory network to extract frequency information and sequence relationships from signals. The proposed model, integrating convolutional neural networks and bidirectional short-term memory networks, efficiently extracts frequency information and sequence relationships from signals. However, when dealing with one-dimensional time series, its final classification accuracy (ACC) is unsatisfactory, and it may face challenges such as high computational complexity and overfitting. This model inputs only a one-dimensional chain time series into the classifier, and the final ACC is unsatisfactory.

The self-attention mechanism weighs input data parts, emphasizing those most influential on the output. This approach assigns higher weights to key inputs, amplifying their impact within the network ^[12]. Today, self-attention is a pivotal concept in deep learning and is widely applied in EEG signal classification ^[13]. Zheng et al. ^[14] introduced an attention-based bidirectional short-term memory network for visual classification. It utilizes self-attention to identify critical EEG segments, thereby enhancing visual processing accuracy. It identifies critical EEG segments via self-attention to enhance a visual ACC. However, it may require extensive training data and resources and faces risks of overfitting and longer training time. Zhang et al. ^[15] simplified the temporal scale by one-dimensional convolution. They combined a bidirectional long short-term memory network with self-attention for arousal-based binary classification, resulting in reduced complexity and improved performance. However, the method relies on sufficient labeled data for effective training. Kim et al. ^[16] combined a long short-term memory network with self-attention to analyze EEG signals and conduct binary classification based on titer and arousal, achieving a good ACC. However, the method may demand substantial labeled data and has a relatively high computational cost. Chang et al. ^[17] employed 3D convolutional neural networks to extract deep EEG features and leveraged dual attention to enhance them, resulting in improved performance. However, the approach comes with higher computational costs and data requirements. Traditional methods extract single-modal features without preserving the structure of EEG signals in the dimensions, time, frequency, and nonlinear kinematics and do not reach the ideal state in multiple classification tasks.

To address the aforementioned challenges, we proposed a multi-modal feature fusion (MMFF) method leveraging a multi-head self-attention mechanism to extract a time domain, frequency domain, and nonlinear dynamic features from epileptic EEG signals. Specifically, the obtained resting EEG signals were preprocessed to extract time series. Second, the time domain features of EEG were extracted by Gaussian kernel principal component analysis (GPCA), while the frequency domain features were extracted by short-time Fourier transform (STFT). Additionally, the nonlinear dynamic features were extracted by SEn. Then, the features of the three modalities were interactively learned by the multi-head self-attention mechanism, and the attention weights were trained. The fused features were derived by amalgamating the value vectors of feature representations, which transform an optimal model and introduce an L₁ norm regularization term.

The major contributions of this study are summarized as follows:

(a) The multi-head self-attention mechanism fused the time domain, frequency domain, and nonlinear dynamic features derived from epileptic EEG signals. Additionally, the introduction of the L₁ norm regularization term served to decrease model complexity, bolster robustness, and mitigate the risk of overfitting.

(b) We explored the variation trends of several parameters in different GPCA, including the bandwidth of the Gaussian kernel function, STFT window length and step size, SEn window length, overlap rate, threshold, and the number of multi-head attention mechanisms.

(c) We examined how these parameters, along with L₁ norm regularization, affected the classification performance of epilepsy patients. Through this comprehensive investigation, an optimal parameter combination was identified, achieving an ACC of 92.76 ± 1.64%.

2.   Materials and methods

2.1.   Research framework

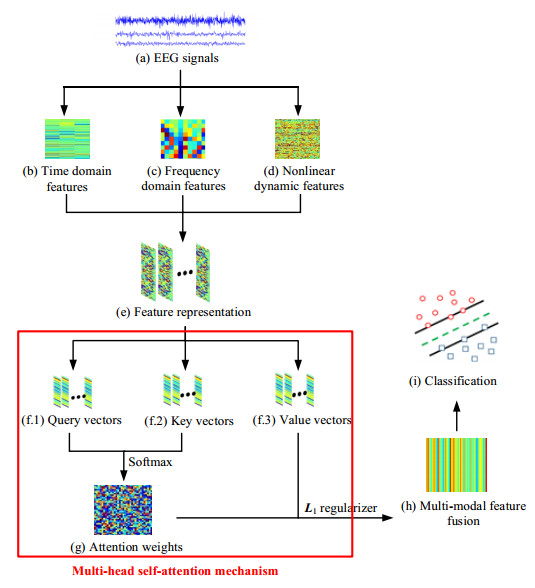
Figure 1 shows the framework diagram. The specific steps are as follows: (a) Preprocess resting epileptic EEG signals to extract time series data; (b) Extract the time domain features of EEG by GPCA and then calculate their self-attention scores and generate the corresponding output; (c) Extract the frequency domain features of EEG by STFT, calculate their self-attention scores, and produce the associated output; (d) Extract the nonlinear dynamic features of EEG by Sen and then calculate their self-attention scores and generate the corresponding output; (e) Derive the feature representation by fusing the self-attention outputs from the three modal features; (f) Obtain the query vector, key vector, and value vector through a linear transformation to the feature representation; (g) Determine the normalized attention weight by scaling the dot product of the query and key vectors, followed by Softmax function; (h) Generate fused features by combining the value vectors of feature representations and then transform them into optimization models with the introduction of L₁ norm regularization terms; and (i) Diagnose epilepsy by the fused features, enabling assessment of classification performance.

Figure 1.  Research framework.

DownLoad: Full-Size Img PowerPoint

2.2.   Data sources

The experimental data was sourced from a widely used epileptic EEG dataset provided by the University of Bonn, Germany (http://epileptologie-bonn.de/cms/upload/workgroup/lehnertz/eegdata.html). The dataset was divided into five subsets from Set A to Set E, with each subset containing 100 samples of the same type and each sample containing 4096 EEG time series. The data sampling frequency was 173.61 Hz, and the duration was 23.6 s. The artifacts had been removed by manual filtering. Set A and Set B were collected from 5 healthy subjects with open and closed eyes, respectively. The Set C and Set D were collected outside the focal area and in the focal area of 5 patients, respectively. Set E was collected from focal areas during the seizure. The Set C, Set D, and Set E subsets were recorded by tape electrodes implanted in the skull and affixed to the surface of the hippocampus. Among them, Set E and Set D were recorded by attaching a strip electrode to the lesion area of the hippocampus structure, and Set C was recorded by attaching a strip electrode to the hippocampus structure of the other brain hemisphere outside the lesion area. Table 1 shows the details.

Table 1.  Details of the Bonn dataset.

Data subset	A	B	C	D	E
Subject	Five healthy volunteers		Five patients with epilepsy
Subject status	Open-eyed	Close-eyed	Interparoxysmal		Paroxysmal
Recording period	Normal		Epileptic interval		Epileptic phase
Electrode type	Non-invasive surface		Intracranial
Electrode arrangement	International 10-20 standard system		Hippocampus structure	Lesion	All seizures

---

 | Show Table

DownLoad: CSV

2.3.   Feature extraction

The features of EEG signals are mainly derived from time domain, frequency domain, time-frequency domain, and nonlinear dynamics ^[18,19,20].

The time domain features were extracted by GPCA ^[21]. GPCA first maps EEG signals to a high-dimensional feature space and then applies principal component analysis for dimensionality reduction. For M samples ${x_1}, {x_2}, ..., {x_M}$ in the input space, each of them is a d-dimensional vector. The similarity matrix K between samples was calculated by the Gaussian kernel function. Calculate the centralized matrix H, whose expression is:

where I is the identity matrix and E is a n-dimensional one-all matrix.

Calculate the centralized similarity matrix K', and its expression is as follows:

The eigenvalue decomposition of the centralized similarity matrix K' was carried out to obtain the eigenvalue and eigenvector. The eigenvector corresponding to the first k largest eigenvalues was selected as the principal component. The projection of all the samples onto k principal components forms a new eigenmatrix ${\boldsymbol{Z}} = {[{z_1}, {z_2}, ..., {z_M}]^T}$, as time domain features.

The frequency domain features were extracted by STFT ^[22]. STFT decomposes EEG signals into components of different frequencies to obtain the amplitude spectrum and phase spectrum within each time window. These features facilitated the description of EEG signals' energy distribution and frequency features across various frequencies.

Set the original EEG signal as x(t), sampling frequency as f_s, time window length as L_s, and time window move step as s. For each time window, the amplitude spectrum and phase spectrum after STFT are calculated. Frequency domain feature ${\boldsymbol{X}} \in {{\boldsymbol{R}}^{{N_t} \times F}}$, where N_t is the number of time windows and F is the frequency resolution of the amplitude spectrum. The specific STFT expression is as follows:

where x(n) is the original EEG signal, w(n-m) is the window function, w is the frequency, m is the time shift factor, and N_t is the number of time windows.

For each time window, set its starting time as t_i, and calculate its amplitude spectrum A(k, i) and phase spectrum P(k, i) at k as follows:

where $| \cdot {|_k}$ represents the module of the kth frequency component of the STFT calculation result, and $\arg {(\cdot)_k}$ represents the angle of the kth frequency component of the STFT calculation result. ${x_{{t_i}}}[n]$ represents a time window of length L_s from time t_i.

Finally, the amplitude spectra of all time windows are splicing together to form the frequency domain feature X, and the ith row is the amplitude spectrum of the ith time window, namely $X(i, k) = A(k, i)$.

The nonlinear dynamic features were extracted by SEn ^[23]. The algorithm requires a small amount of data and takes less time ^[24]. The time series T is divided into m subsequences of length L_e, and the overlap rate is set as R.

The frequency of occurrence is calculated for each subsequence. The similarity between two subsequences is measured according to a distance metric. Calculate the occurrence frequency p:

where ${{\boldsymbol{T}}_i}$ represents the ith sub-sequence, and $C_m^2$ represents the number of 2-combinations from a set with m distinct sequences, that is, $C_m^2 = \frac{{m(m - 1)}}{2}$. r stands for a threshold to determine whether two subsequences are similar, where $[d({{\boldsymbol{T}}_i}, {{\boldsymbol{T}}_j}) < r]$ represent 1 for $d({{\boldsymbol{T}}_i}, {{\boldsymbol{T}}_j}) < r$ and 0 otherwise.

Then, the nonlinear dynamic feature S is concretely expressed as:

Nonlinear dynamic feature ${\boldsymbol{S}} \in {{\boldsymbol{R}}^{M \times N}}$ varies with the window length L_e and the threshold r. In a specific research environment, the parameter setting is certain, where M represents the number of samples and N represents the dimension of nonlinear dynamic features. In general, r ∈ 0.1·std~0.25·std, where std represents the standard deviation of a given time series.

2.4.   Feature fusion

The self-attention mechanism ^[25] is applicable to situations where there are complex and nonlinear dependencies between different modalities and can improve the performance and expressiveness of the fused features, which will contain cross-modal information ^[26].

(a) Calculate query vector ${{\boldsymbol{Q}}_T} = {\boldsymbol{Z}}{{\boldsymbol{W}}_{QT}}$, key vector ${{\boldsymbol{K}}_T} = {\boldsymbol{Z}}{{\boldsymbol{W}}_{KT}}$ and value vector ${{\boldsymbol{V}}_T} = {\boldsymbol{Z}}{{\boldsymbol{W}}_{VT}}$, where ${{\boldsymbol{W}}_{QT}}, {{\boldsymbol{W}}_{KT}}, {{\boldsymbol{W}}_{VT}} \in {{\boldsymbol{R}}^{T \times d}}$ are the weight matrixes and d is the hidden layer dimension. Calculate query vector ${{\boldsymbol{Q}}_F} = {\boldsymbol{X}}{{\boldsymbol{W}}_{QF}}$, key vector ${{\boldsymbol{K}}_F} = {\boldsymbol{X}}{{\boldsymbol{W}}_{KF}}$ and value vector ${{\boldsymbol{V}}_F} = {\boldsymbol{X}}{{\boldsymbol{W}}_{VF}}$, where ${{\boldsymbol{W}}_{QF}}, {{\boldsymbol{W}}_{KF}}, {{\boldsymbol{W}}_{VF}} \in {{\boldsymbol{R}}^{F \times d}}$ are the weight matrixes and d is the hidden layer dimension. Calculate query vector ${{\boldsymbol{Q}}_N} = {\boldsymbol{S}}{{\boldsymbol{W}}_{QN}}$, key vector ${{\boldsymbol{K}}_N} = {\boldsymbol{S}}{{\boldsymbol{W}}_{KN}}$ and value vector ${{\boldsymbol{V}}_N} = {\boldsymbol{S}}{{\boldsymbol{W}}_{VN}}$, where ${{\boldsymbol{W}}_{QN}}, {{\boldsymbol{W}}_{KN}}, {{\boldsymbol{W}}_{VN}} \in {{\boldsymbol{R}}^{N \times d}}$ are the weight matrixes and d is the hidden layer dimension.

(b) Calculate the attention score AT and output OT of time domain features. Calculate attention score AF and the output OF for frequency domain features. Calculate attention score AN and output ON for nonlinear dynamic features. The attention scores A and the output O are respectively expressed as:

where Q is the query vector, K is the key vector, and V is the value vector.

(c) Integrate self-attention output ${\boldsymbol{O}} \in {{\boldsymbol{R}}^{M \times (T + F + N)}}$ to get the feature representation:

Calculate the query vector ${\boldsymbol{Q}} = {\boldsymbol{O}}{{\boldsymbol{W}}_Q}$, the key vector ${\boldsymbol{K}} = {\boldsymbol{O}}{{\boldsymbol{W}}_K}$ and the value vector ${\boldsymbol{V}} = {\boldsymbol{O}}{{\boldsymbol{W}}_V}$, where ${{\boldsymbol{W}}_Q}, {{\boldsymbol{W}}_K}, {{\boldsymbol{W}}_V} \in {{\boldsymbol{R}}^{(T + F + N) \times d}}$ are the weight matrixes and d is the hidden layer dimension.

(d) Enable the model to simultaneously participate and process diverse information from various subspaces to enhance its expression and ability to handle complex tasks. Q, K, and V are split into h heads, each with dimension d/h, and an independent self-attention calculation is performed for each head. Specifically, for each head i, calculate its attention score A_i and the corresponding attention output O_i:

Splice together the attention output O_i of all heads to obtain the final feature fusion matrix Y through a layer of the linear transformation:

where ${{\boldsymbol{W}}_Y} \in {{\boldsymbol{R}}^{d \times {d_Y}}}$is the weight matrix, and d_Y is the dimension of the final output feature fusion.

(e) Introduce the L₁ norm regular term to reduce model complexity, increase robustness, and avoid overfitting. The objective function with a square loss is expressed as:

where ${Y_{\boldsymbol{i}}}$ is the real feature, ${\widehat Y_{\boldsymbol{i}}}$ is the feature predicted by the model, M is the sample size, and ${\boldsymbol{λ }}$ is the weight of the regularization term of the L₁ norm.

Update the weight matrixes ${{\boldsymbol{W}}_Q}, {{\boldsymbol{W}}_K}, {{\boldsymbol{W}}_V}, {{\boldsymbol{W}}_Y}$ by backpropagation algorithm to minimize the objective function in the training process ^[27]. The objective function enabled the model to learn the feature mapping Y and control the sparsity of the features by regularization terms. We measured the square of the Euclidean distance between the predicted and real features by square loss.

3.   Experiment and analysis

We extracted the time domain, frequency domain, and nonlinear dynamic features of EEG by GPCA, STFT, and SEn, respectively. The features of these three modalities were fused by the multi-head self-attention mechanism, and L₁ norm regular term was introduced. In the implementation of STFT, the attention weights were calculated by Hamming window function ^[28] and Softmax function ^[29]. Additionally, the L₁ norm was resolved through the gradient descent algorithm ^[30]. The proposed method was verified by leave-one cross-validation due to the limited EEG samples. Ten repeated experiments were conducted to obtain the average value. The classification performance was assessed according to the ACC index ^[31]. The influence of different parameters on the classification performance was first discussed to verify the classification performance of fused features, and the optimal parameters were determined by a one-to-many strategy for multi-category classification and then compared with other feature extraction methods ^[32].

3.1.   Parameter selection

The proposed method comprises multiple parameters. The mesh search method cannot find the optimal parameters directly. The optimal parameter values were systematically determined through a sequential process. (a) Determine the bandwidth $\sigma$ of the Gaussian kernel function. (b) Set the window length L_s and step size s. (c) Establish the window length L_e, overlap rate R, and threshold r. (d) Finalize the number of heads h and the L₁ norm regularization parameter λ. The optimal classification model was formed by the EEG training set, and the model was assessed using the test set. The average of the test results was calculated to assess the model's performance. Multiple iterations of model training were conducted to ascertain the optimal hyperparameter. Subsequently, the model employing the optimal hyperparameter underwent testing with the original sample.

GPCA has demonstrated superior performance in EEG analysis, thus justifying its selection for this task ^[33]. It differs from traditional principal component analysis in that it does not directly obtain a fixed number of principal components. The input data is mapped to a high-dimensional feature space by the Gaussian kernel function. Then, the eigenvector of the covariance matrix in the feature space is calculated as the kernel principal component. Since there were only 100 samples per class, we considered choosing a smaller Gaussian kernel bandwidth to avoid overfitting ^[34]. Accordingly, the σ was set from 1 to 10, and ACCs of different σ were compared, as shown in Figure 2.

Figure 2.  ACCs of GPCA with different σ.

DownLoad: Full-Size Img PowerPoint

It is observed from Figure 2 that σ has a great impact on the model performance and determines the similarity of the data in the feature space. As σ increased from 1 to 10, the accuracy of the five-category classification increased gradually, reaching a peak and gradually declining. Specifically, when σ increased from 1 to 5, ACCs increased from 65.4% to 80.2%, indicating that increasing σ helped improve ACCs in this interval. While σ increased to 6 and above, ACCs gradually declined, decreasing from 79.4% to 76.2%. With GPCA, σ controlled the "smoothness" between points mapped into a high-dimensional feature space. Smaller σ meant that the points in the high-dimensional space were more dispersed, leading the model to focus too much on details and noise in the training data, i.e., overfitting.

Conversely, larger σ caused the mapped points to be more concentrated, leading the model to fail to capture important features from epileptic EEG signals, that is, underfit. ACCs increased first and then decreased with the increase of σ, indicating an optimal σ range. In this range, the model balanced the deviation and variance well and achieved a higher ACC. When σ was 5, the model reached the highest accuracy of 80.2%. This may indicate that the model complexity at this σ setting is moderate enough to capture key features from epileptic EEG signals without being too affected by noise.

L_s is usually chosen as the power of 2 to obtain better computational efficiency when performing a fast Fourier transform.s is usually set to half L_s or 1/4 of L_s ^[35]. Since there were only 100 samples per category, we considered choosing a smaller L_s and s to retain more time and frequency detail. On that basis, L_s was set to 32, 64,128,256, and s was set to 4, 8, 16, and the ACCs when different L_s s were compared, as shown in Figure 3.

Figure 3.  ACCs of STFT with different L_S and s.

DownLoad: Full-Size Img PowerPoint

It is observed from Figure 3 that when L_s was short (such as 32), ACCs were greatly affected by s to some extent, and ACCs ranged from 56.6% to 73.8%. This suggests that shorter L_s may be sensitive to time resolution, but have lower frequency resolution. When L_s was medium (e.g., 64), a significant increase was observed, especially when s was 8, and the ACCs reached up to 82.5%. This suggests that a moderate L_s may provide a better time-frequency resolution balance. For longer L_s (such as 128 and 256), the ACC changes were more complex, and the overall trend showed that the maximum ACC decreased as L_s increased. This could be attributed to the fact that although a longer L_s enhances frequency resolution, it compromises time resolution, impeding the ability to capture dynamic shifts from epileptic EEG signals accurately. For a given L_s, a shorter s (e.g., 4) yielded better or relatively stable ACCs. This could be attributed to the increased overlap in time, which allows for a more detailed capture of the signal. Conversely, a longer s (e.g., 16) often leads to a lower ACC in most cases. This decline in performance might be due to the reduced time coverage, potentially resulting in the omission of crucial time-frequency information.

It is commonly recommended that L_e be set to a power of 2 during EEG signal processing when extracting nonlinear dynamic features of EEG by SEn. This ensures improved computational efficiency when carrying out fast calculations. The advantage of SEn in capturing local features was reflected by setting the overlap rate R, thereby preserving a richer array of time and frequency details. R chooses a value between 0.5 and 0.9. r thresholds SEn to extract nonlinear dynamic features. Generally, r ranges from 0.1·std to 0.25·std ^[36], where std represents the standard deviation of a given time series. It is advisable to opt for a shorter L_e and a higher overlap rate When working with a limited dataset of 100 samples per category. This approach helped to retain a greater amount of temporal and frequency detail. Then, L_e was set to 32, 64,128,256, R was set to 0.6, 0.7, 0.8, 0.9, and r was set to 0.1·std, 0.15·std, 0.2·std, 0.25·std, and the ACCs of the combination of different L_e, R and r were compared, as shown in Figure 4.

Figure 4.  ACCs of SEn with different L_e, R, and r.

DownLoad: Full-Size Img PowerPoint

It is observed from Figure 4 that when L_e was 64, the ACC was generally higher with the change of R and r, especially when R was 0.8 and r was 0.15·std, reaching the highest ACC of 82.6%. ACCs decreased slightly when L_e increased to 128, suggesting that a shorter L_e may be better suited to capturing dynamic changes in epileptic EEG signals. As L_e was further increased, ACCs decreased even more, particularly when L_e reached 256, leading to a significant reduction in ACCs. This decline could be explained by the fact that a longer L_e decreased the temporal resolution, thereby impeding the effective capture of rapid changes in epileptic EEG signals. Under each L_e setting, ACCs generally increased first and then stabilized or slightly decreased with the increase of R. This suggests that appropriately increasing R can aid in enhancing ACCs. The reason for this improvement lies in the fact that a higher R offers a more extensive data sample, enabling a more detailed capture of signal changes. When R was high (e.g., 0.8), the ACC reached its highest at shorter L_e (e.g., 64). This emphasizes improving the efficiency of feature extraction by increasing R while maintaining a high temporal resolution. The influence of r variations on ACCs exhibits complexity, lacking a discernible universal trend. This complexity can be attributed to the fact that selecting an appropriate r is intricately tied to the inherent dynamic features of epileptic EEG signals. Consequently, an apt r is crucial for distinguishing signals corresponding to different states. The ACC reached its peak when r was set to 0.15 std in certain scenarios, such as when L_e was set to 64, and R was 0.8. This finding suggests that, under these settings, r is optimally suited to the characteristics of the current dataset. This ensures accurate SEn calculation results by limiting the similarity between subsequences and mitigating the influence of noise or other interfering factors.

The multi-head attention mechanism can extract the feature representation of different attention weights to enhance the expression ability of the model; thus, the number of heads h was usually set to a value between 2 and 8 ^[37]. The introduction of L₁ norm regular term makes the model learn sparse feature representation to improve the model's generalization performance. The L₁ norm regularization parameter λ controls how much the regularization term affects the overall loss function, and it is usually set to a value between 0.0001 and 0.1 ^[38]. Since there were only 100 samples per class, h was set to 4, 5, 6, 7, 8, and the value range of λ was set to [2^–5, 2^–3]. They provided sufficient model complexity while avoiding excessive computational burden. We compared the values of ACCs obtained from various combinations of h and λ, as shown in Figure 5.

Figure 5.  ACCs of multi-head self-attention mechanism with different h and λ.

DownLoad: Full-Size Img PowerPoint

When h was 4, ACCs increased somewhat (from 71.4% to 85.0%). λ increased from 2^–5 to 2^–4 but decreased (72.4%) when it was further increased to 2^–3. Smaller regularization parameters may assist the model in better retaining crucial features, whereas substantial regularization parameters have the potential to cause the model to discard an excessive amount of information. When h was 5, ACCs fluctuated in the range from 2^–5 to 2^–3. The highest ACC occurred when the parameter combination was 5-headers and 2^–4 regularized parameters (90.8%), which may be a more desirable combination. The ACC was higher overall when h was 6, and better results were achieved under different regularization parameters. The highest ACC (92.7%) occurred when the parameter combination was 6-head and 2^–4 regularized parameters, indicating that the combination positively impacts the fusion of the time domain, frequency domain, and nonlinear dynamics features. ACCs were generally low when h was 7 and 8, especially when the regularization parameter was 2^–4, and ACCs decreased significantly. An excessive number of heads might result in model complexity or overfitting, explaining the observed performance decline.

To sum up, $\sigma$ was set to 5, L_s was 64, s was 8, L_e was 64, R was 0.8, r was 0.15·std, h was 6, and λ was 2^–4.

3.2.   Comparative experiment

The proposed MMFF method was compared with the out-of-state feature extraction methods for epileptic EEG signals. Ten repeated experiments were conducted to get the average value from leave-one-out cross-validation. Specific methods included fast Fourier transform (FFT) ^[39], wavelet transform (WT) ^[40], mutual correlation power spectral density (RPSD) ^[41], genetic process-based feature extraction system (GPF) ^[42], power spectral density (PSD) ^[43], time-frequency analysis (TFA) ^[44], time-frequency analysis and approximate entropy (TFAE)^[45], and time-frequency domain and spatial feature fusion (TFSF) ^[46]. Table 2 presents the mean ACCs, specificity (SPE), sensitivity (SEN), and respective variance for the five-category classification for epileptic EEG signals.

Table 2.  ACCs of different feature extraction methods.

Dataset	Feature extraction method	Classification method	ACC (%)	SPE(%)	SEN(%)
Set A, Set B, Set C, Set D, Set E	FFT	Decision tree	81.32 ± 3.46	80.02 ± 2.51	82.55 ± 3.04
	WT	Artificial neural network	82.74 ± 2.85	82.61 ± 2.01	83.69 ± 2.53
	RPSD	SVM	83.17 ± 1.55	83.52 ± 1.50	83.44 ± 2.08
	GPF	K-nearest neighbor classifier	78.44 ± 4.28	77.83 ± 3.58	79.48 ± 4.02
	PSD	Gaussian mixture model	86.53 ± 2.62	86.07 ± 2.05	87.09 ± 2.51
	TFA	Artificial neural network	88.21 ± 2.06	88.67 ± 1.53	88.57 ± 1.84
	TFAE	SVM	85.64 ± 1.47	85.32 ± 1.01	86.06 ± 1.53
	TFSF	SVM	89.59 ± 2.13	89.66 ± 1.53	90.83 ± 2.09
	MMFF	SVM	92.76 ± 1.64	92.51 ± 1.73	93.28 ± 1.57

---

 | Show Table

DownLoad: CSV

It is found in Table 2 that different feature extraction methods have a significant impact on ACCs. The ACC (89.59 ± 2.13%) was achieved by TFSF with a support vector machine (SVM) classifier, and 88.21 ± 2.06% was achieved by TFA with an artificial neural network classifier. This indicates that time-frequency domain features or their fusion positively affect epileptic EEG signal classification. The ACC of TFAE achieved 85.64 ± 1.47%, but the ACC with an artificial neural network classifier may not be optimal. The SVM classifier achieved high ACCs in multiple feature extraction methods, which showed that it had good robustness and generalization abilities for epileptic EEG signal classifications. MMFF achieved the highest ACC (92.76 ± 1.64%), indicating that the method had a good classification performance for the extracted features. There were complex interactions between feature extraction methods and classification methods. TFSF attained a high ACC, while other classifiers may not have exhibited optimal performance. This underscores the importance of considering the compatibility between feature extraction methods and the features of specific tasks when choosing them. It is crucial to identify the most suitable combination to ensure optimal performance.

4.   Discussion

Epileptic EEG signals contain a wealth of information when processing biomedical signals. However, this information is often complex and multi-modal. The time domain features were extracted by GPCA to convert the original epileptic EEG signals into a smaller feature subspace with higher differentiation, such as mean value and standard difference. The frequency domain features were extracted by STFT to convert the epileptic EEG signals into the energy distributions at different frequencies, including the power spectral density and the phase of EEG signals. The nonlinear dynamic features were extract by SEn to assesse the complexity and irregularity of epileptic EEG signals, such as self-similarity and complexity.

The MMFF method significantly increased the ACC in epileptic EEG signals classification tasks, reaching 92.76 ± 1.64%. This method verifies that the multi-head self-attention mechanism can effectively learn the time, frequency, and nonlinear dynamic features interactively to better capture the multi-modal features from epileptic EEG signals. In this method, the features of these three modallities were fused to better integrate the information of different modalities and retained the time, frequency, and nonlinear dynamic features of epileptic EEG signals. This strategy improved the robustness and accuracy of feature extraction for epileptic EEG signals.

The proposed method obtained satisfactory results, but some limitations remained. For example, experimental datasets' limited size and origin may affect the model's ability to generalize. Future considerations include expanding the dataset size and further validating the model's applicability across a broader spectrum of scenarios. The calculation time of the model was too long, and each experiment lasted 5 days. We intend to refine the model structure, enhance feature extraction techniques, and investigate more efficacious epileptic EEG signal processing methods. In addition, our model lacks interpretability and requires the integration of clinical data and expert insights from real-world medical settings. In the future, we will advance the feature extraction of epileptic EEG signals in clinical practice to improve acceptability for medical professionals and patients. With a multi-head self-attention mechanism, the result is not perfect yet, so new deep learning methods will be used in the future to improve classification performance ^[47,48]. The available public data was preprocessed without significant noise. In the future, we will explore the sensitivity of the model to noise in EEG data or its performance at different data qualities.

5.   Conclusions

We developed an MMFF method to improve epileptic EEG signal feature classifications. Different modalities of features were extracted from a time domain, frequency domain, and nonlinear dynamics, respectively. These features were interactively learned through the multi-head self-attention mechanism, thereby acquiring attention weights among them. The fused features preserve the time, frequency, and nonlinear dynamics information of epileptic EEG signals to screen out more representative epileptic features. Experimental results show that the proposed method achieves better results for the five-category classification task. This proves the superiority and feasibility of this model in feature extraction. Introducing MMFF with a multi-head self-attention mechanism demonstrated superior performance in the five-category classification task. This study provides a compelling new method in the field of feature extraction for epileptic EEG signals and provides a reference for the diagnosis and treatment of epilepsy.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by National Natural Science Foundation of China (grant No. 51877013), and Jiangsu Provincial Key Research and Development Program (grant No. BE2021636). This work was also sponsored by Qing Lan Project of Jiangsu Province.

Conflict of interest

The authors declare there is no conflict of interest.