Processing and interpretation of magnetic data in the Caucasus Mountains and the Caspian Sea: A review

1.   Introduction

Magnetic prospecting is one of the most productive and cheapest geophysical methods. It does not require a field source. Modern magnetometers are lightweight and allow mobile movement even in very rough terrain. Cesium magnetometers measure the magnetic field with an accuracy of one picoTesla and are stable even at very high magnetic field gradients.

Magnetic prospecting is not only included in complexes of geophysical methods for solving various problems (from studying the deep structure of the Earth's crust on continents and oceans to searching and exploring ore bodies and archaeological objects) but is also often an independent method of geological-geophysical research ^[1,2,3,4]. Using magnetic survey equipment on uncrewed aerial vehicles (considering the high possible frequency of magnetic field measurements—5000 measurements per second or more) allows for the uniform study of large areas quickly.

Modern equipment makes it possible to detect even very weak magnetic anomalies (for example, to differentiate sedimentary rocks or detect pyrite-polymetallic ores). However, as the measurement accuracy increases, the influence of various interferences that complicate the geological interpretation of magnetic survey results also increases.

Traditionally, the methodology for interpreting magnetic anomalies has been based on vertical magnetization. In this case, there is no need to consider the vector nature of magnetic properties. However, in natural conditions, vertical magnetization is the exception (typical only for high latitudes of the Earth) rather than the rule. In Azerbaijan, the average magnetic field inclination is about 58.5°. The ubiquitously developed remanent magnetization, generally oriented arbitrarily relative to the modern magnetic field, further limits the possibility of using the apparatus to interpret magnetic anomalies developed for vertical magnetization. Another essential factor complicating the interpretation of magnetic data is the rugged terrain. Finally, the variety of anomalies of various orders (especially in mountainous areas) does not enable the assessment of the level of the normal field, which is vital in many interpretation procedures.

This article discusses the primary interference during high-precision magnetic surveys and ways to eliminate it. The multi-stage process of interpreting magnetic data is presented, starting with considering time variations and ending with constructing the research object's physical-geological model (PGM). Considering the complex nature of magnetic fields, a combination of probabilistic and deterministic approaches is proposed. Particular attention is paid to methods for quantitative analysis of magnetic anomalies (improved tangent, characteristic point, and areal methods) in conditions of inclined magnetization, rugged terrain relief, and unknown normal field levels.

2.   Formation of the initial model of the medium

An initial medium model should be created, in one form or another, when drawing up a project for magnetic research in a specific area to solve the problem. This allows the selection of the scale of the study and the type of magnetic survey (ground-based, using uncrewed aerial vehicles, or a combined approach) and provides an interpretation methodology. The methodology can be refined as necessary before starting the interpretation process. The stage of forming the initial model of the environment is critical since the final success of the interpretation, and the entire study, largely depends on its optimal implementation.

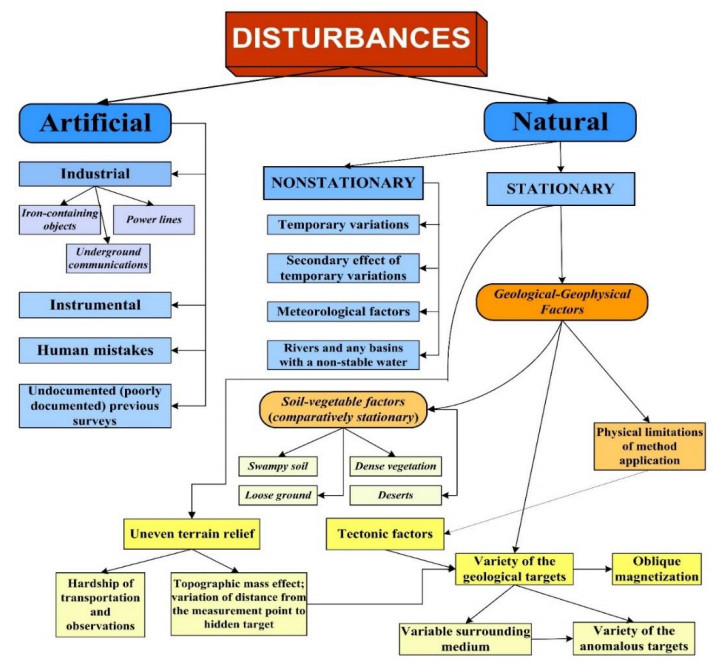
Any rock magnetic model must satisfy two generally contradictory requirements: (1) reflect the essential characteristics (features) of the desired object, and (2) be simple enough to enable its practical use. The petromagnetic (physical-geological) model is a generalized and formalized model of the target of study and its host rocks. The background against which the research object appears is no less important than the target itself and must be considered in the environmental model with the same detail. In addition, the model must consider the manifestations of various complications (the most typical interferences that arise during detailed magnetic studies are shown in Figure 1).

The characteristics of geological environments in open (single-tier) areas indicate the advisability of using stochastic models in many cases. However, when examining observed magnetic fields as random functions, it is essential to consider that they may exclude regular components of a pulsed or periodic nature. Suppose we discard the tasks associated with mapping the territory according to the statistical characteristics of the magnetic field, which are considered random. In that case, a large group of significant geological problems remains, based on isolating the regular component from its combination with the noise of various natures. This component may correspond to a magnetized gabbroic or weakly magnetic acidic intrusion, a zone of hydrothermal alteration, a skarn-magnetite or pyrrhotite-containing lens, etc.

The regular magnetic field component can only be identified by specifying certain model concepts. Research objects such as considerable ore bodies are usually rare, and their statistical characteristics are challenging to determine. Therefore, it is necessary to apply a specific method for processing and interpreting the results of geomagnetic research, which makes it possible to isolate the desired anomalies from a mixture of anomalies and interference based on a deterministic approach to the object being studied (the desired anomaly) and a probabilistic approach to all other features of the environment and geophysical observations considered as interfering factors (interference).

The deterministic study of objects of magnetic research is enabled by the possibility of geometric approximations of objects divided into the main classes being studied (Table 1).

3.   Petrophysical support

The data sources for petrophysical support are primarily the rock magnetic map and rock magnetic sections (if available). Rock magnetic data from core samples and deep mine workings are critical since regular surface changes do not distort them. The most excellent weight should be given to determining magnetic properties based on materials comparing the observed magnetic field with an available geological section.

In the absence of rock magnetic properties in the work area (which should generally be an exception), information is used on the magnetic properties of rocks in the neighboring regions and objects like the object of study, including those obtained from interpretation results. All home media and local geological targets, including ore bodies, must have average values of magnetic parameters with certainty intervals. The same relates to the altered rock zones.

When constructing a rock magnetic model, it is advisable to calculate the magnetization of individual structural and formation complexes using the available geological information. However, the information must satisfy the recognized section's petro- and paleomagnetic data. After this, a model based on rock-magnetic characteristics is generated. The weighted average magnetization values for specific rock complexes are obtained and combined with the magnitude of magnetic properties or magnetization direction (within one paleomagnetic zone). When calculating the weighted average values of the igneous rocks's magnetization, it may be helpful to use the explosiveness coefficient (the ratio in the context of the volumes of lavas and pyroclasts) since lower values of magnetic susceptibility χ and natural remanent magnetization of rocks I_n usually characterize the latter.

When observing a magnetic field under conditions of inclined magnetization, determining the direction of magnetization is of particular importance since both the intensity and the shape of the magnetic anomaly significantly depend on the inclination of the excess magnetization of the object ^[4]. Only inductive magnetization I_i is often assumed when analyzing magnetic properties, and the residual magnetization I_n is relatively tiny. In this case, data on the values of χ of rocks and ores is sufficient. However, contrary to previously held beliefs, remanent magnetization is more the rule than the exception ^[7], especially in volcanic and intrusive rocks, where it can be characterized by large values and directions that differ from the direction of the modern magnetic field of the Earth's region under study.

If the body's and the surrounding medium's magnetization vectors are parallel, then the module of excess magnetization is a simple difference in the absolute values of these vectors, and its direction coincides with the directions of the original vectors. In the case of non-parallel magnetization vectors of the anomalous body and the medium, the components of excess magnetization must be calculated. Some common principles of magnetic map examination are compiled in Table 2.

4.   Signs of the desired objects and interpretation criteria

An important place in compiling a physical-geological model (PGM) of the geological media consists of calculating magnetic effects from anomalous objects against the host environment and comparing them with the observed anomalies. The comparison results allowed us to adjust the PGM and clarify the criteria for identifying the desired targets. We will call criteria for the specific quantitative parameters for the magnetic field examination (amplitude, gradient, observation accuracy, and ruggedness), the values of which exceed a certain level only in the presence of the desired object.

In complex physical-geological conditions, the effects of the desired objects are often minor, and it is necessary to use "weak" interpretive criteria ^[8]. This increases the likelihood of interpretation errors (omission of the desired object or erroneous conclusions about its presence). Integrating geophysical observations makes it possible to reduce the risk of making an incorrect decision several times. Thus, if a "weak" anomaly is recorded by three points and the average square of the anomaly of each geophysical method is equal to the variance of the interference, then value of interpretation reliability q for a single method is 0.61, and for a set of three methods (we assume the effectiveness of all methods is equivalent) increases to 0.87. Considering the false decision γ = 1 – q, we find that making an incorrect decision when using a combination of three methods (compared to one) is reduced by three times ^[8].

Finally, secondary features are of great importance ^[9]—various transformants of the original field and their combinations (smoothed field values, variability, the prevailing extent of isolines, etc.). Secondary features are often more essential than the original observed fields. Commercial economic deposits are usually characterized by a scarce combination of many secondary signatures (e.g., ^[10]).

However, using too many features will increase the complexity and decrease the efficiency of interpretation. As noted by Duda and Hart ^[11], an increase in the number of features upsurges the requirements for the volume of reference information, and many similar standards can only be available in a well-studied geological province, where quantitative forecasting is usually less relevant than in poorly studied areas. There exist known situations when the number of features (signatures) reaches a hundred values or more. Therefore, selecting (justification) the most significant (informative) features is critical in forming PGM.

5.   Brief description of several developed non-standard methods for processing and interpreting magnetic survey data

Several monographs provide standard processing and interpretation methods (for example, calculating the International Geomagnetic Reference Field (IGRF), removing temporal magnetic variations, etc.) ^{[1,2,3,12,13,14]}. Therefore, we focus here only on some developed non-standard procedures.

5.1.   Calculating the secondary effect of temporal variations in the magnetic field

The accuracy of modern field geomagnetic surveys has improved markedly and can vary between 0.05 and 0.5 nanoTesla (nT) ^[15,16]. At the same time, several highly magnetic rocks (basalts, diabases, gabbros, etc.) and artificial objects (iron or iron-containing objects) can create a secondary effect of magnetic variations, the level of which can significantly exceed the above values.

Conventional procedures for accounting for variation ^[1] are based on the use of the following trivial expression:

where t is the time, x and y are the spatial coordinates, ΔT(x, y, t) is the magnetic field recorded along the observation profile, ${\sum }_{i = 1}^{l}{a}_{i}$ is the sum of "useful" anomalies, and ${\sum }_{j = 1}^{k}{n}_{j}$ is the sum of noise components caused by time variations. This interference accounting model only subtracts the direct time variation component from the observed magnetic field and does not allow for estimating the secondary effect of temporal variations.

Because the amplitude of secondary variations also depends on the primary variations intensity, the general model of magnetic observations can be described using the following expression ^[17]:

where ${\sum }_{j = 1}^{k}n\left(j, t\right)$ is the temporal variations of the magnetic field, and ${\sum }_{i = 1}^{l}S\left\{x, y, {a}_{i}\left[{\sum }_{j = 1}^{k}n\left(j, t\right)\right]\right\}$ is the sum of the effects of anomalous bodies and environmental geological inhomogeneities, considering their dependence on time variations.

How can we calculate the effect of secondary variations in high-precision magnetic field measurements? Magnetic field measurements made at different times t (t ≥ 2) allow us to obtain a solvable system of algebraic equations that will enable us to calculate the desired signal ΔT, free from the influence of secondary variations.

5.2.   Correlation method for calculating the influence of terrain relief

In the case of direct magnetization and a homogeneous geological medium, the maxima of the magnetic field correspond to increases in the "magnetic" relief, and the minimums correspond to decreases ^[1,13]. In this case, the influence of the terrain is usually twofold: first, the influence of the shape and physical properties of the topographic layers forming the relief, and second, the influence of the profile observation slope, which causes a change in the distance from the field registration point to the occurrence of an object ^[18].

The correlation technique (see equations 3 and 4) eliminates the influence of the first component. The second component's distorting influence can be neutralized using correction equations to interpret magnetic anomalies ^[6] quantitatively (see section 5.6).

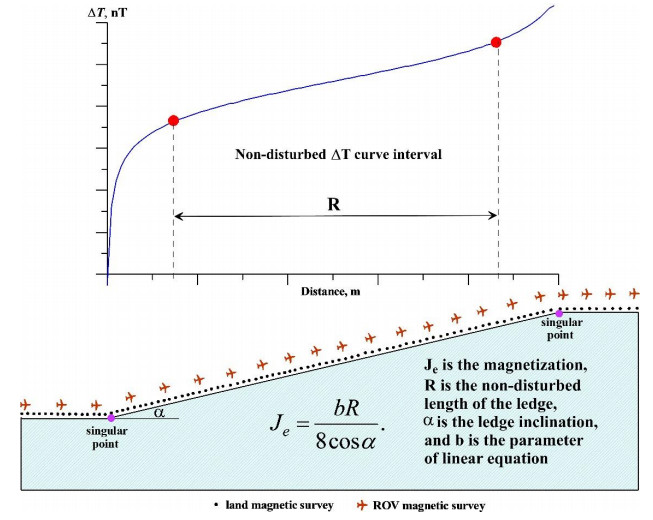
The analytical approach ^[18] showed the possibility of applying the linear relation ΔZ(ΔT) = f(h) (here ΔZ is the vertical component of the magnetic field, ΔT is the total magnetic field, and h is the relative observation height) to a typical relief element—inclined ledge. All major landforms can be approximated using one or an arbitrary combination of slopes (a correlation field can be constructed for each of these slopes). Thus, it is an elementary and prompt way to eliminate the influence of magnetized relief.

To apply this methodology, the correlation between the ΔT and h values is calculated. In general, the approximate field ΔTappr is used to calculate the correction for a rough terrain element ^[18]:

where ΔT is the correction magnetic field, and b and c are the components of the linear equation calculated by the least squares method (LSM).

The magnetic field ΔT_corr corrected for the influence of terrain is defined as:

where ΔT_obser is the observed magnetic field.

Eliminating the topographic effect using the correlation method makes it possible to almost entirely smooth out anomalies caused by the uneven influence of the terrain. Along with the linear approximation of the relationship between the magnetic field and topography, approximations by a quadratic trinomial (parabolic equation) are appropriate here. This method can improve the field's reduction level selection to one plane. When calculating the correlation field, the areas of most extraordinary dispersion relative to the averaging line are compared to the height of the points under which the targets are located. The existence of dispersion indicates hidden heterogeneity in the geological section.

5.3.   Using parameters obtained in the correlation method to assess the medium magnetization

The authors in ^[18] showed that the coefficient "b" from equation (4) can be used to average calculating the magnetization of the upper portion of the geological section:

where J is the magnetization of the upper portion of the geological section (in mA/m), α is the acute angle between the average slope and the horizon (in degrees), R is the length of the inclined scarp along strike (in meters), and the coefficient b has the dimension nT/m.

Since the parameters α and R are identified from field measurements and the coefficient b is calculated using the LSM, I can be easily calculated (1 nT = 0.796 mA/m). The presented scheme was developed for pedestrian (vehicle) surveying with terrain contouring. If we have a horizontal terrain, a combined observation system using uncrewed aerial vehicles can be used ^[19].

Figure 2 shows a model example of determining the magnetization of the upper part of the geological section.

5.4.   Employment of information characteristics

Since solving geophysical problems almost always requires integrating various methods, expressing the obtained data using common measurement units is desirable. This allows for determining the recognition efficiency of individual geophysical methods and calculating various integrated indicators relatively quickly. As shown in ^[8], the theoretically optimal integration for geophysical research consists of two physically independent methods.

Information obtained from various geophysical methods may correspond to different classes of geological objects. In some cases, only comparing fields measured by multiple geophysical methods leads to an "information leap" ^[9], allowing the detection and classification of the desired objects.

Estimating the amount of information and its distribution along the profile (or area) can help identify a target(s) relating to a definite class of objects. These estimates are significant for integrated interpretation since they transform data from various geophysical methods and allow them to be presented in unified information units.

The information theory language ^[20] is the most convenient way to express the essence of geophysical (sometimes geological and environmental) research. Despite the probabilistic nature of geophysical data, the information approach allows us to establish some deterministic characteristics. Geophysical data processing primarily focuses on eliminating (reducing) various kinds of noise. The primary task of magnetic field qualitative interpretation is to identify an object of a particular class ^[8]. In contrast, quantitative interpretation enables the determination of the geometric and physical parameters of the desired target. Solutions to these problems often overlap and are based on interpreter model representations ^[21]. A simplified introduction to the calculation of information characteristics is given below.

At each point, the information amount ${\Omega }_{i}$ obtained from applying the i-th geophysical method can be presented as ^[20]:

Or

where P_j is the relative frequency of occurrence of the j-th interval of the i-th indicator on the distribution histogram, and U_i and ΔU_i are the amplitude and the error of indicator determination, respectively ^[9].

After summing up the information elements, the random geological-geophysical components of positive and negative signs, as a rule (excluding extremal situations), are leveled out (tend to be zero). As a result, the significant and explicit amplitudes distinguish the desired target (targets). To avoid identifying false anomalies, values of ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 n}}\right.} \!\lower0.7ex\hbox{$n$}}{\sum }_{i = 1}^{n}{\Omega }_{i}$ are calculated. When a substantial amount of information is contained in the data of several methods, an integration Ω_integr criterion can be calculated (this is only one of several possible methods for information combination). This choice depends on the number of significant indicators and the technology of reducing their mutual influence ^[9]:

where Ω_p is determined using paired combinations of results from n methods used (I₁ and I₂ are a pair of geophysical observations from the total number of n geophysical methods used):

In some cases, relative frequencies of averaged values at sliding averaging intervals, instead of the values of P_j and U_i, can be used to detect anomalies at small signal-to-noise ratios.

Equation (7) represents a simplified version of the summation. Calculating the sum of informants using expressions (6) and (8) can yield a more significant result. It is important to emphasize that if one method does not identify an anomaly, the decrease in total information is not compensated by any increase in the intensity of anomalies in other integration elements.

Instead, the ${\Omega }_{i}$ value, the relative amount of information (information content coefficient), can be used:

The value ${\overline{\Omega }}_{i}$ determines the information obtained from the result U_j falling into the interval x_j with an equal probability of falling into any R intervals. This value corresponds to the average information ^[22] contained in the results obtained by one physical method,

The difference in amplitudes of various physical fields is considered using the K_i parameter. However, it is necessary to assume that the use of expressions (6) and (8–11) may be ineffective if there are insufficient physical observations.

Besides the informational approach, advanced magnetic data analysis based on applying the wavelet approach, diffusion maps, and machine learning is an established perspective ^{[23,24,25,26,27]}.

5.5.   Magnetic anomaly quantitative interpretation

Most methodologies developed for the quantitative analysis of magnetic anomalies (e.g., ^{[28,29,30,31,32,33,34,35]}) are insufficient for complex physical-geological conditions: oblique magnetization, rugged terrain relief, and an unknown normal field level. Under oblique magnetization conditions, magnetic data are often "polarized" by calculating "pseudogravimetric" anomalies ^[14]. However, this procedure is only suitable if all anomalous bodies in the study area are magnetized parallel to the geomagnetic field and have a subvertical incidence. Magnetic fields can only be correctly recalculated if these limitations are met; this produces symmetrical plots, and further interpretation can be made using conventional techniques. Similar methodologies based on the magnetic field transformations (for example, the analytical signal ^[31] have the same limitations.

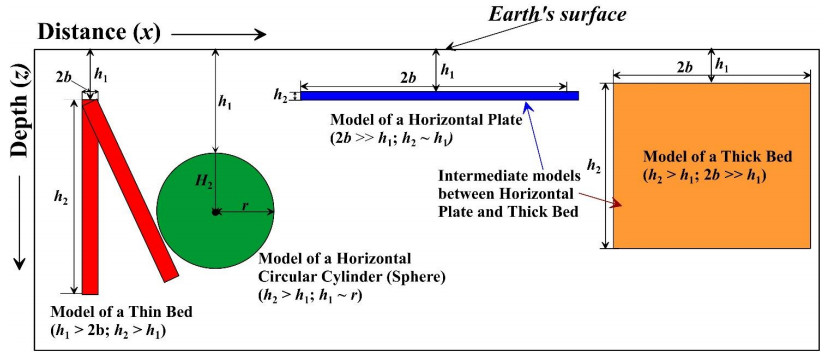
Interpretive methodologies developed for complex physical-geological environments (see above) use advanced modifications of the characteristic point, tangent, and areal methods, and the most commonly used geometric models: (1) thin inclined bed (TIB), (2) horizontal circular cylinder (HCC), (3) sphere, (4) thick bed (TB), (5) thin horizontal plate (THP), and (6) an intermediate model between TB and THP (Figure 3). A detailed explanation of these methodologies is given in ^{[5,17,18,21,36]}. These six geometric models with various modifications can approximate and correspondingly quantitatively interpret anomalies from most geological objects. The necessary procedures for interpreting magnetic anomalies from some of the above models are presented in Tables 3–5.

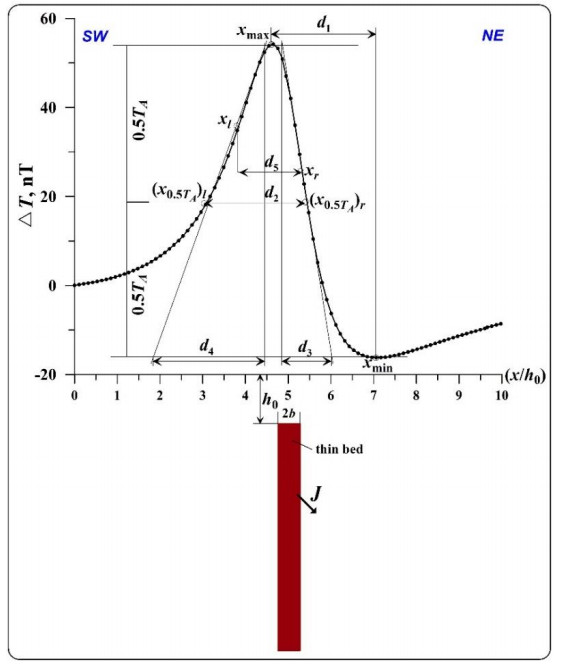
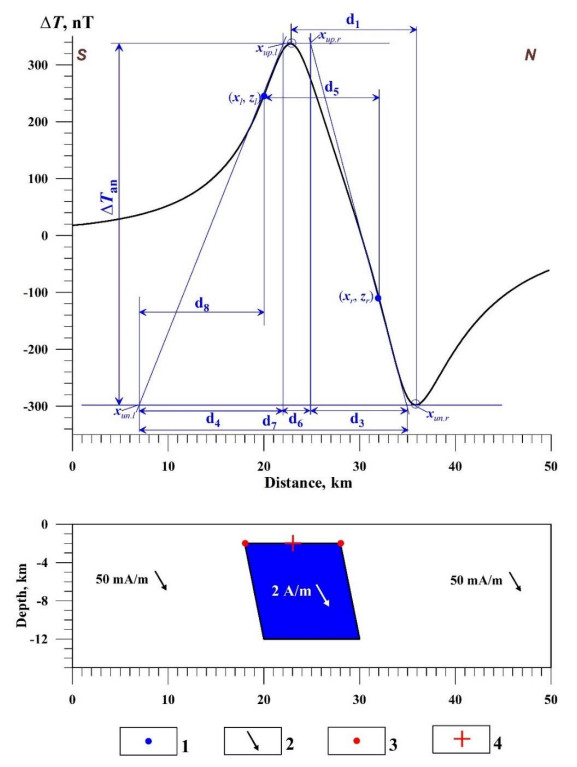
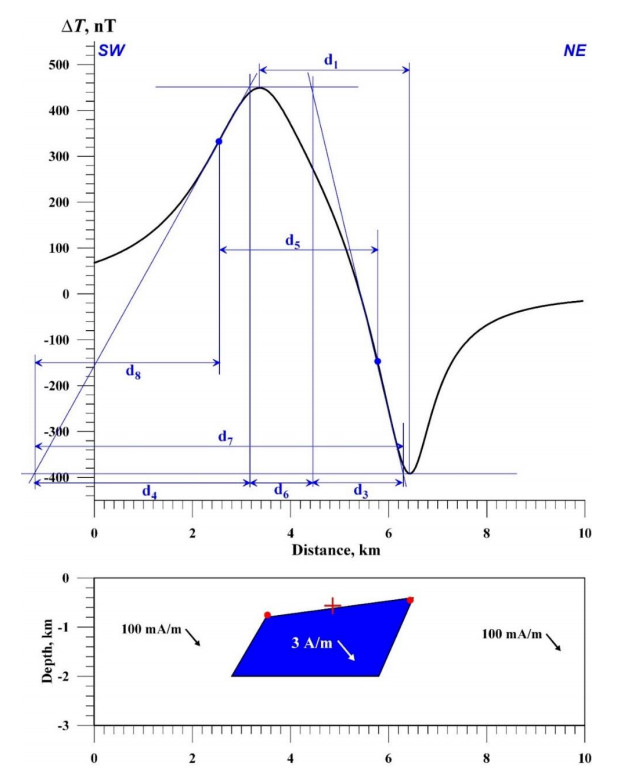
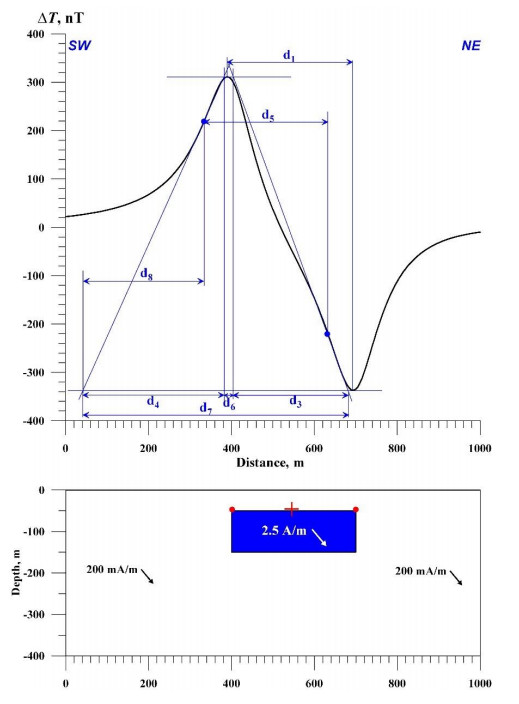
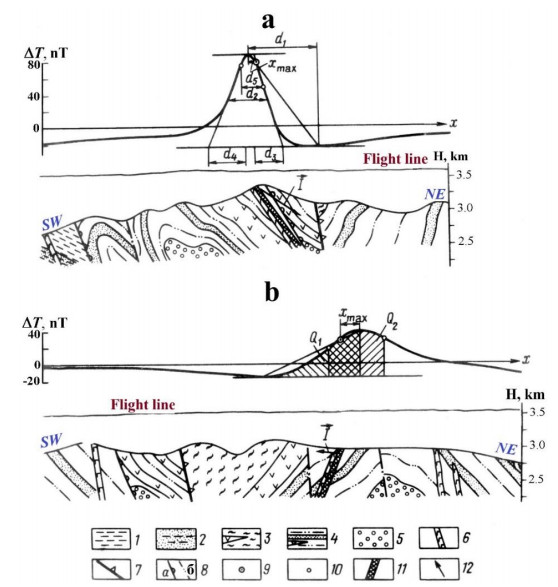
The following parameters are taken from the anomaly graph in the characteristic point method (Figure 4): d₁ = difference in the abscissa of the half-amplitude point, d₂ = difference in the abscissa of the extrema, d₅ = difference in the abscissa of the inflection point.

The tangent method uses four tangents: two horizontal lines relative to the extremes of the anomaly and two inclined lines passing through the inflection points on the left and right branches of the anomaly graph. The following parameters are taken from the graph (Figure 4): d₃ = difference in the abscissa of the points of intersection of the inclined tangent with the horizontal tangents on one branch; d₄ = the same on the other branch (d₃ is selected from the branch of the magnetic anomaly with conjugate extrema).

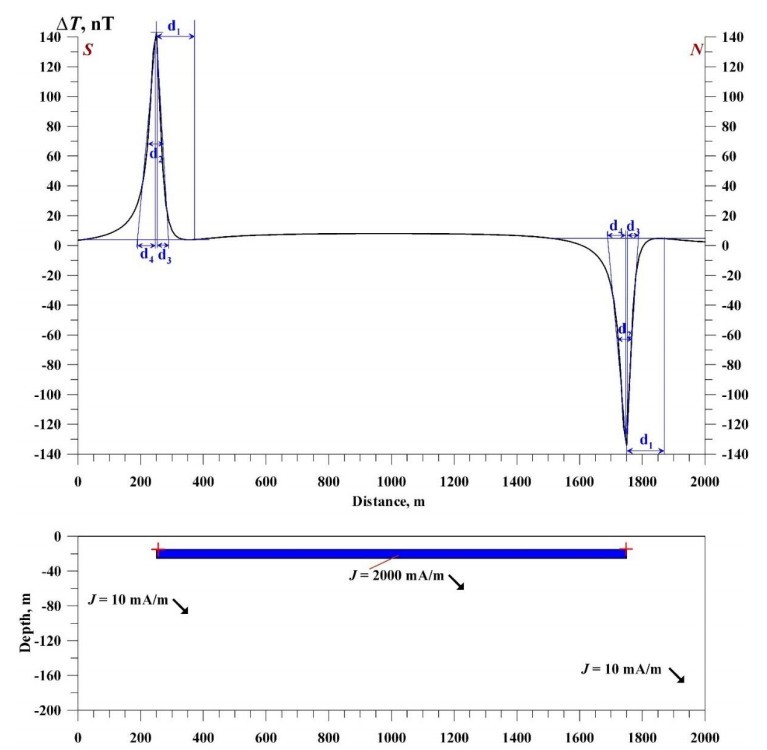
Let us consider the magnetic effect from the thin horizontal plate with a large horizontal thickness 2b, small vertical thickness (h₁ and h₂ ≪ 2b), and near-surface occurrence. This model cannot be interpreted as a "quasi-thick" model. If the parameter 2b is sufficiently large, we observe two independent anomalies; each of them we can interpret using methodologies developed for complex physical-geological conditions for the thin bed model ^[21]. In this case, we assume that the magnetization of the left-hand thin bed is positive and the right-hand thin bed is negative (in this model, determining the magnetization is complicated). As shown in Figure 5, the interpretation results indicate the position of the center of the upper edges of two "fictitious" thin beds on the left butt (positive anomaly) and the right butt (negative anomaly) of the considered thin horizontal plate model.

For the thick bed model, the parameters d₆, the interval between d₃ and d₄, and d₈, the difference in the abscissa between the point of intersection of the left inclined tangent with the lower horizontal tangent, and the inflection point on the left branch, are also used (Figure 6). Eppelbaum ^[17] provides a detailed description of the interpretation of magnetic anomalies from TB, which is undoubtedly more complex than for other models.

Interpretation of a more complex thick bed model with an inclined upper surface is shown in Figure 7.

The next model (Figure 8) is of the most significant interest. This PGM fills an intermediate geometrical position between the thick bed and the thin horizontal plate. It is known that a thin horizontal plate model is challenging to analyze in conditions of oblique magnetization and unknown levels of the normal field (e.g., ^[1,12]). Applying the aforementioned methodology to interpret the magnetic anomaly for a thick bed to this intermediate target enables obtaining the parameters of the anomalous body with the obliged accuracy. This model is more complex, and the determined J_e value comprised 2100 mA/m (the value simulated for the anomalous body in this PGM is 2500 mA/m by the host medium of 200 mA/m).

The areal method calculates individual areas limited by the anomalous magnetic field graph, a horizontal line, and two vertical lines intersecting some special points on the anomalous curve (Table 5). However, this method is not always possible (especially in regions with an angle of the magnetization vector inclination less than 50°).

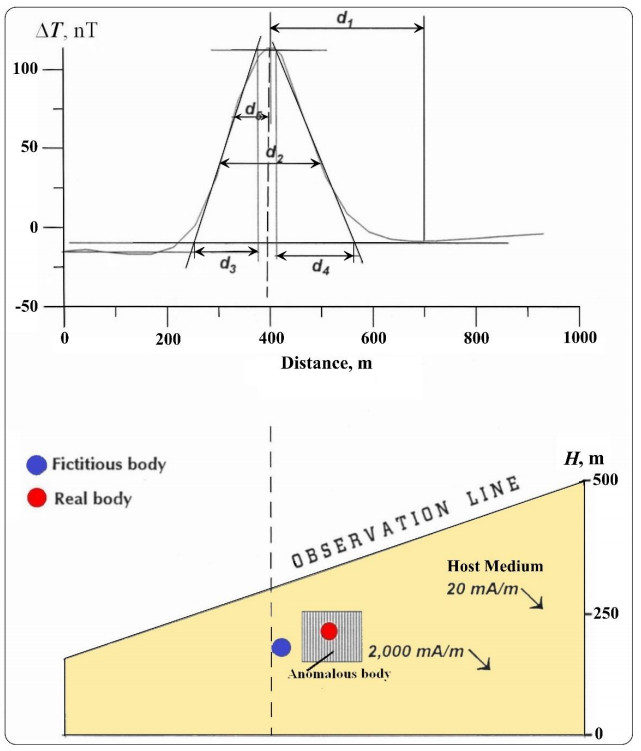
When observing anomalies on an inclined profile, the obtained parameters characterize a fictitious body. The transition from the parameters of a fictitious body to the parameters of a real body is carried out using the following expressions (the index "r" denotes a parameter of a real target):

where h is the depth of the upper edge of the body (or the center of the HCC), x_o is the displacement of the anomaly maximum from the projection of the center of the disturbing body onto the Earth's surface (caused by oblique magnetization), ω_o is the angle of the terrain relief inclination (ω_o > 0 when the inclination is directed toward the side of the positive x-axis direction).

Figure 9 illustrates the mistakes that may appear from the oblique magnetization and inclined terrain relief. The magnetic anomaly max amplitude does not coincide with the anomalous body contour. After introducing the correction for the oblique magnetization (x_o), the situation improved slightly (blue circle). However, the interpretation results still do not coincide with the contour of the anomalous body. Finally, practically ideal results were obtained after calculating a correction for the inclined terrain relief (Equation (12)).

The experience of using these interpretation methods in the Caucasus, the Near East, the Middle East, and several European regions has shown that the tangent method in the presented modification is the most accurate (e.g., ^[4]).

6.   3D modeling of magnetic anomalies

6.1.   Brief description of the developed 3D software

The GSFC-M (Geological Space Field Calculation, modified) program is designed to calculate three-dimensional gravitational and magnetic fields in complex physical-geological conditions ^[4,37]. This program is intended to calculate the gravitational field (observed values, free air, and Bouguer reductions), magnetic field components (ΔZ, ΔX, ΔY), the total magnetic field vector ΔT, and the second derivatives of the gravity potential under conditions of uneven terrain, inclined magnetization, and geological media of any complexity. 3D horizontal polygonal prisms approximate geological bodies, filling the medium under study to a definite deep boundary. Geometrically, each body can be described by 50 characteristic points; the number of bodies in the calculation model is practically unlimited (up to 1000). The geological bodies can be prepared for calculation, in addition to the 3D option, such as 2.5D and 2D (infinite along strike). The body types in the x, z plane can be (1) closed, (2) left-sided open, (3) right-sided open, and (4) open on both sides. Based on the diverse available geological-geophysical data, the strike dimensions for each geological body are estimated, and a particular block in the GSFC program is allocated.

The program has the following main advantages, in addition to those previously listed ^[37]: (1) Simultaneous calculation of magnetic and gravitational fields, (2) description of the terrain relief using unevenly spaced characteristic points, (3) calculation of the influence of the ground-air boundary by selection method directly during the interpretation process, (4) modeling of interpreting profiles flowing around rugged terrain or at various arbitrary levels (at characteristic points), and (5) simultaneous modeling of several profiles (up to ten).

The basic algorithm implemented in the GSFC program is the solution of a direct 3D problem of gravity-magnetic prospecting for a 3D horizontal polygonal prism limited in the strike. In the developed algorithm, integration over the volume is implemented on the surface bounding the anomalous target. Combined modeling of potential fields is carried out through an iterative process in which geological bodies' geometric and physical properties can change. An essential feature of the developed program is the ability to calculate 3D gravity-magnetic effects from bodies lying outside the plane of the studied geological section ^[37].

6.2.   Construction of the final PGM

The construction of the final PGM is based on the results obtained at all previous stages of the study. In this case, the highest priority should be given to the data from (1) surface geology, (2) drilled wells, (3) utilization of other geophysical method results, and (4) 3D modeling of the magnetic field. Involving materials from other geophysical methods and various geological maps and sections will help increase the reliability and accuracy of the final PGM. Of course, we must never forget that the results of magnetic field modeling should not contradict the available geological data and modern geological concepts. The interpreter must be skilled enough to combine all of this data and flexibly apply the data from other methods.

7.   Field examples

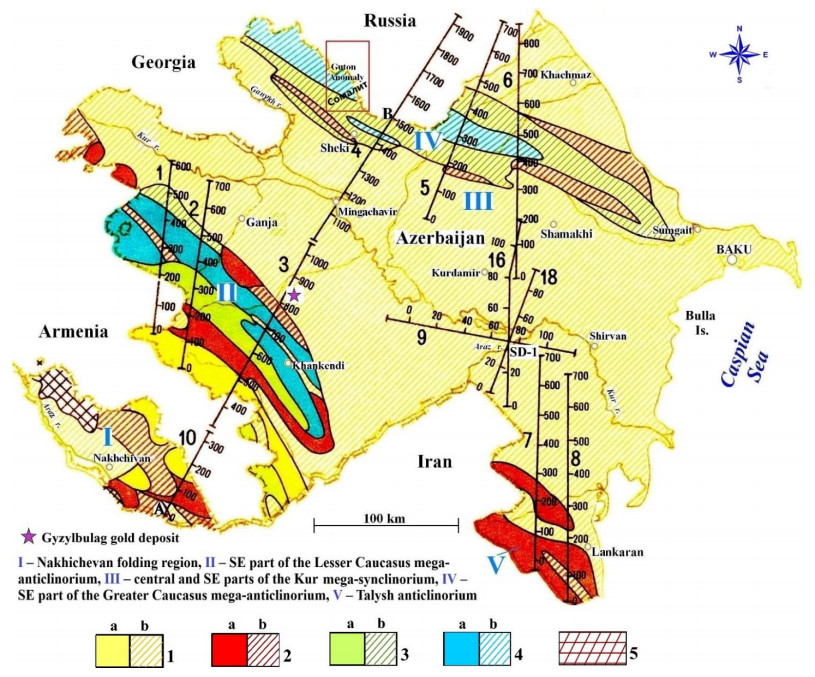
All considered field examples relate to Azerbaijan's territory. The complexity of Azerbaijan's geological structure is exemplified by its location within the highly tectonically active Alpine Himalayan collisional zone (AHCZ). The northeast part of Azerbaijan is part of the Pre-Caucasian foreland filled by the Cenozoic terrigenous sediments. A heterogenic Nakhichevan folding system is in the southwest, where carbonate Paleozoic strata and Cenozoic magmatic formations are mixed (Figure 10). At the Greater Caucasus mega-anticlinorium, stratified Cenozoic and Mesozoic thick (predominantly sedimentary) strata are present. The prevalence of the Mesozoic magmatic formations is typical for the Lesser Caucasus mega-anticlinorium. In the Kur mega-synclinorium, dividing the Greater and Lesser Caucasus, an accumulation of thick (up to several kilometers) Cenozoic terrigenous sediments is recognized.

In Figure 10: (1a) Magmatic formations of orogenic uplifts of the late collisional stage, (1b) molasse deposits of different origins, (2a) formations of collisional rifting of volcano-plutonic belts, (2b) terrigenous carbonate flyschoid, (3a) magmatic formations of continental margins, (3b) terrigenous flysch, (4a) differentiated volcanic and intrusive series, (4b) formations of deep-sea suboceanic basins, (5) subplatform deposits.

The Caspian Sea Basin is a giant depression of the meridional strike, the southern part of which belongs to the AHCZ. The South Caspian Basin (SCB) is an asymmetrical basin, in the deep part of which several anticlinal zones are distinguished—continuations of the tectonic zones of the Baku Archipelago and the Absheron Peninsula. Since the mid-90s, intensive studies of SCB began, but its complex deep tectonic structure makes it challenging to study.

The location of twelve interpretation profiles (Figure 10) onshore Azerbaijan was chosen so that they crossed the Greater and Lesser Caucasus, the Talysh Mountains, and the site of the Saatly superdeep well.

Some examples of magnetic field analysis in the South Caucasus were given, for instance, in ^[6,38,39,40] and the Caspian Sea ^[41,42,43].

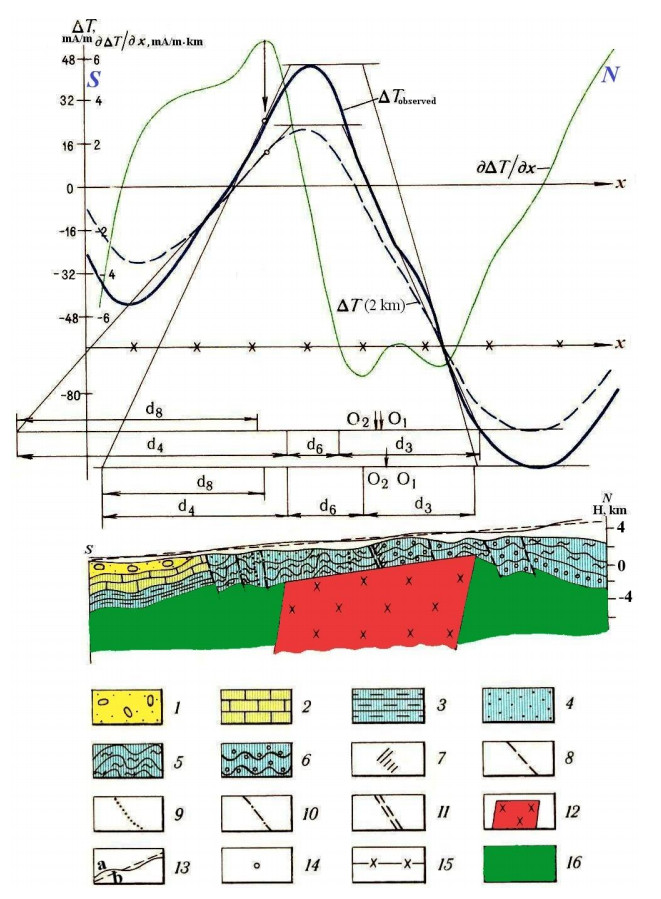
In Figure 11: (1) Alluvial deposits; (2) limestones, tuff sandstones, clay shales (K); (3) mudstones, tuff sandstones (J₃); (4) monolith clay shales and tuff sandstones (J₂); (5) sandy-clay shales with horizons of sand flysch, metamorphosed clay shales and sandstones (J₂); (6) clay shales, sandstones, spilites (J₁); (7) dikes of the gabbro-diabasic association (J₂); (8) regional upthrust-overthrusts; (9) local upthrust-overthrusts; (10) upthrust-overthrusts complicating the longitudinal tectonic steps; (11) transverse fractures; (12) magmatic intrusion of intermediate-acid composition (in the non-segmented J_1-2 complex); (13) flight line (a) and averaging inclined straight line (b); (14) inflection point of the plot ΔT nearest to the maximum on the left; (15) corrected zero line of the plots ΔT; (16) J_1-2 complex. O₁ and O₂ are locations of the origin (middle of the anomalous body's upper edge) obtained from the parameters x_un.r and x_un.l, respectively.

7.1.   Caucasus Mountains

7.1.1.   Guton magnetic anomaly (the southern slope of the Greater Caucasus)

The Guton magnetic anomaly is in northwest Azerbaijan, near the border with the Russian Federation (Figure 10). This anomaly was investigated using fifteen airborne magnetic profiles of the south-north orientation. Figure 11 indicates the obtained results along one of these profiles; an anomalous body was approximated by a model of a thick inclined bed (see subsection 5.6). The data indicate the studied target's low magnetization (250 mA/m), great vertical thickness (~ 30 km), and inclined lateral contacts. The abovementioned characteristics testify to the basic acid composition of the anomalous body (intrusion). The sizeable vertical thickness of this body (granites?) agrees with the obtained depth of the Curie discontinuity in this region (about 30 km) ^[46]. The upper edge of this intrusion is at a depth of 2.6 km (from the Earth's surface) in its middle part. This magmatic intrusion is associated with the rich pyrite-polymetallic deposits of the Belokan-Zakatala ore field ^[36] and possibly other areas in the Greater Caucasus ^[47].

7.1.2.   Somalit area (southern slope of the Greater Caucasus)

Figure 12 shows the results of a quantitative analysis of aeromagnetic anomalies ΔT in the Somalit area in the southern slope of the Greater Caucasus (Azerbaijan). For examination of these anomalies, a model of a thin inclined bed has been used (see subsection 5.6): (12a)—by the method of tangents and characteristic points (Tables 3 and 4), (13b)—by the areal method (Table 5).

In Figure 12: (1) Yalakhkam suite J₂aal₂, (2) Zainkam suite J₂aal₁, (3) Nagab suite J₁toa₃, (4) Tseilakhan suite J₁toa₃, (5) the Lower and Middle Toarcian suite J₁toa_1-2, (6) dikes of the gabbro-diabasic association; , (7) the Major Caucasian Ridge (upthrust-overthrust), (8) ore controlling (a) and ore distributing (b) upthrust-overthrusts, (9) Reford's point ^[29], (10) inflection points on ΔT plots, (11) position of the anomalous body obtained from quantitative interpretation; (12) obtained direction of the magnetization vector projection.

7.1.3.   Regional profile in western Azerbaijan

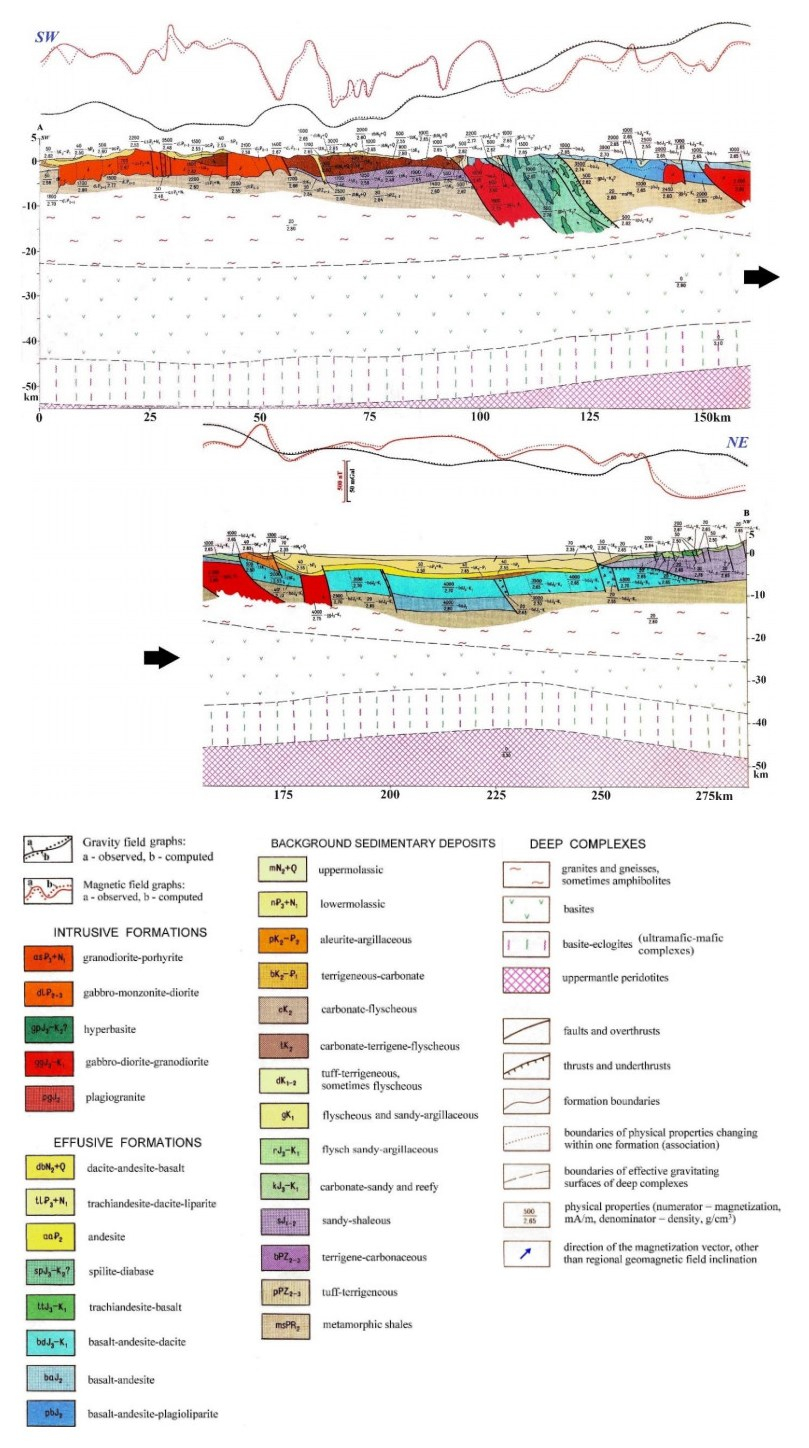
A regional profile A–B (its location is shown in Figure 10) is composed of three profiles (10, 3, and part of profile 4) and nicely demonstrates the complex deep structure of Azerbaijanian land. It starts near the town of Julfa (Nakhchivan Autonomous Republic of Azerbaijan), crosses Armenian territory, and subsequently traverses the Azerbaijanian territory and ends near the town of Sheki (near the border with Georgia) (Figure 13). This profile clearly illustrates the geological complexity of the region under study. The airborne observed magnetic and gravity fields were used in this research. The peculiarities of the combined 3D magnetic-gravity modeling are briefly described in section 6. It should be noted that magnetic field selection is much more complex than gravity field modeling, considering the dipole nature and the variability of the magnetic field characteristics. Combined 3D magnetic-gravity modeling increases the difficulties of the successive interactive selection, but the PGM reliability also increases.

In this PGM, in the Kur depression, a decrease in the Earth's crust thickness was observed. The surface of the "basaltic" layer displays the most uplift in the core of the Lesser Caucasus mega-anticlinorium. Here, Azerbaijan's geological formation stages are reflected in the upper part of the geological section (Figure 13). Orogenic granodiorite-porphyric and pre-orogenic gabbro-monzonite-dioritic intrusive formations developed at the beginning of the southwest profile (Nakhchivan region); orogenic effusive daсite-andesite-basaltic formations are found southwest of the town of Istisu, and orogenic sedimentary deposits (molasse) in the Kur depression, to a thickness of 4–5 km.

Pre-orogenic effusive associations are presented in (1) the southwest part of this profile, where they occur on sub-platform terrigenous-carbonate deposits, (2) in the transfer area from the Lesser Caucasus to the Kur depression, and (3) in the southern slope of the Greater Caucasus immersion. The numerous effusive formations are outcropped in the Lesser Caucasus in the middle of the profile, creating an "ophiolitic zone" ^[47]. 3D physical-geological modeling indicates that these formations can occur under young sedimentary deposits in the Kur depression and under Lower-Middle-Jurassic sand-shale associations in the Greater Caucasus (where these formations were underthrusted because of the tectonic processes). In the Lesser Caucasus, there are presumed to be thick buried intrusives of gabbro-diorite-granodiorite formations; intrusives of these formations are usually metalliferous.

3D magnetic-gravity modeling along this profile (Figure 13) was performed using about 150 successive iterations, with detailed results after each iteration. The strike dimensions of each body were determined using surface geology, borehole data, seismic, magnetotelluric, and thermal data, as well as the magnetic and gravitational fields themselves.

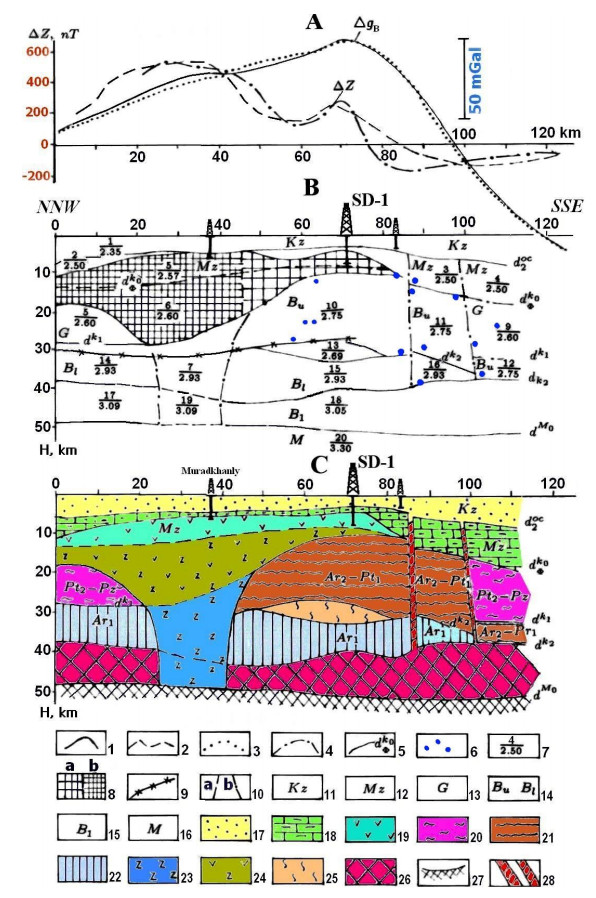
7.2.   The Saatly superdeep borehole

The Kur depression is in the Greater and Lesser Caucasus Intermountain Basin. For many decades, the point of view dominated that in the Kur depression, thick sedimentary deposits were present in the crystalline pre-Alpine basement structures divided by sub-vertical deep faults. On the buried uplift of the basement (a hypothesis based on the positive gravity anomaly and increased seismic velocities) ^[6], the Saatly superdeep borehole SD-1 was designed in 1965; the drilling began in 1977 and stopped in 1991 at a depth of 8324 m ^[48]. The surface ΔZ survey performed in this area was used for comparison with the 3D magnetic field modeling (Figure 14). The magnetic anomaly is mainly produced by a thick magnetoactive body occurring in the NNW part of the profile.

The analysis of the magnetic properties of rocks and the magnetic survey results showed that the basement was not magnetized, and a large part of the geological section of the Middle Kur depression is occupied by the highly magnetized Mesozoic magmatic associations of basic and intermediate composition ^[6].

Jurassic magnetic associations are widely distributed in the northeastern Lesser Caucasus. They have a deep-seated, gently sloping underthrust under the thick sand-shale series of the Greater Caucasus Jurassic rocks.

The validity of the interpretation was fully confirmed by the results of the SD-1 drilling (Figure 14). The borehole exposed Mesozoic volcanogenic rocks at a depth of 3.6 km and did not reach their bottom even at 8.2 km ^[47]. Given the location of the lower edge of the magnetized masses and by analogy of this geological section to ones in the Lesser Caucasian, it is likely that magmatic rocks occur down to 10 km (compatible with the Lower Bajocian rocks of the Lesser Caucasus).

Observed curves: (1) gravity field Δg_B, (2) magnetic field ΔZ, curves computed from the model B, (3) Δg_B, (4) ΔZ, (5) velocity and density boundaries and their indices, (6) diffraction points, (7) body number (numerator) and density, g/cm³ (denominator), (8) magnetized geological bodies: 2,500 mA/m (a) and 2,800 mA/m (b), (9) Curie surface depth obtained from the geothermal data, (10) subvertical boundaries of bodies derived from magnetic (a) and gravity (b) analysis, (11) Cenozoic, (12) Mesozoic, (13) G complex (velocity analogue of the "granitic" layer), (14) B_u and B_l subcomplexes of B complex (velocity analogue of the "basaltic" layer), (15) B₁ complex (basite and high-density ultramafites), (16) M complex (presumed peridotite composition), (17) Cenozoic complex: mainly terrigenous deposits, Mesozoic complex: (18) terrigenous-carbonaceous formations, (19) mainly effusive associations of basic and intermediate composition, (20) mainly Baikalian complex (Pt₂-Pz): metamorphic (primarily terrigenous) associations (the presence of younger deposits in the upper part is possible), (21) Pre-Baikalian complex (Ar₂-Pt₁): mainly gneisses and marbles, (22) ancient complex (Ar₁): gneisses and amphibolites, (23) root of the basic magmatism, (24) undivided effusive-intrusive complex, (25) low density rock complex (serpentinization zone?), (26) complex of magmatic associations corresponding to the crust-to-mantle transition (ultramafic-mafic complexes?), (27) upper mantle roof position, (28) large fault zones.

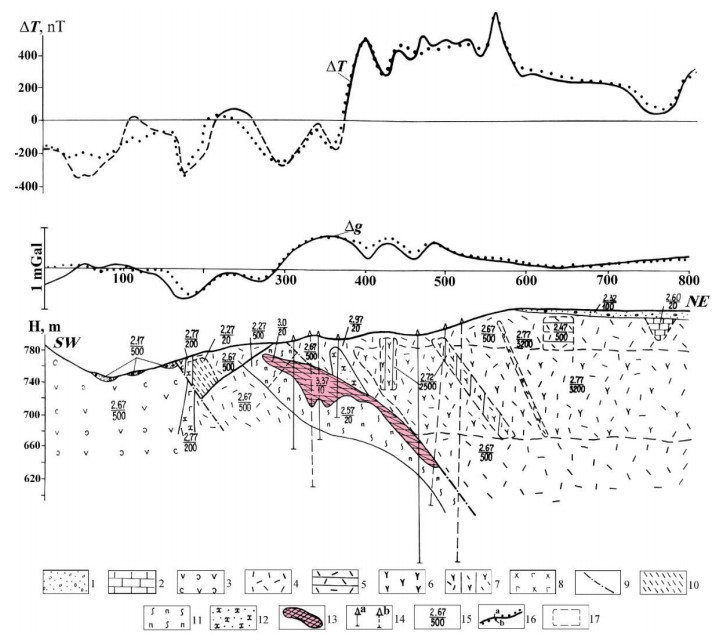
In Figure 15: (1) Quaternary deposits, (2–8) Middle and Upper Jurassic rocks: (2) silicificated limestone lens, (3) tuffs and lavas of andesitic porphyrites, (4) tuffs of liparite-dacitic porphyrites, (5) deconsolidated tuffs of liparite-dacitic porphyrites, (6) lavas of dacitic porphyrites, (7) consolidated lavas of dacite-porphyrites, (8) dikes of andesite-basalts, (9) faults, (10) zone of brecciation and crush, (11) zones of brecciation, crush, and boudinage with lean pyrite-chalcopyrite ore, (12) zone of brecciation, crush, and boudinage with rich impregnating mineralization, (13) massive pyrite-chalcopyrite ore, (14) drilled wells: (a) on the profile, (b) projected on the profile, (15) physical properties of geological bodies (numerator = density, g/cm³, denominator = magnetization, mA/m), (16) gravity and magnetic fields: (a) observed, (b) selected, (17) body contours introduced during the 3D modeling.

7.2.1.   Gyzylbulag gold deposit (Lesser Caucasus, western Azerbaijan)

An example of complex three-dimensional modeling of magnetic and gravity fields at the Gyzylbulag gold deposit (Agdara area of Azerbaijan, the Lesser Caucasus) is illustrated in Figure 15. Based on the data of surface geology, the study of boreholes, and adits rock samples, the strike dimensions were determined for each geological body, for which a particular block was allocated in the GSFC-M program. For example, for the ore body in the center of the presented profile, which has petrophysical parameters (density = 3.37 g/cm³, magnetization = 10 mA/m), the strike dimensions were (−55 m in the NW and +30 m in the SE).

A characteristic petromagnetic feature of this deposit is that the practically non-magnetic (10 mA/m) massive pyrite-chalcopyrite ore body (gold content is ~5 g per ton of ore) occurs in a highly magnetic environment, i.e., we have a negative magnetic anomaly. On the other hand, the density contrast between the ore body and the host medium is about 0.8 g/cm³, which causes the positive gravity anomaly (Figure 15).

7.3.   Caspian Basin

7.3.1.   Bulla-Sea hydrocarbon deposit, Bay of Baku

Using integrated information analysis, Figure 16 shows an example of geophysical data interpretation from a set of fields (including data from a magnetic survey, a first horizontal derivative of gravity, and marine bottom changes).

The Bulla-Sea hydrocarbon field, located in the Bay of Baku (Azerbaijan), is one of the rich deep hydrocarbon reservoirs occurring at depths below 5000 m in the South Caspian Basin ^[49]. To calculate the Ω_integr parameter (see subsection 5.5), three different fields were used: local magnetic anomalies ΔT (the sea ship survey data), the second horizontal derivative of the gravitational potential W_xz (the bottom gravity data), and ΔH/H (the relative changes in the seabed topography). This figure shows that both faults associated with the productive series are reflected in the Ω_integr plot (Figure 16). The larger amplitude of the southwestern anomaly of the Ω_integr parameter compared to the northeastern anomaly can be explained by the proximity of the southwestern fault to the seafloor topography (Figure 16).

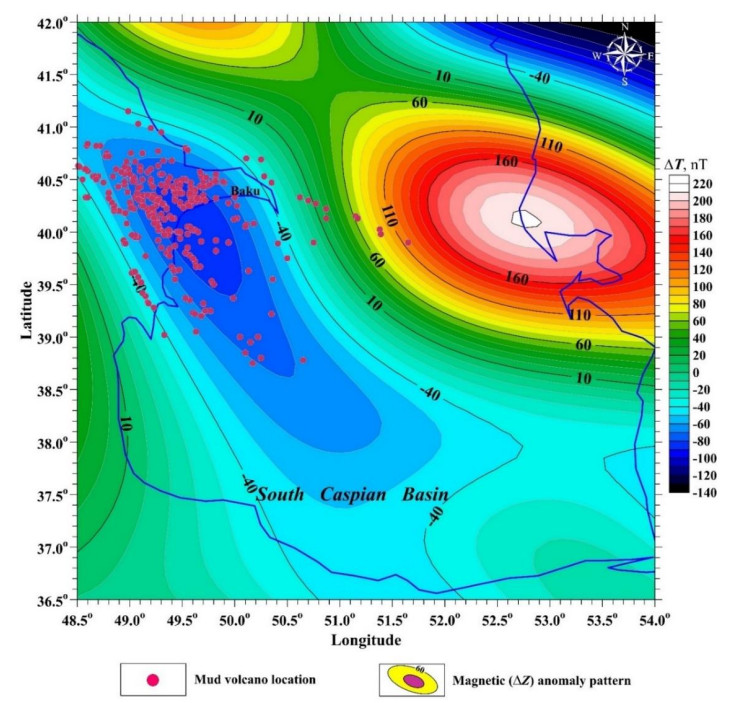
7.3.2.   Azerbaijanian mud volcanoes

Mud volcanism is a natural phenomenon based on the fluid-geodynamic and thermobaric processes at the depth. In Azerbaijan territory, about 35% of all available mud volcanoes on the Earth are disposed of ^[47,50]. The compiled map (Figure 17) first indicates the relationship between the averaged negative magnetic anomaly and the location of most of the Azerbaijani mud volcanoes. Considering the average character of the magnetic field, this map is unsuitable for quantitative analysis. At the same time, it is evident that the sources of this magnetic anomaly occur at a significant depth. Combined geological-geophysical analysis of the obtained phenomenon may shed light on the nature of the formation of many mud volcanoes in a given area.

8.   Discussion

A magnetic survey is an effective, low-cost method for solving various geological-geophysical and environmental problems. Even the limited number of presented examples convincingly shows that the recent decline in interest in magnetic exploration is undeserved.

This review briefly presents the main components of the developed system for interpreting magnetic data under conditions of inclined magnetization, uneven terrain, and unknown magnetic field levels (superpositions from sources of different ranks). Testing interpretative techniques in the challenging conditions of the Caucasus region showed their effectiveness. It is necessary to underline that the author does not include conventional techniques in this paper (e.g., standard calculating initial temporal magnetic variations, removing the International Geomagnetic Reference Field (IGRF), calculating vertical and horizontal gradients, etc.). Nevertheless, the developed non-conventional methodologies must be combined with applying some mandatory procedures.

The article's limited scope did not allow us to present examples of magnetic survey applications in underground, environmental, and archaeological geophysics. A description of the practical methodology of paleomagnetic mapping, which is based on combining magnetic, paleomagnetic, and radiometric data (e.g., ^[7,51]), and classification of buried targets by estimating the character of temporal magnetic variations ^[52], are also outside this article's scope.

Further prospects for high-precision magnetic prospecting are associated with:

(a) widespread use of uncrewed vehicles equipped with high-precision magnetic sensors. Carrying out such surveys at various heights allows us to obtain additional helpful information about the objects of study,

(b) development of detailed databases reflecting the use of magnetic prospecting in various typical situations,

(c) further elaboration of the developed interpretation methodologies (creating an automated quantitative interpreting system),

(d) the use of advanced analysis methods based on avant-garde wavelet methodologies, machine learning, and diffusion maps,

(e) the use of the rapidly developing branch of artificial intelligence in magnetic prospecting.

9.   Conclusions

High-precision magnetic prospecting can solve various geological problems, even under complex physical-geological conditions. A radical increase in the accuracy of magnetic survey equipment, the frequency of magnetic field measurements, and the use of uncrewed equipment makes it possible to obtain magnetic data for large regions without significant financial costs and in a short time. At the same time, the interpretation of magnetic survey data, especially in the complex areas (which includes most of the territory of Azerbaijan: Caucasus Mountains, Middle Kur depression, and South Caspian Basin), is a multi-stage process. Besides the primary assessment of observed magnetic data, the main components of the developed interpreting system are presented, such as the calculation of secondary time variations, correction for terrain relief and its usage to assess the magnetization of the environment, an information approach to the geophysical data analysis, quantitative interpretation of magnetic anomalies under conditions of oblique magnetization, inclined relief, and unknown normal field level, and three-dimensional modeling of the magnetic field is displayed in a shortened form in this article. The interpretative methods presented are illustrated with numerous models and several field examples. Further horizons for the development of magnetic prospecting research are briefly described.

Acknowledgments

The author thanks Prof. I.S. Guliyev and Prof. F.A. Kadirov (Azerbaijan National Academy of Sciences) and their working groups for the data about Azerbaijan's mud volcanoes. The author would also like to thank two anonymous reviewers who thoroughly reviewed the manuscript, and their critical comments and valuable suggestions helped prepare this paper.

Use of AI tools declaration

The author declares that he has not used artificial intelligence (AI) tools in creating this article.

Conflict of interest

The author declares no conflicts of interest.