Forecasting mixture composition in the extractive distillation of n-hexane and ethyl acetate with n-methyl-2-pyrrolidone through ANN for a preliminary energy assessment

1.   Introduction

Steel pipes are important metallurgical products that are widely used in industries such as petroleum, construction, automotive, and power. During the production process for steel pipes, various defects may exist on the surface of the pipes due to factors such as rolling equipment and processes. These defects not only affect the overall aesthetics, it is also true that surface defects such as cracks, corrosion, and holes may have significant impacts during use. For example, steel pipes with crack defects may experience cracks under external forces due to factors such as stress concentration, resulting in safety hazards^[1]. Timely detection of surface defects on steel pipes can effectively improve product quality and reduce the property losses caused by surface defects. Therefore, studying the surface defect detection technology of steel pipes is of great significance ^[2].

To date, many defect detection methods have been developed ^[3,4], and for surface defect detection, vision-based detection methods have a wide range of applications and have been extensively employed in research. Traditional visual based detection methods mainly rely on edge detection ^[5], feature point matching ^[6], template matching ^[7], etc. These methods have high accuracy on specific datasets, but they usually have poor generalization ability. Deep learning technology provides effective solutions to address the aforementioned issues. To date, many excellent deep learning based object detection methods have been developed, such as Faster R-CNN ^[8], YOLO ^[9,10], SSD ^[11], RefineDet ^[12], Transfomers ^[13] etc. After improvement based on specific application scenarios, these methods are widely used to detect defects on surfaces, such as printed circuit boards (PCBs) ^[14], steel plates ^[15], solar cells ^[16], sanitary ceramics ^[17], sawn lumbers ^[18], etc. For example, Hu and Wang et al. ^[14] proposed a defect detection method for PCBs based on the Faster R-CNN, which improves the detection ability of small targets by introducing Garpn and the residual units of ShuffleNetV2. Song et al. ^[15] proposed a steel plate surface defect detection algorithm based on the Faster R-CNN, and it overcomes the problem of a complex shape and high similarity associated with steel plate surface defects by using deformable convolution and background suppression algorithms. Tu et al. ^[18] introduced a Gaussian distribution in YOLOv3 to estimate the coordinates and the localization uncertainty of the prediction box, and they used the complete intersection over union (CIoU) as the loss function to apply the algorithm to apply the algorithm for defect detection in steel pipes. Chen et al. ^[19] introduced an adversarial model for brain vessel segmentation in time-of-flight magnetic resonance angiography (TOF-MRA) imaging, enhancing feature representation by decomposing images into high and low frequencies and thereby addressing sample imbalance.

The method proposed in this paper mainly focuses on the detection of surface defects in steel pipes based on X-ray images, which have the following characteristics. First, natural images generally contain rich textural information, making them suitable for target detection by using deep learning models. However, the X-ray image texture for steel pipes and their surface defects is scarce, with high similarity between normal and defect areas, and small differences between different defect types. For example, an air-hole type defect is a solid small circle, while a hole-head type defect is a hollow small circle. In the process of X-ray image acquisition, there is relative motion between the detected object and the camera. The hollow position of the hollow-bead defect collected by the system often contains motion blur, resulting in high similarity between these two types of defects and difficulty in distinguishing them. Second, the sources of surface defects on steel pipes are different, and the scale of defects varies greatly. For example, during the production process, high temperatures, conveyor belt transportation collisions, and other reasons can lead to the surface of steel pipes containing many small defects such as small pores or scabs. As a comparison, the scale of defects such as surface cracks in steel pipes is relatively large. Third, the frequency of different defects on the surface of steel pipes varies greatly, leading to a serious imbalance in the number of samples with different defects. The above issues pose serious challenges to the surface defect detection of steel pipes based on X-ray images, and they seriously reduce the accuracy of defect detection algorithms.

To address the above issues, we propose a novel steel pipes defect detection method based on the YOLO framework. The contributions of this paper can be summarized as follows.

1) First, a new backbone block is proposed to enhance the feature extraction capacity of the defect detection method. By increasing the high-order spatial interaction and strengthening the capture of internal information, the correlation within steel pipe defect features is fully utilized to extract different features of similar defects, so as to reduce the false detection rate in steel pipe defect detection.

2) Second, a new neck block is proposed to improve the detection performance for small defects in steel pipes. By further strengthening the fusion of spatial feature information and making full use of the feature information of the extracted target, the accuracy of steel pipe defect detection is improved.

3) Third, a novel regression loss function that considers the aspect ratio and scale is proposed to address the issue of large differences in the scale of steel pipe surface defects. Meanwhile, focal loss is introduced to further improve the sample imbalance problem in steel pipe defect dataset.

The remainder of this paper is organized as follows. Section II presents the related works. Section III introduces the data source and the preprocessing method, and Section IV gives the details of the proposed method. In Section V, the effectiveness of the improved method is demonstrated, comparing the experimental results of other target detection algorithms. In Section VI, the paper is summarized and further research directions are given.

2.   Related work

Surface defects constitute a key factor affecting product quality; therefore, surface defect detection is very important. The technology used for surface defect detection is directly related to the characteristics of the product itself. Common surface defect detection technologies include laser based methods, magnetic flux leakage based methods, infrared based methods, ultrasonic based methods, visual based methods, etc. ^[1]. Among these methods, visual based detection methods have become a research feature due to their wide applicability ^[5,6,7]. Particularly since the emergence of deep learning technology ^{[8,9,11,12,13]}, visual based surface defect detection technology has been widely applied ^{[14,15,16,17,18,19,20]}.

The performance of surface defect detection technology is directly related to the characteristics of the defect itself. Therefore, currently, visual based surface defect detection technology is usually developed by improving general visual object detection algorithms based on the characteristics of specific surface defects. Many defects have multiple types, large scale changes, and high similarity between different types of defects. At the same time, in some scenarios, there is a high demand for real-time performance of the algorithm. For example, for PCBs, their surface defects have the characteristics of small targets and high detection speed requirements. To address this issue, Hu and Wang ^[14] proposed a defect detection method for PCBs based on the Faster R-CNN. In this method, a feature pyramid network FPN is used to enhance the algorithm's detection ability for small targets, while the region proposal network is improved to enhance the accuracy of anchor position prediction, thereby reducing the number of anchor points and improving the algorithm's execution efficiency. For surface defects of steel plates, there are many types of defects with complex and irregular shapes, and the sizes of defects are various. Meanwhile, defect areas and normal areas have high similarity. To overcome the above issues, Song et al. ^[15] proposed a surface defect detection algorithm for steel plates based on the Faster R-CNN. In this method, a background suppression algorithm is included to improve the discrimination between defect areas and normal areas, as well as the discrimination between different types of defects. Second, deformable convolution is introduced into the Faster R-CNN algorithm to solve the problems of complex and irregular defect shapes, as well as large changes in defect scale. For the defects of solar cells, they have characteristics such as complex backgrounds, variable defect morphologies, and large scale differences. To overcome these issues, Zhang and Yin et al. ^[16] proposed an improved YOLOv5 algorithm. In this method, deformable convolution is included to overcome the problem of variable defect morphology in solar cells, and modules such as the attention mechanism and small object detection head are included to solve the problem of complex background and large changes in defect scale in solar cells. For weld defects, they have high similarity between different types of defects, large scale changes, and high real-time requirements for the system. To overcome the above issues, Wang et al. ^[21] proposed an improved YOLOv5 method. In this method, the problem of large changes in defect scale is solved by introducing a multi-scale alignment fusion (MSAF) module, and the real-time performance of the system is improved by incorporating it with parallel feature filtering modules. At the same time, in MSAF, the problem of high similarity between different types of defects is solved by aligning features at one level to fuse all other scales. For the surface defects of sanitary ceramics, they have a wide variety of characteristics, and different types of defects have significant differences in morphology and scale. Hang et al. ^[17] proposed a lightweight real-time defect detection network based on the lightweight backbone MobileNetV3, which achieves multi-scale detection of surface defects in sanitary ceramics through multi-layer feature pyramids. A detection head with a channel attention structure and low-level mixed feature classification strategy is used to achieve higher accuracy defect classification, addressing the sample imbalance issue in TOF-MRA imaging, Chen et al. ^[19] proposed a brain vessel segmentation method based on adversarial models. This method involves the separation of TOF-MRA images into high-low frequency components, thereby enhancing the representation of textures and edges. Such separation not only bolsters the model's robustness and regularization, it also significantly improves its capability to extract texture and edge features. Addressing the challenges of 3D object detection, Liu et al. ^[22] proposed an improved PvNet model approach. This method, by integrating per-pixel keypoint voting with depth imaging, enhances the precision and efficiency of object detection. In the field of remote sensing data^{[23,24,25,26]}, object detection also has many challenges. In the classification and identification of surface or subsurface materials in Earth science and remote sensing, the performance of the model is limited by information diversification in some complex scenes. To address this problem, Hong et al. ^[23] adopted a multi-modal deep learning framework and specifically studied cross-modal learning. Through different fusion strategies and deep network training techniques, the classification performance for complex scenes is effectively improved. In a multi-city remote sensing environment, the existing artificial intelligence models, due to a lack of diverse remote sensing information and high generalization ability, do not perform well in cross-city or regional case studies. To address this challenge, Hong et al. ^[24] developed HighDAN, a high-resolution domain adaptation network. This network effectively adapts to the differences in remote sensing images between different cities by combining high-low resolution fusion and adversarial learning, and it improves the segmentation ability and generalization ability of the model. In hyperspectral anomaly detection (HAD), the low-rank representation (LRR) model is limited by the manual selection of parameters and insufficient generalization performance in practical applications. To solve this problem, Li et al. ^[25] proposed a new network that combines an LRR model and deep learning technology: the HAD baseline network (LRR-Net). LRR-Net uses the alternating direction method of multipliers to optimize the LRR model, and it integrates its results into the deep network as prior knowledge. At the same time, the regularization parameters are transformed into trainable parameters to reduce the need for manual parameter tuning. The detection performance and generalization ability of the model are improved. With an increasing amount of remote sensing data being acquired from satellites or airborne platforms, the simultaneous processing and analysis of multi-modal remote sensing data poses new challenges to researchers in the field of remote sensing. In response to this problem, Wu et al. ^[26] proposed a new framework for multi-modal remote sensing data classification based on deep learning, and they used a convolutional neural network as the backbone to develop an advanced cross-channel reconstruction module called the CCR-Net. Through a cross-modal reconstruction strategy, the CCR-Net more compactly fuses different remote sensing data sources to achieve a more effective information exchange. For bubble defects in photoresist, limited by data collection conditions, there are problems such as a small number of samples and high similarity between defect areas and normal areas. Yang et al. ^[27] proposed an improved YOLOv5 algorithm to address the above issues. A method to increase the number of defect samples based on generative adversarial networks has been proposed to address the issue of a small number of defect samples. In response to the problem of high similarity between defect areas and normal areas, which makes the algorithm difficult to train, they optimized the structure and activation function of YOLOv5 to solve the dead zone problem of the activation function, reduce the difficulty of model training, and improve the accuracy of the algorithm.

Compared with the above-mentioned defect detection problems, surface defect detection for steel pipes, as addressed in this paper also faces the problems of multiple defect types, large changes in defect scale, and high similarity between different defects. However, unlike the aforementioned defect detection issues, this work entails the use of X-ray images, while previous algorithms mainly use natural images based on visible light. Natural images based on visible light generally contain rich textural information, making them suitable for target detection by using deep learning models However, the X-ray image texture for steel pipes and their surface defects is scarred, which not only increases the difficulty of the algorithm to capture defect features, it also exacerbates the impact of multiple defect types, large changes in defect scale, and high similarity between different defects on the accuracy of the algorithm.

3.   Data source and preprocessing

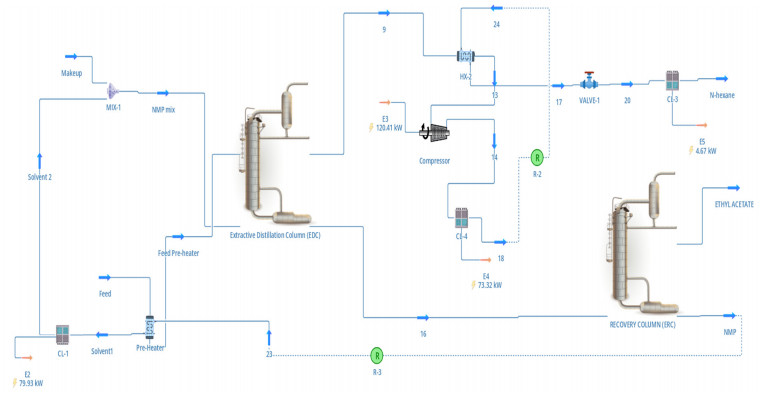
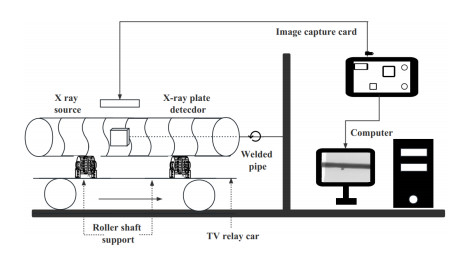
The dataset used in this paper is provided in the RAW format from raw video images by using a real-time X-ray imaging system, as shown in Figure 1. Through batch processing, JPG images of the same width and height were cut and exported, and 3408 original images of steel pipes with eight types of defects were obtained. After that, the defect areas and defect categories of steel pipe welds were marked by using the marking object software LabelMe, and then exported to the YOLO or PASCAL VOC2007 standard dataset format. Deep neural networks require a large number of training samples to accurately and effectively classify and detect targets. In order to increase the amount of training data, data augmentation methods such as rotation, cropping, translation, and mirroring were used for the steel pipe defect dataset in this study. The steel pipe defect dataset was increased to four times the original image, i.e., from 3408 images to 16,528 images. Finally, the dataset contained 16,528 images of eight defect types: 3210 air holes, 1832 broken arcs, 2170 slag inclusions, 1428 cracks, 1784 overlaps, 1050 bite edges, 1624 unfused, 3520 hollow beads, totaling 16,528 images. Some typical defects are shown in Figure 2.

Figure 1.  Real-time X-ray imaging system.

DownLoad: Full-Size Img PowerPoint

Figure 2.  Sample of steel pipe defects.

DownLoad: Full-Size Img PowerPoint

4.   Proposed model

For the target detection models, compared with methods such as the Faster R-CNN, SSD, and other models of the YOLO family, YOLOv5 has the advantage of small models and fast training without any significant decrease in accuracy ^[16,27,28]. It is more suitable for target detection in industry. Therefore, the method proposed in this paper is based on the YOLOv5 model. Figure 3 gives a schematic diagram of the proposed method, where different background colors highlight the proposed "New backbone" and "Neck+" blocks.

Figure 3.  Schematic diagram of the proposed method, where different background colors to highlight the proposed "New backbone" and "Neck+" blocks.

DownLoad: Full-Size Img PowerPoint

4.1.   Overview of the original YOLOv5 model

The network structure of the orignial YOLOv5 can be divided into four parts: input, backbone, neck, and prediction. The methods used at the input include Mosaic data enhancement, adaptive anchor box calculation, and adaptive image scaling. Among them, the backbone is mainly composed of the Conv module, the BottleneckCSP module, and the SPP module, which can be seen in Figure 3. In the model, BottleneckCSP in the backbone is used to extract deep semantic information from images, and BottleneckCSP in the neck is used to fuse feature maps of different scales to enrich semantic information. Bottleneck is composed of two 1*1 convolutional layers plus a 3*3 convolutional layer. There are two 1*1 convolutional layers, where the first 1*1 convolution reduces its dimension, and then a 3*3 convolutional layer is applied to reduce the number of parameters in the calculation process and speed up training, subsequently, a 1*1 convolutional layer is used to restore the original dimension.

4.2.   Model improvements

From Figure 2 it can be seen that the existence of X-ray image texture for steel pipes and their surface defects is scarce, with high similarity between normal and defect areas, and small differences between different defect types. For example, an air-hole type defect is a solid small circle, while a hole-head type defect is a hollow small circle. In the process of X-ray image acquisition, there is relative motion between the detected object and the camera. The hollow position of the hollow-bead defect collected by the system often contains motion blur, resulting in high similarity between these two types of defects and difficulty in distinguishing them. Second, the sources of surface defects on steel pipes are different, and the scale of defects varies greatly. For example, during the production process, high temperatures, conveyor belt transportation collisions, and other reasons can lead to the surface of steel pipes containing many small defects such as small pores or scabs. As a comparison, the scale of defects such as surface cracks in steel pipes is relatively large; Additionally, the frequency of different defects on the surface of steel pipes varies greatly, leading to a serious imbalance in the number of samples with different defects. The above issues pose serious challenges to the surface defect detection for steel pipes based on X-ray images, and they seriously reduce the accuracy of defect detection algorithms.

In order to better adapt to the detection of steel pipe defects, we have made the following improvements to YOLOv5. First, to enhance the feature extraction capacity, the recursive convolutional blocks and BoTBlock are adopted to form a new backbone framework, and the attention module CoordAttention (CA) is embedded in the new framework. By increasing high-order spatial interaction and enhancing the capture of the internal correlations of data features, different feature information for similar defects is extracted, thereby alleviating the false detection rate of the proposed method. Second, a novel C3HB module has been designed based on GnConv_Block, which is embedded in the original FPN to form a new neck structure, namely Neck+. This neck structure can enhance the fusion of spatial feature information and fully utilize the feature information of the target, thus improving the accuracy of steel pipe defect detection. Third, a novel regression loss function that considers the aspect ratio and scale has been designed to address the issue of large differences in the scale of steel pipe surface defects. Meanwhile, the focal loss ^[29] is introduced to further improve the imbalanced sample problem in the steel pipe defect dataset. Focal loss addresses sample imbalance by increasing the gradient contribution of high-quality samples during network training. The above modules can be seen in Figure 3. Details are as follows.

4.2.1.   New backbone block

The location of the proposed new backbone is given in Figure 3, and its schematic diagram is shown in Figure 4. As shown in Figure 3, one key block of the proposed backbone is GnConv_Block, which is a convolutional layer structure that contains group normalization (GN) operations. GN is a normalization operation that is more efficient when processing small batches of data, and it is more robust to the network than traditional batch normalization. GN divides the channel into groups and then independently normalizes the means and variance of the features within each group. This reduces redundancy between features and increases the differentiation of feature representations. The input of GnConv_block is a feature map, and the output feature map is obtained after a convolution operation. Before the convolution operation, a GN operation is performed on the input feature map, that is, GN is used to normalize the feature map. Then the normalized feature map is input into the convolutional layer for the convolution operation. Finally, the feature map obtained after the convolution operation is output. By introducing GN operations before the convolutional layer, GnConv_block is able to improve the expressiveness and discrimination of features. The GN operation helps to reduce correlations between features, making the features of different channels more independent and representative. Gnconv goes through a series of convolutional and fully connected layers to form the GnConv_Block module in the backbone. Following the same meta-architecture as a Transformer to build GnConv_Block, including a spatial mixing layer and feed forward network, under the condition that the accuracy would not change much, it also greatly reduces the amount of ground parameters in the calculation process, and it strengthens the spatial interaction, which is conducive to extracting the effective location information for defects in the dataset. This is very important for the training and learning process of neural networks, as it can improve the performance and robustness of the model. Therefore, GnConv_Block can improve the effect of feature extraction and classification, as well as improve the accuracy and accuracy of model detection and classification. In order to make better use of the feature information extracted by GnConv_block and better retain the position information of small targets, this paper introduces a new architectural BoTCA for the backbone part, where BoTCA consists of a component module BoT in BoTNet and a plug-and-play mobile network attention mechanism (CA). The BoT module replaces the traditional convolutional layer with a Transformer module based on the self-attention mechanism to better capture the global contextual information and improve the representation ability of features. The BoT module consists of several key components: a Bottleneck structure, a BoT block, residual connectivity, and layer normalization. Through the combination of these components, the BoT module can effectively capture global context dependencies in visual data and generate feature representations with strong representation capabilities. Compared with traditional convolutional neural networks, BoT modules have better performance in terms of handling tasks such as long-distance dependence and global information interaction. Because the attention mechanism of the CA module establishes global associations in different locations, it is more sensitive to local information. It achieves the effect of reducing the computational complexity and improving the ability to identify defective targets. In the backbone and head switch, it should be as simple as possible. Not only can the captured location information be fully utilized, but the area of interest can also be captured. Spatial relationships can also be captured effectively. In this way, the accurate position information for the global receptive field coding can be well obtained, the spatial position information for the defect target can be further extracted, and the target omission can be reduced. In the process of developing an image recognition system, it is essential to retain more important semantic information for the next step of feature extraction. This approach helps to ensure that the most relevant and distinguishing characteristics of the images are used when training the model, leading to more accurate and reliable results.

Figure 4.  Schematic diagram of the new backbone block.

DownLoad: Full-Size Img PowerPoint

4.2.2.   Neck+ block

The neck block is the key component for information fusion. The neck block of the original YOLOv5 model is mainly composed of an FPN and a path aggregation network (PAN). In order to further improve the ability of feature extraction and fusion in the model, we have optimized the neck structure by introducing a novel C3GB block based on GnConv_Block (as shown in Figure 5), referred to as Neck+. The location of the proposed Neck+ module is shown in Figure 3, and its structure is given in Figure 6. The C3GB structure consists of three convolutional layers and a sequence of GnConv_Blocks, as shown in Figure 5. It processes the input by using two different paths and then combines the results of the two paths. This design can increase the width of the network without significantly increasing the computational complexity, often helping to improve the performance of the model. Compared to the feature fusion structure of the original FPN and PAN, C3GB allows for dynamic and recursive feature fusion processes. The recursive process allows the block to capture more contextual information across continuous levels, thereby improving the model's ability to detect small targets. Meanwhile, C3GB can flexibly adjust the features of interest based on different input data, further distinguishing targets with similar appearances or shapes. After C3GB fusion, the feature fusion structure leads to more complex feature fusion due to the recursive property of C3GB, which allows the model to distinguish similar categories and reduces the possibility of defect identification errors. It also allows the model to adapt its feature extraction and fusion strategies in the training process, so as to better deal with complex defect detection tasks. Therefore, the Neck+ proposed in this paper can significantly improve the model's detection ability for small defect targets and similar targets.

Figure 5.  Schematic diagram of the proposed C3GB module.

DownLoad: Full-Size Img PowerPoint

Figure 6.  Schematic diagram of the proposed Neck+ block.

DownLoad: Full-Size Img PowerPoint

4.2.3.   Improved loss function

Our algorithm modifies the bounding box parameters, which increases the scale of the length and width of the prediction box to make the prediction box more consistent with the ground truth position.

In the original YOLOv5, the loss function used is the $CIOU$ loss function.The $CIOU$ loss function is shown in Eq (4.2):

In the $CIOU$ loss function, $v$ is the parameter used to measure the consistency of the aspect ratio, and ${\alpha}$ is the parameter used to achieve a trade-off. The $CIOU$ scales the length and width of the prediction box to ensure that the prediction box is closer to the true ground position. However, the aspect ratio in $CIOU$ is a relative value, and it is not clear and does not consider the problem of sample imbalance. Therefore, it is not suitable for surface defect detection for steel pipes. In order to overcome the above problems, a new loss function $ExIOU$ is proposed based on the improved $EIOU$. The original $EIOU$ calculates the difference between width and height based on the $CIOU$ instead of the aspect ratio, and it applies focal loss to solve the problem of sample imbalance. The $EIOU$ loss function is defined as in Eq (4.5):

where $c$ is the diagonal distance between the center points of the predicted bounding box and the ground truth bounding box, and $C_w$ and $C_h$ are the width and height of the smallest enclosing box covering both the predicted and ground truth rectangles.

Although the $EIOU$ directly minimizes the difference in width and height between the target box and the anchor box, it does not account for the scale difference of the target. However, targets at different scales may have different importance in object detection. In steel pipe defects, for defects with small targets and high similarity, the inspection process leads to low accuracy and false detection. To overcome this problem, we have improved the performance of $EIOU$ on te task of identifying steel pipe images by adding a scaling function. The proposed $ExIOU$ loss function is as in Eq (4.9):

where $S$ is the area where the target is detected. $S$ is computed by using label values to ensure that the weights are stable during training and truly represent the size of the object. When $\theta$ decreases, the value of $\theta$ approaches 0, and when $S$ increases, the value of $\theta$ approaches 1. To amplify the size error of smaller targets, 1 - $\theta$ is used as the weight of the size error. This gives smaller targets greater weight.

Regarding the proposed loss function, the weight function can improve the difference between different targets and the importance of identifying smaller defects, thereby improving the detection accuracy of small targets. Then, using the sigmoid nonlinear function to further adjust the scaling function can make the scaling function more flexible, making the fusion more responsive to actual needs. From the subsequent ablation experiments, it can be seen that $ExIOU$ is superior to the original loss function $EIOU$.

5.   Experiment

5.1.   Experimental settings

The experimental settings of this study are as follows. The development environment was Python 3.8, PyTorch (1.12.0+cu102), and CUDA 11.6. Eight percent of samples in the steel pipe defect dataset were used as the training set, and the rest of the data were used as the test set. To fully evaluate the performances of the proposed method and other compared methods, we adopted a series of indicators such as precision, recall, average precision (AP), and mean average precision (mAP). $MAP@0.5$ is the AP calculated for all images in each category for an $IOU$ of 0.5 that is then averaged.

5.2.   Experimental results

5.2.1.   Performance of the proposed method

In this section, first, we give the test results on all types of defects in Table 1 and Figure 7, and we present comparisons of the proposed method with eight other widely used detection methods in Table 2 to prove the effectiveness of the proposed method.

Table 1.  The test results for the proposed method.

f	Air hole	Broken arc	Slag inclusion	Crack	Overlap	Bite edge	Unfused	Hollow bead
Precision	51.3	100.0	93.4	99.0	99.0	100.0	100.0	99.0
Recall	98.0	100.0	100.0	100.0	100.0	100.0	99.0	100.0
AP	99.2	99.5	99.1	99.5	99.5	99.5	92.6	98.7
Computational complexity	179.6 GFLOPS
MAP@0.5	98.9
MAP@0.5_0.95	67.4

---

 | Show Table

DownLoad: CSV

Figure 7.  Some detection results for typical steel pipe defects. (a) Air hole. (b) Broken arc. (c) Slag inclusion. (d) Crack. (e) Overlap. (f) Bite edge. (g) Unfused. (h) Hollow bead.

DownLoad: Full-Size Img PowerPoint

Table 2.  Comparative experimental results on different general object detection methods.

Model name	AP	AP	AP	AP	AP	AP	AP	AP	MAP@0.5
	Air hole	Undercut	Broken arc	Crack	Overlap	Bite edge	Unfused	Hollow bead
Ours	99.2	99.5	99.1	99.5	99.5	99.5	92.6	98.7	98.9
YOLOv3	98.9	99.5	98.1	99.5	99.5	99.6	91.0	98.7	98.1
YOLOv3_spp	99.0	99.5	98.4	99.5	99.5	99.6	91.8	98.8	98.3
YOLOv3_tiny	97.2	99.5	97.2	99.5	99.5	99.5	94.1	98.6	98.1
YOLOv7	98.1	95.5	83.8	99.1	99.5	99.5	81.6	98.6	95.0
YOLOv6	-	-	-	-	-	-	-	-	92.4
SSD	-	-	-	-	-	-	-	-	88.6
Faster_RCNN	-	-	-	-	-	-	-	-	79.21

---

 | Show Table

DownLoad: CSV

From Table 1 and Figure 7, it can be seen that, for the proposed method, the precision and recall of some types of defects can be 100%, and the AP of most types of defects are greater than 99%, which indicates that the proposed method can effectively detect surface defects of steel pipes. In Table 2, we compare the proposed method with eight widely used detection methods, incluidng YOLOv3, YOLOv3_spp, YOLOv3_tiny, YOLOv6, YOLOv7, SSD, and Faster R-CNN. Among these methods, YOLOv3, YOLOv3_spp, YOLOv3_tiny, YOLOv6, and YOLOv7 belong to the YOLO family. SSD and Faster R-CNN are typical one-stage and two-stage high performance detection methods. As shown in Table 2, it can be seen that, compared to other models, the proposed method demonstrates the best performance in terms of steel pipe defect detection. The proposed method does not only improve the mAP, it also significantly improves the APs in multiple defect categories such as the air hole, broken arc, etc.

5.2.2.   Comparisons with other methods

In order to further verify the effectiveness of the proposed model, eight state-of-the-art defect detection methods were tested for comparison ^{[28,30,31,32,33,34,35,36]}, and the results are shown in Table 3; some images of typical detection results are given in Figure 8.

Table 3.  Comparison with other defect detection methods.

Model name (%)	Layer number	MAP@0.5 (%)	GLOPs
Li et al. [35]	235	98.2	12.6
Liu et al.[33]	-	98.2	-
Liu et al.[30]	412	97.8	16.3
Yang et al. [36]	607	93.9	220.6
Cheng et al. [34]	198	98.5	14.8
Ye et al. [32]	604	82.1	314.1
Zhu et al. [28]	567	98.6	145.6
Liu et al. [31]	235	98.2	12.6
Ours	501	98.9	179.6

---

 | Show Table

DownLoad: CSV

Figure 8.  Comparison between the proposed model and the method in ^[36].

DownLoad: Full-Size Img PowerPoint

From Table 3, it can be seen that the results of the proposed method are better than those of the comparison model. Note that some comparison model algorithms have poor detection results for small target defect images of steel pipes. For example, the Image-Adapt-YOLO algorithm has low detection accuracy for small targets. In this study, a new neck network structure was formed by using the C3GB module, which strengthens the ability of the model to perform multi-scale feature fusion and further improves the detection ability of the model for small targets.

Among these eight methods, the model proposed in ^[36] is similar to the method proposed in this paper. In this paper and ^[36], on the premise of using similar steel pipe datasets, YOLOv5x is used for detection. However, ^[36] mainly uses a Hough transform to detect the straight line of the weld edge and improve the detection accuracy of the model for defects. As shown in Table 3, it can be seen that the detection performance of the method in ^[36] is worse than that of the algorithm of this paper. In order to show the advantages of the proposed method in detail, the results of steel pipe defect image detection from ^[36] and this paper's algorithm are shown in detail in Figure 8, where 1 represents the algorithm in this paper, and 2 represents the algorithm proposed in ^[36]. From Figure 8 it can be seen that the performance of the method of ^[36] is worse than that of the model in this paper. It is worth noting that ^[36] reported poor detection ability on broken arc defects, while the model proposed in this paper yielded correct identification results and is more inclusive in special situations. The feasibility of the model is further verified by this set of comparative experiments.

5.2.3.   Ablation experiments

In order to further prove the portability of the model improvement demonstrated in this paper, we conducted ablation experiments on several improvement points; the results are shown in Table 4.

Table 4.  Ablation experiment results.

Result (%)	Model size	Parameters	Layers	MAP@0.5 (%)	MAP@0.5_0.95 (%)
YOLOv5x	169 MB	88,480,857	607	92.2	57.8
YOLOv5x-EIOU	173 MB	88,480,757	607	97.9	65.1
YOLOv5x-Ex_IOU	169 MB	89,607,797	607	98.7	66.8
YOLOv5x-BoT_CA	155 MB	81,268,077	635	98.6	67.4
YOLOv5x-GnConv_Block	167 MB	78,574,877	343	98.5	66.2
YOLOv5x-C3GB	202.8 MB	101,121,077	725	98.7	66.1
YOLOv5x-Ourselves	159 MB	83,244,957	501	98.9	67.4

---

 | Show Table

DownLoad: CSV

From the above ablation experiment, it can be seen that in the case of the improved model, the accuracy of different improved modules is higher than that of the original YOLOv5. In order to further demonstrate the performance of the model in this paper, the convergence processes for different models are shown, as presented in Figure 9. The figure shows the convergence of loss functions of YOLOv5, the improved YOLOv5 model (YOLOv5_EGBC) and the YOLOv7 model during experimental training and verification. It can be seen from the loss convergence diagram in the above figure that the YOLOv5 model tends to converge when the number of epochs is 60 in the steel pipe defect dataset. In the training of each model for the detection of steel pipe images, it can be seen from the convergence diagram for the loss function that the stability of the YOLOv5 series is better than that of YOLOv7, and that YOLOv7 has obvious oscillation during the training process. In the case of YOLOv5, the final improved model stability is maximized in the YOLOv5 series. It can be seen that the improved YOLOv5 model has better performance and is also more stable.

Figure 9.  Visualization of training and validation set loss functions.

DownLoad: Full-Size Img PowerPoint

5.2.4.   Additional experiment

Some experiments were carried out to reflect the difficulties in the X-ray image detection process and demonstrate the advantages of the proposed method. On the basis of the existing X-ray image dataset, we have added natural images to construct a mixed dataset. These natural images have six types of defects, including patches, a pitted surface, roll in scale, scratches, inclusions, and crazing. YOLOv5 was used for training and validation on the mixed dataset. After training, the network model trained on the mixed dataset was used for further testing on the mixed defect images. The results are shown in Table 5.

Table 5.  Mixed dataset training and validation results.

Result (%)	Air hole	Slag inclusion	Broken arc	Crack	Overlap	Bite edge	Unfused	Hollow bead	Patches	Pitted surface	Rolled inscale	Scratch	Inclusion	Crazing
AP	58.2	96.7	82.7	99.2	78.4	91.4	82.7	99.0	99.4	99.3	99.5	99.1	99.1	99.5
Test result	30.0	82.0	52.0	81.0	30.0	59.0	30.0	80.0	81.0	76.0	47.0	76.0	81.0	80.0
MAP@0.5	90.0

---

 | Show Table

DownLoad: CSV

From Table 5, it can be seen that using the same network model and parameter settings, the MAP@0.5 results for X-ray image detection are worse than those of natural images. Table 5 also shows that the defect test results for X-ray images are also worse than those for natural images. Therefore, it can be seen that object detection in X-ray images is more difficult than that in natural images.

Data are often subject to various degradations, noise effects, or variations during imaging. In ^[37], a new spectral mixture model called the augmented linear mixture model is proposed. The inverse problem of hyperspectral unmixing is handled by implementing a data-driven learning strategy, which handles the main spectral variations independently and solves the mixing difficulties due to spectral variations in hyperspectral imaging. Considering that similar interference may also occur in the application of the steel pipe defect detection model, in order to further verify the effectiveness of the proposed model under degradation factors such as noise, we have added the relevant experiments. First, influential factors such as noise were added to the steel pipe image, and then the steel pipe image was detected by using the network model proposed in this paper. The types of added noise, parameter settings and corresponding recognition results were shown in Table 6. Some of the recognition results are shown in Figure 10.

Table 6.  Noise parameter setting and identification results.

Noise type	Noise intensity	Air hole	Slag inclusion	Broken arc	Crack	Overlap	Bite edge	Unfused	Hollow bead
Salt and pepper	0.01	0.72	0.88	0.90	0.88	0.86	0.82	0.94	0.92
Salt and pepper	0.03	0.72	0.88	0.88	0.87	0.89	0.80	0.94	0.92
Gaussian distribution	20	0.78	0.87	0.90	0.88	0.90	0.86	0.94	0.94
Gaussian distribution	50	0.76	0.88	0.87	0.85	0.87	0.78	0.94	0.94
Poisson distribution	20	0.76	0.87	0.89	0.88	0.90	0.83	0.94	0.93
Poisson distribution	50	0.74	0.89	0.89	0.83	0.87	0.76	0.94	0.95

---

 | Show Table

DownLoad: CSV

Figure 10.  Detection results on images with degradation. (a) Air hole. (b) Broken arc. (c) Slag inclusion. (d) Crack. (e) Overlap. (f) Bite edge. (g) Unfused. (h) Hollow bead.

DownLoad: Full-Size Img PowerPoint

It can be ascertained from Table 6 that the proposed model has a good recognition effect on steel pipe images with influential factors, regardless of the addition of Gaussian distribution or salt and pepper noise, and there is no particularly obvious difference between different noises and different noise intensities. It can be seen in Figure 10 that the proposed network model has a good detection effect for various types of steel pipe defects when a variety of different noise and other common degradation factors are added. For example, the detection of small targets such as pores and hollow beads demonstrated high confidence and accurate positioning. There are no instances of erroneous detection of defects such as air holes, hollow beads. Therefore, under the degradation factors, the network model proposed in this paper still has good detection and identification ability, which further reflects the stability and effectiveness of the model in this paper.

6.   Conclusions

This paper first analyzes the features of the surface defects in steel pipes, and then it presents a defect detection method based on the YOLO framework. First, a new feature extraction backbone block was constructed to enhance the feature extraction capacity of the defect detection method. By increasing high-order spatial interaction and enhancing the capture capability of internal correlations of data features, different feature information regarding similar defects is extracted, thereby alleviating the false detection rate of the proposed method. Second, a new neck network structure was designed to improve the detection performance for small defects in steel pipes. By further enhancing the fusion of spatial feature information and fully utilizing the feature information of the target, the accuracy of steel pipe defect detection is improved. Third, a novel regression loss function that considers the aspect ratio and scale was proposed to address the issue of large differences in the scale has been steel pipe surface defects. Meanwhile, the focal loss has been introduced to further improve the imbalanced sample problem in steel pipe defect datasets. Extensive experiments proved the effectiveness of the proposed method. In summary, our research constitutes significant progress in the direction of addressing the challenges of low detection accuracy of small objects in steel pipe images, missed detection, and unbalanced samples, thus improving the accuracy of steel pipe defect detection. Looking forward, several avenues for further research emerge. First, exploring advanced deep learning algorithms can lead to more robust solutions for object detection in complex industrial scenarios. Moreover, integrating more diverse datasets, including those with rare defect types, can further improve the model's ability to handle sample imbalance. Finally, there is a very high possibility that these research results can be translated into real industrial applications. These future research directions not only have the potential to refine defect detection methods, but they will also make a significant contribution to the field of industrial image processing and quality control.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (62273337, 92267205), Liaoning Province Applied Basic Research Program Project(2023JH2/101300183), and Shenyang Youth Science and Technology Innovation Talent Support Program Project (RC210478).

Conflict of interest

The authors declare that there is no conflict of interest.