Data-driven optimal controller design for sub-satellite deployment of tethered satellite system

1.   Introduction

Tethered satellite systems (TSSs) are comprised of multiple satellites connected by tethers and are primarily used for tasks such as collecting cosmic dust particles and observing the mechanisms of the sun's impact on terrestrial climate and weather changes ^[1,2]. Compared with other aircrafts ^[3,4], the TSS has attracted the attention of many researchers due to its unique advantages and practical experiments have been conducted to study the concept of a satellite system ^[5,6].} The TSS mission includes deployment, maintenance, and retrieval phases. During actual works, the space tether may experience severe oscillations with deployment and retrieval phases, which can lead to a decrease in system performance or even system instability. Therefore, achieving a rapid and stable system is a fundamental and challenging task ^[7,8]. The TSS is connected by a flexible tether. Based on different research tasks and purposes, scholars have proposed various tethered system models, such as rigid model, elastic rod model, chain bead model, and the finite element-based model. The rigid model, which assumes that the tether does not experience bending or torsion and neglects its elasticity and flexibility, leads to simplified dynamic equations and is commonly used in control research ^[9,10].

Over the years, a series of control methods have been developed to suppress the oscillation behavior of sub-satellites during the deployment phase of the TSS ^[11,12]. According to the type of control behavior, they can be divided into methods that consider both platform thrusters and tension control and methods that only consider tension control ^[13,14]. For example, Takeichi et al. ^[14] proposed a switch controller to dominate the thrusters installed on the sub-satellites for making the TSS perform periodic motions in orbit. However, due to the high energy consumption and complexity of the propulsion system, adjusting tension alone has become an energy-efficient and effective way to achieve system control. Since the TSS is a nonlinear system, some scholars have considered using sliding mode control strategies ^[15,16]. Xu et al. ^[17] designed a novel fractional-order fuzzy sliding mode control strategy to ensure the TSS stability with input saturation. Zhao et al. ^[18] proposed a pulse adaptive hyper-twisting sliding mode control scheme to complete the tether retrieval action, which can make the state vector converge to the origin in a finite time. Razzaghi et al. ^[19] used adaptive sliding mode control and state-dependent Riccati equation control methods to achieve stability of the TSS system and the dislodging of space debris. Li et al. ^[20] developed a novel fractional-order nonsingular terminal sliding mode control scheme to guarantee the desired deployment performance of the TSS. Moreover, sliding mode control strategies can cause the state trajectory to oscillate around the equilibrium point after reaching the sliding mode surface, which is a major obstacle in practical applications. Compared with other control strategies, the optimal control strategy considers the dynamic changes and uncertainties of the system, has significant advantages in optimization performance, adaptability, and robustness, and is suitable for dealing with complex systems and nonlinear problems. Fujii et al. ^[21] was the first to apply optimal control methodology to tether deployment/retrieval. They formulated an optimization problem where the objective was to minimize a combination of the square of the tether tension and the libration angle. In their work, the tether was assumed to be massless, and the analysis disregarded disturbances such as atmospheric friction, gravitational disturbances, and solar radiation pressure. Additionally, uncertainties in the tether parameters were not taken into account. In ^[22], Koakutsu et al. investigated optimal deployment control for a microsatellite with the objective of minimizing the integral square of the tether length rate. They also incorporated a term in the cost function to ensure a high tether tension. This specific cost function was chosen to enhance the tracking controller's capability to follow the desired trajectory even in the presence of disturbances.

In a multi-network environment ^[23,24,25], some scholars have started considering using data-driven algorithms to solve the TSS control problem. Vafamand et al. ^[26] used the radial basis function to estimate the unmodeled dynamics of the system online and obtained a robust adaptive backstepping controller to mitigate the TSS oscillation. Ji et al. ^[27] proposed a sub-satellite speed control strategy based on adaptive neural dynamics. Ma et al. ^[28] studied a deep learning predictive control method based on the nonlinear model for the derailment behavior of electric TSS. However, the above literature ignores the measurement data with noise, which can cause the iterative bias of data-driven algorithms. These sources of noise can result in measurement errors in attitude estimation or distortion in control commands, thereby affecting the satellite's attitude control. It can be considered to use the Kalman filter to process data and then realize the design of the online control algorithm based on data. Chen et al. ^[29] designed the Kalman filter based on a machine learning algorithm and discovered secondary processing of the standard deviation of inductive signal. Li et al. ^[30] proposed a hybrid method of the deep learning method and Kalman filter for the estimation of state of charge. Kheirandish et al. ^[31] studied the mobile robot with two sensors that are fused using an interacting multiple model Kalman filter based on both unscented and extended Kalman filters. It can be seen that the practical application scope of the Kalman filter is very wide and practical ^[32,33,34], but its combination with TSS is still rare. The advantages of using the unscented Kalman filter (UKF) include their ability to handle nonlinearities without linearization, improved accuracy compared to the extended Kalman filter, robustness to non-Gaussian noise, and reasonable computational complexity. These factors make the UKF a popular choice for state estimation in various fields, including robotics, navigation systems, and control applications. The main purpose of using the UKF in the paper is to provide more accurate measurement data of the tether length and the libration angle through denoising, aiming to enhance the performance and accuracy of the machine learning algorithms.

The subject of this paper stems from practical needs and focuses on addressing the error issue caused by measurement noise during the sub-satellite deployment phase, as well as the stabilization problem of the libration angle. The primary contributions are briefed below:

● Based on the motion behavior of the TSS during the sub-satellite deployment phase, a dynamic equation is established and then transformed into a state equation that incorporates nonlinear functions and disturbances, with a particular focus on the relative variations and relationships among the state variables.

● Due to the nonlinear nature of the TSS, the optimal control gain cannot be solved solely through the Hamiltonian equation. We consider incorporating critic-actor neural networks to utilize the data for discovering the optimal controller.

● Measurement data often contains noise and uncertainty in the TSS. By applying an UKF, the measurement data can be filtered and smoothed, removing or reducing the interference caused by noise and providing more accurate and reliable data as input for critic-actor neural networks.

The rest of this paper is organized as follows. Section 2 gives the tethered satellite dynamics. Section 3 designs the UKF for estimating the state. Section 4 designs the optimal controller. Section 5 gives an approximate solution based on critic-actor neural network. Section 6 simulates the numerical example. Section 7 gives the summary and looks forward to the future work.

2.   Tethered satellite dynamics

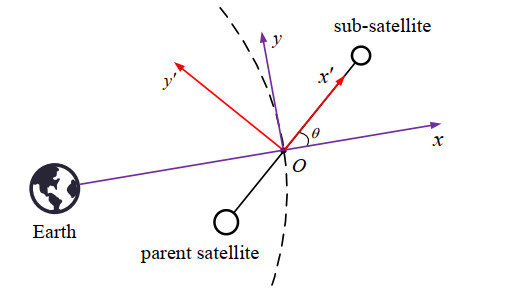
Figure 1 shows the geometric model of the TSS, which mainly includes parent satellites, sub-satellites, tethers, and winch control mechanisms. In this paper, we concentrate on the change of the libration angle and ignore the spin angle. To facilitate the study, the following assumptions are given ^[35,36].

● The TSS and the earth approximately form a two-body system.

● The dumbbell model is used to describe the spatial position state of the TSS; that is, two satellites are regarded as the mass points, the tether mass and the flexural stiffness are not considered, and the tether length direction is rigid.

● The system is orbiting in a circular Keplerian orbit in a central gravitation field of the earth.

Next, the dynamic equation of the TSS is established as follows.

where $l$, $\dot{l}$, and $\ddot{l}$ represent the tether length, the tether velocity, and the tether acceleration, respectively. $\theta$, $\dot{\theta}$ and $\ddot{\theta}$ represent the libration angle, the libration angle velocity, and the libration angle acceleration, respectively. $\Omega$ is the orbital angular velocity. $T$ means the tether tension. ${\bar m} = m_1m_2/\left(m_1+m_2\right)$, where $m_1$ indicates the mass of the sub-satellite and $m_2$ indicates the mass of the parent satellite.

Due to the significant differences in the orders of magnitude of physical systems and the influence of unit selection in equation transformation on controller design and algorithm simulation implementation, it is necessary to perform dimensionless on Eq (1). The dimensionless variables are introduced as follows.

where $\lambda \in [0, 1]$ is the dimensionless tether length, $L$ is the total deployment tether length, and $\tau = \Omega t$ is the dimensionless time, then we get

Define ${\textbf x}\left(\tau \right) = {\left[{\begin{matrix} {{x_1}} & {{x_2}} & {{x_3}} & {{x_4}} \\ \end{matrix} } \right]^{\text{T}}} = {\left[{\begin{matrix} {\lambda - 1} & {\dot \lambda } & \theta & {\dot \theta } \\ \end{matrix} } \right]^{\text{T}}}$ and $u\left(\tau \right) = - \frac{T}{{\bar{m}{\Omega ^2}L}}$, where $x_1 \in [-1, 0]$. Real time measurement of the libration angle is obtained using a sensor, but the measurement data and process data often suffer from the presence of noise, then Eq (3) becomes

where ${\textbf x}(\tau)$, $y(\tau)$, $w(\tau)$, and $v(\tau)$ are system state, measurement output, process noise, and observation noise, respectively. Let $w(\tau)$ and $v(\tau)$ be uncorrelated Gaussian white noise and the covariances are $P$ and $\Gamma$, respectively. The initial expectation of the system state is ${\hat{{\textbf x}}_0}$ and the initial variance is ${{\textbf D}_0}$, and

3.   Design of unscented kalman filter

System (4) has process noise and measurement noise, no matter if it is from the point of view of control or measurement, so the whole process of satellite release requires human intervention. Therefore, it is necessary to use a UKF to estimate the system state and carry out the system robust control.

Referring to ^[37], a UKF is established based on system (4) with the following specific steps:

1) Calculate the sigma point of the state through unscented transformation. We define

where ${\textbf X}(\tau)$ is the sigma point matrix, $\hat{{\textbf x}}(\tau)$ is the state estimation, $\zeta = \sqrt {\left({n + \epsilon } \right){\mathbf D}\left(\tau \right)}$ is a positive semi-definite matrix, $n$ is the state dimension, $\epsilon = {\alpha ^2}\left({n + \beta } \right) - n$, $0.0001 \leqslant \alpha \leqslant 1$ and $\beta$ are designed parameters, and ${\mathbf D}\left(\tau \right)$ is the state variance.

2) Calculate the corresponding weight of the sigma point set. We select the number of sigma points as $2n+1$, then we have

where $W_j, \, j = 0, 1, \ldots, 2n$ are the corresponding weights of the sigma point, respectively, then we can obtain

3) Calculate the Kalman gain ${\mathbf K}\left(\tau \right)$.

4) Update the state and covariance of the system.

where ${\mathbf \digamma}\left({{\mathbf X}, u} \right) = {\mathbf f}\left({\mathbf X }\right) + {\mathbf B}u\left(\tau \right)$.

Based on Eqs (9)–(16), the predicted value of the state at each moment is calculated and then passed to the controller to realize the control of the TSS. The block diagram of control model based on UKF is shown in Figure 2.

4.   Design of optimal controller

From Eqs (3) and (4), it can be seen that the libration angle is mainly realized by the real time adjustment of the tension in the release phase. Therefore, it is necessary to design an optimal control strategy to ensure that the libration angle is finally stabilized. Based on the UKF, we can use $\dot{\hat{{\mathbf x}}}(\tau)$ in system (15) to solve the control problem of system (4). The performance index function is established as

where ${\mathbb{E}}\left\{ \cdot \right\}$ denotes the expectation and ${\mathbf Q}$ and $R$ are both symmetric positive definite matrices. Furthermore, the Hamilton equation can be obtained as

where $\nabla V = \frac{{\partial V\left({\hat{{\mathbf x}}, u} \right)}}{{\partial \hat{{\mathbf x}}\left(\tau \right)}}$.

Based on the Bellman optimality criterion, we have

The optimal controller obtained by (19) may have a positive value, which means that the tether tension is negative. Considering the actual physical constraints, the situation of negative tether tension cannot be realized in practice, so the controller given in (19) is modified as follows:

This indicates that when the control signal is negative, the value remains unchanged, otherwise it updates to 0.

Theorem 1. Considering that ${V^*}\left({\hat{{\mathbf x}}, u} \right)$ is the solution of the Hamilton equation and the optimal control strategy is given by Eq (20), the closed-loop system (15) is an asymptotic stability.

Proof. Letting ${V^*}\left({\hat{{\mathbf x}}, u} \right)$ be a Lyapunov function, we can get

For all cases of Eq (20), it holds true that ${{\dot V}^*}\left({\hat{{\mathbf x}}, u} \right) \leqslant 0$. Therefore, the closed-loop system (15) is an asymptotic stability. The proof is completed. □

5.   Approximate solution based on critic-actor neural network

Since the Hamilton equation is nonlinear and has no explicit solution, then in order to solve the Hamilton equation, this paper considers using the critic neural network to approximate the performance index function and the actor neural network to approximate the control strategy.

5.1.   Critic neural network

First, using a critic neural network to approximate the performance index function, we can obtain

where $\hat{{\mathbf W}}\left(\tau \right)$ is the weight matrix, which is updated in real time during the training process. $\varphi \left(\cdot \right)$ represents the activation function. ${\mathbf \Xi} \left(\tau \right)$ is the input variable composed of $\hat{{\mathbf x}}\left(\tau \right)$ and $u\left(\tau \right)$, that is,

Thus, the Hamilton equation for each step is obtained as

where $\Delta {\varphi ^{\text{T}}}\left({\mathbf \Xi} \right) = {\varphi ^{\text{T}}}\left({{\mathbf \Xi} \left({\tau + \Delta T} \right)} \right) - {\varphi ^{\text{T}}}\left({{\mathbf \Xi} \left(\tau \right)} \right)$ and $\Delta T$ is the sampling interval.

Furthermore, the mean square residual function is given as $E_v(\tau) = \frac{1}{2}e_v^T(\tau)e_v(\tau)$, and for any feasible control strategy, the expected $\hat{{\mathbf W}}$ is selected to ensure the minimum mean square residual based on ^[38].

where ${\alpha _v} > 0$ is the critic neural network gain.

5.2.   Actor neural network

Define an actor neural network for approximating the control strategy

where ${\hat {{\mathbf W}}_u}\left(\tau \right)$ is the weight matrix, which is updated in real time during the training process. $\phi \left(\cdot \right)$ represents the activation function.

In order to find the controller that minimizes $\hat V\left(\tau \right)$, introduce the actor neural network error function

where $g\left(\tau \right)$ is the final utility function, which takes different values in different fields. This paper sets $g\left(\tau \right) = 0$.

According to the actor neural network, define the objective function

For ensuring that the objective function is minimized, the actor neural network weight matrix is updated as

where ${\alpha _u} > 0$ is the actor neural network gain, and

6.   Numerical simulation

The TSS parameters of an actual model (as shown in Table 1) are used for simulation verification. The initial state of system (4) is ${{\mathbf x}_0} = \left[{\begin{matrix} { - 0.99} & 0 & {-1.06} & 0 \\ \end{matrix} } \right]$. Consider the covariance of process noise $w\left(\tau \right)$ and measurement noise $v\left(\tau \right)$ is $P = {0.1^2}$ and $\Gamma = {0.01^2}$, respectively. We set the controller to 0 and obtain the state trajectories of the open-loop system, as shown in Figure 3. It can be seen that the system is divergent.

Next, the initial expectation and variance of the system state are given as ${\hat{{\mathbf x}}_0} = {\left[{\begin{matrix} 0 & 0 & 0 & 0 \\ \end{matrix} } \right]^{\text{T}}}$ and ${{\mathbf D}_0} = 100 \times {{\mathbf I}_{4 \times 4}}$. In views of Eqs (9–16), the optimal control strategy (26) ensure the stability of the closed-loop system (4). The closed loop system state trajectories based on UKF and the true system state trajectories are shown in Figure 4. Let ${\mathbf e}(\tau) = {\mathbf x}(\tau)-\hat{{\mathbf x}}(\tau)$, then we can get the error trajectories between the estimated state and true state, as shown in Figure 5. It can be seen that the control effect of the state and the error between the estimated state and the true state are highly satisfactory, which indicates the accuracy and efficacy of the state estimation and control processes. The measurement output trajectory is shown in Figure 6, and its practical significance is that the libration angle is stabilized to ensure that the TSS is always in a balanced position under the optimal control strategy. The optimal control strategy and the corresponding weights are shown in Figures 7 and 8, which shows that the control strategy is effective for system (1) and the weights are eventually uniformly bounded. Although the system achieves stability through the application of the UKF and controller design, it is important to acknowledge that the libration angle of the satellite may still exhibit oscillations in the vicinity of the equilibrium point. This phenomenon arises due to the system's inherent nonlinearities, time-varying characteristics, or other complex dynamic properties. Additionally, due to the initial instability of the system and the rapid release of the tether during the early stages of satellite deployment, there is a possibility of zero tether tension. Therefore, it is possible for the control input $u(t)$ to be zero during the initial period.

Furthermore, for comparison purposes, the TSS model is linearized, the linear state feedback controller given below will be used under the same initial conditions ^[39],

and we get the estimated state trajectory with controller (31) and the corresponding controller trajectory as shown in Figures 9 and 10. Through comparison, it is observed that the system converges at 2 orbits under controller (31), while the control strategy presented in this paper ensures the system converges at 1.5 orbits. This indicates that the control strategy proposed in this paper achieves faster convergence and better stability compared to controller (31).

To analyze the effects of the controller on tether tension, we conduct simulations where the tether is released at a constant velocity. In this scenario, the sub-satellite separates from the parent satellite as the tether is steadily released, which shows that the speed of the tether is limited. We can then solve the libration angle and tension changes according to Eq (1). We compare the changes in tension with the controller to the changes in tension when the tether is released at a constant velocity. The resulting tether tension is illustrated in Figure 11. By comparing tension trends between two conditions, it becomes evident that the controller significantly influences the tether tension. When the tether is released at a constant velocity, the tension displays fluctuations and potentially reaches higher magnitudes, indicating a lack of control over the tether dynamics. Conversely, with the controller, the tether tension demonstrates a more stable and controlled response. The controller effectively regulates the tether tension, minimizing oscillations and ensuring it remains within the desired range.

In our study, similar to the literature ^[17,27,39], we have chosen a relatively short time horizon, primarily due to computational constraints and the need to demonstrate the feasibility and provide initial validation of the proposed control method. Moreover, since the system has already stabilized within 3 orbits, the effectiveness of this approach has been thoroughly proven. Therefore, extending the time dimension is unnecessary in this paper.

7.   Conclusions

This paper presented a data-driven optimal control method for reducing the libration angle oscillation of a sub-satellite during the deployment process of a TSS. By establishing the dynamic state equation of the TSS, a UKF was utilized to estimate the system state and the optimal control strategy was designed based on the performance index function and the Hamiltonian equation. Since the optimal control strategy cannot be represented by an explicit solution, a data-driven control algorithm based on the critic-actor neural network was implemented to ensure the stability of the closed-loop system. Finally, a simulation showed the applicability and effectiveness of the control strategy in reducing the tether vibration of the disturbed system. In future work, the proposed method can be extended to handle more complex scenarios, such as multi-agent systems, or systems with uncertainties in the dynamics or disturbances. To assess the effectiveness of the control method more accurately in practical applications, we will explore the possibility of utilizing a practical tether model in further research.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was supported in part by the National Natural Science Foundation of China (62173030) and in part by the Beijing Natural Science Foundation (4222050).

Conflict of interest

The authors declare there are no conflicts of interest.