Speaking territories in the cultural landscape: Challenges of transformation in the Central Europe

1.   Introduction

It is getting harder and harder to control the spread of infectious diseases among humans, and accordingly, studies on infectious disease research have been more prevalent in the literature in recent years. Coronaviruses (CoV) are a large family of viruses that cause diseases ranging from the common cold to more serious diseases such as Middle East Respiratory Syndrome (MERS-CoV) and Severe Acute Respiratory Syndrome (SARS-CoV).

The coronavirus disease (COVID-19) was first identified in December 2019 in the city of Wuhan, Hubei province of China, and the World Health Organization (WHO) declared the virus temporarily New Coronavirus-2019 (2019-nCoV) on February 11, 2020 and named the disease Coronavirus Disease-2019. The first confirmed case of the virus was discovered on17 November 2019 in Hubei.As of July 5, 2020, more than 11.1 million cases have been reported in 188 countries around the world, resulting in more than 528,000 deaths [1].

Depending on the age and immune system of each individual, COVID-19 has many features that differ from other infectious diseases, including high infectiousness during incubation, the time delay between real dynamics and the number of confirmed cases observed daily, and the response effects of quarantine and control measures applied. Although the incubation period of COVID-19 varies greatly among patients, it is known that it is between 3–7 days, with a maximum of 14 days. The new coronavirus is believed to be contagious during the incubation period when patients do not show any symptoms. This has been shown to be an important feature that distinguishes COVID-19 from SARS [2].

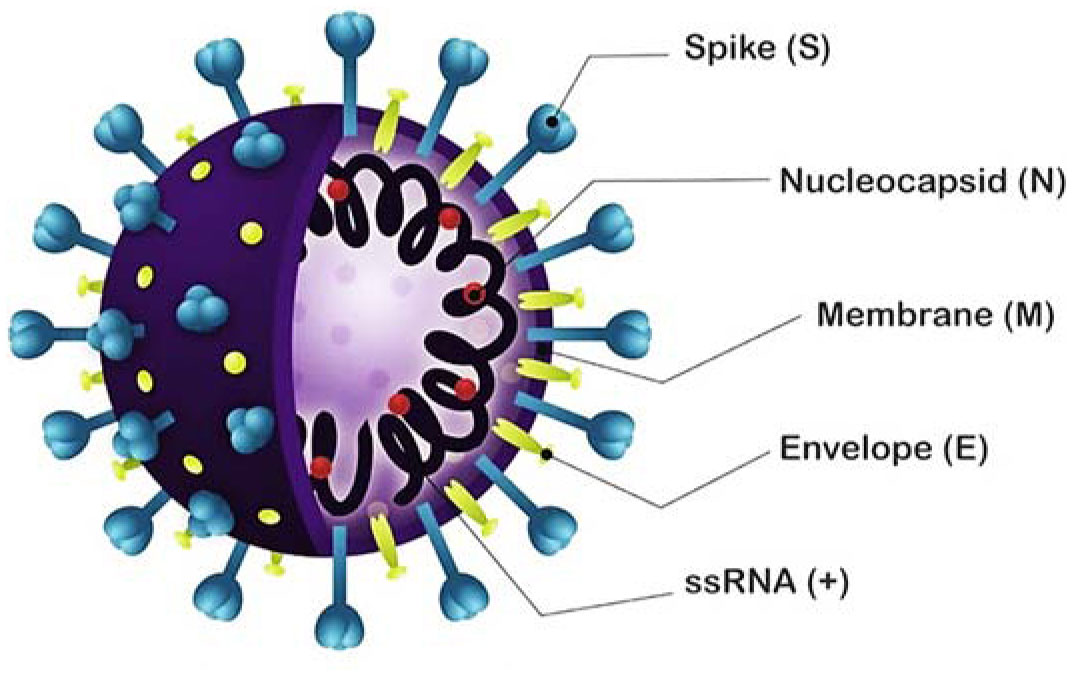
The Scientific Committee of Turkish Republic, which was established under the Ministry of Health General Directorate of Public Health, prepared and published a study on the schematic structure of the COVID-19 virus on March 23, 2020. According to this study, coronaviruses are single-stranded, positive-polarity, enveloped RNA viruses. Because they are positively polarized, they are dependent on RNA, but they do not contain the enzyme RNA polymerase, but encode this enzyme in their genome. They have rod-like extensions on their surface. Based on the Latin meaning of these protrusions, “corona”, that is, “crown”, these viruses were named coronavirus (crowned virus). Details of this virus are shown in the explanations of the Figures 1,2 [3].

Existing modeling studies of COVID-19 often focus on epidemiological issues and help predict the effectiveness of various interventions to reduce the basic reproduction number of the virus and the escalation of the disease [6]. There have been a number of producitve and illustrative studies have been performed by the scientists recently related to the modelling of real-life problems, such as modelling of COVID-19 [7]–[14], global threshold of Kermack-McKendrick model [15], the acute sill of an ecological model [16], wastewater treatment under unstable physical and chemical laboratory conditions [17], a sewage treatment model with general higher-order perturbation [18], synchronization [19], chaos of calcium diffusion [20], stability characterization of a fractional-order viral system [21], distributions with variable transmuting parameter [22], cancer models [23], Uncertainty-based Gompertz growth model for tumor population [24], e-cigarette smoking model [25], transmission of nipah virus dynamics [26], disturbances in the calcium neuronal model [27], generalized diffusion characteristics of calcium model [28], solitary wave solutions [29].

The first coronavirus infection in Iraq was discovered on February 22, 2020, in an Iranian student in the city of Najaf. A family who had just returned from Iran tested positive for COVID-19 in the city of Kirkuk, on February 25, 2020. The death of a 70-year-old cleric in the city of Sulaymaniyah on March 4 has been identified as the first coronavirus death. The disease has spread to all 18 provinces of Iraq as of March 27. Infections were observed to increase continuously after mid-March 2020. Later, the Iraqi government took the necessary measures. Health measures have increased with full or partial curfews and travel restrictions. Schools, universities and cinemas in Iraq were closed. Later, large public and religious gatherings in cities were prohibited. The Iraqi Ministry of Health declared a nationwide curfew on 30 July, except for the Iraqi Kurdistan Regional Government. The large number of reported cases has led us to examine the spread of COVID-19 in Iraq.

Best of our knowledge, there has not been provided any study so far related to the COVID-19 mathematical model using real data from Iraq and contains vaccination and quarantine processes. This can be regarded as one of the major novelties of the paper. The rest of the paper can be summarized as the following: In Section 2, the main mathematical model is formulated. In Section 3, fundamental mathematical analysis is provided. In Section 4, numerical estimations of the model parameters are achieved by using the parameter estimation technique. In Section 5, the sensitivity analysis of the basic reproduction number is discussed. In Section 6, a solution technique to the nonlinear differential equation system is proposed. In Section 7, the numerical solutions and simulations are presented. Finally, in Section 8, concluding remarks and several informative suggestions to the future related papers are given.

2.   Model formulation

Mathematical models can reflect how communicable diseases progress to show possible consequences and can assist public health interventions by informing those concerned. The models use maths together with basic assumptions and aggregated statistics to find various infectious diseases and parameters. Parameters are used to calculate the effects of different interventions. Modeling can help decide which interventions to avoid and which to try, or it can predict future growth patterns. The most widely applied dynamic model in epidemiology is SEIR models. The SEIR model consists of four parts: susceptible individuals S(t) exposed individuals E(t), (infected but not yet infectious, in a latent period), infectious individuals I(t) and recovered individuals R(t) [30]. In this study, to describe the dynamics of the COVID-19 pandemic in Iraq, the SEIQVR model, which is a generalization of the classical SEIR model, was obtained by including two new classes, the vaccinated population V(t) and the quarantined population Q(t). The model shows effect of incubation times, vaccine effect and quarantine period on the spread of COVID-19 in symptomatically contagious sections. Thus, the epidemic model was formulated by dividing the Iraqi population into six. Susceptible individuals (S) are shown in the first compartment.

In the second compartment, there are exposed individuals (E) who have been exposed to the disease but do not show any symptoms and can transmit their diseases to susceptible individuals. In the third compartment are infected individuals (I). In the fourth compartment, there are quarantined individuals (Q) who are quarantined by not making contact with anyone for a period equal to the longest incubation period of the disease. The fifth compartment contains post-vaccinated individuals (V). In the sixth compartment, there are recovered individuals who recovered by gaining immunity against COVID-19 (R). Some of these individuals may be exposed to the disease again. Total population size is represented by N(t). In this case, the total population and the corresponding mathematical model are given by Eqs 1,2, respectively.

The definitions and values of the parameters of the model given in system (2) are presented in Table 1, subject to the initial conditions,

In the system of equations above, η indicates the ineffective vaccine (0 ≤ η ≤ 1). So, (1 − η) represents the vaccine effectiveness. If η = 0, the vaccine provides 100% protection against the disease. Figure 3 shows the flow diagram of the COVID-19 mathematical model created for this study and the details of which are given above.

3.   Analysis of the model

In this section, the non-negative solution region, constraint, equilibrium points, basic reproduction number and stability analysis for the system given in Eq 2 are considered.

3.1.   Non-negative solution region and boundedness

The positivity and boundedness of the solutions of the system given by Eq 2 with the help of the set formed with the following initial conditions

Theorem 3.1. System (2) remains positive in the Ω region.

Proof: Consider the initial conditions (3) and consider that S around t₁ is zero before the other state variables become zero.

This indicates that S is a non-decreasing function of time around t₁. Therefore, S remains non-negative. The same is true for other populations.

Thus, we obtain the non-negative state of all six state variables, from which it follows that ℝ+6 is a positive solution region for the model (2).

Theorem 3.2. System (2) is bounded in the region Ω and moreover,

holds.

Proof. Summing up all the equations of model (2), it is seen that the total population satisfies the following equations:

Thus, N(t)≥Λµ is obtained if dNdt≤0. In particular, if N(t)≤Λµ, then N(t)≤N(0)e−µt+Λµ(1−e−µt). This gives the boundedness of the total population. Also, if N(0)>Λµ, then either the solution enters Ω in finite time or N(t) asymptotically approaches Λµ. Therefore, all solutions in the ℝ+6 fall within the Ω region.

3.2.   Equilibrium points and stability analysis of the proposed system

In this section, firstly, the equilibrium points of the proposed system (2) are given. Then, the stability of healthy and diseased equilibrium points is discussed in the following theorems. The right parts of the system (6) are set to zero and thus equilibrium points are found. If the infected compartments are taken as zero, non-infected, that is, healthy equilibrium points (SDN (disease-free equilibrium)) are obtained. Then the system of equations

takes the form. In system (6) infected compartments (diseased) “E, I, Q” is taken as zero, SDN=(Sd,0,0,0,Vd,0) is found. Here;

is in the form. Another balance point is the infected diseased (endemic) balance point (EDN) known as E*=(S*,E*,I*,Q*,V*,R*) balance point and is calculated as following:

3.3.   Basic reproduction number

Known as the basic reproduction number, R₀, is a parameter that measures the number of people an infected person will infect. It is also known as the secondary infection rate in epidemic diseases and gives important information about the future course of the disease. In this case, all people are sensitive. Determining this ratio is important for mathematical models that examine the spread behavior of a virus such as COVID-19. The reproductive coefficient R₀, which plays an effective role in the spread of the disease related to COVID-19, has a significant impact on modeling such diseases by using data from multiple epidemics such as COVID-19 variants seen during the epidemic and various social epidemic rates determined during the course of the epidemic. The new generation matrix method given in [31] was used to calculate the basic reproduction number of system (2). Then

Let's consider system (2) as:

Here while obtaining matrix ℱ, the first infected individuals in system (2) are taken into account. All remaining parameters form 𝒱 matrix.

With the new generation matrix method, the corresponding Jacobian matrices at the sick equilibrium point of ℱ and 𝒱 matrices are calculated as:

According to the new generation matrix method, the spectral radius (the largest of its eigenvalues) of the FV⁻¹ matrix is called the fundamental reproduction number. To construct this matrix, let's first find the inverse of V

Here, matrix F is a non-negative matrix, and matrix V is a non-singular matrix. Basic reproduction number denoted by and R₀, which is considered the spectral radius of the FV⁻¹ matrix at the disease-free (healthy) equilibrium (SDN) point:

If R₀ = 0, then there is no risk. If R₀ = 1, this is considered a stable situation: the infected person infects only one person, and the newly infected person infects another person. If R₀ < 1, on average an infected individual infects less than one individual during the contagious period, thus reducing the rate of spread of infection. This indicates that the infection will gradually fade and the epidemic will stop. If R₀ > 1, the risk of epidemic increases; In this case, the disease is considered as a pandemic, for example, if R₀ = 2, the infected person transmits the infection to two people, and the number of individuals infected in this way gradually increases. For the proposed model (2), let's state the theorem that gives the stability criteria in order to analyze the stability points obtained by (6):

Theorem 3.3. [32] For the stability of the healthy equilibrium point

Let's consider inequality (10) and define the characteristic equation of SDN consisting of eigenvalues as follows:

In this case, in order for all roots of the characteristic Eq 11 to satisfy the condition (10), that is, to be stable, the following conditions are considered:

a) For w = 1, in Eq 11 must be ξ₁ > 0.

b) For w = 2, the Routh–Hurwitz conditions of Eq 11 or the following conditions must be hold.

c) For w = 3, the necessary and sufficient conditions satisfying (10) if the discriminant of the polynomial D(λ) are positive: ξ1>0,ξ3>0,ξ1ξ2>ξ3.

Theorem 3.4. Healthy equilibrium point of the system (2), if R₀ < 1 is locally asymptotically stable, if R₀ > 1, it is unstable.

Proof. The Jacobian matrix of (2) at the healthy equilibrium point is:

If the healthy equilibrium points (7) in (12) are substituted in the Jacobian matrix, the eigenvalues of this matrix are obtained as:

Since λ_1,2,3,4,5 < 0, it must be λ₆ < 0 for the stability of the healthy equilibrium point. This means R₀ < 1. Thus, if R₀ < 1, since all eigenvalues will be negative, the healthy equilibrium point will be locally and asymptotically stable. When R₀ > 1, although other eigenvalues are negative, the healthy equilibrium point will be unstable since λ₆ > 0.

Now, let's do the stability analysis by substituting the endemic equilibrium point in the Jacobian matrix.

Theorem 3.5. If R₀ > 1, the endemic equilibrium point of the system (2‏) is locally and asymptotically stable. R₀ < 1 is unstable.

Proof. The Jacobian matrix of (2) at the infected equilibrium point E* of the COVID-19 epidemic model is as follows:

The characteristic equation of the matrix is Φ0(λ)=(λ+µ)(λ+µ+θ2)(ϵ2+λ+µ+µ1+θ1)(λ3+A1*λ2+A2*λ+A3*)=0. The first three roots of the above Jacobian matrix −µ,−(µ+θ2) and −(ϵ2+µ+µ1+θ) are negative, for the remaining roots the following equation is obtained:

Here

If this last inequality is satisfied, it follows from the Routh–Hurwitz criterion (Theorem 3.3) that the endemic balance of the system E* is locally and asymptotically stable.

4.   Parameter estimation

The parameter estimation (PE) technique is to provide the best fit curve to the real data. Recently, there have been many studies that allow us to find the parameter values closest to the real data. With the help of the PE method, the most realistic parameter values are calculated for the proposed mathematical model. In most of the studies, the numerical values of the parameters are the estimated parameter values used in the previous studies. As model-specific parameter values are calculated with this method, the use of these specific and more accurate values more clearly shows the consistency of the obtained model. Parameter estimation is very important for a more realistic mathematical model study. Parameter estimation increases the reliability of the model created to better understand the future state of the disease and the transmission dynamics of the epidemic. The PE method is important in terms of calculating the model-specific parameter values and thus discussing the result of the study on the basis of using the most appropriate parameter values. The working process of this method is as follows:

• Determination of constants (c) for problem solving:

minc∥(c,cdata)−ydata∥22=minc∑(X(c,cdatai)−ydatai)2, where cdata and ydata are matrix or vector; X(c,cdata) function is the same dimensional matrix or vector value function as ydata, cdata represents input values (real data), ydata represents output values (numerical solution).

• In case of m-limit in parameters, this lower and upper limit can be shown as lb and ub respectively. Thus, c, lb and ub can be vector or matrix.

• “lsqcurvefit” MATLAB code easily obtains a suitable interface for data fitting problems and requires a user-defined function to calculate the following vector-valued function: By using the “least squares curve fitting technique”, the most accurate (closest to the approximate solution) curve was found by trying to make the parameters based on the principle of minimizing the sum of the squares of the differences between the real values more suitable for the model [33].

Thus, 9 biological parameters estimated with the help of least squares curve fitting method were obtained as shown in Figure 4. Real cases of COVID-19 are shown with red circles in Figure 4, while the curve that best fits the actual data is shown with a blue solid line. The parameter values that make up the curve with the best fitting of the proposed COVID-19‏ ‏model's solution to real cases and graphed in Figure 4 are also listed in Table 1.

While obtaining these values, COVID-19 cases in Iraq between 1–30 June 2022 were taken into account. Thus, by using real data, the curve that best fits these real data was tried to be obtained and the following curve was created:

There are a total of 11 different parameter values in the model created for the COVID-19 epidemic, and the natural death rate (µ) from the parameters was taken according to the data in the literature that were not calculated by the parameter estimation method [5]. The average life expectancy of an Iraqi citizen is 72.4 years [5]. This corresponds to the value µ=1/(72.4×365) on a daily basis. In Addition, the total population of Iraq is 41 million 190 bin 658 people [34] and the limited population in the absence of COVID-19 is Λµ. The (initial conditions) of the compartments are taken as follows, according to the COVID-19 cases published by the Ministry of Health in Iraq (Iraq Ministry of Health, 2022): S(0)=28189333, I(0)=110, V(0)=10696926, R(0)=2302039. However, the initial conditions for exposed individuals and individuals in quarantine are estimated as follows: E(0)=250,Q(0)=2000.

5.   Sensitivity analysis

In this section, the sensitivity of R₀ will be analyzed according to the parameters affecting the basic reproduction number. The sensitivity measure expresses the relative changes in the basic reproduction number caused by a change in a certain parameter. More detailed information on sensitivity analysis of model parameters can be found in [35]. Considering the importance of the basic reproduction number in the calculation of disease spread variation, the sensitivities of the parameters in model (2) are found as follows:

Considering the equations obtained above for sensitivity analysis, it is seen that R₀ value increases for Λ, β and η values, and decreases for other µ, k₁ and ϵ₁ values. This explains that parameters with negative values of the derivative should be maximized in the population to reduce the spread of the disease. Parameter values and basic reproduction number for all graphs created in this section were created by considering the COVID-19 cases in Iraq between 1-30 June 2022 and the results were obtained with the MATLAB R2017b package program.

Figure 5 shows the variation of R₀ with respect to ϵ₁ and β. As β values get closer to 1 (when ϵ₁ values are less than about 0.5), R₀ gets values greater than 1, that is, the disease gradually increases; it is also seen that R₀ is around 1 when both parameters approach towards 1. This means that quarantining individuals exposed to the virus will be effective in controlling the disease, that is, the disease will decrease over time as the number of individuals in quarantine increases.

Figure 6 shows the variation of R₀ with respect to k₁ and β. As β values get closer to 1 (when k₁ values are less than about 0.1), it is seen that R₀ takes values greater than 1, that is, the disease gradually increases. However, Figure 6 indicates that as k₁ values increase, that is, as the number of individuals vaccinated increases, R₀ takes values less than 1. This means that the virus will decrease over time by vaccinating susceptible individuals (those who have not yet been exposed to the virus).

Figure 7 shows the variation of R₀ with respect to µ and β. It is seen that R₀ takes values less than 1 in all cases of both parameters.

6.   A method for numerical solution to the model

Analytical solutions of ordinary differential equations (ODE) systems are not always easy to obtain. Therefore, in cases where analytical solutions cannot be obtained, approximate-analytical or numerical methods are used. In recent years, ODE has found numerous applications in different branches of electrical network, signal routing, control theory of dynamic systems, image routing, science and engineering. One of the most used methods in the literature, especially in recent years, to find approximate or analytical solutions of nonlinear ordinary and partial differential equations is the Adams-Bashforth type of estimation-correction method [36]–[38]. In this study, this method was used as a numerical method. In order to define the basic components of the method and the solution steps, let's first consider the following initial value problem:

m-step method for solving initial value problem; to find the approximate solution of w_i+1 at mesh point t_i+1 has a difference equation indicated by the equation below where m is an integer greater than 1.

For i=m−1,m,...,N−1, h=(b−a)/N, b0,b1,...,bm−1 and a0,a1,...,am−1 values are fixed and initial values are specified as follows:

For the detailed steps regarding the Adams-Bashforth method, one can see the Appendix.

7.   Numerical solution of the model and discussion

Numerical simulation can be defined very simply as the realistic simulation of a physical event in a computer environment. Studies that started in the 1970s have gained great momentum especially in the last ten years in parallel with the rapid development in computer technology. Simulation is also very useful when the real system is out of reach or dangerous, the application is rejected, or systems designed but not yet manufactured or simply not available can be implemented. Key features in simulation include acquiring valid source information on the selection of important aspects and behaviors, as well as the use of convergence and simplification of hypotheses in simulation, or the accuracy and validity of simulation results. The simulation technology used for model validation and/or validation allows testing the effectiveness and thus validity of the established model. As such, simulation is a tool that is frequently used in applied sciences and is gradually gaining importance [5]. In this context, numerical simulation of a model helps to make predictions about the future behavior of the real-life problem on which that model is based.

In this section, numerical solutions of the created COVID-19 model will be discussed. As a solution method, Adams-Bashforth type estimation-correction method, which is detailed in Chapter 8, will be used. Multi-step Adams-Bashforth methods are one of the important methods used in the numerical solution of nonlinear systems. Again, unlike Runge–Kutta methods, Adams–Bashforth methods have smaller stability regions as they go to higher accuracy [40].

In mathematical biology, it is very important to make predictions about the future course of a disease by making numerical simulations and to calculate the numerical solutions of the models created. In this section, the biological significance of the stable equilibrium points of the system given by (2) will be discussed and the behavior of the results obtained will be examined. The initial value conditions in the (4.2) system are taken as S(0)=28189333,E(0)=250,I(0)=110,Q(0)=2000,V(0)=10696926,R(0)=2302039.

With numerical solutions, which parameters play an active role in the spread of the disease were examined. Therefore, the variation of each subpopulation over time was simulated for different β values using the values given in Table 4. In addition, graphs were obtained for various values by considering the parameters that significantly change the behavior of the system dynamics.

In Figure 8, the time-dependent variation of the population in susceptible individuals was investigated for different values of β as β = 0.8326, β = 0.8526, and β = 0.8726, and β = 0.8926, which is the transmission coefficient of the disease in system (2). Here, the most suitable β value for the real data was calculated as β = 0.8326, by parameter estimation method. Considering the values of β in the simulation, it is seen that the number of susceptible individuals decreases as β increases after the 40th day, and the susceptible population exhibits a stable behavior for all β values after the 80th day.

Similarly, in Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, for different values of β β = 0.8326, β = 0.8526, and β = 0.8726, and β = 0.8926, respectively, exposed, infected, time-dependent variation of the population in quarantine, vaccinated, and recovered individuals was studied. When Figure 8 is examined, it is seen that for the value β = 0.8326, obtained by the parameter estimation method, the number of individuals exposed to the virus decreased compared to the other values of β (β = 0.8526, β = 0.8726, β = 0.8926). As the β values increase, the number of exposed individuals also increases significantly. In addition, the reduction in the number of individuals exposed; The effect of the quarantine applied to the exposed individuals can be interpreted as the recovery of the patients and/or the increase in the number of infected individuals. However, it is also seen that the individuals exposed after the 100th day become stable.

When Figure 10 is examined, it is seen that the change in the infected individuals also exhibits similar behavior to the change in the exposed individuals. That is, as β values increase, the number of infected individuals also increases. In other words, for the value of β = 0.8326, it was observed that the number of infected individuals increased significantly compared to other values and the contagiousness increased until about 60 days, then started to decrease and stabilized after a certain period of time.

In Figure 11, the variation of the number of individuals in quarantine for different β values is examined. According to the change in the number of individuals exposed to the virus and infected, the number of individuals quarantined also changes.

When Figure 12 is examined, it is seen that the number of individuals vaccinated for the value β = 0.8326, obtained by the parameter estimation method decreased compared to the other values of β (β = 0.8526, β = 0.8726, β = 0.8926). That is, as β values increase, the number of vaccinated populations decreases.

According to Figure 13, it is observed that the number of recovered individuals corresponding to the value of β found as a result of parameter estimation is less than the other determined values of β. That is, as β values increase, the number of recovered populations also increases. This can be interpreted as an expected situation, as the recovered individuals are the result of quarantined individuals and the infected individuals recovering from the disease (gaining immunity). As a result, increased contagion will lead to an increase in recovering individuals.

However, the variation of the population over time is also considered for different η values. In Figure 14, it is seen that as η values increase, the number of sensitive individuals increases. This situation can be interpreted as the loss of effect of the vaccine (inability of the vaccine) to cause an increase in susceptible individuals. It is also seen that susceptible individuals become stable after the 90th day.

In Figure 15, it was observed that the number of individuals vaccinated for η = 0.0643 was significantly less than the other values and stabilized over time.

8.   Conclusion and recommendations

In this study, a new COVID-19 mathematical model (see system (2)) was analyzed and the parameter values of this model were estimated with real data from Iraq. Numerical simulations were carried out using the estimated parameter values for system (2) and the future processes of the COVID-19 epidemic were tried to be predicted. In this part of the study, the results and recommendations obtained throughout the study are presented. The important results obtained in this study study can be listed as follows:

In our study, a new mathematical structure that models the COVID-19 disease has been created and the efficiency and accuracy of this model has been examined. The resulting structure includes quarantined (Q), vaccinated (V) and recovered individuals (R), as well as susceptible (S), exposed (E) and infected (I) individuals, which are considered the main components of COVID-19 disease. In this context, it can be argued that the model created includes the basic components of the COVID-19 disease, thus being an effective model. It has been seen that the model created as a result of the research accurately models the processes of COVID-19 and provides illustrative predictions about its future course. The non-negative solution region and the boundedness of the model's compartments (populations) are discussed in order to demonstrate the biological relevance of the established system to analyze various aspects of the immune response to infection for COVID-19. Endemic (EDN) and disease-free (SDN) equilibrium points of the model were calculated and local stability analysis of these equilibrium points was performed. Thus, it is revealed under which conditions the equilibrium points of the system are stable.

The basic reproduction number, which is known as the secondary infection rate in epidemics and gives important information about the future course of the disease, was also calculated for the relevant model. Sensitivity analysis of this number was also performed and it was emphasized which parameters were effective on this number and how it affected this number.

On the other hand, the first coronavirus infection in Iraq was discovered on February 22, 2020, in an Iranian student in the city of Najaf. In our study, the parameters (9 parameters) of the model created for COVID-19 using real data from Iraq were estimated by least squares curve fitting method and numerical simulations were made according to these values. The working algorithm of the least squares curve fitting method used to determine the parameter values of the created mathematical model is given. In addition, these estimated parameter values and the curve fitted to the actual data are presented together. For the solution of the model, the Adams-Bashforth type predictive-corrective numerical method was used and with the help of numerical simulations, predictions were made about the future course of COVID-19 and how each compartment affected the parameters.

As future directions and the suggestions for the authors who are dealing with the related areas, the followings can be offered to guide researchers in future similar studies.

Different predictions can be made about the future course of COVID-19 by using a fractional derivative operator instead of the integer order system used in the study. Thus, the relationship of different derivative operators with integer order systems is also revealed. More data sets can be used for parameter estimation on different types of biological models. In addition to the least squares curve fitting method, different methods such as “maximum likelihood” can also be used.