A naive justification of hyperbolic discounting from mental algebraic operations and functional analysis

1.   Introduction

Intertemporal decision-making, the process of making choices between outcomes occurring at different points in time, is a fundamental aspect of human behavior (Ainslie, 1975; Green and Myerson, 2004). For instance, Cadena and Keys (2015) point out that discounting also plays a very important role in the domain of education. In effect, usually impatient people make dynamically inconsistent decisions such as starting an educational program but failing to complete it or dropping out of college. In the same vein, Golsteyn et al. (2013) show a significant negative relationship between high discount rates and school performance, health, labor supply, and lifetime income. Specifically, males and high ability children gain significantly more from being future-oriented. Analogously, Backes-Gellner et al. (2018) show that a low degree of long-term patience is a key determinant of dropping out of upper-secondary school. Finally, one month before termination of their programs, loos averse students are more likely to have a definite job offer. This is because, usually, individuals face some situations where they must weigh the costs and benefits of immediate versus delayed rewards. Understanding the mental processes underlying intertemporal decision-making is essential for unraveling the complexities of human choice behavior.

This article aims to explore the interplay of mental processes, namely cognitive evaluation, subjective valuation, and comparison, involved in intertemporal decision-making, with a particular focus on the discounting process. Cognitive evaluation refers to the initial assessment of the attributes, features, and characteristics of the rewards under consideration (Loewenstein and Prelec, 1992). Subsequently, subjective valuation occurs when individuals assign subjective values to the rewards based on their personal preferences, goals, and priorities (Loewenstein, 1996; Lempert et al., 2016; Friedel et al., 2014). Furthermore, individuals engage in a comparison process to determine the equivalence of the rewards (Malkoc and Zauberman, 2006; Zauberman et al., 2009a; Franco-Watkins et al., 2016).

The discounting process is a crucial component of intertemporal decision-making, involving the mental devaluation or discounting of future rewards relative to immediate rewards. Two types of discounting functions have been formulated: exponential and hyperbolic discounting. These functions play a critical role in shaping decision-making behavior and have implications for various domains, including financial decisions (Cruz Rambaud, 2014; Muñoz et al., 2018), health-related choices (Scharff, 2009; Cheung et al., 2022), and self-control (Bickel et al., 2008; Steward et al., 2017).

Recent research suggests that the hyperbolic discounting function better captures the mental processes involved in intertemporal choices compared to exponential discounting. The hyperbolic function accounts for the tendency of individuals to heavily discount immediate rewards in favor of delayed rewards, with the discount rate decreasing as the delay increases (Berns et al., 2007). This finding supports a growing body of evidence favoring hyperbolic discounting as a more accurate representation of human decision-making behavior.

This paper is organized as follows. Section 2 provides a comprehensive review of the existing literature on the mental and discounting processes involved in intertemporal decisions. In Section 3, specifically Subsection 3.1, the development of the subjective discount rate is described. Subsection 3.2 focuses on the mental algebraic operations used to determine the discounted amount equivalent to a future reward in an intertemporal choice, leading to the derivation of the mathematical expression of the discounting process based on the assumptions presented in Section 2, which supports the concept of hyperbolic discounting. Section 4 derives the hyperbolic discount function using functional analysis. Finally, Section 5 provides a summary and concluding remarks.

2.   Literature review

2.1.   Mental processes on intertemporal decisions

When an individual is faced an intertemporal choice and needs to determine the reward equivalent to another one, several mental processes come into play. These mental processes involve cognitive evaluation, subjective valuation, and comparison (Frederick et al., 2002; Loewenstein, 1988).

Initially, the individual engages in cognitive evaluation, which implies assessing the attributes, features, and characteristics of the rewards under consideration (Loewenstein and Prelec, 1992). This evaluation may include factors such as the magnitude or size of the rewards, and the timing or delay associated with each reward which influence the decision-making process (Malkoc and Zauberman, 2019).

A set of psychological processes may be involved in the process of evaluating the magnitude and time of rewards such as temporal framing (deferral or expedite) (Loewenstein, 1988; Malkoc and Zauberman, 2006), attentional processing (Franco-Watkins et al., 2016; Malkoc et al., 2010), perception of time (Kim and Zauberman, 2009; Zauberman et al., 2009a), or retrieval of memories (Zauberman et al., 2009b).

After that, subjective valuation occurs when the individual assigns a subjective value or importance to each reward based on their personal preferences, goals, and priorities. This valuation process is influenced by various psychological factors, such as emotions (Loewenstein, 1996; Lempert et al., 2016), or past experiences (Harris, 2012), and individual differences (Keidel et al., 2021) such as impulsivity (Friedel et al., 2014; Moreira and Barbosa, 2019; Liu et al., 2022) in decision-making tendencies.

Finally, the individual engages in a comparison process, where they mentally weigh and compare the rewards against each other to determine their equivalence. This comparison may involve evaluating the trade-offs between immediate gratification and delayed rewards (Malkoc and Zauberman, 2006), considering the potential benefits and drawbacks of each option (Zauberman et al., 2009a), and weighing the perceived value of the rewards over time (Franco-Watkins et al., 2016). Bias may affect this process, such as loss aversion (Tversky and Kahneman, 1991) and relative risk aversion (Dyer and Sarin, 1982).

2.2.   Discounting process

The process of discounting refers to the tendency of individuals to devalue or discount future rewards relative to immediate rewards. This process involves the evaluation of the subjective value of rewards over time giving rise to different mathematical models to describe discounting. However, the main objective of this paper is to describe the underlying process leading to the temporal devaluation of rewards.

One model used to describe the process of discounting is exponential discounting, which assumes a constant rate of discounting over time. According to this model, the value of a future reward is discounted exponentially as a function of its delay (Frederick et al., 2002). However, the exponential discounting assumes that people have a fixed time horizon beyond which they do not discount the value of rewards, which is inconsistent with real-life behavior (Laibson, 1997).

Another widely used model is hyperbolic discounting, which suggests that the subjective value of a delayed reward decreases more rapidly in the short-term compared to the long-term (Ainslie, 1975). This process leads to impulsive decision-making behavior, where individuals prioritize immediate rewards over delayed ones.

A new model called "arithmetic discounting" has been used used to explain the process of discounting. This model is a specific instance of Killeen's model (2009). The analogy of the excess wages needed for waiting, rather than analogies of simple (hyperbolic discounting) or compound interest (exponential discounting), underpins the underlying behavioral model (Doyle and Chen, 2010).

Whilst the arithmetic model is simpler to calculate than the hyperbolic or exponential model, hyperbolic discounting has been found to provide a more accurate description of real-life decision-making behaviors. This is due to its ability to account for the observation that individuals discount the value of future rewards more heavily as the time to receipt approaches (Mazur, 1987; Green and Myerson, 2004).

Moreover, hyperbolic discounting has been found to have evolutionary advantages over exponential discounting (Kable and Glimcher, 2007). It has been argued that hyperbolic discounting may have evolved as an adaptation to decision-making in a changing environment, where immediate rewards are more certain and long-term rewards are more uncertain (Stevens and Stephens, 2010). This is consistent with the idea that hyperbolic discounting may be a more accurate model for explaining decision-making behaviors in real-life situations than exponential discounting (Cruz Rambaud, 2014).

In addition, hyperbolic discounting has been shown to better explain choices related to health behaviors, such as smoking and exercise (Chapman and Weber, 2006). Similarly, hyperbolic discounting has been found to be a better predictor of impulsive consuming behaviors compared to exponential discounting (Zauberman et al., 2009b). These findings suggest that hyperbolic discounting may provide a more accurate model for predicting and understanding intertemporal decision-making phenomena in real-life situations. However, hyperbolic discounting may be influenced by social and cultural factors, which may vary across different populations (Muñoz et al., 2018).

2.3.   The link between mental processes and discounting process on intertemporal decisions

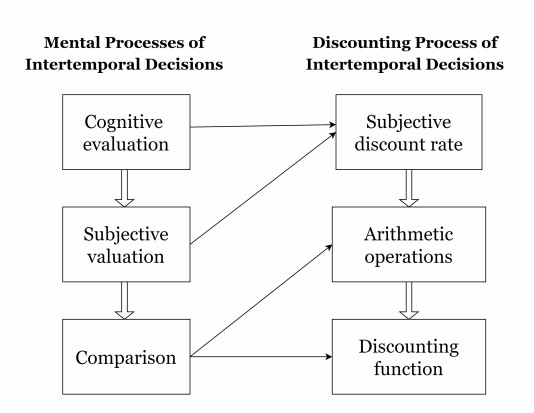
The process of discounting is influenced by various factors, including cognitive, affective, and situational factors. Therefore, the discounting process is closely intertwined with the cognitive evaluation, subjective valuation, and comparison of different rewards in the context of intertemporal decisions (see Figure 1).

Within the cognitive evaluation process, mental discounting occurs as individuals mentally weigh the value of immediate rewards against delayed rewards. They assess how the delay to receive a reward affects its perceived value and the trade-offs between immediate gratification and delayed but potentially larger rewards.

For example, mental processes such as mental representation and framing play a role in discounting. Malkoc and Zauberman (2006) propose that the temporal frame and mental concreteness of an intertemporal choice can explain individuals' discounting rates. The way individuals mentally represent and frame the options affects their valuation and decision-making. Attentional processing also participates in discounting process. Franco-Watkins et al. (2016) conclude that individuals with attentional biases towards immediate rewards are more likely to exhibit present-biased preferences and choose immediate rewards over delayed rewards. Additionally, perception of time is involved in discounting process. Individuals tend to discount the value of delayed rewards more steeply when there is a greater discrepancy between their subjective perception of time and the objective duration of the rewards (Kim et al., 2009). Additionally, memories, as valuable assets, participate in discounting. Zauberman et al. (2009b) suggest that the discounting process in intertemporal decision-making is influenced by individuals' strategic use of memories. By leveraging positive memories, individuals can attenuate the negative impact of temporal discounting and make more patient choices that align with their long-term goals. Additionally, language has a role in the process of discounting. According to Chen (2013), languages requiring future-time reference cause their speakers to process future-oriented decisions differently than speakers of languages requiring present-time reference. This was confirmed by Sutter et al. (2015; 2018) and Herz et al. (2021) after controlling for cultural variables.

The discounting process is an integral part of subjective valuation as individuals assign different values to immediate and delayed rewards. The discounting process involves devaluing the subjective worth of delayed rewards compared to immediate rewards due to factors like time preference, uncertainty, and impatience. For example, Loewenstein (1996) highlights the role of emotions in discounting, suggesting that individuals may have a positively-valenced arousal response toward immediate rewards compared to delayed ones. In the other hand, impulsivity, as a trait associated with impulsive decision-making, also influences the discounting process in different context such as smoking. In effect, smokers demonstrate higher levels of impulsivity compared to non-smokers. Furthermore, smokers exhibit steeper discounting of both monetary rewards and consumable outcomes (e.g., cigarettes) compared to non-smokers (Friedel et al., 2014).

In the process of comparing different rewards, mental discounting comes into play. Individuals consider the temporal aspects, such as the delay to receive a reward, and apply discounting functions or mental heuristics to adjust the perceived value of rewards based on their temporal distance. This comparison helps individuals make trade-offs between immediate rewards and delayed rewards. However, bias may influence this process, such as through loss aversion (Tversky and Kahneman, 1991) and relative risk aversion (Dyer and Sarin, 1982). Whilst individuals tend to prefer avoiding losses rather than acquiring equivalent gains (loss aversion), the subjective value of a gain or loss decreases as the size of the gain or loss increases in the comparison process. In uncertain situations, people tend to decrease their risk tolerance as their wealth increases (relative risk aversion). Consequently, individuals with greater risk aversion are more reluctant to undertake risky ventures, even if they have the potential for significant gains.

3.   A justification with elemental algebraic operations

3.1.   Cognitive evaluation and subjective valuation processes: Subjective discount rate

Most experiments are designed as follows. An individual is asked about the amount equivalent today to another reward available at a future time. The individual assesses the attributes, features, and characteristics of the rewards under consideration. After that, the individual assigns a subjective value or importance to reward based on their personal preferences, goals, and priorities. Based on both processes (cognitive evaluation and subjective valuation), the individual determines a fixed discount percentage $r$ (see Figure 1).

3.2.   Comparison process: Assumptions of discounting process

First assumption. In the comparison process, the subject tends to use elemental algebraic operations (sums, subtractions, multiplications and divisions) only. More specifically, her mental discounting process will be to subtract $r$ from the initial reward (see Figure 1). Thus, if the initial delayed reward is $A$, the successive discounted amounts are shown in Table 1.

Therefore, for the sake of simplicity, if the initial reward is $A = fanxiexian_myfh1$ at time $t$, the discounted amount will be the subjective discount function, $\tilde{F}(t)$. Thus, under this assumption, $\tilde{F}(t)$ will be linear discounting:

Nevertheless, despite this initial assumption is logical, the subject has to slightly correct her first assumption in the following way.

Second assumption. The subject realizes that, after a certain number of the experiment replications, the chosen reward can reach the value $0$ and even negative records. Thus, she proposes the following expression for the subjective discount function:

where $r(t)$ is decreasing and $r(1) = r$ is the initial percentage chosen by the decision maker. Observe that this requirement is in line with Harvey(1986, 1994). In effect, Harvey (1992) states: "We have in mind any method with positive discount rates that decrease and tend to zero as time tends to infinity. Such a method will be called slow discounting. We will not argue that people should have values in accord with slow discounting. Rather, we will argue that if people do have such values, then a slow discounting model can be reasonable and insightful as part of a public policy study".

Third assumption. Taking into account Equation (2), although $r(t)$ is decreasing, $r(t)t$ must be increasing as it represents the discount of fanxiexian_myfh1 and this amount must be increasing with $t$.

Fourth assumption. The discounted amount must vanish at infinity. Therefore, the following identity holds:

This is the most difficult question to be checked because the involved time is infinity. However, in Subsection 3.3, we will show that this is a necessary and sufficient condition to derive a discounting model with a single parameter, similarly to constant discounting. This feature is relevant in Harvey (1994) when defining the so-called proportional discounting, improving the tractability of the model.

A summary of the assumptions is the following:

1. $\tilde{F}(t) = 1- r(t)t$.

2. $r(t)$ is decreasing.

3. $r(0) < +\infty$.

4. $r(1) = r$.

5. $\lim_{t \to +\infty} [r(t)t] = 1$.

3.3.   Derivation of the hyperbolic model

As indicated in Section 2, it is assumed that the subject is only willing to do elemental algebraic operations. Therefore, she must start from the expression of the type $r(t) = \frac{a}{b+ct}$ which, as formerly indicated, only includes elemental operations. Thus, the requirements #4 and #5 proposed in Section 2 lead to the following equations:

● $\frac{a}{b+c} = r$.

● $a = c$.

Observe that $a = c$ becomes $r(t)$ an expression depending on a single parameter, as formerly indicated in the proportional discounting (Harvey, 1994): $r(t) = \frac{1}{m+t}$ where $m = \frac{b}{a}$. Consequently,

and

where $i = \frac{r}{1-r}$, which is the well-known expression of the hyperbolic discounting.

4.   A justification with functional analysis

Traditionally, the paradigm of discounting models has been the exponential discount function. The use of this model has been justified from different points of view. One of them has been that the exponential function is the solution of the functional equation:

The idea underlying to this functional equation is that the individual uses the same rate independently of the instant at which she chooses the equivalent reward. Based on this approach, we can think about a discounting model which successively applies a lesser interest rate. In effect, let us consider a generic interval $[r, r+s]$, where $r > 0$ is variable and $s > 0$ is fixed. If decreasing impatience (or, equivalently, increasing patience) holds, then the financial factor in the interval $[r, r+s]$

must be increasing with respect to $r$ (Cruz Rambaud and Muñoz Torrecillas, 2016). Indeed, an easy way to propose a function of $r$ and $s$, increasing with respect to $r$, is

from which:

giving rise to the following functional equation:

It can be shown that the solution of Equation (7) is (Aczél, 1987):

which is the well-known hyperbolic discounting model.

Finally, an immediate generalization of Equation (7) is:

whose solution is (Aczél, 1987):

which is the well-known generalized hyperbolic discount:

5.   Conclusions

The objective of this paper has been to identify the three stages of mental processes in intertemporal choice environments. In effect, these phases (cognitive evaluation, subjective valuation and comparison) have been concreted in a series of logical rules which individuals use to determine the discounting of a delayed reward. As a result, we have found that the hyperbolic discounting better fits the mental processes involved in intertemporal choices. This reinforces the wide set of arguments in favor of hyperbolic instead of exponential discounting.

This objective has been also treated by transforming the thoughts of individual about discounting into a functional equation whose solution aldo leads to hyperbolic discounting.

As a future research line, our aim is to administer suitable questionnaires in order to determine the discount function to be applied by a group of individuals. Specifically, our aim is to convert the traditional quantitative experiments into a qualitative questionnaire able to elucidate the four assumptions discussed in Section 2. In effect, most experiments deduce the concrete expression of a discount function asking for a significant number of amounts equivalent to another constant reward at different dates. This methodology presents a noteworthy inconvenience: the only meditated answer could be the corresponding to the first questions, and the rest of answers can be "the first thing that comes into her head". In this way, our proposal is to find a set of tendencies and mental processes of the group, and then to deduce the mathematical expression of the function that better fits the intertemporal choices.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

We would like to thank the financial support from the Mediterranean Research Center for Economics and Sustainable Development (CIMEDES).

Conflict of interest

All authors declare no conflicts of interest in this paper.