A Pontryagin maximum principle for terminal state-constrained optimal control problems of Volterra integral equations with singular kernels

1.   Introduction

1.1.   Motivation

In this paper, we consider the following bistable three-species competition systems.

The above system describes the population distribution of predators over time when three predators compete for two prey. $u, v,$ and $w$ represent the nonnegative population distributions of the three predators. Three distributions usually have values less than 1. $\left\{a_i\right\}_{i = 1}^{3}$ and $\left\{d_i\right\}_{i = 1}^{3}$ denote each predator's diffusion coefficient and net growth rate, respectively. Finally, $\left\{b_i\right\}_{i = 1}^{3}$ refers to the proportion of population decline caused by one predator competing with another. In this system, we assume that predators corresponding to $u$ and $w$ do not compete with each other.

We aim to approximate the monotone traveling wave solution for the above system through the definite integral of positive functions. The traveling wave solution, a particular solution of partial differential equations (PDE), may exist in several forms for a single equation because there is no constraint on the wave speed. The most common case is when traveling wave solutions always exist for speeds higher than a specific value, called minimum wave speed. The exact minimum wave speed was revealed in the case of the Keller-Segel model with logistic growth dynamics ^[1]. The authors in ^[2] investigated the presence of a minimum wave speed and a sharp bound for a non-KPP type reaction-diffusion system. The authors in ^[3] identified the necessary and sufficient conditions for the maximum delay time to assure the existence of the traveling wave solution to the Lotka-Volterra competition system. It turns out that only monotone solutions are possible in this system.

In contrast to the previous examples, there are several equations where a solution and wave speed are uniquely determined. A monotone traveling wave solution exists uniquely for the Keller-Segel model with a chemotactic sensitivity term in the form of a logarithmic function ^[4]. The same results hold for the Allen-Cahn model with relaxation terms and Lotka Volterra competition diffusion system ^[5,6]. When several functions can satisfy constraints, it is challenging to predict to which solution the trained neural network will converge. Since the three-species competition systems covered in this paper ensure the uniqueness of the solution under the assumption of monotonicity, we solve the well-posed forward-inverse problem that simultaneously approximates a solution and speed.

For all positive integers $n$, shallow neural networks without bias are dense in $C^n(\cdot)$, representing the set of functions whose all $n$ th partial derivatives are continuous ^[7]. It suggests that neural networks can approximate the PDE or ODE solution with an arbitrarily small error. Modifying a fully connected neural network can also impose boundedness or monotonicity on neural networks. Therefore, the deep neural network (DNN) approach becomes a flexible method for solving differential equations with additional constraints.

1.2.   Related works

The authors in ^[8] presented a physics informed neural networks (PINN) in which neural networks simultaneously learn solutions and coefficients of partial differential equations. They employed automatic differentiation ^[9] in computing the derivatives of neural networks and optimized the mean squared loss corresponding to initial and boundary conditions. Since it can estimate a high-order differential coefficient of neural networks at all points, the method does not have a constraint to be trained on a fixed grid.

Several recent studies have shown that minimizing the loss function designed above is equivalent to finding an approximator near a solution in terms of pointwise error. The authors in ^[10] first proved the existence of a neural network with a sufficiently small loss for quasilinear parabolic partial differential equations. Assuming the regularity of the solution, they concluded that the neural network eventually converges to the solution when the residual loss decreases to zero. Subsequently, studies showing that the neural network approximation sequence converges to a solution of PDE through the Gronwall inequality have emerged. The authors in ^[11] discussed the 1-dimensional kinetic Fokker-Planck equation for inflow and specular boundary conditions. The second-order parabolic equation of the zero Dirichlet boundary problem was analyzed in ^[12]. The authors in ^[13] employed monotonicity to set the point where the solution necessarily passes and perform estimates of traveling wave solutions for various equations. Furthermore, estimates for the unique continuation problem, including additional observation of the ill-posed forward problem, have also been recently studied. The authors in ^[14] identified the number of training points required to reduce residual loss, considering the errors which arise from the quadrature rule.

1.3.   Outline of the paper

In Section 2, we introduce the structure of a fully connected neural network model. We construct a residual loss to approximate the solution of the system and describe the monotonic neural network. In Section 3, existing theoretical results are first provided, such as the uniqueness of the traveling wave solution and the sign of wave speed. Then we prove that our model can minimize the loss function and that the sequence of DNN solutions approaches the actual solution. In section 4, corresponding experiments of several methods are addressed, that impose monotonicity. We offer the shortcomings of each method and experimental results, which prove that our model can overcome them. Finally, we conclude the article by summarizing the results and discussing how to supplement the paper and develop future research topics.

2.   Preliminaries

In this section, we describe our neural network model to approximate the solutions of the system and the wave speed. The construction of the loss function is fundamentally based on PINN^[8] and follows the detailed settings in ^[13].

Consider the system (1.1) with the traveling wave ansatz

where $s$ denotes the wave speed. Then, traveling wave solution $(U, V, W)(z)$ of the system (1.1) with the boundary condition (1.2) is a solution of the following system.

In this paper, we set the two constant states $(u_-, v_-, w_-)$ and $(u_+, v_+, w_+)$ in the asymptotic boundary conditions (2.2) to $(1, 0, 1)$ and $(0, 1, 0)$ respectively. If the sign of wave speed $s$ is positive, the predator corresponding to $V$ disappears, and the predators corresponding to $U$ and $W$, which do not compete with each other, survive. In the opposite case, only the predator corresponding to $V$ survives. It should be noted that in this research, we are only concerned with the study of monotone traveling wave solutions. That is, $U_z < 0, V_z > 0, W_z < 0$.

2.1.   Neural network model & Loss function

The fully connected neural network $U^{nn}$, an approximator of the solution $U(t, x)$, is formulated as a recurrence relation with a linear affine transformation and a nonlinear activation function $\sigma$.

$\left\{W_{i} \in \mathbb{R}^{h_i}\times \mathbb{R}^{h_{i+1 }}\right\}_{i = 1}^{L}$ denotes the sequence of matrices where $\left\{h_{i}\right\}$ denotes the number of hidden neurons in each layer. Since $h_1$ and $h_{L+1}$ denote the dimension of input and output respectively, they are set to 1. $s^{nn}$ is an approximator of the wave speed $s$ in our method, which varies by optimizing the loss functions provided below. The other two networks, $V^{nn}$ and $W^{nn}$, are defined similarly.

Now we define the following three operators $P(U, V, W; s), Q(U, V, W; s)$ and $R(U, V, W; s)$.

We use the truncated interval as the domain instead because we cannot consider all the points on a infinite real line. For a sufficiently large interval $[-L, L]$, the residual loss function for each governing equation in (2.1) is defined by

where $\{z_i\}_{i}$ represents the set of sample points over the spatial domain used for computing the integral expression of the mean squared loss. At each iteration of the training process, new points are randomly selected for use in the Monte Carlo integration method.

It is also challenging to consider asymptotic boundary conditions on the real line. Therefore, we assign boundary conditions to both endpoints of the truncated domain instead. The residual boundary loss function is formulated as follows.

In this paper, we propose a Neumann boundary condition the solution inherently satisfies. Multiplying both sides of the first equation in (2.1) by $U_{z}$ and integrating them over a truncated interval $[-c, b]$, we can derive the convergence of $U_z$ through the following computation. First, the last term on the right side of the equation must be finite when $b$ goes to infinity.

where last integral must be finite since $V(z)$ should be less than 1 and $UU_z$ is a negative integrable function. Therefore, the definite integral $\int_{-c}^{b}s U_z ^2 +d_1 U_z U_{zz} dz = \int_{-c}^{b} s U_z ^2 dz + d_1(U_z ^2 (b)-U_z ^2 (-c))/2$ must converge.

When we consider the asymptotic boundary condition, the only possibility is that $U_{z}(b)$ converges to zero regardless of the sign of $s$. For $s = 0$, the convergence of $U_z(b)$ permits the case only when $U_z(+\infty) = 0$. When $s$ is positive, the increasing function $\int_c ^{b} sU_z ^2 dz$ should converge so that $1/2 U_{z}(b)^2$ also converge. For negative $s$, we focus on the first equation of (2.1). Since $sU'(z)+d_1U''(z)$ goes to zero, there exists an arbitrary small $\epsilon > 0$ such that for all sufficiently large $z$,

Suppose that there exists large $z_1$ such that $U'(z_1) < (d_1/s) \epsilon$. Then, the inequality $d_1\epsilon+d_1U''(z_1) < sU'(z_1)+d_1U''(z_1) < \frac{d_1}{2} \epsilon$ results in the negativity of $U''(z_1)$. This contradicts to the asymptotic boundary condition (2.2) since $U'(z)$ cannot maintain values indefinitely below a certain negative constant. Therefore, we put forward the following Neumann boundary condition (2.3).

The loss function for the boundary condition of the derivative is defined as follows.

We note that the translation of a traveling wave solution is still a traveling wave solution. To consider a wide interval on the real line in both directions, it is necessary to fix a point through which the solution must pass. If the monotone function's left and right limits on the real line are $0$ and $1$ respectively, the range of the function must contain $1/2\in \mathbb{R}$. For the symmetric interval $[-L, L]$ about the origin, it would be natural to enforce a value of $1/2$ at $x = 0.$

Finally, we optimize the total loss function aggregating the above losses. Changes in weights included in neural networks follow the ADAM^[15] based on gradient descent.

2.2.   Monotonic neural network

The original monotonic network in ^[16] was constructed by combining positive constrained weights and min-max operation. In the case of simply forcing the positivity of the weights, a neural network with a popular activation function, such as ReLU^[17] or ELU^[18], can only represent a convex function ^[19]. In contrast, the above min-max monotonous neural network has universal properties for monotone functions in $C ^{1}([0, 1]^D; \mathbb{R})$. Some studies propose a method of considering the regularizer for monotonicity^[20]. The authors in ^[21] revealed that in multi-dimensional spaces, the upper envelope of the function must be a monotone function. They employed a monotone function in prediction by directly constructing the upper envelope of the counterexample.

In this paper, we transform the unconstrained monotonic neural network ^[22], which devised the integration of the positive function. By replacing numerical integration with DeepONet-based operator learning without using the quadrature rule, the neural network becomes a smoother function suitable for representing solutions to differential equations.

We generate $m$ variables $\left\{p_i\right\}_{i = 1}^{m}$ to represent the values of a positive function at $m$ positions $\left\{x_i \right\}_{i = 1}^{m}$. To find a fully connected neural network representing the primitive function, we perform operator learning for the integration based on DeepONet. The overall structure of our neural network model is formulated as follows.

It is worth noting that the structure of this method is the same as that of DeepONet, which is capable of learning general operators. In this research, it is specifically designed to learn integral operators. We construct a monotonic neural network model $U^{mon}$ as an inner product of Branch Net and Trunk Net, which are fully connected neural networks in Section 2.1. Branch Net receives a discretization of function as an input to determine which positive function to integrate. Trunk Net takes the point of the domain as input and queries the location of interest. Due to the high expressivity for compact operators, combining the two networks will improve the approximation possibility for monotone functions. We remark that Branch Net and Trunk Net are called shallow networks when they are two-layered fully connected neural networks (i.e. $L = 2$).

3.   Theory

In this section, we introduce existing theories about the system and provide results on the convergence of our model. The first part discusses the assumption that guarantees uniqueness other than the initial and boundary conditions. The following part addresses the theory obtained based on DeepONet's universality ^[23] and Grönwall inequality.

3.1.   Existing theoretical results

In the case of an original bistable three-species competition System (1.1), we cannot guarantee the monotonicity and uniqueness of traveling wave solutions. The authors in ^[24] additionally assume one of the two following conditions.

It may be straightforward to show that the former condition implies the latter when $U$, $V$, $W$ are traveling wave solutions of the system (1.1). The authors in ^[24] remarked that the above two inequalities are indeed equivalent conditions. Under the above assumption, the following theorem states the uniqueness of a traveling wave solution.

Theorem 1. (Thm 3.1 in ^[24]) The three-species competition system (1.1) has a traveling wave solution that is unique up to translation with the unique wave speed.

In several cases, the sign of wave speed was revealed without knowing the exact value. The theorem below presents that $U$ and $W$ should become extinct when the predators corresponding to $U$ and $W$ are relatively less competitive than the predator corresponding to $V$.

Theorem 2. (Thm 3.2 in ^[24]) Suppose that $a_1 = d_1, a_3 = d_3, b_3 = b_1.$ If $0 < b_1 < 1 < 2 \leq b_2$, then the sign of wave speed $s$ for the system (1.1) is negative.

Similar to the above, there is a theorem describing the sign of wave speed for various parameter settings. In particular, the theorem provides the presence of a solution with a wave speed of zero. If the condition $b_2 = 2b_1$ is satisfied, it will be used as a validation example to verify the accuracy of proposed method.

Theorem 3. (Thm 3.4 in ^[24]) Suppose that $a_1 = d_1 = a_3 = d_3$ and $0 < b_1 < 1 < b_2 < 2.$ Then, the sign of wave speed $s$ for the system (1.1) is the same as the sign of $(2b_1-b_2)$. In particular, the wave speed $s$ is precisely zero when $b_2$ is identical to $2b_1$.

3.2.   Convergence of neural network model

We now introduce theoretical results on the performance of our model when we optimize the loss introduced in Section 2.1. Our monotonic neural network in Section 2.2 replaces the original fully connected neural network. When approximating each traveling wave solution, we maintain the weights of Branch Net and Trunk Net, and only a sequence $\left\{p_i \right\}_{i = 1}^{m}$ depends on the solution. In the above situation, our model capabilities embrace uniform convergence.

Corollary 1. Assume that an activation function $\sigma$ is continuous and non-polynomial. Let $S(U)\in C^1 ([-L, L])$ denote the set which contains traveling wave solutions $U$ of the first predator in the system (2.1). Suppose the set of derivatives $D(U)$ of elements in $S(U)$ is compact in $C([-L, L])$. Then for any arbitrary small $\epsilon > 0$, there exists a large positive integer $m$ with shallow Branch Net and Trunk Net such that for any $U\in S(U)$, our monotonic neural network $U^{mon}(z)( = \langle \mathit{\text{ Branch Net }}(p_1, \cdots, p_m), \mathit{\text{ Trunk Net }}(z)\rangle)$ with an appropriate sequence $\left\{p_i\right\}_{i = 1}^{m}$ satisfies the following.

Proof. The compactness of the set of derivatives implies the compactness of $S(U)$ since the integral operator is continuous when the domain of functions is a finite closed interval. Define a operator $G:D(U)\rightarrow S(U)$ as $G(f)(z) = \int_{L}^{z} f dz$ for $z\in [-L, L]$. As in Theorem 5 in ^[23], we can choose $m$ grid points $\left\{x_i \right\}_{i = 1}^{m}$ for $G$ which guarantees

We then achieve the desired result by setting $f$ and $\left\{f(x_i)\right\}_{i = 1}^{m}$ to $U'(z)$ and $\left\{p_i\right\}_{i = 1}^{m}$, respectively.

Remark 1. As a representative example of $D(U)$ that satisfies the requirement, we have considered the case of a finite-dimensional space $S(U)$ with bounded properties, which can be achieved through the use of sequentially compact bounded intervals. However, it should be noted that due to the unbounded differential values of the monotone traveling wave solution, it is not possible to search the entire traveling wave solution within the solution space using a single DeepONet. The size of D(U) is determined by the user of the theorem. The assumption becomes necessary from the fact that a single DeepONet structure, comprising of parameters with appropriate values, was employed to approximate the integration of multiple functions.

Proposition 1 suggests that if DeepONet approximates the integral operator with proper performance, our monotonic neural network does not deviate significantly from the possible solutions. In other words, we can assume the boundness of the approximator when the loss for operator learning becomes sufficiently reduced. Given the optimized residual loss with the assumption, we estimated the pointwise error for the solution of the approximator. Note that the same results hold for fully connected neural networks where $s^{mon}$ denotes our method's approximation of speed $s$.

Theorem 4. Suppose that our monotonic networks $U^{mon}, V^{mon}, W^{mon}$ are bounded by a constant $C$. Denote $|(U(z), V(z), W(z))-(U^{mon}(z), V^{mon}(z), W^{mon}(z))|$ by $E(z)$. Then, the following holds.

where $K_1, K_2$ are constants depending on $E(-L)$, $Loss_{GE}$, $Loss_{BC}, Loss_{limit}$, $L$, $s$, $s^{mon}$, and the parameters of the system (2.1).

Proof. Integrating the first equation of the system (2.1), we derive the followings.

With the residual loss for governing equation, our monotonic neural network satisfies a similar system above. The detailed form of a system can be written as follows.

where $\int_{-L}^{L} \left\{f(y)\right\}^2 + \left\{g(y)\right\}^2+\left\{h(y) \right\}^2dy = Loss_{GE}$ as in Section 2.1. We now leverage the boundedness of the solutions and triangular inequalities to estimate how similarly $U$ and $U^{mon}$ follow the system of ordinary differential equations. First of all, the difference in the first equation of the system can be decomposed into three terms as follows.

The last term $f_3$ can be bounded by a constant via the boundedness of solutions.

Therefore, we complete the estimates of $|F(z, U)-F(z, U^{mon})|$ by triangular inequalities.

Estimates of the second and third equations can be obtained by using a similar manner. We combine all the results to obtain the following inequality,

where a constant $C_1$ depends on $s$ and the diffusion coefficients of system and a constant $C_2$ depends on the parameters of system, $|U'-(U^{mon})'|(-L)$, $L$ and $C$.

Finally, we would like to complete the proof by presenting the upper bound for the growth of the error function $E(z)$.

where $C_3$ is a constant depending on $C$, $(U^{mon})'(-L)$, and the diffusion coefficients of the system. {Therefore, we can get the following inequalities.

By the Grönwall's inequality in section 17.3 of ^[25] with two constants $E(-L)+2LC_2+\int_{-L}^{L} \frac{{(f(y))}^2}{d_1} +\frac{(g(y))^2}{d_2}+\frac{(h(y))^2}{d_3} +C_{3}|s-s^{mon}|dy$ and $C_1$,

We remark that Grönwall's inequality can be modified by considering the opposite direction. The estimate above states that the trained neural network effectively represents the solution near the boundary, assuming that $s^{mon}$ approximates $s$ within a small error. We conclude this section by introducing the existence of our monotonic network model that reduces the $Loss_{total}$ for the solution of the finite-dimensional space.

Theorem 5. Assume that an activation function $\sigma$ is continuous and non-polynomial. Consider a finite-dimensional space $\mathcal{O}\subset C^{2}([-L, L])$ which is bounded. Then for any positive $\epsilon$, there exists a large positive integer $m$ with shallow Branch Net and Trunk Net such that for any traveling wave solution $(U, V, W)$ of 2.1 where $U, V, W\in \mathcal{O}$, our monotonic neural network $U^{mon}(z)( = \langle \mathit{\text{ Branch Net }}(p_1, \cdots, p_m), \mathit{\text{ Trunk Net }}(z)\rangle)$ with an appropriate sequence $\left\{p_i\right\}_{i = 1}^{m}$ satisfy the following.

Proof. For any $\epsilon > 0$, we first note that Trunk Net learns the basis of the function space, and Branch Net learns the coefficients for each basis. Denote the ornormal basis of $\mathcal{O}$ by $\left\{o_i\right\}_{i = 1}^{n}$. By universal properties of neural network in ^[7], there exists a sequence of neural networks $\left\{NN_{i}\right\}_{i = 1}^{n}$ such that

Suppose that Trunk Net represents the $NN_{i}$. Then by the Theorem $5$ in ^[23], we can choose $m$ values $\left\{p_i \right\}_{i = 1}^{m}$ as in the proof of proposition 1 which guarantees

Since $\left\{NN_{i} \right\}_{i = 1}^{n}$ is the approximator of $\left\{o_i \right\}_{i = 1}^{n}$ in $C^{2}([-L, L])$, the above inequality implies that Branch Net estimates the appropriate coefficients, resulting the uniform convergence in $C^{2}([-L, L])$ for all $U\in \mathcal{O}$.

If $(U^{mon}, V^{mon}, W^{mon})$ are efficient approximations of $(U, V, W)$ in $C^{2}([-L, L])$, $Loss_{limit}$, $Loss_{BC}$ and $Loss_{trans}$ should be small (t.e. less than a constant multiple of $\epsilon$). {For the term $Loss_{GE}$, we only consider the loss function $Loss_{GE}^{(1)}$ for the first equation in the governing equation. For the traveling wave solution $(U, V, W)$ of the system (2.1),

Since we may assume the boundedness of $(U^{mon}, V^{mon}, W^{mon})$ by Corollary 1, we can decompose the nonlinear product term in the system (2.1) as $|UV-U^{mon}V^{mon}| \le |U-U^{mon}||V|+|V-V^{mon}||U^{mon}|$. By observing this type of triangular inequality, we can conclude that the convergence in $C^{2}([-L, L])$ indeed guarantees an arbitrary small $Loss_{GE}$.

4.   Experiments

In this section, we present experimental results that our model can be more accurately trained than previous min-max monotonic networks ^[16] or fully connected neural networks. Before interpreting the tables and figures, we describe experimental settings in detail. In all cases, the ADAM optimization algorithm, as outlined in the literature by Kingma and Ba^[15], was utilized with a learning rate of 1e-2 to minimize the loss function. By employing the StepLR scheduler, the learning rate decreased by 0.9 per 300 epochs. All experimental results were adopted using an optimal model based on the value of the loss function in training up to 10000 epochs. The 5-layered neural network has 48 hidden neurons for each hidden layer. The initial weights were set in accordance with the default initialization method provided by PyTorch.

Training of the DeepONet in Section 2.2 utilized the 20th-order Chebyshev polynomials. The model learns the integral of Chebyshev polynomials in the closed interval [0, 1] and derives the primitive function on [-50, 50] using a linear transformation. For the discretization of the function on 300 points, a dataset was generated by odeint implemented in the module named Scipy in Python. Trunk Net and Branch Net are 5-layer neural networks with a width of 256 and a latent dimension of 64. For the integration, we used an Adam optimizer and StepLR scheduler with a learning rate of 1e-3 and a rate of 0.9.

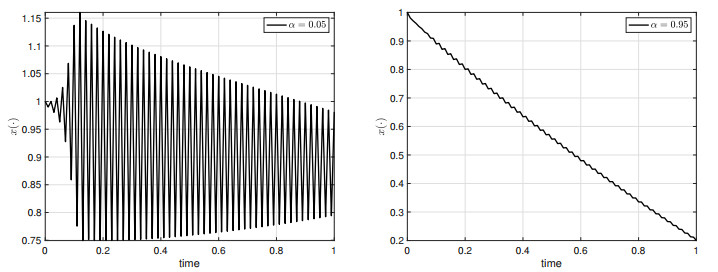
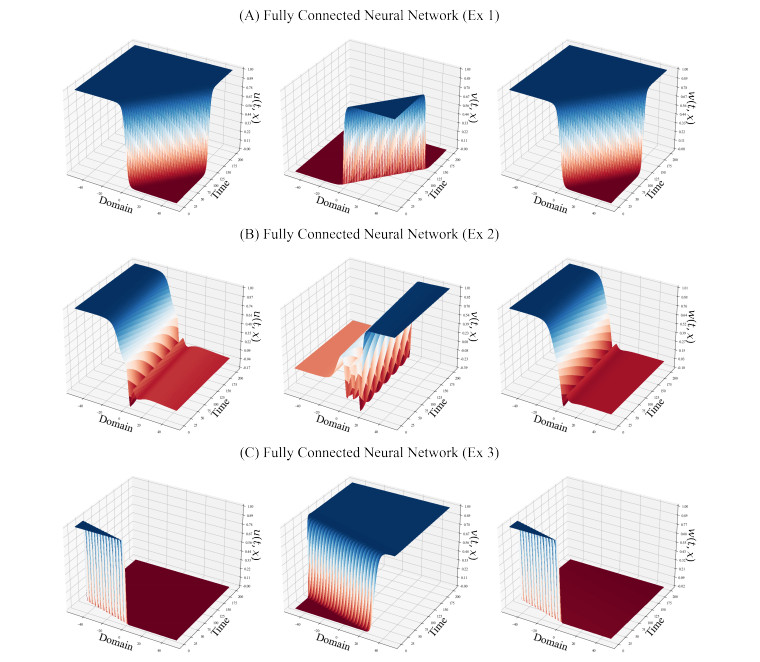
If we optimize only the residual loss of Section 2.1 without any restrictions, the fully connected neural network proceeds with unstable training. Figure 1 shows the results of the convergence of the fully connected neural network for three different seeds provided by Pytorch and Numpy. Theorem 3 implies that the wave speed is precisely zero for $(a_1, d_1, a_3, d_3, b_1, b_2, b_3) = (1, 1, 1, 0.6, 1.2, 0.6)$. Although the fully connected neural network seems to extract the corresponding wave speed in the second experiment, the approximations do not have monotonicity. In the case of the first and third experiments, as seen in Table 1, the model achieves the approximations with a small loss function. This result raises the possibility that the system without monotonicity may admits another solution.

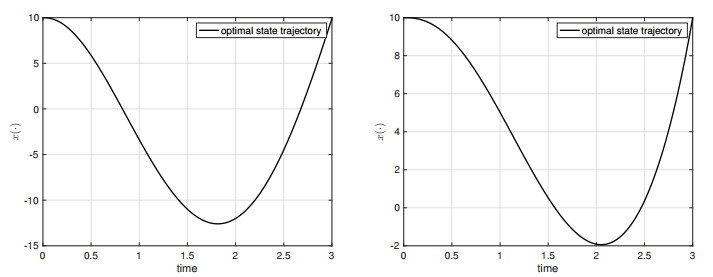
In contrast to the above, our method showed outstanding performance. Figure 2(B) shows that our model indeed approximates smooth function. By observing that our model predicts an accurate speed with a small loss in Table 1, the results of Theorem 4 suggest that our model exists near the solution. min-max monotonic networks have failed to predict the exact speed and reduce loss. We analyzed that the network cannot satisfy the governing equation because max or min operation hinders differentiability.

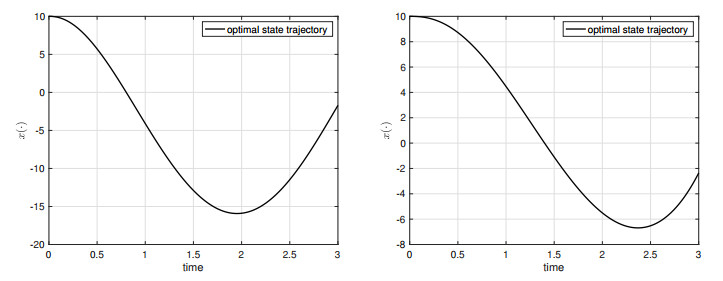
When the sign is known instead of the exact value of wave speed, our model has performed feasible predictions. Figures 3 and 4 show the experimental results of our model when $(a_1, d_1, a_3, d_3, b_1, b_2, b_3)$ is determined to (1, 1, 1, 1, 0.75, 0.75, 1.25) and (1, 1, 1, 1, 0.75, 0.75, 1.75), respectively. Our model predicted the correct sign, and the loss function converged to zero for the above cases. However, stabilization of learning requires more hyperparameter search. The learning and decay rates used in this paper are searched by performing a grid search on $Loss_{Total}$. The segmentation and extension of the set of hyperparameters may contribute to the convergence of the model.

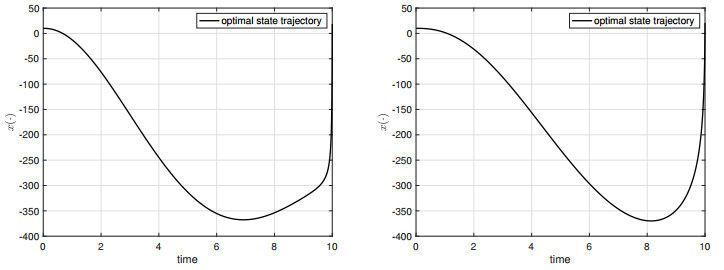
Finally, for analysis of negative wave speeds related to Theorem 2, we set $(a_1, d_1, a_3, d_3, b_1, b_2, b_3)$ to $(1, 1, 1, 1, 0.99, 0.99, 2.01)$. In this case, Figure 5 shows that the solution is challenging to approximate through our methods. Although the estimated speed seems to converge to -0.2, we can observe a phenomenon in which the value of the loss function increases rapidly before reaching an acceptable level of convergence. We observed that in the majority of experiments, it was necessary for the loss function values to be less than 1e-5 to ensure convergence to accurate solutions. The experimental results presented in Table 1 demonstrate that The training of neural networks with loss function values around 1e-3 can result in a failure to predict an adequate wave speed. This raised the question of whether our method indeed approximates real solutions in this negative speed case.

5.   Conclusions

In this paper, we construct the monotonic neural network to impose constraints on the monotonicity. In all experiments, our method performed better than other methods, suggesting that it effectively represents real solutions based on a theoretical basis.

To verify that this approach is universal, we require supplementary experiments on various equations in which a unique monotone solution exists. We anticipate that the proof techniques or algorithm can be applied to several equations without significant modifications, provided that the uniqueness of the traveling wave solution is guaranteed. As a future research direction, it would be valuable to develop a neural network structure that can approximate the traveling wave solution with the minimum wave speed when multiple solutions exist.

Recently, the number of studies attempting to transform the residual loss of PINN has been increasing. The optimization problem for PDE was interpreted as a boundary constraint problem, with empirical evidence that minimizing the loss function for boundary conditions is quite challenging. Reflecting this trend, we will conduct a convergence analysis of algorithms that consider regularization rather than constraints. There exist a few traveling wave solutions which possess monotonicity as a property, rather than as an imposed constraint. In future work, we will investigate the variations that result from training with Physics-informed Neural Networks (PINNs) for this regularized problem.

Acknowledgments

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (RS-2022-00165268) and by Institute for Information & Communications Technology Promotion (IITP) grant funded by the Korea government(MSIP) (No.2019-0-01906, Artificial Intelligence Graduate School Program (POSTECH)).

Conflict of interest

The authors declare there is no conflict of interest.