Modelling and analysis of fractional-order vaccination model for control of COVID-19 outbreak using real data

1.   Introduction

Mathematical models are the foremost technique to investigate the transmission dynamics of COVID-19 to control and develop a new strategy or policy to prevent the spread of the disease. Several mathematical models have been developed and formulated in the last two years to understand the novel infection surge by COVID-19 such as understanding the transmission dynamics ^{[1,2,3,4,5,6,7,8,9,10]}, the efficiency of lockdown ^[11,12], the impact of social distancing ^[13,14], the effect of isolation and quarantine ^{[15,16,17,18,19,20,21]}, the impact of facemask ^[22,23], media effect ^[24,25], the impact of the environment ^[26,27].

A vaccine is a kind of medicine that develops a body's immune system before catching the disease. Clinically there are four types of COVID-19 vaccine as follows: 1) whole virus, 2) protein subunit, 3) viral vector, and 4) RNA and DNA (Nucleic acid). The entire world is taken a challenge to prepare a vaccine to prevent COVID-19. In this short span, various vaccinations are developed and approved for emergency use such as Covaxin, Moderna, Sputnik Light, Sputnik V, Covishield, Ad26.COV2.S, Convidecia, Zifivax, Novavax, Comirnaty, Covilo, CoronaVac, etc. At present, the world health organization (WHO) approved eleven vaccines for emergency use to fight or reduce the spread of COVID-19 ^[28]. Among these eleven approved vaccines, Covishield, and Covaxin are manufactured in India. Covishield is manufactured by the Serum Institute of India along with Oxford University and approved by 49 countries in the world whereas Covaxin is manufactured by Bharat Biotech and approved by 14 countries in the world ^[28]. About 61% population of India is vaccinated by dose-I and 44% population of India is vaccinated by dose-II up to 1 January 2022. According to the Indian Council of Medical Research (ICMR), two-dose of Covishield or Covaxin significantly mitigate the risk of COVID-19 ^[29].

Mathematical models to understand the effect of vaccination, the efficiency of vaccination, and the vaccination campaign on COVID-19 have been developed and analyzed by the authors ^{[30,31,32,33,34,35,36,37,38,39]} to prevent the disease. Recently, a few mathematical models are reported to study the effect of multi-vaccination or two-dose of vaccination on COVID-19 to control or built an efficient strategy ^[40,41,42]. Best of our knowledge there is none of the attempts is registered to investigate the impact of two-dose of vaccination on COVID-19 with Caputo derivative using real data from the Republic of India. Hence in this attempt, we have proposed a mathematical model to study the effect of two-dose of vaccination on the transmission dynamics of COVID-19.

The rest of the paper is organized as follows: Section 2 provides the preliminary of fractional calculus. The SV₁V₂EIR model formulation for dose-I and dose-II of vaccination with Caputo derivative is presented in Section 3. The local and global stability of the equilibrium points of the SV₁V₂EIR model and the positivity of the solution are provided in Section 4. The Laplace-Adomian decomposition method for the numerical solution of the proposed SV₁V₂EIR model is given in Section 5. The estimation of SV₁V₂EIR model parameters, sensitivity analysis, and numerical simulations are presented in Section 6. Finally, a conclusion of the present work is given in Section 7.

2.   Preliminaries

In this section, the basic definition of fractional calculus is presented which uses to describe and formulate the SV₁V₂EIR model for COVID-19 ^[43,44,45].

Definition 2.1 Let $y \in {L^1}([0, T], \mathbb{R}),$ then the Riemann-Liouville fractional integral of order $\alpha$ is defined by

Definition 2.2 The Caputo fractional derivative of a function $y(t)$ on the interval $[0, T]$ is defined by

where $n = [\alpha] + 1$ and $[\alpha]$ denotes the integer part of $\alpha.$

Definition 2.3 The Laplace transform of Caputo fractional derivative of a function $y(t)$ is defined by

where $n - 1 < \alpha < n$ and $n \in \mathbb{N}.$

3.   Mathematical model

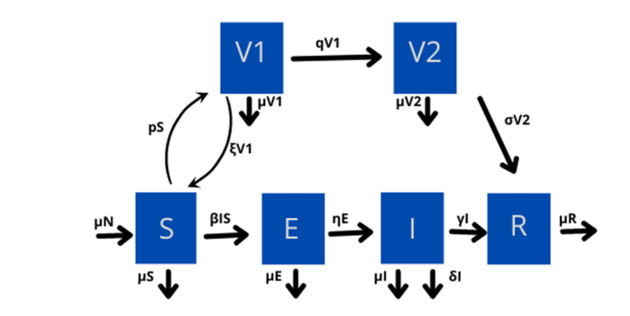
Mathematical modelling of transmission dynamics of COVID-19 is ubiquitous to control the spread of the disease. A series of models are reported to explore the impact of vaccines on the treatment of disease. In this section, we propose a deterministic two-dose vaccination model to analyze the overall dynamics of COVID-19. We divide the total population into six compartments namely susceptible individuals $S(t)$, vaccinated individuals after dose-I ${V_1}(t)$, vaccinated individuals after dose-II ${V_2}(t)$, exposed individuals $E(t)$, infected individuals $I(t)$, and recovered individuals $R(t)$. The size of the compartment class varies with time $t$ but the total size of the population $N(t) = S(t) + {V_1}(t) + {V_2}(t) + E(t) + I(t) + R(t)$ is constant.

The susceptible individuals increase due to new birth and the inflow of vaccinated individuals after dose-I at rates $\xi$. It decreases due to an infection, acquires dose-I of vaccine, and natural death at the rate $\beta$, $p$ and $\mu$ respectively. The vaccinated individuals after dose-I are increased due to a susceptible individual who acquires dose-I of the vaccine. It decreases due to a vaccinated transfer back to the susceptible, acquiring dose-II of vaccine, and natural death at the rate $\xi$, $q$ and $\mu$ respectively. The vaccinated individuals after dose-II are increased due to an individual who acquires dose-II of the vaccine. It decreases due to an individual who acquires two-dose of vaccines and natural death at the rate $\sigma$ and $\mu$ respectively. It is assumed that a two-dose of vaccine develops hard immunity in the body and thus an individual recovers from the disease. The exposed individual increase due to susceptible individual who carries the virus but yet not developed clinical symptoms. It decreases due to the development of clinical symptoms in exposed individuals and natural death at the rate $\eta$ and $\mu$ respectively. The infected individual increased due to exposed individuals who got the symptoms of COVID-19. It decreases due to natural recovery, death due to vaccines, and natural death at the rate $\gamma$, $\delta$ and $\mu$ respectively. The recovered individual is increased due to recovery of infected individuals and an individual who acquire two-dose of vaccines at the rate $\gamma$ and $\sigma$ respectively and decrease due to natural death. The flow diagram of the transmission between different individuals is shown in Figure 1. Therefore the resulting mathematical model for COVID-19 is described by the following system of nonlinear ordinary differential equations.

With the initial conditions $S(0) > 0, {V_1}(0) > 0, {V_2}(0) > 0, E(0) > 0, I(0) > 0, R(0) > 0$ and the variables or parameters and a description of the parameter is given in Table 1.

The susceptible individuals in transmission of COVID-19 use their memory to prevent or reduce infection. But an integer-order derivative is not able to acquire it due to its local behaviour. Fractional-order derivatives acquire the information of present and past due to their non-local nature and are involved to prevent infection ^{[43,44,45,46,47,48]}. Motivated by the importance of fractional calculus, we converted the classical model to the fractional SV₁V₂EIR transmission model of COVID-19. First, we replace the classical derivative in the system (4) with the Caputo fractional derivative of order $\alpha$, where $\alpha$ can take any value in the interval $(0, 1]$. Thus, the dimension of a newly developed Caputo SV₁V₂EIR model does not remain the same. In this situation, we use the auxiliary parameter $\chi$ to adjust the inconsistency that arises in the dimensions of the left and right sides of the system. By applying these a balance fractional SV₁V₂EIR transmission model of COVID-19 is given by

with the initial conditions

4.   Model analysis

In mathematical epidemiology, we ensure that the solutions of the model (5) are nonnegative and bounded at all future times. In model (5), all the individual populations are independent of the recovery population so we focus only on susceptible, vaccinated after dose-I, vaccinated after dose-II, exposed, and infected. Hence for this reason we consider the following feasible region for system (5) as $\Omega = \left\{ {(S, {V_1}, {V_2}, E, I) \in R_ + ^5|S, {V_1}, {V_2}, E, I \geqslant 0} \right\}.$

Theorem-1 The closed set $\Omega$ is a positive invariant with respect to the fractional model (5).

Proof: From the first equation of the system (5), we have

as $\mu$ and $\xi$ are natural death rate and progression rate form ${V_1}$ to $S$ respectively, and both parameters are non-negative.

Similarly, we observed that

The Eqs (7)-(8) hold for any point of the region $\Omega$. Thus the set $\Omega$ is positive invariant with respect to the fractional model (5).

Basic reproduction number :the number of infections spread by a single individual is referred to as a basic reproduction number and it plays a vital role in controlling the spread of disease. The disease-free equilibrium point of the SV₁V₂EIR model (5) is given by ${E^0} = ({S^0}, V_1^0, V_2^0, 0, 0),$ where

To compute the basic reproduction number using the next generation method ^[49], we consider the right-hand side of the infected class $E$ and $I$ at ${E^0}$ as $F$ and $V$ where $F = \left({\begin{array}{*{20}{c}} 0 & {\beta {S^0}} \\ 0 & 0 \end{array}} \right)$ and $V = \left({\begin{array}{*{20}{c}} { - (\eta + \mu)} & 0 \\ \eta & { - (\gamma + \delta + \mu)} \end{array}} \right).$ The basic reproduction number is the spectral radius of the next generation matrix $F{V^{ - 1}} = \left({\begin{array}{*{20}{c}} {\frac{{\beta {S^0}\eta }}{{(\eta + \mu)(\gamma + \delta + \mu)}}} & {\frac{{\beta {S^0}}}{{(\gamma + \delta + \mu)}}} \\ 0 & 0 \end{array}} \right).$

Hence the basic reproduction number is defined as

Theorem-2 The disease-free equilibrium point ${E^0}$ of the SV₁V₂EIR model (5) is locally asymptotically stable if ${R_0} < 1.$

Proof: The Jacobian matrix of the model (5) is obtained as follows

So the Jacobian matrix at ${E^0}$ is

The characteristic equation of the Jacobian matrix at the disease-free equilibrium point $J({E^0})$ is ${\chi ^{1 - \alpha }} \cdot \det (J({E^0}) - \lambda I) = 0.$

The third column suggests that one of the eigenvalues is $- (\sigma + \mu)$ and the remaining four eigenvalues can be obtained from the following submatrix of $J({E^0})$ defined as

The matrix ${J_1}({E^0})$ can be rewritten in block form as

where

${B_1} = \left[{\begin{array}{*{20}{c}} { - p - \mu } & \xi \\ p & { - \xi - q - \mu } \end{array}} \right], {B_2} = \left[{\begin{array}{*{20}{c}} 0 & { - \beta {S^0}} \\ 0 & 0 \end{array}} \right], {B_3} = \left[{\begin{array}{*{20}{c}} 0 & 0 \\ 0 & 0 \end{array}} \right],$ and ${B_4} = \left[{\begin{array}{*{20}{c}} { - \eta - \mu } & {\beta {S^0}} \\ \eta & { - \gamma - \delta - \mu } \end{array}} \right].$

The characteristic equation of the block matrix ${J_1}({E^0})$ is given by

Since block matrix, ${B_3} = \left[{\begin{array}{*{20}{c}} 0 & 0 \\ 0 & 0 \end{array}} \right]$ the characteristic equation of ${J_1}({E^0})$ is reduced as

For block matrix ${B_1},$ $Trace({B_1}) = - (p + \mu + \xi + q + \mu) < 0,$ and $Det({B_1}) = (p + \mu)(\xi + q + \mu) - p\xi = p(q + \mu) + \mu (\xi + q + \mu) > 0.$

For block matrix ${B_4},$ $Trace({B_4}) = - (\eta + \mu + \gamma + \delta + \mu) < 0,$ and $Det({B_4}) = (\eta + \mu)(\gamma + \delta + \mu) - \eta \beta {S^0} = 1 - \frac{{\eta \beta {S^0}}}{{(\eta + \mu)(\gamma + \delta + \mu)}} = 1 - {R_0},$

Hence it is clear that $Det({B_4}) > 0$ if ${R_0} < 1.$

Thus by the Routh-Hurwitz criteria of stability, the disease-free equilibrium point of the SV₁V₂EIR model (5) is locally asymptotically stable if ${R_0} < 1$ otherwise unstable.

Theorem-3 The SV₁V₂EIR model (5) possesses at most two equilibrium points, 1) A disease-free equilibrium point ${E^0} = ({S^0}, V_1^0, V_2^0, 0, 0),$ where

2) An endemic equilibrium point ${E^*} = ({S^*}, V_1^*, V_2^*, {E^*}, {I^*})$ where

Proof: To find the equilibrium points of the model (5), we solve the following equations

Thus, we get the following algebraic system

By simple algebraic manipulation, we obtain two solutions to the system (20). The first is a disease-free equilibrium point ${E^0} = ({S^0}, V_1^0, V_2^0, 0, 0),$ where

and the second is an endemic equilibrium point ${E^*} = ({S^*}, V_1^*, V_2^*, {E^*}, {I^*})$,

Theorem-4 The endemic equilibrium point ${E^*}$ of the SV₁V₂EIR model (5) is locally asymptotically stable if ${R_0} > 1.$

Proof: The Jacobian matrix of the model (5) is obtained as follows

So the Jacobian matrix at ${E^*}$ is

The third column suggests that one of the eigenvalues is $- (\sigma + \mu)$ and the remaining four eigenvalues can be obtained from the following sub matrix of $J({E^*})$ defined as

The characteristic equation of the sub matrix ${J_1}({E^*})$ is defined as ${\chi ^{1 - \alpha }} \cdot \det ({J_1}({E^*}) - \lambda I) = 0.$

Thus we have

where

The simplification gives

the simplification gives

and

the simplification gives

Now, it is easily seen that ${a_i} > 0, i = 1, 2, 3, 4$ provided ${I^*} > 0.$ Also, from Eq (18) it is clear that ${I^*} > 0$ if ${R_0} > 1.$

Thus by the Routh-Hurwitz criteria of stability, the endemic equilibrium point of the SV₁V₂EIR model (5) is locally asymptotically stable if ${R_0} > 1$ otherwise unstable.

Theorem-5 The disease-free equilibrium point ${E^0}$ of the SV₁V₂EIR model (5) is globally asymptotically stable if ${R_0} < 1.$

Proof: We consider the appropriate positive definite Lyapunov function $L(S, {V_1}, {V_2}, E, I):\Omega \to {\mathbb{R}^ + }$ defined as

The Caputo fractional derivative of the Lyapunov function is

From (5) we get,

The simplification gives

Since $S = {S^0} \leqslant N,$ it follows that

Therefore

Hence if ${R_0} < 1,$ then ${}_0^CD_t^\alpha L(t) < 0$ and ${}_0^CD_t^\alpha L(t) = 0$ when $I = 0.$ Thus by LaSalle's extension to Lyapunov's principle ^[50], the disease-free equilibrium point of the SV₁V₂EIR model (5) is globally asymptotically stable if ${R_0} < 1$ otherwise unstable.

Next, to prove the global stability of an endemic equilibrium point ${E^*}$ of the SV₁V₂EIR model (5) we use the following result.

Lemma: 6 ^[51] Let $g(t) \in {\mathbb{R}^ + }$ be a differentiable and continuous function then for any ${g^*} \in {\mathbb{R}^ + }$ and $\alpha \in (0, 1)$ it satisfies,

Theorem-7 The endemic equilibrium point ${E^*}$ of the SV₁V₂EIR model (5) is globally asymptotically stable if ${R_0} > 1.$

Proof: We consider the appropriate positive definite Lyapunov function $L(S, {V_1}, {V_2}, E, I):\Omega \to {\mathbb{R}^ + }$ defined as

where ${W_1} = \frac{1}{{p + \mu }}$, ${W_2} = \frac{{({R_0} - 1)}}{{\eta + \mu }}$, ${R_0} > 1$ and ${W_3} = \frac{1}{{\gamma + \delta + \mu }}$ are positive constants.

The Caputo fractional derivative of the Lyapunov function is

Then by using Lemma 6 we have

From (5) we get,

From the endemic equilibrium points, we get the following relationship

Substitute the values of Eq (36) in Eq (35) then we obtain

It follows that if ${R_0} > 1$ then we have ${}_0^CD_t^\alpha L(t) \leqslant 0,$ and if $S = {S^*}, E = {E^*}$ and $I = {I^*}$ then we have ${}_0^CD_t^\alpha L(t) = 0.$ Thus by LaSalle's extension to Lyapunov's principle ^[50], the endemic equilibrium point of the SV₁V₂EIR model (5) is globally asymptotically stable if ${R_0} > 1$ otherwise unstable.

5.   Solution of the SV₁V₂EIR model by the Laplace-Adomian Decomposition method

The LADM is an efficient technique to obtain an approximate solution for non-linear systems of differential equations ^{[52,53,54,55,56,57,58,59]}.

5.1.   Numerical method

The present section shows the general procedure to provide a numerical solution of the SV₁V₂EIR model (5) with the initial condition

$S(0) = {n_1}, {V_1}(0) = {n_2}, {V_2}(0) = {n_3}, E(0) = {n_4}, I(0) = {n_5},$ and $R(0) = {n_6}.$ By applying the Laplace transform to both sides of the model (5) we have

Now by using the property of Laplace transform, we have

Then by simple rearrangement of the system (39) we have

It is clear that the LADM gives the solution in the form of an infinite series given by

And the nonlinear term $I(t)S(t)$ involved in the model are decomposed by the Adomian polynomial given by

where

Substitution of Eqs (41) and (42) to Eq (40) yields the following results

Next matching the two sides of Eq (44) yields the following iterative algorithm

For vaccinated class after dose-I we have

For the vaccinated class after dose-II we have

For exposed class we have

For infected class we have

For recovered class we have

Then by inverting the Laplace transform of Eqs (45)-(50) along with the initial condition we have an iterative formula as

Therefore the approximate solution of the SV₁V₂EIR model (5) is

where

5.2.   Convergence analysis of LADM

The solution of the SV₁V₂EIR model (5) is obtained in infinite series (52), which rapidly and uniformly converge to the exact solution. To check the convergence of the series solution we use the classical technique ^[60,61]. For this purpose, the obtained solution (52) can be recast as

Next, we present Theorem 8 to prove the convergence of LADM.

Theorem 8 Let $X$ be a Banach space and $F:X \to X$ a contractive map with $0 < k < 1$ then $F$ has a unique point $x$ such that $F(x) = x,$ where $x = (S, {V_1}, {V_2}, E, I, R).$ Let ${x_0} \in {B_r}(x),$ where ${B_r}(x) = \{ x' \in X:||x' - x|| < r\}$ then we have ${x_n} \in {B_r}(x)$ and $\mathop {\lim }\limits_{n \to \infty } {\text{ }}{x_n} = x.$

Proof: We used mathematical induction to prove the result. For $n = 1,$ we have

Let's assume the result is true for $n - 1,$ then

We get

That is

It means that ${x_n} \in {B_r}(x).$

Moreover, $||{x_n} - x|| \leqslant {k^n}||{x_0} - x||$ and $\mathop {\lim }\limits_{n \to \infty } ||{x_n} - x|| = 0$ as $\mathop {\lim }\limits_{n \to \infty } {\text{ }}{k^n} = 0,$ therefore we have $\mathop {\lim }\limits_{n \to \infty } {\text{ }}{x_n} = x.$

This completes the proof.

6.   Numerical results

6.1.   Estimation of SV₁V₂EIR model parameters

To investigate a numerical simulation of the model (5) for India in the Caputo sense we have considered a few parametric values from the literature and the rest are estimated or fitted by the least-squares curve fitting method. We have to use the total population of India N = 1, 408, 044, 253 as of 1 January 2022 ^[63]. The birth rate in India for the year 2022 is 17.163 births per 1000 people ^[64], so we estimate a new recruitment rate $\frac{{Birth{\text{ }}rate*N}}{{365}}$. The mortality rate for India in 2022 is 27.695 deaths per 1000 live births ^[65], so we estimate a natural death rate $\frac{{27.695}}{{1000}} = 0.0277$. The goal is to estimate the remaining parameters of the SV₁V₂EIR model to approximate our numerical results to fit real data. For this purpose, we have considered real data of cumulative covid-19 cases in India from 1 January 2022 to 30 April 2022 provided by worldometer ^[62] and grouped them as weekly in Table 2.

The model (5) was fitted to the daily cumulative covid-19 cases for India to minimize the summation of square error given by the model solution over a considered period and reported real data. We have taken t = 1 day as of 1 January 2022 and t = 120 days as of 30 April 2022. Figure 2 shows the model fitting of daily cumulative confirmed cases of COVID-19 in India.

6.2.   Sensitivity analysis

We have performed the sensitivity analysis of the reproduction number ${R_0}$ of the SV₁V₂EIR model (5) to provide a good strategy and prevent the spread of the disease. A sensitivity index measure provides the proportion that relative changes that may occur in a parameter lead to the relative change in a variable. The normalized forward sensitivity index of ${R_0}$ with a parameter $x$ is defined as follows ^[66]

For the basic reproduction number ${R_0},$ we compute the following sensitivity index as

From the Eq (59), we note that as there is an increase or decrease in transmission rate $\beta$ by a certain percentage say $k$ then the reproduction number ${R_0}$ also increases or decreases by the same percentage $k$. The sensitivity indices of ${R_0}$ with parameters of the SV₁V₂EIR model were evaluated at the parameter values listed in Table 3 and reported in Table 4.

Figure 3 shows the graphical analysis of the sensitivity indices of ${R_0}$ with respect to the model parameters. This analysis suggests that the transmission rate of disease, mortality rate, progression rate form $E$ to $I$, the total population of India, and progression rate form ${V_1}$ to $S$ are in positive correlation with ${R_0}$ whereas the rate of dose-I of vaccine, rate of dose-II of vaccine, vaccines related death rate, and the natural recovery rate are in negative correlation with ${R_0}.$ Also, the sensitivity analysis suggests that the most influential parameter are disease transmission rate and rate of dose-I of vaccine, and the least influential parameter is vaccines related death rate. Hence based on this analysis we can develop a suitable strategy to control and prevent the spread of disease.

6.3.   Numerical simulation

In this subsection, we have employed the LADM scheme to obtain a numerical simulation of the SV₁V₂EIR model (5). To analyze the model (5) we simulate it for various biological parameters mentioned in Table 3.

First, we performed a numerical simulation for various values of the rate of dose-I of the vaccine $(p)$ to explore its impact on the infected population. In Figure 4, the values of $p$ taken into consideration are $p = 0, 0.30, 0.60$ and $0.94.$ In the absence of dose-I of vaccine, there is a giant peak in a number of an infected population near to 20, 190, 000. As values of rate of dose-I of vaccine increase then there is dramatically declined in a number of an infected population. The estimated value of $p = 0.94$ and the number of an infected population is around 7, 570, 000. The model is also simulated for $\alpha = 0.9$ and $\alpha = 0.8$ to analyze the impact of rate of dose-I of the vaccine on the infected population. For $\alpha = 0.9$ and $p = 0$ the number of an infected population is around 19, 410, 000 whereas it is dramatically decreased for $p = 0.94$ around 7, 378, 000 For $\alpha = 0.8$ and $p = 0$ the number of an infected population is around 18, 730, 000 whereas it is dramatically decreased for $p = 0.94$ around 7, 365, 000. Thus there is a strong negative correlation between the rate of dose-I of vaccine and infected population.

Figure 5 shows the impact of the rate of dose-II of the vaccine $(q)$ on the infected population. The values of $q$ taken into consideration are $q = 0, 0.30, 0.62$ and $0.90.$ In the absence of dose-II of vaccine, there is a giant peak in a number of an infected population near to 18, 640, 000. As values of rate of dose-II of vaccine increase then there is dramatically declined in a number of an infected population. The estimated value of $q = 0.62$ and the number of an infected population is around 7, 597, 000. The model is also simulated for $\alpha = 0.9$ and $\alpha = 0.8$ to analyze the impact of the rate of dose-II of the vaccine on the infected population. For $\alpha = 0.9$ and $q = 0$ the number of an infected population is around 18, 000, 000 whereas it is dramatically decreased for $q = 0.62$ around 7, 412, 000. For $\alpha = 0.8$ and $q = 0$ the number of an infected population is around 17, 270, 000 whereas it is dramatically decreased for $q = 0.62$ around 7, 407, 000. Thus there is a strong negative correlation between the rate of dose-II of vaccine and infected population.

Figure 6 shows the impact of disease transmission rate $(\beta)$ on the infected population for various transmission rates such as 9.25 × 10^-8, 8.25 × 10^-8, 7.25 × 10^-8, and 6.25 × 10^-8. As the disease transmission rate decrease the number of an infected population is decreased. Thus there is a strong positive correlation between the disease transmission rate and the infected population. The impact of $\beta$ on the infected population is also evaluated for fractional-order $\alpha = 0.9$ and $0.8.$ The same strong positive correlation is observed between the disease transmission rate and the infected population.

Figure 7 shows the impact of the rate of dose-I and dose-II of the vaccine on the infected population. Figure 7 is simulated for the estimated value of $p$ and $q$ for fractional-order $\alpha = 1, 0.9$ and $0.8.$ For $\alpha = 1,$ the infected population after getting dose-I of vaccine is around 485, 100, 000 whereas after getting dose-II of vaccine is around 263, 300, 000. For $\alpha = 0.9,$ the infected population after getting dose-I of vaccine is around 454, 500, 000 whereas after getting dose-II of vaccine is around 240, 400, 000. For $\alpha = 0.8,$ the infected population after getting dose-I of vaccine is around 432, 600, 000 whereas after getting dose-II of vaccine is around 219, 600, 000. Thus there is a dramatically declined in a number of an infected population after getting dose-II of vaccine as compare to dose-I of the vaccine. Also, we observed that as the fractional order decreased the number of the infected population is also gradually decreased due to a non-local property of fractional derivative.

7.   Conclusions

In this paper, we have investigated the SV₁V₂EIR model to reveal the impact of dose-I, and dose-II vaccination on COVID-19 by using the Caputo fractional derivative. The basic reproduction number of the model is derived by using the next-generation matrix method. The local and global stability analysis is investigated for both the disease-free and endemic equilibrium points. Next, we have to consider real data of cumulative COVID-19 cases in India from 1 January 2022 to 30 April 2022 then the model (5) was fitted to the daily cumulative COVID-19 cases for India to minimize summation of square error by least-squares curve fitting method to estimate model parameters. Then we performed a sensitivity analysis to examine the effects of model parameters that affect the basic reproduction number. From a sensitivity index, we analyze that the most influential parameters are disease transmission rate and rate of dose-I of vaccine, and the least influential parameter is the vaccine-related death rate. Finally, the LADM is implemented to obtain a numerical result of an SV₁V₂EIR model. The numerical results suggest that there is a strong negative correlation between the rate of dose-I of the vaccine and the infected population. Thus dose-I of the vaccine is necessary to control the spread of COVID-19. According to numerical results, the dose-II of the vaccine is the most efficient to restrict the wide spread of disease. Furthermore, the numerical results suggest that there is a strong positive correlation between the disease transmission rate and the infected population. Thus by following the proper guideline declared by the WHO and the government we decrease the disease transmission rate and ultimately restrict the spread of the pandemic. The fractional-order model provides accurate results due to a non-local property and reveals the precise number of infected population and hence in advanced intimate to develop a most efficient strategy to prevent an outbreak.

Conflict of interest

The authors declare there is no conflict of interest.