Deterministic-Stochastic modeling: A new direction in modeling real world problems with crossover effect

Abdon ATANGANA; Seda İĞRET ARAZ; Abdon ATANGANA; Seda İĞRET ARAZ

doi:10.3934/mbe.2022163

Mathematical Biosciences and Engineering

2022, Volume 19, Issue 4: 3526-3563. doi: 10.3934/mbe.2022163

Previous Article Next Article

Research article Special Issues

Deterministic-Stochastic modeling: A new direction in modeling real world problems with crossover effect

Abdon ATANGANA ^{1,2
,
,},
Seda İĞRET ARAZ ^1,3

1.
Faculty of Natural and Agricultural Sciences, University of the Free State, South Africa
2.
Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan
3.
Department of Mathematics Education, Siirt University, Siirt, Turkey

Received: 30 October 2021 Revised: 11 December 2021 Accepted: 22 December 2021 Published: 07 February 2022

Many real world problems depict processes following crossover behaviours. Modelling processes following crossover behaviors have been a great challenge to mankind. Indeed real world problems following crossover from Markovian to randomness processes have been observed in many scenarios, for example in epidemiology with spread of infectious diseases and even some chaos. Deterministic and stochastic methods have been developed independently to develop the future state of the system and randomness respectively. Very recently, Atangana and Seda introduced a new concept called piecewise differentiation and integration, this approach helps to capture processes with crossover effects. In this paper, an example of piecewise modelling is presented with illustration to chaos problems. Some important analysis including a piecewise existence and uniqueness and piecewise numerical scheme are presented. Numerical simulations are performed for different cases.

Keywords:

Citation: Abdon ATANGANA, Seda İĞRET ARAZ. Deterministic-Stochastic modeling: A new direction in modeling real world problems with crossover effect[J]. Mathematical Biosciences and Engineering, 2022, 19(4): 3526-3563. doi: 10.3934/mbe.2022163

Related Papers:

[1]	Abdon Atangana, Seda İĞRET ARAZ . Rhythmic behaviors of the human heart with piecewise derivative. Mathematical Biosciences and Engineering, 2022, 19(3): 3091-3109. doi: 10.3934/mbe.2022143
[2]	Abdon ATANGANA, Seda İǦRET ARAZ . Piecewise derivatives versus short memory concept: analysis and application. Mathematical Biosciences and Engineering, 2022, 19(8): 8601-8620. doi: 10.3934/mbe.2022399
[3]	Tingting Yu, Sanling Yuan . Dynamics of a stochastic turbidostat model with sampled and delayed measurements. Mathematical Biosciences and Engineering, 2023, 20(4): 6215-6236. doi: 10.3934/mbe.2023268
[4]	Simone Göttlich, Stephan Knapp . Modeling random traffic accidents by conservation laws. Mathematical Biosciences and Engineering, 2020, 17(2): 1677-1701. doi: 10.3934/mbe.2020088
[5]	Linda J. S. Allen, P. van den Driessche . Stochastic epidemic models with a backward bifurcation. Mathematical Biosciences and Engineering, 2006, 3(3): 445-458. doi: 10.3934/mbe.2006.3.445
[6]	Jiang Li, Xiaohui Liu, Chunjin Wei . The impact of fear factor and self-defence on the dynamics of predator-prey model with digestion delay. Mathematical Biosciences and Engineering, 2021, 18(5): 5478-5504. doi: 10.3934/mbe.2021277
[7]	Dawid Czapla, Sander C. Hille, Katarzyna Horbacz, Hanna Wojewódka-Ściążko . Continuous dependence of an invariant measure on the jump rate of a piecewise-deterministic Markov process. Mathematical Biosciences and Engineering, 2020, 17(2): 1059-1073. doi: 10.3934/mbe.2020056
[8]	Fathalla A. Rihan, Hebatallah J. Alsakaji . Analysis of a stochastic HBV infection model with delayed immune response. Mathematical Biosciences and Engineering, 2021, 18(5): 5194-5220. doi: 10.3934/mbe.2021264
[9]	Azmy S. Ackleh, Shuhua Hu . Comparison between stochastic and deterministic selection-mutation models. Mathematical Biosciences and Engineering, 2007, 4(2): 133-157. doi: 10.3934/mbe.2007.4.133
[10]	Tingting Xue, Long Zhang, Xiaolin Fan . Dynamic modeling and analysis of Hepatitis B epidemic with general incidence. Mathematical Biosciences and Engineering, 2023, 20(6): 10883-10908. doi: 10.3934/mbe.2023483

Abstract

1. Introduction

Deterministic models have been initiated to replicate processes in nature. They have been applied with great success in the last decades. However, when dealing with processes following randomness, indeed these deterministic models cannot be in use as they have failed to model random behaviors. However they are very useful to depict processes exhibiting power-law, fading memory to power law, passage from fading memory to power-law. They are also useful to depict memory processes. Stochastic differential equations have been introduced to deal with processes exhibiting randomness. They have been used in many real world problems with great success. Noting that, these models are obtained using the concept of differentiation and integral. In particular, the concept of differentiation with the generalized Mittag-Leffler function was developed in ^[1], while Caputo and Fabrizio suggested a differential operator with exponential decay function ^[2]. Atangana generalized the concept of rate of change in his paper ^[3]. Atangana and Seda have suggested piecewise differential and integral operators in their work ^[4]. An analysis of a new chaos model was presented in ^[5]; Atangana and Gomez presented some important properties of fractional differential and integral operators with no singular kernel in ^[6]. Chaos in a turbulent swirling flow was investigated in ^[7], another important analysis of chaos with stochastic properties was presented in ^[8]. A comparative study between chaos and stochastic dynamics was presented in ^[9], Daniel et al, presented a simple method to detect chaos in nature ^[10], another important analysis of stochastic chaos was performed in ^[11]. However there exist in nature processes that exhibit passage from power-law to fading memory, or even from memoriless to power-law, indeed such processes cannot be replicated using either stochastic models or deterministic models. Very recently Atangana and Seda introduced new concepts called piecewise differentiation and integration, where a derivative or an integral is defined as a piecewise within a given interval ^[4]. Such a concept is indeed a new mathematical weapon to model complex real world problems exhibiting complex cross-over behaviors. The new type of modeling will be able to handle many complex problems. For example, we observe a very strange way of spread exhibiting by Covid-19, where in some cases, the spread shows a sign of deterministic within a given period of time then later it shows sign of stochastic randomness. A clear indication of complex cross-over. In this paper, we aim at modeling behaviors of real world exhibiting cross-over from deterministic to stochastic or vice versa.

2. Modeling cross-over from deterministic to stochastic and vice versa

In this section, we discuss different possible scenarios that could possibly occur in nature ^[4].

Case 1. Assume that a real world problem exhibiting cross-over from memoriless process to randomness with no steady state. A general Cauchy problem associated to this is given as

$\begin{equation} \left\{ \begin{array}{c} \frac{dy\left( t\right) }{dt} = f\left( t, y\left( t\right) \right) \;, \; 0\leq t\leq t_{1} \\ y\left( 0\right) = y_{0} \\ dy\left( t\right) = f\left( t, y\left( t\right) \right) dt+\sigma y\left( t\right) dB\left( t\right) \;{\rm{ , }}\;t_{1}\leq t\leq T \\ y\left( t_{1}\right) = y_{1} \end{array} \right. \end{equation}$

(2.1)

where $\sigma$ and $B\left(t\right),$ are density of randomness and environmental noise respectively.

Case 2. Assuming that a real world problem exhibits cross-over from power-law to stochastic processes, then the Cauchy problem associated to this problem can be defined as

$\begin{equation} \left\{ \begin{array}{c} _{0}^{C}D_{t}^{\alpha }y\left( t\right) = f\left( t, y\left( t\right) \right) \;, \;0 < t\leq t_{1} \\ y\left( 0\right) = y_{0} \\ dy\left( t\right) = f\left( t, y\left( t\right) \right) dt+\sigma y\left( t\right) dB\left( t\right) \;{\rm{ , }}\;t_{1}\leq t\leq T \\ y\left( t_{1}\right) = y_{1} \end{array} \right. \end{equation}$

(2.2)

where $0 < \alpha \leq 1.$

Case 3. Assuming that a real world problem exhibits cross-over from fading memory to stochastic processes, then the general Cauchy problem associated to this real world problem can be defined as

$\begin{equation} \left\{ \begin{array}{c} _{0}^{CF}D_{t}^{\alpha }y\left( t\right) = f\left( t, y\left( t\right) \right) \;, \;0 < t\leq t_{1} \\ y\left( 0\right) = y_{0} \\ dy\left( t\right) = f\left( t, y\left( t\right) \right) dt+\sigma y\left( t\right) dB\left( t\right) \;{\rm{ , }}\;t_{1}\leq t\leq T \\ y\left( t_{1}\right) = y_{1} \end{array} \right. \end{equation}$

(2.3)

where $0 < \alpha \leq 1.$

Case 4. Assuming that a complex real world problem is exhibiting cross-over from Mittag-Leffler process to stochastic processes, then the general Cauchy problem associated to such problem is defined as

$\begin{equation} \left\{ \begin{array}{c} _{0}^{ABC}D_{t}^{\alpha }y\left( t\right) = f\left( t, y\left( t\right) \right) \;, \;0 < t\leq t_{1} \\ y\left( 0\right) = y_{0} \\ dy\left( t\right) = f\left( t, y\left( t\right) \right) dt+\sigma y\left( t\right) dB\left( t\right) \;{\rm{ , }}\;t_{1}\leq t\leq T \\ y\left( t_{1}\right) = y_{1} \end{array} \right. \end{equation}$

(2.4)

where $0 < \alpha \leq 1.$

In the stochastic part, the classical derivative can be replaced by global derivative to capture more complex behaviors. To accommodate readers that are not use to fractional calculus, we present the following definitions

$\begin{equation} _{0}^{C}D_{t}^{\alpha }y\left( t\right) = \frac{1}{\Gamma \left( 1-\alpha \right) }\int_{0}^{t}y\prime \left( \tau \right) \left( t-\tau \right) ^{-\alpha }d\tau \end{equation}$

(2.5)

where $0 < \alpha \leq 1.$

$\begin{equation} _{0}^{CF}D_{t}^{\alpha }y\left( t\right) = \frac{M\left( \alpha \right) }{ 1-\alpha }\int_{0}^{t}y\prime \left( \tau \right) \exp \left[ -\frac{\alpha }{1-\alpha }\left( t-\tau \right) \right] d\tau \end{equation}$

(2.6)

where $0 < \alpha \leq 1, M\left(0\right) = M\left(1\right)$ and $M\left(\alpha \right)$ is defined as normalized function. The space within which such is defined is well presented in ^[12]

$\begin{equation} _{0}^{ABC}D_{t}^{\alpha }y\left( t\right) = \frac{AB\left( \alpha \right) }{ 1-\alpha }\int_{0}^{t}y\prime \left( \tau \right) E_{\alpha }\left[ -\frac{ \alpha }{1-\alpha }\left( t-\tau \right) ^{\alpha }\right] d\tau \end{equation}$

(2.7)

where $0 < \alpha \leq 1, AB\left(0\right) = AB\left(1\right)$ and $AB\left(\alpha \right) = 1-\alpha +\frac{\alpha }{\Gamma \left(\alpha \right) }$ $.$

Finally a global derivative of a function $f$ with respect to a function $g$ where $g$ is positive continuously increasing function is defined as

$\begin{equation} D_{g}f\left( t\right) = \lim\limits_{t\rightarrow t_{1}}\frac{f\left( t\right) -f\left( t_{1}\right) }{g\left( t\right) -g\left( t_{1}\right) }. \end{equation}$

(2.8)

If $f$ and $g$ are differentiable with $g\prime \left(t\right) \neq 0,$ then

$\begin{equation} D_{g}f\left( t\right) = \frac{f\prime \left( t\right) }{g\prime \left( t\right) }. \end{equation}$

(2.9)

Case 5. Assuming that a real world problem exhibits random walk processes from $\left[0, t_{1}\right]$ , then later the process follows changes within region in $\left[t_{1}, T\right]$ . A mathematical model associate to this will be

$\begin{equation} \left\{ \begin{array}{c} dy\left( t\right) = f\left( t, y\left( t\right) \right) dt+\sigma y\left( t\right) dB\left( t\right) \;, \;0 < t\leq t_{1} \\ y\left( 0\right) = y_{0} \\ D_{g}y\left( t\right) = f\left( t, y\left( t\right) \right) \;{\rm{ , }}\; t_{1}\leq t\leq T \\ y\left( t_{1}\right) = y_{1}. \end{array} \right. \end{equation}$

(2.10)

where $D_{g}$ can be fractional also.

3. Analysis of deterministic-stochastic models

In this section, we present a discussion regarding numerical solution of each defined deterministic-stochastic model. For each suggested deterministic-stochastic model, the analysis of existence and uniqueness of solutions can be performed piecewisely according to each interval. A proper space of the function can be chosen and a suitable methodology for proving existence and uniqueness of such a model can be performed within each interval. This will not be the object of discussion in our paper, however some examples will be considered later and the existence and uniqueness of their solutions will be presented accordingly. In this section, our focus will be to provide a numerical solution to each model using the Newton polynomial interpolation formula ^[12].

3.1. Numerical scheme for Case 1

We consider the following problem to present numerical scheme

(3.1)

The above is converted to

$\begin{equation} y\left( t\right) = \left\{ \begin{array}{c} y\left( 0\right) +\int_{0}^{t}f\; \;\left( \tau , y\right) d\tau \; \; \\ y\left( t_{1}\right) +\int_{t_{1}}^{t}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\int_{t_{1}}^{t}\sigma y\left( \tau \right) dB\left( \tau \right) \end{array} \right. \end{equation}$

(3.2)

$\begin{equation} y\left( t_{n+1}\right) = \left\{ \begin{array}{c} y\left( 0\right) +\int_{0}^{t}f\; \;\left( \tau , y\right) d\tau \; \; \\ y\left( t_{1}\right) +\int_{t_{1}}^{t}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\int_{t_{1}}^{t}\sigma y\left( \tau \right) B\prime \left( \tau \right) d\tau \end{array} \right. . \end{equation}$

(3.3)

At $t = t_{n+1}$ , we write

$\begin{equation} y\left( t_{n+1}\right) = \left\{ \begin{array}{c} y\left( 0\right) +\int_{0}^{t}f\; \;\left( \tau , y\right) d\tau \\ y\left( t_{1}\right) +\int_{t_{1}}^{t_{n+1}}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\int_{t_{1}}^{t_{n+1}}\sigma y\left( \tau \right) B\prime \left( \tau \right) d\tau \; \; \end{array} \right. \end{equation}$

(3.4)

and

$\begin{equation} y\left( t_{n+1}\right) = \left\{ \begin{array}{c} y\left( 0\right) +\sum_{k = 0}^{i}\int_{t_{k}}^{t_{k+1}}f\; \;\left( \tau , y\right) d\tau \\ y\left( t_{1}\right) +\sum_{k = i+1}^{n}\int_{t_{k}}^{t_{k+1}}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\sum_{k = i+1}^{n}\int_{t_{k}}^{t_{k+1}}\sigma y\left( \tau \right) B\prime \left( \tau \right) d\tau \; \; \end{array} \right. . \end{equation}$

(3.5)

We approximate $f$ $\left(t, y\right)$ within $\left[t_{k}, t_{k+1}\right]$ when $0 < t\leq t_{1}$ using the Newton interpolation polynomial

$\begin{eqnarray} f\left( t, y\right) & = &P_{k}\left( t\right) \simeq f\left( t_{k-1}, y\left( t_{k-1}\right) \right) +\frac{f\left( t_{k-1}, y\left( t_{k-1}\right) \right) -f\left( t_{k-2}, y\left( t_{k-2}\right) \right) }{\Delta t}\left( t-t_{k-2}\right) \\ &&+\frac{f\left( t_{k}, y\left( t_{k}\right) \right) -2f\left( t_{k-1}, y\left( t_{k-1}\right) \right) +f\left( t_{k-2}, y\left( t_{k-2}\right) \right) }{2\left( \Delta t\right) ^{2}}\left( t-t_{k-1}\right) \left( t-t_{k-2}\right) . \end{eqnarray}$

(3.6)

Replacing $f$ $\left(t, y\right)$ by $P_{k}\left(t\right)$ within $\left[t_{k}, t_{k+1}\right]$ , we have following scheme

$\begin{equation} y\; \;\left( t_{n+1}\right) = \left\{ \begin{array}{c} y\left( 0\right) +\sum_{k = 2}^{i}\left\{ \begin{array}{c} \frac{5}{12}f\left( t_{k-2}, y^{k-2}\right) \Delta t-\frac{4}{3}f\left( t_{k-1}, y^{k-1}\right) \Delta t \\ +\frac{23}{12}f\left( t_{k}, y^{k}\right) \Delta t \end{array} \right\} \\ \left[ \begin{array}{c} y\left( t_{1}\right) +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}f\left( t_{k-2}, y^{k-2}\right) \Delta t-\frac{4}{3}f\left( t_{k-1}, y^{k-1}\right) \Delta t \\ +\frac{23}{12}f\left( t_{k}, y^{k}\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B\left( t_{k-1}\right) -B\left( t_{k-2}\right) \right) \sigma y^{k-2} \\ -\frac{4}{3}\left( B\left( t_{k}\right) -B\left( t_{k-1}\right) \right) \sigma y^{k-1} \\ +\frac{23}{12}\left( B\left( t_{k+1}\right) -B\left( t_{k}\right) \right) \sigma y^{k} \end{array} \right\} \end{array} \right] \; \; \end{array} \right. . \end{equation}$

(3.7)

3.2. Numerical scheme for Case 2

We deal with the following problem where first part is with Caputo fractional derivative and second part is stochastic. Such model is given by

(3.8)

The above is converted to

$\begin{equation} y\left( t\right) = \left\{ \begin{array}{c} \frac{1}{\Gamma \left( \alpha \right) }\int_{0}^{t}f\left( \tau , y\right) \left( t_{1}-\tau \right) ^{\alpha -1}d\tau \\ y\left( t_{1}\right) +\int_{t_{1}}^{t}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\int_{t_{1}}^{t}\sigma y\left( \tau \right) B\prime \left( \tau \right) d\tau \end{array} \right. . \end{equation}$

(3.9)

At $t = t_{n+1}$ , we write

$\begin{equation} y\left( t_{n+1}\right) = \left\{ \begin{array}{c} \frac{1}{\Gamma \left( \alpha \right) }\int_{0}^{t_{n+1}}f\left( \tau , y\right) \left( t_{1}-\tau \right) ^{\alpha -1}d\tau \\ y\left( t_{1}\right) +\int_{t}^{t_{n+1}}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\int_{t}^{t_{n+1}}\sigma y\left( \tau \right) B\prime \left( \tau \right) d\tau \; \; \end{array} \right. \end{equation}$

(3.10)

and

$\begin{equation} y\left( t_{n+1}\right) = \left\{ \begin{array}{c} \frac{1}{\Gamma \left( \alpha \right) }\sum_{k = 0}^{i}\int_{t_{k}}^{t_{k+1}}f \; \;\left( \tau , y\right) \left( t_{n+1}-\tau \right) ^{\alpha -1}d\tau \\ y\left( t_{1}\right) +\sum_{k = i+1}^{n}\int_{t_{k}}^{t_{k+1}}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\sum_{k = i+1}^{n}\int_{t_{k}}^{t_{k+1}}\sigma y\left( \tau \right) B\prime \left( \tau \right) d\tau \; \; \end{array} \right. . \end{equation}$

(3.11)

Replacing $f$ $\left(t, y\right)$ by its Newton polynomial, we can approximate $f$ $\left(t, y\right)$ within $\left[t_{k}, t_{k+1}\right]$ as follows

$\begin{equation} y\; \;\left( t_{n+1}\right) = \left\{ \begin{array}{c} \left\{ \begin{array}{c} \frac{\left( \Delta t\right) ^{\alpha -1}}{\Gamma \left( \alpha +1\right) } \sum_{k = 2}^{i}f\left( t_{k-2}, y^{k-2}\right) \Pi \\ +\frac{\left( \Delta t\right) ^{\alpha -1}}{\Gamma \left( \alpha +2\right) } \sum_{k = 2}^{i}\left[ f\left( t_{k-1}, y^{k-1}\right) -f\left( t_{k-2}, y^{k-2}\right) \right] \Sigma \\ +\frac{\alpha \left( \Delta t\right) ^{\alpha -1}}{2\Gamma \left( \alpha +3\right) }\sum_{k = 2}^{i}\left[ \begin{array}{c} f\left( t_{k}, y^{k}\right) -2f\left( t_{k-1}, y^{k-1}\right) \\ +f\left( t_{k-2}, y^{k-2}\right) \end{array} \right] \Delta \end{array} \right\} \\ \left[ \begin{array}{c} y\left( t_{1}\right) +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}f\left( t_{k-2}, y^{k-2}\right) \Delta t-\frac{4}{3}f\left( t_{k-1}, y^{k-1}\right) \Delta t \\ +\frac{23}{12}f\left( t_{k}, y^{k}\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B\left( t_{k-1}\right) -B\left( t_{k-2}\right) \right) \sigma y^{k-2} \\ -\frac{4}{3}\left( B\left( t_{k}\right) -B\left( t_{k-1}\right) \right) \sigma y^{k-1} \\ +\frac{23}{12}\left( B\left( t_{k+1}\right) -B\left( t_{k}\right) \right) \sigma y^{k} \end{array} \right\} \end{array} \right] \; \; \end{array} \right. . \end{equation}$

(3.12)

3.3. Numerical scheme for Case 3

In this subsection, we present numerical approximation for stochastic-deterministic Cauchy problem given by

(3.13)

where the first part is Caputo-Fabrizio fractional derivative and second part is stochastic. Such problem can be integrated as

$\begin{equation} y\left( t\right) = \left\{ \begin{array}{c} \frac{1-\alpha }{M\left( \alpha \right) }f\; \;\left( t, y\right) +\frac{ \alpha }{M\left( \alpha \right) }\int_{0}^{t}f\; \;\left( \tau , y\right) d\tau \; \; \\ y\left( t_{1}\right) +\int_{t_{1}}^{t}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\int_{t_{1}}^{t}\sigma y\left( \tau \right) dB\left( \tau \right) \end{array} \right. \end{equation}$

(3.14)

$\begin{equation} y\left( t\right) = \left\{ \begin{array}{c} \frac{1-\alpha }{M\left( \alpha \right) }f\; \;\left( t, y\right) +\frac{ \alpha }{M\left( \alpha \right) }\int_{0}^{t}f\; \;\left( \tau , y\right) d\tau \; \; \\ y\left( t_{1}\right) +\int_{t_{1}}^{t}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\int_{t_{1}}^{t}\sigma y\left( \tau \right) B\prime \left( \tau \right) d\tau \end{array} \right. . \end{equation}$

(3.15)

At $t = t_{n+1}$ , we write

$\begin{equation} y\left( t_{n+1}\right) = \left\{ \begin{array}{c} \frac{1-\alpha }{M\left( \alpha \right) }f\; \;\left( t, y\right) +\frac{ \alpha }{M\left( \alpha \right) }\int_{0}^{t_{n+1}}f\; \;\left( \tau , y\right) d\tau \\ y\left( t_{1}\right) +\int_{t_{1}}^{t_{n+1}}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\int_{t_{1}}^{t_{n+1}}\sigma y\left( \tau \right) B\prime \left( \tau \right) d\tau \; \; \end{array} \right. \end{equation}$

(3.16)

and

$\begin{equation} y\left( t_{n+1}\right) = \left\{ \begin{array}{c} \frac{1-\alpha }{M\left( \alpha \right) }f\; \;\left( t_{n}, y^{n}\right) + \frac{\alpha }{M\left( \alpha \right) }\sum_{k = 0}^{i}\int_{t_{k}}^{t_{k+1}}f \; \;\left( \tau , y\right) d\tau \\ y\left( t_{1}\right) +\sum_{k = i+1}^{n}\int_{t_{k}}^{t_{k+1}}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\sum_{k = i+1}^{n}\int_{t_{k}}^{t_{k+1}}\sigma y\left( \tau \right) B\prime \left( \tau \right) d\tau \; \; \end{array} \right. . \end{equation}$

(3.17)

We can approximate $f$ $\left(t, y\right)$ within $\left[t_{k}, t_{k+1} \right]$ as follows

$\begin{equation} y\; \;\left( t_{n+1}\right) = \left\{ \begin{array}{c} \frac{1-\alpha }{M\left( \alpha \right) }f\; \;\left( t_{n}, y^{n}\right) + \frac{\alpha }{M\left( \alpha \right) }\sum_{k = 2}^{i}\left\{ \begin{array}{c} \frac{5}{12}f\left( t_{k-2}, y^{k-2}\right) \Delta t-\frac{4}{3}f\left( t_{k-1}, y^{k-1}\right) \Delta t \\ +\frac{23}{12}f\left( t_{k}, y^{k}\right) \Delta t \end{array} \right\} \\ \left[ \begin{array}{c} y\left( t_{1}\right) +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}f\left( t_{k-2}, y^{k-2}\right) \Delta t-\frac{4}{3}f\left( t_{k-1}, y^{k-1}\right) \Delta t \\ +\frac{23}{12}f\left( t_{k}, y^{k}\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B\left( t_{k-1}\right) -B\left( t_{k-2}\right) \right) \sigma y^{k-2} \\ -\frac{4}{3}\left( B\left( t_{k}\right) -B\left( t_{k-1}\right) \right) \sigma y^{k-1} \\ +\frac{23}{12}\left( B\left( t_{k+1}\right) -B\left( t_{k}\right) \right) \sigma y^{k} \end{array} \right\} \end{array} \right] \; \; \end{array} \right. . \end{equation}$

(3.18)

3.4. Numerical scheme for Case 4

To obtain numerical scheme for following problem with piecewise derivative, we consider the following problem

(3.19)

The above problem can be converted as

$\begin{equation} y\left( t\right) = \left\{ \begin{array}{c} \frac{1-\alpha }{AB\left( \alpha \right) }f\left( t, y\right) +\frac{\alpha }{ AB\left( \alpha \right) \Gamma \left( \alpha \right) }\int_{0}^{t}f\left( \tau , y\right) \left( t_{1}-\tau \right) ^{\alpha -1}d\tau \\ y\left( t_{1}\right) +\int_{t_{1}}^{t}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\int_{t_{1}}^{t}\sigma y\left( \tau \right) B\prime \left( \tau \right) d\tau \end{array} \right. . \end{equation}$

(3.20)

At $t = t_{n+1}$ , we write

$\begin{equation} y\left( t_{n+1}\right) = \left\{ \begin{array}{c} \frac{1-\alpha }{AB\left( \alpha \right) }f\left( t, y\right) +\frac{\alpha }{ AB\left( \alpha \right) \Gamma \left( \alpha \right) }\int_{0}^{t_{n+1}}f\left( \tau , y\right) \left( t_{1}-\tau \right) ^{\alpha -1}d\tau \\ y\left( t_{1}\right) +\int_{t_{1}}^{t_{n+1}}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\int_{t_{1}}^{t_{n+1}}\sigma y\left( \tau \right) B\prime \left( \tau \right) d\tau \; \; \end{array} \right. \end{equation}$

(3.21)

and

$\begin{equation} y\left( t_{n+1}\right) = \left\{ \begin{array}{c} \frac{1-\alpha }{AB\left( \alpha \right) }f\; \;\left( t_{n}, y^{n}\right) +\frac{\alpha }{AB\left( \alpha \right) \Gamma \left( \alpha \right) } \sum_{k = 0}^{i}\int_{t_{k}}^{t_{k+1}}f\; \;\left( \tau , y\right) \left( t_{n+1}-\tau \right) ^{\alpha -1}d\tau \\ y\left( t_{1}\right) +\sum_{k = i+1}^{n}\int_{t_{k}}^{t_{k+1}}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\sum_{k = i+1}^{n}\int_{t_{k}}^{t_{k+1}}\sigma y\left( \tau \right) B\prime \left( \tau \right) d\tau \; \; \end{array} \right. . \end{equation}$

(3.22)

Replacing $f$ $\left(t, y\right)$ by its Newton polynomial, we can get the following scheme

$\begin{equation} y\; \;\left( t_{n+1}\right) = \left\{ \begin{array}{c} \left\{ \begin{array}{c} \frac{1-\alpha }{AB\left( \alpha \right) }f\left( t_{n}, y^{n}\right) +\frac{ \alpha }{AB\left( \alpha \right) }\frac{\left( \Delta t\right) ^{\alpha -1}}{ \Gamma \left( \alpha +1\right) }\sum_{k = 2}^{i}f\left( t_{k-2}, y^{k-2}\right) \Pi \\ +\frac{\alpha }{AB\left( \alpha \right) }\frac{\left( \Delta t\right) ^{\alpha -1}}{\Gamma \left( \alpha +2\right) }\sum_{k = 2}^{i}\left[ f\left( t_{k-1}, y^{k-1}\right) -f\left( t_{k-2}, y^{k-2}\right) \right] \Sigma \\ +\frac{\alpha }{AB\left( \alpha \right) }\frac{\left( \Delta t\right) ^{\alpha -1}}{2\Gamma \left( \alpha +3\right) }\sum_{k = 2}^{i}\left[ \begin{array}{c} f\left( t_{k}, y^{k}\right) -2f\left( t_{k-1}, y^{k-1}\right) \\ +f\left( t_{k-2}, y^{k-2}\right) \end{array} \right] \Delta \end{array} \right\} \\ \left[ \begin{array}{c} y\left( t_{1}\right) +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}f\left( t_{k-2}, y^{k-2}\right) \Delta t-\frac{4}{3}f\left( t_{k-1}, y^{k-1}\right) \Delta t \\ +\frac{23}{12}f\left( t_{k}, y^{k}\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B\left( t_{k-1}\right) -B\left( t_{k-2}\right) \right) \sigma y^{k-2} \\ -\frac{4}{3}\left( B\left( t_{k}\right) -B\left( t_{k-1}\right) \right) \sigma y^{k-1} \\ +\frac{23}{12}\left( B\left( t_{k+1}\right) -B\left( t_{k}\right) \right) \sigma y^{k} \end{array} \right\} \end{array} \right] \; \; \end{array} \right. . \end{equation}$

(3.23)

3.5. Numerical scheme for Case 5

In this paper, we consider the following problem with piecewise derivative

(3.24)

which is transformed into

$\begin{equation} y\left( t\right) = \left\{ \begin{array}{c} y\left( 0\right) +\int_{0}^{t}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\int_{0}^{t}\sigma y\left( \tau \right) dB\left( \tau \right) \; \; \\ y\left( t_{1}\right) +\int_{t_{1}}^{t}f\; \;\left( \tau , y\left( \tau \right) \right) dg\left( \tau \right) \end{array} \right. \end{equation}$

(3.25)

$\begin{equation} y\left( t\right) = \left\{ \begin{array}{c} y\left( 0\right) +\int_{0}^{t}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\int_{0}^{t}\sigma y\left( \tau \right) B\prime \left( \tau \right) d\tau \\ y\left( t_{1}\right) +\int_{t_{1}}^{t}f\; \;\left( \tau , y\left( \tau \right) \right) g\prime \left( \tau \right) d\tau \end{array} \right. . \end{equation}$

(3.26)

At $t = t_{n+1}$ , we write

$\begin{equation} y\left( t_{n+1}\right) = \left\{ \begin{array}{c} y\left( 0\right) +\int_{0}^{t}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\int_{0}^{t}\sigma y\left( \tau \right) B\prime \left( \tau \right) d\tau \\ y\left( t_{1}\right) +\; \;\int_{t_{1}}^{t_{n+1}}f\; \;\left( \tau , y\right) g\prime \left( \tau \right) d\tau \end{array} \right. \end{equation}$

(3.27)

and

$\begin{equation} y\left( t_{n+1}\right) = \left\{ \begin{array}{c} y\left( 0\right) +\sum_{k = 0}^{i}\int_{t_{k}}^{t_{k+1}}f\; \;\left( \tau , y\left( \tau \right) \right) d\tau +\sum_{k = 0}^{i}\int_{t_{k}}^{t_{k+1}}\sigma y\left( \tau \right) B\prime \left( \tau \right) d\tau \\ y\left( t_{1}\right) +\; \;\sum_{k = i+1}^{n}\int_{t_{k}}^{t_{k+1}}f\; \; \left( \tau , y\left( \tau \right) \right) g\prime \left( \tau \right) d\tau \end{array} \right. . \end{equation}$

(3.28)

The function $f$ $\left(t, y\right)$ can be approximated as follows

$\begin{equation} y\; \;\left( t_{n+1}\right) = \left\{ \begin{array}{c} \left[ \begin{array}{c} y\left( 0\right) +\sum_{k = 2}^{i}\left\{ \frac{5}{12}f\left( t_{k-2}, y^{k-2}\right) \Delta t-\frac{4}{3}f\left( t_{k-1}, y^{k-1}\right) \Delta t+\frac{23}{12}f\left( t_{k}, y^{k}\right) \Delta t\right\} \\ +\sum_{k = 2}^{i}\left\{ \begin{array}{c} \frac{5}{12}\left( B\left( t_{k-1}\right) -B\left( t_{k-2}\right) \right) \sigma y^{k-2}-\frac{4}{3}\left( B\left( t_{k}\right) -B\left( t_{k-1}\right) \right) \sigma y^{k-1} \\ +\frac{23}{12}\left( B\left( t_{k+1}\right) -B\left( t_{k}\right) \right) \sigma y^{k} \end{array} \right\} \end{array} \right] \\ y\left( t_{1}\right) +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}f\left( t_{k-2}, y^{k-2}\right) \left( g\left( t_{k-1}\right) -g\left( t_{k-2}\right) \right) \\ -\frac{4}{3}f\left( t_{k-1}, y^{k-1}\right) \left( g\left( t_{k}\right) -g\left( t_{k-1}\right) \right) \\ +\frac{23}{12}f\left( t_{k}, y^{k}\right) \left( g\left( t_{k+1}\right) -g\left( t_{k}\right) \right) \end{array} \right\} \; \; \end{array} \right. . \end{equation}$

(3.29)

4. Analysis with illustrative example with Hindmarsh-Rose model of neuronal activity

Case 1, we assume that the process follow classical mechanical behavior from $\left[0, 12\right]$ , then later follows the randomness from $\left[12, 25 \right].$ Thus the model can be formulated as

$\begin{eqnarray} \left\{ \begin{array}{c} \frac{dx}{dt} = y+\phi \left( x\right) -z+I \\ \frac{dy}{dt} = \psi \left( x\right) -y \\ \frac{dz}{dt} = r\left[ s\left( x-x_{R}\right) -z\right] \\ x\left( 0\right) = x_{0}, y\left( 0\right) = y_{0}, z\left( 0\right) = z_{0} \end{array} \right. \;{\rm{ if }}\;0\leq t\leq 12 \end{eqnarray}$

(4.1)

$\begin{eqnarray} \left\{ \begin{array}{c} dx = \left( y+\phi \left( x\right) -z+I\right) dt+\sigma _{1}xdB_{1}\left( t\right) \\ dy = \left( \psi \left( x\right) -y\right) dt+\sigma _{2}ydB_{2}\left( t\right) \\ dz = \left( r\left[ s\left( x-x_{R}\right) -z\right] \right) dt+\sigma _{3}zdB_{3}\left( t\right) \\ x\left( 12\right) = x_{12}, y\left( 12\right) = y_{12}, z\left( 12\right) = z_{12} \end{array} \right. \;{\rm{if }}\;12\leq t\leq 25. \end{eqnarray}$

(4.2)

Here $\phi \left(x\right) = -ax^{3}+bx^{2}, \psi \left(x\right) = c-dx^{2}.$

We define the norm $\left\Vert \varphi \right\Vert _{\infty } = \sup_{t\in D_{\varphi }}\left\vert \varphi \left(t\right) \right\vert$ , we consider a Banach space. We present here the existence and uniqueness of the solution piecewisely. However to achieve this, we verify the linear-growth and Lipschitz condition properties. We also assume that $\forall t\in \left[0, 12 \right]$ , there exists $3$ positive constant $M_{1}, M_{2}$ and $M_{3} < \infty$ such that $\left\Vert x\right\Vert _{\infty } < M_{1}, \left\Vert y\right\Vert _{\infty } < M_{2}$ and $\left\Vert z\right\Vert _{\infty } < M_{3}$ .

$\begin{equation} \left\{ \begin{array}{c} \overset{\cdot }{x} = f_{1}\left( x, y, z, t\right) \\ \overset{\cdot }{y} = f_{2}\left( x, y, z, t\right) \\ \overset{\cdot }{z} = f_{3}\left( x, y, z, t\right) \end{array} \right. \;{\rm{ if }}\;0\leq t\leq 12. \end{equation}$

(4.3)

$\forall i = 1, 2, 3,$ we first verify that

$\begin{equation} \left\vert f_{i}\left( x, t\right) \right\vert ^{2} < k_{i}\left( \left\vert x_{i}\right\vert ^{2}+1\right) \end{equation}$

(4.4)

and

$\begin{equation} \left\vert f_{i}\left( x^{1}, t\right) -f_{i}\left( x^{2}, t\right) \right\vert ^{2} < \overline{k_{i}}\left\vert x^{1}-x^{2}\right\vert ^{2}. \end{equation}$

(4.5)

For proof, we consider the function $f_{1}\left(x, y, z, t\right)$

$\begin{eqnarray} \left\vert f_{1}\left( x, y, z, t\right) \right\vert ^{2} & = &\left\vert y+bx^{2}-ax^{3}-z+I\right\vert ^{2} \end{eqnarray}$

(4.6)

$\begin{eqnarray} &\leq &4\left\vert y\right\vert ^{2}+4\left\vert bx^{2}-ax^{3}\right\vert ^{2}+4\left\vert z\right\vert ^{2}+4I^{2} \\ &\leq &4\left( \sup\limits_{t\in \left[ 0, 12\right] }\left\vert y^{2}\right\vert +\left\vert bx-ax^{2}\right\vert ^{2}\left\vert x\right\vert ^{2}+\sup\limits_{t\in \left[ 0, 12\right] }\left\vert z^{2}\right\vert +I^{2}\right) \\ &\leq &4\left( \left\Vert y^{2}\right\Vert _{\infty }+\left\Vert bx-ax^{2}\right\Vert _{\infty }\left\vert x\right\vert ^{2}+\left\Vert z^{2}\right\Vert _{\infty }+I^{2}\right) \\ &\leq &4\left( \left\Vert y^{2}\right\Vert _{\infty }+\left\Vert z^{2}\right\Vert _{\infty }+I^{2}\right) \left( 1+\frac{\left\Vert bx-ax^{2}\right\Vert _{\infty }}{\left\Vert y^{2}\right\Vert _{\infty }+\left\Vert z^{2}\right\Vert _{\infty }+I^{2}}\left\vert x\right\vert ^{2}\right) \notag\end{eqnarray}$

(4.7)

under the condition that $\frac{\left\Vert bx-ax^{2}\right\Vert _{\infty }}{ \left\Vert y^{2}\right\Vert _{\infty }+\left\Vert z^{2}\right\Vert _{\infty }+I^{2}} < 1$ , then

$\begin{equation} \left\vert f_{1}\left( x, y, z, t\right) \right\vert ^{2}\leq k_{1}\left( 1+\left\vert x\right\vert ^{2}\right) . \notag \end{equation}$

Using same routine,

$\begin{eqnarray} \left\vert f_{2}\left( x, y, z, t\right) \right\vert ^{2} & = &\left\vert c-dx^{2}-y\right\vert ^{2} \end{eqnarray}$

(4.8)

$\begin{eqnarray} &\leq &3c^{2}+3d^{2}\left\vert x^{2}\right\vert ^{2}+3\left\vert y\right\vert ^{2} \\ &\leq &3\left( c^{2}+d^{2}\sup\limits_{t\in \left[ 0, 12\right] }\left\vert x^{4}\right\vert +\left\vert y^{2}\right\vert \right) \\ &\leq &3\left( c^{2}+d^{2}\left\Vert x^{4}\right\Vert _{\infty }+\left\vert y^{2}\right\vert \right) \\ &\leq &3\left( c^{2}+d^{2}\left\Vert x^{4}\right\Vert _{\infty }\right) \left( 1+\frac{1}{c^{2}+d^{2}\left\Vert x^{4}\right\Vert _{\infty }} \left\vert y\right\vert ^{2}\right)\end{eqnarray}$

(4.9)

under the condition that $\frac{1}{c^{2}+d^{2}\left\Vert x^{4}\right\Vert _{\infty }} < 1$ , then

$\begin{equation} \left\vert f_{2}\left( x, y, z, t\right) \right\vert ^{2}\leq k_{2}\left( 1+\left\vert y\right\vert ^{2}\right) . \notag \end{equation}$

For the function $F_{3},$

$\begin{eqnarray} \left\vert f_{3}\left( x, y, z, t\right) \right\vert ^{2} & = &\left\vert r\left[ s\left( x-x_{R}\right) -z\right] \right\vert ^{2} \\ &\leq &2r^{2}s^{2}\left\vert x-x_{R}\right\vert ^{2}+2r^{2}\left\vert z\right\vert ^{2} \\ &\leq &2\left( r^{2}s^{2}\sup\limits_{t\in \left[ 0, 12\right] }\left\vert x-x_{R}\right\vert ^{2}+\left\vert z\right\vert ^{2}\right) \\ &\leq &2r^{2}\left( s^{2}\left\Vert x-x_{R}\right\Vert _{\infty }^{2}+\left\vert z\right\vert ^{2}\right) \\ &\leq &2r^{2}\left( s^{2}\left\Vert x-x_{R}\right\Vert _{\infty }^{2}\right) \left( 1+\frac{1}{s^{2}\left\Vert x-x_{R}\right\Vert _{\infty }^{2}} \left\vert z\right\vert ^{2}\right) \end{eqnarray}$

(4.10)

under the condition that $\frac{1}{s^{2}\left\Vert \left(x-x_{R}\right) ^{2}\right\Vert _{\infty }} < 1$ , then

$\begin{equation} \left\vert f_{3}\left( x, y, z, t\right) \right\vert ^{2}\leq k_{3}\left( 1+\left\vert z\right\vert ^{2}\right) . \notag \end{equation}$

Therefore the condition of linear growth is verified if

$\begin{equation} \max \left\{ \frac{\left\Vert bx-ax^{2}\right\Vert _{\infty }}{\left\Vert y^{2}\right\Vert _{\infty }+\left\Vert z^{2}\right\Vert _{\infty }+I^{2}}, \frac{1}{c^{2}+d^{2}\left\Vert x^{4}\right\Vert _{\infty }}, \frac{1}{ s^{2}\left\Vert x-x_{R}\right\Vert _{\infty }^{2}}\right\} < 1. \end{equation}$

(4.11)

4.1. Numerical scheme for stochastic-deterministic model of Hindmarsh-Rose model

We consider the Hindmarsh-Rose model in piecewise where the first part is classical and the second part is stochastic such that the stochastic-deterministic model of Hindmarsh-Rose model^[13] is given as

$\begin{eqnarray} \left\{ \begin{array}{c} \frac{dx}{dt} = y-ax^{3}+bx^{2}-z+I \\ \frac{dy}{dt} = c-dx^{2}-y \\ \frac{dz}{dt} = rs\left( x-x_{R}\right) -rz \\ x\left( 0\right) = x_{0}, y\left( 0\right) = y_{0}, z\left( 0\right) = z_{0} \end{array} \right. \;{\rm{ if }}\;0\leq t\leq t_{1} \end{eqnarray}$

(4.12)

$\begin{eqnarray} \left\{ \begin{array}{c} dx = \left( y-ax^{3}+bx^{2}-z+I\right) dt+\sigma _{1}xdB_{1}\left( t\right) \\ dy = \left( c-dx^{2}-y\right) dt+\sigma _{2}ydB_{2}\left( t\right) \\ dz = \left( rs\left( x-x_{R}\right) -rz\right) dt+\sigma _{3}zdB_{3}\left( t\right) \\ x\left( t_{1}\right) = x_{1}, y\left( t_{1}\right) = y_{1}, z\left( t_{1}\right) = z_{1} \end{array} \right. \;{\rm{if }}\;t_{1}\leq t\leq T. \end{eqnarray}$

(4.13)

Using the numerical scheme presented in Case 1, the numerical solution of the stochastic-deterministic Hindmarsh-Rose model is given as follows:

$\begin{equation} x\left( t_{n+1}\right) = \left\{ \begin{array}{c} x^{0}+\sum_{k = 2}^{i}\left\{ \begin{array}{c} \frac{5}{12}\left( y^{k-2}-ax^{3k-6}+bx^{2k-4}-z^{k-2}+I\right) \Delta t \\ -\frac{4}{3}\left( y^{k-1}-ax^{3k-3}+bx^{2k-2}-z^{k-1}+I\right) \Delta t \\ +\frac{23}{12}\left( y^{k}-ax^{3k}+bx^{2k}-z^{k}+I\right) \Delta t \end{array} \right\} , \;{\rm{if }}\;0 < t\leq t_{1} \\ \left[ \begin{array}{c} x^{1}+\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( y^{k-2}-ax^{3k-6}+bx^{2k-4}-z^{k-2}+I\right) \Delta t \\ -\frac{4}{3}\left( y^{k-1}-ax^{3k-3}+bx^{2k-2}-z^{k-1}+I\right) \Delta t \\ +\frac{23}{12}\left( y^{k}-ax^{3k}+bx^{2k}-z^{k}+I\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B_{1}\left( t_{k-1}\right) -B_{1}\left( t_{k-2}\right) \right) \sigma _{1}x^{k-2} \\ -\frac{4}{3}\left( B_{1}\left( t_{k}\right) -B_{1}\left( t_{k-1}\right) \right) \sigma _{1}x^{k-1} \\ +\frac{23}{12}\left( B_{1}\left( t_{k+1}\right) -B_{1}\left( t_{k}\right) \right) \sigma _{1}x^{k} \end{array} \right\} \end{array} \right] \;{\rm{ , if }}\;t_{1}\leq t\leq T \end{array} \right. . \end{equation}$

(4.14)

$\begin{equation} y\; \;\left( t_{n+1}\right) = \left\{ \begin{array}{c} y^{0}+\sum_{k = 2}^{i}\left\{ \begin{array}{c} \frac{5}{12}\left( c-dx^{2k-4}-y^{k-2}\right) \Delta t \\ -\frac{4}{3}\left( c-dx^{2k-2}-y^{k-1}\right) \Delta t \\ +\frac{23}{12}\left( c-dx^{2k}-y^{k}\right) \Delta t \end{array} \right\} , \;{\rm{if }}\;0 < t\leq t_{1} \\ \left[ \begin{array}{c} y^{1}+\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( c-dx^{2k-4}-y^{k-2}\right) \Delta t \\ -\frac{4}{3}\left( c-dx^{2k-2}-y^{k-1}\right) \Delta t \\ +\frac{23}{12}\left( c-dx^{2k}-y^{k}\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B_{2}\left( t_{k-1}\right) -B_{2}\left( t_{k-2}\right) \right) \sigma _{2}y^{k-2} \\ -\frac{4}{3}\left( B_{2}\left( t_{k}\right) -B_{2}\left( t_{k-1}\right) \right) \sigma _{2}y^{k-1} \\ +\frac{23}{12}\left( B_{2}\left( t_{k+1}\right) -B_{2}\left( t_{k}\right) \right) \sigma _{2}y^{k} \end{array} \right\} \end{array} \right] \;{\rm{ , if }}\;t_{1}\leq t\leq T \end{array} \right. . \end{equation}$

(4.15)

$\begin{equation} z\; \;\left( t_{n+1}\right) = \left\{ \begin{array}{c} z^{0}+\sum_{k = 2}^{i}\left\{ \begin{array}{c} \frac{5}{12}\left( rs\left( x^{k-2}-x_{R}\right) -rz^{k-2}\right) \Delta t \\ -\frac{4}{3}\left( rs\left( x^{k-1}-x_{R}\right) -rz^{k-1}\right) \Delta t \\ +\frac{23}{12}\left( rs\left( x^{k}-x_{R}\right) -rz^{k}\right) \Delta t \end{array} \right\} , \;{\rm{if }}\;0\leq t\leq t_{1} \\ \left[ \begin{array}{c} z^{1}+\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( rs\left( x^{k-2}-x_{R}\right) -rz^{k-2}\right) \Delta t \\ -\frac{4}{3}\left( rs\left( x^{k-1}-x_{R}\right) -rz^{k-1}\right) \Delta t \\ +\frac{23}{12}\left( rs\left( x^{k}-x_{R}\right) -rz^{k}\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B_{3}\left( t_{k-1}\right) -B_{3}\left( t_{k-2}\right) \right) \sigma _{3}z^{k-2} \\ -\frac{4}{3}\left( B_{3}\left( t_{k}\right) -B_{3}\left( t_{k-1}\right) \right) \sigma _{3}z^{k-1} \\ +\frac{23}{12}\left( B_{3}\left( t_{k+1}\right) -B_{3}\left( t_{k}\right) \right) \sigma _{3}z^{k} \end{array} \right\} \end{array} \right] \;{\rm{ , if }}\;t_{1}\leq t\leq T \end{array} \right. . \end{equation}$

(4.16)

4.2. Numerical simulation for stochastic-deterministic model of Hindmarsh-Rose model

We provide the numerical simulations for the Hindmarsh-Rose model^[13] with piecewise derivative

(4.17)

(4.18)

where the first part is classical and the second part is stochastic. Here initial data is taken as

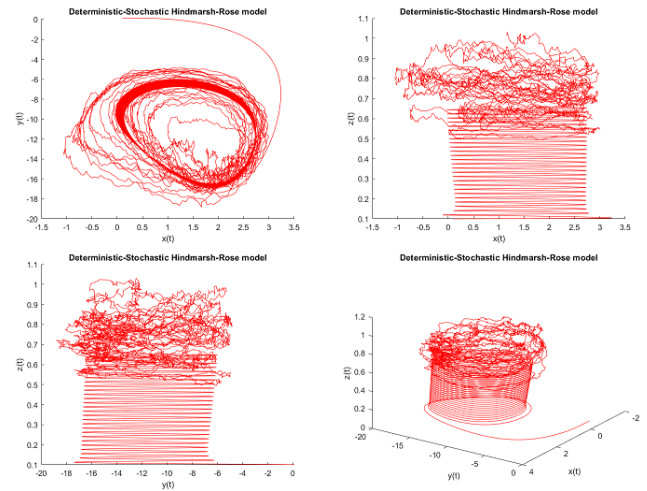
$\begin{equation} x\left( 0\right) = 0.1, y\left( 0\right) = 0.1, z\left( 0\right) = 0.1. \end{equation}$

(4.19)

In , the numerical simulations are depicted with the parameters $a = 1, b = 3, c = 1, d = 5, s = 4, x_{R} = -8/5, r = 10^{-3}, I = 6.$

Figure 1. Numerical visualization of Hindmarsh-Rose model for

$\alpha = 1, \sigma _{1} = 0.01, \sigma _{2} = 0.015, \sigma _{3} = 0.012$ .

DownLoad: Full-Size Img PowerPoint

4.3. Numerical scheme for stochastic-deterministic model of Hindmarsh-Rose model

We present the numerical solution for Hindmarsh-Rose model^[13] in piecewise where the first part is with Caputo fractional derivative and the second part is stochastic. Such model is represented by

$\begin{eqnarray} \left\{ \begin{array}{c} _{0}^{C}D_{t}^{\alpha }x = y-ax^{3}+bx^{2}-z+I \\ _{0}^{C}D_{t}^{\alpha }y = c-dx^{2}-y \\ _{0}^{C}D_{t}^{\alpha }z = rs\left( x-x_{R}\right) -rz \end{array} \right. \;{\rm{ if }}\;0 < t\leq t_{1} \\ \left\{ \begin{array}{c} dx = \left( y-ax^{3}+bx^{2}-z+I\right) dt+\sigma _{1}xdB_{1}\left( t\right) \\ dy = \left( c-dx^{2}-y\right) dt+\sigma _{2}ydB_{2}\left( t\right) \\ dz = \left( rs\left( x-x_{R}\right) -rz\right) dt+\sigma _{3}zdB_{3}\left( t\right) \end{array} \right. \;{\rm{if }}\;t_{1}\leq t\leq T. \end{eqnarray}$

(4.20)

The numerical solution of such model is given by

$\begin{equation} x\left( t_{n+1}\right) = \left\{ \begin{array}{c} \left\{ \begin{array}{c} \frac{\left( \Delta t\right) ^{\alpha -1}}{\Gamma \left( \alpha +1\right) } \sum_{k = 2}^{i}\left( y^{k-2}-ax^{3k-6}+bx^{2k-4}-z^{k-2}+I\right) \Pi \\ +\frac{\left( \Delta t\right) ^{\alpha -1}}{\Gamma \left( \alpha +2\right) } \sum_{k = 2}^{i}\left[ \begin{array}{c} \left( y^{k-1}-ax^{3k-3}+bx^{2k-2}-z^{k-1}+I\right) \\ -\left( y^{k-2}-ax^{3k-6}+bx^{2k-4}-z^{k-2}+I\right) \end{array} \right] \Sigma \\ +\frac{\alpha \left( \Delta t\right) ^{\alpha -1}}{2\Gamma \left( \alpha +3\right) }\sum_{k = 2}^{i}\left[ \begin{array}{c} \left( y^{k-2}-ax^{3k-6}+bx^{2k-4}-z^{k-2}+I\right) \\ -2\left( y^{k-1}-ax^{3k-3}+bx^{2k-2}-z^{k-1}+I\right) \\ +\left( y^{k}-ax^{3k}+bx^{2k}-z^{k}+I\right) \end{array} \right] \Delta \end{array} \right\} , \;{\rm{if }}\;0 < t\leq t_{1} \\ \left[ \begin{array}{c} x^{1}+\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( y^{k-2}-ax^{3k-6}+bx^{2k-4}-z^{k-2}+I\right) \Delta t \\ -\frac{4}{3}\left( y^{k-1}-ax^{3k-3}+bx^{2k-2}-z^{k-1}+I\right) \Delta t \\ +\frac{23}{12}\left( y^{k}-ax^{3k}+bx^{2k}-z^{k}+I\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B_{1}\left( t_{k-1}\right) -B_{1}\left( t_{k-2}\right) \right) \sigma _{1}x^{k-2} \\ -\frac{4}{3}\left( B_{1}\left( t_{k}\right) -B_{1}\left( t_{k-1}\right) \right) \sigma _{1}x^{k-1} \\ +\frac{23}{12}\left( B_{1}\left( t_{k+1}\right) -B_{1}\left( t_{k}\right) \right) \sigma _{1}x^{k} \end{array} \right\} \end{array} \right] \;{\rm{ , if }}\;t_{1}\leq t\leq T \end{array} \right. \end{equation}$

(4.21)

$\begin{equation} y\left( t_{n+1}\right) = \left\{ \begin{array}{c} \left\{ \begin{array}{c} \frac{\left( \Delta t\right) ^{\alpha -1}}{\Gamma \left( \alpha +1\right) } \sum_{k = 2}^{i}\left( c-dx^{2k-4}-y^{k-2}\right) \Pi \\ +\frac{\left( \Delta t\right) ^{\alpha -1}}{\Gamma \left( \alpha +2\right) } \sum_{k = 2}^{i}\left[ \begin{array}{c} \left( c-dx^{2k-2}-y^{k-1}\right) \\ -\left( c-dx^{2k-4}-y^{k-2}\right) \end{array} \right] \Sigma \\ +\frac{\alpha \left( \Delta t\right) ^{\alpha -1}}{2\Gamma \left( \alpha +3\right) }\sum_{k = 2}^{i}\left[ \begin{array}{c} \left( c-dx^{2k-4}-y^{k-2}\right) \\ -2\left( c-dx^{2k-2}-y^{k-1}\right) \\ +\left( c-dx^{2k}-y^{k}\right) \end{array} \right] \Delta \end{array} \right\} , \;{\rm{if }}\;0 < t\leq t_{1} \\ \left[ \begin{array}{c} x^{1}+\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( c-dx^{2k-4}-y^{k-2}\right) \Delta t \\ -\frac{4}{3}\left( c-dx^{2k-2}-y^{k-1}\right) \Delta t \\ +\frac{23}{12}\left( c-dx^{2k}-y^{k}\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B_{2}\left( t_{k-1}\right) -B_{2}\left( t_{k-2}\right) \right) \sigma _{2}y^{k-2} \\ -\frac{4}{3}\left( B_{2}\left( t_{k}\right) -B_{2}\left( t_{k-1}\right) \right) \sigma _{2}y^{k-1} \\ +\frac{23}{12}\left( B_{2}\left( t_{k+1}\right) -B_{2}\left( t_{k}\right) \right) \sigma _{2}y^{k} \end{array} \right\} \end{array} \right] \;{\rm{ , if }}\;t_{1}\leq t\leq T \end{array} \right. . \end{equation}$

(4.22)

$\begin{equation} z\left( t_{n+1}\right) = \left\{ \begin{array}{c} \left\{ \begin{array}{c} \frac{\left( \Delta t\right) ^{\alpha -1}}{\Gamma \left( \alpha +1\right) } \sum_{k = 2}^{i}\left( rs\left( x^{k-2}-x_{R}\right) -rz^{k-2}\right) \Pi \\ +\frac{\left( \Delta t\right) ^{\alpha -1}}{\Gamma \left( \alpha +2\right) } \sum_{k = 2}^{i}\left[ \begin{array}{c} \left( rs\left( x^{k-2}-x_{R}\right) -rz^{k-2}\right) \\ -\left( rs\left( x^{k-1}-x_{R}\right) -rz^{k-1}\right) \end{array} \right] \Sigma \\ +\frac{\alpha \left( \Delta t\right) ^{\alpha -1}}{2\Gamma \left( \alpha +3\right) }\sum_{k = 2}^{i}\left[ \begin{array}{c} \left( rs\left( x^{k-2}-x_{R}\right) -rz^{k-2}\right) \\ -2\left( rs\left( x^{k-1}-x_{R}\right) -rz^{k-1}\right) \\ +\left( rs\left( x^{k}-x_{R}\right) -rz^{k}\right) \end{array} \right] \Delta \end{array} \right\} , \;{\rm{if }}\;0 < t\leq t_{1} \\ \left[ \begin{array}{c} x^{1}+\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( rs\left( x^{k-2}-x_{R}\right) -rz^{k-2}\right) \Delta t \\ -\frac{4}{3}\left( rs\left( x^{k-1}-x_{R}\right) -rz^{k-1}\right) \Delta t \\ +\frac{23}{12}\left( rs\left( x^{k}-x_{R}\right) -rz^{k}\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B_{3}\left( t_{k-1}\right) -B_{3}\left( t_{k-2}\right) \right) \sigma _{3}z^{k-2} \\ -\frac{4}{3}\left( B_{3}\left( t_{k}\right) -B_{3}\left( t_{k-1}\right) \right) \sigma _{3}z^{k-1} \\ +\frac{23}{12}\left( B_{3}\left( t_{k+1}\right) -B_{3}\left( t_{k}\right) \right) \sigma _{3}z^{k} \end{array} \right\} \end{array} \right] \;{\rm{ , if }}\;t_{1}\leq t\leq T \end{array} \right. . \end{equation}$

(4.23)

4.4. Numerical simulation for stochastic-deterministic model of Hindmarsh-Rose model

We present the numerical simulations for the Hindmarsh-Rose model^[13] in piecewise

(4.24)

where initial data is considered as

$\begin{equation} x\left( 0\right) = 0.1, y\left( 0\right) = 0.1, z\left( 0\right) = 0.1. \end{equation}$

(4.25)

In , the numerical simulations are provided with the parameters $a = 1, b = 3, c = 1, d = 5, s = 4, x_{R} = -8/5, r = 10^{-3}, I = 6.$

Figure 2. Numerical visualization of Hindmarsh-Rose model for

$\alpha = 1, \sigma _{1} = 0.01, \sigma _{2} = 0.015, \sigma _{3} = 0.012$ .

DownLoad: Full-Size Img PowerPoint

4.5. Numerical scheme for stochastic-deterministic model of Hindmarsh-Rose model

We consider the Hindmarsh-Rose model^[13] where the first part is Caputo-Fabrizio derivative and the second part is stochastic as follows

(4.26)

$\begin{eqnarray} \left\{ \begin{array}{c} dx = \left( y-ax^{3}+bx^{2}-z+I\right) dt+\sigma _{1}xdB_{1}\left( t\right) \\ dy = \left( c-dx^{2}-y\right) dt+\sigma _{2}ydB_{2}\left( t\right) \\ dz = \left( rs\left( x-x_{R}\right) -rz\right) dt+\sigma _{3}zdB_{3}\left( t\right) \end{array} \right. \;{\rm{if }}\;t_{1}\leq t\leq T. \end{eqnarray}$

(4.27)

Using the numerical scheme presented in Case 3, the numerical scheme for stochastic-deterministic Hindmarsh-rose model is given as follows:

$\begin{equation} x\left( t_{n+1}\right) = \left\{ \begin{array}{c} \frac{1-\alpha }{M\left( \alpha \right) }\left( y^{n}-ax^{3n}+bx^{2n}-z^{n}+I\right) \\ +\frac{\alpha }{M\left( \alpha \right) }\sum_{k = 2}^{i}\left\{ \begin{array}{c} \frac{5}{12}\left( y^{k-2}-ax^{3k-6}+bx^{2k-4}-z^{k-2}+I\right) \Delta t \\ -\frac{4}{3}\left( y^{k-1}-ax^{3k-3}+bx^{2k-2}-z^{k-1}+I\right) \Delta t \\ +\frac{23}{12}\left( y^{k}-ax^{3k}+bx^{2k}-z^{k}+I\right) \Delta t \end{array} \right\} , \;{\rm{if }}\;0 < t\leq t_{1} \\ \left[ \begin{array}{c} x^{1}+\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( y^{k-2}-ax^{3k-6}+bx^{2k-4}-z^{k-2}+I\right) \Delta t \\ -\frac{4}{3}\left( y^{k-1}-ax^{3k-3}+bx^{2k-2}-z^{k-1}+I\right) \Delta t \\ +\frac{23}{12}\left( y^{k}-ax^{3k}+bx^{2k}-z^{k}+I\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B_{1}\left( t_{k-1}\right) -B_{1}\left( t_{k-2}\right) \right) \sigma _{1}x^{k-2} \\ -\frac{4}{3}\left( B_{1}\left( t_{k}\right) -B_{1}\left( t_{k-1}\right) \right) \sigma _{1}x^{k-1} \\ +\frac{23}{12}\left( B_{1}\left( t_{k+1}\right) -B_{1}\left( t_{k}\right) \right) \sigma _{1}x^{k} \end{array} \right\} \end{array} \right] , \;{\rm{ if }}\;t_{1}\leq t\leq T\; \; \end{array} \right. . \end{equation}$

(4.28)

$\begin{equation} y\; \;\left( t_{n+1}\right) = \left\{ \begin{array}{c} \frac{1-\alpha }{M\left( \alpha \right) }\left( c-dx^{2n}-y^{n}\right) \\ +\frac{\alpha }{M\left( \alpha \right) }\sum_{k = 2}^{i}\left\{ \begin{array}{c} \frac{5}{12}\left( c-dx^{2k-4}-y^{k-2}\right) \Delta t \\ -\frac{4}{3}\left( c-dx^{2k-2}-y^{k-1}\right) \Delta t \\ +\frac{23}{12}\left( c-dx^{2k}-y^{k}\right) \Delta t \end{array} \right\} , \;{\rm{if }}\;0 < t\leq t_{1} \\ \left[ \begin{array}{c} y^{1}+\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( c-dx^{2k-4}-y^{k-2}\right) \Delta t \\ -\frac{4}{3}\left( c-dx^{2k-2}-y^{k-1}\right) \Delta t \\ +\frac{23}{12}\left( c-dx^{2k}-y^{k}\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B_{2}\left( t_{k-1}\right) -B_{2}\left( t_{k-2}\right) \right) \sigma _{2}y^{k-2} \\ -\frac{4}{3}\left( B_{2}\left( t_{k}\right) -B_{2}\left( t_{k-1}\right) \right) \sigma _{2}y^{k-1} \\ +\frac{23}{12}\left( B_{2}\left( t_{k+1}\right) -B_{2}\left( t_{k}\right) \right) \sigma _{2}y^{k} \end{array} \right\} \end{array} \right] , \;{\rm{ if }}\;t_{1}\leq t\leq T\; \; \end{array} \right. . \end{equation}$

(4.29)

$\begin{equation} z\; \;\left( t_{n+1}\right) = \left\{ \begin{array}{c} \frac{1-\alpha }{M\left( \alpha \right) }\left( rs\left( x^{n}-x_{R}\right) -rz^{n}\right) \\ +\frac{\alpha }{M\left( \alpha \right) }\sum_{k = 2}^{i}\left\{ \begin{array}{c} \frac{5}{12}\left( rs\left( x^{k-2}-x_{R}\right) -rz^{k-2}\right) \Delta t \\ -\frac{4}{3}\left( rs\left( x^{k-1}-x_{R}\right) -rz^{k-1}\right) \Delta t \\ +\frac{23}{12}\left( rs\left( x^{k}-x_{R}\right) -rz^{k}\right) \Delta t \end{array} \right\} , \;{\rm{if }}\;0 < t\leq t_{1} \\ \left[ \begin{array}{c} z^{1}+\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( rs\left( x^{k-2}-x_{R}\right) -rz^{k-2}\right) \Delta t \\ -\frac{4}{3}\left( rs\left( x^{k-1}-x_{R}\right) -rz^{k-1}\right) \Delta t \\ +\frac{23}{12}\left( rs\left( x^{k}-x_{R}\right) -rz^{k}\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B_{3}\left( t_{k-1}\right) -B_{3}\left( t_{k-2}\right) \right) \sigma _{3}z^{k-2} \\ -\frac{4}{3}\left( B_{3}\left( t_{k}\right) -B_{3}\left( t_{k-1}\right) \right) \sigma _{3}z^{k-1} \\ +\frac{23}{12}\left( B_{3}\left( t_{k+1}\right) -B_{3}\left( t_{k}\right) \right) \sigma _{3}z^{k} \end{array} \right\} \end{array} \right] , \;{\rm{ if }}\;t_{1}\leq t\leq T\; \; \end{array} \right. . \end{equation}$

(4.30)

4.6. Numerical simulation for stochastic-deterministic model of Hindmarsh-Rose model

In this subsection, we consider stochastic-deterministic the Hindmarsh-Rose model^[13]

$\begin{eqnarray} \left\{ \begin{array}{c} _{0}^{CF}D_{t}^{\alpha }x = y-ax^{3}+bx^{2}-z+I \\ _{0}^{CF}D_{t}^{\alpha }y = c-dx^{2}-y \\ _{0}^{CF}D_{t}^{\alpha }z = rs\left( x-x_{R}\right) -rz \end{array} \right. \;{\rm{ if }}\;0 < t\leq t_{1} \\ \left\{ \begin{array}{c} dx = \left( y-ax^{3}+bx^{2}-z+I\right) dt+\sigma _{1}xdB_{1}\left( t\right) \\ dy = \left( c-dx^{2}-y\right) dt+\sigma _{2}ydB_{2}\left( t\right) \\ dz = \left( rs\left( x-x_{R}\right) -rz\right) dt+\sigma _{3}zdB_{3}\left( t\right) \end{array} \right. \;{\rm{if }}\;t_{1}\leq t\leq T \end{eqnarray}$

(4.31)

where initial data is considered as

$\begin{equation} x\left( 0\right) = 0.1, y\left( 0\right) = 0.1, z\left( 0\right) = 0.1. \end{equation}$

(4.32)

In , we perform the numerical simulations with the parameters $a = 1, b = 3, c = 1, d = 5, s = 4, x_{R} = -8/5, r = 10^{-3}, I = 6.$

Figure 3. Numerical visualization of Hindmarsh-Rose model for

$\alpha = 1, \sigma _{1} = 0.01, \sigma _{2} = 0.015, \sigma _{3} = 0.012$ .

DownLoad: Full-Size Img PowerPoint

4.7. Numerical scheme for stochastic-deterministic model of Hindmarsh-Rose model

In this section, we present the numerical scheme for Hindmarsh-Rose model ^[13] with piecewise derivative

$\begin{eqnarray} \left\{ \begin{array}{c} _{0}^{ABC}D_{t}^{\alpha }x = y-ax^{3}+bx^{2}-z+I \\ _{0}^{ABC}D_{t}^{\alpha }y = c-dx^{2}-y \\ _{0}^{ABC}D_{t}^{\alpha }z = rs\left( x-x_{R}\right) -rz \end{array} \right. \;{\rm{ if }}\;0 < t\leq t_{1} \\ \left\{ \begin{array}{c} dx = \left( y-ax^{3}+bx^{2}-z+I\right) dt+\sigma _{1}xdB_{1}\left( t\right) \\ dy = \left( c-dx^{2}-y\right) dt+\sigma _{2}ydB_{2}\left( t\right) \\ dz = \left( rs\left( x-x_{R}\right) -rz\right) dt+\sigma _{3}zdB_{3}\left( t\right) \end{array} \right. \;{\rm{if }}\;t_{1}\leq t\leq T. \end{eqnarray}$

(4.33)

Stochastic-deterministic Hindmarsh-Rose model can be solved by the following scheme

$\begin{equation} x\left( t_{n+1}\right) = \left\{ \begin{array}{c} \left\{ \begin{array}{c} \frac{1-\alpha }{AB\left( \alpha \right) }\left( y^{n}-ax^{3n}+bx^{2n}-z^{n}+I\right) \\ +\frac{\alpha }{AB\left( \alpha \right) }\frac{\left( \Delta t\right) ^{\alpha -1}}{\Gamma \left( \alpha +1\right) }\sum_{k = 2}^{i}\left( y^{k-2}-ax^{3k-6}+bx^{2k-4}-z^{k-2}+I\right) \Pi \\ +\frac{\alpha }{AB\left( \alpha \right) }\frac{\left( \Delta t\right) ^{\alpha -1}}{\Gamma \left( \alpha +2\right) }\sum_{k = 2}^{i}\left[ \begin{array}{c} \left( y^{k-1}-ax^{3k-3}+bx^{2k-2}-z^{k-1}+I\right) \\ -\left( y^{k-2}-ax^{3k-6}+bx^{2k-4}-z^{k-2}+I\right) \end{array} \right] \Sigma \\ +\frac{\alpha }{AB\left( \alpha \right) }\frac{\left( \Delta t\right) ^{\alpha -1}}{2\Gamma \left( \alpha +3\right) }\sum_{k = 2}^{i}\left[ \begin{array}{c} \left( y^{k-2}-ax^{3k-6}+bx^{2k-4}-z^{k-2}+I\right) \\ -2\left( y^{k-1}-ax^{3k-3}+bx^{2k-2}-z^{k-1}+I\right) \\ +\left( y^{k}-ax^{3k}+bx^{2k}-z^{k}+I\right) \end{array} \right] \Delta \end{array} \right\} , \;{\rm{if }}\;0 < t\leq t_{1} \\ \left[ \begin{array}{c} x^{1}+\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( y^{k-2}-ax^{3k-6}+bx^{2k-4}-z^{k-2}+I\right) \Delta t \\ -\frac{4}{3}\left( y^{k-1}-ax^{3k-3}+bx^{2k-2}-z^{k-1}+I\right) \Delta t \\ +\frac{23}{12}\left( y^{k}-ax^{3k}+bx^{2k}-z^{k}+I\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B_{1}\left( t_{k-1}\right) -B_{1}\left( t_{k-2}\right) \right) \sigma _{1}x^{k-2} \\ -\frac{4}{3}\left( B_{1}\left( t_{k}\right) -B_{1}\left( t_{k-1}\right) \right) \sigma _{1}x^{k-1} \\ +\frac{23}{12}\left( B_{1}\left( t_{k+1}\right) -B_{1}\left( t_{k}\right) \right) \sigma _{1}x^{k} \end{array} \right\} \end{array} \right] \;{\rm{ , if }}\;t_{1}\leq t\leq T \end{array} \right. , \end{equation}$

(4.34)

$\begin{equation} y\left( t_{n+1}\right) = \left\{ \begin{array}{c} \left\{ \begin{array}{c} \frac{1-\alpha }{AB\left( \alpha \right) }\left( c-dx^{2n}-y^{n}\right) + \frac{\alpha }{AB\left( \alpha \right) }\frac{\left( \Delta t\right) ^{\alpha -1}}{\Gamma \left( \alpha +1\right) }\sum_{k = 2}^{i}\left( c-dx^{2k-4}-y^{k-2}\right) \Pi \\ +\frac{\alpha }{AB\left( \alpha \right) }\frac{\left( \Delta t\right) ^{\alpha -1}}{\Gamma \left( \alpha +2\right) }\sum_{k = 2}^{i}\left[ \begin{array}{c} \left( c-dx^{2k-2}-y^{k-1}\right) \\ -\left( c-dx^{2k-4}-y^{k-2}\right) \end{array} \right] \Sigma \\ +\frac{\alpha }{AB\left( \alpha \right) }\frac{\left( \Delta t\right) ^{\alpha -1}}{2\Gamma \left( \alpha +3\right) }\sum_{k = 2}^{i}\left[ \begin{array}{c} \left( c-dx^{2k-4}-y^{k-2}\right) \\ -2\left( c-dx^{2k-2}-y^{k-1}\right) \\ +\left( c-dx^{2k}-y^{k}\right) \end{array} \right] \Delta \end{array} \right\} , \;{\rm{if }}\;0 < t\leq t_{1} \\ \left[ \begin{array}{c} x^{1}+\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( c-dx^{2k-4}-y^{k-2}\right) \Delta t \\ -\frac{4}{3}\left( c-dx^{2k-2}-y^{k-1}\right) \Delta t \\ +\frac{23}{12}\left( c-dx^{2k}-y^{k}\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B_{2}\left( t_{k-1}\right) -B_{2}\left( t_{k-2}\right) \right) \sigma _{2}y^{k-2} \\ -\frac{4}{3}\left( B_{2}\left( t_{k}\right) -B_{2}\left( t_{k-1}\right) \right) \sigma _{2}y^{k-1} \\ +\frac{23}{12}\left( B_{2}\left( t_{k+1}\right) -B_{2}\left( t_{k}\right) \right) \sigma _{2}y^{k} \end{array} \right\} \end{array} \right] \;{\rm{ , if }}\;t_{1}\leq t\leq T \end{array} \right. , \end{equation}$

(4.35)

$\begin{equation} z\left( t_{n+1}\right) = \left\{ \begin{array}{c} \left\{ \begin{array}{c} \frac{1-\alpha }{AB\left( \alpha \right) }\left( rs\left( x^{n}-x_{R}\right) -rz^{n}\right) \\ +\frac{\alpha }{AB\left( \alpha \right) }\frac{\left( \Delta t\right) ^{\alpha -1}}{\Gamma \left( \alpha +1\right) }\sum_{k = 2}^{i}\left( rs\left( x^{k-2}-x_{R}\right) -rz^{k-2}\right) \Pi \\ +\frac{\alpha }{AB\left( \alpha \right) }\frac{\left( \Delta t\right) ^{\alpha -1}}{\Gamma \left( \alpha +2\right) }\sum_{k = 2}^{i}\left[ \begin{array}{c} \left( rs\left( x^{k-2}-x_{R}\right) -rz^{k-2}\right) \\ -\left( rs\left( x^{k-1}-x_{R}\right) -rz^{k-1}\right) \end{array} \right] \Sigma \\ +\frac{\alpha }{AB\left( \alpha \right) }\frac{\left( \Delta t\right) ^{\alpha -1}}{2\Gamma \left( \alpha +3\right) }\sum_{k = 2}^{i}\left[ \begin{array}{c} \left( rs\left( x^{k-2}-x_{R}\right) -rz^{k-2}\right) \\ -2\left( rs\left( x^{k-1}-x_{R}\right) -rz^{k-1}\right) \\ +\left( rs\left( x^{k}-x_{R}\right) -rz^{k}\right) \end{array} \right] \Delta \end{array} \right\} , \;{\rm{if }}\;0 < t\leq t_{1} \\ \left[ \begin{array}{c} x^{1}+\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( rs\left( x^{k-2}-x_{R}\right) -rz^{k-2}\right) \Delta t \\ -\frac{4}{3}\left( rs\left( x^{k-1}-x_{R}\right) -rz^{k-1}\right) \Delta t \\ +\frac{23}{12}\left( rs\left( x^{k}-x_{R}\right) -rz^{k}\right) \Delta t \end{array} \right\} \\ +\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( B_{3}\left( t_{k-1}\right) -B_{3}\left( t_{k-2}\right) \right) \sigma _{3}z^{k-2} \\ -\frac{4}{3}\left( B_{3}\left( t_{k}\right) -B_{3}\left( t_{k-1}\right) \right) \sigma _{3}z^{k-1} \\ +\frac{23}{12}\left( B_{3}\left( t_{k+1}\right) -B_{3}\left( t_{k}\right) \right) \sigma _{3}z^{k} \end{array} \right\} \end{array} \right] \;{\rm{ , if }}\;t_{1}\leq t\leq T \end{array} \right. . \end{equation}$

(4.36)

4.8. Numerical simulation for stochastic-deterministic model of Hindmarsh-Rose model

We provide the numerical simulations for the Hindmarsh-Rose model^[13] in piecewise

(4.37)

where the first part is with Mittag-Leffler kernel and the second part is stochastic. Initial data is considered as

$\begin{equation} x\left( 0\right) = 0.1, y\left( 0\right) = 0.1, z\left( 0\right) = 0.1. \end{equation}$

(4.38)

In , the numerical simulations are depicted with the parameters $a = 1, b = 3, c = 1, d = 5, s = 4, x_{R} = -8/5, r = 10^{-3}, I = 6.$

Figure 4. Numerical visualization of Hindmarsh-Rose model for

$\alpha = 1, \sigma _{1} = 0.01, \sigma _{2} = 0.015, \sigma _{3} = 0.012$ .

DownLoad: Full-Size Img PowerPoint

4.9. Numerical scheme for stochastic-deterministic model of Hindmarsh-Rose model

In this section, we deal with the Hindmarsh-Rose model^[13] where the first part is stochastic and the second part is global derivative. The stochastic-deterministic model of Hindmarsh-Rose model is represented by

$\begin{eqnarray} \left\{ \begin{array}{c} dx = \left( y-ax^{3}+bx^{2}-z+I\right) dt+\sigma _{1}xdB_{1}\left( t\right) \\ dy = \left( c-dx^{2}-y\right) dt+\sigma _{2}ydB_{2}\left( t\right) \\ dz = \left( rs\left( x-x_{R}\right) -rz\right) dt+\sigma _{3}zdB_{3}\left( t\right) \\ x\left( 0\right) = x_{0}, y\left( 0\right) = y_{0}, z\left( 0\right) = z_{0} \end{array} \right. \;{\rm{ if }}\;0\leq t\leq t_{1} \end{eqnarray}$

(4.39)

$\begin{eqnarray} \left\{ \begin{array}{c} D_{g}^{\alpha }x = \left( y-ax^{3}+bx^{2}-z+I\right) \\ D_{g}^{\alpha }y = \left( c-dx^{2}-y\right) \\ D_{g}^{\alpha }z = \left( rs\left( x-x_{R}\right) -rz\right) \\ x\left( t_{1}\right) = x_{1}, y\left( t_{1}\right) = y_{1}, z\left( t_{1}\right) = z_{1} \end{array} \right. \;{\rm{if }}\;t_{1}\leq t\leq T. \end{eqnarray}$

(4.40)

Using the numerical scheme presented in Case 5, we can have the following scheme for the stochastic-deterministic Hindmarsh-Rose model

$\begin{equation} x\left( t_{n+1}\right) = \left\{ \begin{array}{c} \left[ \begin{array}{c} x^{0}+\sum_{k = 2}^{i}\left\{ \begin{array}{c} \frac{5}{12}\left( y^{k-2}-ax^{3k-6}+bx^{2k-4}-z^{k-2}+I\right) \Delta t \\ -\frac{4}{3}\left( y^{k-1}-ax^{3k-3}+bx^{2k-2}-z^{k-1}+I\right) \Delta t \\ +\frac{23}{12}\left( y^{k}-ax^{3k}+bx^{2k}-z^{k}+I\right) \Delta t \end{array} \right\} \\ +\sum_{k = 2}^{i}\left\{ \begin{array}{c} \frac{5}{12}\left( B_{1}\left( t_{k-1}\right) -B_{1}\left( t_{k-2}\right) \right) \sigma _{1}x^{k-2} \\ -\frac{4}{3}\left( B_{1}\left( t_{k}\right) -B_{1}\left( t_{k-1}\right) \right) \sigma _{1}x^{k-1} \\ +\frac{23}{12}\left( B_{1}\left( t_{k+1}\right) -B_{1}\left( t_{k}\right) \right) \sigma _{1}x^{k} \end{array} \right\} \end{array} \right], \;{\rm{ if }}\;0 < t\leq t_{1} \\ x^{1}+\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( y^{k-2}-ax^{3k-6}+bx^{2k-4}-z^{k-2}+I\right) \left( g\left( t_{k-1}\right) -g\left( t_{k-2}\right) \right) \\ -\frac{4}{3}\left( y^{k-1}-ax^{3k-3}+bx^{2k-2}-z^{k-1}+I\right) \left( g\left( t_{k}\right) -g\left( t_{k-1}\right) \right) \\ +\frac{23}{12}\left( y^{k}-ax^{3k}+bx^{2k}-z^{k}+I\right) \left( g\left( t_{k+1}\right) -g\left( t_{k}\right) \right) \end{array} \right\} , \;{\rm{ if }}\;t_{1}\leq t\leq T \end{array} \right. , \end{equation}$

(4.41)

$\begin{equation} y\; \;\left( t_{n+1}\right) = \left\{ \begin{array}{c} \left[ \begin{array}{c} y^{0}+\sum_{k = 2}^{i}\left\{ \begin{array}{c} \frac{5}{12}\left( c-dx^{2k-4}-y^{k-2}\right) \Delta t \\ -\frac{4}{3}\left( c-dx^{2k-2}-y^{k-1}\right) \Delta t \\ +\frac{23}{12}\left( c-dx^{2k}-y^{k}\right) \Delta t \end{array} \right\} \\ +\sum_{k = 2}^{i}\left\{ \begin{array}{c} \frac{5}{12}\left( B_{2}\left( t_{k-1}\right) -B_{2}\left( t_{k-2}\right) \right) \sigma _{2}y^{k-2} \\ -\frac{4}{3}\left( B_{2}\left( t_{k}\right) -B_{2}\left( t_{k-1}\right) \right) \sigma _{2}y^{k-1} \\ +\frac{23}{12}\left( B_{2}\left( t_{k+1}\right) -B_{2}\left( t_{k}\right) \right) \sigma _{2}y^{k} \end{array} \right\} \end{array} \right] , \;{\rm{if }}\;0 < t\leq t_{1} \\ y^{1}+\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( c-dx^{2k-4}-y^{k-2}\right) \left( g\left( t_{k-1}\right) -g\left( t_{k-2}\right) \right) \\ -\frac{4}{3}\left( c-dx^{2k-2}-y^{k-1}\right) \left( g\left( t_{k}\right) -g\left( t_{k-1}\right) \right) \\ +\frac{23}{12}\left( c-dx^{2k}-y^{k}\right) \left( g\left( t_{k+1}\right) -g\left( t_{k}\right) \right) \end{array} \right\} \;{\rm{, if }}\;t_{1}\leq t\leq T \end{array} \right. , \end{equation}$

(4.42)

$\begin{equation} z\; \;\left( t_{n+1}\right) = \left\{ \begin{array}{c} \left[ \begin{array}{c} z^{0}+\sum_{k = 2}^{i}\left\{ \begin{array}{c} \frac{5}{12}\left( rs\left( x^{k-2}-x_{R}\right) -rz^{k-2}\right) \Delta t \\ -\frac{4}{3}\left( rs\left( x^{k-1}-x_{R}\right) -rz^{k-1}\right) \Delta t \\ +\frac{23}{12}\left( rs\left( x^{k}-x_{R}\right) -rz^{k}\right) \Delta t \end{array} \right\} \\ +\sum_{k = 2}^{i}\left\{ \begin{array}{c} \frac{5}{12}\left( B_{3}\left( t_{k-1}\right) -B_{3}\left( t_{k-2}\right) \right) \sigma _{3}z^{k-2} \\ -\frac{4}{3}\left( B_{3}\left( t_{k}\right) -B_{3}\left( t_{k-1}\right) \right) \sigma _{3}z^{k-1} \\ +\frac{23}{12}\left( B_{3}\left( t_{k+1}\right) -B_{3}\left( t_{k}\right) \right) \sigma _{3}z^{k} \end{array} \right\} \end{array} \right], \;{\rm{if }}\;0 < t\leq t_{1} \\ z^{1}+\sum_{k = i+3}^{n}\left\{ \begin{array}{c} \frac{5}{12}\left( rs\left( x^{k-2}-x_{R}\right) -rz^{k-2}\right) \left( g\left( t_{k-1}\right) -g\left( t_{k-2}\right) \right) \\ -\frac{4}{3}\left( rs\left( x^{k-1}-x_{R}\right) -rz^{k-1}\right) \left( g\left( t_{k}\right) -g\left( t_{k-1}\right) \right) \\ +\frac{23}{12}\left( rs\left( x^{k}-x_{R}\right) -rz^{k}\right) \left( g\left( t_{k+1}\right) -g\left( t_{k}\right) \right) \end{array} \right\}, \;{\rm{if }}\;t_{1}\leq t\leq T \end{array} \right. . \end{equation}$

(4.43)

$a = 1, b = 3, c = 1, d = 5, s = 4, x_{R} = -8/5, r = 10^{-3}, I = \left[-10, 10\right].$

4.10. Numerical simulation for stochastic-deterministic model of Hindmarsh-Rose model

In this subsection, we provide the numerical simulations for the following Hindmarsh-Rose model^[13]

$\begin{eqnarray} \left\{ \begin{array}{c} dx = \left( y-ax^{3}+bx^{2}-z+I\right) dt+\sigma _{1}xdB_{1}\left( t\right) \\ dy = \left( c-dx^{2}-y\right) dt+\sigma _{2}ydB_{2}\left( t\right) \\ dz = \left( rs\left( x-x_{R}\right) -rz\right) dt+\sigma _{3}zdB_{3}\left( t\right) \\ x\left( 0\right) = x_{0}, y\left( 0\right) = y_{0}, z\left( 0\right) = z_{0} \end{array} \right. \;{\rm{ if }}\;0\leq t\leq t_{1} \end{eqnarray}$

(4.44)

(4.45)

where $g\left(t\right) = t$ and initial data is considered as

$\begin{equation} x\left( 0\right) = 0.1, y\left( 0\right) = 0.1, z\left( 0\right) = 0.1. \end{equation}$

(4.46)

In , the numerical simulations are depicted with the parameters $a = 1, b = 3, c = 1, d = 5, s = 4, x_{R} = -8/5, r = 10^{-3}, I = 6.$

Figure 5. Numerical visualization of Hindmarsh-Rose model for

$\alpha = 1, \sigma _{1} = 0.01, \sigma _{2} = 0.015, \sigma _{3} = 0.012$ .

DownLoad: Full-Size Img PowerPoint

5. Applications for stochastic-deterministic 4D Sinusoidally Driven Lorenz system model

In this section, we present illustrative examples for stochastic-deterministic 4D driven Lorenz system^[14] by taking into account all cases presented in this work.

5.1. Numerical simulation for stochastic-deterministic 4D Sinusoidally Driven Lorenz system model

We present the numerical solution for 4D sinusoidally Driven Lorenz model ^[14] in piecewise where the first part is considered with classical and the second part is stochastic. Such model is represented by

$\begin{eqnarray} \left\{ \begin{array}{c} \frac{dx}{dt} = -a\left( x-y-c\sin u\right) \\ \frac{dy}{dt} = bx-xz-y \\ \frac{dz}{dt} = xy-dz \\ \frac{du}{dt} = w \end{array} \right. \;{\rm{ if }}\;0\leq t\leq t_{1} \\ \left\{ \begin{array}{c} dx = \left( -a\left( x-y-c\sin u\right) \right) dt+\sigma _{1}xdB_{1}\left( t\right) \\ dy = \left( bx-xz-y\right) dt+\sigma _{2}ydB_{2}\left( t\right) \\ dz = \left( xy-dz\right) dt+\sigma _{3}zdB_{3}\left( t\right) \\ du = wdt+\sigma _{4}udB_{4}\left( t\right) \end{array} \right. \;{\rm{if }}\;t_{1}\leq t\leq T \end{eqnarray}$

(5.1)

where initial data is considered as

$\begin{equation} x\left( 0\right) = 0.1, y\left( 0\right) = 0.1, z\left( 0\right) = 0.1, u\left( 0\right) = 0.1. \end{equation}$

(5.2)

For Case 1, the numerical simulations are performed in . Here the parameters are chosen as $a = 10, b = 30, d = 8/3, c = 17, w = 0.5.$

Figure 6. Numerical visualization of 4D Sinusoidally Driven Lorenz system for

$\alpha = 1, \sigma _{1} = 0.012, \sigma _{2} = 0.013, \sigma _{3} = 0.015, \sigma _{4} = 0.014$ .

DownLoad: Full-Size Img PowerPoint

5.2. Numerical simulation for stochastic-deterministic 4D Sinusoidally Driven Lorenz system model

In this subsection, numerical simulations for 4D sinusoidally Driven Lorenz model^[14] with piecewise derivative are presented

$\begin{eqnarray} \left\{ \begin{array}{c} _{0}^{C}D_{t}^{\alpha }x = -a\left( x-y-c\sin u\right) \\ _{0}^{C}D_{t}^{\alpha }y = bx-xz-y \\ _{0}^{C}D_{t}^{\alpha }z = xy-dz \\ _{0}^{C}D_{t}^{\alpha }u = w \end{array} \right. \;{\rm{ if }}\;0 < t\leq t_{1} \\ \left\{ \begin{array}{c} dx = \left( -a\left( x-y-c\sin u\right) \right) dt+\sigma _{1}xdB_{1}\left( t\right) \\ dy = \left( bx-xz-y\right) dt+\sigma _{2}ydB_{2}\left( t\right) \\ dz = \left( xy-dz\right) dt+\sigma _{3}zdB_{3}\left( t\right) \\ du = wdt+\sigma _{4}udB_{4}\left( t\right) \end{array} \right. \;{\rm{if }}\;t_{1}\leq t\leq T \end{eqnarray}$

(5.3)

where initial conditions are as follows

$\begin{equation} x\left( 0\right) = 0.1, y\left( 0\right) = 0.1, z\left( 0\right) = 0.1, u\left( 0\right) = 0.1. \end{equation}$

(5.4)

In , the numerical simulations are depicted for the parameters $a = 10, b = 30, d = 8/3, c = 17, w = 0.5.$

Figure 7. Numerical visualization of 4D Sinusoidally Driven Lorenz system for

$\alpha = 1, \sigma _{1} = 0.012, \sigma _{2} = 0.013, \sigma _{3} = 0.015, \sigma _{4} = 0.014$ .

DownLoad: Full-Size Img PowerPoint

5.3. Numerical simulation for stochastic-deterministic 4D Sinusoidally Driven Lorenz system model

To give numerical simulation for 4D sinusoidally Driven Lorenz model^[14], we deal with the following problem

$\begin{eqnarray} \left\{ \begin{array}{c} _{0}^{CF}D_{t}^{\alpha }x = -a\left( x-y-c\sin u\right) \\ _{0}^{CF}D_{t}^{\alpha }y = bx-xz-y \\ _{0}^{CF}D_{t}^{\alpha }z = xy-dz \\ _{0}^{CF}D_{t}^{\alpha }u = w \end{array} \right. \;{\rm{ if }}\;0 < t\leq t_{1} \\ \left\{ \begin{array}{c} dx = \left( -a\left( x-y-c\sin u\right) \right) dt+\sigma _{1}xdB_{1}\left( t\right) \\ dy = \left( bx-xz-y\right) dt+\sigma _{2}ydB_{2}\left( t\right) \\ dz = \left( xy-dz\right) dt+\sigma _{3}zdB_{3}\left( t\right) \\ du = wdt+\sigma _{4}udB_{4}\left( t\right) \end{array} \right. \;{\rm{if }}\;t_{1}\leq t\leq T \end{eqnarray}$

(5.5)

where first part is with exponential decay kernel and the second part is stochastic. Initial conditions are as follows

$\begin{equation} x\left( 0\right) = 0.1, y\left( 0\right) = 0.1, z\left( 0\right) = 0.1, u\left( 0\right) = 0.1. \end{equation}$

(5.6)

In , we provide the numerical simulations for 4D Sinusoidally Driven Lorenz system with the parameters $a = 10, b = 30, d = 8/3, c = 17, w = 0.5.$

Figure 8. Numerical visualization of 4D Sinusoidally Driven Lorenz system for

$\alpha = 1, \sigma _{1} = 0.012, \sigma _{2} = 0.013, \sigma _{3} = 0.015, \sigma _{4} = 0.014$ .

DownLoad: Full-Size Img PowerPoint

5.4. Numerical simulation for stochastic-deterministic 4D Sinusoidally Driven Lorenz system model

In this subsection, we present the numerical simulation for the following 4D sinusoidally Driven Lorenz model^[14]

$\begin{eqnarray} \left\{ \begin{array}{c} _{0}^{ABC}D_{t}^{\alpha }x = -a\left( x-y-c\sin u\right) \\ _{0}^{ABC}D_{t}^{\alpha }y = bx-xz-y \\ _{0}^{ABC}D_{t}^{\alpha }z = xy-dz \\ _{0}^{ABC}D_{t}^{\alpha }u = w \end{array} \right. \;{\rm{ if }}\;0 < t\leq t_{1} \\ \left\{ \begin{array}{c} dx = \left( -a\left( x-y-c\sin u\right) \right) dt+\sigma _{1}xdB_{1}\left( t\right) \\ dy = \left( bx-xz-y\right) dt+\sigma _{2}ydB_{2}\left( t\right) \\ dz = \left( xy-dz\right) dt+\sigma _{3}zdB_{3}\left( t\right) \\ du = wdt+\sigma _{4}udB_{4}\left( t\right) \end{array} \right. \;{\rm{if }}\;t_{1}\leq t\leq T \end{eqnarray}$

(5.7)

where initial conditions are as follows

$\begin{equation} x\left( 0\right) = 0.1, y\left( 0\right) = 0.1, z\left( 0\right) = 0.1, u\left( 0\right) = 0.1. \end{equation}$

(5.8)

In , the numerical simulations for the considered system are performed with the parameters $a = 10, b = 30, d = 8/3, c = 17, w = 0.5.$

Figure 9. Numerical visualization of 4D Sinusoidally Driven Lorenz system for

$\alpha = 1, \sigma _{1} = 0.012, \sigma _{2} = 0.013, \sigma _{3} = 0.015, \sigma _{4} = 0.014$ .

DownLoad: Full-Size Img PowerPoint

5.5. Numerical simulation for stochastic-deterministic 4D Sinusoidally Driven Lorenz system model

We consider 4D sinusoidally Driven Lorenz model^[14] with piecewise derivative where the first part is stochastic and the second part is global derivative

$\begin{eqnarray} \left\{ \begin{array}{c} dx = \left( -a\left( x-y-c\sin u\right) \right) dt+\sigma _{1}xdB_{1}\left( t\right) \\ dy = \left( bx-xz-y\right) dt+\sigma _{2}ydB_{2}\left( t\right) \\ dz = \left( xy-dz\right) dt+\sigma _{3}zdB_{3}\left( t\right) \\ du = wdt+\sigma _{4}udB_{4}\left( t\right) \end{array} \right. \;{\rm{ if }}\;0\leq t\leq t_{1} \\ \left\{ \begin{array}{c} D_{g}^{\alpha }x = -a\left( x-y-c\sin u\right) \\ D_{g}^{\alpha }y = bx-xz-y \\ D_{g}^{\alpha }z = xy-dz \\ D_{g}^{\alpha }u = w \end{array} \right. \;{\rm{if }}\;t_{1}\leq t\leq T \end{eqnarray}$

(5.9)

such that $g\left(t\right) = t.$ Here initial conditions are as follows

$\begin{equation} x\left( 0\right) = 0.1, y\left( 0\right) = 0.1, z\left( 0\right) = 0.1, u\left( 0\right) = 0.1. \end{equation}$

(5.10)

In , the numerical simulations are depicted for the considered problem where the parameters are chosen as $a = 10, b = 30, d = 8/3, c = 17, w = 0.5.$

Figure 10. Numerical visualization of 4D Sinusoidally Driven Lorenz system for

$\alpha = 1, \sigma _{1} = 0.012, \sigma _{2} = 0.013, \sigma _{3} = 0.015, \sigma _{4} = 0.014$ .

DownLoad: Full-Size Img PowerPoint

6. Applications for stochastic-deterministic model of Bouali system

In this section, we present applications of stochastic-deterministic Bouali system for all cases ^[15].

6.1. Numerical simulation for stochastic-deterministic model of Bouali system

We consider the Bouali model^[15] in piecewise where the first part is classical and the second part is stochastic as follows

$\begin{eqnarray} \left\{ \begin{array}{c} \frac{dx}{dt} = ax\left( 1-y\right) -\beta z \\ \frac{dy}{dt} = -y\left( 1-x^{2}\right) \\ \frac{dz}{dt} = \mu x \end{array} \right. \;{\rm{ if }}\;0\leq t\leq t_{1} \end{eqnarray}$

(6.1)

$\begin{eqnarray} \left\{ \begin{array}{c} dx = \left( ax\left( 1-y\right) -\beta z\right) dt+\sigma _{1}xdB_{1}\left( t\right) \\ dy = \left( -by\left( 1-x^{2}\right) \right) dt+\sigma _{2}ydB_{2}\left( t\right) \\ dz = \mu xdt+\sigma _{3}zdB_{3}\left( t\right) \end{array} \right. \;{\rm{if }}\;t_{1}\leq t\leq T \end{eqnarray}$

(6.2)

where initial conditions are taken as

$\begin{equation} x\left( 0\right) = 1, y\left( 0\right) = 1, z\left( 0\right) = -0.02. \end{equation}$

(6.3)

In and , the numerical simulations are depicted for the parameters $a = 3,$ $\beta = 2.2, b = 1, \mu = 0.001.$

Figure 11. Numerical visualization of Bouali system for

$\alpha = 1, \sigma _{1} = 0.02, \sigma _{2} = 0.022, \sigma _{3} = 0.025$ .

DownLoad: Full-Size Img PowerPoint

Figure 12. Numerical visualization of Bouali system for

$\alpha = 1, \sigma _{1} = 0.02, \sigma _{2} = 0.022, \sigma _{3} = 0.025$ .

DownLoad: Full-Size Img PowerPoint

Figure 13. Numerical visualization of Bouali system for

$\alpha=1,\sigma _{1}=0.02,\sigma _{2}=0.022,\sigma _{3}=0.025$ .

DownLoad: Full-Size Img PowerPoint

In , we present the numerical simulations for stochastic-deterministic Bouali system for the parameters $a = 3,$ $\beta = 2.2, b = 1, \mu = 1.51.$

Figure 14. Numerical visualization of Bouali system for

$\alpha = 1, \sigma _{1} = 0.02, \sigma _{2} = 0.022, \sigma _{3} = 0.025$ .

DownLoad: Full-Size Img PowerPoint

6.2. Numerical simulation for stochastic-deterministic model of Bouali system

We consider the Bouali model^[15]

$\begin{eqnarray} \left\{ \begin{array}{c} _{0}^{C}D_{t}^{\alpha }x = ax\left( 1-y\right) -\beta z \\ _{0}^{C}D_{t}^{\alpha }y = -y\left( 1-x^{2}\right) \\ _{0}^{C}D_{t}^{\alpha }z = \mu x \end{array} \right. \;{\rm{ if }}\;0 < t\leq t_{1} \end{eqnarray}$

(6.4)

(6.5)

where the first part is Caputo and the second part is stochastic. Initial conditions are taken as

$\begin{equation} x\left( 0\right) = 1, y\left( 0\right) = 1, z\left( 0\right) = -0.02. \end{equation}$

(6.6)

In , the numerical simulations are depicted for the parameters $a = 3,$ $\beta = 2.2, b = 1, \mu = 0.001.$

Figure 15. Numerical visualization of Bouali system for

$\alpha = 1, \sigma _{1} = 0.02, \sigma _{2} = 0.022, \sigma _{3} = 0.025$ .

DownLoad: Full-Size Img PowerPoint

6.3. Numerical simulation for stochastic-deterministic model of Bouali system

We consider the Bouali model^[15] with piecewise derivative

$\begin{eqnarray} \left\{ \begin{array}{c} _{0}^{CF}D_{t}^{\alpha }x = ax\left( 1-y\right) -\beta z \\ _{0}^{CF}D_{t}^{\alpha }y = -y\left( 1-x^{2}\right) \\ _{0}^{CF}D_{t}^{\alpha }z = \mu x \end{array} \right. \;{\rm{ if }}\;0 < t\leq t_{1} \end{eqnarray}$

(6.7)

(6.8)

Initial conditions are given by

$\begin{equation} x\left( 0\right) = 1, y\left( 0\right) = 1, z\left( 0\right) = -0.02. \end{equation}$

(6.9)

In , the numerical simulations are provided for Bouali system where the parameters are taken as $a = 3,$ $\beta = 2.2, b = 1, \mu = 0.001.$

Figure 16. Numerical visualization of Bouali system for

$\alpha = 1, \sigma _{1} = 0.02, \sigma _{2} = 0.022, \sigma _{3} = 0.025$ .

DownLoad: Full-Size Img PowerPoint

6.4. Numerical simulation for stochastic-deterministic model of Bouali system

We deal with the stochastic-deterministic Bouali model^[15]

$\begin{eqnarray} \left\{ \begin{array}{c} _{0}^{AB}D_{t}^{\alpha }x = ax\left( 1-y\right) -\beta z \\ _{0}^{AB}D_{t}^{\alpha }y = -y\left( 1-x^{2}\right) \\ _{0}^{AB}D_{t}^{\alpha }z = \mu x \end{array} \right. \;{\rm{ if }}\;0 < t\leq t_{1} \end{eqnarray}$

(6.10)

(6.11)

Here the first part is Atangana-Baleanu fractional derivative and the second part is stochastic. Also initial conditions are taken as

$\begin{equation} x\left( 0\right) = 1, y\left( 0\right) = 1, z\left( 0\right) = -0.02. \end{equation}$

(6.12)

In , we provide simulations for Bouali system with the parameters $a = 3,$ $\beta = 2.2, b = 1, \mu = 0.001.$

Figure 17. Numerical visualization of Bouali system for

$\alpha = 1, \sigma _{1} = 0.02, \sigma _{2} = 0.022, \sigma _{3} = 0.025$ .

DownLoad: Full-Size Img PowerPoint

6.5. Numerical simulation for stochastic-deterministic model of Bouali system

We consider the Bouali model^[15] with piecewise derivative

(6.13)

$\begin{eqnarray} \left\{ \begin{array}{c} D_{g}^{\alpha }x = ax\left( 1-y\right) -\beta z \\ D_{g}^{\alpha }y = -y\left( 1-x^{2}\right) \\ D_{g}^{\alpha }z = \mu x \end{array} \right. \;{\rm{if }}\;t_{1}\leq t\leq T \end{eqnarray}$

(6.14)

such that $g\left(t\right) = t.$ Also initial conditions are as follows

$\begin{equation} x\left( 0\right) = 1, y\left( 0\right) = 1, z\left( 0\right) = -0.02. \end{equation}$

(6.15)

In , the numerical simulations are presented for the parameters $a = 3,$ $\beta = 2.2, b = 1, \mu = 0.001.$

Figure 18. Numerical visualization of Bouali system for

$\alpha = 1, \sigma _{1} = 0.02, \sigma _{2} = 0.022, \sigma _{3} = 0.025$ .

DownLoad: Full-Size Img PowerPoint

7. Conclusion

Using the concept of piecewise differentiation and integration suggested by Atangana and Seda recently, we suggested classes of nonlinear ordinary differential equations. These classes are called piecewise deterministic stochastic equations. We suggested five classes, of course more classes can be obtained depending on how the piecewise differential and integral operators are defined with given intervals. We informed that, of each class presented, a suitable method to prove existence and uniqueness of piecewise solution can be performed in suitable spaces. However, we also informed that such discussion was not presented in general in our paper. Nevertheless, we considered a few chaotic models and extended each one of the five classes suggested, for some we presented conditions under which existence and unique solutions are obtained. General numerical solutions using the Newton polynomial interpolation were obtained. Illustrative examples are presented together with simulations. The obtained solutions leave us no chose to conclude that, this approach is the future of modelling complex real world problems.

Conflict of interest

The authors declare there is no conflict of interest.

References

[1]	A. Atangana, D. Baleanu, New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model, Therm. Sci., 20 (2016), 763–769. https://doi.org/10.98/TSCI160111018A doi: 10.98/TSCI160111018A
[2]	M. Caputo, M. Fabrizio, A new definition of fractional derivative without singular kernel, Prog. Fract. Differ. Appl., 1 (2015), 73–85. https://doi.org/10.12785/pfda/010201 doi: 10.12785/pfda/010201
[3]	A. Atangana, Extension of rate of change concept: From local to nonlocal operators with applications, Results Phys., 19 (2021), 103515. https://doi.org/10.1016/j.rinp.2020.103515 doi: 10.1016/j.rinp.2020.103515
[4]	A. Atangana, S. Igret Araz, New concept in calculus: Piecewise differential and integral operators, Chaos Solit. Fract., 145 (2021), 110638. https://doi.org/10.1016/j.chaos.2020.110638 doi: 10.1016/j.chaos.2020.110638
[5]	M. Ababneh A new four-dimensional chaotic attractor Ain Shams Eng. J., 9 (2018), 1849–1854. https://doi.org/10.1016/j.asej.2016.08.020 doi: 10.1016/j.asej.2016.08.020
[6]	A. Atangana, J. F. Gómez-Aguilar, Fractional derivatives with no-index law property: Application to chaos and statistics, Chaos Solit. Fract., 114 (2018), 516–535. https://doi.org/10.1016/j.chaos.2018.07.033 doi: 10.1016/j.chaos.2018.07.033
[7]	D. Faranda, Y. Sato, B. Saint-Michel, C. Wiertel, V. Padilla, B. Dubrulle, et.al., Stochastic chaos in a turbulent swirling flow, Phys. Rev. Lett., 119 (2017), 014502. https://doi.org/10.1103/PhysRevLett.119.014502 doi: 10.1103/PhysRevLett.119.014502
[8]	E. K. Kosmidis, K. Pakdaman, Stochastic Chaos in a neuronal model, Int. J. Bifurcat. Chaos, 16 (2006), 395–410. https://doi.org/10.1142/S0218127406014873 doi: 10.1142/S0218127406014873
[9]	C. C. Canavier, P. D. Shepard, Chaotic versus stochastic dynamics: A critical look at the evidence for nonlinear sequence dependent structure in dopamine neurons, J. Neural Transm. Suppl., 73 (2009), 121–128. https://doi.org/10.1007/978-3-211-92660-4 doi: 10.1007/978-3-211-92660-4
[10]	D. Toker, F. T. Sommer, M. D'Esposito, A simple method for detecting chaos in nature, Commun. Biol., 3 (2020). https://doi.org/10.1038/s42003-019-0715-9
[11]	W. Cunli, L. Youming, F. Tong, Stochastic chaos in a Duffing oscillator and its control, Chaos Solit. Fract., 27 (2006), 459–469. https://doi.org/10.1016/j.chaos.2005.04.035 doi: 10.1016/j.chaos.2005.04.035
[12]	A. Atangana, S. Igret Araz, New numerical scheme with Newton polynomial: Theory, Methods and Applications, Academic Press, (2021). Available from: https://www.sciencedirect.com/book/9780323854481/new-numerical-scheme-with-newton-polynomial
[13]	J. L. Hindmarsh, R. M. Rose, A model of neuronal bursting using three coupled first order differential equations, Proc. Royal Soc. B. P. Roy. Soc. B. Biol. Sci. 221, (1984), 87–102. https://doi.org/10.1098/rspb.1984.0024 doi: 10.1098/rspb.1984.0024
[14]	Han Chunyan, Yu Simin, Wang Guangyi, A Sinusoidally Driven Lorenz System and Circuit Implementation, Math. Probl. Eng., 2015 (2015), Article ID 706902. https://doi.org/10.1155/2015/706902 doi: 10.1155/2015/706902
[15]	S. Bouali, A 3D Strange Attractor with a Distinctive Silhouette. The Butterfly Effect Revisited, 24th ABCM International Congress of Mechanical Engineering, (2013).

Reader Comments

Your name:*

Email:*
© 2022 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

Mathematical Biosciences and Engineering

3.9

Metrics

Article views(2093) PDF downloads(105) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Abstract

Introduction

Modeling cross-over from deterministic to stochastic and vice versa

Analysis of deterministic-stochastic models

Analysis with illustrative example with Hindmarsh-Rose model of neuronal activity

Applications for stochastic-deterministic 4D Sinusoidally Driven Lorenz system model

Applications for stochastic-deterministic model of Bouali system

Conclusion

Conflict of interest

References

Figures and Tables

Figures(18)

Mathematical Biosciences and Engineering

Deterministic-Stochastic modeling: A new direction in modeling real world problems with crossover effect

Related Papers:

Abstract

1. Introduction

2. Modeling cross-over from deterministic to stochastic and vice versa

3. Analysis of deterministic-stochastic models

3.1. Numerical scheme for Case 1

3.2. Numerical scheme for Case 2

3.3. Numerical scheme for Case 3

3.4. Numerical scheme for Case 4

3.5. Numerical scheme for Case 5

4. Analysis with illustrative example with Hindmarsh-Rose model of neuronal activity

4.1. Numerical scheme for stochastic-deterministic model of Hindmarsh-Rose model

4.2. Numerical simulation for stochastic-deterministic model of Hindmarsh-Rose model

4.3. Numerical scheme for stochastic-deterministic model of Hindmarsh-Rose model

4.4. Numerical simulation for stochastic-deterministic model of Hindmarsh-Rose model

4.5. Numerical scheme for stochastic-deterministic model of Hindmarsh-Rose model

4.6. Numerical simulation for stochastic-deterministic model of Hindmarsh-Rose model

4.7. Numerical scheme for stochastic-deterministic model of Hindmarsh-Rose model

4.8. Numerical simulation for stochastic-deterministic model of Hindmarsh-Rose model

4.9. Numerical scheme for stochastic-deterministic model of Hindmarsh-Rose model

4.10. Numerical simulation for stochastic-deterministic model of Hindmarsh-Rose model

5. Applications for stochastic-deterministic 4D Sinusoidally Driven Lorenz system model

5.1. Numerical simulation for stochastic-deterministic 4D Sinusoidally Driven Lorenz system model

5.2. Numerical simulation for stochastic-deterministic 4D Sinusoidally Driven Lorenz system model

5.3. Numerical simulation for stochastic-deterministic 4D Sinusoidally Driven Lorenz system model

5.4. Numerical simulation for stochastic-deterministic 4D Sinusoidally Driven Lorenz system model

5.5. Numerical simulation for stochastic-deterministic 4D Sinusoidally Driven Lorenz system model

6. Applications for stochastic-deterministic model of Bouali system

6.1. Numerical simulation for stochastic-deterministic model of Bouali system

6.2. Numerical simulation for stochastic-deterministic model of Bouali system

6.3. Numerical simulation for stochastic-deterministic model of Bouali system

6.4. Numerical simulation for stochastic-deterministic model of Bouali system

6.5. Numerical simulation for stochastic-deterministic model of Bouali system

7. Conclusion

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog