A study on the (2+1)–dimensional first extended Calogero-Bogoyavlenskii- Schiff equation

1.   Introduction

Non-linear differential equations continue to play a vital role in today's world as they are used as mathematical models that describe natural phenomena, for example in astronomy, fluids, plasmas, solid-state materials, meteorology and climate, operations research, system theory and control, continuum mechanics, and oceanography, just to mention a few. Some of these models include the pair transition coupled non-linear Schrödinger equations that are used to illustrate the spreading of the optical waves in isotropic medium ^[1]; Boussinesq equation that arises in the vibrations of a non-linear string ^[2]; Boiti-Leon-Manna-Pempinelli equation that models incompressible fluid ^[3]; and Hirota-Satsuma equation that models the unidirectional propagation of shallow water waves ^[4]. Lie symmetry analysis was carried out in ^[5,6,7,8] on some non-linear partial differential equations (NPDEs) and Boussinesq type equations were studied in ^[9,10,11]. Painlevé integrability was studied for the three dimensional Date-Jimbo-Kashiwara-Miwa equations with constant and time-dependent coefficients and for Sakovich equation in ^[12,13], respectively. Conservation laws and exact solutions were obtained in ^[14,15,16] for double dispersion equations in (1+1) and (2+1) dimensions, an extended Korteweg–de Vries equation and the (3+1)-dimensional negative-order KdV equation, respectively. New exact solutions to the nonlinear Schrödinger equation with variable coefficients were derived in ^[17], whereas symmetry reductions were performed in ^[] for the (3+1)-dimensional modified Zakharov-Kuznetsov equation. Bounded and unbounded travelling wave solutions of the (3+1)-dimensional Jimbo-Miwa equation were obtained in ^[19] and exact solutions for the short pulse equation were constructed in ^[20].

Due to the fact that a lot of phenomena of real world are represented by NPDEs, it is paramount that we are able to solve them and find their closed-form solutions for a better understanding of such equations. There is no standard theory that can be utilized to find such solutions. Nevertheless, over the years, researchers have developed several methods which can lead us to special solutions of NPDEs. These include the power series method ^[20], the inverse scattering transform method ^[21], bifurcation method ^[22], the simplest equation technique ^[23], the extended simplest equation technique ^[24], Kudryashov's technique ^[25], Hirota's method ^[26], Bäcklund transformation ^[27], Darboux transformation ^[28], the homogeneous balance technique ^[29], $(G'/G)-$expansion technique ^[30], Lie symmetry method ^[31,32,33] and so on.

In the middle years of the nineteenth century, Sophus Lie invented the theory of continuous groups together with its applications to differential equations (DEs). This investigation resulted in one of the significant branches of the twentieth-century mathematics, which is called theory of Lie groups as well as Lie algebras. Lie introduced what is called the Lie symmetries and used them to solve ordinary differential equations (ODEs). Moreover, utilizing Lie symmetries, systems of DEs can be reduced to simpler form. In fact, Lie's method is the most effective and powerful technique for obtaining closed-form solutions to NPDEs ^[31,32,33].

Conservation laws are beneficial in the investigation of DEs ^[33,34]. Conservation laws are physical laws that state that certain physical properties remain unchanged in the course of time within an isolated system. For example, in physics such laws govern momentum, energy, angular momentum, and electric charge. With the help of conservation laws one can recognize whether or not a given partial differential equation (PDE) is completely integrable. The validity of numerical solution methods can be checked by the aid of conservation laws ^[35]. Moreover, conservation laws can be used in constructing exact solutions of PDEs ^[36,37]. For systems that have Lagrangian formulation, Noether theorem gives an elegant way to construct conservation laws ^[38,39,40]. However, the multiplier method ^[32] and the theorem due to Ibragimov ^[41,42,43] can be utilized to derive conservation laws for any system of equations whether or not the system has a Lagrangian formulation.

Two NPDEs that model real-life situations, that is to say, the (2+1)–dimensional Calogero-Bogoyavlenskii-Schiff (CBS) equations that read ^[44]

and

describe the interplay of long propagating wave in the $x$-axis with the Riemann propagating wave along $y$-axis. Bogoyavlenskii in ^[45] derived (1.1) using Lax formulation and went further to utilize some form of Lax representations which made it possible for the introduction of equation (1.2). Besides, the researcher established an indication that equation (1.1) possesses soliton as well as N-soliton solutions which are smooth in one coordinate. In ^[44], Wazwaz invoked Hirota's bilinear approach and derived solutions of (1.1) and later travelling wave solutions were obtained in ^[46]. In ^[47], the authors derived Bäcklund transformation alongside Lax pair of a form of CBS equation (1.1) via the singular manifold method. Moreover, some travelling wave solutions to (1.1) were derived in ^[48] using tanh function technique and $(G'/G)-$expansion technique.

However, a generalized version of (1.1), namely

has been studied by many researchers. For instance, in ^[49], $(G'/G)-$expansion method was invoked and travelling wave solutions of (1.3) were constructed. Furthermore, in ^[50], the Hirota's bilinear technique and homoclinic test method were employed to secure breather-type as well as certain analytic soliton solutions. Using tanh-coth approach, the authors of ^[51] found some closed-form solution of (1.3). The sine-cosine and complex techniques were used in ^[52,53] to derive, respectively, the analytic and meromorphic exact solutions of (1.3).

Recently, by including $u_{xy}$ to CBS equation (1.1), the author of ^[54] introduced the equation that reads

Here $t$ is an independent variable representing time, $x$ and $y$ are independent variables that represent spatial coordinates and $u(t, x, y)$ denotes the elongation of the wave at any point $(t, x, y)$. We call it (2+1)–dimensional first extended CBS (eCBS) equation. This new integrable eCBS equation (1.4) appears in propagation of waves and provide a variety of multiple real and complex soliton solutions. Painlevé analysis has been employed to justify the integrability and furthermore, multiple soliton solutions were derived in ^[54].

Here we investigate eCBS equation (1.4). In Section 2, we present solutions of eCBS (1.4) using different methods and Section 3 deals with the conservation laws of the equation, obtained by two approaches. Thereafter, we bestow concluding remarks.

2.   Solutions of the eCBS equation

This section firstly determines the Lie point symmetries of eCBS equation (1.4) which are then utilized to reduce the equation and subsequently enables us to find its exact solutions.

2.1.   Symmetry reductions

The eCBS equation (1.4) will admit the infinitesimal group generator

on condition that

where ${\cal S}^{[4]}$ is fourth extension of (2.1) defined by ^[32]

Thus, from equation (2.2), we obtain

and when expanding and separating on appropriate derivatives of $u$, we get fourteen linear homogeneous PDEs:

The solution of above PDEs yields the symmetries of the eCBS equation (1.4) given as

One-parameter groups and transformed solutions

Using the Lie equations ^[33], the corresponding one-parameter groups are

Consequently, if $u = \psi(t, x, y)$ is a solution of eCBS equation (1.4), then so are

We now perform symmetry reductions of the eCBS equation (1.4) by utilizing its three translation symmetries. Consider the combination ${\cal S} = {\cal S}_{1}+ a {\cal S}_{2}+ b {\cal S}_{3}$, with $f(t) = 1/2$ and constants $a$ and $b$. The symmetry ${\cal S}$ provides three invariants, namely

and using them reduces (1.4) to

Clearly $\Gamma_1 = {\partial}/{\partial p}$ and $\Gamma_{2} = {\partial}/{\partial q}$ are Lie point symmetries of equation (2.6) as $p$ and $q$ do not appear explicitly in the equation. Utilizing the symmetry $\Gamma = \Gamma_1+ d \Gamma_2$, $d$ being an arbitrary constant, we can reduce equation (2.6). The symmetry $\Gamma$ provides us with two invariants

which reduces equation (2.6) to 4th-order nonlinear ordinary differential equation (NODE)

2.2.   Solution of (1.4) by direct integration

We rewrite equation (2.8) in the form

where $A = d - bd + a d^2$. Integrating equation (2.9) twice, we get

where $K_{1}$ and $K_{2}$ are arbitrary constants. Let $G' = {\Phi}$, then equation (2.10) becomes

If the algebraic equation

has the roots $r_{1} > r_{2} > r_{3}$, then (2.11) can be written as

whose solution is ^[55,56]

with ${\rm{cn}}$ denoting the cosine elliptic function. Since $\Phi = G'$ we integrate equation (2.13) and going back to the variables $t$, $x$ and $y$ the eCBS equation (1.4) acquires a periodic solution

where $r = (ad-b)t- dx+ y$, $C_3$ a constant and

is the incomplete elliptic integral ^[57]. We present the wave profile of the periodic solution (2.14), for the parametric values $a = -4$, $b = 0.2$, $d = 0.6$, $r_1 = 100$, $r_2 = 50.05$, $r_3 = -60$, $C_3 = 100$ in Figure 1.

When the roots satisfy $r_1 > r_2 = r_3$, the solution of the eCBS equation (1.4) becomes

where $r = (ad-b)t- dx+ y$ and $C$ is a constant of integration.

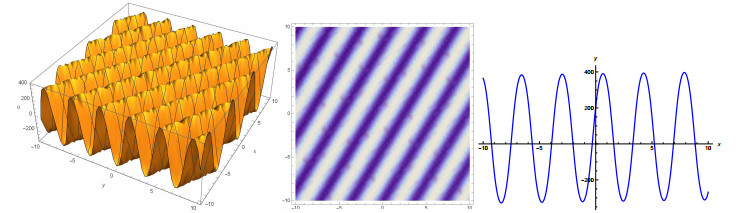
When $r_1 = 2k^2$ ($k$ a constant) and $r_2 = r_3 = 0$, the solution of the eCBS equation (1.4) becomes

where $r = (ad-b)t- dx+ y$ and $C_0$ is an integration constant. We represent the wave profile of (2.16) in Figure 2 with 3D and 2D plots taking the parametric values $a = 0.1$, $b = 0.1$, $d = 1.5$, $k = 1$, $C_0 = 10$ with $t = 10$.

2.3.   Solution of (1.4) by Kudryashov's method

We invoke Kudryashov's method ^[25] to construct a closed-form solution of eCBS equation (1.4). This method is an effective technique for finding closed-form solutions of NPDEs. The first step is to reduce the nonlinear eCBS equation (1.4) to NODE, which we have already done using the Lie symmetries in the previous section. Thus, we work with the NODE (2.8). We assume a solution of (2.8) is structured as

where $H(r)$ satisfies the first-order NODE

We observe that the solution of (2.18) is

The balancing procedure ^[25] for (2.8) yields $N = 1$. Thus, from (2.17), we have

Now substituting (2.20) into (2.8) and using (2.18), we obtain, with the aid of Mathematica

Now separating on powers of $H(r)$, we acquire the following algebraic equations for the coefficients $A_0$ and $A_1$:

whose solution is

Consequently, the solution of eCBS equation (1.4) associated with (2.23) is

where $A_0$ represents arbitrary constant. The wave profile solution (2.24) for different values of parameters $b = 0$, $d = 0.05$, $A_0 = 0$ with $t = 0$ is shown in Figure 3.

2.4.   Solution of (1.4) by $(G'/G)-$expansion method

Here we invoke the $(G'/G)-$expansion method ^[30] to acquire closed-form solutions of eCBS equation (1.4). Assume solution of the form

where $H(r)$ satisfies

with $\lambda$, $\mu$ constants. The value of $M$ is determined by the use of balancing procedure ^[30]. Here $A_0, \cdots, A_M$, are undetermined parameters which will be found.

For (2.8), the balancing procedure yields $M = 1$ and hence (2.25) becomes

Substitution of the expression for $G(r)$ from (2.27) into (2.8) and using (2.26) provides an algebraic equation, which when separated on powers of $H'(r)/H(r)$ gives five algebraic equations:

Solving with Mathematica, gives

Accordingly, we have the following three kinds of solutions to eCBS equation (1.4):

When $\lambda^2-4\mu > 0,$ we gain hyperbolic function solution

where $r = (ad-b)t- dx+ y$, $\Delta_{1} = \frac{1}{2}\sqrt{\lambda^2-4\mu}$ together with $C_1$ and $C_2$ arbitrary constants. The wave profile of the solution (2.28) for parametric values $a = 1$, $b = 0.1$, $d = 1$, $\lambda = -0.01$, $\mu = 0.05$, $A_0 = 1$, $C_1 = 1$, $C_2 = 4$ with $t = 1$ is shown in Figure 4.

When $\lambda^2-4\mu < 0,$ we achieve trigonometric function solution

where $r = (ad-b)t- dx+ y$, $\Delta_{2} = \frac{1}{2}\sqrt{4\mu-\lambda^2}$ and $C_1$, $C_2$ arbitrary constants. The wave profile of the solution (2.29) for parametric values $a = 0.1$, $b = 0.01$, $d = 1$, $\lambda = 0.01$, $\mu = 0.05$, $A_0 = 1$, $C_1 = 3$, $C_2 = 5$ with $t = 1$ is shown in Figure 5.

When $\lambda^2-4\mu = 0,$ we gain rational function solution

where $r = (ad-b)t- dx+ y$ and $C_1$, $C_2$ arbitrary constants. The wave profile of the solution (2.30) for parametric values $a = 0.01$, $b = 0.01$, $d = 1$, $\lambda = 0.01$, $\mu = 0.05$, $A_0 = 1$, $C_1 = 3$, $C_2 = 0$ with $t = 0.4$ is shown in Figure 6.

Remark. It should be noted that Kudryashov's method (also called exponential rational function method) and the $(G'/G)-$expansion method are particular cases of an earlier Riccati expansion technique ^{[58,59,60,61]}.

3.   Conservation laws

We now invoke multiplier method and Noether's theorem to derive conservation laws of eCBS equation (1.4).

3.1.   Use of multiplier method

In this subsection, we determine conserved quantities of eCBS equation (1.4) by invoking multiplier method ^[32,42]. We attempt to find first-order multipliers $\cal Q$, that is

The multipliers are determined from

where

is the Euler operator with $D_{t}$, $D_{x}$, $D_{y}$ being the total derivative operators ^[33].

Expanding (3.1) and separating on appropriate derivatives of $u$, we obtain twenty five PDEs:

Solving the above PDEs, we obtain

with $C_{1}, \dots, C_6$ as constants whereas $f$, $g$ are functions of $t$. Conserved quantities of equation (1.4) are now derived using the divergence expression

with $T^{t}$ conserved density and $T^{x}$, $T^{y}$ spatial fluxes. As a result we get the following low-order conserved vectors $(T^t, T^x, T^y)$ corresponding to the eight multipliers:

Case 1. For ${\cal Q}_{1} = -4 t^2 u_t -2tx u_x-4ty u_y -2 tu-tx+xy$,

we have the corresponding conserved vector as

Case 2. For ${\cal Q}_{2} = 4\, tu_t +xu_x + 2t u_y + 2 y u_y + u$, we have the conserved vector given by

Case 3. For ${\cal Q}_{3} = x- 4 t u_y$, we have the conserved vector

Case 4. For ${\cal Q}_{4} = u_t$, we have the conserved vector

Case 5. For ${\cal Q}_{5} = u_x$, we have the corresponding conserved vector as

Case 6. For ${\cal Q}_{6} = u_{y}$, we have the conserved vector given by

Case 7. For ${\cal Q}_{7} = f'(t) y-2 f(t)u_x$, we have the conserved vector

Case 8. For ${\cal Q}_{8} = g(t)$, we have the conserved vector

3.2.   Use of Noether's theorem

We now utilize the classical Noether's theorem ^[38] to construct conservation laws for the eCBS equation (1.4).

A 2nd-order Lagrangian of equation (1.4) is

Thus, the Noether symmetries

of eCBS equation (1.4) are constructed by employing the Lagrangian (3.3) on the determining equation

with $N^{[2]}$ being the second extension of $N$ and $B^t, B^x, B^y$ are gauge functions. Expanding (3.4) and solving the resultant PDEs, we obtain the following Noether symmetries and the corresponding gauge functions:

Now using the above Noether symmetries and invoking ^[38,39]

the corresponding conserved vectors are, respectively, given by

4.   Concluding remarks

In this paper, we investigated the eCBS equation $(1.4)$. We determined the Lie point symmetries of this equation, which were then used to construct group of transformations. Thereafter, symmetry reductions were performed and eCBS equation $(1.4)$ was reduced to the NODE $(2.8)$. This NODE was solved by direct integration and the solution was obtained in terms of incomplete elliptic integral, which represents periodic solution. Moreover, Kudrayshov's along with $(G'/G)-$expansion methods were employed to obtain solutions of the NODE. These solutions were presented graphically and we also included the parametric values of the parameters involved in the solutions. Finally, we used the multiplier method and Noether's theorem to derive the conservation laws of (1.4). The multiplier method yielded eight multipliers which gave eight local conservation laws for eCBS equation $(1.4)$ whereas Noether's theorem gave six local conservation laws. The conservation laws obtained contain the conservation of energy and momentum. It is worth mentioning here, that Noether's theorem has a limitation when it is applied to some differential equations. The limitation is that differential equations should come from a variational problem. On the other hand, the multipliers approach can be applied to any differential equation irrespective of it being variational or not.

Acknowledgments

The authors would like to thank OD Adeyemo for fruitful discussions and the authorities of North-West University, Mafikeng campus for their continued support. Also, the authors thank the reviewers for their positive suggestions, which helped to improve the paper enormously.

Conflict of interest

The authors declare that there is no conflict of interest.