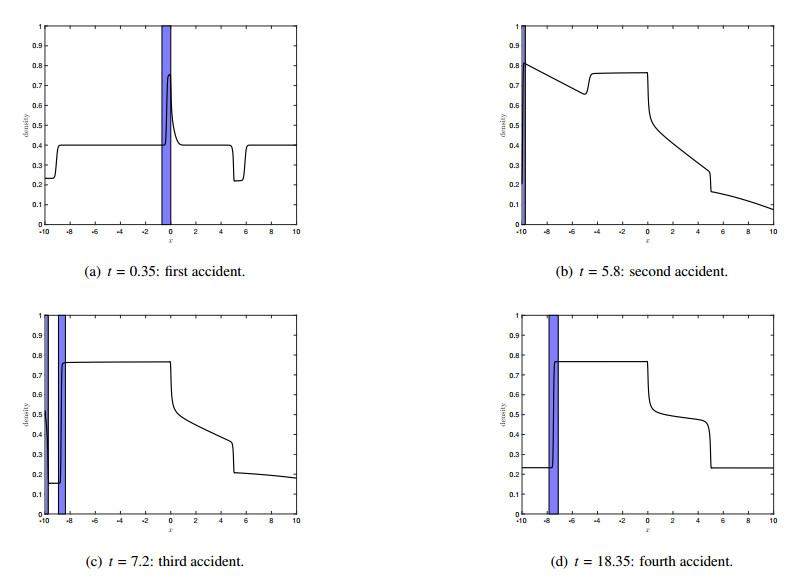
We introduce a stochastic traffic flow model to describe random traffic accidents on a single road. The model is a piecewise deterministic process incorporating traffic accidents and is based on a scalar conservation law with space-dependent flux function. Using a Lax-Friedrichs discretization, we show that the total variation is bounded in finite time and provide a theoretical framework to embed the stochastic process. Additionally, a solution algorithm is introduced to also investigate the model numerically.
1.
Introduction
Hepatocellular carcinoma (HCC), which is the most common type of primary liver cancer in adults, is the most common cause of death in people with cirrhosis [1]. It is related to chronic viral hepatitis, alcohol abuse, steatohepatitis, and liver immunodeficiency [2]. The cure rate of HCC is low (18%) [3], and major treatments include surgical resection and liver transplantation. However, less than 20% of patients can undergo surgical resection, and the lack of suitable liver source limits liver transplantation. Therefore, local ablation treatments of HCC have noteworthy clinical significance [4,5,6]. It has been established as the third major treatment for liver tumors, following surgical resection and liver transplantation [7].
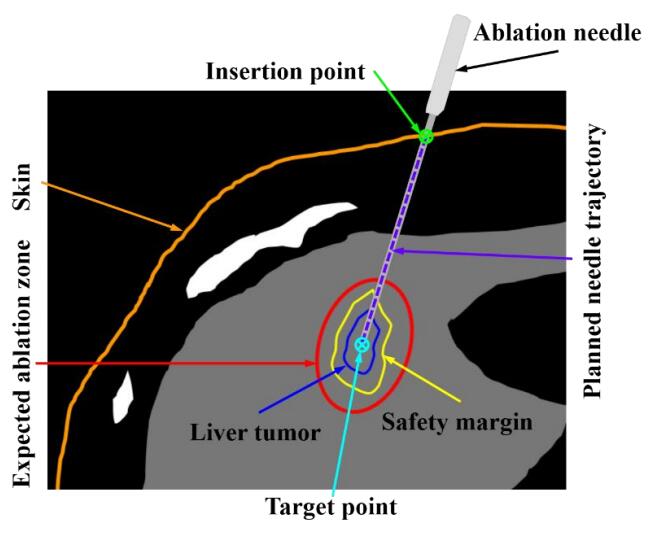
Local ablation can be divided into energy-based ablation and chemical ablation [6,8]. Energy-based ablation includes thermal ablation and non-thermal ablation. Thermal ablation includes hyperthermic ablation (radiofrequency ablation, microwave ablation, laser ablation, and high-intensity focused ultrasound ablation) and hypothermic ablation (cryoablation). Non-thermal ablation mainly refers to irreversible electroporation. Radiofrequency ablation (RFA) and microwave ablation (MWA) have become the key ablation treatments for liver tumors [2]. RFA and MWA are a minimally invasive therapy which involves an ablation applicator or needle (i.e., radiofrequency electrode or microwave antenna) inserted percutaneously into a tumor to destroy the tumor in situ by heating-induced coagulation necrosis (Figure 1). A heating-induced ablation zone is generated to cover the tumor with a 5-10 mm safety margin. Medical imaging, such as computed tomography (CT), is generally used to guide RFA and MWA procedures.
RFA and MWA of liver tumor consists of three steps: pre-intervention, peri-intervention and post-intervention. Pre-intervention involves two critical missions for treatment planning. The first mission is to determine the anatomical structures of abdominal cavity and the relative location of the ablation zone. This relies on medical image processing to segment and reconstruct extrahepatic structures (including the rib, celiac artery/vein, spine, lung, stomach, and spleen) and intrahepatic tissues (including the liver, liver vessel, and liver tumor) [9,10,11]. The second mission of pre-intervention is to plan the needle trajectory (path) and the treatment parameters (e.g., ablation power and duration). Peri-intervention involves inserting the ablation needle along the planned trajectory, which is called targeting, and monitoring and controlling the ablation treatment. Post-intervention involves evaluating the efficacy of the ablation treatment. Treatment planning, particularly needle trajectory planning, is crucial to RFA and MWA [12,13,14,15,16,17]. In the clinical ablation procedures, however, needle trajectory planning still relies on the personal experience of clinicians. Manual needle trajectory planning is tedious and may cause inter-operator difference. Therefore, computer-assisted needle trajectory planning techniques are of clinical value and have been extensively explored.
In 2010, a review of computer-assisted planning, intervention, and assessment of liver tumor ablation was presented [16]. However, a survey that focuses on computer-assisted needle trajectory planning for liver tumor RFA and MWA has not been reported. In this paper, we conducted an extensive review on computer-assisted needle trajectory planning for RFA and MWA of liver tumors. Fundamentals of needle trajectory planning are summarized (Section 2). Algorithms for single-needle and multi-needle trajectory planning are analyzed (Sections 3 and 4). Shortcomings of current algorithms are discussed and future developments are suggested (Section 5).
2.
Fundamentals of computer-assisted needle trajectory planning
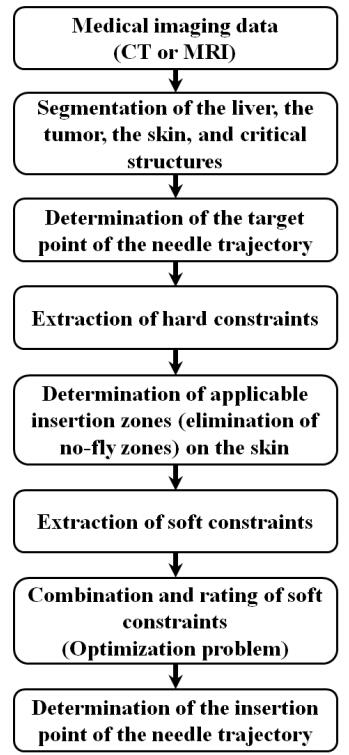
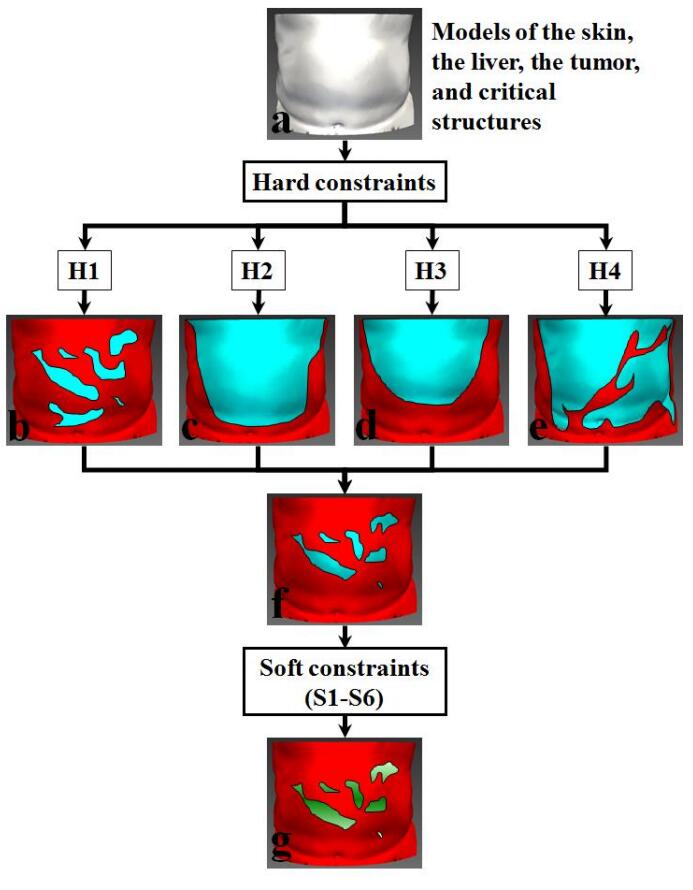
Figure 2 shows the flow chart of computer-assisted needle trajectory planning. Firstly, the liver, the liver tumor, the skin, and critical structures are segmented and reconstructed from the patient's CT or magnetic resonance (MR) images. Subsequently, the target point of the needle trajectory is determined, usually as the center or the centroid of the tumor. Then, hard constraints for needle insertion (puncture) are extracted to determine applicable insertion zones, or to eliminate inapplicable zones, or no-fly zones on the skin. Next, soft constraints for needle insertion are extracted. Finally, the soft constraints are combined and rated to determine the insertion point on the skin for the needle trajectory, which is formulated mathematically as an optimization problem.
2.1. Constraints for needle insertion
Constrains for needle insertion include hard constraints and soft constraints [17,18]. Hard constraints refer to the conditions that must be met in treatment planning. Any violation from hard constraints may lead to a failure of needle intervention. Soft constraints refer to the requirements that should be satisfied as much as possible in treatment planning. Failing to satisfy soft constraints may not directly lead to the failure of needle intervention, but the planned needle trajectory would not be optimal. Hard constraints and soft constraints are summarized as below.
2.1.1. Hard constraints
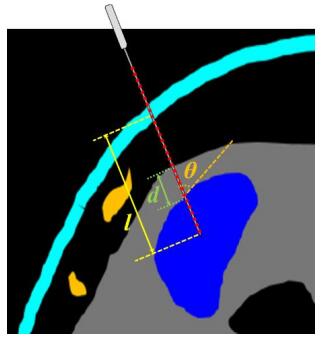
The length of the needle trajectory (l), the trans-hepatic route depth (d), and the angle between the ablation needle and the liver capsule (θ) are illustrated in Figure 3. Four hard constrains for needle insertion (H1-H4) are summarized as below.
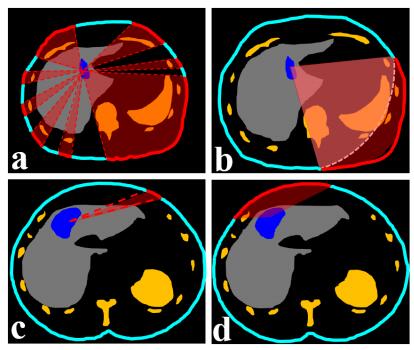
H1. The needle trajectory should avoid critical structures including the heart, lung, stomach, spleen, kidney, rib, spine, and vessel (Figure 4a).
H2. The length of the needle trajectory l should be less than that of the ablation needle (Figure 4b).
H3. The angle between the ablation needle and the liver capsule θ should be large enough (>20°) [19,20] (Figure 4c). If θ is too small, the ablation needle may glide on the liver capsule.
H4. The needle trajectory should ensure an enough trans-hepatic route depth d (>5 mm) (Figure 4d).
2.1.2. Soft constraints
Six soft constrains for needle insertion (S1-S6) are summarized as below.
S1. The needle trajectory should be far enough away from critical structures.
S2. The length of the needle trajectory should be small enough.
S3. The angle between the needle trajectory and the liver capsule should be large enough.
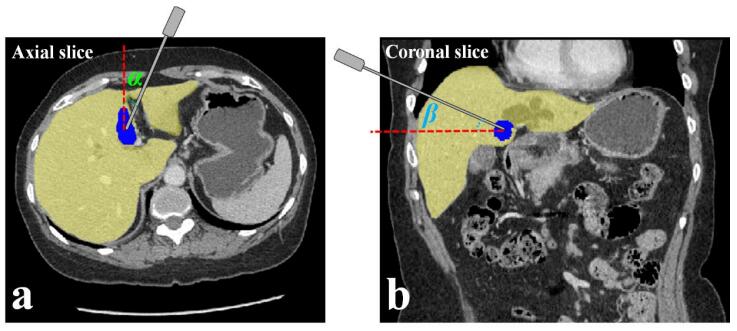
S4. The horizontal and vertical deflection angles (defined as α and β in Figure 5) should small enough.
S5. An ablation zone that conformally covers the tumor with a 5-10 mm safety margin should be generated.
S6. Ablation damage to healthy liver tissue should be minimized.
2.2. Multi-objective decision-making and numerical optimization
After defining the constraints, the goal is to plan the optimal needle path under the constraints. The mathematical model of needle trajectory planning is briefly described here. Needle trajectory planning can be abstracted into decision-making and numerical optimization problems. The goal of numerical optimization is to identify a variable x∈Rn for which the value of an objective function f(x) is optimal. Based on an initial guess of x, a sequence of improved estimation is generated consequently, hopefully terminating with an optimal solution [21]. Its mathematical expression is as follows:
subject to:
where g(x) and h(x) are the inequality and equality constraints functions, respectively; m and e are the number of inequality and equality constraints, respectively. The problem described in Equation (1) is the basis of numerical optimization, which is called single-objective optimization (SOO). However, the actual needle trajectory planning involves the decision-making and numerical optimization of multiple-objective functions fi(x) (multiple constraints). Note that some objective functions are contradictory to each other. In this case, the optimization problem turns into multi-objective optimization (MOO) [22]:
where F(x) is the vector of k-objective functions fi(x). The objective function fi(x) does not have priority difference in spatial Rk, so the MOO problem usually does not have a single optimal solution, but a series of relatively optimal solutions can be obtained by the pre-definition of optimization [23,24].
The solution of MOO problem usually follows the idea of scalar quantization, which integrates the multi-objective vector function F(x) into a scalar objective function F'(x), and makes MOO problem degenerate into SOO problem. Then, the SOO problem can be solved by using classical derivative or non-derivative strategies. Newton algorithm is often used as derivation strategy. For non-derivative strategy, Powell algorithm [25], Nelder-Mead simplex algorithm [26], simulated annealing algorithm [27], and exhaustive algorithm are common in needle trajectory planning.
The process of needle trajectory planning can be summed up as follows. The hard constraints are used to initialize the needle trajectory x, and the value space of x is divided into two categories. The value space satisfying hard constraints is called feasible solution space (corresponding to applicable insertion zones on the skin), denoted as χ. The value space that does not satisfy hard constraints is marked as infeasible solution space (corresponding to no-fly zones on the skin). Figure 6 illustrates hard and soft constraints. Figures 6b-6e represent the classification of applicable insertion zones and no-fly zones based on hard constraints H1-H4, respectively. Figure 6f shows the applicable insertion zones after combining H1-H4. With optimization strategy, local or global optimal solution set χ* is searched in the applicable insertion zones χ (Figure 6f). Figure 6g shows the combination of multiple soft constraints S1-S6 and rating of the applicable insertion zones χ on the skin. The better to worse ratings are shown in darker to lighter green.
3.
Single-needle trajectory planning algorithms
Villard et al. [28] used ideal ellipsoid to simulate the ablation zone of RFA, and searched the optimized needle path that could conformally cover liver tumors (S5,
S6) with Nelder-Mead simplex algorithm [26]. The planning algorithm also involved critical structures avoidance (H1). A pickup function derived from graphics rendering technology was customized, which returned the collision and depth information between the needle path and the critical structures in the search process. The algorithm was tested on 9 cases of clinical data, and it was found that the validity heavily depended on the initial search location of the planning path. Therefore, Villard et al. then proposed an improved algorithm [29] to initialize the search space of simplex algorithm [26] by avoiding the critical structures (H1). The algorithm rendered polygonal surfaces of the patient's skin, treated the tumor as a light source and treated the critical structures as opaque shelters. If the light emitted from the tumor was not obscured by the critical structures, the light could be received by a number of polygons surfaces. All the polygons covered by light constituted the initial applicable insertion zones. Five cases of clinical data were selected to validate the algorithm. The result showed that the initialization to simplex algorithm [26] could make the planned needle trajectory far away from the gaps surrounding the critical structures.
Baegert et al. [30] used quasi-exhaustive algorithm to optimize the needle path in the applicable insertion zones, and converted the soft constraint of conformal coverage (S5) into the angle between the planned needle trajectory and the long axis of the tumor. Results of needle trajectory planning of 7 cases of clinical data showed that the quasi-exhaustive algorithm has the same conformal coverage ability as exhaustive method. Then Baegert et al. [19] extended hard constraints in needle trajectory planning. When initializing the applicable insertion zone, three hard constraints were added: the depth (H2) and the angle (H3) of the needle path, and the reserved trans-hepatic route distance (H4). They also proposed a multi-scale refinement strategy on polygonal meshes reconstructed for the patient skin surface. The algorithm compared the effect of needle trajectory planning with and without multi-scale refinement strategy with 7 cases of retrospective clinical data (18 tumors). The results showed that the multi-scale refinement strategy expanded the applicable insertion zone, and the additional operation time was acceptable. In another work, Baegert et al. [18] constructed an evaluation function to measure soft constraints by considering the actual needle depth and the actual distance from the needle path to the critical structures, and integrated the soft constraints (S1, S2, S6) with weighted sum algorithm. The algorithm was qualitatively evaluated by 7 cases of retrospective clinical data. It was found that one case of the needle path planned by the computer-assisted system is significantly better than that planned manually by experts. In the remaining cases, the planning performance is comparable.
For the MOO problem, there is some controversy about the weighted summation algorithm [31,32], as the ideal weighted result is not equivalent to the cooperative optimization of multi-objective vector function. In addition, the weighting factors depend on subjective experience, which will cause planning deviation. For these reasons, Seitel et al. [20] introduced Pareto optimality concept [33,34,35] into needle trajectory planning of umbrella ablation electrode. The planning algorithm constructed Pareto frontier from pairs of soft constraints (S1 and S2, or S2 and S4) in the applicable insertion zone (H1-H4), and guided the clinician to select the optimal needle path on Pareto frontier. The algorithm was retrospectively verified by 10 cases of clinical data which were ablated unsuccessfully (with complications). The results showed that the manually planned trajectories of 6 patients were invalid (violating hard constraints), and the rest manually planned trajectories were not the optimal choice (dissatisfying soft constraints). The concepts and algorithms involved in solving the optimal needle path problem by Pareto optimality were discussed, and detailed mathematical proofs were given. At the same time, the authors also proposed an adaptive hyper-boxing algorithm [35], which could rapidly deploy Pareto frontier based on pairwise soft constraints.
The needle trajectory planning algorithms introduced above are based on polygonal surface rendering of the segmented structures using the patient's medical images. This makes the accuracy and efficiency of trajectory planning heavily depend on the resolution and quality of polygon surface rendering, which limits the potential of the needle trajectory planning algorithms. To overcome these drawbacks, Schumann and colleagues proposed the idea of needle trajectory planning based on perspective projection. In a preliminary study, Schumann et al. [36] proposed a needle trajectory planning algorithm based on the cylindrical projection [37,38] of multiple constraints (H1-H4 and S1-S6). The projection discretized the needle path space into alternative path list by two deflection angles, and generated constraint maps for each constraint. The final planned needle trajectory was obtained from the weighted product of the constraint maps. In order to consider the rationality of the weighted coefficient, the coefficient functions of each constraint were also designed. The algorithm was validated by 25 cases of clinical data. Radiologists were invited to grade the needle path with a score of 1-6 (1: best; 6: worst). The results showed that 84% of the planned trajectory scored within 2 (mean value 1.77).
Generally, the teaching and practice of needle trajectory planning accepted by clinician were carried out on two-dimensional (2D) slices of medical images. In order to facilitate the integration of computer-assisted needle trajectory planning algorithm into this workflow, Schumann et al. [39] proposed a visualized needle trajectory planning algorithm which could rapidly project the no-fly zone onto patient image slices. The algorithm only aimed at avoiding critical structures (H1). After defining the reconstruction scene of target point and related critical structures, using the cube mapping algorithm [40], the critical structures mapping was obtained by accelerating volume rendering with graphics processing unit (GPU) [41]. Then, the mapping result was projected onto the medical image slices. In the evaluation of 20 cases of liver RFA, three experienced radiologists indicated that the visualized planning algorithm had a significant assistant effect on 55% of cases, and two radiologists pointed out that the algorithm significantly reduced the time-consumption of needle trajectory planning. Subsequently, Schumann et al. [42] designed a needle trajectory planning system based on slider interactive interface, which could accommodate all the alternative needle paths with the according constraint parameters in each constraint maps (H1, H2, S1,
S2, S4). The clinician could remove the unsatisfactory needle path by dragging the slider to set the corresponding parameter. At the same time, the needle path selected by the slider would be rendered in real-time in the three-dimensional (3D) reconstructed scene. The algorithm was evaluated by two radiologists without clinical puncture background and an expert in the field of human-computer interaction by User Experience Questionnaire [43]. The score of six aspects ranged from 1.75 to 2.41.
In order to design a more practical computer-assisted planning system, Schumann et al. [44] took the lead in replacing the ellipsoid ablation zone with the simplified temperature field simulation model for the first time, which further studied the conformal coverage to the liver tumor. The computer-assisted planning system divided the needle trajectory planning into two steps. The 'seed' path was selected firstly by multi-constraint maps, and a new Pareto slider was designed by combining the Pareto optimality [35]. Clinicians could search the Pareto optimality path with compromised multi-constraints interactively. The performance of the system was validated by 19 cases of clinical data. Compared with the needle path manually planned by experts, 32% of the computer-assisted needle paths were superior. The six items score of the User Experience Questionnaire [43] were between 1.375 and 2.0. Then, Helck and colleagues [45] reported clinical trials of the system.
The accuracy of the needle trajectory planning algorithms proposed by Schumann and colleagues depends on the cylindrical projection. Because the horizontal and vertical deflection angles are discretely resampled during projection to obtain a list of candidate needle paths, the degree of discretization will affect the precision of needle trajectory planning.
Liu et al. [46] used spherical coordinates to investigate the reachable area of the fix-length ablation needle without touching the critical structures. In the algorithm, the needle, the critical structures and the patient's skin were sampled at discrete points to construct the ablation scene. With two soft constraints about needle insertion depth and distance to critical structures (S1,
S2), the Newton algorithm was used to obtain the optimal needle path. The planning algorithm was specially designed for surgical manipulator with three degrees of freedom. However, the algorithm has not been verified on clinical data.
4.
Multi-needle trajectory planning algorithms
The needle trajectory planning algorithms in Section 3 plans a single-needle path for a single liver tumor, assuming that a single ablation can destroy the whole tumor. In fact, this hypothesis is incomplete. Studies have shown that a single ablation could completely destroy a liver tumor whose radial length is less than 2 cm [47,48]. Once the radial length of the tumor is longer than 3 cm, a single ablation could not completely ablate the whole tumor [49,50,51,52,53]. In this case, a multi-needle ablation is required for the large tumor. In this section, needle trajectory planning algorithms of multi-needle ablation are reviewed.
Butz et al. [54] were the first to study the needle trajectory planning algorithm for the large tumor. The algorithm reconstructed the 3D scene of abdominal cavity based on MR images. In the scene, a simulated ablation needle could be placed interactively to generate simulated ablation zones of cryoablation without collision with skeleton and blood vessel. Powell algorithm [25] was used to optimize the external insertion points for the large liver tumor. This semi-automatic needle trajectory planning algorithm involved the simulation scenario of multi-needle ablation for the large tumor, but complicated human interaction is needed in the planning process.
Automated conformal coverage planning for large tumors were initially based on two assumptions. Hypothesis I: Assume that the shape of the tumor is an ideal sphere. Hypothesis II: Assume that the simulated ablation zone is an ideal sphere or ellipsoid. The coverage models proposed by Dodd et al. [55] and Khajanchee et al. [56] can be regarded as the foundation of the conformal coverage planning for large tumors. Dodd et al. [55] constructed standard 6-ball, 14-ball and columnar ablation zone coverage model. The effective coverage of each simulation ablation zone models was demonstrated. Khajanchee et al. [56] proposed that the number of surfaces on the basis of circumscribed regular polyhedron greater or equal to the diameter of the tumor is the minimum number of ablations required for conformal coverage of the large tumor. The minimum number of ablations required for conformal coverage tumors (3-6.23 cm) by simulated spherical ablation zones (3-7 cm) were discussed.
In order to make the planning more realistic, researchers relaxed the hypothesis of tumor morphology (Hypothesis I) and began to study the conformal coverage of irregular tumors. Mundeleer et al. [47] proposed a large tumor coverage planning algorithm independent of target points and tumor shapes. By constructing a cost function to represent the effective ablation volume, simplex algorithm [26] was used to obtain the optimal target points. Chen et al. [57] used the regular prism or polyhedron models to calculate the minimum number of punctures required for RFA of liver tumors. Then, the optimal overlap of ablation zones and the optimal target points were planned. The planning was based on covering the tumor center firstly, and then complementary ablation covered the tumor edge or bulge.
However, the above algorithms [47,55,56,57] only consider the conformal coverage of the large tumor, but it is not integrated into the needle trajectory planning. The following work overcomes this limitation.
RFA planning toolkit 'RF-Sim' developed by Villard et al. [48] involved multi-needle ablation needle trajectory planning for the large tumor. The initial target points were used as the clustering centers, and the large tumor was clustered into multiple lesion sub-regions according to voxel spacing by means of distance transformation [58]. Then the simplex optimization algorithm [26] was used to find the final target point and the planned needle trajectory for each lesion sub-region. Trovato et al. [59] proposed a large tumor coverage planning algorithm which took into account the effective ablation zone and the over-ablation of the liver tissues. Firstly, the algorithm arranged enough spherical simulated ablation zones to cover the tumor on bounding box of the ablation zone. Then, it attracted the simulated ablation zones to the expected ablation zone center by means of the attractors which were located at the target points and the center of simulated ablation zones. Finally, it iteratively updated the coverage of the simulated ablation zones, deleted redundant ablations, and finally fed back the location of external insertion points.
Yang et al. [60] proposed a large tumor conformal coverage planning based on the 'voxel growth', which adaptively generated multiple target points according to the contour of a tumor. In order to reduce the number of ablations and the degree of over-ablation, 'growth regions' needed to best fit the geometric shape of the ablation zone. The algorithm divided the tumor voxels into several continuous voxel cubes. Each cube grew layer by layer along the contour of the tumor. Its growth centers were the corresponding target points, and its external growth regions were the corresponding simulated ablation zones. In subsequent work of the same team, Duan et al. [61] integrated this algorithm into the surgical manipulator system, and realized multi-needle trajectory planning through a single incision at the skin. The feasibility of the algorithm was verified by the experiment of swine liver ex vivo. Liu et al. [62] designed a multi-needle collaborative ablation system based on a single incision at the skin. In order to effectively cover the large irregular tumor, a sphere-propagation algorithm was proposed. Based on the hexagonal close packing theory [63], a series of simulated spherical ablation zones covering the tumor were automatically generated by the volume of effective ablation and over-ablation.
The MWA planning system proposed by Liu et al. [64] could automatically calculate the minimum ablation times according to the selected external insertion points and the volume of liver tumors. The simulated ablation zones were modeled as an ellipsoid whose radius varied with ablation power and duration. The cost function reflected the volume of under-ablation and over-ablation. The additional penalty was inflicted by the paths colliding critical structures (H1). The Limited Memory Broyden Fletcher Goldfarb Shanno with Bounds (LMBFGSB) optimization approach [65,66] was used to select optimally the planned trajectories. Wang et al. [67] theoretically improved the ablation planning of larger irregular liver tumors by geometric optimization model. They pointed out that it was almost impossible to plan more than three needle paths for the same tumor. Therefore, the conformal coverage of simulated ablation zones was modeled by 2D inscribed triangle method and subdivision method. Finally, the coverage problem could be classified into four categories: single-needle ablation, double-needle ablation, three-needle ablation, and untreatable ablation. The algorithm optimized the needle path after determining the number of ablation times.
Ren et al. [68] proposed a needle trajectory planning method by solving integer programming model on the basis of previous work [69,70]. The initial insertion points were labeled by the clinician. The algorithm consisted of two parts: the minimum trajectories integer program and the minimum ablations integer program. The minimum radial trajectory required to cover the tumor and the minimum ablation times along the selected radial trajectory were obtained respectively. The algorithm could generate several feasible schemes, which needed to be decided by clinicians after parameter evaluation and visual comparison. In the same year, Ren et al. [71] also proposed a planning system for liver tumor ablation, which used genetic algorithm to heuristically solve the optimal coverage problem. Chen et al. [72] investigated the conformal coverage planning of large tumors by using improved clustering algorithm and coverage iteration optimization algorithm in applicable insertion zones. The clustering algorithm initialized the ablation zone into several sub-regions with the approximate volume, and the shape of each sub-region was similar to that of the simulated ablation zone. Coverage optimization algorithm minimized the simulated ablation zone of each sub-region and iteratively calculated the minimum number of ablation. In order to avoid collision between planned path and critical structures (H1), the algorithm attached a conical needle region for fine-tuning.
5.
Discussion
The single-needle and multi-needle trajectory planning algorithms reviewed in this paper are listed in Table 1, in terms of the constraints involved in each needle trajectory planning methods, the strategy of combining hard or soft constraints, and the validation data of each algorithm. Although some progress has been made in the research of needle trajectory planning algorithms, they are rarely used in the clinic. There is still a gap between the current research and clinical practice. Next, we will analyze the shortcomings of existing needle trajectory planning algorithms and discuss future developments from three aspects: needle trajectory planning, ablation zone simulation, and deformation model.
5.1. Needle trajectory planning algorithms
Table 2 compares the constraints involved in single-needle and multi-needle needle trajectory planning. For hard constraints, current single-needle planning methods consider them more comprehensively, while most of multi-needle planning methods only consider the constraint of avoiding critical structures (H1). For soft constraints, single-needle planning takes into account the actual distance between the needle path and the critical structures, the actual puncture depth and angle. Among them, Villard et al. and Baegert et al. [28,29,30] based their research on the conformal coverage of tumors. However, Schumann et al. [39,42,44] neglected the coverage of tumors; in the preliminary study [36], the conformal coverage problem was handled by the simplified constraint that the direction of the needle path was best parallel to the direction of the long axis of a tumor. Seitel et al. [20] and Teichert [35] also lacked consideration of the conformal coverage of liver tumors. Multi-needle planning just focused on avoiding under-ablation of liver tumors and over-ablation of healthy tissues. In future developments, the conformal coverage should be considered more in single-needle trajectory planning (for small tumors). Multi-needle trajectory planning (for large tumor) should be based on the conformal coverage of tumors and establish a relationship with needle trajectory planning.
The reconstruction scene of abdominal critical structures can determine the accuracy of the applicable insertion zone. Multi-needle planning has not yet involved the complete needle trajectory planning process, so here we only analyze the single-needle trajectory planning algorithm (Table 3), which can be roughly divided into two categories. Firstly, the abdominal skin and critical structures were reconstructed by surface rendering. Villard et al. [28] proposed reconstructing the ablation scene by triangular mesh surface rendering. The connection between the vertex of the triangle meshes and the target point is used as the candidate needle trajectories. This strategy has higher rendering efficiency and lower requirement for computer hardware. However, the quantity and quality of the triangular meshes are directly related to the accuracy and generation efficiency of the applicable insertion zone and candidate needle paths. The surface rendering is also limited by the resolution of the used screen. Off-screen rendering may be a solution for this problem [20]. In addition, the strategy of surface rendering of critical structures and sampling them into discrete points was proposed by Liu et al. [46]. The discrete points were combined with the spherical coordinates to plan the needle trajectory. However, their method was not validated by clinical data. Secondly, cylindrical projection based on direct volume rendering was conducted. The accuracy and efficiency of candidate needle trajectories do not depend on the rendering algorithm, but they depend on the discreteness of horizontal and vertical deflection angles in the projection process. Schumann et al. [6] pointed out that the critical structures could be made through dilation operation or the constraint maps could be filtered by a proper threshold, but it does not solve the problem essentially.
Table 4 compares the strategies of combining the multiple soft constraints. The optimization to conformal coverage problem of multi-needle ablation is only an incomplete optimization problem, so we only summarize these related algorithms in Table 1. The optimization problem discussed here is mainly rationally planned needle trajectory within the applicable insertion zone. Villard et al. compared Powell algorithm [25], Nelder-Mead simplex algorithm [26] and simulated annealing algorithm [27] in both the research of single-needle [28] and multi-needle [48] trajectory planning. Their study showed that the search efficiency of Powell algorithm and simulated annealing algorithm was lower. The parameters of simulated annealing algorithm were difficult to set. Therefore, Nelder-Mead simplex algorithm was chosen to select the optimal path. Although it was relatively sensitive to initialization, Villard et al. [29] pointed out that Nelder-Mead simplex algorithm could be reasonably initialized by searching the applicable insertion zone. Baegert et al. [18] and Seitel et al. [20] tried weighted summation strategy. Although the algorithm complexity of weighted summation is simple, there are still some shortcomings in solving MOO problems, because it is difficult to ensure that multiple objectives achieve coordination optimal. Weighted product can alleviate this shortcoming to some extent, but both weighted summation or product need to set weight factors artificially, which will lead to the deviation of needle trajectory planning due to the difference of human experience. Pareto optimality can avoid this kind of artificial interference, but the solution of MOO problem based on Pareto optimality concept has not been recognized clinically [31]. In addition, Pareto optimality is applicable to deal with the paired clinical soft constraints, and it still needs manual interaction when selecting the final planned trajectory. Although Newton algorithm adopted by Liu et al [46] is theoretically suitable for solving local optimization problems, in practice, it may be difficult to satisfy the ideal premise of derivation. The approximation of finite difference leads to increased computational complexity [21]. LMBFGSB algorithm [65,66] adopted by Liu et al. [64] is a quasi-Newton method, which the computational cost is lower, and the memory requirement is also lower than other online quasi-Newton methods. However, it is not fast convergent and requires a lot of function calculation to converge on difficult problems [66]. The concept of Genetic algorithm is easy to understand, and it supports multi-objective optimization, so Ren et al. [71] carried out simple needle trajectory planning based on Genetic algorithm. However, the construction of objective function reflecting constraints in genetic algorithm is complex, the calculation of genetic algorithm is time-consuming, and it may fall into local extremum. To sum up, there is no recognized optimization algorithm to search for the optimal needle path in the applicable insertion zone, which is one of the reasons that limit the clinical application of needle trajectory planning algorithms. In future developments, this issue should be addressed.
5.2. Ablation zone simulation
In order to further relax the assumption of the standard model for simulating ablation zones in needle trajectory planning (Hypothesis II) and make the ablation zone more realistic, it is necessary to use the simulation of the temperature field in ablation zones. However, the environment of liver cancer ablation is complex and involves many characteristics of liver tissues (including electrical conductivity, thermal conductivity, thermal capacity, tissue density, tissue temperature, water content and protein status). The simulation of ablation zones has developed into a new research field. It is generally accepted that the finite element simulation of thermal ablation temperature field can be carried out by using the bio-heat transfer equation in the existing simulation studies of ablation zones.
Most bio-heat simulation is based on the Penne's bioheat equation (PBE) [73]. The heat conduction term is derived from classical Fourier heat conduction law. Considering metabolic heat production and blood perfusion heat transfer, it is the most concise model for calculating the temperature field of bio-heat transfer. However, Fourier heat conduction law implies the following assumption: the velocity of heat transfer in the medium is infinite, which is inconsistent with the heat conduction in the process of thermal ablation. With the deepening of the research, the Hyperbolic bioheat equation (HBE) based on the non-Fourier heat conduction law has been proposed [74,75]. The main idea is that there exists a constant delay time τ between heat flux and temperature gradient in biological tissues. In the early years, HBE has been used to calculate 3D temperature distribution in radiofrequency ablation of cornea and arrhythmia [76].
Temperature field simulation of RFA and MWA is generally based on PBE, and a finite element model of ablation is established. Because the individual difference of tumor is significant, it is necessary to establish accurate 3D temperature field simulation to determine the optimal heating parameters in MWA [77]. For the simulation accuracy of temperature field in MWA, the research mainly focuses on the accuracy distribution of specific absorption rate (SAR) [78,79], the setting of thermophysical parameters of liver tissues [78,80], the influence of blood perfusion and vaporization [81]. Similarly, in order to establish the finite element model of RFA, the temperature change in the thermal lesion is predicted by the coupled analysis of electric-thermal field in the simulation software, and there are also many studies on the simulation of temperature field of RFA [82,83,84,85,86].
At present, there is a lack of research on the combination of simulated ablation zones and needle trajectory planning for liver tumor ablation. Only Schumann et al. [44] used the approximation of the numerical simulation [87] to take the conformal coverage of simulated ablation zones as a clinical constraint condition of needle trajectory planning for the initialization of needle path. Researchers either tend to simplify the model (ellipsoid simulation ablation zone), or speed up the simulation with GPU [87,88,89]. Simplified simulation model of ablation zones will reduce the accuracy of needle trajectory planning and limit the application of planning algorithm in the clinic. GPU computing is a direct means to accelerate the simulation of temperature field in ablation zones, and it can also make the real geometry of temperature field more ideal through interdisciplinary means. A new nano-cryoablation technique using nanoparticles was proposed [90]. A theoretical 3D simulation of the freezing ablation zone incorporating nanoparticles was conducted [91,92]. The phenomenon of heat conduction caused by blood flow in large vessels was fully considered. In vitro animal experiments showed that injecting nanoparticles with high thermal conductivity into the freezing ablation zone could significantly reduce the heat-sink effect caused by blood flow, shorten the ablation duration, and expand the effective range of cryoablation. This technique may be introduced into RFA and MWA in the future.
5.3. Linear needle trajectory planning and curved needle trajectory planning
The needle trajectory planning algorithms in Sections 3 and 4 abstract the path as a line segment between the insertion point and the target point. However, in the actual puncture process, linear needle trajectory planning is not enough to meet the clinical needs, because the puncture process is bound to face two types of deformation. Deformation I: The pressure on the body surface or viscera surface caused by the needle tip and the friction force produced by the needle-tissue interaction will force the needle and tissues to be deformed.
Deformation II: The patient's respiratory function causes the liver to produce similar periodic displacement and deformation, which changes the relative position of the liver tumor to the body surface. Due to the complexity of the two types of deformation, curved needle trajectory planning is challenging.
The needle trajectory planning methods considering deformation I is still rare. Hamzé et al. [93] proposed a needle trajectory planning model for liver tumor ablation under the condition of needle-tissue interaction force. Tan et al. [94] planned the needle path of flexible needle based on Markov decision. Modeling of needle-tissue interaction can be found in a recent review [95], but the models are rarely used in needle trajectory planning for liver tumor ablation.
There are no literatures reporting the needle trajectory planning considering deformation II. Only respiratory deformation models are reported. For curved needle trajectory planning, the trend is to effectively build dynamic atlas of liver tissues. The planning can introduce medical image sequence with motion information to realize multi-modal medical image fusion, such as ultrasound-CT/MR [96,97,98,99]. During the acquisition of CT or MR images, ultrasound image sequence of several respiratory cycles is acquired simultaneously. The periodic trajectory of the target point can be obtained by an efficient registration algorithm. For single-modality medical image sequence, the construction of four-dimensional motion maps including anatomical structure and motion characteristics was conducted [100,101,102]. Besides, the periodic displacement of the tumor can be tracked by the feedback signal of the labeled sensor [103,104,105]. However, compared with the image processing methods [96,97,98,99,100,101,102], the ways of adding labels or auxiliary needles pose additional challenges.
It should be noted that there are some clinical considerations that are challenging in current needle trajectory planning. (i) Patient breathing, patient movement, and interventional radiologists skill at replicating angle are variables that mathematical modeling cannot currently predict. (ii) As the actual ablation zone is dependent on the ablation device used, the expected ablation zone with a 5-10 mm safety margin (Figure 1) prior to needle placement may not be realized. (iii) Tissue shrinkage [106,107,108,109,110] and hydrodissection have not been taken into account in current needle trajectory planning.
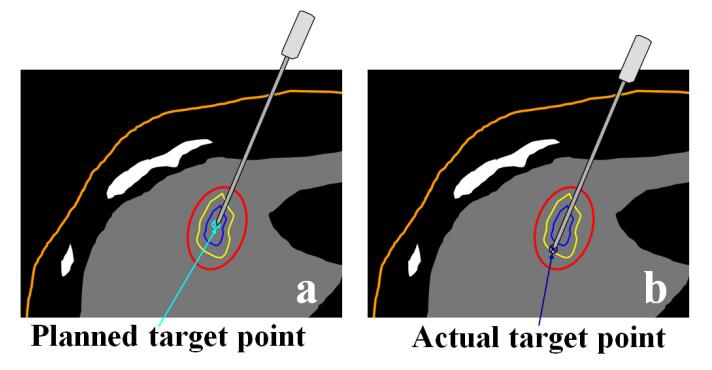
In addition, the current trajectory planning algorithms still have the following shortcomings. (ⅰ) The target point of the needle trajectory is set as the center or the centroid for small tumors, or as the sub-region for large tumors. However, in the clinic, the needle tip usually punctures through the tumor (Figure 7). There is no mathematical model for the actual target point. Additionally, as the needle tip penetrates through the tumor, the outside part of the needle involves key constraints such as whether to touch the critical structure. (ⅱ) In the needle trajectory planning for large tumors, the default multiple ablation effect is equivalent to multiple superimposition of single-needle ablation effect, but in fact, the ablation zone generated by multi-needle ablation will be more complex. (ⅲ) Finite element simulation, respiratory motion model and needle-tissue interaction deformation model are still difficult to meet the actual clinical needs. To effectively integrate the multi-level mathematical model into needle trajectory planning is also a problem. (ⅳ) There is no accepted criterion for the evaluation of needle trajectory planning algorithms. In future developments, these shortcomings should be overcome.
Acknowledgments
The authors would like to thank the anonymous reviewers for their insightful comments and suggestions. This work was supported partially by the National Natural Science Foundation of China (Grant Nos. 61801312, 61871005, 11804013, and 71661167001), the Beijing Natural Science Foundation (Grant No. 4184081), the International Research Cooperation Seed Fund of Beijing University of Technology (Grant No. 2018A15), the Basic Research Fund of Beijing University of Technology, and the Intelligent Physiological Measurement and Clinical Translation, Beijing International Base for Scientific and Technological Cooperation.
Conflict of interest
The authors declared they have no competing interests. The authors alone are responsible for the content and writing of the paper.









 DownLoad:
DownLoad: