Hoop tensile strength behaviour between different thicknesses E-glass and S-glass FRP rings

Abbreviations: σhtu: Ultimate hoop tensile strength (MPa); P_max: Maximum load earlier than failure (Kn); Amax: Least cross-sectional area of the two decreased segments, l × b (m); E: Apparent modulus of elasticity (MPa); ΔL: length difference before and after test (mm); A: Initial cross section area of the specimen (mm²); L: Initial length of the specimen (mm); P: Total load (kg); r: Average radius of the ring (cm); b: Ring width (cm); d: Ring thickness (cm); Δ: Total deflection of head (cm); S: Pipe stiffness (N/mm); D_m: Mean diameter (m); F: Force in Newtons; d_v: Deflection in metres; f: Deflection coefficient

1.   Introduction

Filament winding can be stated as a constant fiber reinforced composite fabrication process in which epoxy resin is saturated into the continuous fiber, and the fiber roll is rotated over the mandrel. The procedure was prolonged with the winding of added layers until the design parameters were obtained. The production of the GFRP was accomplished by curing the filament wound element in an oven and by using a mandrel. This procedure is mainly employed for hollow tubular fabrications such as pressure vessels and pipes which are commonly operated under internal pressure heading to elevated hoop stresses. The performance of GFRP under hoop stresses was analysed using various methods such as filament-wound fibrous composites containing the hydrostatic burst pressure test, split disk test with poly-tetra fluoro ethylene rings, and examinations with inflatable systems and mechanical regions.

Filament wound glass composite erections were examined to accomplish two key constraints. The first constraint is to deliver the essential fabric and strength records for design intentions, and the second one is to authenticate the precision of the finished design studies. For these reasons, a test specimen design must be carefully selected based of the test outcomes and the provision of material properties beneficial in the design platform. Basically, the three categories of testing methods usually operated in the testing of filament-wound composite assemblies are ring specimens, flat (coupon) specimens and tubular specimens. Shear, axial and bending reply of individual testing method can be decided by using an appropriate type of loading. Tests concerning combined/biaxial loading are also achievable. To supplement these tests, torsion and internal pressure tests can be employed to the tubular samples. The section below indicates the experimental investigation of the different ring and cylindrical samples.

Investigations on the hoop stress, hoop stiffness and void volume fraction distribution through thickness and interlaminar shear strength of the fiber reinforced filament wound ring samples were done by Cohen and his co-workers ^[1] in which during the tests, hoop stiffness and hoop strength of the samples were gained by performing forced ring tests on filament winded rings. They found that composite intensity surged for cylinders, wound lacking of winding gradient, wound in short time, with high winding tension. However, it was also found that the consequences of these parameters on strength were very little, with the outcome of the winding tension in actuality was major during the tests. Wang et al. ^[2] carried out ring hoop tension tests on ring specimens through a single concentrated part of an area. In evaluating and determining the hoop stress–strain curves of the specimens, they decided that the ring hoop tension test was a perfect test to calculate the transverse tensile parameters of tubular samples. Bai et al. ^[3] carried out a research on the mechanical performance of G558 filament wounded glass fiber/epoxy resin reinforced pipes under three various stress states: pure internal pressure, pure axial tensile load and combined loading. As the performance of the samples increased its ultimate tensile strength about twenty to fifty percent, this indicated that the central damage initiation mechanisms were due to delamination and micro cracking. Depending on the loading stages, one of the mechanisms governs over the other. Relevant to the above work, another experimental study regarding G558 filament wounded composite pipes was carried out by Caroll et al. ^[4]. Glass fiber/epoxy tubes used were checked in a biaxial testing machine with different ratios of hoop stress to axial stress. The subsequent stress/strain curves were studied, and biaxial failure areas in terms of strain and stress were created. The study indicated that the performance of the tubes was hard to predict, and the ratio and rate of biaxial loading consequences could lead to the reduction in the monotonic failure strength, damage reduction and a failure pattern of the specimens. Ramesh and his co-researchers ^[5] investigated the characterization of FRP composites using the modified spilt disk method and finally concluded that the average ultimate strains of the FRP rings using spilt disk test were lower than the ultimate hoop strains observed in FRP cylindrical specimens. Rafiee et al. ^[6] had developed a model to predict the hoop tensile strength modelling of glass fiber-reinforced polyester pipes which integrated the lamination theory and damage modelling.

Other than the efforts cited above, the purpose of this investigation was to find out the effects/consequences of the stiffness of the three different diameters of E-glass and S-glass fiber ring specimens: fiber type, resin type, and winding angle by contrasting the mechanical operation such as the hoop tensile strength and hoop tensile modulus of various samples under split-disk tests which accomplished the inducement of hoop stresses as if they were under internal pressure.

2.   Sample fabrication

For all the sequences of the course parameters cited above, tube-shaped samples were fabricated by means of a winding technique (wet) on the filament-winding machine at Aceon fiber glass Sdn. Bhd. as shown in Figure 1. Winding operations were performed on a 100 mm diameter steel mandrel with a computer-controlled Roth filament-winding machine. One of the mats used for the preparation of pipes was made of E-glass while the other was made with S-glass fiber. Polyester resin was used as a matrix along with hardener to finish the pipes fabrication with a winding angle of 90° as suggested by the previous work performed by Kaynak et al. ^[7]. The filament-wounded pipes were placed in ovens along with the mandrel for the curing operation. After curing, the composite tubes were removed from their mandrels. Split-disk test samples were then created by decreasing these composite pipes following the methods in ISO 8521 ^[8] or ASTM D 2290 ^[9] with three different thickness rings of each pipe. The properties of the glass fibers are shown in Table 1 below.

Figure 1.  Fabrication process of E-glass and S-glass tubular specimens: (a) Applying fabric on the mandrel, (b) coating with polyester resin, (c) curing operation.

DownLoad: Full-Size Img PowerPoint

Table 1.  Mechanical properties of glass fibers (As provided by the manufacturers).

Data provided by the manufacturer	E-glass	S-glass
Thickness of the glass fiber in GSM	900	630
Tensile strength, MPa	2000	4750
Density, g/cm3	2.55	2.43
Ultimate strain, %	4.5	3.2

---

 | Show Table

DownLoad: CSV

3.   Split-disk tests

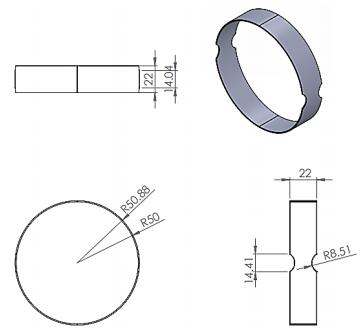
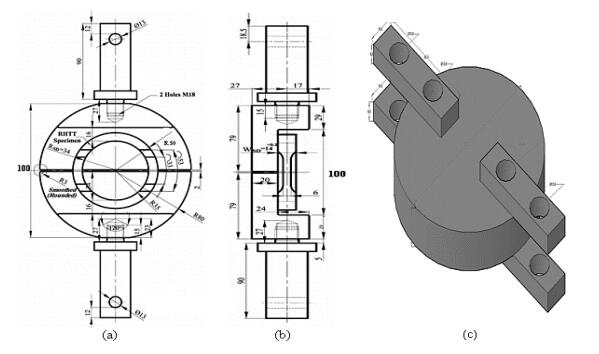
The most important purpose of this analysis is to determine the hoop tensile properties of two different filament wound composite pipes (E-glass and S-glass) by split-disk method. Split disk as shown in Figure 2 with a diameter of 100 mm is used instead of 50 mm as specified in the ASTM D2290 and ISO 8521 to be closer to typical strengthening applications. Three different specimens with various thicknesses were tested for each method of combination. The ultimate hoop tensile modulus of elasticity and hoop tensile strength of the specimens were determined. As shown in Figure 3, test samples have full diameter and full wall thickness rings, with an inner diameter of 100 mm and an average outer diameter of 101.75 mm. Figure 2 shows the split-disk test specimen's geometry with dimensions. Each test ring comprises two segments of decreased area, which were positioned 180° apart from one another. The glass fiber/epoxy rings were created free from machining spots, and each was uniform in cross-section. The test fixture shown in Figures 4 and 5 which was produced through CNC Lathe machine has two half semi-circle shaped metal plates which were attached to the upper and lower connecting arms of the test fixture with pins. Bending moment imposed during the test at the split between the split disk test fixtures can produce mainly the values of apparent tensile strength rather than the true tensile strength in each test. The test fixture was therefore designed to minimize the effect of this bending moment.

Figure 2.  Split-disk test specimens' geometry with dimensions.

DownLoad: Full-Size Img PowerPoint

Figure 3.  E-glass and S-glass composite test rings for split disk tests fabricated according to ASTM D 2290 standard.

DownLoad: Full-Size Img PowerPoint

Figure 4.  Split-disk fixture fabricated by using CNC Lathe machine.

DownLoad: Full-Size Img PowerPoint

Figure 5.  Design of the test rig with geometry: (a) Front view, (b) Side view, (c) Designed test rig view.

DownLoad: Full-Size Img PowerPoint

4.   Test procedure

A universal testing machine INSTRON 3382 with a loading capacity of 600 kN and fitted with drive mechanism with a constant rate of 2 mm/min cross head drive was used to find out apparent HTS as shown in Figure 6. All the tests were performed at a room temperature of 23.7 ℃. The load, displacement, and strain gauge signals were acquired from the testing machine.

Figure 6.  Universal testing machine INSTRON 3382 with attached split disk fixture.

DownLoad: Full-Size Img PowerPoint

The process of flow throughout split disk tests were as follows:

(ⅰ) E-glass and S-glass composite rings which are cut from the glass/epoxy composite pipe were measured by means of digital callipers. For each composite pipe, thickness widths were noted at five places with three of them in the gage segments. The sizes of all the decreased pieces were noted. Composite pipe decreased sections are shown in Figure 3 above.

(ⅱ) Glass/epoxy composite pipe rings were fixed on the split-disk test fitting with the decreased sections. Attention was taken to support the test ring on the split disk frame so that it was in the center along the line linking the contacts of connection with the fixture to the test apparatus.

(ⅲ) Load up level of the experimenting apparatus was fixed to a steady level, and the test was commenced. Strain data and axial force were considered till failure occurred in the E- and S-glass composite rings.

(ⅳ) Once attaining axial force-strain graphs of all the E-glass and S-glass FRP rings, the average mean value of the hoop tensile modulus and ultimate hoop tensile strength values were determined, and the standard deviations were noted for each experiment.

5.   Results and discussion

5.1.   Study of the hoop strain distribution in the E-glass and S-glass composite rings

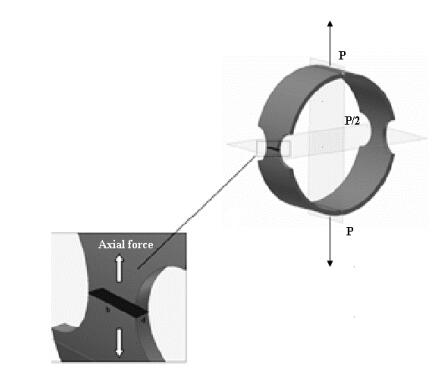
The strain distribution in the GFRP rings was analysed by the strain gauges located on the machine and the test rig. Figure 7 shows the structural analysis view through load and stress analysis.

Figure 7.  Hoop tensile strength analysis through load and stress analysis.

DownLoad: Full-Size Img PowerPoint

The strain formation in the split and the overlapping region until rupture is shown in the graphs below. The analysis of the results from the graph show that strain is non-uniform around the circumference of the fixture which is connected to the UTM. The apparent hoop tensile was analysed by distributing ultimate applied load by two times of the decreased section width. The apparent hoop tensile strength (HTS) of the samples can be calculated using the following Eq 1:

It is important to state that the apparent hoop tensile strength can be achieved by the method rather than true tensile strength method due to the bending moment imposed during the test at the split between split disk fixtures ^[10]. By performing mechanical assessments on filament wound GRFP rings, hoop tensile modulus at ambient temperature was determined for all GFRP ring samples. The hoop tensile modulus was decided by the following Eq 2 ^[11]:

By using the slopes in the initial linear part of the stress–strain curves, the apparent modulus of elasticity can be calculated by the Eq 3 ^[12]:

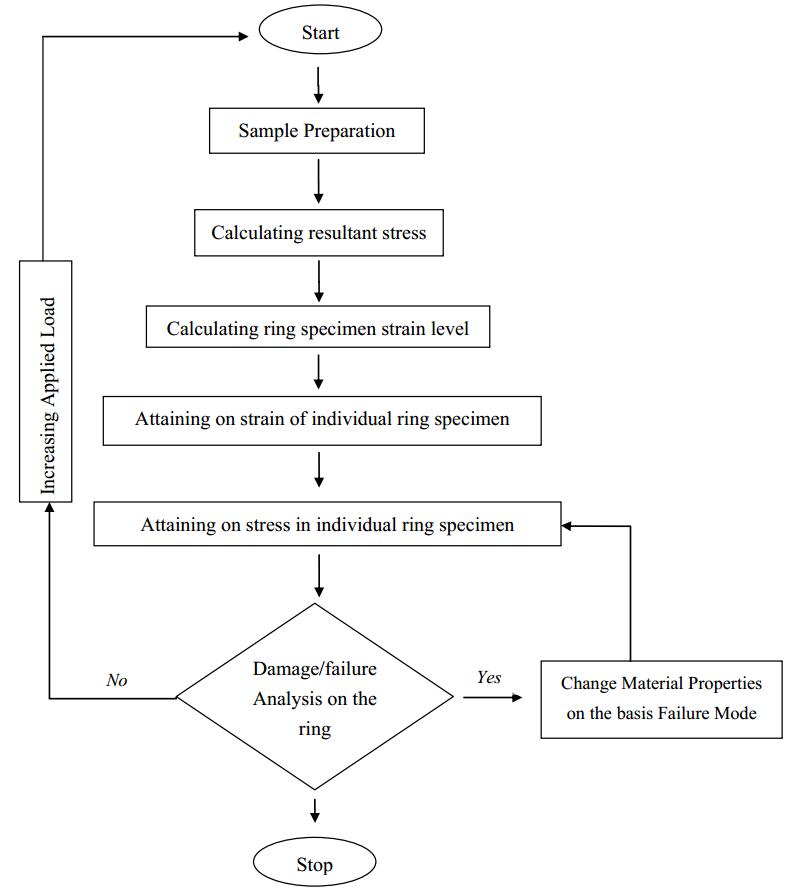
A successive damage model (SDM) was used to calculate the apparent hoop tensile strength. The process flow chart from the acquired SDM is shown in Figure 8 below. This developed model comprises four major levels: model fabrication, stress evaluation, damage analysis, and material properties deprivation.

Figure 8.  Flowchart of sequential damage modelling ^[6].

DownLoad: Full-Size Img PowerPoint

5.2.   Characterization of E- and S-glass fiber/epoxy pipe rings with split-disk tests

The rings which were thicker showed some non-linearity which can be predicted by the cracking phenomenon while straightening the ring at the split. The failure mode of the rings that are made of S-glass showed more strength to control rather than those fabricated with E-glass fabric polymer. Another point was that the failure pattern of the rings made of thicknesses 1.75 mm and 3.50 mm showed the same patterns both in E-glass and S-glass fiber reinforced polymer. The tensile strength, ultimate strain and elastic modulus were averaged for a set of two sets of specimens, where repeated tests were conducted to get the accurate value to predict the result.

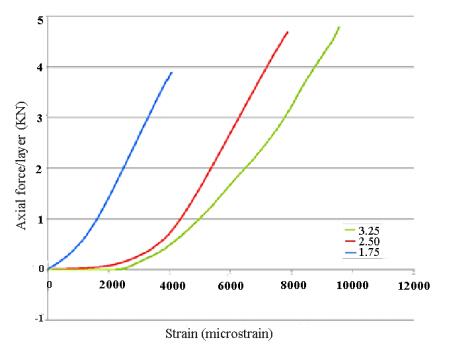
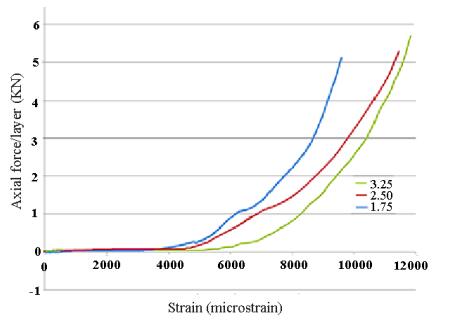
Corresponding to Figures 9 and 10, it can be confirmed that the samples produced by S-glass fiber exhibited a better mechanical performance compared to the one reinforced with E-glass fiber. Different thicknesses of ring samples fabricated with E-glass fiber were observed to have more axial force than the ones fabricated with S-glass fiber. However, when it comes to the strain/load extension, S-glass rings showed good conduct when compared with the E-glass ring samples. Therefore, it can be predicted that ring specimens made of S-glass fiber have higher ultimate strain and elastic modulus of rigidity as opposed to the rings fabricated with E-glass fiber.

Figure 9.  Axial force–strain curves of the rings fabricated with E-glass fiber/epoxy composite.

DownLoad: Full-Size Img PowerPoint

Figure 10.  Axial force–strain curves of the rings fabricated with S-glass fiber/epoxy composite.

DownLoad: Full-Size Img PowerPoint

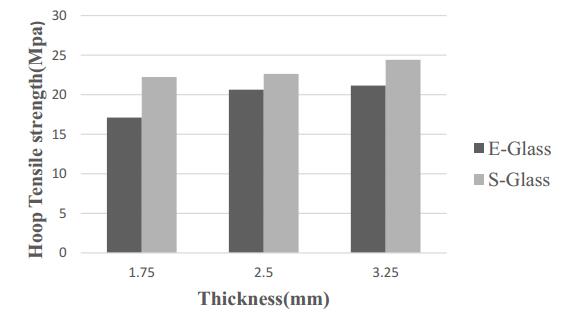
Figure 11 shows that thickness is dependent on the hoop tensile strength of the specimen for two different materials with which the rings are fabricated. As expected, the highest strength values were obtained for specimens fabricated with S-glass material with a maximum thickness of 3.25 mm. Conversely, the lowest strength was noticed in the specimens fabricated with E-glass fabric with a thickness of 1.75 mm. The specimens fabricated with ring thickness exhibited intermediate performance between the two extremes. Based on Figure 11, it can also be stated that the effect of the polyester resin system on the hoop tensile strength of the rings is negligible. As the thickness increased, the load-carrying capacity increased to some extent, with the ultimate load. Therefore, it appears that tests on S-glass specimens, in the characterization of GFRP, would give conservative results over E-glass GFRP rings and in their applications. This confirms the conclusions stated by earlier researchers ^[13,14,15]. Average experimental results of apparent hoop tensile strength, elastic modulus, and hoop tensile modulus during split disk tests are shown in Table 2 below.

Figure 11.  Assessment of hoop tensile strength of E-glass and S-glass samples with three different thickness rings.

DownLoad: Full-Size Img PowerPoint

Table 2.  Average experimental results for apparent hoop tensile strength (HTS), elastic modulus, and hoop tensile modulus of split disk test.

Type of Material	Thickness (mm)	Maximum load prior to failure (kN)	Average Apparent HTS (MPa)	Average Apparent modulus of elasticity (MPa)	Average Ultimate strain (%)
E-glass	1.75	3.92	17.11	0.122	1.25 × 10−2
	2.50	4.73	20.63	0.145	1.45 × 10−2
	3.25	4.85	21.15	0.149	1.65 × 10−2
S-glass	1.75	5.10	22.24	0.152	1.74 × 10−2
	2.50	5.19	22.63	0.156	1.79 × 10−2
	3.25	5.59	24.41	0.167	1.99 × 10−2

---

 | Show Table

DownLoad: CSV

As observed from Figures 12 and 13, failures occurred in both E-glass and S-glass composite pipe rings. For specimens fabricated with S-glass fiber, fiber-matrix de-bonding corresponded to the fiber's direction and loading axis which resulted in fiber fracture. For example, fabricated E-glass fiber with a similar mechanism was observed during the delamination stage. The external surface was noticed to be completely damaged.

Figure 12.  Typical failure pattern observed in E- and S-GFRP rings during testing.

DownLoad: Full-Size Img PowerPoint

Figure 13.  Dominant failure mechanisms observed on split-disk specimens: (a) E-Glass, (b) S-glass.

DownLoad: Full-Size Img PowerPoint

6.   Conclusion

This analysis was planned to satisfy the conditions of the investigational data with different characterizations of both E-glass and S-glass filament wound epoxy composite pipes. Split disk tests were accomplished for different thicknesses, and the following conclusions were achieved:

● The strain values in the rings of S-glass polymer show more elasticity than the rings made of E-glass fiber polymer.

● From the ultimate strain and elastic modulus, we can also conclude that Poisson's ratio of the rings fabricated with the proposed S-glass fiber is higher than the existing E-glass fiber.

● The failure is generally brittle, with the load bearing ability which dropped rapidly after the peak owing to the rupture of the glass fibers.

● Both hoop tensile modulus of elasticity and hoop tensile strength can be determined by the thickness of the samples. Specimens having a thickness of 3.25 showed higher values than others, both in E-glass and S-glass specimens.

● The consequences of the epoxy resin usage have no impact on the mechanical performance, and it was insignificant because the properties of these structures were relatively small with a minor variance in the viscosity of the resin and the transition temperature of the glass.

● Sample prepared using S-glass fabric demonstrated much developed mechanical properties when matched with rings fabricated by E-glass fabric for loading conditions near the path of loading.

● Split-disk test is a successful approach to determine the hoop tensile strength of filament-wounded tube-shaped shapes. Consistent results were attained with a little standard deviation. Experiments with S-glass fiber/epoxy reinforced rings gave a relatively greater deviation values when compared to E-glass reinforced specimens.

Acknowledgment

The author would like to thank the Universiti Putra Malaysia and Department of Mechanical and Manufacturing Engineering, UPM for supporting this project under Grant by UPM Scheme, Vot No 9556200.

Conflict of interest

The authors declare no conflict of interest.