Design of sensor and actuator fault tolerant control system on wind turbine benchmark for Region II

1.   Introduction

The operation of wind turbine systems requires high reliability and long-term sustainability. Moreover, to ensure the safety, the maintenance cost of wind turbine is remarkably expensive compared to that of other energy resources ^[1]. The development of the wind turbine power generation system is absolutely one of the most notable issues to expand the utilization of wind turbine power generation. The key challenge is to yield the electricity production as large as possible over a broad range of weather and operation condition as well as to minimize manufacturing and maintenance costs.

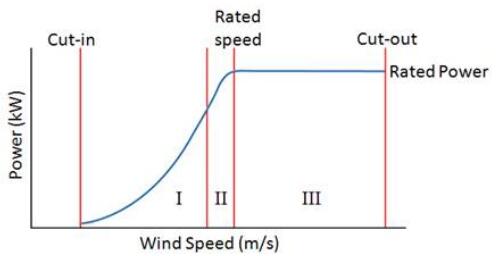
Basically, generator of wind turbine system operates in four operational regions with respect to wind speed value, as shown in Figure 1. In Region Ⅰ, the turbine is at the standstill as it is very low wind power condition. In both Region Ⅱ and Ⅲ, the turbine has rotated, but in different condition. Regions Ⅱ is an operational mode where the maximum power is desirable to achieve. Hence, tracking for optimum speed is necessary to gain the maximum power. The power optimization for regions Ⅱ is the main issue. Meanwhile, in region Ⅲ, the turbine should limit the maximum power so as not to exceed the mechanical and electrical load. In this region, constant power production is maintained. In Region Ⅳ, the turbines are pitched out to stop their rotation because of high wind speed.

As regards to the electricity improvement, the wind energy system performance should be maintained, especially for wind power decrement which commonly occurs in Region Ⅱ. The development of wind turbine control system seems to be the promising technique to resolve this issue. However, due to the component faults including sensor and actuator, the output response of control system is unforeseen. Since there is no treatment which is carried out, these minor faults might turn out to be major faults, causing the system operation failure. For example, the sensor faults around wind turbine drive train could produce the increase in friction and the wear of the drive train. Over the years, the accumulation of wear leads to the total breakdown which not only needs high-cost maintenance but also results in long downtime of the wind turbine. Meanwhile, the wind turbines are expected to generate energy in very short downtimes. The robust control system is highly necessary to overcome this issue so that the good performance wind turbine system could be achieved. This study proposes an innovative generator speed control system for a wind turbine benchmark which capable to accommodate the minor faults (called fault tolerant control or FTC) in its speed sensor and its converter.

The FTC is known as a control scheme which is able to accommodate fault component automatically and maintain the desired performance and the stability when fault occurs ^[2]. Indeed, many methods regarding the FTC system have been offered. Recently, compensation method which employs fault estimates to fix the fault effect has been developed. Here a large computational burden can be avoided since the fault detection and reconfigurable control scheme are designed in an integrated way ^[3].

In wind turbine system, the fault compensation method is a relatively new field of research. Sami et.al developed a robust FTC strategy based on an adaptive gain sliding mode control (SMC) for a wind turbine operating at low wind speed ^[4]. They proposed a robust descriptor observer to simultaneously estimate the states and the "unknown outputs". In ^[5], a set of unknown input observers was proposed to estimate generator speed in FTC scheme. Literature ^[6] proposed a novel strategy whose architecture was based on the combination of proportional multiple integral observers and dynamic output feedback control. However, all previous studies have not considered actuator faults.

In ^[7], an active fault-tolerant control scheme for handling actuator faults in a wind turbine benchmark was presented. The scheme was based on the adaptive filters which are obtained via the non-linear geometric approach in order to obtain interesting decoupling property with respect to uncertainty affecting the wind turbine system. The implementation of linear parameter varying (LPV) fault tolerant control (FTC) approach for hydraulic pitch actuator of a wind turbine system has been suggested in ^[8]. The study included two separate actuator fault scenarios, i.e. stuck fault which was addressed to a fault hiding approach; and loss effectiveness which was solved by synchronizing all three pitch systems to prevent further damage caused by the unbalanced structural loads. Nevertheless, both schemes were only for accommodating actuator faults.

Researchers which focus on the utilization of FTC on the wind turbine are still limited, especially for sensor and actuator faults that occur simultaneously. Literature ^[9] conducted research focusing on the control strategy based on the virtual sensor/actuator concept in which encapsulates the actual sensors and actuators in a software module. It could be considered as an annihilating signal for the fault. This signal exists in the virtual sensor/actuator, hence the effect of the fault is reduced. Since this scheme relies on FDI, the fault must first be identified. Another scheme is using adaptive control concept as proposed in ^[10]. This controller was designed by means of the online identification in which the controller reconfiguration mechanism depends on its estimation result. But the adaptive nature may produce a lot of negative spikes in the output responses as reported by ^[11]. Furthermore, there is no information about the location of the faults whether it is in the sensors or in the actuators or in the others.

Our previous study had designed an active fault tolerant tracking control system to accommodate both sensor and actuator fault simultaneously for a DC series motor speed drive ^[12]. Due to the losses related to false alarm and reconfiguration time, the proposed fault tolerant strategy was based on robust fault estimation and compensation without FDI scheme. The reconfigurable control was obtained by compensating the received sensor signal and the delivered control signal using the fault estimates. For this purpose, a single robust fuzzy observer was proposed to estimate both the state and the fault simultaneously. This observer was designed based on the extended system expression. The determination of the observer gain was conducted by employing Linear Matrix Inequalities (LMI) technique.

In ^[13] and ^[14], the similar method is applied for wind turbine plans. To overcome nonlinearities, a fuzzy model approach is used in ^[13], thus making the system more complex and depending on the accuracy of the fuzzy models used; while the LPV model approach is used in ^[14] so that the accuracy of the model depends on the relationship of parameters with wind speed, where this relationship is difficult to obtain. In addition, the used effective wind speed must be limited to predetermined values.

The objective of this study is to design a robust control system based on Fault Tolerant Control (FTC) aiming to overcome the fault of rotor speed sensor and converter by implementing a modified version of the algorithm in ^[15]. Here the linear model approach is still used in order to get a simpler control system. A studied wind turbine benchmark is considered consists of blade and pitch systems, drive train, generator, and converter. The used benchmark model is adopted from ^[16] in order to get a realistic generic model of the horizontal variable-speed wind turbine with a full-scale converter coupling. This plant operates in Region Ⅱ with the wind speed of 4–11 m/s.

2.   System description

2.1.   Wind turbine benchmark

The extracted wind power of the horizontal axis wind turbine system is ^[17]:

where, ρ_air = air density, A_r = blade impact area, V_w = wind speed, C_p is the non-dimensional power coefficient whose value is approached using this experiment equation, given in equation ^[18]

where

C₁ = 0.6450; C₂ = 116; C₃ = 0.4; C₄ = 5; C₅ = 21; C₆ = 0.00912; C₇ = 0.08; C₈ = 0.035;

where, β = blade pitch angle, w_t = turbine shaft speed, R = blade length.

The hydraulic pitch system is considered as a closed loop system whose transfer function is in the range of pitch angle (β) and its reference (β_r). Basically, it is a piston servo system which could be modelled using a second order transfer function:

where ζ is the damping factor and ω_n is the natural frequency.

The relations of wind power to turbine torque T_t and turbine shaft speed (blade rotation) is given in the following equation:

The wind turbine mechanical model is considered to have a two-mass system behavioral, namely generator and drive train whose the gearbox and the bearing attenuation are ignored, that is:

T_m = generator mechanical torsion

Δθ = torsion angle

H = inertia constant of the whole mechanical system

ω_g = generator speed

D_m = mutual damping

K_sh = stiffness constant

The turbine and the generator speed are the same in the steady condition, or mathematically express as ω_t = ω_g = ω. In the dynamic condition, the generator speed is given in equation:

where, H_g = inertia constant of the generator, F = friction factor, T_g = the generator electrical torsion

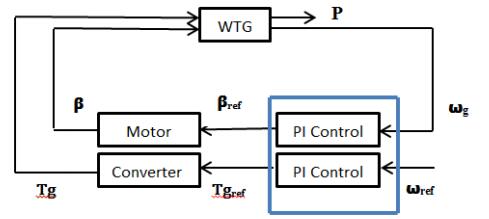
2.2.   Nominal control system

In the optimization of power generation, the designed control system is responsible for varying the speed of turbine and generator so as to track the wind speed. This system has two levels of control, i.e. operational and subsystem control. As regards the operational control, it assigns how the control objectives are attained by the turbine in the specified Region. The generator, power electronics, pitch drive and other actuators can well-perform as desired due to the existence of the subsystem controllers. This paper considers only the operational controls working in the Region Ⅱ while the subsystem controllers are apart from the scope of the paper. This is because the benchmark model works at the system level in which the subsystem controllers have the fast control loops.

The WTG (Wind Turbine Generator) power levels are below the rated value (1 pu) in Region Ⅱ. In order to produce the maximum power, the speed of turbine should be set at its optimum point. The speed reference should slowly track the changes of power with a time constant of approximately 5 seconds. In this study, the turbine speed reference is reduced for power levels below 75% by using the following equation:

For Region Ⅱ, the active operational controller is a generator torque control which provides generator torque reference to maximize the power coefficient C_p by examining the turbine speed. The pitch angle is maintained at zero degrees (the optimal efficiency point) by the pitch control so that the wind turbine captures all available wind power. Although the rotor's net torque depends on the wind input torque and the generator load torque, the generator torque could be utilized to influence the rotor accelerations and deceleration.

Both the torque and the pitch control are performed using a proportional-integral (PI). Furthermore, the block diagram of the control scheme is depicted in Figure 2. The transfer function is required and it is highlighted in the frequency domain of the PI-controllers as formulated in the following:

In terms of variable-speed operations, the generator torque is driven by applying a power electronic as an actuator. Hence it could be changed quickly. This study considers a converter as a studied actuator. The converter has a subsystem controller accommodating the generator with particular torque. Therefore, the approach of a simplified design of the converter is depicted by the first order system as follow:

where τ_g is generator-converter time constant.

Another prominent device influencing the process in control system is sensor. Indeed, the rotor speed must be accurately gauged to gain the true value of the system. Moreover, the speed sensor is formulated by the first-order system along with certain time constant, τ_ω. The transfer function for the speed sensor is represented as:

From the function, the speed variable being measured is then defined as the output function being appended with certain Gaussian noise.

The converter fault could make the wind turbine generator system does not work properly and damage the system when it is stopped suddenly. Moreover, it could damage the machine due to the setting of the rotor brakes to stop blade's position in the desired position at maximum pitch rate. Meanwhile, sensor fault will certainly cause a false reading followed by faulty decision, which may be harmful to the whole system. Therefore, the utilization of redundant sensors seems to be a promising technique to exacerbate the whole reliability of the measurement system. But it requires more cost.

3.   Fault tolerant control scheme

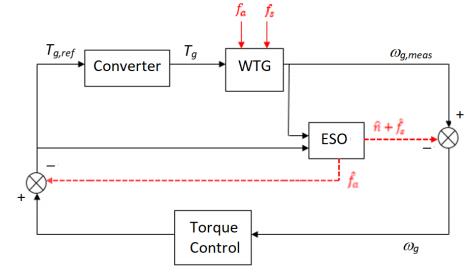
In this study, the proposed FTC system model is the modification of control method developed in reference ^[12]. The distinction between the previous study and the current study is on the plant, i.e. the wind turbine generator system. The focus of the current study is to control the turbine rotor (w) in terms of the rotational speed which is known as the controlled output.

The proposed design of FTC system comprises a modest configuration as illustrated in Figure 3. The WTG Plant includes the wind turbine generator, the pitch motor, the converter and the speed sensor. To accommodate the speed sensor and converter faults simultaneously, the FTC system automatically executes the reconfiguration of control law. The first approach employs suitable corrective measurement signal ω_g to the nominal control system in order to compensate the sensor fault. The second approach compensates the converter fault directly by utilizing the suitable corrective control signal Tg_ref. Meanwhile, β_ref is kept to zero in Region Ⅱ so the pitch motor does not work. For this FTC strategy, an observer is required to supply fault estimate.

3.1.   State space model

The modelled observer is evolved according to a model which pictures the controller input Tg_ref to the output of generator rotor speed ω_g. This design is taken into account as the succeeding multivariable linear time-invariant system (LTI) along with disturbance, noise, actuator and sensor fault represented in following state space equation:

where x(t), y(t), u(t), d(t) ∈ R, n(t) ∈ R, f_s(t) ∈ R, are the state vector, the input vector, the output vector, the unknown disturbance (including the actuator fault f_a), the measurement noise, and the sensor fault, in turn. A and B are constant real matrices of appropriate dimension hailed from the wind turbine generator (WTG) design.

In order the proposed observer could work on a wide range, the no-fault WTG system is represented in the state space model as follows

The short definition of all used parameters in (17) can be seen in Table 1.

The wind aerodynamic torque (T_a) is unknown and can't be measured. Because of its nonlinearity, in order to get a linear state space model, T_a is considered as a disturbance input (not a state variable) that affects the rotor speed state variable. While, the fault of actuator affects the generator torque state variable (T_g). Both those disturbances can be put together in one vector as a disturbance vector. Thus, the state space equation (17) can be re-written as

The equation (18) has the same form as (15) in which:

If the measured outputs are T_g, ω_r, and ω_g, then referring (16) the matrix output becomes

It is assumed that the faults of sensor only occurs in the generator speed sensor so the distribution matrix of sensor fault is written

3.2.   Extended state observer

The designed observer estimating the fault value is evolved according to an extended state observer as described in ^[15]. The observer then acquainted the updated x_z ∈ R as follows:

Establishing the augmented state of X becoming X = [x x_z]^T, it is then gained the augmented states of both (17) and (18) as follows:

with ${A_a} = \left[{\begin{array}{*{20}{c}} A&O\\ C&{ - I} \end{array}} \right], {B_a} = \left[{\begin{array}{*{20}{c}} B\\ O \end{array}} \right], {C_a} = \left[{\begin{array}{*{20}{c}} O&I \end{array}} \right], {D_{an}} = \left[{\begin{array}{*{20}{c}} O\\ {{D_n}} \end{array}} \right],$ ${E_a} = \left[{\begin{array}{*{20}{c}} {{D_d}}&O\\ O&{{F_s}} \end{array}} \right], f = \left[{\begin{array}{*{20}{c}} {{f_a}}\\ {{f_s}} \end{array}} \right], {D_{ad}} = \left[{\begin{array}{*{20}{c}} {{D_d}}\\ O \end{array}} \right]$

I is the matrix of identity with appropriate dimension. The design of observer can be therefore presented from (23) as shown in the (24):

where $\hat X, \, \hat f, \; \hat Y$ are the estimates of augmented state, the fault, and the output in turn.

To estimate states of the system correctly even in the existence of both the disturbance and the fault, the next step is to calculate the gain of observer L_X and L_f so that the exogenous inputs are enervated under the desired level γ leading to robust stability. Therefore the utilization of H_∞ approach which is famed as the Bounded Real Lemma, is suggested. The detail description of the technique will not be discussed in this research, yet it was studied in ^[15].

4.   Simulation results

In this section, the proposed method is evaluated by applying it to a horizontal axis of the wind turbine benchmark through simulation. Table 1 is the list of numerical values of the WTG plant model parameters. Per unit system (pu) is used to express the comparison of the studied quantities with their normal values. For a given quantity, per unit value is the value related to a base quantity. The measurement noise is presented to be the band limited white noise signal with the value of noise power is 10⁻⁴ W.

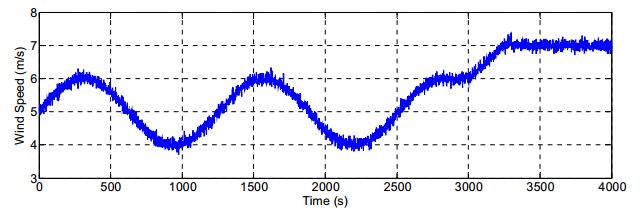
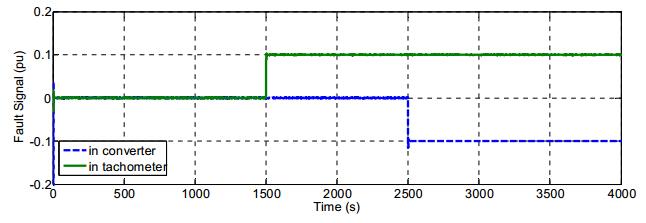
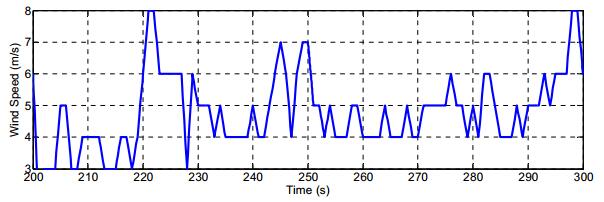
The test series was conducted to exhibit how the proposed method handles divergent operating conditions while the faults were issuing. Therefore, a predefined wind speed sequence is implemented. The wind sequence contains the simulated data of wind which could be observed in Figure 4. The wind speed ranges from 4 to 6 m/s, which represents Region Ⅱ. The simulations of the speed sensor and converter faults are shown as either constant offset or bias with 0.1 pu at time 1500 s and −0.1 pu at time 2500 s respectively.

It can be proven easily that all requirements stated in ^[15] are satisfied. The proposed observer (24) is developed in which the observer gain is determined by using LMI technique, namely:

The fault estimates using the proposed observer are shown in Figure 5, i.e. the solid line for the speed sensor fault and dashed line for the converter fault. Figure 5 confirms that the suggested technique results in good estimation. Although time-varying operation occurs due to the wind speed dynamic, the observer keeps the correctness of estimation when the steady-state operation is reached, i.e. 0.1 pu for the sensor fault estimate and −0.1 pu for the actuator fault estimate. It is also seen that the converter fault estimate is not affected by both input changes and sensor fault, but by the actuator fault dynamic only as shown at the time of 2500 second. The sensor fault estimate is noisy signal because it is a total addition of the sensor fault and the noise signal. Moreover, it is portrayed that there is no amplification from the noise by the observer, hence it is beneficial to gain the true value of measurement for control objective.

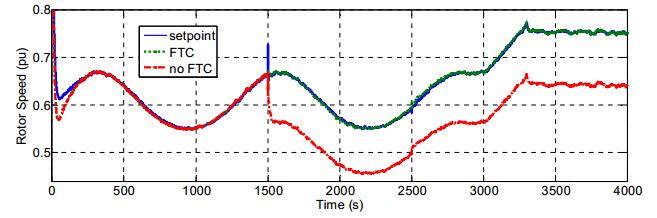
Figure 6 illustrates the true responses of speed (not its measured response) for the performed test series. In the initial phase, using both FTC system and the conventional control system without FTC can maintain the turbine speed around the setpoint (the green solid line). On the contrary, when the sensor fault happens, the system without FTC cannot maintain the turbine speed approaches to the desired value. This is because the error steady state of the response exists due to the false data received by the PI controller regarding the actual speed. The FTC system indeed is able to keep the turbine speed closes to the desired value even in the transient condition. Furthermore, when the actuator fault is occurred (at 2500 s), the FTC system still tracks the setpoint while the conventional system does not evaluate because it is hidden by the sensor fault effect.

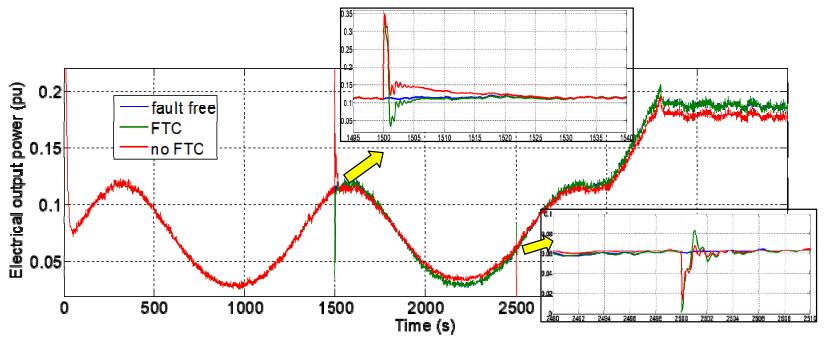
The same result is obtained for the power response as described in Figure 7. The zoomed versions of the response describe the more detail response when the faults happen. The FTC system has the capability to recover the generated power as soon as possible when the speed sensor fault and the converter fault occur. Furthermore, the WTG system with the conventional control produces less power (the red line) than one with the FTC (the green line). The FTC has been proven to maintain the power production such as the WTG system without any faults (the blue line).

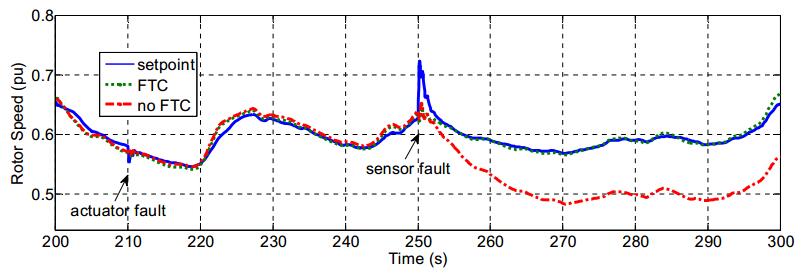
The proposed method is also applied in simulation to wind farms in the East Java region, Indonesia. The daily wind speed profile is shown in Figure 8. The comparison of control system response of FTC and no-FTC is shown in Figure 9. This time, the simulated actuator fault occurs first in the 210th second, being followed by a sensor fault in the 250th second. The simulation results show that minor actuator fault does not affect the performance of the control system, in this case the FTC performs the same as no-FTC, which is tracking the setpoint. Only when there is a sensor fault, the FTC produces a better response than the no-FTC as explained in the previous experiment.

5.   Conclusion

The designed FTC system successfully compensates the minor faults occurred in the speed sensor and the converter system of the wind turbine. The valid information is provided by the extended observer for the PI controller, so that this makes the wind turbine can generate the peak power while a sensor fault exists. The observer also generates the suitable signal that reconfigures the PI controller output of the torque control to fit the real needs. It is noticed that the responses of the speed and power of the FTC system are better than those of the system without FTC. This is because the FTC system has minimum error compared to the conventional control system. The wind turbine benchmark system with FTC performs well as the free fault one. Moreover, the power output is more generated with the FTC system than that of the conventional system.

Acknowledgments

This study has been supported in part by the Indonesian Ministry of Research and Higher Education through PU ITS research scheme (contract number: 706/PKS/ITS/2017).

Conflict of interest

The authors declare no conflict of interest.