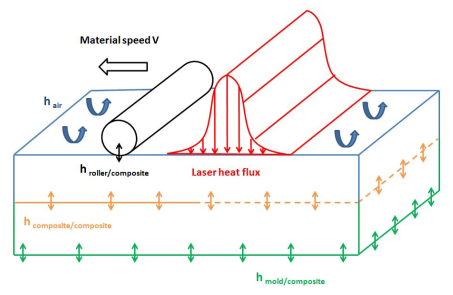
Nowadays, the production of large pieces made of thermoplastic composites is an industrial challenging issue as there are yet several difficulties associated to their processing. The laser-assisted tape placement (LATP) process is an automated manufacturing technique to produce long-fiber reinforced thermoplastic matrix composites. In this process, a tape is placed and progressively welded on the substrate. The main aim of the present work is to solve an almost state of the art thermal model by using an efficient numerical technique, the so-called Proper Generalized Decomposition (PGD) that considers parameters (geometrical and material) as model extra-coordinates. Within the PGD rationale the parametric temperature field is expressed in a separated form, as a finite sum of functional products, where each term depends on a single coordinate (space, time or each one of the parameters considered as extra-coordinates). Such a separated representation allows the explicit expression of the sensitivity fields, from the temperature derivative with respect to each parameter. These sensitivity fields represent a very valuable methodology to analyze and establish the influence of the critical input parameters on the thermal response, and therefore, for performing process optimization and control, as well as for evaluating the effect of parameters variability on the thermal response.
1.
Introduction
The process of selecting appropriate and applicable variable values for a specific task is known as optimization [1,2,3]. Optimization exists in almost every domain, including job shop scheduling [4], feature selection [5,6,7], image processing [8,9], face detection and recognition [10], predicting chemical activities [11], classification [12,13], network allocation [14], internet of vehicles [15], routing [16], and neural network [17]. Due to the nature of real-world problems, Optimization becomes very challenging and has many difficulties such as multiobjectivity [18], memetic optimization [19], large-scale optimization [20], fuzzy optimization [21], uncertainties [22] and parameter estimation [23]. Metaheuristics algorithms have been used to solve such problems due to their advantages such as flexibility, efficiency and getting a near-optimal solution in a reasonable time.
Examples of metaheuristics algorithms include particle swarm optimization (PSO) [24], artificial bee colony [25], coot bird [26], genetic algorithms (GAs) [27], the krill herd algorithm [28], the harmony search (HS) algorithm [29], the snake optimizer [30], monarch butterfly optimization [31], the slime mold algorithm [32], the moth search algorithm [33], the hunger games search [34], the Runge-Kutta method [35], the weighted mean of vectors [36], the virus colony search [37], the lightning search algorithm [38], ant lion optimization [39], the crow search algorithm [40], moth-flame optimization [41], the wild horse optimizer [42], the remora optimization algorithm [43], the artificial rabbit Optimizer [44], the artificial hummingbird algorithm [45], grasshopper optimization algorithm (GOA) [46], grey wolf optimizer (GWO) [47] and the whale optimization algorithm (WOA) [48].
The Aquila optimizer (AO) is the latest developed algorithm proposed by Abualigah et al. [49] which simulates the four different phases of Aquila hunting behavior. Wang et al. [50] developed an improved version of the AO by replacing AO's original exploitation phase with the Harris hawks optimizer's exploitation phase. Moreover, they embedded a random opposition-learning strategy and nonlinear escaping operator in their proposed algorithm. They argued that the proposed algorithm is able to achieve the best results compared with the other five metaheuristic optimizers. Also, Mahajan et al. [51] hybridized the AO with the arithmetic optimization algorithm (AOA) [52]. They tested their algorithm which is called AO-AOA with original AO, original AOA, WOA, GOA and GWO. Another hybrid work between AO and AOA has been done by Zhang et al. [53]. Likewise, Zhao et al. [54] developed another version of the AO called the simplified AO algorithm by removing the control equation of the exploitation and exploration procedures (latter strategies) and keeping the former two techniques. They said their developed algorithm IAO achieved better results than many newly developed swarm algorithms. Another enhancement has been done by Ma et al. [55] in which grey wolf optimizer is hybridized using Aquila algorithm that allows some wolves to be able to fly, improving their search techniques, and avoiding getting stuck in local optima. They tested their developed algorithm with many optimizers using 23 functions. Also, Gao et al. [56] employed three different strategies to enhance the AO algorithm. These strategies are Gaussian mutation (GM), random-opposition learning, and developing a search control operator. They argued that their algorithm, an improved AO, has superior results compared to other optimizers.
The AO has been successfully used in many applications. For example, AlRassas et al. [57] tried to forecast oil production by using the AO to optimize the adaptive neuro-fuzzy inference system model. Also, Abdelaziz et al. [58] tried to classify COVID-19 images using the AO algorithm and MobilNet3. Likewise, Fatani et al. [59] developed an extraction and selecting approach for features using the AO and deep learning for iot detection intrusion systems.
Despite the powerfulness and superiority of the algorithm, and as stated by the no free lunch theorem, the AO cannot solve all optimization issues. So, the AO still needs more enhancements and developments.
This paper introduces a novel version of the AO in which three different strategies have been used to overcome the original optimizer drawbacks such as getting stuck in local optima and slow convergence. These strategies are the chaotic local search (CLS), opposition-based learning (OBL) and the restart strategy (RS). Using OBL and the RS enhances the AO exploratory search capabilities whereas the CLS improves AO exploitative search abilities.
The main contributions of this paper are as follows:
● A novel Aquila algorithm has been developed using three strategies: OBL, the RS and the CLS.
● The developed optimizer has been compared with the original AO and nine other algorithms, namely, the CSA [40], EHO [60], GOA [46], LSHADE [61], Lshade-EpSin [62], MFO [63], MVO [64], and PSO [24].
● A scalability test and removing one strategy from the developed algorithm experiments have been carried out.
● mAO was tested using 29 functions and five constrained ones.
This paper is organized as follows: Section 2 discusses the background and preliminaries of the original algorithm, OBL, the CLS and the RS, whereas Section 3 introduces the structure of the modified optimizer and its complexity. Sections 4 and 5 discuss the results of the proposed mAO and other competitors in CEC2017 and five different constrained engineering problems whereas Section 6 concludes the paper.
2.
Preliminaries
2.1. Aquila optimizer (AO)
Aquila algorithm is one of the latest population-based swarm intelligence optimizers developed by Abualigah et al. [49]. Aquila can be considered among the most well-known prey birds existed in north hemisphere. Aquila is brown with a golden back body. Aquila uses its agility and strength with its wide nails and strong feet to catch various types ofprey usually squirrels, rabbits, marmots, and hares [65].
Aquila optimizer (AO) simulates the four different Aquila strategies in hunting. The next subsection shows Aquila's mathematical model.
2.2. Mathematical model
AO begins with a random set of individuals that can be represented mathematically as follows:
where X is an agent position (solution) that can be computed using the following equation:
where D refers to the number of decision variables, N indicates the number of agents, UBj and LBj are the jth upper and lower boundaries, and xi refers to the ith value of the decision variable.
AO simulates Aquila hunting in four different phases where the optimizer can easily move from exploration and exploitation using the following condition:
IF, {t≤(23)×TPerform explorationOtherwisePerform exploration
2.2.1. Expanded exploration (X1)
In this phase, Aquila will determine the area to hunt the prey and select it by a vertical stoop and high soar. The mathematical formula for such a behavior is given by the following two equations:
where XM(t) indicates the mean position in the ith generation, Xbest is the best Aquila position founded in this iteration, r is a randomly generated number in the interval [0,1], t is the current generation where T is the maximum generation number, and N is the Aquilas number.
2.2.2. Narrowed exploration (X2)
This technique is the most technique used by Aquila for hunting. To attack the prey, a short gliding is used with contour flight. Aquila position's will be updated as follows:
where XR indicates a position of Aquila generated randomly, rand is a random real number between 0 and 1, D is the number of variables, and Levy refers to a lévy function which is presented as follows:
where s is a fixed value and equals 0.01, u and μ are random numbers between 0 and 1 and β is a constant and equals 1.5. Both y and x are used to model the spiral shape and can be computed using the following two equations:
where r and θ can be calculated as follows:
where U equals 0.00565, ω equals 0.005, and r1 has a value between 1 and 20.
2.2.3. Expanded exploitation (X3)
In the 3rd technique, the prey area is determined and agents can vertically perform a preliminary attack with low flight. Agents can attack the prey as follow:
where XM(t) indicates the mean position in the i-th generation, Xbest is the best Aquila position founded in this iteration, rand is a randomly generated number in the interval [0,1], α and β are exploitation parameters that are equal 0.1, and UB and LB refer to the upper and lower boundaries.
2.2.4. Narrowed exploitation (X4)
In this phase, Aquila can easily chase the prey and attack attacks it using escape trajectory light which can be modeled as follows:
where QF(t) is the quality value, G1 refers to various AO motions, and G2 refers to chasing prey flight slope.
2.3. Opposition-based learning
Opposition-based learning strategy is a technique introduced by Tizhoosh [66] which has been employed by many researchers to improve many swarm optimizers. For example, Hussien [67] embedded OBL in SSA to overcome getting trapped in local optima. Moreover, Hussien and Amin used OBL with chaotic local search to improve the exploration abilities of HHO [7]. Zhao et al. employed OBL with arithmetic optimization algorithm [1]. OBL works by comparing the original solution with its opposite one. Let x is a real number that falls in the interval [lb,ub], then its opposite can be calculated from the following equation:
where lb and ub are lower boundary and upper one respectively, and ˉx indicates the opposite solution. If x is a vector that has multi values, then ˉx can be computed from the following equation:
where xj indicates the jth value of x and ubj and lbj refer to upper and lower boundaries respectively.
2.4. Chaotic local search
The chaotic local search (CLS) technique has been integrated with many swarm optimizers such as WOA [68], HHO [7], brain storm optimization [69], and Jaya Algorithm (JAYA) [70]. CLS technique is almost used with the logistic map which is given in the following equation:
where s is the number of the current iteration, C is a control parameter that equals 4, o1≠ 0.25, 0.50 and 0.75. Local search is used to search in the neighborhood area of the already founded optimal solution. CLS can be represented by the following equation:
where Cs refers to the value generated by CLS in iteration i and `Ci can be easily calculated as follows:
μ is a shrinking factor and can be computed from the following below equation:
where t and T refer to the current and maximum number of iterations.
2.5. Restart strategy
During the search operation, some agents may not be able to find a better location as they may get trapped in local optimum regions. Such agents may affect the overall search as they take many generation resources and don't enhance the search process. Restart strategy (RS) at this point which is proposed by Zhang et al. [71] can help worse agents to jump out from local regions. RS counts the number of times for each individual that has been enhanced and updated. So, if the i-th agent has updated, then the trial value will be zero, otherwise, the trial value will be increased by 1. If the trial is equal to a certain threshold, then the individual position will be changed using the following 2 equations:
where ub and lb refer to upper and lower boundaries and rand indicates a random number in the number [0,1].
3.
Enhanced Aquila optimizer
3.1. Shortcoming of Aquila algorithm
AO similar to other swarm optimizers may get stagnation in sub-optimal areas and have a slow convergence, especially when addressing and handling complicated & complex problems that have high dimensional features.
3.2. Architecture of modified AO
Our proposed algorithm which is termed mAO tries to solve the original optimizer limitations. In the proposed mAO, three different strategies are used to improve the classical AO namely: opposition-based Learning, restart strategy, and chaotic local search. OBL strategy is used in both the initialization phase and updating agent position process. OBL is used in initialization by selecting the best N solutions from the pool of X∪ˉx to ensure the algorithm starts with a good set of agents whereas it is embedded in the updating process to improve algorithm exploration abilities. Moreover, a chaotic local search mechanism is used to improve the best solution and existed until now which will lead to the enhancement of the whole individuals. On the other hand, a restart strategy is employed in AO to change the position of the worst individuals if they have already get fallen in local regions. The pseudo-code of the developed optimizer can be seen in algorithm 1.
3.3. Complexity of mAO
The complexity of the proposed algorithm can be computed by calculating the complexity of each phase separately, i.e., initialization, evaluation, and updating process. So O(mAO)=O(Initialization)+O(Evaluation)+O(Updating Position)+O(CLS+OBL+RS). If D is the number of dimensions, N is the number of individuals, and T is the max iteration number, the following can be obtained.
O(Initialization)=O(N)
O(Evaluation)=O(N×T)
O(Updating Position)=O(N×T×D)
O(CLS)=O(N×T)
O(OBL)=O(N×T×D)
O(RS)=O(N×D)
O(CLS+OBL+RS)=O(N×T×D)
O(mAO)=O(N)+O(N×T)+O(N×T×D)+O(N×T×D)=O(N×T×D)
4.
Experiments and discussion
4.1. Parameter setting
To validate our proposed approach, 29 functions from CEC2017 have been used to test mAO performance. These CEC2017 functions are very challenging and contain different types of functions (Unimodal, multimodal, composite, and hybrid). The description of CEC2017 functions is shown in Table 4 where opt. refers to the global optimal value. All experiments have been performed on Matlab 2021b using Intel Corei7 and 8.00 G of RAM. The parameter setting of all experiments is shown in Table 2. mAO is compared with the original Aquila Optimizer and other nine well-known and powerful swarm algorithms namely: crow search algorithm [40], elephant herd optimizer [60], grasshopper optimization algorithm [46], LSHADE [61], Lshade-EpSin [62], moth-flame optimization [63], multi-verse optimization [64], and particle swarm algorithm [24]. The parameter of each mentioned algorithm is given in Table 3.
4.2. CEC2017
The developed optimizer and its competitors' results are shown in Table 5 in terms of best (min), worst (mac), mean (average), and standard deviation. From the above-mentioned table, it can be seen that the suggested technique has good results and performs well in solving all functions type. For example, in term of average, it ranked first in all unimodal functions (F1 and F3), and all multimodal functions (F4 and F10). On the other hand, it can be noticed that mAO achieved better results compared to the original optimizer and others. It ranked first in almost functions whereas it ranked first in solving composite problems in 5 functions out of 10. Besides the statistical measures, convergence curve can be seen as a powerful tool to compare any new algorithm with its competitors to see if it has a good convergence or slow one. mAO has been recognized to achieve a fast convergence curve in all mentioned function types as shown in Figures 1–3.
Furthemore, a statistical comparsion using Wilcoxon test [72,73] has been carried out between the developed algorithm and all other competitors. Table 6 shows the p-values which show a big diffeence in the outputs between different optimizers. From Table 6, results prove the mAO algorithm superiority in finding near-optimal solutions when compared with others. To show the powerful and efficient of the proposed algorithm, a scalability test has been performed on 10 and 50 dimensions using the same functions and the same comparing algorithms. The results of this scalability test are shown in Table 7. It can be seen that mAO is better than other competitors in almost functions.
To show the powerfulness of our suggested optimizer by intergrating three strategies with AO, we test the standard AO with each operator seperately. Table 8 shows the average and standard deviation of four algorithms: AO with OBL (AOOBL), AO with CLS (AOCLS), AO with RS (AORS), and the developed algorithm mAO that contains AO with CLS, RS, and OBL.
5.
Engineering problems
In this section, the performance of the developed optimizer is tested using many real-world constrained problems which contain many inequalities. These problems are Welded beam design problem, Pressure vessel design problem, Tension/compression spring design problem, Speed reducer design problem, and Three-bar truss design problem. The mathematical formulas for the above problems are existed in [68,74,75].
5.1. Welded beam design problem
The first constrained problem used in this study is welded beam design (WBD) which is proposed by Coello [76]. The aim of this problem is to find the minimum welded beam cost and its design structure is shown in Figure 4. WBD has 7 constraints and 4 design variables namely: bar thickness (b), bar height (t), weld thickness (h), and attached bar part length (l). The mathematical representation of WBD can be formulated as follows:
Consider→x=[x1x2x3x4]=[hltb]
Minimize f(→x)=1.10471x21x2+0.04811x3x4(14.0+x2)
Subject to:
g1(→x)=τ(→x)−13600≤0
g2(→x)=σ(→x)−30000≤0
g3(→x)=x1−x4≤0
g4(→x)=0.10471(x21)+0.04811x3x4(14+x2)−5.0≤0
g6(→x)=δ(→x)−0.25≤0
g7(→x)=6000−pc(→x)≤0
where
τ(→x)=√(τ′)+(2τ′τ″)x22R+(τ″)2
τ′=6000√2x1x2
τ″=MRJ
M=6000(14+x22)
R=√x224+(x1+x32)2
j=2{x1x2√2[x2212+(x1+x32)2]}
σ(→x)=504000x4x23
δ(→x)=65856000(30×106)x4x33
pc(→x)=4.013(30×106)√x23x6436196(1−x3√30×1064(12×106)28)
with 0.1≤x1,x4≤2.0and0.1≤x2,x3≤10.0
Results of WBD are shown in Table 9 where mAO is compared with classical AO, GSA [46], GA [77], SSA [78], MPA [79], HHO [80,81], WOA [82], and CSA [40]. From the pre-mentioned table, it's notable that mAO has outperformed other swarm optimizers with an objective value of 1.6565 and decision values (x1,x2,x3,x4) = (0.1625, 3.4705, 9.0234, 0.2057, 1.6565).
5.2. Pressure vessel design problem
The 2nd constrained problem introduced in this study is one of the mixed integer optimization problems which is termed as Pressure Vessel Design (PVD) problem proposed by Kannan and Kramer [83]. PVD aims to select the lowest cost of raw materials for the cylindrical vessel as shown in Figure 5. PVD has 4 parameters namely: head thickness (Th), shell thickness (Ts), cylindrical strength (L), and inner radius (R). To mathematically model PVD, the following formula is designed:
Minimize f(x)=0.6224x1x3x4+1.7781x2x23+3.1661x21x4+19.84x21x3
Subject to:
g1(x)=−x1+0.0193x
g2(x)=−x2+0.00954x3≤0
g3(x)=−πx23x4−(4/3)πx33+1,296,000≤0
g4(x)=x4−240≤0
0≤xi≤100,i=1,2
10≤xi≤200,i=3,4
$ Results of PVD exists in table 10 where the suggested optimizer is compared with original AO, WOA [82], PSO-SCA [84], HS [85], SMA [86], CPSO [87], GWO [47], HHO [80], GOA [46], TEO [88], and SO [30]. From the pre-mentioned table, it can be seen that the developed optimizer ranked first with a value of 5946.3358 and decision values (x1,x2,x3,x4) = (1.0530, 0.181884, 58.619, 38.8080, 5946.3358).
5.3. Tension/compression spring design problem
The 3rd constrained engineering problem discussed here is Tension/Compression Spring Design (TCSD) which was introduced by Arora [89] and its main objective is to decrease the tension spring weight by determining the optimal design variables' values that satisfy its constrained requirements. TCSD has different 3 variables namely: diameter of mean coil (D), the diameter of the wire (d), and active coils number (N). TCSD design is given in Figure 6 and its mathematical formulation is given as follows:
Consider:
→x=[x1x2x3]=[dDN]
Minimize f(→x)=(x3+2)x2x21
subjectto:
g1(→x)=1−x32x371785x41≤0
g2(→x)=4x22−x1x212566(x2x31−x41)+15108x21−1≤0
g3(→x)=1−140.45x1x22x3≤0
g4(→x)=x1+x21.5−1≤0
with 0.05≤x1≤2.0,0.25≤x2≤1.3,and2.0≤x3≤15.0
Table 11 shows the results of TCSD where mAO is compared with RO [90], WOA [82], PSO [87], MVO [64], ES [91], OBSCA [92], GSA [93], and CPSO [87].
From the previously mentioned table, we can conclude that mAO has achieved better results compared to original and other competitors. It achieves a fitness value with 0.011056 and decision values (x1,x2,x3) = (0.0502339, 0.32282, 10.5244).
5.4. Speed reducer design problem
The 4th engineering problem discussed in this section is the speed reducer design [94] (SRD) whose main aim is to minimize speed reducer weight with respect to curvature stress of gear teeth, shafts stress, and shafts transverse deflections. It has seven different variables and its design is shown in Figure 7. The formulation of the SRD can be descriped mathematically as follows:
Minimize:f(→z)=0.7854z1z22(3.3333z23+14.9334z3−43.0934)−1.508z1
(z26+z27)+7.4777(z36+z37)+0.7854(z4z26+z5z27)
Subject to:
g1(→z)=27z1z22z3−1≤0
g2(→z)=397.5z1z22z3−1≤0
g3(→z)=1.93z34z2z3z46−1
g4(→z)=1.93z35z2z3z47−1≤0
g5(→z)=1110z36√(745z4z2z3)2+16.9×106−1≤0
g6(→z)=185z37√(745z5z2z3)2+157.5×106−1≤0
g7(→z)=z2z340−1≤0
g8(→z)=5z2z1−1≤0
g9(→z)=z112z2−1≤0
g10(→z)=1.5z6+1.9z4−1≤0
g11(→z)=1.1z7+1.9z5−1≤0
with
2.6≤z1≤3.6
0.7≤z2≤0.8
17≤z3≤28
7.3≤z4≤8.3
7.8≤z5≤8.3
2.9≤z6≤3.9
and5≤z7≤5.5
mAO is compared with different metaheuristics optimizers including PSO [95], MDA [96], GSA [93], HS [29], SCA [97], SES [98], SBSM [99], and hHHO-SCA [100] as shown in Table 12. From this table, it's obvious that mAO outperformed other algorithms. mAO ranked first with a fitness value of 3002.7328 and decision values (x1,x2,x3,x4,x5,x6,x7) = (3.5012, 0.7, 17, 7.3100, 7.8873, 3.0541, 5.2994).
5.5. Three-bar truss design problem
The last engineering problem addressed in this manuscript is called the Three-bar truss design (TBD) problem. TBD is a fraction and nonlinear civil engineering problem introduced by Nowcki [101]. Its objective is to find the minimum values of truss weight. It has two variables and its mathematical formulation is shown below:
Minimize: f(x)=(2√2x1+x2)∗l
Subject to: g1(x)=√2x1+x2√2x21+2x1x2P−σ≤0
g2(x)=x2√2x21+2x1x2P−σ≤0
g3(x)=1√2x21+2x1x2P−σ≤0
Variable Range
0≤x1,x2≤1
mAO results are compared with CS [102], GOA [46], DEDS [103], MBA [104], PSO-DE [84], AAA [105], PSO-DE [84], DEDS [103] and AO. The results of TBD are listed in table 13 in which mAO results outperformed other competitors. mAO ranked first with a fitness value of 231.8681 and decision values (x1,x2) = (30.7886, 0.3844).
6.
Conclusions and future work
In this study, a novel AO version is suggested called mAO to tackle various optimization issues. mAO is based on 3 different techniques: 1) Opposition-based Learning to improve optimizer exploration phase 2) Restart Strategy to remove the worse agents and replace them with totally random agents. 3) Chaotic Local Search to add more exploitation abilities to the original algorithm. mAO is tested using 29 CEC2017 functions and different five engineering optimization problems. Statistical analysis and experimental numbers show the significance of the suggested optimizer in solving various optimization issues. However, mAO like other swarm-based algorithms has a slow convergence in high-dimensional problems so, it won't be able to solve all optimization problem types.
In future, we can apply mAO to feature selection, job scheduling, combinatorial optimization problems, and stress suitability. Binary and multi-objective versions may be proposed in future.
Acknowledgments
The authors would like to thank the support of Digital Fujian Research Institute for Industrial Energy Big Data, Fujian Province University Key Lab for Industry Big Data Analysis and Application, Fujian Key Lab of Agriculture IOT Application, IOT Application Engineering Research Center of Fujian Province Colleges and Universities, Sanming City 5G Innovation Laboratory, and also the anonymous reviewers and the editor for their careful reviews and constructive suggestions to help us improve the quality of this paper. Educational research projects of young and middle-aged teachers in Fujian Province (JAT200648), Fujian Natural Science Foundation Project (2021J011128).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: