1. Introduction

Transposons, which are elements that can self-replicate and move from one chromosomal location to another, are a major source of genetic variation in both animal and plant genomes [1, 2, 3], and, as such, are significant contributors to evolutionary change [4, 5]. It is now generally recognized that in addition to genetic variation, epigenetic variation also affects evolution [7], especially in a fluctuating environment [8, 9, 10]. There has been much interest in transgenerational epigenetic effects caused by input from the environment (for a review see [7]). However, the treatment presented here does not depend on transgenerational epigenetic effects. Strong evidence is accumulating that epigenetic variation caused by genetic changes, such as the insertion of transposons, can affect expression of nearby genes, and importantly, epigenetic variation and transposons have been linked with human disease [11]. Transposons expression is usually, but not always, silenced and kept harmless by epigenetic mechanisms. We have commented on the interplay between evolution, epigenetic variation and transposon activity before, but not to the extent of mathematical modelling presented here [11, 12, 13, 14, 15].

In this paper we continue our study of the impact of Stochastic Epigenetic Modifications (SEM) during developmental windows of opportunity in the early embryo [12]. Two critical assumptions of the SEM model are that stochastic epigenetic changes take place during a window of opportunity in the developing embryo, and then, after closure of the developmental window, the epigenetic state of the affected locus is propagated faithfully for the life of the organism, at least in some cell lineages, thereby altering function of the adult. This allows selection to be applied to any genetic change affecting the probability of establishment of an altered epigenetic state controlling expression of a gene. Our previous work [12, 13, 14], focused on evolution by gene duplication, with the finding that SEM can both enhance the fixation of duplicates and prevent pseudogenization. In our most recent paper, we also presented some preliminary analysis of the effect of transposons [12] after they were fixed in the population. Here we extend this work to a consideration of the probability of fixation, and average time of fixation, under the assumption that insertion of a transposon will affect, in cis, the probability of epigenetic modification and thus expression level of a nearby gene.

Though the exact nature of the epigenetic modification need not be specified for the SEM model, for simplicity we will henceforth assume that the modification is DNA methylation, since the stable somatic inheritance of 5-methylcytosine patterns in CpG doublets is well established. (However, it should be noted that other, similar, mechanisms would automatically fit into the model, because while our mathematical framework is well-defined, it's quite flexible). There are numerous examples of stochastic DNA methylation changes during developmental windows of opportunity followed by faithful inheritance after the window closes. One example is caused by a partial duplication of the H19/Igf2 imprint control region and results in two phenotypes, large and small mice, with the same genotype [15]. However, the best studied example of this is X chromosome inactivation [16]. In the very early embryo, at about the time of implantation of the blastocyst into the uterine wall, a random choice is made in each cell as to whether the maternal or paternal X chromosome is inactivated. Once this choice is made it is fixed. If the parent cell in the early embryo has the maternal X inactive, all daughter cells derived from this parent cell will not express most genes on the maternal X chromosome. It is well established that the extremely stable somatic heritability of X inactivation is due to DNA methylation specific to the inactive X chromosome [17]. It addition to X-linked genes, several hundred autosomal genes show random mono-allelic expression; this also is determined during early differentiation, and, once established, is highly stable and can contribute to changed function in a proportion of cells [18, 19, 20]. Beyond this, there are several examples of epialleles that affect mouse phenotype, and there is evidence in both mouse and human that maternal nutrition during pregnancy can have life-long effects on the expression of certain genes, with a correlated change in DNA methylation [21]. Though the importance of nutrition in an epigenetic context is important, we emphasize that our modeling assumes that the epigenetic landscape is reset entirely each generation, i.e., there is no transgenerational effects. As reviewed in [22], several murine epialleles (e.g. A^vy, A^xinFu, Cabp^IAP) have been identified in which the activity of a retrotransposon controls expression of an adjacent gene [23]. Variable expressivity results from stochastic epigenetic modification of the 5' long terminal repeat (LTR) of the retrotransposon, producing genetically identical individuals with different phenotypes. The epigenetic state of the retrotransposon varies between individuals but, in a given individual, the epigenetic state is similar between tissues. The difference between epialleles (and adult individuals) is thought to arise from stochastic events in the early embryo, in a window of opportunity before the three primary germ layers are determined. After the window closes the epigenetic state of the retroposon is progagated faithfully in somatic cells. In the case of A^vy it seems clear that DNA methylation at the LTR of a retroposon upstream of the the agouti yellow gene affects expression of agouti. If the LTR is umethylated, the mice are obese with yellow coat color; if the LTR is methylated, the mice are normal weight, with agouti coat color. It should be noted that the location of the transposon can be quite far from the affected gene and can be either upstream or downstream. For example, the A^vy insertion is located 100 Kb upstream of the Agouti gene, with the LTR providing an alternative promoter if unmethylated [24]. In addition to alternate promoters, it is now known that long noncoding RNAs (lncRNAs) are common, often in antisense orientation, and these can affect cis-located genes [25]. For example, the Tsix promoter, which is involved in X chromosome inactivation, drives transcription of a lncRNA that prevents, in cis, expression of Xist, whose promoter is located over 30 kb from the Tsix promoter [26]. There is also evidence that in embryonic stem cells certain sequences in LTRs act as binding sites for zinc finger proteins, which then attract additional proteins that favor formation of repressive heterochromatin, expression silencing and DNA methylation [27]. In such systems, the repressive heterochromatin has been shown to spread and silence genes at least 1 kb from the site of insertion. One major function of DNA methylation in mammals is to help control the activity of transposons, especially in somatic cells, which have a relatively high level of methylation [28]. However, both mouse and human DNA becomes relatively less methylated (hypomethylated) at two developmental stages, early gametogenesis and between fertilization and late blastocyst [28, 29, 30]. Though DNA in primordial germ cells is hypomethylated, it becomes highly methylated again during gamete maturation; both oocyte and sperm DNA are highly methylated. After fertilization, there is a wave of active and passive demethylation, first on the paternal genome and then on the maternal, leading to a low methylation state in the blastocyst just before implantation. After implantation, a wave of de novo methylation occurs, again creating a relatively high level of DNA methylation, with a pattern that then is mostly conserved by maintenance methylation during further cell divisions, lineage specification and maturation to specific cell types. Most transposons are demethylated along with the rest of the genomic DNA in the zygote and early embryo, and increased expression of transposons correlates with their demethylation. At least some demethylated LTRs function as promoters and are active in the early embryo. However the demethylation of transposons in the early embryo is incomplete; for mouse and humans 30-40% methylation remains, increasing to 80% or more after differentiation [28, 29, 30]. While it is not yet certain whether demethylation (and then remethylation) of transposon LTRs takes place stochastically and independently on the maternal or paternal genome, as we assume here, it is known that the phenotype of Agouti yellow mice, which is due to the A^vy transponson, is variable and consistent with stochastically incomplete and variable demethylation and/or remethylation events at the LTR in the early embryo, before specification of the three primary germ layers [24].

2. Modeling

Our intention was to expand the existing models of evolutionary behavior of a transposon sequence (T), and the role it might play in a regulation of a downstream gene (A). We were specifically interested in (i) the probability, and (ii) time of fixation of locus TA initially present in the population at frequency P in a randomly mating diploid population of effective size N_e. 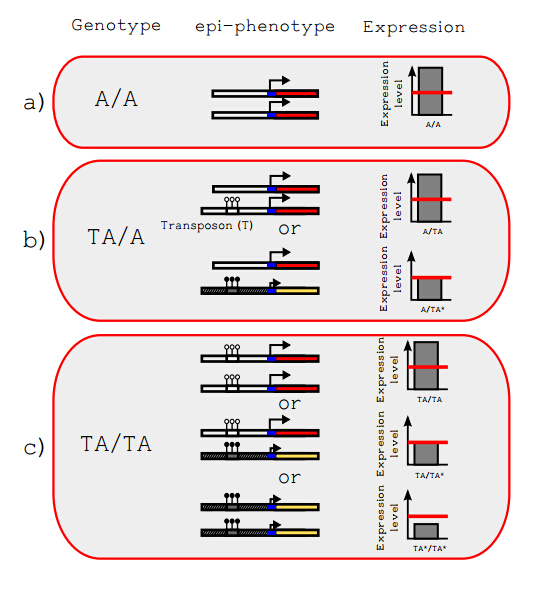The probability of fixation, and the time of fixation, of a locus are two factors that determine whether the locus in question will be maintained in a population. For modeling purposes we assume an initial state where the expression level of the gene A is higher than the "optimal" level (Fig 1). Such a situation could occur for any number of reasons that disrupt the status quo: environmental changes, migration; in general, everything that can alter the fitness landscape of the population (species) in question. We assume that the epigenetic effect of transposon T triggers the establishment of repressive heterochromatin whose influence extends to gene A. We further assume that gene silencing is manifested during development and that the status of the locus TA (silenced or active) is preserved during the life of the organism. At each generation, however, the epigenetic memory is effectively "reset" and the probability of silencing (or not) of the locus depends only on the presence or absence of transposon T and its own probability to be silenced. Thus, the fixation of T leads to a much higher fixation probability of A. The process is still driven by a selection mechanism, but a stochastic event during development is introduced that leads to multiple phenotypes from a single genotype.

Figure 1. Transposon silencing model. a) The original homozygous A/A before transposon insertion. b) The heterozygous TA/A with the transposon inserted upstream the gene A. The sthocastic epigenetic (methylation) modifications of the transposons modulate the expresion of gene A. The central column shows the alternative epi-phenotype resulting from the different possible epigenetic configurations (silencing, or not, of the transposon). c) The homozygous TA/TA and alternative epi-phenotype. This configuration will only be present when the transposon gets fixed in the population. Red horizontal line in Expression Level is the optimal expression level. Closed circles, unmethylated CpG sites; Open circles, methylated CpG sites. The transposon (T) is the rectangle below the circles. The epigenetic state of T is proposed to spread, possibly as repressive heterochromatin, to affect gene A, the function of which is dosage dependent. Blue represents the promoter region of the gene. Red and yellow represent the gene with full or reduced expression level, respectively.

DownLoad: Full-Size ImgPowerPoint

We pursued two avenues of investigation: analytical framework (diffusion equation) and computer simulations. Once again, the goal was to estimate the probability, and average time, of fixation for the locus TA. The relative frequencies of the corresponding epi-phenotypes (and their fitnesses) are shown in Table 1 (genotype/epi-phenotype/fitness map). Assuming the average fitness (W) associated with each genotype TA/TA, TA/A and A/A, we used the standard diffusion equation framework to model the evolution of the system.

Table 1. Transposon model 1 genotype/epi-phenotype/fitness map.

 | Show Table

DownLoad: CSV

2.1 SEM Affects the Probability of Fixation.

The probability of fixation u(P) for the locus TA is

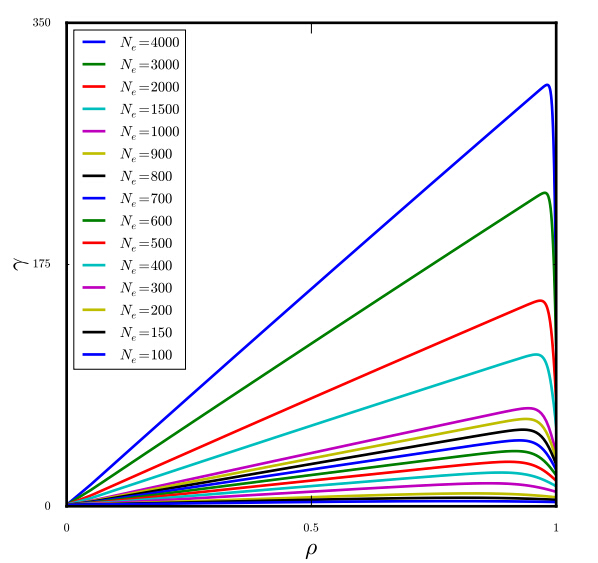
Results of the numerical integration of equation (3) are shown in Figure 2 where γ the scaled probability of fixation (given by γ=2N_eu(P)) of locus TA is plotted vs probability of epigenetic silencing ρ. Calculations were performed with initial frequency of TA given by P = 1/2N_e and s=0.01. From Figure 2 we can observe that γ exhibits behaviour corresponding to a positive selection drive increasing with N_e. Moreover, when ρ equals zero, the system behaves statically, meaning that if the transposon has no chance to be epigenetically silenced (ρ=0), it has consequentially no effect on locus A, and therefore the fixation in such a situation is equivalent to a neutral event (i.e. γ=1. As ρ increases, γ increases as well, reaching a maximum value when ρ is between 0.5 and 1, depending on the population size. Thus γ measures the relative advantage of the TSM model over standard neutral drift. We conclude that SEM with TSM is advantageous for fixation, with the relative advantage increasing with effective population size.

Figure 2. Scaled probability of fixation γ(2N_eu(P)) of TA as a function of ρ, the probability of epigenetic silencing. P=1/2N_e for effective population size N_e and selection coefficient s = 0.01; ρ is probability of epigenetic silencing.

DownLoad: Full-Size ImgPowerPoint

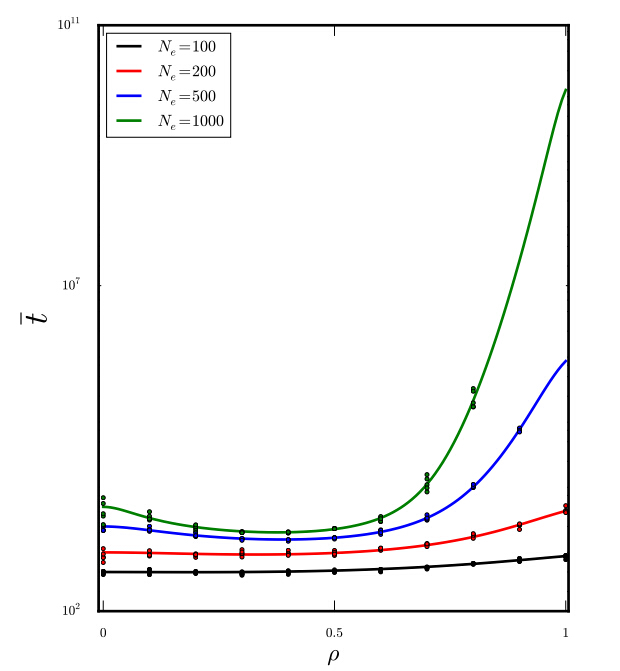
2.2 SEM Affects the Time of Fixation.

In order to better understand the evolutionary dynamics of the system, we have also computed the average time of fixation (t) of the locus with the inserted transposon.

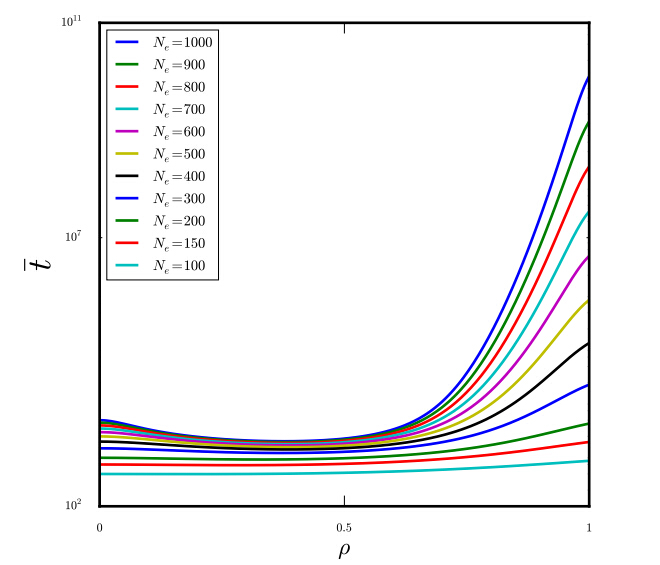
Results of numerical integration of equation (4) are shown in Figure 3. When ρ equals zero, fixation of TA essentially becomes a neutral evolution process. For larger values of N_e the time of fixation t(ρ) appears to attain a minimum and exhibits exponential growth towards the end of the interval. This behavior is interesting and makes perfect biological sense when one considers the relative fitness of TA/TA (W₁₁), A/A (W₁₂]) and A/A (W₂₂) as ρ changes. With ρ = 0 W₁₁=W₁₂=W₂₂ the system is essentially into the neutral evolution mode. With 0 < ρ < 0.5, W₁₁ > W₁₂ > W₂₂ the fixation of TA is positively driven by selection. When ρ = 0.5, W₁₁=W₁₂>W₂₂ and the system behaves as "dominant" in regard to fixation of TA. Finally, for ρ > 0.5 the insertion of TA has an "overdominant" effect, W₁₂ > W₂₂ ≥ W₁₁ i.e. the heterozygotes have a larger selective advantages than both homozygotes, with the special case W₂₂=W₁₁ for ρ=1.

Figure 3. Average time of fixation t of TA as a function of ρ, the probability of epigenetic silencing. P = 1/2N_e for effective population size N_e and selection coefficient s = 0.01.

DownLoad: Full-Size ImgPowerPoint

2.3. Computer Simulation and Comparison with Analytical Approach.

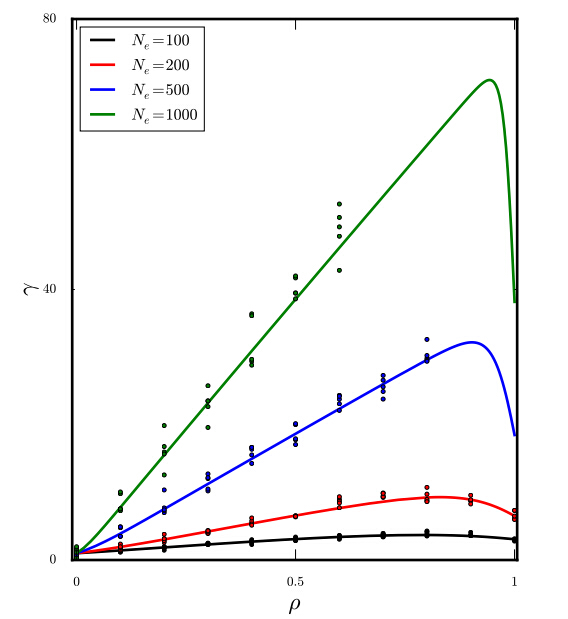
To confirm the results obtained by the diffusion approximation we also performed a Monte Carlo simulation and compared the results with those generated by equations (3) and (4) for γ and t. Simulation entailed the following steps:

1. A population is initialized starting with 2N_e - p gametes A and P gametes TA (with 2N_e p=1).

2. 2N_e gametes are sampled with replacement (i.e., the infinite pool model) following their corresponding fitness and epi-phenotype frequencies. Subsequently, the adult individuals produce gametes following their corresponding allele frequencies.

3. Steps 2 is repeated until fixation of A or TA.

4. To obtain an estimate of γ and t, simulations are repeated 100, 000 times for each set of parameters.

5. Repeat the entire procedure five times.

Results of simulation experiments are shown in Figure 4 and 5, where it can be seen that there is an agreement with equation (3) and (4), respectively.

Figure 4. Scaled probability of fixation γ (2N_eu(P)) of TA P = 1/2N_e for effective population size N_e and selection coefficient s = 0.01; ρ is probability of epigenetic silencing; solid lines are obtained by equation (3); circles reflect the results of simulation experiments.

DownLoad: Full-Size ImgPowerPoint

3. Discussion

We find that stochastic epigenetic modification (SEM) of a newly inserted transposon during a developmental window can greatly increase both the rate and probability of fixation of the new element (and associated expression of a nearby gene), with the advantage provided by SEM increasing with N_e. These conclusions are based on quantitative calculations of γ, the scaled probability of fixation, and t, the time to fixation, for different values of ρ, the probability of transposon silencing. The two approaches in the study are, first, an analytical treatment based on diffusion equations, and, second, a simulation-based analysis.

Figure 5. Average time of fixation t of TA for initial frequency P = 1/2N_e for different effective population size N_e and selection coefficient s = 0.01; ρ is probability of epigenetic silencing, solid lines are obtained by equation (3); circles reflect the results of simulation experiments.

DownLoad: Full-Size ImgPowerPoint

Assumptions. A key question is whether the following biological assumptions are reasonable: (1) stochastically incomplete epigenetic silencing takes place only during a transient, relatively short developmental window, (2) stable somatic inheritance of the resultant epigenetic state, and (3) full resetting of epigenetic marks at each generation. Without question, epigenetic modifications affect function and can be somatically heritable; this is the case for both DNA methylation and for histone/chromatin modifications [31, 32] DNA methylation, which is strongly associated with transcriptional silencing, is considered to be the most stable and heritable of these epigenetic marks. Moreover, a major function of DNA methylation is thought to be the control of transposon activity [1]. However, for mammals there is solid evidence for a wave of DNA demethylation (removal of epigenetic mark) following fertilization and then remethylation (re-addition of the mark) at about the time of implantation of the early embryo into the uterine wall. Waves of demethylation and remethylation also are seen during gametogenesis. In addition, there is evidence for specific changes in DNA methylation at key regulatory elements during later lineage commitment stages [34]. Genome-wide studies of DNA methylation in the early preimplantation embryo suggest that demethylation of transposons is usually incomplete. Transposons are highly methylated in the gametes (~ 80%, declining after fertilization to 30-40% methylation by late blastocyst). Even for specific genes and gene control elements, a general feature of DNA methylation, when analyzed at single nucleotide resolution by bisulfite sequencing, is an apparently stochastic variation between molecules, as molecules with multiple CpG sites very often have somewhat different methylation patterns. This suggests that there is variation between cells. For X-linked genes subject to X chromosome inactivation, it is very clear that the variation in DNA methylation seen at promoters in adult somatic cells is in large part derived from a stochastic epigenetic event(s) in the preimplantation embryo, which is fixed at the time of implantation and then faithfully propagated in somatic cells [16]. At about the time of implantation there is choice made in each cell as to which X chromosome is to become inactive. The choice usually is random; in each cell both the maternal and paternal X chromosome have a 50 percent chance of inactivation, and studies of the percent of cells expressing either the maternal or paternal X have established that the inactivation is indeed stochastic. Thus this phenomenon is an excellent example of a stochastic event in the early embryo that becomes fixed (and thereafter mitotically stable) in the late blastocyst. DNA methylation at promoters correlates with the inactive state and is the epigenetic mark responsible for the stable inheritance of X inactivation. Also of interest is that the entire inactive X chromosome becomes condensed and cytologically recognizable as heterochromatin. As mentioned in the Introduction, several alleles in the mouse are known to cause two phenotypes from one homozygous genotype [15, 16, 22]. Most relevant for this paper is the fact that a transposon inserted 100 Kb upstream of the Agouti gene can cause two different adult phenotypes, depending on whether or not the transposon insertion is methylated.

With regard to the third assumption, it is now well recognized that in both plants and animals epigenetic changes, such as those caused by repetitive elements, are often difficult to distinguish from "true" genetic changes except by their response to inhibitors of DNA methylation [35]. Two examples highly relevant for this paper are random monallelic expression of autosomal genes [16], and metastable epi-alleles that are sensitive to maternal nutrition or stress [22]. Much recent interest has focused on the fact that maternal nutrition can cause epigenetic changes in the offspring, and these may persist for more than one generation. This brings to the fore the possibility of Lamarckian genetics. We do not argue against this, but our analysis does not depend on any such transgenerational effects, since we assume full resetting of epigenetic marks at each generation. The advantages of epigenetic variability in a fluctuating environment have been modeled [8], but this analysis focuses only on genes that affect the overall, genome-wide probability of epigenetic modification. We focus on cis-action, although gene-specific trans-activity is not excluded. Chess et al. have recognized that random mono-allelic expression of autosomal genes has implications for evolution [16, 19], but we are not aware of any work other than ours that has suggested a mathematical treatment for encompassing cis-acting elements.

Generalizability. Transposons carry promoters and transcription termination signals that can affect expression of cis-located genes, and they also tend to be rendered inactive by epigenetic modifications [1]. Enhancers act at a distance, are often epigenetically modified, and the modification is changed during development [36]. As a general principle, it should be possible to adapt / expand the TSM/SEM model to any genetic change(s) (or combination thereof) that acts at a distance and is stochastically and incompletely modified during a developmental window. A mutation that affects the spread of heterochromatin could, for example, cause position-effect variegation, similar to that seen in Drosophila [37]. Figure 1 could be interpreted as the variable spread of heterochromatin from any new element, duplication or mutation, and it could be modeled by the equations derived. In fact, any genetic alteration that affects the probability of changed expression at another genetic element (protein coding genes, lncRNA, miRNA, etc.) that could be selected for or against during evolution, would fit into our modeling framework. Transposons are just one (although very likely) way to change the probability of expression; other factors (enhancers, promoters, unidentified SNPs) can lead to the same result. The model is robust with regard to the specific mechanism. For example, if the new element or mutation affects expression only when unmethylated, rather than methylated, the mathematical approach and biological results would remain the same. As an independent biological validation of our model, it is worth noting that an element has been found, the X controlling element (Xce), which has alleles that change the probability of X chromosome inactivation from 50:50 to, for example, 70:30 [38]. Whether DNA methylation is involved in the function of this element is not known, but is clear that a genetic element can change the probability of an epigenetic event controlling expression only of cis-located genes; in this case X-linked genes.

Overdominance and population polymorphisms. It should be noted that the behavioral pattern of an inserted element can vary from neutral to dominant to overdominant as ρ varies from 0 to near 1.0. Under the "overdominant" model, heterozygotes have a selective advantage: while the probability of fixation is increasing, the "time" of fixation becomes exceedingly remote. The element might become common in the population, but will never become homozygous in a stable environment under constant selection pressure. This means that heterozygotes do indeed have a selective advantage: under the given constraints (e.g., see Figures 2 and 3) while the probability of fixation is increasing, the time of fixation becomes unrealistic: the element might become common in the population, but will never become homozygous in a constant environment, under constant selection pressure.

In all cases considered here expression of locus A starts as bi-allelic and evolves (under selection drive) to the final (random) mono-allelic stage.

Analysis of a two-step process, where first a polymorphism accumulates and then selection changes, will be the subject of future work, which has implications for macro-evolution including evolution of mono-allelic expression, nervous system function, and the immune system, both innate and adaptive.

It should be mentioned that interaction between epigenetic regulation, transposons and (micro-) evolution has long been recognized as an important topic in A. thaliana} and other agricultural plant research [3, 39, 40, 41]. However, only recently have attempts been made to extend the concept to other species [42, 43]. We feel very strongly that a robust mathematical framework is needed to support the conjectures regarding the above interplay, and we present some of it in this paper. To our knowledge, this is the first attempt to do so. Our analyses are "generic" with respect to the species, so by adjusting standard population genetics parameters (effective population size, fitness, etc.) they can be generalized to various organisms. This study in general, and our methodology in particular, were intentionally designed to work on a larger (macro-) evolutionary scale.

Hence, the connection to the neo-functionalization and sub-functionalization by gene duplication. A number of plausible scenarios have been proposed (see [44] and [45] for some recent perspective), but the general consensus is that there are many mechanisms that can potentially aid emergence and fixation of new genes and functions (escaping pseudogenization). We do not intend to claim that the mechanism modelled in this report is the only mechanism; however, our belief is that it is a strong, perhaps at times decisive, factor, and this belief is supported by both analytical and simulation experiments results. Our main conclusion is this: under realistic evolutionary / population genetics conditions and parameters, transposon insertion can create a stable polymorphism in the population, and, that the behavior of the retrotransposon strongly depends on the epigenetic regulation.

Caveats. Three caveats should be considered, which also brings us to the following prospective future research directions: One, the system under consideration is fundamentally a multifactorial system that, at this time, we are treating in a unifactorial way. As a follow-up to this research, we plan to use Dynamic Bayesian (Belief) Networks [46] to expand on our modeling, including visualization of the dynamics of the evolutionary processes. We also intend to explore other alternatives, such as entropic analysis, which we believe is a promising direction, and although there is only one study to that effect [47], we feel that combining the multifactorial entropic (non-parametric) analysis of large-scale data with epigenetic modeling is arguably the most promising venue. In a more general sense, a quantitative data analysis framework that includes "standard" phylogenetics (or perhaps coalescent, depending on the evolutionary scale) and epigenetic data is desperately needed. While there are some notable recent advances [48, 49], they are few and far between. There has been substantial progress in incorporating different data types and levels of biological abstraction in computational evolution data analysis machinery, ranging from next generation sequencing to metabolomics --- sadly, epigenetics is not quite "there" yet.

The second caveat has to do with our inadequate ability to deal with extremely large effective population size when it comes to the simulation. There are computational limits to that, even with the latest-generation workstations and clusters. We intend to address this in the future by parallelizing some of our computations, improving tractability of the problem.

The third caveat is that one cannot be certain to what extent the epigenetic process is fully a Markov one. However, the model presented here is probably the best (compact) fit, considering the biological knowledge we have right now and, as the field progresses, we intend to expand the model accordingly. We should emphasize that our model is in essence "non-Lamarckian" because at each generation the memory of epigenetic marks is reset. At this time, our intent is that the proposed model does not imply (or need) any epigenetic-based transgenerational effects, although it could certainly be expanded to accommodate such if the need arises.

Predictions and Experimental Testing. Our earlier paper on SEM emphasized duplications [12], with the assumption that they were epigenetically marked during gametogenesis and then subject to stochastic events during a developmental window. There is recent experimental evidence that duplicates are indeed epigenetically marked. Keller and Yi [10] have demonstrated that evolutionary young duplicate genes are initially heavily methylated and then gradually lose DNA methylation with evolutionary age. Chang and Liao [50] found that duplicate genes tend to be heavily methylated and concluded that DNA methylation plays a dominant role in dosage rebalance after gene duplication. With respect to developmental windows for stochastic changes, it is becoming increasingly apparent that, in addition to random X chromosome inactivation, random mono-allelic gene expression (RMAE) can be detected in 5-10% of autosomal genes [16, 19]. RMAE studies of cloned cells have clearly shown variability consistent with stochastic events during developmental windows, and the number of genes showing RMAE has been found to increase upon stem cell differentiation [18], [20]. Of great interest is a recent report by Toyoda et al. [51] showing stochastic selection in neurons of individual promoters of the clustered protocadherin family, with the probability of expression being controlled by DNA methylation in the early embryo. As a result of recent advances, it is now possible, though technically challenging, to directly measure DNA methylation changes in single cells [52, 53, 54]. In fact, on the basis of their single-cell studies, Lorthongpanich et al. [52] have concluded that there is epigenetic chimerism in preimplantation embryos. Thus single-cell analysis of both expression and DNA methylation may enable direct testing of the prediction that duplicates, transposons, and probably other DNA elements will show stochastic variability between individual cells in the preimplantation embryo and in some cell lineages. Another promising approach, only now becoming practical, is the use of CRISPR and TALEN technology [55] to make locus-specific transposon insertions, mutations and duplications in ES cells and then assay for methylation and expression at the single cell level during in vitro and in vivo differentiation. Thus, the key assumptions, and the conclusions of modeling addressed in this paper are experimentally testable, and it is our intention to continue pursuing this research direction.

4. Conclusion

We conclude that stochastic modifications of a newly inserted transposon element during a developmental window could significantly affect both the rate and the probability of fixation of the transposon and nearby gene alleles. We used two approaches in the study. First, an analytical treatment based on diffusion equations, and, second, a simulation-based analysis. Importantly, both approaches are in agreement, which bodes well for future research in this area. In summary, we present a laconic but flexible quantitative framework that, while generalizable, was first and foremost developed to assess whether the combination of epigenetic effects and transposons could be one of the principal factors in both macro- and micro- evolution. We show the evidence to that effect. We also advocate development of the evolutionary data analysis algorithms and methods that incorporates epigenetic data, as it is long overdue.

Acknowledgments

S.B. is a Susumu Ohno Distinguished Fellow and A.S.R. holds the Susumu Ohno Chair in Theoretical Biology at Beckman Research Institute of the City of Hope. We would like to acknowledge the late Sergei N. Rodin who was instrumental in starting this work.