1. Introduction

Sparse representation and compressed sensing has achieved tre-mendous success in practice. They naturally fit for order-one data, such as voices and feature vectors. However, in applications we are often faced with various types of data, such as images, videos, and genetic microarrays. They are inherently matrices or even tensors. Then we are naturally faced with a question: how to measure the sparsity of matrices and tensors?

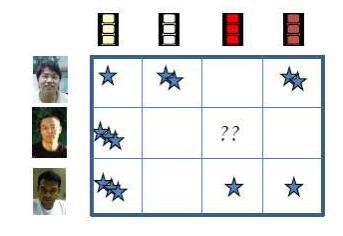
Low-rank models are recent new tools that can robustly and efficiently handle high-dimensional data. Although rank has been used in statistics as a regularizer of matrices, e.g., reduced rank regression (RRR) [61], and in three-dimensional stereo vision [50], rank constraints are ubiquitous, the surge of low-rank models in recent years was inspired by sparse representation and compressed sensing. There has been systematic development on new theories and applications. In this background, rank is interpreted as the measure of the second order (i.e., matrix) sparsity¹, rather than merely a mathematical concept. To illustrate this, we take image and video compression as an example. To achieve effective compression, we have to fully utilize the spatial and temporal correlation in images or videos. Take the Netflix challenge² (Figure 1) as another example, to infer the unknown user ratings on videos, one has to consider both the correlation between users and the correlation between videos. Since the correlation among columns and rows is closely connected to matrix rank, it is natural to use rank as a measure of the second order sparsity.

¹ The first order sparsity is the sparsity of vectors, whose measure is the number of nonzeros, i.e., the $\ell_0$ norm $\|\cdot\|_0$.

² Netflix is a video-renting company, which owns a lot of users' ratings on videos. The user/video rating matrix is very sparse. The Netflix company offered one million US dollars to encourage improving the prediction on the user ratings on videos by 10%. See https://en.wikipedia.org/wiki/Netflix_Prize

In the following, I review the recent development on low-rank models³. I first introduce linear models in Section 2, then nonlinear ones in Section 3, where the former are classified as single subspace models and multi-subspace ones. Theoretical analysis on some linear models, including exact recovery, closed-form solutions, and block-diagonality structure, is also provided in Section 2. Then I introduce commonly used optimization algorithms for solving low-rank models in Section 4, which can be classified as convex, non-convex, and randomized ones. Next, I review representative applications in Section 5. Finally, I conclude the paper in Section 6.

³ There has been an excellent review on low-rank models in image analysis by Zhou et al. [82]. However, my review differs significantly from [82]. My review introduces much more low-rank models, e.g., tensor completion and recovery, multi-subspace models, and nonlinear models, while [82] mainly focuses on matrix completion and Robust PCA. My review also provides theoretical analysis and randomized algorithms.

---

2. Linear models

The recent boom of low-rank models started from the matrix completion (MC) problem [6] proposed by E. Candès in 2009. We introduce linear models first. Although they look simple, theoretical analysis show that linear models are very robust to strong noises and missing values. In real applications, they also have sufficient data representation power.

---

2.1. Single subspace models

Single subspace models are to extract one overall subspace from data. The most famous one may be the MC problem, proposed by E. Candès. It is as follows. Given the values of a matrix $\mathbf{D}$ at some locations, whether we can recover the whole matrix? This is a very general mathematical model for various problems, such as the above-mentioned Netflix challenge and the measurement of genetic microarrays. Obviously, the answer to this question is non-unique. Observing that we should consider the correlation among matrix columns and rows, E. Candès suggested to choose the solution $\mathbf{A}$ with the lowest rank:

$\min\limits_{\mathbf{A}} {\rm{rank}}(\mathbf{A}), \;\;\;\;s.t.\;\;\;\; \pi_{\Omega}(\mathbf{A}) = \pi_{\Omega}(\mathbf{D}),$

(1)

where $\Omega$ is the set of indices where the entries are known, $\pi_{\Omega}$ is the projection operator that keeps the values of entries in $\Omega$ while filling the remaining entries with zeros. The MC problem is to recover the low-rank structure in the case of missing values. Shortly, E. Candès further considered MC with noise [5]:

$\min\limits_{\mathbf{A}} {\rm{rank}}(\mathbf{A}), \;\;\;\;s.t.\;\;\;\; \|\pi_{\Omega}(\mathbf{A})-\pi_{\Omega}(\mathbf{D})\|_F^2\leq\varepsilon,$

(2)

in order to handle the case when the observed data are noisy, where $\|\cdot\|_F$ is the Frobenius norm.

When considering the low-rank recovery problem in the case of strong noises, it seems that this problem is well solvable by the traditional Principal Component Analysis (PCA). However, the traditional PCA is effective in accurately recovering the underlying low-rank structure only when the noises are Gaussian. If the noises are non-Gaussian and strong, even a few outliers can make PCA fail. Due to the great importance of PCA in applications, many scholars spent a lot effort on robustifying PCA, proposing many so-called "robust PCAs." However, none of them has a theoretical guarantee that under certain conditions the underlying low-rank structure can be exactly recovered. In 2009, Chandrasekaran et al.[7] and Wright et al. [68] proposed Robust PCA (RPCA) simultaneously. The problem they considered is how to recover the low-rank structure when the data have sparse and large outliers:

$\min\limits_{\mathbf{A}, \mathbf{E}} {\rm{rank}}(\mathbf{A})+\lambda\|\mathbf{E}\|_0, \;\;\;\;s.t.\;\;\;\; \mathbf{A}+\mathbf{E} = \mathbf{D},$

(3)

where $\|\mathbf{E}\|_0$ stands for the number of nonzeros in $\mathbf{E}$. Shortly, E. Candè joined J. Wright et al.'s work and obtained stronger results. Namely, the matrix can have missing values. The generalized model is [4]:

$\min\limits_{\mathbf{A}, \mathbf{E}} {\rm{rank}}(\mathbf{A})+\lambda\|\mathbf{E}\|_0, \;\;\;\;s.t.\;\;\;\; \pi_{\Omega}(\mathbf{A}+\mathbf{E}) = \pi_{\Omega}(\mathbf{D}).$

(4)

In their paper, they also discussed a generalized RPCA model which involves dense Gaussian noises [4]:

$\min\limits_{\mathbf{A}, \mathbf{E}} {\rm{rank}}(\mathbf{A})+\lambda\|\mathbf{E}\|_0, \;\;\;\;s.t.\;\;\;\; \|\pi_{\Omega}(\mathbf{A}+\mathbf{E})-\pi_{\Omega}(\mathbf{D})\|_F^2\leq\varepsilon.$

(5)

Chen et al. [9] considered the case that noises cluster in sparse columns and proposed the Outlier Pursuit model, which replaces $\|\mathbf{E}\|_0$ in the RPCA model with $\|\mathbf{E}\|_{2, 0}$, i.e., counting how many $\ell_2$ norms of columns of $\mathbf{E}$ are zeros.

When the data are tensor-like, Liu et al. [42] generalized matrix completion to tensor completion. Although tensors have a mathematical definition of rank, which is based on the CP decomposition [31], it is not computable. So Liu et al. proposed a new rank for tensors, which is defined as the sum of the ranks of matrices unfolded from the tensor in different modes. Their tensor completion model is thus: given the values of a tensor at some entries, recover the missing values by minimizing this new tensor rank. Also using the same new tensor rank, Tan et al. [60] generalized RPCA to tensor recovery. Namely, given a tensor, decompose it as a sum of two tensors, one having a low new tensor rank, the other being sparse.

There are also matrix factorization based models, such as nonnegative matrix factorization [34]. Such models could be casted as low-rank models. However, they are better viewed as optimization techniques, as mentioned at the end of Section 4.2. So I will not elaborate them here. Interested readers may refer to several excellent reviews on matrix factorization based methods, e.g., [11,59,65].

To sum up, single-subspace models could be viewed as extensions of the traditional PCA, which is mainly for denoising data and finding common components.

---

2.2. Multi-subspace models

MC and RPCA can only extract one subspace from data. They cannot describe finer details of data within this subspace. The simplest case of finer structure is the multi-subspace model, i.e., data distribute around some subspaces. We need to find these subspaces. This problem is called the Generalized PCA (GPCA) problem [62] or subspace clustering [63], which has a lot of solution methods, such as the algebraic method and RANSAC [63], but none of them have a theoretical guarantee. The emergence of sparse representation offers a new way to this problem. In 2009, E. Elhamifar and R. Vidal proposed the key idea of self-representation, i.e., using other samples to represent every sample. Based on self-representation, they proposed the Sparse Subspace Clustering (SSC) model [14,15] such that the representation matrix is sparse:

$\min\limits_{\mathbf{Z}, \mathbf{E}} {\rm{rank}}(\mathbf{Z})+\lambda\|\mathbf{E}\|_{0}, \;\;\;\; s.t. \;\;\;\;\mathbf{D} = \mathbf{D}\mathbf{Z}+\mathbf{E}, {\rm{diag}}(\mathbf{Z}) = 0,$

(6)

where the constraint ${\rm{diag}}(\mathbf{Z}) = 0$ is to prevent using the sample itself to represent a sample. Inspired by their work, Liu et al. proposed the Low-Rank Representation (LRR) model [38,39]:

$\min\limits_{\mathbf{Z}, \mathbf{E}} {\rm{rank}}(\mathbf{Z})+\lambda\|\mathbf{E}\|_{2, 0}, \;\;\;\; s.t.\;\;\;\; \mathbf{D} = \mathbf{D}\mathbf{Z}+\mathbf{E}.$

(7)

The reason of enforcing the low-rankness of $\mathbf{Z}$ is to enhance the correlation among the columns of $\mathbf{Z}$ so as to boost the robustness against noise. The optimal representation matrix $\mathbf{Z}^*$ of SSC and LRR could be used as a measure of similarity between samples. Utilizing $(|\mathbf{Z}^*|+|\mathbf{Z}^{*, T}|)/2$⁴ to define the similarity between samples ($|\mathbf{Z}^*|$ is the matrix whose entries are the absolute values of those of $\mathbf{Z}^*$), one can cluster the data into several subspaces via spectral clustering. Zhuang et al. further required $\mathbf{Z}^*$ to be nonnegative and sparse, and applied $\mathbf{Z}^*$ to semi-supervised learning [84].

⁴ In their later work [38], Liu et al. changed to use $|\mathbf{U}_{Z^*}\mathbf{U}_{Z^*}^T|$ as the similarity matrix, where the columns of $\mathbf{U}_{Z^*}$ are the left singular vectors of the skinny SVD of $\mathbf{Z}^*$. For the reason, please refer to Section 2.3.2.

LRR requires that the samples are sufficient. In the case of insufficient samples, Liu and Yan [41] proposed the Latent LRR model:

$\min\limits_{\mathbf{Z}, \mathbf{L}, \mathbf{E}} {\rm{rank}}(\mathbf{Z})+{\rm{rank}}(\mathbf{L})+\lambda\|\mathbf{E}\|_{0}, \;\;\;\; s.t.\;\;\;\; \mathbf{D} = \mathbf{D}\mathbf{Z}+\mathbf{L}\mathbf{D}+\mathbf{E}.$

(8)

They call $\mathbf{D}\mathbf{Z}$ as the Principal Feature and $\mathbf{L}\mathbf{D}$ the Salient Feature. $\mathbf{Z}$ is used for subspace clustering and $\mathbf{L}$ is used for extracting discriminant features for recognition. As an alternative way, Liu et al. [44] proposed the Fixed Rank Representation (FRR) model:

$\min\limits_{\mathbf{Z}, \tilde{\mathbf{Z}}, \mathbf{E}} \|\mathbf{Z}-\tilde{\mathbf{Z}}\|_F^2+\lambda\|\mathbf{E}\|_{2, 0},\;\;\;\; s.t.\;\;\;\; \mathbf{D} = \mathbf{D}\mathbf{Z}+\mathbf{E}, {\rm{rank}}(\tilde{\mathbf{Z}})\leq r,$

(9)

where $\tilde{\mathbf{Z}}$ is used for measuring the similarity between samples.

To further improve the accuracy of subspace clustering, Lu et al. [45] proposed using Trace Lasso to regularize the representation vector:

$\min\limits_{\mathbf{Z}, \mathbf{E}} \|\mathbf{D}{\rm{diag}}(\mathbf{Z}_i)\|_*+\lambda\|\mathbf{E}_i\|_{0}, \;\;\;\; s.t. \;\;\;\;\mathbf{D}_i = \mathbf{D}\mathbf{Z}_i+\mathbf{E}_i, i = 1, \cdots, n,$

(10)

where $\mathbf{Z}_i$ is the $i$th column of $\mathbf{Z}$, $\|\mathbf{D}{\rm{diag}}(\mathbf{Z}_i)\|_*$ is called the Trace Lasso of $\mathbf{Z}_i$, and $\|\cdot\|_*$ is the nuclear norm of a matrix (sum of singular values). When the columns of $\mathbf{D}$ are normalized in the $\ell_2$-norm, Trace Lasso has an appealing interpolation property:

$\|\mathbf{Z}_i\|_2\leq \|\mathbf{D}{\rm{diag}}(\mathbf{Z}_i)\|_* \leq \|\mathbf{Z}_i\|_1.$

Moreover, the left hand side is achieved when the data are completely correlated (the columns being the same vector or the negative of the vector), while the right hand side is achieved when the data are completely uncorrelated (the columns being orthogonal). Therefore, Trace Lasso has the characteristic of being adaptive to the correlation among samples. This model is called Correlation Adaptive Subspace Segmentation (CASS).

For better clustering of tensor data, Fu et al. proposed the Tensor LRR model [19], so as to fully utilize the information of tensor in different modes.

In summary, multi-subspace models can model the data structure much better than the single-subspace ones. Their main purpose is to cluster data, drastically in contrast to that of single-subspace ones, i.e., to denoise data.

---

2.3. Theoretical analysis

The theoretical analysis on low-rank models is relatively rich. It consists of the following three parts.

---

2.3.1. Exact recovery

The above-mentioned low-rank models are all discrete optimization problems, most of which are NP-hard, which incurs great difficulty in efficient solution. To overcome this difficulty, a common way is to approximate discrete low-rank models as convex programs. Roughly speaking, the convex function (over the unit ball of $\ell_\infty$ norm) "closest" to the $\ell_0$ pseudo-norm $\|\cdot\|_0$ is the $\ell_1$ norm $\|\cdot\|_1$, i.e., the sum of absolute values of entries, and the convex function (over the unit ball of matrix spectral norm) "closest" to rank is the nuclear norm $\|\cdot\|_*$. Thus, all the above discrete problems can be converted into convex programs, which can be solved much more efficiently. However, this naturally brings a question: can solving a convex program result in the ground truth solution? For most low-rank models targeting on a single subspace, such as MC [6], RPCA [4], RPCA with missing values [4], and Outlier Pursuit [9,74], the answer is affirmative. Briefly speaking, if the outlier is sparse and uniformly random and the ground truth matrix is of low rank, then the ground truth matrix can be exactly recovered. What is surprising is that the exact recoverability is independent on the magnitude of outliers. Instead, it depends on the sparsity of outliers. Such results ensure that the low-rank models for single subspace recovery are very robust. This characteristic is unique when compared with the traditional PCA. Unfortunately, for multi-subspace low-rank models, only LRR has relatively thorough analysis [40]. However, Liu et al. only proved that when the proportion of outliers does not exceed a threshold, the row space of $\mathbf{Z}_0$ and which samples are outliers can be exactly known, where $\mathbf{Z}_0$ is given by $\mathbf{U}_{Z^*}\mathbf{U}_{Z^*}^T$, in which $\mathbf{U}_{Z^*}\mathbf{\Sigma }_{Z^*}\mathbf{V}_{Z^*}^T$ is the skinny SVD of $\mathbf{Z}^*$. The analysis did not answer whether $\mathbf{Z}_0$ and $\mathbf{E}_0$ themselves can be exactly recovered. Fortunately, when applying LRR to subspace clustering, we only need the row space of $\mathbf{Z}_0$.

When data are noisy, it is inappropriate to use the noisy data to represent the data themselves. A more reasonable way is to denoise the data first and then apply self-representation on the denoised data, resulting in modified LRR and Latent LRR models:

$\min\limits_{\mathbf{Z}, \mathbf{A}, \mathbf{E}} \|\mathbf{Z}\|_*+\lambda\|\mathbf{E}\|_{2, 1}, \;\;\;\; s.t. \;\;\;\;\mathbf{D} = \mathbf{A}+\mathbf{E}, \mathbf{A} = \mathbf{A}\mathbf{Z},$

(11)

and

$\min\limits_{\mathbf{Z}, \mathbf{L}, \mathbf{A}, \mathbf{E}} \|\mathbf{Z}\|_*+\|\mathbf{L}\|_*+\lambda\|\mathbf{E}\|_{1}, \;\;\;\;s.t.\;\;\;\; \mathbf{D} = \mathbf{A}+\mathbf{E}, \mathbf{A} = \mathbf{A}\mathbf{Z}+\mathbf{L}\mathbf{A}.$

(12)

By utilizing the closed-form solutions discovered in the following subsection, Zhang et al. [76] proved that the solutions of modified LRR and Latent LRR can be expressed as that of corresponding RPCA models:

$\min\limits_{\mathbf{A}, \mathbf{E}} {\rm{rank}}(\mathbf{A})+\lambda\|\mathbf{E}\|_{2, 1}, \;\;\;\; s.t. \;\;\;\;\mathbf{D} = \mathbf{A}+\mathbf{E},$

(13)

and

$\min\limits_{\mathbf{A}, \mathbf{E}} {\rm{rank}}(\mathbf{A})+\lambda\|\mathbf{E}\|_{1}, \;\;\;\; s.t.\;\;\;\; \mathbf{D} = \mathbf{A}+\mathbf{E},$

(14)

respectively. So the exact recovery results of RPCA [4] and Outlier pursuit [9,74] can be applied to the modified LRR and Latent LRR models, where again only the column space of $\mathbf{D}$ and which samples are outliers can be recovered.

---

2.3.2. Closed-form solutions

An interesting property of low-rank models is that they may have closed-form solutions when the data are noiseless. In comparison, sparse models do not have such a property. Wei and Lin [66] analyzed the mathematical properties of LRR. They first found that the noiseless LRR model:

$\min\limits_{\mathbf{Z}} \|\mathbf{Z}\|_*, \;\;\;\; s.t.\;\;\;\; \mathbf{D} = \mathbf{D}\mathbf{Z},$

(15)

has a unique closed-form solution. Let the skinny SVD of $\mathbf{D}$ be $\mathbf{U}_D\mathbf{\Sigma }_D\mathbf{V}_D^T$, then the solution is $\mathbf{V}_D\mathbf{V}_D^T$, which is called the Shape Interaction Matrix in structure from motion. Liu et al. [38] further found that the LRR with a general dictionary:

$\min\limits_{\mathbf{Z}} \|\mathbf{Z}\|_*, \;\;\;\; s.t.\;\;\;\; \mathbf{D} = \mathbf{B}\mathbf{Z},$

(16)

also has a unique closed-form solution: $\mathbf{Z}^* = \mathbf{B}^{+}\mathbf{D}$, where $\mathbf{B}^+$ is the Moore-Penrose pseudo-inverse of $\mathbf{B}$. This result is generalized by Yu and Schuurmans [72] to general unitary invariant norms, in which they found mode low-rank models with closed-form solution. Favaro et al. also found some low-rank models which are related to subspace clustering and have closed-form solutions [16]. Zhang et al. [73] further found that the solution to noiseless Latent LRR (both discrete and convex approximation) is non-unique and gave the complete closed-form solutions. In the paper, they also found that discrete noise-less LRR (the $\mathbf{E}$ in (7) being 0) is actually not NP-hard and further gave the complete closed-form solutions. To remedy this issue of Latent LRR, based on their analysis, Zhang et al. [75] further proposed to find the sparsest solution among the solution set of Latent LRR.

---

2.3.3. Block-diagonal structure

Multi-subspace clustering models all result in a representation matrix $\mathbf{Z}$. For SSC and LRR, it can be proven that under the ideal conditions, i.e., the data are noiseless and the subspaces are independent (i.e., none of the subspaces can be represented by other subspaces), the optimal representation matrix $\mathbf{Z}^*$ is block-diagonal. As each block corresponds to one subspace, the block-structure of $\mathbf{Z}^*$ is critical to subspace clustering. Surprisingly, Lu et al. [47] proved that if $\mathbf{Z}$ is regularized by the squared Frobenius norm (the corresponding model is called Least Squared Representation (LSR)), then under ideal conditions the optimal representation matrix $\mathbf{Z}^*$ is also block-diagonal. Lu et al. further proposed the Enforced Block-Diagonal (EBD) Conditions. As long as the regularizer for $\mathbf{Z}$ satisfies the EBD conditions, the optimal representation matrix under the ideal conditions is block-diagonal [47]. The EBD conditions greatly extended the range of possible choices of $\mathbf{Z}$, which is no longer limited to sparsity or low-rankness constraints. For subspace clustering models whose representation matrix $\mathbf{Z}$ is solved column-wise, e.g., Trace-Lasso-based CASS (10), Lu et al. also proposed the Enforced Block-Sparse (EBS) Conditions. As long as the regularizer on the columns of $\mathbf{Z}$ satisfies the EBS conditions, the optimal representation matrix under the ideal conditions is also block-diagonal [45]. However, all the above results are obtained under the ideal conditions. If the ideal conditions do not hold, i.e., when the data are noisy or when the subspaces are not independent, the optimal $\mathbf{Z}$ will not be exactly block-diagonal, which may cause difficulty in the subsequent subspace pursuit. To address this issue, based on the basic result in the spectral graph theory that the algebraic multiplicity of the eigenvalue zero of the Laplacian matrix equals the number of diagonal blocks in the weight matrix, Feng et al. [17] proposed the block-diagonal prior. Adding the block-diagonal prior to the subspace clustering models, an exactly block-diagonal representation matrix $\mathbf{Z}$ can be ensured even under non-ideal conditions, thus significantly improved the robustness against noise.

The grouping effect among the representation coefficients, i.e., when the samples are similar their representation coefficient vectors should also be similar, is also helpful for maintaining the block-diagonal structure of the representation matrix $\mathbf{Z}$ when the data are noisy. SSC, LRR, LSR, and CASS are all proven to have the grouping effect. Hu et al. proposed general Enforced Grouping Effect (EGE) Conditions [24], with which one can easily verify whether a regularizer has the grouping effect.

To conclude, linear models are relatively simple yet powerful enough to model complex data distributions. They can also have good mathematical properties and theoretical guarantees.

---

3. Nonlinear models

Linear models assume that the data distribute near some low-dimensional subspaces. Such assumption can be easily violated in real applications. So developing nonlinear models is necessary. However, low-rank models for clustering nonlinear manifolds are relatively few. A natural idea is to utilize the kernel trick, proposed by Wang et al. [64]. The idea is as follows. Suppose that via a nonlinear mapping $\phi$, the set $\mathbf{X}$ of samples is mapped to linear subspaces in a high dimensional space. Then the LRR model can be applied to the mapped sample set. Suppose that the noises are Gaussian, the model is:

$\min\limits_{\mathbf{Z}}\|\phi(\mathbf{X})-\phi(\mathbf{X})\mathbf{Z}\|_F^2 + \lambda\|\mathbf{Z}\|_*.$

Since $\|\phi(\mathbf{X})-\phi(\mathbf{X})\mathbf{Z}\|_F^2 = {\rm{tr}}\left[(\phi(\mathbf{X})-\phi(\mathbf{X})\mathbf{Z})^T(\phi(\mathbf{X})-\phi(\mathbf{X})\mathbf{Z})\right]$, we obtain inner products $\phi(\mathbf{X})^T\phi(\mathbf{X})$. So we can introduce a kernel function $K(\mathbf{x}, \mathbf{y})$, such that $K(\mathbf{x}, \mathbf{y}) = \phi^T(\mathbf{x})\phi(\mathbf{y})$. Therefore, the above model can be written in a kernalized form without introducing the nonlinear mapping $\phi$ explicitly. However, when the noises are not Gaussian, the above kernel trick does not apply.

The other heuristic approach is to add Laplacian or hyper-Laplacian to the corresponding linear models. It is claimed that Laplacian or hyper-Laplacian can capture the nonlinear geometry of the data distribution. For example, Lu et al. [49] added the Laplacian regularization ${\rm{tr}}(\mathbf{Z}\mathbf{L}_{\mathbf{W}}\mathbf{Z}^T)$ to the objective function of LRR, where $\mathbf{L}_{\mathbf{W}}$ is the Laplacian matrix of the weight matrix $\mathbf{W}$ in which $W_{ij} = \exp\left(-\|\mathbf{x}_i-\mathbf{x}_j\|^2/\sigma\right)$. Zheng et al. [81] added another form of Laplacian regularization ${\rm{tr}}(\mathbf{D}\mathbf{L}_{\tilde{\mathbf{Z}}}\mathbf{D}^T)$ to the objective function of LRR, where $\mathbf{D}$ is the data matrix and $\mathbf{L}_{\tilde{\mathbf{Z}}}$ is the Laplacian matrix of $\tilde{\mathbf{Z}} = (|\mathbf{Z}|+|\mathbf{Z}^T|)/2$. Yin et al. considered both Laplacian and hyper-Laplacian regularization in the nonnegative low-rank and sparse LRR model [71].

Although the modifications on linear models result in more powerful nonlinear models, it is hard to analyze their properties. So their performance may heavily depend on the choice of parameters.

---

4. Optimization algorithms

Once we have a mathematical model, we need to solve it efficiently. The discrete low-rank models in Section 2 are mostly NP-hard. So most of the time they could only be solved approximately. A common way is to convert them into continuous optimization problems. There are two ways to do so. The first way is to convert them into convex programs. For example, as mentioned above, one may replace the $\ell_0$ pseudo-norm $\|\cdot\|_0$ with the $\ell_1$ norm $\|\cdot\|_1$ and replace rank with the nuclear norm $\|\cdot\|_*$. Another way is to convert to non-convex programs. More specifically, it is to use a non-convex continuous function to approximate the $\ell_0$ pseudo-norm $\|\cdot\|_0$ (e.g., using the $\ell_p$ pseudo-norm $\|\cdot\|_p (0<p<1)$) and rank (e.g., using the Schatten-$p$ pseudo-norm (the $\ell_p$ pseudo-norm of the vector of singular values)). There is still another way. It is to represent the low-rank matrix as a product of two matrices, the number of columns of the first matrix and the number of rows of the second matrix both being the expected rank, and then update the two matrices alternately until they do not change. This special type of algorithm does not appear in the sparsity based models. The advantage of convex programs is that their global optimal solutions can be relatively easy obtained. The disadvantages include that the solution may not be sufficiently low-rank or sparse. In contrast, the advantage of non-convex optimization is that lower-rank or sparser solutions can be obtained. However, their global optimal solution may not be obtained. The quality of solution may heavily depend on the initialization. So the convex and non-convex algorithms complement each other. By fully utilizing the characteristics of problems, it is also possible to design randomized algorithms so that the computation complexity can be greatly reduced.

---

4.1. Convex algorithms

Convex optimization is a relatively mature field. There are a lot of polynomial complexity algorithms, such as interior point methods. However, for large scale or high dimensional data, we often need $O(n\mbox{polylog}(n))$ complexity, where $n$ is the number or the dimensionality of samples. Even $O(n^2)$ complexity is unacceptable. Take the RPCA problem as example, if the matrix size is $n\times n$, then the problem has $2n^2$ unknowns. Even if $n = 1000$, which corresponds to a relatively small matrix, the number of unknowns already reaches two millions. If we solve RPCA with the interior point method, e.g., using the CVX package [22] by Stanford University, then the time complexity of each iteration is $O(n^6)$, while the storage complexity is $O(n^4)$. If solved on a PC with 4GB memory, the size of matrix will be limited to $80\times 80$. So to make low-rank models practical, we have to design efficient optimization algorithms.

Currently, all the optimization methods for large scale computing are first order methods. Representative algorithms include Accelerated Proximal Gradient (APG) [2,54], the Frank-Wolfe algorithm [18,26], and the Alternating Direction Method (ADM) [36,37].

APG is basically for unconstrained problems:

$\begin{equation}\min\limits_{\mathbf{x}} f(\mathbf{x}), \end{equation}$

(17)

where the objective function is convex and $C^{1, 1}$, i.e., differentiable and its gradient is Lipschitz continuous:

$\|\nabla f(\mathbf{x})-\nabla f(\mathbf{y})\|\leq L_f\|\mathbf{x}-\mathbf{y}\|, \;\;\;\;\forall \mathbf{x}, \mathbf{y}.$

(18)

The convergence rate of traditional gradient descent can only be $O(k^{-1})$, where $k$ is the number of iterations. However, Nesterov constructed an algorithm [54]:

$\begin{array}{l} \mathbf{x}_k = \mathbf{y}_k-L_f^{-1}\nabla f(\mathbf{y}_k), \\ t_{k+1} = \dfrac{1+\sqrt{1+4t_k^2}}{2}, \\ \mathbf{y}_{k+1} = \mathbf{x}_k+\dfrac{t_k-1}{t_{k+1}}(\mathbf{x}_k-\mathbf{x}_{k-1}), \end{array}$

(19)

where $\mathbf{x}_0 = \mathbf{y}_1 = 0$ and $t_1 = 1$. whose convergence rate can achieve $O(k^{-2})$. Later, Beck and Teboulle generalized Nesterov's algorithm for the following problem:

$\min\limits_{\mathbf{x}} g(\mathbf{x})+f(\mathbf{x}),$

(20)

where $g$ is convex, whose proximity operator $\min_{\mathbf{x}} g(\mathbf{x})+\frac{\alpha}{2}\|\mathbf{x}-\mathbf{w}\|^2$ is easily solvable, and $f$ is a $C^{1, 1}$ convex function [2], thus greatly extended the applicable range of Nesterov's method. APG needs to estimate the Lipschitz coefficient $L_f$ of the gradient of the objective function. If the Lipschitz coefficient is estimated too conservatively (too large), the convergence speed will be affected. So Beck and Teboulle further proposed a back-tracking strategy to estimate the Lipschitz coefficient adaptively, so as to speed up convergence [2]. For some problems with special structures, APG can be generalized (Generalized APG, GAPG) [85], such that different Lipschitz coefficients could be chosen for different variables, thus the convergence can be made faster. For problems with linear constraints:

$\min\limits_{\mathbf{x}} f(\mathbf{x}), \;\;\;\; s.t. \;\;\;\;\mathcal{A}(\mathbf{x}) = \mathbf{b},$

(21)

where $f$ is convex and $C^{1, 1}$ and $\mathcal{A}$ is a linear operator, one may add the squared constraint to the objective function as a penalty, converting the problem to an unconstrained one:

$\min\limits_{\mathbf{x}} f(\mathbf{x})+\dfrac{\beta}{2}\| \mathcal{A}(\mathbf{x}) - \mathbf{b}\|^2,$

(22)

then solve (22) by APG. To speed up, the penalty parameter $\beta$ should increase gradually along with iteration, rather than being set at a large value from the beginning. This important trick is called the continuation technique [20].

For problems with a convex set constraint:

$\min\limits_{\mathbf{x}} f(\mathbf{x}),\;\;\;\; s.t.\;\;\;\; \mathbf{x}\in C,$

(23)

where $f$ is convex and continuously differentiable and $C$ is a compact convex set, Frank-Wolfe-type algorithms [18,26]:

$\mathbf{g}_k = \underset{\mathbf{g}\in C}{\mathop{\text{argmin}}}\, \langle \mathbf{g}, \nabla f(\mathbf{x}_k)\rangle, \\ \mathbf{x}_{k+1} = (1-\gamma_k)\mathbf{x}_k + \gamma_k \mathbf{g}_k, \;\;\;\;\mbox{where } \gamma_k = \dfrac{2}{k+2},$

(24)

can be used to solve (23). In particular, when the constraint set $C$ is a ball of bounded nuclear norm, $\mathbf{g}_k$ can be relatively easily computed by finding the singular vectors associated to the leading singular values of $\nabla f(\mathbf{x}_k)$ [26]. Such a particular problem can also be efficiently solved by transforming it into a positive semi-definite program [27], where only the eigenvector corresponding to the largest eigenvalue of a matrix is needed.

ADM fits for convex problems with separable objective functions and linear or convex-set constraints:

$\min\limits_{\mathbf{x}, \mathbf{y}} f(\mathbf{x})+g(\mathbf{y}), \;\;\;\; s.t.\;\;\;\; \mathcal{A}(\mathbf{x})+\mathcal{B}(\mathbf{y}) = \mathbf{c},$

(25)

where $f$ and $g$ are convex functions and $\mathcal{A}$ and $\mathcal{B}$ are linear operators. ADM is a variant of the Lagrange Multiplier method. ADM first constructs an augmented Lagrangian function [37]:

$\mathcal{L}(\mathbf{x}, \mathbf{y}, \mathbf{\lambda }) = f(\mathbf{x})+g(\mathbf{y})+\ <\mathbf{\lambda }, \mathcal{A}(\mathbf{x})+\mathcal{B}(\mathbf{y})-\mathbf{c}\> + \dfrac{\beta}{2}\|\mathcal{A}(\mathbf{x})+\mathcal{B}(\mathbf{y})-\mathbf{c}\|^2,$

(26)

where $\mathbf{\lambda }$ is the Lagrange multiplier and $\beta>0$ is the penalty parameter, then updates the two variables alternately by minimizing the augmented Lagrangian function with the other variable fixed [37]:

$\begin{array}{rcl} \mathbf{x}_{k+1}& = &\underset{\mathbf{x}}{\mathop{\text{argmin}}}\,\mathcal{L}(\mathbf{x}, \mathbf{y}_k, \mathbf{\lambda }_k), \\ \mathbf{y}_{k+1}& = &\underset{\mathbf{y}}{\mathop{\text{argmin}}}\,\mathcal{L}(\mathbf{x}_{k+1}, \mathbf{y}, \mathbf{\lambda }_k). \end{array}$

(27)

Finally, ADM updates the Lagrange multiplier [37]:

$\mathbf{\lambda }_{k+1} = \mathbf{\lambda }_k+\beta(\mathcal{A}(\mathbf{x}_{k+1})+\mathcal{B}(\mathbf{y}_{k+1})-\mathbf{c}).$

(28)

The advantage of ADM is that its subproblems are simpler than the original problem. They may even have closed-form solutions. When the subproblems are not easily solvable, one may consider approximating the squared constraint $\dfrac{\beta}{2}\|\mathcal{A}(\mathbf{x})+\mathcal{B}(\mathbf{y})-\mathbf{c}\|^2$ in the augmented Lagrangian function with its first order Taylor expansion plus a proximal term, to make the subproblem even simpler. This technique is called the Linearized Alternating Direction Method (LADM) [37]. If after linearizing the squared constraint in the augmented Lagrangian function the subproblem is still not easily solvable, one may further linearize the $C^{1, 1}$ component of the objective function [36]. For multi-block (the number of blocks of variables is greater than 2) convex programs, a naive generalization of the two-block ADM may not converge [8]. However, if we change the serial update with parallel update and choose some parameters appropriately, the convergence can still be guaranteed, even if linearization is used [36]. In all the above-mentioned ADM algorithms, the penalty parameter $\beta$ is allowed to increase dynamically so that the convergence can be accelerated and the difficulty in tuning an optimal penalty parameter can be overcome [36,37].

When solving the low-rank models with convex surrogates, we often face with the following subproblem:

$\min\limits_{\mathbf{X}} \|\mathbf{X}\|_* + \dfrac{\alpha}{2}\|\mathbf{X}-\mathbf{W}\|_F^2,$

which has a closed-form solution [3]. Suppose that the SVD of $\mathbf{W}$ is $\mathbf{W} = \mathbf{U}\mathbf{\Sigma }\mathbf{V}^T$, then the optimal solution is $\mathbf{X} = \mathbf{U}\Theta_{\alpha^{-1}}(\mathbf{\Sigma })\mathbf{V}^T$, where

$\Theta_{\varepsilon}(x) = \left\{ \begin{array}{ll} x-\varepsilon, &\mbox{if }x>\varepsilon, \\ x+\varepsilon, &\mbox{if }x <-\varepsilon, \\ 0, &\mbox{if }-\varepsilon\leq x\leq \varepsilon. \end{array} \right.$

(29)

So solving low-rank models with nuclear norm, SVD is often indispensable. For $m\times n$ matrices, the time complexity of full SVD is $O(mn\min(m, n))$. So in general the computation cost for solving low-rank models with nuclear norm is large. This issue is more critical when $m$ and $n$ is large. Fortunately, from (29) one can see that it is unnecessary to compute the singular values not exceeding $\alpha^{-1}$ and their associated singular vectors, because these singular values will be shrunk to zeros, thus do not contribute to $\mathbf{X}$. So we only need to compute singular values greater than $\alpha^{-1}$ and their corresponding singular vectors. Such partial SVD computation can be achieved by PROPACK [33] and accordingly the computation cost reduces to $O(rmn)$, where $r$ is the expected rank of the optimal $\mathbf{Z}$. It is worth noting that PROPACK can only provide expected number of leading singular values and their singular vectors. So we have to dynamically predict the value of $r$ when calling PROPACK [37]. When the solution is not sufficiently low-rank, such as Transform Invariant Low-Rank Textures (TILT) [78] ((30) and Section 5.5) which has wide applications in image processing and computer vision, one can use incremental SVD [58] for acceleration.

Convex algorithms have the advantage of being independent of initialization. However, the quality of their solutions may not be good enough. So exploring nonconvex algorithms is another hot topic in low-rank models.

---

4.2. Nonconvex optimization algorithms

Nonconvex algorithms trade the initialization independency for better solution quality and possibly faster speed as well. For unconstrained problems which use the Schatten-$p$ norm to approximate rank and the $\ell_p$ norm to approximate the $\ell_0$ norm, an effective way is the Iteratively Reweighted Least Squares (IRLS) [46]. To be more precise, approximate ${\rm{tr}}\left((\mathbf{X}\mathbf{X}^T)^{p/2}\right)$ with ${\rm{tr}}\left((\mathbf{X}_k\mathbf{X}_k^T)^{(p/2)-1}(\mathbf{X}\mathbf{X}^T)\right)$ and $|\mathbf{x}_i|^p$ with $|\mathbf{x}_i^{(k)}|^{p-2}\mathbf{x}_i^2$, where $\mathbf{X}_k$ is the value of low-rank matrix $\mathbf{X}$ at the $k$th iteration and $\mathbf{x}_i^{(k)}$ is the $i$th component of the sparse vector $\mathbf{x}$ at the $k$th iteration. So each time to update $\mathbf{X}$, a matrix equation needs to be solved, while updating $\mathbf{x}$ needs solving a linear system. Another way is to apply the idea of APG. To be specific, linearize the $C^{1, 1}$ component of the objective function. Then in each iteration one only needs to solve the following subproblem:

$\min\limits_{\mathbf{X}}\sum\limits_{i = 1}^n g(\sigma_i(\mathbf{X}))+\dfrac{\alpha}{2}\|\mathbf{X}-\mathbf{W}\|_F^2,$

where $g$ is a non-decreasing concave function on $\{x\geq 0\}$, such as $x^p (0 <p <1)$. Lu et al. [48] provided an algorithm to solve the above subproblem. Another function that approximates rank is the Truncated Nuclear Norm (TNN) [25]: $\|\mathbf{X}\|_r = \sum\limits_{i = r+1}^{\min(m, n)}\sigma_i(\mathbf{X})$. TNN does not involve the largest $r$ singular values. So it is not a convex function. The intuition behind TNN is obvious. By minimizing TNN, the tailing singular values will be encouraged to be small, while the magnitudes of the first $r$ singular values are unaffected. So a solution closer to a rank $r$ matrix can be obtained. TNN can be generalized by adding larger weights to smaller singular values, obtaining the Weighted Nuclear Norm (WNN) [23]: $\|\mathbf{X}\|_{w, *} = \sum\limits_{i = 1}^{\min(m, n)}w_i\sigma_i(\mathbf{X})$. However, in this case in general the subproblem

$\min\limits_{\mathbf{X}}\sum\limits_{i = 1}^n \|\mathbf{X}\|_{w, *}+\dfrac{\alpha}{2}\|\mathbf{X}-\mathbf{W}\|_F^2,$

does not have a closed-form solution. Instead, a small-scale optimization w.r.t. the singular values need to be solved numerically.

The third kind of methods for low-rank problems is to represent the expected low-rank matrix $\mathbf{X}$ as $\mathbf{X} = \mathbf{A}\mathbf{B}^T$, where $\mathbf{A}$ and $\mathbf{B}$ both have $r$ columns. Then $\mathbf{A}$ and $\mathbf{B}$ can be updated alternately until they do not change [67]. The advantage of this kind of methods is its simplicity. However, we have to estimate the rank of low-rank matrix apriori and $A$ and $B$ may easily get stuck.

Nonconvex algorithms for low-rank models are much richer than convex ones. The price paid is that their performance may heavily depend on initialization. In this case, prior knowledge is important for proposing a good initialization.

---

4.3. Randomized algorithms

All the above-mentioned methods, no matter for convex or non-convex problems, their computation complexity is at least $O(rmn)$, where $m\times n$ is the size of the low-rank matrix that we want to compute. This is not fast enough when $m$ and $n$ are both very large. To break this bottleneck, we have to resort to randomized algorithms. However, we cannot reduce the whole computation complexity simply by randomizing each step of a deterministic algorithm, e.g., simply replacing SVD with linear-time SVD [13], because some randomized algorithms are very inaccurate. So we have to design randomized algorithms based on the characteristics of low-rank models. As a result, currently there is limited work on this aspect. For RPCA, Liu et al. proposed the $\ell_1$-filtering method [43]. It first randomly samples a submatrix $\mathbf{D}^s$, with an appropriate size, from the data matrix $\mathbf{D}$. Then it solves a small-scale RPCA on $\mathbf{D}^s$, obtaining a low-rank $\mathbf{A}^s$ and a sparse $\mathbf{E}^s$, Next, it processes the sub-columns and sub-rows of $\mathbf{D}$ that $\mathbf{D}^s$ resides on, using $\mathbf{A}^s$, as they should belong to the subspaces spanned by the columns or rows of $\mathbf{A}^s$ up to sparse errors. Finally, the low-rank matrix $\mathbf{A}$ that corresponds to the original matrix $\mathbf{D}$ can be represented by the Nyström trick, without explicit computing. The complexity of the whole algorithm is $O(r^3)+O(r^2(m+n))$, which is linear with respect to the matrix size. For LRR and Latent LRR, Zhang et al. found that if we denoise the data first with RPCA and then apply LRR or Latent LRR on the denoised data, then their solutions can be expressed by the solution of RPCA and vice versa. So the solutions of LRR and Latent LRR can be greatly accelerated by reducing to RPCA [76].

Randomized algorithms could bring down the order of computation complexity. However, designing randomized algorithms often needs to consider the characteristic of the problems.

---

5. Representative applications

Low-rank models have found wide applications in data analysis and machine learning. For example, there have been a lot of papers on NIPS 2011 which discussed low-rank models. Below I introduce some representative applications.

---

5.1. Video denoising [29]

Image and video denoising can be conveniently formulated as a matrix completion problem. In [29], Ji et al. first broke each of the video frames into patches, then grouped the similar patches. For each group, the patches are reshaped into vectors and assembled into a matrix. Next, the unreliable (noisy) pixels are detected as those whose values deviate from the means of their corresponding row vectors and the remaining pixels are considered reliable (noiseless). The unreliable pixel values can be estimated by applying the matrix completion model (2) to the matrix by marking them as missing values. After denoising all the patches, each frame is restored by averaging the pixel values in overlapping patches. Part of the results of video denoising are shown in Figure 2.

---

5.2. Keyword extraction [51]

In document analysis, it is important to extract keywords from documents. Let $\mathbf{D}$ be the unnormalized term frequency matrix, where the row indices are the document IDs and the column indices are the term IDs and the $(i, j)$-th entry is the frequency of the $j$-th term in the $i$-th document. Then for documents of similar topics, many of the words are common, forming the "background" topic, and each document should have its unique keywords to discriminate it from others. This phenomenon makes keyword extraction naturally fit for the RPCA model (3), where the sparse error $\mathbf{E}$ identifies keywords in each document. One example of keyword extraction is shown in Figure 3.

---

5.3. Background modeling [4]

Background modeling is to separate the background and the foreground from a video. The simplest case is that the video is taken by a fixed video camera. It is easy to see that the background hardly changes. So if putting each frame of the background as a column of a matrix, then the matrix should be of low rank. As the foreground consists of moving objects, it often occupies only a small portion of pixels. So the foreground corresponds to the sparse "noise" in the video. So we can obtain the RPCA model (3) for background modeling, where each column of $\mathbf{D}$, $\mathbf{A}$, and $\mathbf{E}$ is a frame of the video, the background, and the foreground, respectively, rearranged into a vector. Part of the results of background modeling is shown in Figure 4.

---

5.4. Robust Alignment by Sparse and Low-Rank decomposition (RASL) [56]

The RPCA model for background modeling has to assume that the background has been aligned so as to obtain a low-rank background video. In the case of misalignment, we may consider aligning the frames via appropriate geometric transformation. So the mathematical model is:

$\min\limits_{\tau, \mathbf{A}, \mathbf{E}} \|\mathbf{A}\|_* + \lambda\|\mathbf{E}\|_1, \;\;\;\; s.t.\;\;\;\; \mathbf{D}\circ\tau = \mathbf{A}+\mathbf{E},$

(30)

where $\mathbf{D}\circ\tau$ represents applying frame-wise geometric deformation $\tau$ to each frame, which is a column of $\mathbf{D}$. Now (30) is a nonconvex optimization problem. For efficient solution, Peng et al. [56] proposed to linearize $\tau$ locally and update the increment of $\tau$ iteratively. That is to say, first solve $\Delta\tau_k$ from:

$\min\limits_{\Delta\tau_k, \mathbf{A}, \mathbf{E}} \|\mathbf{A}\|_* + \lambda\|\mathbf{E}\|_1, \;\;\;\;s.t.\;\;\;\; \mathbf{D}\circ\tau_k + \mathbf{J}\Delta\tau_k = \mathbf{A}+\mathbf{E},$

(31)

then add $\Delta\tau_k$ to $\tau_k$ as $\tau_{k+1}$, where $\mathbf{J}$ is the Jacobian of $\mathbf{D}\circ\tau$ with respect to the parameters of transformation $\tau$. Under the affine transformation, part of the results of facial image alignment are shown in Figure 5.

---

5.5. Transform Invariant Low-rank Textures (TILT) [78]

The purpose of Transform Invariant Low-rank Textures (TILT) is to rectify an image patch $\mathbf{D}$ with a geometric transformation $\tau$, such that the content in patch becomes regular, such as being rectilinear or symmetric. Such regularity could be depicted by low-rankness. The mathematical formulation of TILT is the same as that of RASL (30). The solution method is also identical. The difference resides in the interpretation on the matrix $\mathbf{D}$, which is now a rectangular image patch in a single image. Figure 6 gives examples of rectifying image patches under the perspective transform.

In principle, TILT should work for any parameterized transformations. Zhang et al. [79] further considered TILT under generalized cylindrical transformations, which can be used for texture unwarping from buildings. Some examples are shown in Figure 7.

TILT is also widely applied to geometric modeling of buildings [78], camera self-calibration, and lens distortion auto-correction [80]. Due to its importance in applications, Ren and Lin [58] proposed a fast algorithm for TILT to speed up its solution by more than five times.

---

5.6. Motion segmentation [38,39]

Motion segmentation means to cluster the feature points on moving objects in a video, such that each cluster corresponds to an independent object. Then an object can be identified and tracked. For each feature point, its feature vector consists of its image coordinate in each frame and is a column of the data matrix $\mathbf{D}$. Then subspace clustering models, such as those in Section 2.2, could be applied to cluster the feature vectors and hence the corresponding feature points. LRR (7) is regarded as one of the best algorithms for segmenting the motion of rigid bodies [1]. Some of the examples of motion segmentation are shown in Figure 8.

---

5.7. Image segmentation [10]

Image segmentation is to partition an image into homogenous regions. It can be viewed as a special clustering problem. Cheng et al. [10] proposed to oversegment the image into superpixels, then extract usual features from the superpixels. Next, they fused multiple features via an integrated LRR model, where basically each feature corresponds to an LRR model. After obtaining the global representation matrix $\mathbf{Z}^*$, they applied normalized cut to a graph whose weights are given by the similarity matrix $(|\mathbf{Z}^*|+|\mathbf{Z}^{*T}|)/2$ to cluster the superpixels into clusters, each corresponding to an image region. Part of the results of image segmentation are shown in Figure 9.

---

5.8. Gene clustering [12]

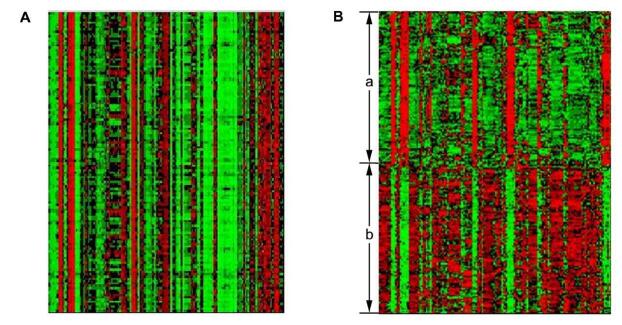
Gene clustering is to group genes with similar functionality. Identifying gene clusters from the gene expression data is helpful for the discovery of novel functional gene interactions. Let $\mathbf{D}$ be the transposed gene expression data matrix, whose columns contain the expression levels of a gene in all the samples and whose rows are the expression levels of all the genes in one sample. Cui et al. [12] then applied the LRR model to $\mathbf{D}$ to cluster the genes. Two examples of gene clustering are shown in Figure 10.

---

5.9. Image saliency detection [32]

Saliency detection is to detect the visually salient regions in an image without understanding the content of the image. Motion segmentation, image segmentation, and gene clustering all utilize the representation matrix $\mathbf{Z}$ in LRR. In contrast, Lang et al. [32] proposed to utilize the sparse "noise" $\mathbf{E}$ in LRR for image saliency detection. Note that salient regions in an image is the "larruping" region. So if using other regions to "predict" salient regions, there will be relatively large errors. Therefore, by breaking an image into patches and extracting their features, the salient regions should correspond to those with large sparse "noise" $\mathbf{E}$ in the LRR model, where the data matrix $\mathbf{D}$ consists of the feature vectors. Part of the examples of saliency detection are shown in Figure 11.

---

5.10. Other applications

There have been many other applications of low-rank models, such as partial duplicate image search [70], face recognition [57], structured texture repairing [35], man-made object upright orientation [30], photometric stereo [69], image tag refinement [83], robust visual domain adaption [28], robust visual tracking [77], feature extraction from 3D faces [52], ghost image removal in computed tomography [21], semi-supervised image classification [84], image set co-segmentation [53], and even audio analysis [53,55], protein-gene correlation analysis, network flow abnormality detection, robust filtering and system identification. Due to the space limit, I omit their introductions.

---

6. Conclusions

Low-rank models have found wide applications in many fields, including signal processing, machine learning, and computer vision. In a few years, there has been rapid development in theories, algorithms, and applications on low-rank models. This review is only a sketchy introduction to this dynamic research topic. Many real problems, if combining the characteristic of problem with proper low-rankness constraints, very often we could obtain better results. In some problems, the raw data may not have a low-rank property. However, the low-rankness could be enhanced by incorporating appropriate transforms (like the improvement of RASL/TILT over RPCA). Some scholars did not check whether the data have low-rank property or do proper pre-processing before claiming that low-rank constraints do not work well. This should be avoided. From the above review, we can see that low-rank models still lack research in the following aspects: generalization from matrices to tensors, nonlinear manifold clustering, and low-complexity (polylog$(n)$) randomized algorithms, etc. Hope this review can attract more research in these aspects.

---

Acknowledgments

Z. Lin is supported by NSF China (grant nos. 61272341 and 61231002), 973 Program of China (grant no. 2015CB352502), and Microsoft Research Asia Collaborative Research Program.

---