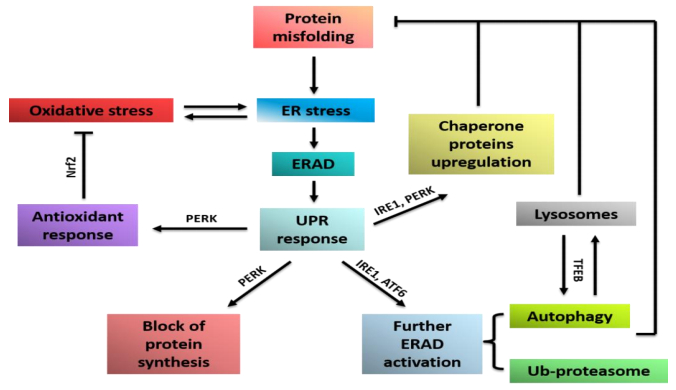
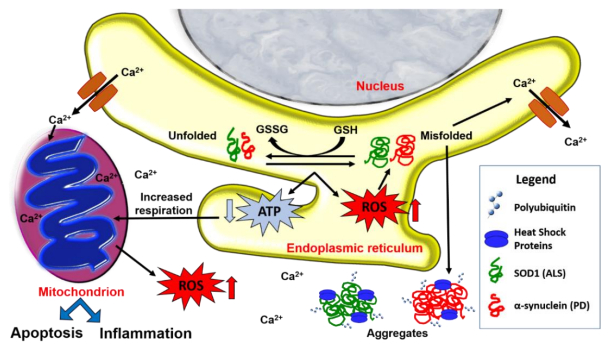
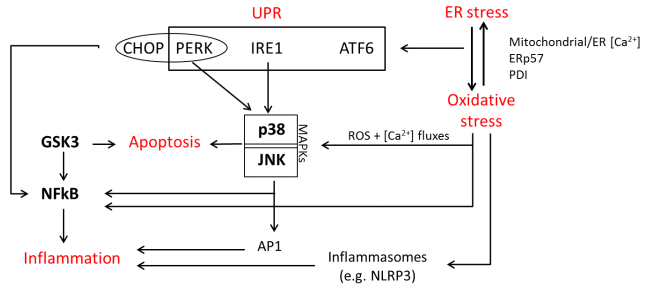
Cellular stress caused by protein misfolding, aggregation and redox imbalance is typical of neurodegenerative disorders such as Parkinson’s disease (PD) and Amyotrophic Lateral Sclerosis (ALS). Activation of quality control systems, including endoplasmic reticulum (ER)-mediated degradation, and reactive oxygen species (ROS) production are initially aimed at restoring homeostasis and preserving cell viability. However, persistent damage to macromolecules causes chronic cellular stress which triggers more extreme responses such as the unfolded protein response (UPR) and non-reversible oxidation of cellular components, eventually leading to inflammation and apoptosis. Cell fate depends on the intensity and duration of stress responses converging on the activation of transcription factors involved in the expression of antioxidant, autophagic and lysosome-related genes, such as erythroid-derived 2-related factor 2 (Nrf2) and transcription factor EB respectively. In addition, downstream signaling pathways controlling metabolism, cell survival and inflammatory processes, like mitogen activated protein kinase and nuclear factor-kB, have a key impact on the overall outcome.
Molecular chaperones and ER stress modulators play a critical role in protein folding, in the attenuation of UPR and preservation of mitochondrial and lysosomal activity. Therefore, the use of chaperone molecules is an attractive field of investigation for the development of novel therapeutic strategies and disease-modifying drugs in the context of neurodegenerative diseases such as PD and ALS.
1.
Introduction
This paper is concerned with a mathematical model for a gene regulatory network involved in the regulation of DNA transcription. DNA transcription is part of the mechanism by which a sequence of the nuclear DNA is translated into the corresponding protein. The transcription is initiated by the binding of a transcription factor, which is usually another protein, onto the gene's DNA-binding domain. Once bound, the transcription factor promotes the transcription of the nuclear DNA into a messenger RNA (further denoted by mRNA), which, once released, is translated into the corresponding protein by the ribosomes. This process is subject to a high level of noise due to the large variability of the conditions that prevail in the cell and the nucleus at the moment of the transcription. Yet, a rather stable amount of the final protein is needed for the good operation of the cell. The processes that regulate noise levels and maintain cell homeostasis have been scrutinized for a long time. Recently, micro RNAs (further referred to as μRNAs) have occupied the front of the scene. These are very short RNAs which do not code for proteins. Many different sorts of μRNAs are involved in various epigenetic processes. But one of their roles seems precisely the reduction of noise level in DNA transcription. In this scenario, the μRNAs are synthesized together with the mRNAs. Then, some of the synthesized μRNAs bind to the mRNAs and de-activate them. These μRNA-bound mRNA become unavailable for protein synthesis. It has been proposed that this paradoxical mechanism which seems to reduce the efficiency of DNA transcription may indeed have a role in noise regulation (see [1,2,3] and the review [4]). The goal of the present contribution is to propose a mathematical model of the μRNA-mRNA interaction and to use it to investigate the role of μRNAs as potential noise regulators.
Specifically, in this paper, we propose a stochastic chemical kinetic model for the mRNA and μRNA content in a cell. The production of mRNAs by the transcription factor and their inactivation through μRNA binding are taken into account. More precisely, our model is a simplified version of the circuit used in [5,Figure 2A,A']. We consider a ligand involved in the production of both an mRNA and a μRNA, the μRNA having the possibility to bind to the mRNA and deactivate it. By contrast to [5], we disregard the way the ligand is produced and consider that the ligand is such that there is a constant production rate of both mRNA and μRNA. A second difference to [5] is that we disregard the transcription step of the mRNA into proteins. While [5] proposes to model the μRNA as acting on translation, we assume that the μRNA directly influences the number of mRNA available for transcription. Therefore, we directly relate the gene expression level to the number of μRNA-free mRNA also referred to as the number of unbound mRNA. In order to model the stochastic variability in the production of the RNAs, a multiplicative noise is added to the production rate at all time. From the resulting system of stochastic differential equations, we introduce the joint probability density for mRNA and μRNA which solves a deterministic Fokker-Planck equation. The mathematical object of interest is the stationary density solving the Fokker-Planck equation and more precisely the marginal density of the mRNA. The coefficient of variation (also called cell-to-cell variation) of this mRNA density, which is its standard deviation divided by its the expectation, is often considered as the relevant criterion for measuring the robustness of gene expression (see for instance [5]).
Our main goal in this contribution is to provide theoretical and numerical evidence that the robustness of the gene expression is increased in the presence of μRNA. At the theoretical level we derive a number of analytical formulas either for particular subsets of parameters of the model or under some time-scale separation hypotheses. From these formulas we can easily compute the cell to cell variation numerically and verify the increased robustness of gene expression when binding with μRNA happens in the model. For general sets of parameters, the solution cannot be computed analytically. However we can prove well-posedness of the model and solve the PDE with a specifically designed numerical scheme. From the approximate solution, we compute the coefficient of variation and verify the hypothesis of increased gene expression.
Another classical approach to the study of noise in gene regulatory networks is through the chemical master equation [6] which is solved numerically by means of Gillespie’s algorithm [7], see e.g., [5,8]. Here, we use a stochastic chemical kinetic model through its associated Kolmogorov-Fokker-Planck equation. Chemical kinetics is a good approximation of the chemical master equation when the number of copies of each molecule is large. This is not the case in a cell where sometimes as few as a 100 copies of some molecules are available. Specifically, including a stochastic term in the chemical kinetic approach is a way to retain some of the randomness of the process while keeping the model complexity tractable. This ultimately leads to a Fokker-Planck model for the joint distribution of mRNAs and μRNAs. In [9], a similar chemical kinetic model is introduced with a different modelling of stochasticity. The effect of the noise is taken into account by adding some uncertainty in the (steady) source term and the initial data. The authors are interested in looking at how this uncertainty propagates to the mRNA content and in comparing this uncertainty between situations including μRNA production or not. The uncertainty is modeled by random variables with given probability density functions. Compared to [9], the Fokker-Planck approach has the advantage that the random perturbations do not only affect the initial condition and the source term, but are present at all times and vary through time. We believe that this is coherent with how stochasticity in a cell arises through time-varying ecological or biological factors.
While Fokker-Planck equations are widely used models in mathematical biology [10], their use for the study of gene regulatory network is, up to our knowledge, scarce (see e.g., [11]). Compared to other approaches, the Fokker-Planck model enables us to derive analytical formulas for solutions in certain cases. This is particularly handy for understanding the role of each parameter in the model, calibrating them from real-world data and perform fast numerical computations. Nevertheless, in the general case, the theoretical study and the numerical simulation of the model remains challenging because of the unboundedness of the drift and diffusion coefficients. We believe that we give below all the tools for handling these difficulties, and that our simple model provides a convincing mathematical interpretation of the increase of gene expression in the presence of μRNAs.
The paper is organized as follows. In Section 2, we introduce the system of SDEs and the corresponding Fokker-Planck models. In Section 3, we discuss the well-posedness of the Fokker-Planck equations and derive analytical formulas for solutions under some simplifying hypotheses. In Section 4, we use the analytical formulas for solutions to give mathematical and numerical proofs of the decrease of cell-to-cell variation in the presence of μRNA. In Section 5, we propose a numerical scheme for solving the main Fokker-Planck model and gather further evidence confirming the hypothesis of increased gene expression from the simulations. Finally, in Section 6 we discuss the particular choice of multiplicative noise (i.e., the diffusion coefficient in the Fokker-Planck equation) in our model. In the appendix, we derive weighted Poincaré inequalities for gamma and inverse-gamma distributions which are useful in the analysis of Section 3. The code used for numerical simulations in this paper is publicly available on GitLab [12].
2.
Presentation of the models
In this section, we introduce three steady Fokker-Planck models whose solutions describe the distribution of unbound mRNA and μRNA within a cell. The solutions to these equations can be interpreted as the probability density functions associated with the steady states of stochastic chemical kinetic systems describing the production and destruction of mRNA and μRNA. In Section 2.1 we introduce the main model for which the consumption of RNAs is either due to external factors in the cell (translation, {etc.}) or to binding between the two types of mRNA and μRNA. Then, for comparison, in Section 2.2 we introduce the same model without binding between RNAs. Finally in Section 2.3, we derive an approximate version of the first model, by considering that reactions involving μRNAs are infinitely faster than those involving mRNAs, which amplifies the binding phenomenon and mathematically allows for the derivation of analytical formulas for solutions. The latter will be made explicit in Section 3.
2.1. Dynamics of mRNA and μRNA with binding
We denote by rt the number of unbound mRNA and μt the number of unbound μRNA of a given cell at time t. The kinetics of unbound mRNA and μRNA is then given by the following stochastic differential equations
with cr, cμ, kr, kμ, σr, σμ being some given positive constants and c being a given non-negative constant. Let us detail the meaning of each term in the modeling. The first term of each equation models the constant production of mRNA (resp. μRNA) by the ligand at a rate cr (resp. cμ). The second term models the binding of the μRNA to the mRNA. Unbound mRNA and μRNA are consumed by this process at the same rate. The rate increases with both the number of mRNA and μRNA. In the third term, the parameters kr and kμ are the rates of consumption of the unbound mRNA or μRNA by various decay mechanisms. The last term in both equations represents stochastic fluctuations in the production and destruction mechanisms of each species. It relies on a white noise dBt/dt where Bt=(B1t,B2t) is a two-dimensional standard Brownian motion. The intensity of the stochastic noise is quantified by the parameters √2σrrt and √2σμμt. Such a choice of multiplicative noise ensures that rt and μt remain non-negative along the dynamics. The Brownian motions B1t and B2t are uncorrelated. The study of correlated noises or the introduction of extrinsic noise sources would be interesting, but will be discarded here.
In this paper we are interested in the invariant measure of Eq (2.1) rather than the time dynamics described by the above SDEs. From the modelling point of view, we are considering a large number of identical cells and we assume that mRNA and μRNA numbers evolve according to Eq (2.1). Then we measure the distribution of both RNAs among the population, when it has reached a steady state f≡f(r,μ). According to Itô's formula, the steady state should satisfy the following steady Fokker-Planck equation
where the Fokker-Planck operator is given by
Since we do not model the protein production stage, we assume that the observed distribution of gene expression level is proportional to the marginal distribution of mRNA, i.e..
By integration of Eq (2.2) in the μ variable, ρ satisfies the equation
The quantity jμ(r) is the conditional expectation of the number of μRNA within the population in the presence of r molecules of mRNA and it is given by
Before ending this paragraph, we note an alternate way to derive the Fokker-Planck Eq (2.2) from the chemical master equation through the chemical Langevin equation. We refer the interested reader to [13].
2.2. Dynamics of free mRNA without binding
In the case where there is no μRNA binding, namely when c=0, the variables r and μ are independent. Thus, the densitites of the invariant measures satisfying Eq (2.2) are of the form
where λ(μ) is the density of the marginal distrubution of μRNA. From the modelling point of view, it corresponds to the case where there is no feed-forward loop from μRNA. Therefore, only the dynamics on mRNA, and thus ρ0, is of interest in our study. It satisfies the following steady Fokker-Planck equation obtained directly from Eq (2.4),
It can be solved explicitly as we will discuss in Section 3.2.
2.3. Dynamics with binding and fast μRNA
The Fokker-Planck Eq (2.2) cannot be solved explicitly. However, one can make some additional assumptions in order to get an explicit invariant measure providing some insight into the influence of the binding mechanism with μRNA. This is the purpose of the model considered hereafter.
Let us assume the μRNA-mRNA binding rate, the μRNA decay and the noise on μRNA are large. Since the sink term of the μRNA equation is large, it is also natural to assume that the μRNA content is small. Mathematically, we assume the following scaling
for some small constant ε>0. Then (rt,˜μt) satisfies
whose corresponding steady Fokker-Planck equation for the invariant measure then writes, dropping the tilde,
In the limit case where ε→0, one may expect that at least formally, the density fε converges to a limit density ffast satisfying
As r is only a parameter in the previous equation and since the first marginal of fε still satisfies Eq (2.4) for all ε, one should have (formally)
3.
Well-posedness of the models and analytical formulas for solutions
In this section, we show that the three previous models are well-posed. For the Fokker-Planck Eqs (2.6) and (2.7), we explicitly compute the solutions. They involve inverse gamma distributions.
3.1. Gamma and inverse gamma distributions
The expressions of the gamma and inverse gamma probability densities are respectively
and
for x,y∈(0,∞). The normalization constant is given by Cα,β=βα/Γ(α) where Γ is the Gamma function. Observe that by the change of variable y=1/x one has
which justifies the terminology. Let us also recall that the first and second moments of the inverse gamma distribution are
Interestingly enough, we can show (see Appendix A.1 for details and additional results) that inverse gamma distributions with finite first moment (α>1) satisfy a (weighted) Poincaré inequality. The proof of the following proposition is done in Appendix A.1 among more general considerations.
Proposition 3.1. Let α>1 and β>0. Then, for any function v such that the integrals make sense, one has
where for any probability density ν and any function u on (0,∞), the notation ⟨u⟩ν denotes ∫uν.
3.2. Explicit mRNA distribution without binding
In the case of free mRNAs, a solution to Eq (2.6) can be computed explicitely and takes the form of an inverse gamma distribution.
Lemma 3.2. The following inverse gamma distribution
is the only classical solution to Eq (2.6).
Proof. First observe that
Therefore a solution of Eq (3.1) must be of the form
for some constants C1,C2. The first term decays like 1/r at infinity, thus the only probability density ρ0 of this form is obtained for C1=0 and C2=1.
The Poincaré inequality (3.5) tells us that the solution of Lemma 3.2 is also the only (variational) solution in the appropriate weighted Sobolev space. Indeed, we may introduce the natural Hilbert space associated with Eq (2.6),
with a squared norm given by
Then the following uniqueness result holds.
Lemma 3.3. The classical solution ρ0=g1+krσr,crσr is the only solution of Eq (2.6) in X1+krσr,crσr.
Proof. If ρ0 and ~ρ0 are two solutions of Eq (2.6), a straightforward consequence of inequality (3.5) is that ‖ρ0−~ρ0‖X1+krσr,crσr=0. This is obtained by integrating the difference between the equation on ρ0 and ~ρ0 against (ρ0−~ρ0)g−11+krσr,crσr.
Another consequence of the Poincaré inequality is that if we consider the time evolution associated with Eq (2.6) then solutions converge exponentially fast towards the steady state ρ0. This justifies our focus on the stationary equations. The transient regime is very short and equilibrium is reached quickly. We can quantify the rate of convergence in terms of the parameters.
Proposition 3.4. Let ξ solve the Fokker-Planck equation
starting from the probability density ξ(0,r,μ)=ξin(r,μ). Then for all t≥0,
Proof. Observe that ξ−ρ0 solves the unsteady Fokker-Planck equation, so that by multiplying the equation by (ξ−ρ0)g−11+krσr,crσr and integrating in r one gets
Then by using the Poincaré inequality Eq (3.5) and a Gronwall type argument, one gets the result.
3.3. Explicit mRNA distribution in the presence of fast μRNA
Now we focus on the solution of Eq (2.7). The same arguments as those establishing Lemma 3.3 show that the only function M satisfying Eq (2.7) is the following inverse gamma distribution
Then an application of Eq (3.3) yields
It remains to find ρfast which is a probability density solving the Fokker-Planck equation
Arguing as in the proof of Lemma 3.2, one observe that integrability properties force ρfast to actually solve
which yields
where C≡C(cr,cμ,kr,kμ,σr,σμ,c) is a normalizing constant making ρfast a probability density function.
3.4. Well-posedness of the main Fokker-Planck model
Now we are interested in the well-posedness of Eq (2.2), for which we cannot derive explicit formulas anymore. Despite the convenient functional framework introduced in Section 3.2, classical arguments from elliptic partial differential equation theory do not seem to be adaptable to the case c>0. The main obstruction comes from an incompatibility between the natural decay of functions in the space Xα,β and the rapid growth of the term crμ when |(r,μ)|→∞.
However, thanks to the results of [14] focused specifically on Fokker-Planck equations, we are able to prove well-posedness of the steady Fokker-Planck Eq (2.2). The method is based on finding a Lyapunov function for the adjoint of the Fokker-Planck operator and relies on an integral identity proved by the same authors in [15]. The interested reader may also find additional material and a comprehensive exposition concerning the analysis of general Fokker-Planck equations for measures in [16].
First of all let us specify the notion of solution. A weak solution to Eq (2.2) is an integrable function f such that
where the adjoint operator is given by
A reformulation and combination of [14,Theorem A and Proposition 2.1] provides the following result.
Proposition 3.5 ([14]). Assume that there is a smooth function U:Ω→[0,+∞), called Lyapunov function with respect to L, such that
and
where ¯∂Ω=∂Ω∪({+∞}×R+)∪(R+×{+∞}). Then there is a unique f satisfying Eq (3.10). Moreover f∈W1,∞loc(Ω).
Remark 3.6. The method of Lyapunov functions is a standard tool for proving well-posedness of many problems in the theory of ordinary differential equations, dynamical systems... For diffusion processes and Fokker-Planck equations its use dates back to Has'minskii [17]. We refer to [16,Chapter 2], [14] and references therein for further comments on the topic. Let us stress however that Lyapunov functions are not related (at least directly) to the Lyapunov (or entropy) method for evolution PDEs in which one shows the monotony of a functional to quantify long-time behavior.
Remark 3.7. Thanks of the degeneracy of the diffusivities at r=0 and μ=0 and the Lyapunov function condition, one doesn't need supplementary boundary conditions in Eq (3.10) for the problem to have a unique solution. This is different from standard elliptic theory where boundary conditions are necessary to define a unique solution when the domain and the coefficients are bounded with uniformly elliptic diffusivities. Further comments may be found in [14].
Lemma 3.8. Choose any two constants br>ckμ and bμ>ckr. Then, the function U:Ω→R defined by
is a Lyapunov function with respect to L (i.e., it is positive on Ω and it satisfies Eqs (3.12) and (3.13)).
Proof. First observe that condition (3.12) is clearly satisfied. Also, U is minimal at (b−1r,b−1μ) where it takes the value 2 and thus it is positive on Ω. Finally a direct computation yields
and Eq (3.13) follows. Now we state our well-posedness result for the Fokker-Planck Eq (3.10).
Proposition 3.9. There is a unique weak solution f to the steady Fokker-Planck Eq (2.2). Moreover, f is indefinitely differentiable in Ω.
Proof. The existence and uniqueness of a solution f∈W1,∞loc(Ω) is a combination of Proposition 3.5 and Lemma 3.8. From there in any smooth compact subdomain K⊂⊂Ω, we get from standard elliptic theory [18] that f∈C∞(K), since the coefficents are smooth and the operator is uniformly elliptic.
4.
Noise reduction by binding : The case of fast μRNA
In this section we focus on the comparison between the explicit distributions given by Eqs (3.6) and (3.9). We are providing theoretical and numerical evidence that the coefficient of variation (which is a normalized standard deviation) of distribution (3.9) is less than that of distribution (3.6). This quantity called cell to cell variation in the biological literature [5] characterizes the robustness of the gene expression level (the lower the better). We start by performing a rescaling in order to extract the dimensionless parameters which characterize the distributions.
4.1. Dimensional analysis
In order to identify the parameters of importance in the models, we rescale the variables r and μ around characteristic values ˉr and ˉμ chosen to be
These choices are natural in the sense that they correspond to the steady states of the mRNA and μRNA dynamics without binding nor stochastic effects, that is respectively drt=(cr−kr rt)dt and dμt=(cμ−kμ μt)dt. When the noise term is added, it still corresponds to the expectation of the invariant distribution, that is the first moment of ρ0 in the case of mRNA. We introduce fad such that for all (r,μ)∈Ω one has
After some computations one obtains that the Fokker-Planck Eqs (2.2) and (2.3) can be rewritten in terms of fad as
The marginal distributions ρ0 and ρfast are rescaled into dimensionless densities
where Cad0 and Cadfast are normalizing constants depending on the parameters of the model and δ, p and γ are dimensionless parameters. The first parameter
only depends on constants that are independent of the dynamics of μRNAs. The two other dimensionless parameters appearing in the marginal distribution of mRNA in the presence of fast μRNA are
and
Let us give some insight into the biological meaning of these parameters. The parameter γ measures the relative importance of the two mechanisms of destruction of μRNAs, namely the binding with mRNAs versus the natural destruction/consumption. A large γ means that the binding effect is strong and conversely. The parameter p compares the production rate of μRNAs with that of mRNAs. Large values of p mean that there are much more μRNAs than mRNAs produced per unit of time.
Finally, in the Fokker-Planck model (4.2), there are also two other parameters which are
and
The parameter κ compares consumption of μRNA versus that of mRNA by mechanisms which are not the binding between the two RNAs. The parameter ν compares the amplitude of the noise in the dynamics of μRNA versus that of the mRNA.
Remark 4.1. Observe that the approximation of fast μRNA leading to the model discussed in Section 2.3 in its dimensionless form amounts to taking ν=κ=1/ε and letting ε tend to 0.
4.2. Cell to cell variation (CV)
For any suitably integrable non-negative function ν, let us denote by
its k-th moment. The coefficient of variation or cell to cell variation (CV) is defined by
where Exp(⋅) and Var(⋅) denote the expectation and variance. Let us state a first lemma concerning some cases where the coefficient of variation can be computed exactly.
Lemma 4.2. Consider the dimensionless distributions defined in Eqs (4.3) and (4.4). Then one has that
where the variance and coefficient of variation are well-defined only for δ>1. Then for any δ>1, the following limits holds
Proof. The formulas for the moments follow from Eqs (3.3) and (3.4). Then observe that for all r, one has
and
and one can then take limits in integrals by dominated convergence.
Let us give a biological interpretation of the previous lemma. When γ=0 or p=0, which respectively corresponds to the cases where there is no binding between mRNA and μRNA or there is no production of μRNA, the coefficient of variation is unchanged from the case of free mRNAs. The last limit states that if the μRNA production is weaker than the mRNA production, then in the regime where all μRNA is consumed by binding with mRNA, the coefficient of variation is also unchanged.
Outside of these asymptotic regimes, the theoretical result one would like to have is the following.
Conjecture 4.3. For any δ>1, γ,p>0 and one has CV(ρδ,γ,pfast) ≤ CV(ρδ0).
At the moment, we are able to obtain the following uniform in γ and p bound
which holds for all δ>2, γ>0 and p≥0. The result is proved in Proposition in the Appendix. Observe that Cδ≥CV(ρδ0) but asymptotically
so that Cδ is fairly close to CV(ρδ0) for large δ.
In the next section we provide numerical evidence that it should be possible to improve the right-hand side of the bound (4.12) and prove Conjecture 4.3. Let us also mention that using integration by parts formulas it is possible to establish a recurrence relation between moments. From there one can infer the inequality of Conjecture 4.3 for subsets of parameters (γ,p). As the limitation to these subsets is purely technical and do not have any particular biological interpretation we do not report these results here.
4.3. Exploration of the parameter space
Now, we explore the space of parameters (δ,γ,p) in order to compare the cell to cell variation in the case of fast μRNA and in the case of free mRNA.
In order to evaluate numerically the cell to cell variation we need to compute mk(ρδ,γ,pfast), for k=0,1,2. Observe that after a change of variable these quantities can be rewritten (up to an explicit multiplicative constant depending on parameters)
with fk(s)=s2−k(1+s/(γδ))pγδ. For the numerical computation of these integrals, we use a Gauss-Laguerre quadrature
which is natural and efficient as we are dealing with functions integrated against a gamma distribution. We refer to [19] and references therein for the definition of the coefficients ωNi and quadrature points xNi. The truncation order N is chosen such that the numerical error between the approximation at order N and N+1 is inferior to the given precision 10−8 when p≤1. For p≥1, the function fk may take large values and it is harder to get the same numerical precision. In the numerical results below the mean error for the chosen sets of parameters with large values of p is around 10−4 and the maximal error is 10−2. This is good enough to comment on qualitative behavior. The code used for these numerical simulations is publicly available on GitLab [12].
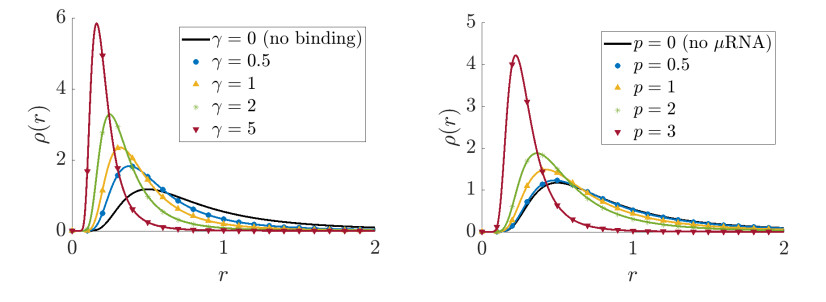
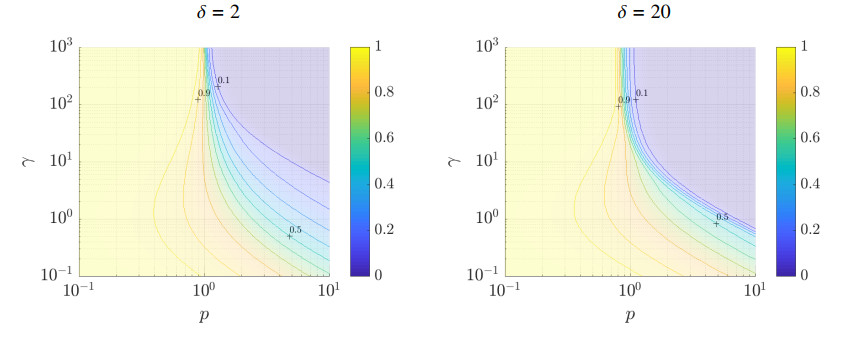
We plot the relative cell to cell variation CV(ρδ,γ,pfast)/CV(ρδ0) with respect to γ and p for two different values of δ. The results are displayed on Figure 1. Then, on Figure 2, we draw the explicit distributions ρδ,γ,pfast for various sets of parameters and compare it with ρδ0.
The numerical simulations of Figure 1 suggest that the bound (4.12) is non-optimal and Conjecture 4.3 should be satisfied. Observe also that the asymptotics of Lemma 4.2 are illustrated.
From a modeling point of view, these simulations confirm that for any choice of parameter, the presence of (fast) μRNA makes the cell to cell variation decrease compared to the case without μRNA. Moreover, the qualitative behavior with respect to the parameters makes sense. Indeed we observe that whenever enough μRNA is produced (p≥1), the increase of the binding phenomenon (γ→∞) makes the cell to cell variation decay drastically.
5.
Noise reduction by binding for the main Fokker-Planck model: numerical evidence
In this section, we compute the gene expression level of the main model described by Eq (2.2). In this case, as there is no explicit formula for the solution, we will compute an approximation of it using a discretization of the Fokker-Planck equation. In order to compute the solution in practice, we restrict the domain to the bounded domain Ωb=[rmin,rmax]×[μmin,μmax]. Because of the truncation, we add zero-flux boundary conditions in order to keep a conservative equation. It leads to the problem
5.1. Reformulation of the equation
In order for the numerical scheme to be more robust with respect to the size of the parameters, we discretize the equation in dimensionless version according to Eq (4.2). It will also allow for comparisons with numerical experiments of the previous sections.
As the coefficients in the advection and diffusion parts of Eq (4.2) grow rapidly in r, μ and degenerate when r=0 and μ=0, the design of an efficient numerical solver for Eq (4.2) is not straightforward. Moreover a desirable feature of the scheme would be a preservation of the analytically known solution corresponding to γ=0. Because of these considerations we will discretize a reformulated version of the equation in which the underlying inverse gamma distributions explicitly appear. It will allow for a better numerical approximation when r and μ are either close to 0 or large. The reformulation is the following
with the associated no-flux boundary conditions and where the functions h(1) and h(2) are given by
and
5.2. Presentation of the numerical scheme
We use a discretization based on the reformulation (5.2). It is inspired by [20] and is fairly close to the so-called Chang-Cooper scheme [21].
We use a finite-volume scheme. The rectangle Ωb is discretized with a structured regular mesh of size Δr and Δμ in each respective direction. The centers of the control volumes are the points (ri,μj) with ri=Δr/2+iΔr and μj=Δμ/2+jΔμ for i∈{0,…,Nr−1} and j∈{0,…,Nμ−1}. We also introduce the intermediate points ri+1/2 with i∈{−1,…,Nr−1} and μj+1/2 with j∈{−1,…,Nμ−1} defined with the same formula as before. The approximation of the solution on the cell (i,j) is denoted by
The scheme reads, for all i∈{0,…,Nr−1} and j∈{0,…,Nμ−1},
where the fluxes are given by a centered discretization of the reformulation (5.2), namely
and
One can show that the scheme (5.5) possesses a unique solution which is non-negative by following, for instance, the arguments of [22,Proposition 3.1]. Moreover, by construction, the scheme is exact in the case γ=0.
Remark 5.1 (Choice of rmin, rmax, μmin, μmax). Clearly f decays faster at infinity than ρ0 since the convection term coming from the binding phenomenon brings mass closer to the origin. Therefore an appropriate choice for rmax and μmax, coming from the decay of the involved inverse gamma distributions, should be (say) r−δmax≤10−8 and μ−δκ/νmax≤10−8 so that the error coming from the tails of the distributions in the computation of moments is negligible. Similarly, near the origin the distributions decay very quickly to 0 (as exp(−1/⋅)). Therefore μmin, rmin can be taken not too small without influencing the precision in the computation of moments of the solution. In practice, we chose μmin=rmin=0.06. Observe that even if nothing prevents the choice μmin=rmin=0 on paper, one experiences in practice a bad conditioning of the matrix which has to be inverted for solving the scheme.
Remark 5.2 (Implementation). Observe that the matrix which has to be inverted in order to solve the scheme is not a square matrix because of the mass constraint (which is necessary to ensure uniqueness of the solution). In practice, in order to solve the corresponding linear system MF=B where F=(fij)ij and B=(0,…,0,1)∈RNrNμ+1 and M∈R(NrNμ+1)×NrNμ we use the pseudo-inverse yielding F=(MtM)−1MtB. Finally the use of a sparse matrix routine greatly improves the computation time. Our implementation was made using Matlab. The code is publicly available on GitLab [12].
5.3. Numerical results
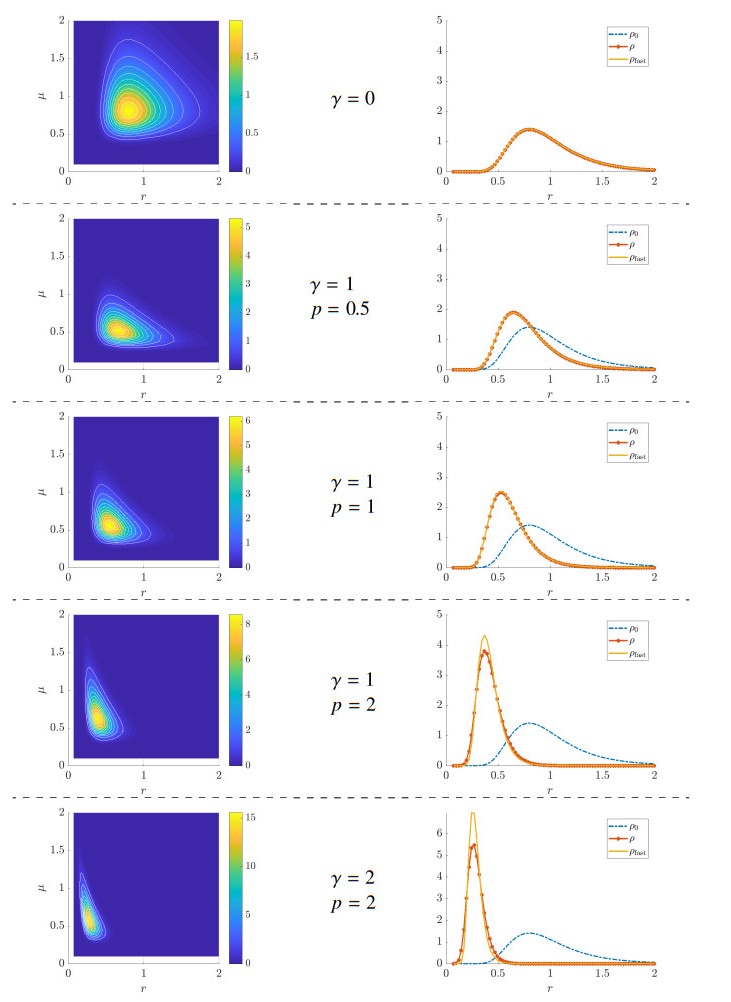
In our test cases we use the following parameters: rmin=0.06, rmax=5, μmin=0.05, μmax=5, δ=8, Nr=70, Nμ=200, κ=1, ν=1.
On Figure 3 we compare the distribution functions f(r,μ) obtained for various sets of parameters (p,γ). We also draw the corresponding marginal ρ(r) as well as ρ0 and ρfast. We observe that for small values of p, ρfast is a good approximation of ρ. For larger values it tends to amplify the phenomenon of variance reduction.
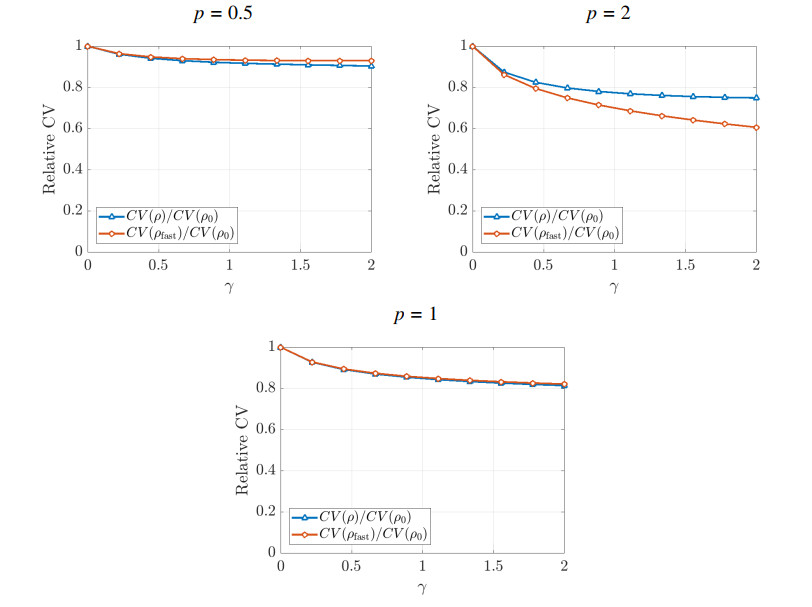
In order to confirm that the main Fokker-Planck model reduces the coefficient of variation as soon as γ>0 we draw on Figure 4 the coefficient of variation for each distribution ρ,ρfast relatively to that of ρ0 for several values of p. We observe that indeed, the coefficient of variation is reduced. As in the case of fast μRNA, the decay is more pronounced when the production of μRNA is higher than that of mRNA, namely when p>1. Interestingly enough, one also notices that the approximation ρfast increases the reduction of CV when p>1 and diminishes it when p<1. A transition at the special value p=1 was already observed on Figure 1.
6.
Comments on the choice of noise
In this section, we discuss the influence of the type of noise in the Fokker-Planck models. Let us go back to the system of stochastic differential equations considered at the beginning and generalize it as follows
with D some given function. In the models of the previous sections we chose D(x)=x2. On the one hand it is natural to impose that D(x) vanishes when x→0 in order to preserve the non-negativity of rt and μt. On the other hand it is clear that the growth at infinity influences the tail of the equilibrium distribution which solves the corresponding Fokker-Planck equation. With a quadratic D we obtained algebraically decaying distributions.
Nevertheless one may wonder if the decay of cell to cell variation due to μRNA would still be observed if D is changed so that it involves distributions with faster decay at infinity. In order to answer this question, we choose a simple enough function D so that we can still derive analytical formulas for distributions of mRNA without binding and mRNA in the presence of "fast" μRNA. Let us assume that
6.1. Explicit formulas for distribution of mRNAs
In terms of modeling we may argue as in Section 2 and Section 3 in order to introduce the stationary probability distribution of mRNA without binding ˜ρ0 which solves
It may still be solved analytically and one finds a gamma distribution
instead of an inverse gamma distribution in the quadratic case. The normalization constant is given in Section 3.1.
In the case of fast μRNA, we may once again follow the method of Section 2 and Section 3 and introduce ˜ρfast solving
where the conditional expectation of the number of μRNA within the population with r mRNA is given by
A direct computation then yields
with C≡C(cr,cμ,c,kr,kμ,σr,σμ) a normalizing constant.
Remark 6.1. Observe that the conditional expectation of the number of μRNA within the population with r mRNA is unchanged, namely ˜jfast(r)=jfast(r). More generally, the expectation of a univariate process (Xt)t satisfying an SDE with linear drift dXt=(a+bXt)dt+√2σ(Xt)dBt does not depend on the diffusion coefficient σ as its density g satisfy ∂tg(t,x)+∂x((a+bx)g(t,x))−∂2xx(σ(x)g(t,x))=0, so that multiplying by x and integrating yields dE[Xt]=(a+bE[Xt])dt on its expectation E[Xt]. The argument also holds for multivariate processes.
6.2. Dimensional analysis
Once again we seek the parameters of importance among the many parameters of the model by a dimensional analysis. The characteristic value of r remains ˉr=cr/kr as it is the expectation of ˜ρ0. After rescaling we find the new distribution
and
where the parameters p and γ are given by Eqs (4.7) and (4.6) respectively and still quantify the intensity of the binding and the respective production of μRNA versus mRNA. The new parameter η is given by
In the context of a dimensional analysis, let us mention that it would be inaccurate to compare η and δ as the σr (and σμ) do not represent the same quantity depending on the choice of D. For D(r)=r2 it has the same dimension as kr so δ=kr/σr is the right dimensionless parameter. Here it has the same dimension as cr, which justifies the introduction of η.
6.3. Numerical computation of the cell to cell variation
The expectation, variance and coefficient of variation of ˜ρ0 are explicitly given by
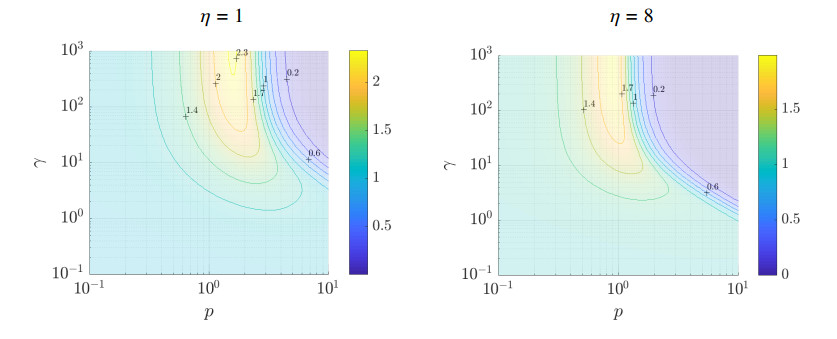
As there is no explicit formula for the coefficient of variation of ˜ρfastη,γ,p we evaluate it numerically as in Section 4.3. The results are displayed on Figure 5. We observe that unlike the case of a quadratic diffusion coefficient the relative cell to cell variation, i.e., the cell to cell variation in the presence of μRNA relative to cell to cell variations of the free case, is not unconditionally less than 1. For a large enough production of μRNA, it eventually decays when the binding effect is very strong. However for smaller production of μRNA or when the binding is weak, the effect is the opposite as the relative cell to cell variation is greater than 1. This is not satisfactory from the modeling point of view.
In conclusion the choice of noise is important in this model. An unconditional cell to cell variation decay in the presence of μRNA is observed for quadratic noise only. While other choices of noise may still lead to similar qualitative results, the choice D(r)=r2 allowed us to derive explicit formulas for the approximate density ρfast which, as numerical simulations show, is fairly close to the marginal ρ corresponding to the solution of the main Fokker-Planck model.
7.
Concluding remarks and perspectives
In this paper, we introduced a new model describing the joint probability density of the number of mRNA and μRNA in a cell. It is based on a Fokker-Planck equation arising from a system of chemical kinetic equations for the number of two RNAs. The purpose of this simple model was to provide a mathematical framework to investigate how robustness in gene expression in a cell is affected by the presence of a regulatory feed-forward loop due to production of μRNAs which bind to and deactivate mRNAs.
Thanks to the combined use of analytical formulas and numerical simulations, we showed that robustness of gene expression is indeed affected by the presence of a feed-forward loop involving μRNA production. However, whether the effect is regulatory or de-regulatory strongly depends on the assumptions made on the type of noise affecting both mRNA and μRNAs production. In the case of geometric noise (the diffusivity being quadratic in the solution itself), the effect is to reduce the spread of the distribution as the reduction of the coefficient of variation shows. In the case of sub-geometric noise (the diffusivity being only linear in the solution itself), the effect increases the spread as shown by the increase of the coefficient of variation. We may attempt an explanation by comparing the mRNA distribution in the absence of μRNA and in the limit of fast μRNA in the two cases. In the quadratic diffusivity case, both distributions are fat-tailed (i.e., they decay polynomially with the number of unbound mRNA molecules r, see Eqs (3.6) and (3.9)) but the rate of decay at infinity is modified by the presence of μRNAs. On the other hand, in the linear diffusivity case, both decay exponentially fast (see Eqs (6.1) and (6.2)) and the exponential rate of decay is the same with or without μRNAs. We propose that this might be the reason of the difference: In the quadratic diffusivity case, the change in polynomial decay allows to greatly reduce the standard deviation without affecting too much the mean, which results in a reduction of the coefficient of variation. In the linear diffusivity case, the exponential tail is not modified, which implies that the core of the distribution must be globally translated towards the origin, which affects the mean and the standard deviation in a similar way and does not systematically reduce the coefficient of variation. Which type of noise corresponds to the actual data is unknown at this stage. While quadratic diffusivity seems a fairly reasonable assumption (it is used in a number of contexts such as finance), it would require further experimental investigations to be fully justified in the present context. This discussion shows that the effect of μRNA on noise regulation of mRNA translation is subtle and not easily predictable.
Along the way we provided theoretical tools for the analysis of the Fokker Planck equation at play and robust numerical methods for simulations. As the main biological hypothesis for the usefulness of μRNA in the regulation of gene expression is based on their ability to reduce external noise, we also discussed the particular choice of stochasticity in the model.
There are several perspectives to this work. A first one would be the calibration of the parameters of the model from real-world data. This would allow to quantify more precisely the amount of cell-to-cell variation reduction due to μRNA, thanks to the thorough numerical investigation done in this contribution of the effects of the parameters of the model. Besides, another perspective would be an improvement of inequality (4.12) to the conjecture (4.3). This would bring a definitive theoretical answer to the hypothesis of increased gene expression level in the simplified model of "fast" μRNAs. One may also look into establishing a similar inequality for the general model. Finally, the gene regulatory network in a cell is considerably more complex than the simple, yet enlightening in our opinion, dynamics proposed in this paper. A natural improvement would be the consideration of more effects in the model, such as the production of the transcription factor, or the translation of mRNA into proteins, among many others.
Acknowledgments
PD acknowledges support by the Engineering and Physical Sciences Research Council (EPSRC) under grants no. EP/M006883/1 and EP/N014529/1, by the Royal Society and the Wolfson Foundation through a Royal Society Wolfson Research Merit Award no. WM130048 and by the National Science Foundation (NSF) under grant no. RNMS11-07444 (KI-Net). PD is on leave from CNRS, Institut de Mathématiques de Toulouse, France. MH acknowledges support by the Labex CEMPI (ANR-11-LABX-0007-01). SM acknowledges support by the CNRS–Royal Society exchange projects "CODYN" and "Segregation models in social sciences" and the Chaire Modélisation Mathématique et Biodiversité of Véolia Environment - École Polytechnique - Museum National d’Histoire Naturelle - Fondation X. All authors would like to thank Prof. Matthias Merkenshlager from Imperial College Institute of Clinical Sciences for bringing this problem to their attention and stimulating discussions.
Conflict of interest
The authors declare no conflict of interest.
Data statement
No new data were collected in the course of this research.
Appendix
A. Complementary results
A.1. Poincaré inequalities for gamma and inverse gamma distributions
In this section we give a elementary proof of the 1D version of the Brascamp and Lieb inequality (see [23,Theorem 4.1], [24]), which is an extension of the Gaussian Poincaré inequality in the case of log-concave measures. This allows us to derive a weighted Poincaré inequality for the gamma distribution and deduce, by a change of variable, a similar functional inequality for the inverse gamma distribution.
Proposition A.1. Let I⊂R be an open non-empty interval and V:I→R a function of class C2. Assume that
(i) V is strictly convex;
(ii) e−V is a probability density on I;
(iii) V tends to +∞ at the extremities of I.
Then, for any suitably integrable function u, one has
where for a density ν the notation ⟨u⟩ν denotes ∫uν.
Proof. Without loss of generality, as one may replace u with u−⟨u⟩e−V, we assume that ⟨u⟩e−V=0. We also assume that u is of class C1 and compactly supported in I and one can then extend a posteriori the class of admissible function by a standard density argument. Then, using (ii) one has
Now using the Cauchy-Schwarz inequality and assumption (i) one has
Then take any point x0∈I and define
so that the inequality rewrites
Now just expand the right-hand side and use Fubini's theorem on each term as well as assumptions (ii) and (iii) to obtain
One concludes by integrating the right-hand side by parts and observing that boundary terms vanish again by assumption (iii).
Remark A.2. The proof is an adaptation of the original proof of the (flat) Poincaré-Wirtinger inequality by Poincaré.
Observe that for I=R and V(x)=x2/2, one recovers the classical Gaussian Poincaré inequality.
Remark A.3. The inequality is sharp. It is an equality for functions of the form u(x)=aV′(x)+b, with a,b∈R if V is such that V′(x)e−V(x) tends to 0 at the boundaries, and only for constant functions otherwise (i.e., a=0 and b∈R).
From the Brascamp-Lieb inequality, we now infer Poincaré inequalities for gamma and inverse gamma distributions.
Proposition A.4. Let α>1 and β>0. Then, for any functions u,v such that the integrals make sense, one has
and
where for a probability density ν the notation ⟨u⟩ν denotes ∫uν.
Proof. The first inequality is an application of Eq (A.1) with V(x)=βx−(α−1)ln(x)−ln(Cα,β), where Cα,β=βα/Γ(α). Then take v(y)=u(1/y) and make the change of variable y=1/x in all the integrals of Eq (A.2) to get the result.
Remark A.5. To the best of our knowledge the classical Bakry and Emery method does not seem to apply to show directly the functional inequalities of Proposition A.4. Let us give some details. In order to show a Poincaré inequality of the type
for V as in Proposition A.1, it is sufficient that D and V satisfy the following curvature-dimension inequality
for some positive constant λ1>0. We refer to [25,26] for the general form of the latter Bakry-Emery condition (for multidimensional anisotropic inhomogeneous diffusions) and to [27] or [28] for the simpler expression in the case of isotropic inhomogeneous diffusion, as discussed here. In the case of the inequalities (A.2) and (A.3), one has respectively D(x)=x2/(α−1), V(x)=βx−(α−1)ln(x)−ln(Cα,β) and D(y)=y2/(α−1), V(y)=β/y+(α+1)ln(y)−ln(Cα,β), which yields respectively R(x)=βx3/(α−1)2 and R(y)=βy/(α−1)2. As claimed above, neither Eq (A.2) nor Eq (A.3) satisfy the condition (A.4). One also observes that in both cases the curvature-dimension inequality fails because of a degeneracy at one end of the interval.
Let us finally mention that there are in the literature other occurrences of Poincaré and more generally convex Sobolev inequalities for gamma distributions [29,30,31,32]. However, we found out that the diffusion coefficient is always taken of the form D(x)=4x/β. This weight, associated with the gamma invariant measure, corresponds to the Laguerre diffusion Lα,βf(x)=βxf"(βx)−(α−βx)f′(βx). This operator differs from the adjoint of the one appearing in our model given by Eq (2.6). In this case, one can check that the curvature-dimension condition of Bakry and Emery is satisfied as soon as α≥1/2.
A.2. An upper bound for the relative cell to cell variation
Proposition A.6. One has the bound
which holds for all δ>2, γ>0 and p≥0.
Proof. The bound is a consequence of the Prékopa-Leindler inequality (see [23] and references therein) which states that if f,g,h:Rd→[0,+∞) are three functions satisfying for some λ∈(0,1) and for all x,y,
then
We use it with λ=1/2, f(x)=(1+x)γpδxδ−2e−δγx if x≥0 and f(x)=0 if x<0, g(x)=x2f(x) and h(x)=(1+C2δ)1/2xf(x). The condition (A.5) is then equivalent to
which is satisfied as the term between brackets is always greater than 1 and the function z↦z[(z+z−1)/2]δ−1, z>0 is bounded from below by (1+C2δ)−1/2, where Cδ is given in Eq (4.12). Then with the change of variable x′=1/(γx) in the integrals of Eq (A.6), one recovers Eq (4.12).









 DownLoad:
DownLoad: