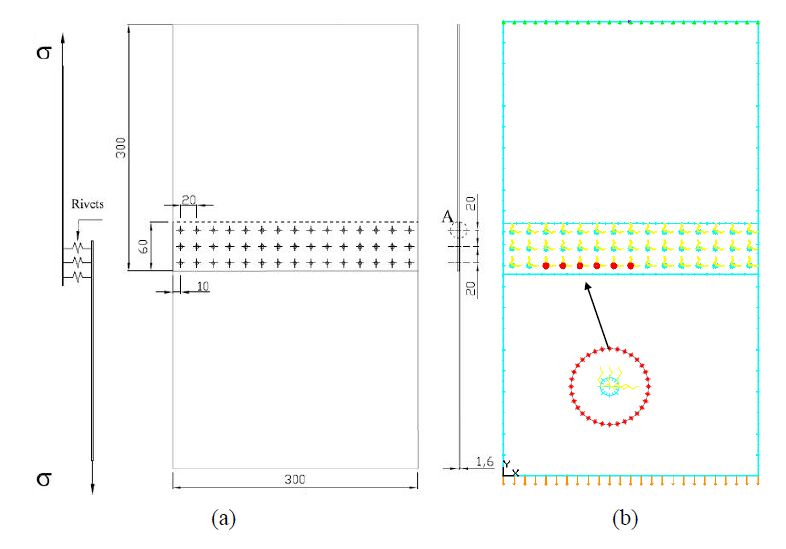
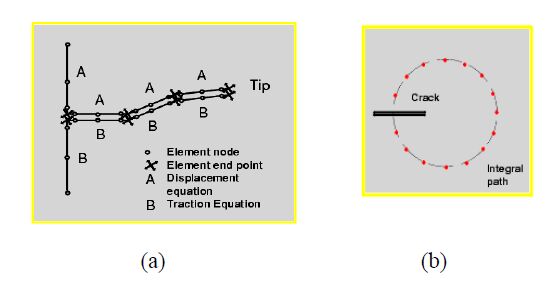
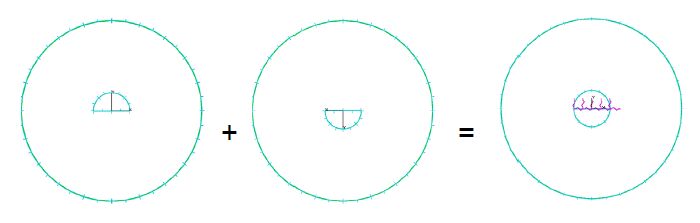
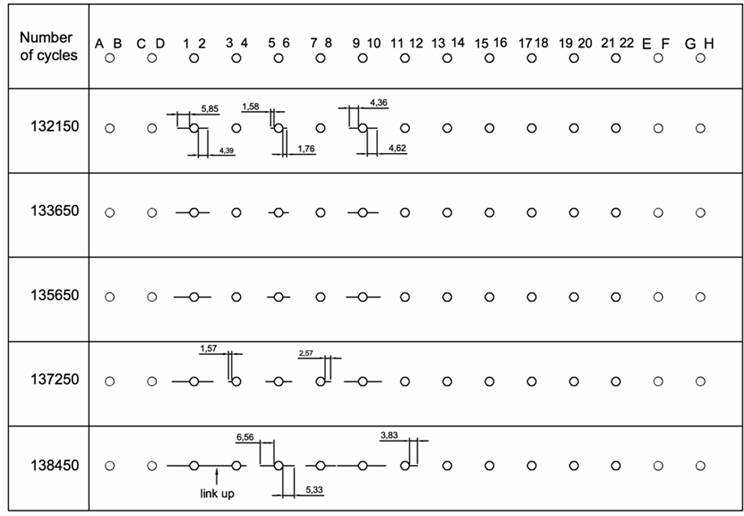
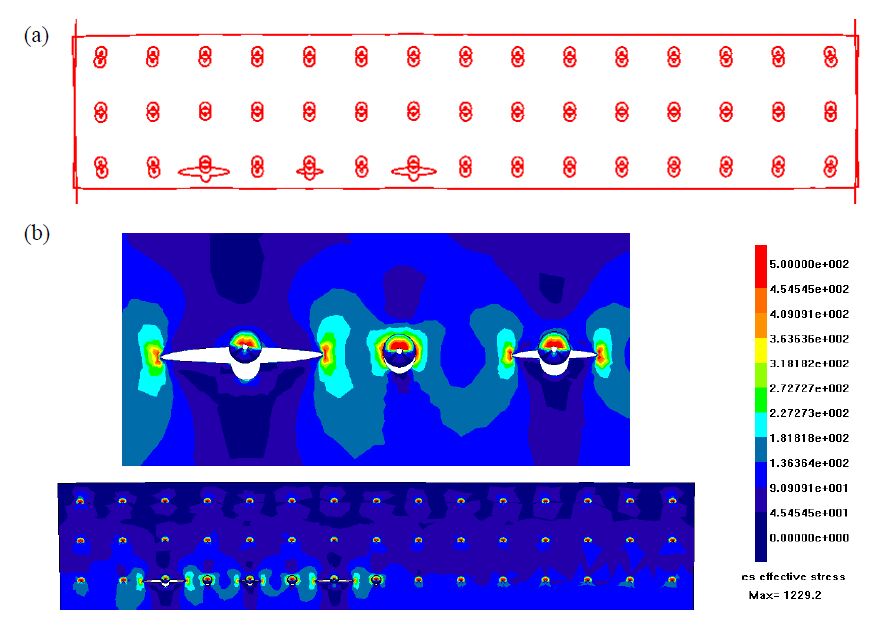
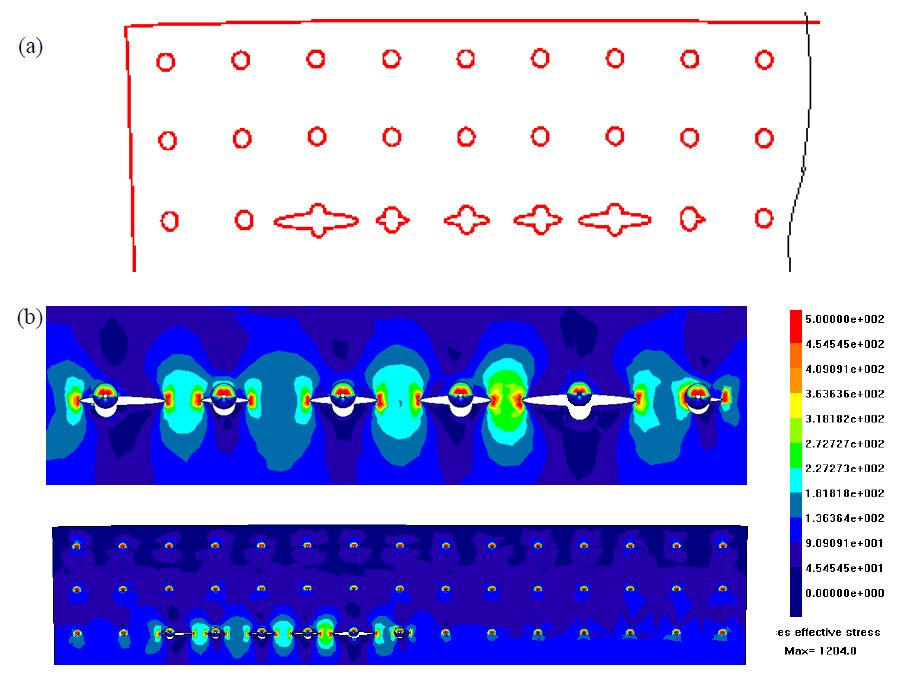
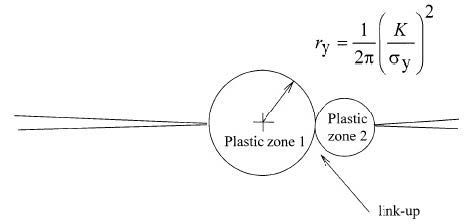
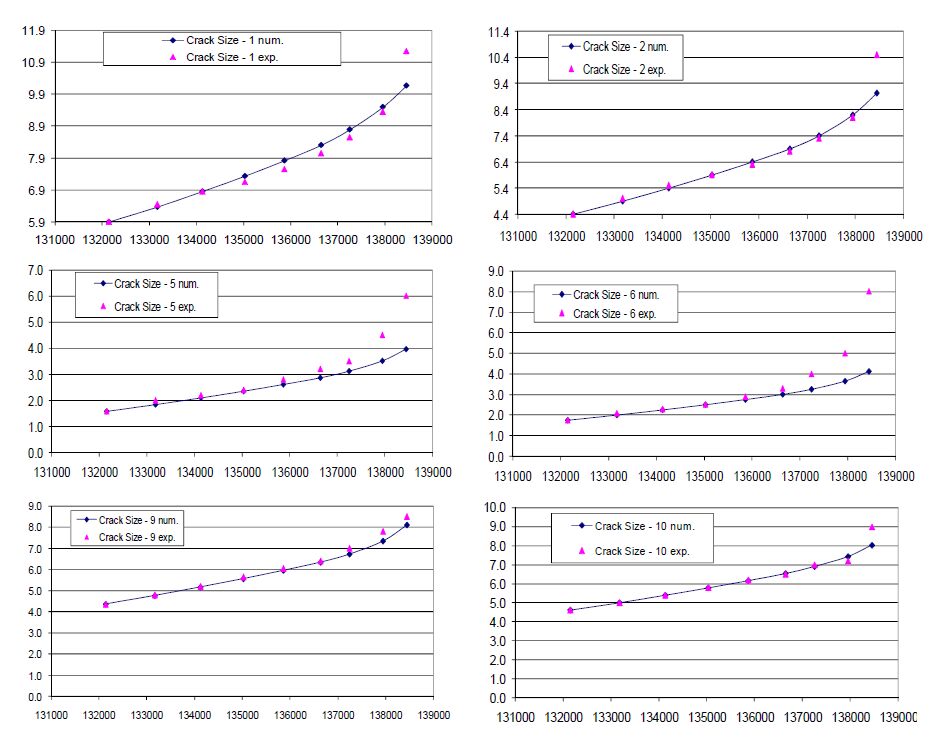
The fatigue behavior of a riveted lap joint is analyzed with the Dual Boundary Element Method (DBEM). A Multiple Site Damage (MSD) scenario is obtained from the simultaneous initiation, from the most loaded holes, and propagation of different cracks. The analysis is bidimensional, with no allowance for secondary bending effects that are judged negligible, due to the reduced thicknesses of the involved plates. The lap joint considered has three rivet rows and undergoes a uniaxial fatigue load. When the cracks are short in comparison to plate thickness and hole diameters the allowance for nonlinear pin-rivet contact condition is provided. Crack faces are meshed using “discontinuous” quadratic elements and Stress Intensity Factors (SIFs) are calculated by the J-integral approach. The crack growth rate is calculated by the well-known Paris’ law, getting a satisfactory correlation between numerical and experimental findings (the latter available from literature).
1.
Introduction
The first cases of AIDS were reported in the United States in June 1981, and even after four decades, HIV/AIDS continues to be one of the biggest global epidemic of infectious disease the world faces. Since the beginning of the epidemic, 79.3 million (55.9–110 million) people have been infected with the HIV virus and 36.3 million (27.2–47.8 million) people have died of HIV. Globally, 37.7 million (30.2–45.1 million) people were living with HIV at the end of 2020 [1]. Extensive research has been performed by researchers from different disciplines, e.g., Biology, Mathematics, Medicine, Public Health and Pharmaceutical Industries, trying to suppress the infection, while curbing or even eliminating the spread of HIV [2,3,4,5,6].
Opioids are a broad group of pain-relieving drugs that work by interacting with opioid receptors in human cells, resembling opium in addictive properties or physiological effects. This class of drugs include the illegal drug heroin, synthetic opioids such as fentanyl, and pain relievers available legally by prescription, such as oxycodone, hydrocodone, codeine, morphine, and many others. The opioid epidemic is one of the greatest public health problems in the USA. Opioid overdose death rates have increased steadily for more than a decade and doubled in the period 2013–2017, when the highly potent synthetic opioid fentanyl entered the drug supply [7]. Evidence supports that using prescription opioids can lead to opioid use disorder, and before 2010, the majority of deaths were linked to prescription opioids. Opioid use disorder is chronically relapsing, and requires chronic disease management [8].
In 1972, Hughes and Crawford introduced epidemiological field methodology to describe research and intervention in urban heroin spread. They concluded that "contagious" individuals tend to be in the early stages of heroin experimentation or addiction and to curb the spread, prevention and early intervention, along with more availability of treatment option would be effective [9]. In 1979, Mackintosh and Stewart introduced an exponential model to show that the spread of heroin usage follows an epidemic pattern and concluded that early intervention is key to stop the heroin epidemic from spreading [10]. Battista et al. investigated a mathematical model that considered opioid addiction originating from prescribed drug usage. The model considered illicit drug usage and treatment as well [11]. They reached the conclusion that to curb the prescription generated opioid epidemic, combatting addiction should be the primary control strategy.
The HIV and opioid epidemics are intimately linked, and not just because the demographic suffering most from both the epidemics are similar, people who are young, previously healthy and already stigmatized in some way [12]. People living with HIV often suffer from chronic pain. They are therefore prescribed opioids more often and at higher doses than people who do not have HIV, and disproportionately experience risk factors for substance use disorder, which suggests they could be at increased risk of the misuse of opioids. Opioid misuse among adults receiving ART (Anti-retroviral Therapy) is associated with inadequate ART adherence, insufficient durable viral suppression, and higher risk of HIV transmission to sexual partners [13]. Certain prescribed opioids for pain management also work as immunosuppressants, and increase infection risks, and HIV infected people are more susceptible to these effects [14]. It is also possible that HIV related neuropathogenesis in patients may be more severe, in case of significant opioid usage interfering with the ART treatment [15].
Opioids are associated with HIV risk behaviors such as needle sharing when infected and risky sexual behaviors, and have been linked to outbreaks of HIV and viral hepatitis. People who are addicted to opioids are also at risk of turning to other ways to get the drug, including trading sex for drugs or money, which increases HIV risk [16].
If the HIV infected and opioid dependent person is receiving treatment for both ailments simultaneously, research has shown that treatment for Opioid Use Disorder can help with HIV viral suppression, adherence to antiretroviral therapy, and overall mortality for patients [17].
In 2020, Duan et al. proposed a model of coinfection, featuring the joint spread of HIV and Heroin usage, and concluded that in the United States, the two disease are in a state of coexistence. Further conclusion was the best control strategies would be to target the drug abuse epidemic, and to neutralize HIV risky behavior among drug users [18].
To model the spread of the disease in the population, it is to be noted that the pathogen is in dynamic interplay with each host body's immune system. The host's propensity to transmit the pathogen or die from it depends on the amount of the pathogen in the system as well as the intensity of the immune response. The spread of diseases on a population level therefore depends on these within-host disease characteristics of infectious individuals [19]. Following a method similar to Gilchrist and Sasaki's nested approach [20], in this paper we form an immuno-epidemiological model, where the within-host model is a simple pharmacokinetic model depicting both HIV and opioid usage. The between host model is an age structured expansion of the model utilized in [18]. The model developed addresses the question, "What control strategies will best combat the inter-connected spread of both the epidemics?"
The paper is organized as follows: In Section 2 the within-host model of HIV, and the subsequent modification to include opioid drug usage is introduced. Further, parameters for the models are estimated by fitting to data, and identifiability analysis is performed on both the models. In Section 3 the between-host model is introduced, along with the linking parameters to create the immuno-epidemiological model; Basic reproduction numbers for both the epidemics are defined, and stability analysis is performed for the disease free equilibrium. Both invasion numbers are defined and stability analysis is done on the boundary equilibriums. In Section 4 the parameters of the between-host model are estimated and sensitivity analysis is conducted on the invasion numbers, with respect to important parameters of the between-host model. Section 5 summarizes our results obtained, and Section 6 contains the Appendix.
2.
Within-host models of HIV infection and opioid addiction
Before introducing a within-host model of HIV infection and opioid addiction, we first start with the well-known model of HIV [4,21].
Here, T(t) denotes the number target cells, specifically the number of CD4 cells per ml, Ti(t) denotes the number of infected target cells and V(t) denotes the virus (HIV), measured as vRNA copies per ml of plasma. Target cells are produced at rate λ and cleared at rate d. Virus infection of target cells is modeled by the mass action term βVT. Infected cells die at a rate δ and new viral particles are produced at a rate π. The clearance rate of the virus is denoted by c.
We modify the within-host model (M1) by explicitly including the opioid drug concentration, C(t), (mg of opioid per kg of the host), and its impact on the average susceptibility of target cells:
Opioid is taken at doses Λ and it is degraded at rate dc. Prior within-host models of HIV and opioids have been developed in [22], where the authors suggests that the morphine increases the susceptibility of target cells to HIV. Based on that result, we model the infection rate of target cells by HIV in the presence of opioid as
where C0 is the half saturation constant, β is the transmission coefficient in the absence of opioid and β1 is a maximal increase in infection rate due to opioids. The resulting within-host model is a pharmacokinetic type of model.
2.1. Parameter estimation
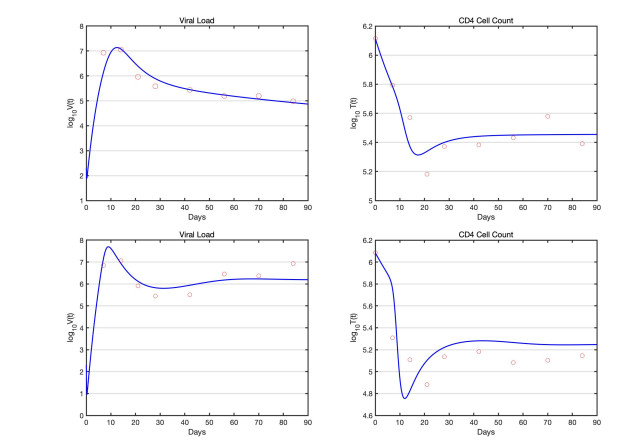
We use the viral load and CD4 measurements collected from 12 rhesus macaques in the experiment [23] to validate the within-host model of HIV and opioid addiction. The 12 animals were divided into two equal groups: six monkeys were morphine addicted and six monkeys served as controls. The simian-human immunodeficiency (SIV) virus was administered intravenously to all 12 animals, while 6 of them were given 5 mg/kg morphine three times a day to induce morphine addiction [23]. The averaged viral load and CD4 count of both the morphined and control groups are used to estimate within-host model parameters, which are as shown in Table 1.
In compact form the within-host models (M1) and (M2) can be rewritten as
where x denote the state variables of the system. The system (x(t)) evolves in time, depending on the parameters (p) and the initial conditions (x0), while we observe the quantities (y) which are functions of the state variables and model parameters. We assume that both observations, y(t)=(y1(t),y2(t)), (viral load and CD4 count) are contaminated with measurements errors Ei and Ej respectively
Clearly,
The measurement errors cause the observations to deviate from their smooth path V(t) and T(t) and satisfy the following form
where ϵi and ϵj are independent and identically distributed with mean zero and constant variance σ20. Thus the observations, Yi1 and Yj2 have mean h1(x(ti),p), h2(x(tj),p) and variances h1(x(ti),p)2σ20, h2(x(tj),p)2σ20, respectively. We estimate the parameters of the within-host models (M1) and (M2) by fitting the logarithm of the predicted viral load and CD4 count to the log of the data in Table 1 via the following optimization problem.
where ω1 and ω2 are appropriate weights. The optimization problem is just a least squares on the logarithms of data points. The weights are picked so that the range of the expressions in two summation terms are about the same magnitude.
The structural identifiability analysis of model (M2) revealed that the within-host model is unidentifiable due to parameter correlations given in (2.11) and (2.12) (explained in detail in the following section). To improve the parameter identifiability, we fix parameters, c,Λ and dc. It is worth mentioning at this point that, this would only improve the identifiability, but it would not result in structurally identifiable model because of the correlations between β,β1 and C0 in models (2.11) and (2.12). We fix the viral clearance rate as c=23 day−1 [22], and Λ=15 mgkgday. The half life of morphine is 3 hours, thus we fixed dc=5.5 day−1. Estimating the within-host model M2 parameters, when c,Λ and dc are fixed, reveals that β=0 (see Table 2). So we update the HIV infection rate of target cells in an addicted host to
We then refit the within-host model (M2) by setting β=0, and the estimated values are presented in Table 2. The fit of within-host models (M1) and (M2) are given in Figure 1.
2.2. Structural identifiability
In order to validate the within-host models with data, it is crucial to perform identifiability analysis. The first step in identifiability analysis is the structural identifiability. Structural identifiability is the property of the within-host model and the analysis assumes ideal, noise free data. To be specific it assumes that the smooth observations for the whole time interval are given. We use differential algebra approach in studying the structural identifiability analysis of the within-host models (M1) and (M2). For a review of other structural identifiability methods, we refer the reader to [24]. The first step in differential algebra approach is to obtain the input-output equations. We eliminate the unobserved state variable which is the infected target cell population, Ti from model (M1) to obtain the following equivalent model (2.5). Within the identifiability analysis literature, we call the resulting equivalent system as input-output equations.
input-output equations for the within-host model (M1):
Solving input-output equations is equivalent to solving the model (M1) for the viral load and target cell population. In the equivalent system, the viral load and target cell states depend on the parameters p={λ,β,d,δ,π,c}. Structural identifiability of a within-host model using differential algebra approach has the following definition [24,25,26,27].
Definition 2.1. Let c(p) denote the coefficients of the input-output equations where p is the vector of model parameters. We say that the within-host model is structured to reveal its parameters from the observations if and only if
Following the definition of the structural identifiability, suppose that another set of parameters q={ˆλ,ˆβ,ˆd,ˆδ,ˆπ,ˆc} would produce the same viral load and target cell populations. Thus first we would have
Let c(p) and c(q) denote the coefficients of the differential polynomials in models (2.5) and (2.6) respectively. Since both models (2.5) and (2.6) are assumed to produce the same observations, solving the system of nonlinear equations c(p)=c(q),
we obtain two sets of solutions,
and
So, we conclude that the model (M1) is not structured to reveal all its parameters from the viral load and CD4 count data. Only the parameters λ,β,π and d can be uniquely identified. The within-host model (M1) is a locally identifiable model, since solving c(p)=c(q), resulted in two sets of solutions. As it is clear from the two sets of solutions, by fixing viral clearance rate to c=ˆc, we would obtain a structurally identifiable model. Thus we have showed the following Proposition 2.1.
Proposition 2.1. The within-host model (M1) is not structured to reveal its parameters from the viral load and target cell observations. Only the parameters λ,β,π and d can be uniquely identified. If the viral clearance rate is fixed, c=ˆc, then the model (M1) reveals all its parameters uniquely.
We continue with identifiability analysis of model (M2). This time eliminating the unobserved state variables which are the infected target cell population and the concentration of opioid from the model is not a trivial task. We use DAISY to obtain the following equivalent system to model (M2);
input-output equations for the within-host model (M2):
Setting c(p)=c(q), we get
together with
Solving the nonlinear systems (2.9) and (2.10), we obtain the following two sets of nonzero positive solutions,
and
This concludes that the model (M2) is not structurally identifiable. It only reveals the parameters, λ,d and π from the viral load and CD4 cell count data.
Proposition 2.2. The within-host model (M2) is not structurally identifiable from the viral load and CD4 cell count observations.
Since validating model (M2) with data revealed that β=0, we continue our analysis by modifying model (M2), by setting β=0. We obtain the following input-output equations in this case.
input-output equations for the within-host model (M2) with β=0:
Note that c(p)=c(q) is the same as systems (2.9) and (2.10) with β=0. Solving c(p)=c(q) we obtain,
and
So, the within-host model (M2) with β=0 is also not structurally identifiable from viral load and CD4 cell counts. It is not possible to identify parameters C0 and Λ individually. It is only possible to identify their ratio C0Λ. If Λ is fixed, then C0 would be identified. But even then, the within-host model (M2) with β=0 becomes locally identifiable since there exist two sets of solutions to c(p)=c(q). We summarize the structural identifiability in the following proposition.
Proposition 2.3. The within-host model (M2) with β=0 is not structurally identifiable from the viral load and CD4 cell count observations.
If the viral clearance and morphine recruitment rates are fixed, that is c=ˆc and Λ=ˆΛ, then the model (M2) with β=0 becomes structurally identifiable.
2.3. Practical identifiability
Structural identifiability is a property of the within-host model and the analysis is performed without the actual data. A within-host model which is structurally identifiable may not be practically identifiable when the actual data is used in the parameter estimation problem. We continue our identifiability analysis with practical identifiability of within-host models (M1) and (M2) using Monte Carlo simulations (MCS). Using the estimated parameters ˆp as presented in Table 2; we generate synthetic data sets Y=(Yi1,Yj2) which are contaminated with error. In particular, we generate M=1000 data sets of viral load and CD4 cell counts using normal distribution whose mean is the model predictions and standard deviations are y1(ti)σ0 and y2(tj)σ0 respectively. That is;
where N(μ,σ) denotes the normal distribution with mean μ and standard deviation σ. The synthetic viral load and CD4 cell count data sets are generated for each measurement errors, by increasing the errors gradually from σ0=1%, to σ0=5%,10% to σ0=30%. We then fit the within-host models (M1) and (M2) to each M=1000 data sets by solving the optimization problem (2.4) and then calculate the Average Relative Errors (AREs) of each parameter for each noise level. The AREs are computed as
where pk is the kth parameter in p and ˆp are the parameters that generate the random variables Yi1 and Yj2. Since a population of parameter estimates results for each measurement error is obtained, we also compute the 95% confidence intervals. AREs of the parameters together with the confidence intervals for each measurement error are presented in Tables 3–6. Examining the AREs and the confidence intervals of the MCS for the within-host model (M1) as presented in Table 3, we see that the AREs of parameters π and c are higher compared to measurement error levels (σ0). Note that the within-host model (M1) is only locally identifiable (see Proposition 2.1) and this is observed in AREs in Table 3. Next, we fix the viral clearance rate and run the MCS again for the within-host model (M1), and as a result AREs of all parameters have decreased significantly (see Table 4). We conclude that the within-host model (M1) is practically identifiable when the clearance rate is fixed. MCS results for the within-host model (M2) with β=0 and when Λ, dc and c are fixed are presented in Table 5. As seen from AREs in Table 5 the parameters β1 and C0 have higher AREs especially when the measurement error is 30%, even though the model is structurally identifiable in that case (see Proposition 2.3). If in addition to Λ,dc,c the half-saturation constant C0 is fixed, then the within-host model (M2) becomes practically identifiable as evident from Table 6.
3.
A multi-scale model of opioid and HIV epidemics
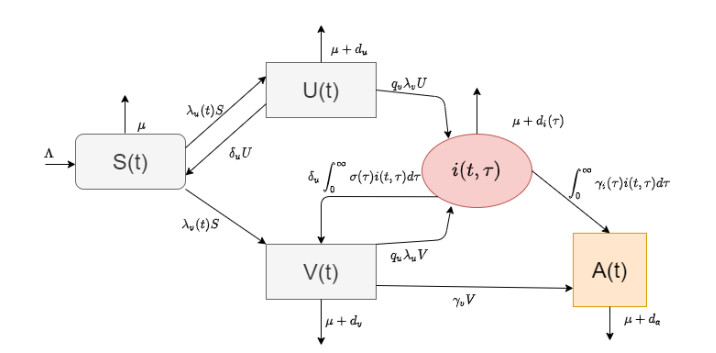
Research shows that HIV infected individuals who use drugs of abuse maintain a higher HIV viral load and treatment is not as effective for them [22,28]. The goal of this study is to understand the interplay between the two epidemics; HIV and opioid addiction. We use the term "co-affected" to characterize the individuals who are living with HIV and are also opioid drug users. Our previous research suggests that the role of the co-affected class is very important in the symbiotic relationship between the two epidemics [18]. To study the interplay of these two epidemics, we develop a multi-scale epidemic model where the total population is divided into five non-intersecting classes; susceptible individuals S(t), opioid addicted individuals U(t), HIV infected individuals V(t), co-affected individuals I(t), and individuals with AIDS A(t). To understand the impact of within-host level opioid addiction on the population level HIV dynamics, we structure the co-affected class with time-since-co-affection parameter τ. The density of opioid addicted individuals who are also infected with HIV is then denoted by i(t,τ). The number of co-affected individuals is determined by
The multi-scale HIV-opioid epidemic model takes the following form;
where ks is a scaling factor such that τ=kst. Note that τ for the within-host scale is measured in days, while the between-host scale time t is measured in years. The scaling factor ks allows us to convert between the two time units. Thus, ks allows us to properly "zoom" on each scale and to consider both scales simultaneously in dynamic regime. The parameter ΛS denotes the recruitment/birth rate and μ denotes the natural death rate of the population. A susceptible individual can get into contact with a HIV infected or opioid addicted individual and move to the corresponding class upon effective transmission of infection or addiction. The force of HIV-infection takes into account the different infectivity of co-affected individuals;
Here βv1 denotes the HIV infection rate of individuals living with HIV and βv2(τ) denotes the HIV infection rate of co-affected individuals which is assumed to vary with infection age τ. We use the data in [29] to determine the form of the linking for the transmission coefficient βv2(τ) to the viral load [19]. Fitting to data, we obtain the following form for βv2(τ);
where V(τ) is the viral load in an HIV-infected host who is also opioid user. That is we obtain the transmission coefficient of the co-affected individual using the within-host model (M2).
We suppose that individuals with AIDS are isolated and consider the following form for the total number of active population;
The force of opioid addiction, λu(t), has a similar formulation. Thus
where βu denotes the rate at which an effective contact with an opioid user will result in addiction. In system (3.1), the term qvλv denotes the force of infection of an opioid user to HIV infection. Similarly, the term quλu denotes the force of addiction of an HIV-infected individual to opioid dependence.
The parameters du,dv and da denote additional death rates induced by addiction, HIV infection and AIDS respectively. Death rate of co-affected individuals is composed of two sources of additional death rates; HIV-infection which varies with infection age and opioid addiction. Namely,
where d0(T(0)−T(τ)) represents death rate due to HIV and d1 represents death rate due to addiction. The disease induced death rate does not depend explicitly on the viral load because the viral load is high during the acute HIV phase but the death rate is low during the same stage. The same relationship is also suggested in [30]. We assume that the opioid users recover at rate δu and move to the susceptible class. Similarly, co-affected individuals recover from addiction and move to the HIV infected class, with a rate δuσ(τ) depending on their HIV infection age τ. γv denotes the transition into AIDS. As before, the transition into AIDS of co-affected individuals γi(τ) varies with infection age. We use the following function as suggested in [30]
Similarly, transition into AIDS does not depend explicitly on the viral load, because an HIV infected individual develop AIDS at average 8 to 10 years after the infection [31], and the viral load usually is not high during that transition time. The flowchart of the model is given in Figure 2. We previously proved the existence, uniqueness, positivity and boundedness of multi-scale models such as studied in this paper in [32,33,34]. Similar analysis can be adapted to this model (3.1) to establish the same results.
3.1. Basic reproduction numbers and stability of disease-addiction free equilibrium
We analyze the system (3.1) by first determining the equilibrium points. We set the differentials with respect to t equal to zero and obtain the following system. Since the individuals with AIDS are isolated, we study the following equivalent system.
When both HIV infection and addiction disappear in the population, we obtain the disease-addiction-free equilibrium for which the compartments U(t), V(t) and i(t,τ) are zero. The disease-addiction-free equilibrium for the system (3.4) is given as E0=(S0,0,0,0)=(ΛSμ,0,0,0).
To determine the stability, we linearize the system around the disease-addiction-free equilibrium. We take S(t)=S0+x(t), U(t)=u(t), V(t)=v(t), N(t)=N0+n(t) and i(t,τ)=y(t,τ), where x(t),u(t),v(t),y(t,τ) and n(t) denote the perturbations around E0. The linearized system for perturbations takes the following form,
where
We look for solutions of the form x(t)=x0eλt, u(t)=u0eλt, v(t)=v0eλt, y(t,τ)=y(τ)eλt and obtain the following eigenvalue problem,
Solving the fourth equation of system (3.6) we get
where
Using Eq (3.7) and the second equation of system (3.6), we obtain,
Solving this equation we obtain,
Since u0≠0, we set the following equation,
We define the basic reproduction number of opioid addiction Ru as
Similarly using Eq (3.7) and the third equation of system (3.6), we obtain,
Then, we define the basic reproduction number of HIV-infection Rv as
Now we state the following theorem,
Theorem 1. If max{Ru,Rv}<1 then disease-addiction-free equilibrium E0 is locally asymptotically stable. If max{Ru,Rv}>1 then the equilibrium E0 is unstable.
Proof. Suppose
Then we notice that G1(0)=Ru, G2(0)=Rv, limλ→∞G1(λ)=0, limλ→∞G2(λ)=0. We claim that if max{Ru,Rv}<1 then the disease free equilibrium is locally asymptotically stable, that is all the roots of system (3.6) have negative real parts. To show this, we proceed by way of contradiction. Suppose system (3.6) has a root λ0 with ℜ(λ0)≥0. Then,
This is a contradiction. Hence E0 is locally asymptotically stable when max{Ru,Rv}<1.
3.2. Stability of boundary equilibria and invasion numbers
To obtain the opioid-only boundary equilibrium E∗1=(S∗1,U∗1,0,0), we set S(t)=S∗1, U(t)=U∗1, V(t)=0 and i(t,τ)=0 in system (3.4), then the system reduces to the following,
Solving system (3.13) we obtain,
At the HIV-only equilibrium, E∗2=(S∗2,0,V∗2,0), the system (3.4) reduces to
Solving system (3.14) we obtain,
We state the following lemma,
Lemma 1. Given min{Ru,Rv}>1, then there exist an opioid-only boundary equilibrium, and an HIV-only boundary equilibrium of system (3.1).
To find the invasion number of HIV and stability of E∗1 we linearize the system (3.1) around E∗1. We set S(t)=x(t)+S∗1, U(t)=u(t)+U∗1, V(t)=v(t), i(t,τ)=y(t,τ) and N(t)=n(t)+N∗1, then the system for the perturbations becomes,
where,
We look for solutions of the form x(t)=xeλt, u(t)=ueλt, v(t)=veλt, y(τ,t)=y(τ)eλt and obtain the following eigenvalue problem,
where,
From the third, fourth and fifth equation of system (3.16) we obtain,
From the second equation of system (3.17) we get y(τ)=y(0)π(τ)e−λτ/ks. Setting
the first and third equations of system (3.17) become,
Solving for v and y(0) we obtain,
Substituting these values into the following equation,
and cancelling λv(v,y) from both sides of the equation, we obtain;
We then define invasion number of HIV infection, R1vi as
Let
Clearly, ˆβ(λ) is bounded above by ˆβ(0) and Q(λ) is bounded above by Q(0) for λ real. Note that, Gvi(0)=R1vi and limλ→∞Gvi(λ)=0. Suppose system (3.19) has a root λ=x+iy with ℜ(λ)=x>0. We first, prove the following inequaltiy.
To prove inequality (Eq 3.21) we write down the left hand side of the inequality,
where, C1=U∗1N∗1, C2=S∗1N∗1 and z=√(x+μ+dv+γv+K)2+y2 where z=x+yi. Since f′(|z|)<0, f(|z|) is a decreasing function. That is when z(0,0)≤z(x,y), f(z(0,0))≥f(z(x,y)) when x≥0. But f(z(0,0)) is just the right hand side of inequality (Eq 3.21). This proves the inequality (Eq 3.21). Using inequality (Eq 3.21) we now state the following,
This is a contradiction. So system (3.19) can only have roots with non-negative real parts when R1vi<1. If R1vi>1 then Gvi(λ)→0 as λ→0 and λ real. Thus E∗1 is unstable. Note that,
To find the further eigenvalues, satisfying the third, fourth and fifth equation of system (3.16), y(t,τ)=0 and v(t)=0. The first two equations in system (3.16) then reduce to
Adding the two equations and solving for n we get
Replacing x and n in the second equation of system (3.16) we get,
Multiplying both sides of the equation 1N∗1,
uN∗1=0 implies from system (3.24) u would be zero, which would not be of interest. Thus uN∗1≠0 and canceling the expression on both sides, then the characteristic equation becomes,
Rewriting this equation as a quadratic equation, we get
Simplifying the equation, we have λ2+bλ+c=0 where b=βu−du−δu>0 and
since βu>(μ+du+δu) when Ru>1. Hence this quadratic equation has only roots with negative real parts.
Combining the work above we can conclude,
Theorem 2. The unique boundary equilibrium E∗1 is locally asymptotically stable if R1vi<1, and it is unstable if R1vi>1.
To find the invasion number of Opioid addiction and stability of E∗2 we first linearize the system (3.1) around E∗2. We set S(t)=x(t)+S∗2, U(t)=u(t), V(t)=v(t)+V∗2, i(t,τ)=y(t,τ) and N(t)=n(t)+N∗2, the system for the perturbations become,
Where,
and
We look for solutions of the form x(t)=xeλt, u(t)=ueλt, v(t)=veλt, y(τ,t)=y(τ)eλt and obtain the following eigenvalue problem,
Where,
From the fourth equation of system (3.29) we get
Let Q(λ)=∫∞0π(τ)e−λτ/ksdτ.
From the second equation of system (3.29) we get
Multiplying both sides of this equation with 1N∗2 we get,
From the fifth equation of system (3.29) we get,
Supplying these values in the equation,
and canceling λ2u(u,y) from both sides we obtain,
We then define the invasion number of opioid epidemic as,
where Π=∫∞0π(τ)dτ and C1=βv1V∗2N∗2. We call R2ui the invasion number of opioid addiction. We claim that when R2ui<1, the boundary equilibrium E∗2 is locally asymptotically stable, that is all the roots of Eq (3.32) have negative real parts.
Suppose
Then Gui(0)=R2ui and limλ→∞Gui(λ)=0.
Assume the Eq (3.32) has roots with non-negative real part ℜ(λ)>0. The Eq (3.32) satisfies,
This is a contradiction. Hence all roots of Eq (3.32) have negative real parts when R2ui<1.
Now let us suppose, R2ui>1. Then since G′ui(λ)<0 when λ>0 and real, Gui(λ) is decreasing when λ>0 and real. But we have, Gui(0)=R2ui>1 and limλ→∞Gui(λ)=0. Then Eq (3.32) has at least one positive root when R2ui>1.
If λ is not a solution of characteristic Eq (3.32), we have u=0, y(0)=0, the first two equations of system (3.29) reduce to
Adding the two equations and solving for n we get
i.e.
Using these values in the second equation of system (3.35) we get,
Since v≠0 we can cancel vλ+μ from both sides and get the following equation,
Now we know for the boundary equilibrium E∗2, S∗2+U∗2=N∗2, i.e both S∗2N∗2 and U∗2N∗2 are less than one. We also have the following,
and since Rv>1, βv1>μ+dv+γv. Assume the Eq (3.37) has roots with non-negative real part. With ℜ(λ)≥0 the Eq (3.37) satisfies,
This is a contradiction. So we can state the following theorem,
Theorem 3. The unique boundary equilibrium E∗2 is locally asymptotically stable if R2ui<1, and it is unstable if R2ui>1.
3.3. Estimating parameters of the multi-scale model of HIV and opioid epidemics
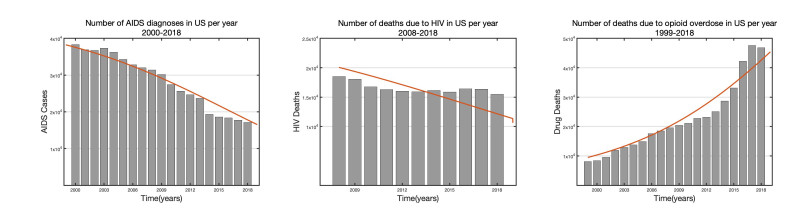
The Centers for Disease Control (CDC) collects and reports the surveillance data on persons diagnosed with HIV infection. The time series data of HIV diagnoses, which is defined by CDC as the number of HIV infections, confirmed by laboratory or clinical evidence in one calendar year, regardless of the stage of HIV-infection [31] is available at their website [35] starting from 2008. AIDS diagnoses are the individuals who were diagnosed with HIV infection and classified as AIDS. We obtain the HIV deaths and AIDS diagnoses from the CDC website to estimate the parameters of the multi-scale model (3.1) [35]. We report the time series data in Appendix Table A. National Center for Health Statistics reports the drug overdose deaths in the US from 1999–2018 [36]. The report gives any drug overdose mortality, but we used only the opioid deaths as given in complimentary pdf file [37]. We present the time series opioid overdose data in Appendix Table A.
We would like to estimate the parameters of the multi-scale model (3.1). As explained above the parameters of the co-affected class are linked to the viral load and target cell population within-infected host who abuse opioid drugs. Let pe denote the parameters of the between host model (3.1) and let p denote the parameters of the within-host model M2, then using the multi-scale data, we will estimate the following parameters;
For simplicity, we set σ(τ)=σ. Recruitment and natural death rates are fixed at ΛS=50,000,000μ and μ=1/75. To define the multi-scale parameter estimation problem based on the data available in US, we set yp(t)=(yp1(t),yp2(t),yp3(t)) to denote the observations. Observations for the between-host model parameter estimation are AIDS cases, denoted by yp1(t), HIV deaths denoted by yp2(t) and deaths due to opioid addiction denoted by yp3(t). Based on the model (3.1) observations are given as the following
Clearly, each observation depends on both the between-host parameters pe and within-host parameters p. Let tik={ti1,ti2,ti3,⋯,tini}, for i=1,2,3 denote the discrete time points measured in years when the AIDS diagnoses, (i=1), HIV deaths (i=2) and opioid deaths (i=3) are reported. Let Zik denote the number of AIDS diagnoses (i=1), HIV deaths (i=2) and opioid deaths (i=3) at the corresponding discrete times. Then we use the following optimization problem to estimate the parameters of the multi-scale system (3.1).
Note that we use multi-scale data to estimate parameters of the multi-scale model. The within-host scale data and population scale data have different magnitudes. For instance, the weekly log viral load data is within range 5–8, and the yearly AIDS cases is within range 1×104−4×104. Furthermore, the number of data points varies significantly for each observation. In such a case, the iterative numerical algorithm which approximates the minimization problem (3.40) tends to minimize the data with the highest magnitude at price of deviating from the small magnitude data. To overcome this issue, we normalize with the average data value. Thus in problem (3.40),
Also note, that in problem (3.40), ω1,…,ω5 are weights given to each data sets.
3.4. Sensitivity analysis
In this section we are interested in performing elasticity analysis of the invasion numbers with respect to the reproduction numbers as well as several important parameters. In article [18], we computed the elasticities of the two invasion numbers of an ODE model similar to the one here with parameters estimated from fitting to data. We found out that the invasion numbers are most sensitive to the parameter qv that gives the enhancement of HIV infection of opioid-addicted individuals. We concluded that "decreasing the HIV infection in drug users is the most efficient way to decouple the two epidemics". In this section, we want to see whether the results from [18] can be confirmed. Thus, in this section we compute the corresponding elasticities. To do that we set, M1=μ+du+δu, M2=μ+dv+γv, and βv2=∫∞0βv2(τ)π(τ)dτ. The analytical expressions of the derivatives of the invasion reproduction numbers with respect to the corresponding parameters are given as in the following.
Expressions for R2ui
Expressions for R1vi
Where,
To determine the best control measures, knowledge of the relative importance of the different parameters responsible for transmission is useful. Elasticity is a measure of the relative change of a quantity Q with respect to the parameter p, and it is defined as follows:
We denote the elasticities of the invasion numbers with respect to the reproduction numbers as follows:
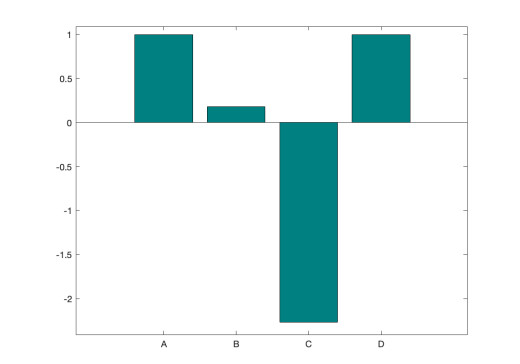
Figure 4 gives the elasticities of the invasion number with respect to the reproduction numbers. One immediate observation is that these elasticities are not all positive. In particular, the elasticity of R1vi with respect to Ru is negative which means that increase in opioid addicted individuals decreases the invasibility of HIV and may decouple the two pandemics. The negative sign is in a sense natural because it signifies competition between the two diseases. At the same time Figure 4 reveals that the elasticity of R2ui with respect to Rv is positive but very small. This means that an increase in HIV-infected individuals barely affects the invasion capabilities of the opioid affected. Looking at Table 9 the largest number in magnitude is the elasticity of R2ui with respect to qv. This is the same elasticity that in [18] had maximal magnitude. This suggests that the key to controlling these two pandemics is to decrease the HIV infection in drug users – this is the point where the control measures will have maximum impact. Decreasing qv will increase the invasion capabilities of opioid addiction. To counter that effect, we have to simultaneously control the opioid epidemic.
Parameters not involved in the reproduction numbers but potentially important for control are qu and qv. We denote the elasticities of the invasion numbers with respect to these parameters as follows:
4.
Discussion and conclusions
In this paper we formulate a multi-scale immuno-epidemiological model of HIV-Opioid epidemics coinfection using the nested approach [20]. The system consists of a within-host model of ordinary differential equations describing the dynamics within the co-affected individuals. The within-host model is linked with an epidemiological model via epidemiological parameters. The multi-scale model here is an extension of the ODE model considered in [18].
To estimate the parameters for the within-host model, the viral load and CD4 measurements obtained from [23] are utilized. Structural identifiability analysis is performed for the estimated parameters, and we conclude that model (M2) is not structurally identifiable as developed. Validation of the model (M2) with data suggests that β=0. Then the within-host model with β=0, is structural identifiable if we fix the drug-infusion and the viral clearance rates. Furthermore the model becomes practically identifiable, when the opioid clearance rate and saturation constant are fixed. We fit the full multi-scale model to the within-host data [23] and the number of AIDS diagnoses in the US, number of HIV deaths and number of opioid deaths. We choose to fit the within-host and between-host models simultaneously to all five data sets because our prior research suggests that simultaneous fitting improves the identifiability of the parameters [26]. This allows us to determine the parameters of the full model.
We study the multi-scale immuno-epidemiological model analytically. We compute the reproduction numbers of HIV and opioid epidemics. We show that the unique disease-addiction-free equilibrium is locally stable if both reproduction numbers are below one and unstable if an least one reproduction number is grater than one. If the reproduction number of HIV is greater than one, there is a unique equilibrium corresponding to HIV only. We show further that the HIV only equilibrium is locally asymptotically stable if the opioid invasion number is smaller than one, and it is unstable if the opioid invasion number is greater than one. Similarly, if the reproduction number of the opioid is greater than one there exists a unique equilibrium corresponding to the opioid epidemic only. We show that the opioid-only equilibrium is locally asymptotically stable if the HIV invasion number is smaller than one. If the HIV invasion number is greater than one, the opioid only equilibrium is unstable. Simulations suggest that there is an interior equilibrium potentially under the condition that both invasion numbers are larger than one; however proving that analytically has not been possible. In the ODE case [18], simulation suggested that the interior equilibrium may not be unique. Thus we expect possible non-uniqueness in this case too.
Using the fitted parameters we compute the elasticities of the invasion numbers with respect to the reproduction numbers as well as with respect to some of the parameters. The elasticities of the invasion number of the opioid with respect to the reproduction number of HIV is very small and positive. In terms of control the HIV epidemic has very little impact on the invasion capabilities of the opioid epidemic. On the other hand, the elasticity of the invasion number of HIV with respect to the opiod reproduction number is very large and negative suggesting that the opioid epidemic has a big impact on the invasion capabilities of HIV. In particular decreasing HIV prevalence increases the opioid epidemic invasion capabilities and strengthens the opioid epidemic. This is what we observe in reality – HIV incidence and deaths drop but the opioid deaths rise in numbers. The largest in modulus elasticity is that of the opioid invasion number with respect to qv – the coefficient of enhancement of HIV infection of opioid affected individuals. This coefficient is already very large – we estimate it at 30, but it also has a very large effect on the invasion capabilities of the opioid epidemic. We find that this elasticity is the largest also in our previous article [18] and we surmise that targeting HIV infection of opioid affected individuals will have the largest impact on the both epidemics. Decreasing HIV-infection of opioid affected individuals will strengthen the invasion capabilities of the opioid epidemic and should be coupled with systematic control of the opioid epidemic alone. Thus, even though our model is different and our data are different in this article compared to [18], we reach similar conclusion about control strategies for the coupled epidemics.
Acknowledgments
Necibe Tuncer was partially supported by NSF DMS-1951626. Maia Martcheva was partially supported by NSF DMS-1951595.
Conflict of interest
All authors declare that there is no conflict of interest.
Appendix









 DownLoad:
DownLoad: