Citation: Zoubir Chaieb, Ould Mohamed Ouarda, Azzeddine Abderrahmane Raho, Mouhyddine Kadi-Hanifi. Effect of Fe and Si impurities on the precipitation kinetics of the GPB zones in the Al-3wt%Cu-1wt%Mg alloy[J]. AIMS Materials Science, 2016, 3(4): 1443-1455. doi: 10.3934/matersci.2016.4.1443
| [1] | Faiza Lourdjane, Mouhyddine Kadi-Hanifi, Azzeddine Abderrahmane Raho . Precipitation of the metastable phases in a tin microalloyed Al-10at%Ag alloy. AIMS Materials Science, 2017, 4(1): 1-15. doi: 10.3934/matersci.2017.1.1 |
| [2] | Sabah Senouci, Mouhyddine Kadi-Hanifi, Azzeddine Abderrahmane Raho . Effect of a plastic deformation on the Guinier-Preston zones growth in Al-5at%Ag alloy. AIMS Materials Science, 2017, 4(1): 16-26. doi: 10.3934/matersci.2017.1.16 |
| [3] | Sabah Senouci, Azzeddine Abderrahmane Raho . Effect of the supersaturation on the precipitation kinetics of the Guinier-Preston zones in Al-rich Ag alloys. AIMS Materials Science, 2017, 4(1): 137-146. doi: 10.3934/matersci.2017.1.137 |
| [4] | Hugo F. Lopez . Microstructural features associated with the effect of temperature on the dimensional stability of an automotive Al-A319 alloy. AIMS Materials Science, 2016, 3(2): 634-644. doi: 10.3934/matersci.2016.2.634 |
| [5] | Piyada Suwanpinij, Audtaporn Worabut, Ratchadaporn Supruangnet, Hans Henning Dickert . Analysis of precipitation and dissolution of the microalloying elements by X-ray absorption spectroscopy (XAS). AIMS Materials Science, 2017, 4(4): 856-866. doi: 10.3934/matersci.2017.4.856 |
| [6] | Nur Farah Bazilah Wakhi Anuar, Mohd Shukor Salleh, Mohd Zaidi Omar, Saifudin Hafiz Yahaya . Mechanical properties and dry sliding wear behaviour of Al–Si–Mg alloy by equal channel angular pressing. AIMS Materials Science, 2022, 9(5): 733-749. doi: 10.3934/matersci.2022045 |
| [7] | Nuriya Mukhamedova, Yernat Kozhakhmetov, Mazhyn Skakov, Sherzod Kurbanbekov, Nurzhan Mukhamedov . Microstructural stability of a two-phase (O + B2) alloy of the Ti-25Al-25Nb system (at.%) during thermal cycling in a hydrogen atmosphere. AIMS Materials Science, 2022, 9(2): 270-282. doi: 10.3934/matersci.2022016 |
| [8] | Ya-Ting Tsu, Yu-Wen Chen . Preparation of gold-containing binary metal clusters by co-deposition-precipitation method and for hydrogenation of chloronitrobenzene. AIMS Materials Science, 2017, 4(3): 738-754. doi: 10.3934/matersci.2017.3.738 |
| [9] | M. P. Lavin-Lopez, L. Sanchez-Silva, J. L. Valverde, A. Romero . CVD-graphene growth on different polycrystalline transition metals. AIMS Materials Science, 2017, 4(1): 194-208. doi: 10.3934/matersci.2017.1.194 |
| [10] | Jie Sun, Tzvetanka Boiadjieva-Scherzer, Hermann Kronberger, Kevin Staats, Johannes Holinka, Reinhard Windhager . Surface modification of Ti6Al4V alloy for implants by anodization and electrodeposition. AIMS Materials Science, 2019, 6(5): 713-729. doi: 10.3934/matersci.2019.5.713 |
A supersaturated solid solution Al-Cu-Mg evolves towards an equilibrium state following the sequence [1,2,3,4]:
α (supersaturated) → GPB (Guinier-Preston-Bagaryatsky) zones → S’ metastable phase → S equilibrium phase
where the GPB zones consists on Cu-Mg co-clusters. The metastable phase S’ (Al2CuMg) is an hexagonal lattice and the equilibrium phase S (Al2CuMg), is an hexagonal lattice. This precipitation sequence is controlled by the diffusion of solute atoms. As GPB zones are coherent with the matrix, their interfacial energy with the matrix is weak and they form firstly. It is well known that the formation of the GPB zones in aluminium alloys is closely linked with the excess vacancies. A model of GPB zones precipitation assisted by vacancies has been developed by several authors. GPB zones formation is governed by a transport mechanism of solute atoms by solute atom-vacancy complexes [5,6,7]. In commercial Al-Cu-Mg alloys, two groups of phases, soluble such Al2Cu and Mg2Si, and insoluble particles such Al12Fe3Si, Al7Cu2Fe and Al6(Fe, Cu) during heat treatment, may be distinguished according to their stabilities [8,9]. The insoluble phases arise mostly from Fe and Si impurities, which, in commercial alloys for structural applications, are very often present. These constituent particles are insoluble because of the low solubility of Fe in aluminium and the low solubility of Si in Al alloyed with Mg. The soluble constituent phases can be dissolved during heat treatment, by virtue of the high solubility of Cu and Mg in Al [10].
Our purpose is to study the influence of the Fe and the Si impurities on the precipitation kinetics of the GPB zones in a supersaturated Al-Cu-Mg solid solution using a technique based on microhardness measurements.
Al-Cu-Mg alloys were prepared by melting aluminium, copper and magnesium elements under an argon protection. Aluminium with a purity of 99.99% and aluminium of commercial quality with a purity of 99.7% are used for the preparation of the pure Al-Cu-Mg and commercial Al-Cu-Mg alloys respectively. The pure aluminium contains less than 0.005% Fe and 0.005% Si and the commercial aluminium contains 0.094% Fe and 0.069% Si. The copper and the magnesium used have a purity of 99.99%. After homogenization, during 15 days at 540 °C and an ice water quenching, the alloys are cutinto platelets specimen which are mechanically polished, homogenized 6 hours at 540 °C and quenched into ice water. The Vickers microhardness measurements were carried out under a load of 100 g on specimen treated during different times at different aged temperatures (90, 130, 160 and 200 °C) and quenched into ice water. The Vickers hardness measurements were made using a microhardness tester type SHIMADZU provided with a square pyramidal penetrator. The average value of ten readings was used for each data point.
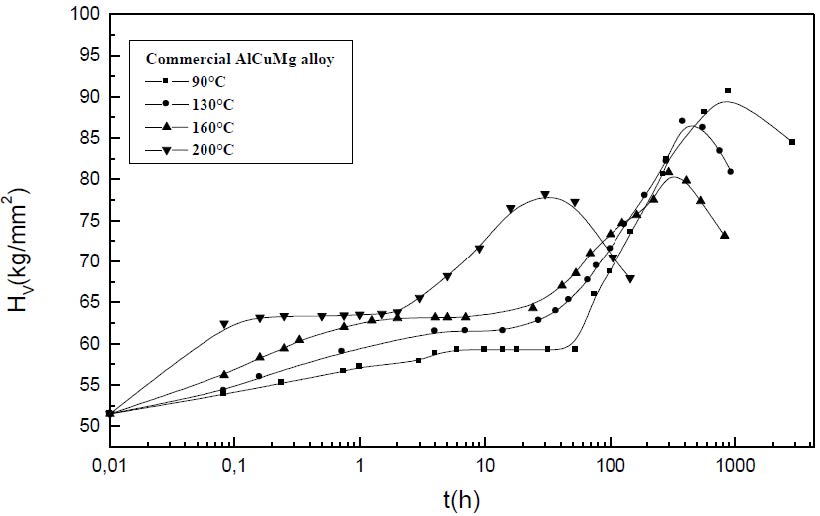
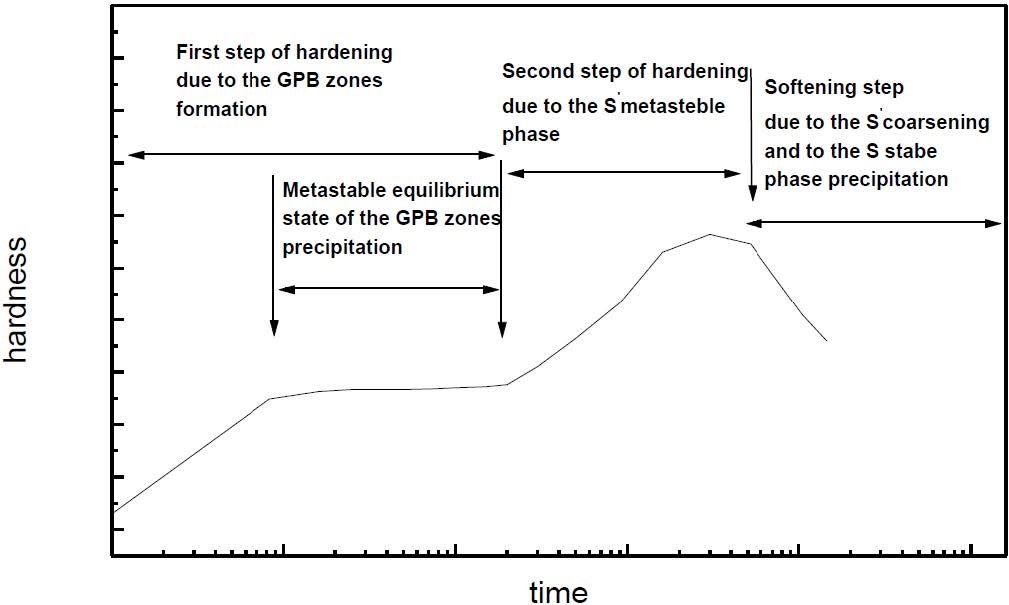
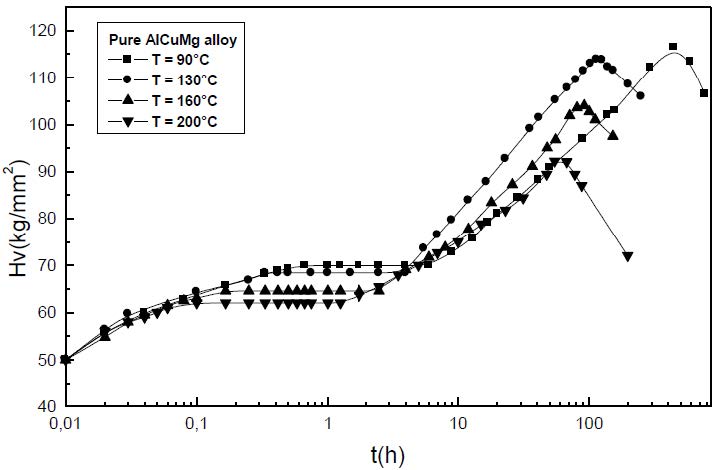
In both pure and commercial alloys, the isothermal hardness curves, established at 90, 130, 160 and 200 °C show two steps of hardening (Figures 1 and 2). The first one is due to the formation of the GPB zones while the second one, more important, is attributed to the precipitation of the metastable S’ phase. The softening occurs at the coarsening of the S’ particles and at the precipitation of the equilibrium phase S. The intermediate plateau observed between the two steps hardening corresponds to the equilibrium state of the GPB zones precipitation. The hardening observed is due to the interaction between GPB zones and S’ particles with moving dislocations [5,11,12,13,14,15,16]. The hardening evolution is schematized in the Figure 3.
Figure 1. Isothermal hardness curves of the pure Al-Cu-Mg alloy.
Figure 2. Isothermal hardness curves of the commercial Al-Cu-Mg alloy.
Figure 3. Schematic description of the hardening steps in the Al-Cu-Mg alloy.During the precipitation of the GPB zones, in a non deformed alloy, the hardening results from the contribution of the solid solution, the GPB zones and the insoluble particles. Since the presence of these particles will remove some of the Cu and Mg atoms from the solid solution, the effective solute concentration in the matrix during the heat treatment is reduced leading in a small reduction of the matrix contribution to the alloy hardening due to the small proportions of Fe and Si in the alloy. Due to the presence of Fe and Si, the reduction of the alloys hardness is not significative.
Precipitation transformation in Al-Cu-Mg alloys are considered as nucleation and growth type transformations. In such a case, the volume fraction of transformed solid solution, F, may be expressed by Johnson-Mehl [17], Avrami [18] and Kolmogorov [19] (JMAK) kinetics: F=1 -exp[-(kt)n], where n and k are the growth parameters. The growth parameter n is a numerical temperature independent exponent. For the diffusional controlled growth n is in the range 0.5-2.5 [20,21]. The growth parameter k is a strongly temperature dependent constant whose value depend on both nucleation and growth rates includes nucleation and growth rates. The growth parameter k characterizes the precipitation kinetics and is expressed by an Arrhenius-type relationship with temperature as follows [22]: k=A·exp[-(Q/RT)], where A is a constant, Q is the activation energy, R is the gas constant and T is the temperature.
During the precipitation of the GPB zones, the transformed fraction, F, which represents the ratio between the volume occupied by the GPB zones at a time t and their volume at the metastable equilibrium state, is given by the Merle relation [23]:
Hv(t)=F·Hv(metastable equilibrium state) + (1−F)·Hv(0), where Hv(0) is the as quenched hardness, Hv(t) is the hardness of the alloy at the time t during the precipitation of the GPB zones, and Hv(metastable equilibrium state) is the hardness of the alloy at the metastable equilibrium state of the GPB zones precipitation.
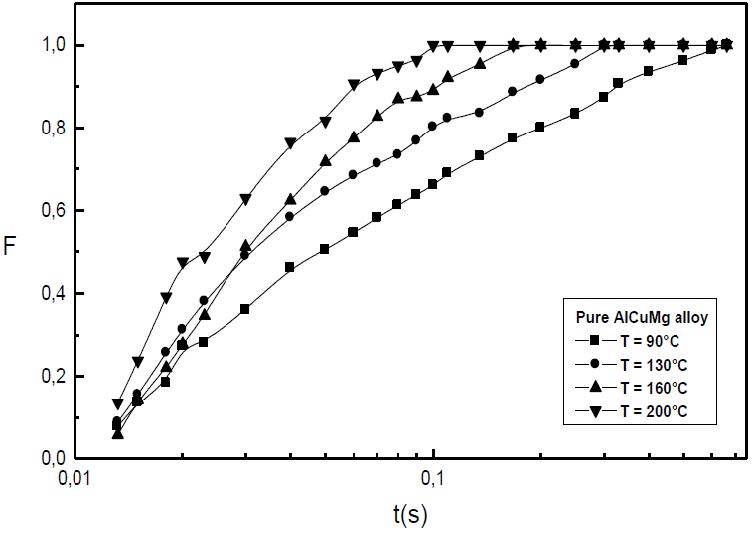
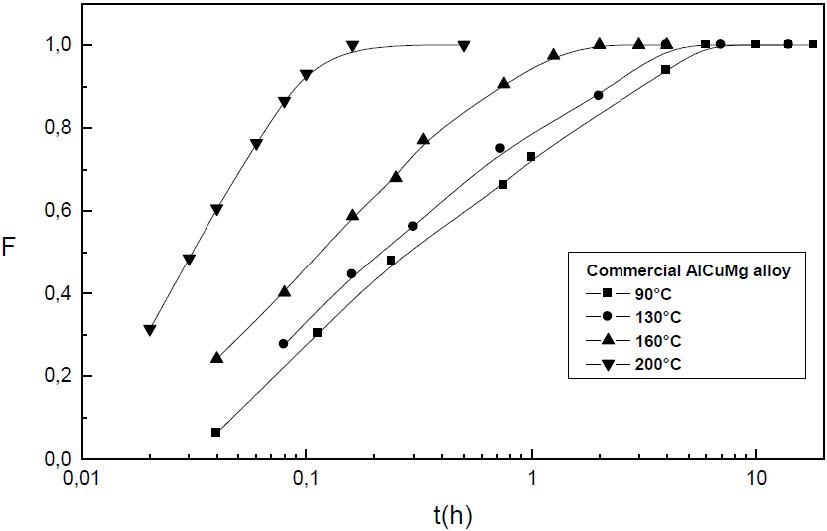
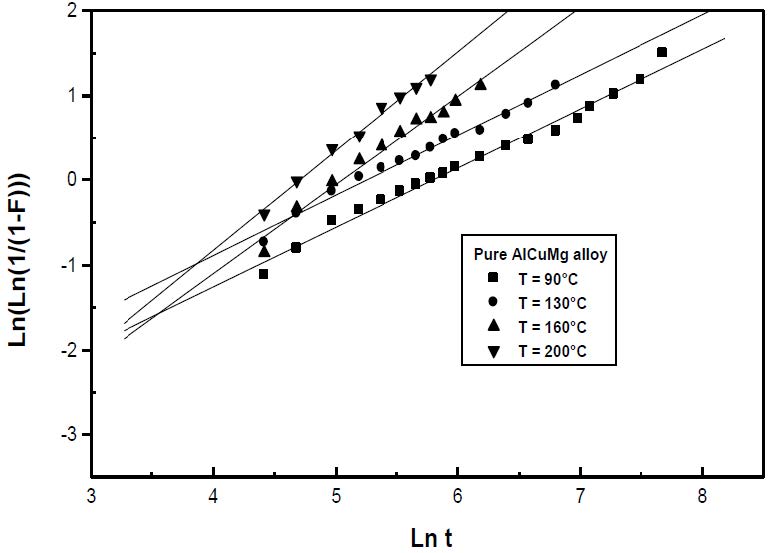
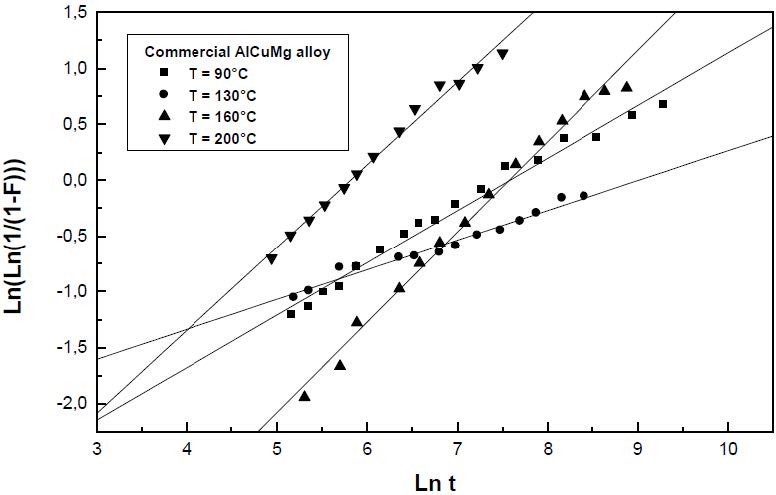
In both pure and commercial alloys, the results show that the GPB precipitation kinetics obeys to the JMAK law of the growth controlled by the diffusion of solute atoms: F=1 -exp[-(kt)n] (Figures 4 and 5).
Figure 4. Transformed fraction during the GPB zones precipitation in the pure Al-Cu-Mg alloy.
Figure 5. Transformed fraction during the GPB zones precipitation in the commercial Al-Cu-Mg alloy.The growth parameters n and k are determined from the slopes of the Ln(Ln(1/(1−F))) curves (Figures 6 and 7). The values of the growth parameter n which varies between 0.47 and 1.17 in both pure and commercial Al-Cu-Mg alloys are characteristics of a growth controlled by the diffusion and an heterogeneous precipitation of the GPB zones [20,21] while the values of k show that the precipitation of the GPB zones is faster at elevated temperature (Table 1).
Figure 6. Determination of the growth parameters during the GPB zones precipitation in the pure Al-Cu-Mg alloy.
Figure 7. Determination of thegrowth parameters during the GPB zones precipitation in the commercial Al-Cu-Mg alloy.| T (°C) | 90 | 130 | 160 | 200 |
| n (commercial alloy) | 0.47 | 0.37 | 0.81 | 0.74 |
| n (pure alloy) | 0.7 | 0.71 | 1.04 | 1.17 |
| k (commercial alloy) (s-1) | 4.61 × 10-4 | 2.23 × 10-4 | 5.16 × 10-4 | 2.9 × 10-3 |
| k (pure alloy) (s-1) | 30 × 10-4 | 52 × 10-4 | 62 × 10-4 | 90 × 10-4 |
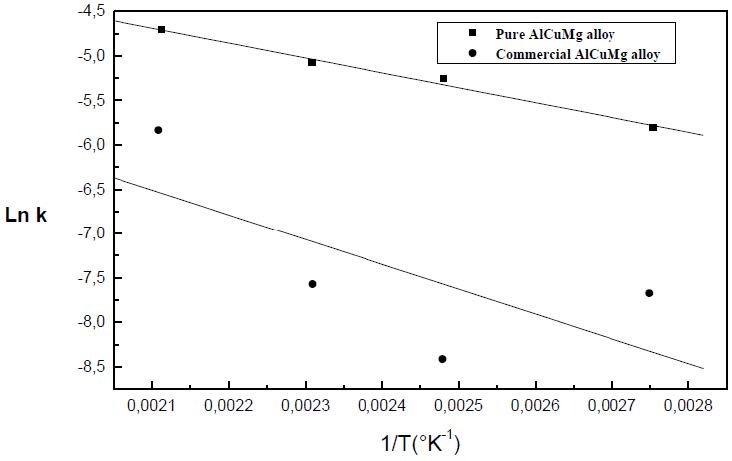
DownLoad: CSVOn the basis of the Arrhenius type expression of the growth parameter k=A·exp[-(Q/RT)] [22], the activation energy during the GPB zones growth, determined from the slopes of the curves Ln(k) against 1/T, is in the order of 14±4.2 kJ/mol and 23±6.9 kJ/mol during the GPB zones growth in the pure and in the commercial Al-Cu-Mg alloys respectively (Figures 8) showing that the reaction is slower in the commercial Al-Cu-Mg alloy. This is due to the reduction of the driving force of the GPB nucleation and growth and the reduction of the free vacancies available for the diffusion of the solute atoms. The presence of Fe and Si atoms leads to the formation of the soluble and the insoluble particles mentioned above. So, some of the Cu and Mg atoms are removed from the solid solution and the effective solute atom concentration in the matrix during the heat treatment is reduced leading a reduction in the driving force of the GPB nucleation and growth and a slowing down the nucleation growth reaction. Due to the strong binding energy of the vacancy to the Si atoms, in the order of 0.28-0.30 eV [24,25], some of the free vacancy available for the diffusion of the solute atoms are trapped by Si atoms therefore reducing the rate of the GPB formation and the rate of the diffusion.
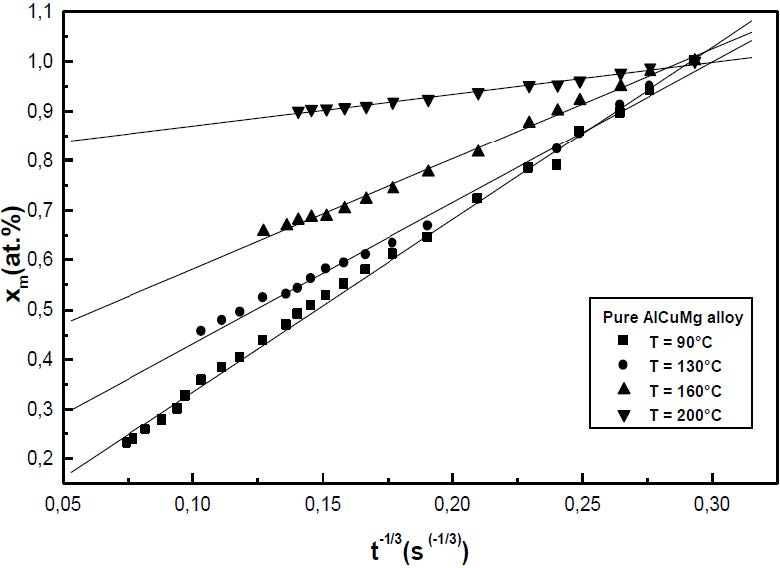
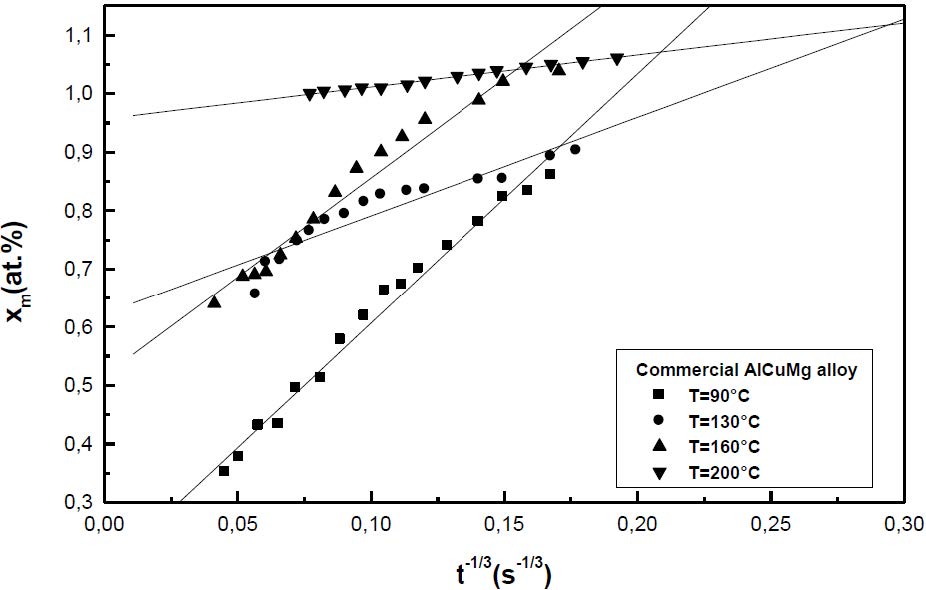
Figure 8. Determination of the apparent activation energy during the GPB zones growth in the pure Al-Cu-Mg alloy and in the commercial Al-Cu-Mg alloy.Coarsening of the precipitates occurs by the growth of large precipitates at the expense of small ones. This process is driven by a reduction in the total interfacial energy. The driving force of the coarsening reaction is due to the interfacial energy showing that there is no supersaturation of the solute atoms during the coarsening reaction. The classical theory of coarsening was developed based on the Gibbs-Thomson equation by Lifshitz and Slyosov [26] and Wagner [27], the so-called LSW theory. Assuming a weak precipitate volume fraction, fv, which corresponds to a highly diluted system and a precipitate volume fraction close to its equilibrium value, when the precipitation of the GPB zones is close to the completion, the LSW theory predicts that during coarsening the matrix supersaturation is given the relation: xm -xe=(kt)−1/3 where xm is the solute matrix concentration at a time t, xe is the solute matrix concentration at the metastable equilibrium state and k=D(RT)2/9σ2xe2Vm. In the k expression, D is the diffusion coefficient, T is the temperature, σ is the interfacial energy between the GPB zones and the matrix and Vm is the molar fraction of the GPB zones. The solute atom concentration of the matrix during the precipitation of the GPB zones is determined from the transformed fraction results using the relation F=(x0 − xm)/(x0 − xe) where x0 is the alloy solute atom concentration, xm is the matrix solute atom concentration and xe is the matrix solute atom concentration at the metastable equilibrium state. According to the metastable equilibrium concentration of the matrix during GPB formation is given by the relation xCu/xMg=1.6 × 104·exp(−38000/RT) [28]. Since the alloy atomic solute concentration ratio xCu/xMg is close to one, we can assume that the Cu and Mg concentrations in the matrix remains equal during the GPB zones precipitation. Thus, the solute matrix concentration at the metastable equilibrium state of the GPB zones precipitation is given by the relation xe=(1.6 × 104·exp(−38000/RT))1/2 [28]. The diffusion coefficients of the solute atoms, determined from the slopes of the variation curves xm against t−1/3 (Figures 9 and 10) using an interfacial energy between the GPB zones and the matrix of 0.1 J/m2 [29] and a molar fraction of the GPB zones, Vm=10−5 m3/mol, are given in the Table 2.
Figure 9. Matrix concentration xm variation in the pure alloy during the GPB coarsening regime.
Figure 10. Matrix concentration xm variation in the commercial alloy during the GPB coarsening regime.| T (°C) | 90 | 130 | 160 | 200 |
| commercial alloy | (6.7 ± 2) × 10-20 | (3.1 ± 1) × 10-18 | (7.2 ± 2.2) × 10-19 | (3.5 ± 1) × 10-16 |
| pure alloy | (1.2 ± 0.4) × 10-19 | (6.6 ± 2) × 10-19 | (2.6 ± 0.7) × 10-18 | (2.2 ± 0.6) × 10-16 |
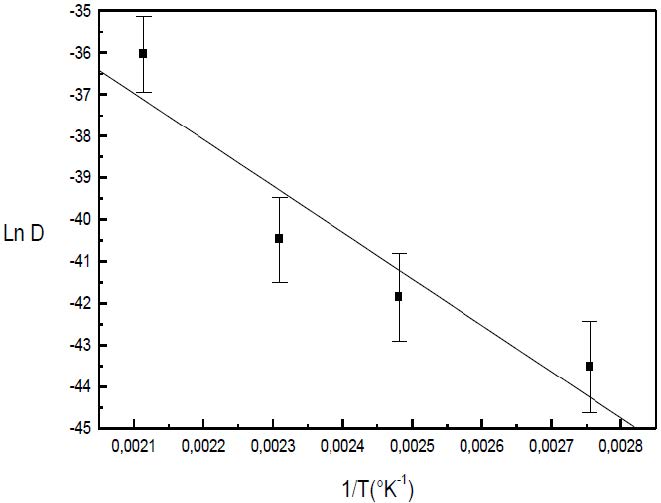
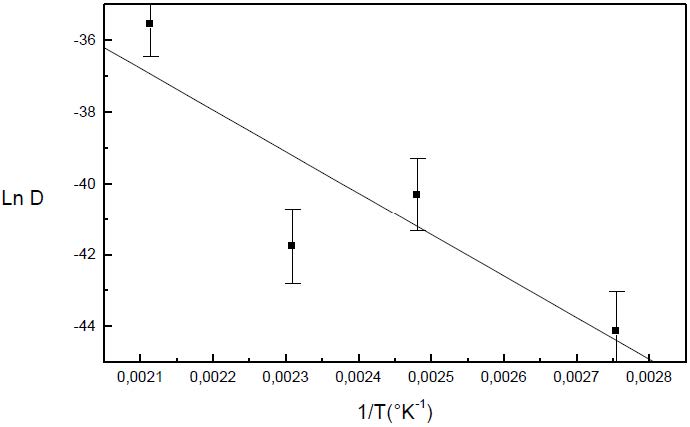
DownLoad: CSVAccording to the relation D=D0·exp(−Q/RT), where D0 is the pre exponential factor, T is the temperature and R is the gas constant, we determine a value of the pre exponential factor in the order of (1.2±0.3) × 10−6 m2/s and (4.2±1.1) × 10−6 m2/s and a value of the activation energy in the order of 93±27 kJ/mol and 96.6±29 kJ/mol (Figure 11 and 12) during the GPB coarsening regime in the pure and in the commercial Al-Cu-Mg alloys respectively (Table 3). These results may be compared with the results of the diffusion coefficient of Cu atoms an Mg atoms in pure Al (Table 4).
Figure 11. Determination of the pre exponential factor, D0, and the activation energy, Q, in the pure Al-Cu-Mg alloy.
Figure 12. Determination of the pre exponential factor, D0, and the activation energy, Q, in the commercial Al-Cu-Mg alloy.| Alloy | D0 (m2/s) | Q (kJ/mol) | Q (eV) |
| Commercial alloy | (4.2 ± 1.2) × 10-6 | 96.6 ± 29 | 1 ± 0.3 |
| Pure AlCuMg alloy | (1.2 ± 0.3) × 10-6 | 93 ± 27 | 0.97 ± 0.29 |
DownLoad: CSV| Element | D0 (m2/s) | Q (eV) |
| Al (self diffusion) | 6.6 × 10-6 [30] | 1.29 [30] |
| Cu | 4.37 × 10-6 [31] | 1.25 [31] |
| 6.47 × 10-5 [32] | 1.4 ± 0.01 [32] | |
| 6.5 × 10-5 [38] (computational result) | 1.4 [38] (computational result) | |
| 2.9 × 10-5 [33] | 1.35 ± 0.07 [33] | |
| 4.44 × 10-5 [34] | 1.18 [40] | |
| 1.39 [34] | ||
| Mg | 1.19 × 10-5[31] | 1.27 [31] |
| 6.23 × 10-5 [41] | 1.19 [41] | |
| 1.24 × 10-4 [38] (computational result) | 1.35 [38] (computational result) | |
| 1.24 × 10-4 [35] | 1.35 ± 0.05 [36] | |
| 1×10-4 [36] | 1.2 [37] | |
| 6.6 × 10-5 [39] | 1.29 ± 0.015 [39] | |
| 1.49 × 10-5 [34] | 1.13 [40] (computational result) | |
| 1.25 [34] |
DownLoad: CSVThe activation energy of the diffusion of the solute atoms during the GPB zones coarsening is characteristic of a slower reaction than that during the GPB zones growth in both pure and commercial Al-Cu-Mg alloys because some of quenched in vacancies are eliminated at the different sinks during the aging. In the presence of the GPB zones, as well as in the pure Al-Cu-Mg alloy and in the commercial Al-Cu-Mg alloy, the diffusion of the solute atoms is faster than that in the pure aluminium. In fact, the activation energy of the Cu atom and that of the Mg atom in the pure aluminium (Table 4) are greater than the activation energy determined in the pure and in the commercial Al-Cu-Mg alloys (Table 3).
The results show that the GPB precipitation kinetics obeys to the JMAK law of the growth controlled by the diffusion of solute atoms and during the coarsening regime and the supersaturation of the matrix obeys to the LSW theory in both pure and commercial Al-Cu-Mg alloys. The growth regime is a faster reaction than the coarsening regime in both pure and commercial Al-Cu-Mg alloys. The growth regime is a faster reaction in the pure Al-Cu-Mg alloy than the growth reaction in the commercial Al-Cu-Mg alloy. The diffusion coefficients of the solute atoms are determined during the coarsening of the GPB zones in both pure and commercial Al-Cu-Mg alloys. In the presence of the GPB zones, the diffusion of the solute atoms in the pure Al-Cu-Mg alloy and in the commercial Al-Cu-Mg alloy is faster than that in the pure aluminium.
The authors declare that there is no conflict of interest regarding the publication of this manuscript.
| [1] | Silcock JM (1960) The structural ageing characteristics of Al-Cu-Mg alloys with copper: Magnesium weight ratios of 7:1 and 2.2:1. J Inst Met 89: 203–210. |
| [2] |
Gupta AK, Gaunt P, Chaturvedi MC (1987) The crystallography and morphology of the S’-phase precipitate in an Al (CuMg) alloy. Phil Mag A 55: 375–387. doi: 10.1080/01418618708209875
|
| [3] |
Radmilovic V, Thomas G, Shiflet GJ, et al. (1989) On the nucleation and growth of Al2CuMg (S’) in AlLiCuMg and AlCuMg alloys. Scripta Mater 23: 1141–1146. doi: 10.1016/0036-9748(89)90315-3
|
| [4] |
Ringer SP, Sakura T, Polmear IJ (1997) Origins of hardening in aged Al-Cu-Mg-(Ag) alloys. Acta Mater 45: 3731–3744. doi: 10.1016/S1359-6454(97)00039-6
|
| [5] |
Federighi T (1958) Quenched-in vacancies and rate of formation of zones in aluminum alloys. Acta Metall 6: 379–381. doi: 10.1016/0001-6160(58)90078-6
|
| [6] |
Federighi T, Thomas G (1962) The interaction between vacancies and zones and the kinetics of pre-precipitation in Al-rich alloys. Phil Mag 7: 127–131. doi: 10.1080/14786436208201864
|
| [7] |
Girifalco LA, Herman H (1965) A model for the growth of Guinier-Preston zones-the vacancy pump. Acta Metall 13: 583–590. doi: 10.1016/0001-6160(65)90120-3
|
| [8] | Wang SC, Li CZ, Yan MG (1990) Precipitates and intermetallic phases in precipitation hardening Al-Cu-Mg alloys. Acta Metall Sin 3A: 104–109. |
| [9] | Starke EA, Staley JT (1996) Application of modern aluminum alloys to aircraft. Prog Aerosp Sci 32: 131–172. |
| [10] | Leschiner LN, Kovalyov VG (1990) Effect of Iron and Silicon in Aluminium and Its Alloys. Key Eng Mater 44-45: 299–310. |
| [11] |
Guo Z, Sha W (2005) Quantification of precipitate fraction in Al-Si-Cu alloys. Mater Sci Eng A 392: 449–452. doi: 10.1016/j.msea.2004.09.020
|
| [12] |
Waterloo G, Hansen V, Gjonnes J, et al. (2001) Effect of predeformation and preaging at room temperature in Al-Zn-Mg-(Cu, Zr) alloys. Mater Sci Eng A 303: 226–233. doi: 10.1016/S0921-5093(00)01883-9
|
| [13] |
Wang G, Sun Q, Feng L, et al. (2007) Influence of Cu content on ageing behavior of AlSiMgCu cast alloys. Mater Design 28: 1001–1005. doi: 10.1016/j.matdes.2005.11.015
|
| [14] |
Novelo-Peralta O, Gonzalez G, Lara Rodriguez GA (2008) Characterization of precipitation in Al-Mg-Cu alloys by X-ray diffraction peak broadening analysis. Mater Charact 59: 773–780. doi: 10.1016/j.matchar.2007.06.012
|
| [15] | Shokuhfar S, Ahmadi S, Arabi H, et al. (2009) Mechanisms of precipitates formation in an Al-Cu-Li-Zr alloy using DSC technique and electrical resistance measurements. Iran J Mater Sci Eng 6: 15–20. |
| [16] | Anjabin N, Taheri AK (2010) The effect of aging treatment on mechanical properties of AA6082 alloy: modelling experiment. Iran J Mater Sci Eng 7: 14–21. |
| [17] | Johnson WA, Mehl RF (1939) Reaction kinetics in processes of nucleation and growth. Trans Am Inst Mining Metall Eng 135S: 416–458. |
| [18] | Avrami M (1941) Kinetics of phase change. III: Granulation, Phase Change and Microstructure. J Chem Phys 9: 177–184 |
| [19] | Kolmogorov AN (1937) Statistical theory of crystallization of metals. Bull Acad Sci USSR Ser Math 1: 355–359. |
| [20] | Doherty RD (1996) Diffusive phase transformations in the solid state, in Physical Metallurgy 4th edition, eds., Cahn RW, Hassen P, North Holland, Amsterdam, 2: 1364–1505. |
| [21] | Christian JW (1975) The theory of phase transformations in metals and alloys, Pergamon Press, Oxford, 542–546. |
| [22] | Esmaeili S, Lloyd DJ, Poole WJ (2003) A yield strength model for the Al-Mg-Si-Cu alloy AA6111. Acta Mater 51: 2243–2257. |
| [23] |
Merlin J, Merle P (1978) Analistic phenomena and structural state in aluminium silver alloys. Scripta Metal 12: 227–232. doi: 10.1016/0036-9748(78)90103-5
|
| [24] | Wilson RN, Moore DM, Forsyth PJE (1967) Effect of 0.25% silicon on precipitation processes in an aluminium-2.5% copper-1.2% magnesium alloy. J Inst Met 95: 177–183. |
| [25] |
Hutchinson CR, Ringer SP (2000) Precipitation processes in AlCuMg alloys microalloyed with Si. Metall Mater Trans A 31: 2721–2733. doi: 10.1007/BF02830331
|
| [26] |
Lifshitz IM, Slyosov VV (1961) The kinetics of precipitation from supersaturated solid solutions. J Phys Chem Solids 19: 35–50. doi: 10.1016/0022-3697(61)90054-3
|
| [27] | Wagner C (1961) Theorie der Alterung von Niderschlagen durch Umlösen (Ostwald Reifung). Z Electrochem 65: 581–591. |
| [28] |
Khan IN, Starink MJ (2008) Microstructure and strength modelling of Al-Cu-Mg alloys during non-isothermal treatments: Part 1—controlled heating and cooling. Mater Sci Technol 24: 1403–1410. doi: 10.1179/174328408X317020
|
| [29] |
Khan IN, Starink MJ, Yan JL (2008) A model for precipitation kinetics and strengthening in Al-Cu-Mg alloys. Mater Sci Eng A 472: 66–74. doi: 10.1016/j.msea.2007.03.033
|
| [30] | Mantina M, Wang Y, Arroyave R, et al. (2008) First-principles calculation of self-diffusion coefficients. Phys Rev Lett 100: 5901–5904. |
| [31] |
Mantina M, Wang Y, Chen LQ, et al. (2009) First principles impurity diffusion coefficients. Acta Mater 57: 4102–4108. doi: 10.1016/j.actamat.2009.05.006
|
| [32] |
Peterson NL, Rothman SJ (1970) Impurity diffusion in aluminum. Phys Rev B 1: 3264–3273. doi: 10.1103/PhysRevB.1.3264
|
| [33] | Murphy JB (1961) Interdiffusion in dilute aluminium-copper solid solutions. Acta Metall 9: 563–569. |
| [34] |
Du Y, Chang YA, Huang B, et al. (2003) Diffusion coefficients of some solutes in fcc and liquid Al: Critical evaluation and correlation. Mater Sci Eng A 363: 140–151. doi: 10.1016/S0921-5093(03)00624-5
|
| [35] | Rothman SJ, Peterson NL, Nowicki LJ, et al. (1974) Tracer diffusion of Magnesium in Aluminum single crystals. Phys Status Solidi B 63K: 29–33. |
| [36] |
Moreau G, Cornet JA, Calais D (1971) Acceleration de la diffusion chimique sous irradiation dans le systeme aluminium-magnesium. J Nucl Mater 38: 197–202. doi: 10.1016/0022-3115(71)90043-2
|
| [37] |
Sandberg N, Holmestad R (2006) First-principles calculations of impurity diffusion activation energies in Al. Phys Rev B 73: 014108. doi: 10.1103/PhysRevB.73.014108
|
| [38] | Adams JB, Foiles SM, Wolfer WG (1989) Self-diffusion and impurity diffusion of FCC metals using the 5-frequency model and the Embedded Atom Method. J Mater Res 4: 102–112. |
| [39] | Verlinden J, Gijbbels R (1980) Impurity diffusion in aluminum as determined from ion-probe mass analysis. Adv Mass Spectrom 8A: 485–495. |
| [40] | Simonovic D, Sluiter MHF (2009) Impurity diffusion activation energies in Al from first principles. Phys Rev B 79: 054304. |
| [41] |
Fujikawa S, Hirano K (1977) Diffusion of 28 Mg in aluminum. Mater Sci Eng 27: 25–33. doi: 10.1016/0025-5416(77)90190-2
|
| 1. | Jose Alvarez-Antolin, Elvira Segurado-Frutos, Hilario Neira-Castaño, Juan Asensio-Lozano, Heat Treatment Optimization in Al-Cu-Mg-Si Alloys, with or without Prior Deformation, 2018, 8, 2075-4701, 739, 10.3390/met8100739 |
Figures(12) / Tables(4)
Zoubir Chaieb, Ould Mohamed Ouarda, Azzeddine Abderrahmane Raho, Mouhyddine Kadi-Hanifi. Effect of Fe and Si impurities on the precipitation kinetics of the GPB zones in the Al-3wt%Cu-1wt%Mg alloy[J]. AIMS Materials Science, 2016, 3(4): 1443-1455. doi: 10.3934/matersci.2016.4.1443
| T (°C) | 90 | 130 | 160 | 200 |
| n (commercial alloy) | 0.47 | 0.37 | 0.81 | 0.74 |
| n (pure alloy) | 0.7 | 0.71 | 1.04 | 1.17 |
| k (commercial alloy) (s-1) | 4.61 × 10-4 | 2.23 × 10-4 | 5.16 × 10-4 | 2.9 × 10-3 |
| k (pure alloy) (s-1) | 30 × 10-4 | 52 × 10-4 | 62 × 10-4 | 90 × 10-4 |
DownLoad: CSV| T (°C) | 90 | 130 | 160 | 200 |
| commercial alloy | (6.7 ± 2) × 10-20 | (3.1 ± 1) × 10-18 | (7.2 ± 2.2) × 10-19 | (3.5 ± 1) × 10-16 |
| pure alloy | (1.2 ± 0.4) × 10-19 | (6.6 ± 2) × 10-19 | (2.6 ± 0.7) × 10-18 | (2.2 ± 0.6) × 10-16 |
DownLoad: CSV| Alloy | D0 (m2/s) | Q (kJ/mol) | Q (eV) |
| Commercial alloy | (4.2 ± 1.2) × 10-6 | 96.6 ± 29 | 1 ± 0.3 |
| Pure AlCuMg alloy | (1.2 ± 0.3) × 10-6 | 93 ± 27 | 0.97 ± 0.29 |
DownLoad: CSV| Element | D0 (m2/s) | Q (eV) |
| Al (self diffusion) | 6.6 × 10-6 [30] | 1.29 [30] |
| Cu | 4.37 × 10-6 [31] | 1.25 [31] |
| 6.47 × 10-5 [32] | 1.4 ± 0.01 [32] | |
| 6.5 × 10-5 [38] (computational result) | 1.4 [38] (computational result) | |
| 2.9 × 10-5 [33] | 1.35 ± 0.07 [33] | |
| 4.44 × 10-5 [34] | 1.18 [40] | |
| 1.39 [34] | ||
| Mg | 1.19 × 10-5[31] | 1.27 [31] |
| 6.23 × 10-5 [41] | 1.19 [41] | |
| 1.24 × 10-4 [38] (computational result) | 1.35 [38] (computational result) | |
| 1.24 × 10-4 [35] | 1.35 ± 0.05 [36] | |
| 1×10-4 [36] | 1.2 [37] | |
| 6.6 × 10-5 [39] | 1.29 ± 0.015 [39] | |
| 1.49 × 10-5 [34] | 1.13 [40] (computational result) | |
| 1.25 [34] |
DownLoad: CSV| T (°C) | 90 | 130 | 160 | 200 |
| n (commercial alloy) | 0.47 | 0.37 | 0.81 | 0.74 |
| n (pure alloy) | 0.7 | 0.71 | 1.04 | 1.17 |
| k (commercial alloy) (s-1) | 4.61 × 10-4 | 2.23 × 10-4 | 5.16 × 10-4 | 2.9 × 10-3 |
| k (pure alloy) (s-1) | 30 × 10-4 | 52 × 10-4 | 62 × 10-4 | 90 × 10-4 |
| T (°C) | 90 | 130 | 160 | 200 |
| commercial alloy | (6.7 ± 2) × 10-20 | (3.1 ± 1) × 10-18 | (7.2 ± 2.2) × 10-19 | (3.5 ± 1) × 10-16 |
| pure alloy | (1.2 ± 0.4) × 10-19 | (6.6 ± 2) × 10-19 | (2.6 ± 0.7) × 10-18 | (2.2 ± 0.6) × 10-16 |
| Alloy | D0 (m2/s) | Q (kJ/mol) | Q (eV) |
| Commercial alloy | (4.2 ± 1.2) × 10-6 | 96.6 ± 29 | 1 ± 0.3 |
| Pure AlCuMg alloy | (1.2 ± 0.3) × 10-6 | 93 ± 27 | 0.97 ± 0.29 |
| Element | D0 (m2/s) | Q (eV) |
| Al (self diffusion) | 6.6 × 10-6 [30] | 1.29 [30] |
| Cu | 4.37 × 10-6 [31] | 1.25 [31] |
| 6.47 × 10-5 [32] | 1.4 ± 0.01 [32] | |
| 6.5 × 10-5 [38] (computational result) | 1.4 [38] (computational result) | |
| 2.9 × 10-5 [33] | 1.35 ± 0.07 [33] | |
| 4.44 × 10-5 [34] | 1.18 [40] | |
| 1.39 [34] | ||
| Mg | 1.19 × 10-5[31] | 1.27 [31] |
| 6.23 × 10-5 [41] | 1.19 [41] | |
| 1.24 × 10-4 [38] (computational result) | 1.35 [38] (computational result) | |
| 1.24 × 10-4 [35] | 1.35 ± 0.05 [36] | |
| 1×10-4 [36] | 1.2 [37] | |
| 6.6 × 10-5 [39] | 1.29 ± 0.015 [39] | |
| 1.49 × 10-5 [34] | 1.13 [40] (computational result) | |
| 1.25 [34] |
