On the mod p Steenrod algebra and the Leibniz-Hopf algebra

1.   Introduction

COVID-19 is a pandemic that started in December 2019 and it is killing numerous people all over the world. There are multiple vectors of coronavirus such as population density, temperature, absolute humidity, climate suitability, cross-border human mobility, and region-specific COVID-19 susceptibility ^[1,2,3]. Additionally, numerous studies revealed that Bacillus Calmette-Guérin (BCG) vaccination might have protected beneficiaries and it is considered to provide broad protection apart from the one related to tuberculosis ^[4,5,6]. However, other authors gave the contrary conclusion ^[7,8]. Instead of focusing much on the causes of the virus spread, it will be essential to discover what can stop it. Considering the dangerousness manifestations of COVID-19, it is a ruthless killer ^[9,10]. The pandemic has affected every sector in the world. For instance, we have Education ^[11], Economy ^[12], Agriculture ^[13,14], Psychosocial issues ^[15,16], Environment ^[17], and Statistics ^[18,19]. Those problems delay every prediction whatever the domain and authorities are eager to control the spread of coronavirus. Numerous studies ^[20,21,22] emphasized the use of mathematics to understand the spread of COVID-19 and the results of vaccinations. From a number of works ^{[23,24,25,26]}, authors found that the pandemic tendency will be unstable (decreasing and increasing as well within years). Consequently, many countries have been working to develop a vaccine that can help handle the virus spread. In other words, the rapid development of a vaccine is a general imperative. If that solution is set, it will improve the immunity of people against that virus. To facilitate the actions that researchers have been taken, many activities were initiated, namely, we have the development of a global landscape for COVID-19 vaccines ^[27].

The misinformation about COVID-19 vaccine is a great issue that delays the acceptance of that solution ^[28]. Widespread misinformation became one of the most serious global health problems during these last days ^[29]. In this study ^[30], researchers investigated the association between public governance and COVID-19 immunization in the early months of 2021 to evaluate how well-prepared nations are for prompt policy responses to handle pandemic events. A recent paper ^[31] stipulated that policymakers and health authorities should strongly think of an effective strategic vaccine acceptance messaging. There is a considerable hesitancy because people think that such kind of rapid solutions might be very dangerous and full of medical mistakes ^[32,33]. In a survey among medical students in Egypt, researchers found that 96.8 and 93.3% of the respondents, respectively, had concerns about the vaccine's adverse effects and ineffectiveness ^[34]. Thus, they think it is not worthy to take the risk. The significant determinants about that hesitancy are multiple and they vary over time in a single country or among countries. Furthermore, it is compulsory to identify effective approaches and tools ^[35] to make people trust vaccines against COVID-19 ^[36]. Different papers discussed modelling of COVID-19 as ^{[37,38,39,40,41,42]}.

In December 2020, there were more than a hundred COVID-19 vaccines in laboratories. To produce any vaccine, expert implement three methods such as the use of the whole virus, some parts of the germ, or a genetic material. In the context of COVID-19, we have Viral vector vaccine, Messenger ribonucleic acid (RNA) vaccine, and Sub-unit protein vaccine. To give some examples of coronavirus vaccines, we can cite PfizerBioNTech, Moderna, Johnson and Johnson, AstraZeneca, or Spoutnik V. Data about each vaccine are essential when a study would like to focus on the pandemic evolution but, we do not have access to them.

In terms of similar studies to ours, a recent work ^[43] did a meta-regression and systematic review of the duration of effectiveness of primary series COVID-19 vaccination against omicron. Some other authors checked on paper written from Dec 3, 2021, to April 21, 2022 about the same topic and with random-effects meta-regression, they found that the mean change in vaccine effectiveness is between 1 month to 6 months or 1 month to 4 months respectively, for primary vaccine series completion or for booster vaccination. In this paper ^[44], authors investigated the best immunization rates to lower the number of COVID-19 cases and fatalities. Another study ^[45] has used the data of 2,099,871 vaccinated persons receiving care in the Veterans Affairs health care system and matched them to unvaccinated controls. Vaccine effectiveness was, respectively, around 69 and 86% against SARS-CoV-2 infection and SARS-CoV-2–related deaths. Even in the United States of America (USA), some authors worked on the effects of vaccination using data from 50 US states and the District of Columbia ^[46]. Considering findings, authors discovered that the death toll may have been 1.67–3.33 fold if there was no vaccine. In addition, using data from Europe and Israel, authors work on vaccination effectiveness related to deaths. They got 72% of protection against deaths related to the variant. Considering those works that have been doing, there is no body of knowledge that gives scientific evidence in a global context about the influence of vaccination on the spread of the pandemic among new cases. To overcome that issue, the current work proposes a statistical modeling as a longitudinal monitoring of new cases and vaccinated people solution to check how effective vaccination is globally. Indeed, this study aims to check whether the number of daily vaccinated people had an influence on the number of new cases all around the world. It is the first of its kind and it will help policymakers to strengthen the evidence related to the effectiveness of the new campaign for COVID-19 vaccines.

The structure of the present work is as follows: Data and methods clarifications are provided in Section 2. Section 3 lists the results of the study. In Section 4, we discussed the findings. Conclusions and perspectives are presented in Section 5. In other words, the latter gives final outputs of the study and highlights next research questions.

2.   Materials and methods

2.1.   Datasets underlying our modeling

In this current study, we used the dataset "Coronavirus Pandemic (COVID-19)" from "Our World in Data" ^[47] (https://ourworldindata.org/coronavirus). Variables were accessed on 24/03/2021 and we have new cases ($NC$) as the dependent variable and the number of vaccinated people ($VP$) as a predictor. $NC$ means the number of registered infections on a given day while $VP$ is the number of registered people that got a vaccine on a given day. Actually, the study period (98 days) is from 2020-12-14 to 2021-03-21. The dataset is daily updated and made available by the European Center for Disease Prevention and Control (ECDC), that is, an agency of the European Union. Considering the data quality, it is mostly related to the fact that ECDC collects data from World Health Organization (WHO), The European Surveillance System (TESSy), the Early Warning and Response System (EWRS), and email exchanges with other international stakeholders. The used data can be put at disposal if requested. A summary about the data's components can be found in the Table 1.

2.2.   Generalized Linear Model (GLM) for count time series

The main idea is to propose a model that cointegrates the number of $NC$ and of $VP$. Actually, we have $NC_t$ and $VP_t$, respectively, as the dependent variable at day $t$ and the explanatory variable at day $t$. To model the count time series, researchers use several approaches regarding each variable in a study. In our current case, $NC_t$ and $VP_t$ are each integrated of order 1, but the residual series of their regression model is not stationary. We would like to recall that the variable of interest is a count time series, therefore, we computed the Generalized log-Linear Model (count time series) to check to what extend $VP$ might influence $NC$. We are not computing Zero-Inflated Poisson or Zero-Inflated Negative Binomial because the data is the whole world daily sum of Cases or Vaccinated people and there is no issue about a number of zeros in the series. We hypothesized that our variable of interest distribution per time $t$ represents a collection of random variables ($Y_1, \dots, Y_{98}$) that are independent and identically distributed. It is the reason that we worked on stationarity as a property that allows us to check how stable is the joint probability distribution when $t$ changes. We would like to model the conditional mean $E(Y_t| \mathcal{F}_{t-1})$ of $NC$ time series by a process, such that $E(Y_t| \mathcal{F}_{t-1}) = w_t$. We mean by $\mathcal{F}_{t-1}$ the history of the joint process $\{Y_t, w_t, X_{t+1}: t \in {\rm I\!N} \}$ with $VP$ at $t+1$. It means that, if $Y_t| \mathcal{F}_{t-1}\sim Poisson (w_t)$, we have:

In other words, for a Poisson process, the conditional mean is equal to the conditional variance. In case $Y_t| \mathcal{F}_{t-1}\sim NegBin(w_t, \rho)$, we have:

The package we used in R is tscount ^[48]. The general model is set as follows:

where $Y_t$ is the time series, $w_t$ is the latent mean process, $\alpha_0$ is the intercept, $\alpha_k$ is the parameter vector related to the autoregressive components, $\beta_l$ is the parameter vector related to the moving average components, $\{ X_t: t \in {{\rm I\!N}} \}$ with $X_t = (VP_t, VP_{t-1}, VP_{t-2})^T$, $\rho^{\intercal}$ is the transpose of the matrix about covariates parameters. We also have:

The transformation function is useful for the autoregressive modeling part of Eq (2.7) because it plays the same role as the link function on the variable of interest. Actually, to estimate the parameters, we use conditional maximum likelihood for the Poisson distribution and the conditional maximum quasi-likelihood approach for the negative binomial distribution. There are two possible distributional assumptions. In the case of Poisson model (PM), the conditional mean and variance are the same and the overdispersion coefficient is null. However, in the context of Negative Binomial model (NBM) with parameters $(w_t, \rho)$, the variance is a quadratic function of the mean. In addition, a process $z_t$ is said weakly stationary if :

● $E(z_t) = \mu$ (which is independent of $t$),

● $Var(z_t) = \sigma^2 (\mbox{constant}$), and

● $Cov(z_t, z_{t+k}) = \gamma_k$ (which is independent of $t$ and depends only on the lag $k$).

Considering both distributions, we have the summary in the Table 2.

In our investigation, we employed the Augmented Dickey Fuller test to determine if a time series is stationary or not ^[49]. Additionally, the property of co-integration enables us to determine whether there is a long-term relationship between the two series. Two time series $x_t$ and $y_t$, both integrated of order one (I(1)), are co-integrated when it exists $\alpha \in {\rm I\!R}$ such that $u_t = y_t-\alpha x_t$, with $u_t$ which is a stationary process. We entered the modeling phase after verifying the stationary and co-integration.

2.3.   Analysis process

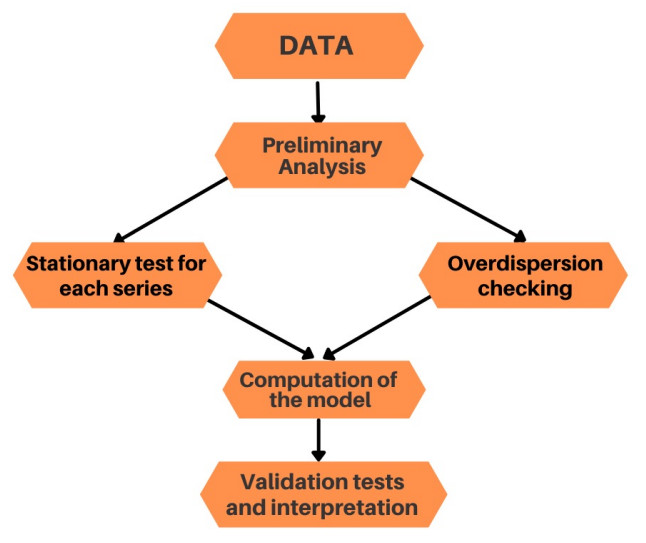
To analyze whether there is a decrease of COVID-19 cases while vaccination got increased needs analysis process. Consequently, we performed stationary analysis and GLM for count time series. To evaluate the model's performance, we used Akaike information criterion (AIC), Bayesian information criterion (BIC), and Mean Absolute Percentage Error (MAPE). The whole analysis was performed in R software (version 3.4.0) on a quadcore Intel Core i5-10210U with 12 GB RAM. We used the packages such as ResourceSelection (function: seastests (function: combined_test), tseries (function: adf.test), MLmetrics (function: MAPE), AER (function: dispersiontest). The execution time was less than one second. The whole analysis procedure is in Figure 1.

3.   Results

3.1.   Preliminary analysis

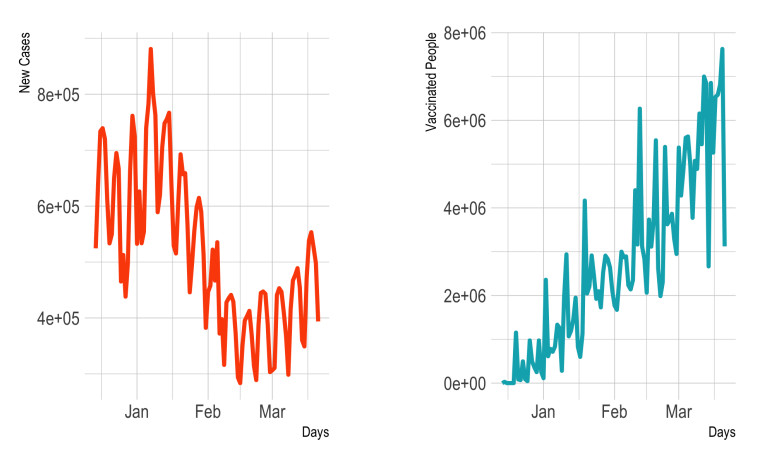
The illustration in Figure 2 shows that while $NC$ gets a decreasing trend, $VP$ increases. In addition, the Pearson correlation coefficient between the two time series (TS) gave a negative value of -0.48. The elements we mentioned strengthen our hypothesis about the influence of vaccination on the spread of COVID-19. Actually, we need to deepen the analysis on the modeling of those TS.

3.2.   Modeling

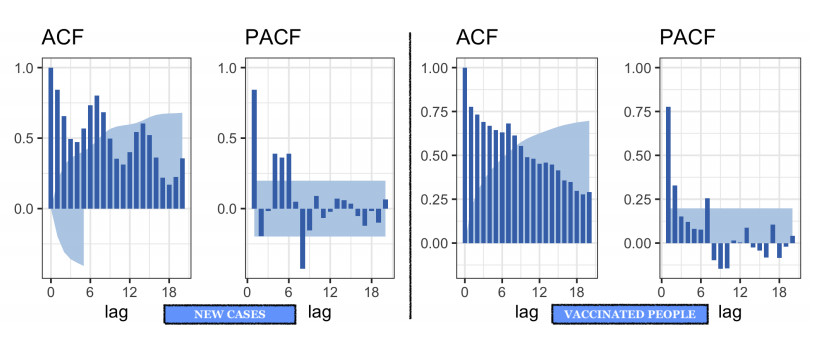
We checked the order of integration and noticed that $NC$ and $VP$ are both I$(1)$ in the Table 3. The regression between series gave a significant coefficient ($p$-value $\approx$ 0.00) of -0.0349 and the residuals were also I$(1)$ in the Table 3. The partial autocorrelation functions (PACFs) and the autocorrelation functions (ACFs) of $NC$ and $VP$ people are shown in Figure 3. When we look at the Figure 3, we can notice that the PACF for $NC$ exhibits a significant coefficient at lag 1 (the band is beyond the threshold), a gap (non significant partial autocorrelation function) at lag 2, and then exhibits significant coefficients once more for some of the subsequent lags. The situation is the same for $VP$ with a significant coefficient at lag 1 and a gap followed by a significant coefficient at lag 6. Therefore, we hypothesized that the optimal choice will be considering the order immediately higher than 1, that is 2. The first 8 autocorrelation coefficients are shown to be significant on the ACFs. As a result, we can assume generally that a level's present value depends on its past value. This explains why order 1 autocorrelation was chosen. In sum, the study of Figure 3 makes it clear that orders 1 and 2 are present in the modeling outputs. In addition, we suspected seasonality in Figure 2 and computed the Ollech and Webel's combined seasonality test (WO-test) on $NC$ and $VP$. It combines the seasonality test (QS-test) and the Kruskall Wallis test (kw-test). We used (combined_test() from the package seastests) and got $p$-values greater than 0.05 meaning that we do not have evidence of a significant season.

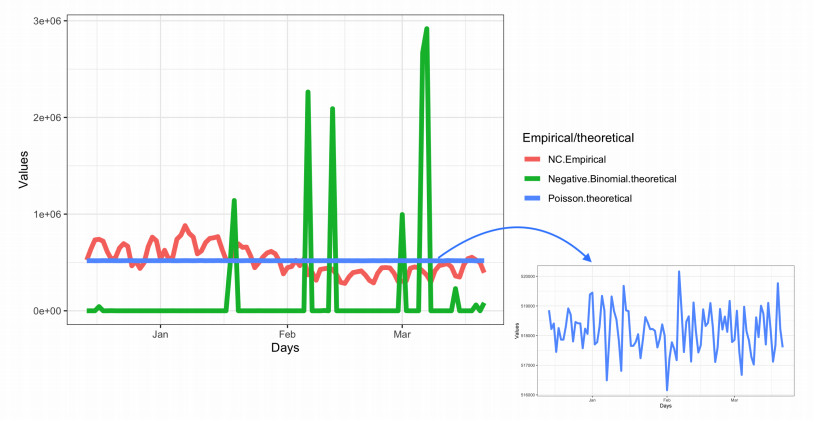
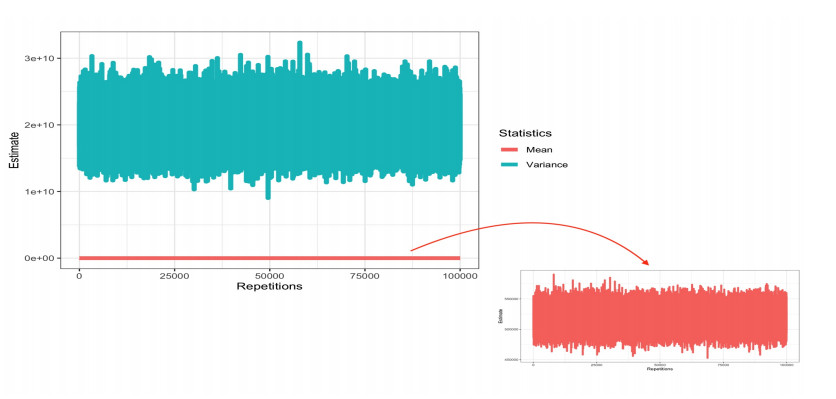
The checking of over-dispersion made us compute the mean and variance of $NC$. We got, respectively, 516786.7 and 20188965808. It is obvious that the mean is far equal to the variance and their ratio (variance/mean) gives $39066.34$ (a confirmation of the over-dispersion doubt). Moreover, in Figure 4 and Table 4, we can notice that the theoretical values of Poisson (516786.7) have a mean (518185) that is similar to the mean of $NC$ (518095), but their variances are far different ($1.99.10^{10}$, $5.65.10^{5}$). However, with the theoretical values of Negative binomial (516786.7, 0.018), we have different means (518095 and 384806) but much more similar variances ($1.99 \times 10^{10}$, $2.71 \times 10^{12}$). Solely on the Figure 4, the simulated values from Poisson seems to fit better $NC$ than Negative binomial values that were simulated. We also used a bootstrap technique of 100,000 repetitions and we could notice Table 5 and Figure 5 that the variance estimates are far greater than the mean estimates. Finally, the dispersion test (function dispersiontest() and package AER) gave a statistic test $z = 7.5365$ and a $p$-value $\approx$ 0.00. To model and compare goodness-of-fit, we will compute Poisson and Negative binomial models. The first results of PM and NBM that we got are in the Tables 6 and 7.

To consider that a coefficient is significant in the Tables 6–9, we need to not have 0 in the 95% confidence interval (CI-lower and CI-upper are either both negative or both positive). In the Table 7, we got every coefficient significant but the one about $VP_{t-1}$ is not. Consequently, we will remove it and compute again the model. It will help to have a model with significant coefficients. The results of the new model are in the Table 8.

In the Table 8, we got a model with each coefficient that is significant. Before interpreting, we need to validate the model. The residuals of the final model are stationary (Dickey-Fuller = -5.0057) with a $p$-value smaller than 0.01. Moreover, we got a MAPE of 10.68% meaning how the forecast is off by 10%. When we look at Poisson accuracy statistics in the Tables 6 and 9, we can notice that NBM in the Table 8 gets smaller (AIC and BIC) and equal (MAPE). Additionally, Pearson residuals test gave a $p$-value of 0.48. We can admit that the model is well adapted to the data. By the way, we got the evidence that we chose the good model. Then, considering the coefficient of $VP_{t-2}$ that is significantly negative with a value approximately equal to 1 ($e^{-5.14.10^{-08}} = 0.999$), we can confirm that when the number of $VP$ increases by 1 new vaccination at time $t$, $NC$ decreases by 1 at $t+2$. On the same day of a vaccination, the trend of virus contamination stays increased and it is the meaning of the significant positive coefficient of $VP_t$. Furthermore, we have the coefficients of $NC_{t-1}$ and $NC_{t-2}$ that are, respectively, positive and negative. In other words, we can understand that in the presence of vaccination, there is no decrease at $t-1$. It is two days after the decrease is noticeable.

4.   Discussion

The main idea of this study is to check whether the vaccination of COVID-19 has a significant influence on the number of new cases. This work uses the time series of $NC$ and $VP$ with an adapted generalized model to check our principal motivation. In the Table 8, it is easy to notice that there is a significant negative relation between the vaccination of people at $t-2$ and the spread of COVID-19 at $t$. This result confirms the target of vaccine creation because the motivation has been to increase the strength of people's immune system. The latter is to protect them from being infected and decrease deaths related to the virus. Several studies ^{[50,51,52,53]} have been promoting those vaccines and this work is the first statistical confirmation of the benefit of vaccination using the world data. When we also take into account the current data, we got a decrease by one $NC_{t}$ when $VP_{t-2}$ increases by one new vaccination. It is the statistical confirmation of how effective is the vaccination. It clarifies that there is a considerable COVID-19 transmission decrease during the process of vaccination. Additionally, this estimate is the first of its kind and needs to be recomputed with greater data sets.

There are many works ^[54,55] that explain how presymptomatic cases can infect effectively others individuals. Recently, in India some authors have found a reproduction number of 2.6 (95% CI: 2.34– 2.86) and after lockdown they got 1.57 (95% CI: 1.30–1.84) ^[56]. Especially, in federal states in Italy, researchers found that the reproduction number decreased to a range below 1 ^[57]. In February 2020, a study ^[58] collected many reproduction numbers and showed that the estimates are from 1.40 to 6.49. Actually, the coefficient 0.999 that we got stipulates that vaccination should be really increased to control the spread of COVID-19 in people who can infect many other ones. Moreover, the findings revealed that the influence of vaccination on new cases is significant after two days. The influence is not notable on the same day and it is understandable because even in the studies we have just cited about reproduction number, there is a period of infection that is probably different from the day of contamination. Firstly, the limitation related to this work might be in the fact that we are concluding without each observation (human being) tracking data. However, as we are using longitudinal data, it gives a strength to our findings. Secondly, some people may also state that the world data is heterogeneous, but we think that the greatest part of the beneficiaries in our data set is from developed countries.

A recent work in Portugal ^[59] discovered that despite the increase of vaccination, non-pharmaceutical interventions are essential to be maintained, otherwise new cases will increase. Furthermore, an author ^[60] noticed that two different control approaches with (feedback and non-feedback control methods) vaccination enabled the decrease of infected people successfully. In terms of vaccination strategies, authors ^[61] have even proposed that it will be much effective to allocate a single dose to adults regardless before the second dose. And it raises a limitation in this work because our findings do not consider the age of individuals. We would like to recall that this work is a longitudinal evidence and it does not provide how an individual avoided to be contaminated or did not suffer from complicated infections. Indeed, we found a strong scientific evidence that while there is an increase of vaccinated people, there is a decrease of the number of cases. Considering new infections due to omicron, it is understandable because there are non vaccinated people or many other vaccinated people. Another limitation of this research is that it does not take into account the individuals that are not vaccinated or the number of vaccinations per individual. To fight COVID-19, factors such as economic status, racism, and underlying medical conditions ^[62] or seasonal patterns ^[63] or variety of measures such as control measures and therapeutic drugs including vaccination ^[60,64] or community lockdown ^[65] are of interest. COVID-19 is not a matter of vaccine solely but a variety of policies. However, this work has put forward the fact that vaccination is effective and should be highlighted.

5.   Conclusions and perspectives

This work gave longitudinal evidence that when the number of vaccinated people increases, the number of new cases decreases significantly with a lag of two days considering worldwide data. It is an evidence on how effective vaccination is against the spread of COVID-19. In terms of perspectives, we can work on vaccinations' effectiveness per type of vaccine. Doing it will help researchers, clinicians, vaccine specialists, and different national leaders to better fight against the spread of coronavirus.

Acknowledgments

Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R299), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (22UQU4310268DSR03). The first author would also like to thank Saudi electronic university for providing facilities.

Conflict of interest

The authors declare there is no conflict of interest.