Mainstreaming resilience to flood risk among households in informal settlements in Kisumu City, Kenya

1.   Introduction

With the development of neuroscience, the controlling mechanism and mode of biological motion have been paid much attention by biologists ^[1,2,3,4], and rhythmic movement is a common mode of motion in biology. Rhythmic movement refers to periodic movement with symmetry of time and space, such as walking, running, jumping, flying, swimming and so on. Biologists have shown that rhythmic movement is not related to the consciousness of the brain, but to the self-excitation of the lower nerve centers. It is a spatiotemporal motion mode controlled by a central pattern generator located in the spinal cord of vertebrates or in the thoracic and abdominal ganglia of invertebrates ^[5]. They have the ability to automatically generate complex high dimensional control signals for the coordination of the muscles during rhythmic movements ^[6,7,8,9].

In engineering, CPG can be regarded as a distributed system consisting of a group of coupled nonlinear oscillators. The generation of rhythmic signals can be realized by phase coupling. Changing the coupling relationship of oscillators can produce spatiotemporal sequence signals with different phase relations, and realize different movement modes. CPG of animals lays a foundation for the research of bionic robots. For example, in ^[10,11] the gait control of quadruped robots based on CPG is studied. Mathematically, there are several common types of CPG oscillators systems, such as Hopf oscillators systems ^[12,13], Kimura oscillators systems, Rayleigh oscillators systems, Matsuoa oscillators systems and VDP oscillator systems ^[14,15], etc.

Quadrupedal gait is a kind of gait that people are very concerned. The gait of quadruped is an important type described by a symmetrical system ^[16,17,18]. For example, in ^[17,18], base on the symmetry property, the primary and secondary gait modes of quadruped are described, respectively. In animal gait movement, the legs are coupled with each other, and the coupling strength affects the complexity of animal gait. In this paper, the delay of leg signal is considered according to CPG model, the basic gait CPG model of a class of quadruped is constructed by using VDP oscillators, and the ranges of coupling strength between legs under four basic gaits are given. This paper is organized as follows. Firstly, a kind of delay CPG network system is constructed by using VDP oscillator. Secondly, the conditions of Hopf bifurcation in VDP-CPG network corresponding to the four basic gaits are given, and the coupling ranges between legs in four basic gaits are given. Finally, the theoretical results are supported by numerical simulations.

2.   Delay VDP-CPG network architecture

CPG, as the control center of rhythmic motion, is a kind of neural network that can generate the output of rhythmic mode without sensor feedback. It sends out motion instructions from the high-level center to control the initial state of rhythmic motion, and integrates the feedback information and perception information of CPG to regulate the motion organically. The CPG network in this paper adopts the following network structure ^[14].

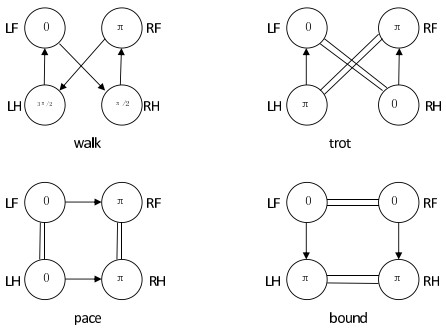
In Figure 1, LF, RF, LH and RH represent the animal's left foreleg, right foreleg, left hind leg and right hind leg, respectively. The black arrows represent the leg raising sequence, and the numbers in the circles are the phase difference between other legs and LF leg. In order to generate the rhythmic signal of each leg, the VDP oscillator used in this paper can refer to ^[14], the equation is as follows.

where $x$ is the output signal from oscillator, $\alpha$, $p$ and $w$ are variable parameters which can influence the character of oscillators. Commonly, the shape of the wave is affected by parameter $\alpha$, and the amplitude of an output counts on the parameter $p$ mostly. The output frequency is mainly relying on the parameter $w$ when the amplitude parameter $p$ is fixed. But the alteration of parameter $p$ can lightly change the frequency of the signal, and $\alpha$ also can effect the output frequency.

Four-legged muscle groups are regarded as VDP oscillators for feedback motion signals, respectively. The animal's left foreleg, right foreleg, right hind leg and left hind leg are recorded as oscillator $x_1, x_2, x_3$ and $x_4$, respectively.

Then the oscillator of the $i$th leg is as follows

where $x_{ki} = x_i+\sum\limits_{j = 1, j\neq i}^4 K_{ij}x_j$ denotes the coupling variable. Here $K_{ij}$ is the coupling coefficient, which represents strength of coupling from $j$ oscillator to $i$ oscillator.

Because the motion state of each leg depends on the motion state of the other three legs in the past short time, the time delay is introduced as follows

Assuming that the biological mechanism of each leg is similar and the degree of excitation or inhibition is the same between legs, and the excitation is positive coupling, then the inhibition is negative coupling. Therefore,

Thus, we study the following VDP-CPG system

where $i = 1, 2, 3, 4$. It is clear that the origin (0, 0, 0, 0, 0, 0, 0, 0) is an equilibrium of Eq (1).

3.   VDP-CPG structures and Hopf bifurcations in rhythmic gaits

In this section, we construct a VDP-CPG network which is used for generation four basic gaits patterns (walk, trot, pace and bound). Then we analyze the conditions for four gait systems to produce Hopf bifurcation.

In order to analyses the four basic gaits, we make the following assumptions.

(H1) $h < 0$,

(H2) $2s-h^2 > 0, \frac{1}{9}m < K^2 < \frac{1}{9}$,

(H3) $K^2 < m,$

where $h = \alpha p^2, s = w^2, m = \frac{4h^2s-h^4}{4s^2}$.

3.1.   Walk

In walking gait, one leg is inhibited by the other three legs, then there are

So the VDP-CPG network in walking gait is as follows

This is a symmetric system. We first explore the symmetry of system (2), then study the existence of Hopf bifurcation of system (2).

Let $Y_i = \left(\begin{array}{c} x_i \\ y_i \\ \end{array} \right)\in R^2, i = 1, 2, 3, 4,$ system (2) can be written in block form as follows

where

Let $\Gamma$ be a compact Lie group. It follows from ^[19], system $\dot{u}(t) = G(u_t)$ is said to be $\Gamma-$ equivariant if $G(\gamma u_t) = \gamma G(u_t)$ for all $\gamma\in \Gamma$. Let $\Gamma = D_4$ be the dihedral group of order 8, which is generated by the cyclic group $Z_4$ of order 4 together with the flip of order 2. Denote by $\rho$ the generator of the cyclic subgroup $Z_4$ and $k$ the flip. Define the action of $D_4$ on $R^8$ by

Then it is easy to get the following lemma.

Lemma 3.1. System (3) is $D_4-$ equivariant.

The linearization of Eq (3) at the origin is

The characteristic matrix of Eq (4) is given by

where $I_2$ is a $2\times 2$ identity matrix. This is a block circulant matrix, from ^[20], we have

where $\chi_j = e^{\frac{\pi j}{2}{\mathrm{i}}}, \; {\mathrm i}$ is the imaginary unit. The characteristic equation of Eq (4) at the zero solution is

with

Lemma 3.2. If (H1) and (H2) hold, for the equation $\Delta_1 = 0$, we have the following results.

(1) when $\tau = 0$, all roots of equation $\Delta_{1} = 0$ have negative real parts,

(2) when $\tau > 0$, there exist $\tau^j$, such that when $\tau = \tau^j (j = 0, 1, 2, \dots)$, $\Delta_1(\pm {\mathrm{i}}\beta) = 0$ holds,

(3) the transversality condition:

where

Proof. (1) When $\tau = 0$, equation $\Delta_{1} = 0$ becomes $\lambda(\lambda-h)+s(1-3K) = 0$, and the solution is obtained as follows

By (H1) and (H2), the roots of equation $\Delta_{1} = 0$ have negative real parts.

(2) When $\tau > 0$, let $\lambda = {\mathrm{i}}\beta(\beta > 0)$ be a root of $\Delta_1 = 0$. Substituting ${\mathrm{i}}\beta$ into $\Delta_1 = 0$, then we have

Separating the real and imaginary parts, we get the following form

If (H2) holds, by solving the above equation, we have

(3) Let $\lambda(\tau) = \alpha(\tau)+{\mathrm{i}}\beta(\tau)$ be the root of equation $\Delta_1 = 0$, satisfying $\alpha(\tau^j) = 0$ and $\beta(\tau^j) = \beta$. Taking the derivative of the equation $\Delta_1 = 0$ with respect to $\tau$, we can get

Then

by (6) and (7), we have

which means that the transversality condition holds at $\tau_{walk\pm}^j, j = 0, 1, 2, \dots$.

The lemma 3.2 holds.

Lemma 3.3. For $\Delta_2 = 0$, we have the following results.

(1) if (H1) holds, when $\tau = 0$ all roots of equation $\Delta_{2} = 0$ have negative real parts,

(2) if (H3) holds, when $\tau > 0$ equation $\Delta_2 = 0$ has no pure imaginary root.

Proof. (1) When $\tau = 0$, equation $\Delta_{2} = 0$ becomes $\lambda(\lambda-h)+s(1+K) = 0$, and the solution is obtained as follows

By (H1), the roots of equation $\Delta_{2} = 0$ have negative real parts.

(2) When $\tau > 0$, let $\lambda = {\mathrm{i}}\beta(\beta > 0)$ be a root of $\Delta_2 = 0$. Substituting ${\mathrm{i}}\beta$ into $\Delta_2 = 0$ then we have

The real and imaginary parts of the above equation are separated, then we obtain

By solving the above equation, we have

By (H3), we obtain $(h^2-2s)^2-4s^2(1-K^2) < 0$, then the formula above is not valid. So the lemma 3.3 holds.

From lemma 3.2 and 3.3, we have following theorem.

Theorem 3.1. If (H1), (H2) and (H3) hold, then we have the following results.

(1) all roots of Eq (5) have negative real parts for $0\leq\tau < \tau_{walk}^0$, and at least a pair of roots with positive real parts for $\tau\in(\tau_{walk}^0, \tau_{walk}^0+\varepsilon)$, for some $\varepsilon > 0,$

(2) zero equilibrium of system (2) is asymptotically stable for $0\leq\tau < \tau_{walk}^0$, and unstable for $\tau\in(\tau_{walk}^0 , \tau_{walk}^0+\varepsilon)$, for some $\varepsilon > 0$,

(3) when $\tau = \tau_{walk}^0$, system (2) undergoes a Hopf bifurcation at zero equilibrium, where $\tau_{walk}^0 = \min\{\tau_{walk+}^0, \tau_{walk-}^0\}.$

Remark 3.1. Near the critical value $\tau = \tau_{walk}^0$, the periodic solution of system (2) at the origin accords with walking gait.

3.2.   Trot

In a trot, a leg on the same diagonal as the current leg stimulates the current leg, and two legs on the other diagonal suppress the current leg, thus

The VDP-CPG network for trotting is as follows.

This is also a symmetric system. Similarly, by lemma 3.1, we have

Lemma 3.4. System (8) is $D_4-$ equivariant.

The characteristic matrix of linearization of Eq (8) is given by

This is a block circulant matrix, and we have

with $\chi_j = e^{\frac{\pi j}{2}{\mathrm{i}}}.$

The characteristic equation of linearization of Eq (8) at zero solution is

where

Similarly, by lemma 3.2 and 3.3, we have following lemmas.

Lemma 3.5. For the equation $\Delta_3 = 0$, we have the following results.

(1) if (H1) holds, when $\tau = 0$, all roots of equation $\Delta_3 = 0$ have negative real parts,

(2) if (H2) holds, when $\tau > 0$, there exist $\tau^j$, such that when $\tau = \tau^j (j = 0, 1, 2, \dots)$, $\Delta_3(\pm {\mathrm{i}}\beta) = 0$ holds,

(3) the transversality condition:

where

Lemma 3.6. For $\Delta_4 = 0$, we have the following results.

(1) if (H1)and $K < 1$ hold, when $\tau = 0$, all roots of equation $\Delta_4 = 0$ have negative real parts,

(2) if (H3) holds, when $\tau > 0$, equation $\Delta_4 = 0$ has no pure imaginary root.

From lemma 3.5 and 3.6, we have following theorem.

Theorem 3.2. If (H1), (H2) and (H3) hold, we have the following results.

(1) all roots of Eq (9) have negative real parts for $0\leq\tau < \tau_{trot}^0$, and at least a pair of roots with positive real parts for $\tau\in(\tau_{trot}^0, \tau_{trot}^0+\varepsilon)$, for some $\varepsilon > 0,$

(2) zero equilibrium of Eq (8) is asymptotically stable for $0\leq\tau < \tau_{trot}^0$, and unstable for $\tau\in(\tau_{trot}^0, \tau_{trot}^0+\varepsilon)$, for some $\varepsilon > 0,$

(3) when $\tau = \tau_{trot}^0$, system (8) undergoes a Hopf bifurcation at zero equilibrium, where $\tau_{trot}^0 = \min\{\tau_{trot+}^0, \tau_{trot-}^0\}$

Remark 3.2. Near the critical value $\tau = \tau_{trot}^0$, the periodic solution of system (8) at the origin accords with trotting gait.

3.3.   Pace

In a pace, the leg on the same side (left or right) of the current leg stimulates the current leg, and the other two legs inhibit the current leg, thus

Thus Eq (1) becomes the following VDP-CPG pacing system.

and the linearization of Eq (10) at the origin is

the characteristic equation of system (11) is

where

Similarly, by theorem 3.1, we have following theorem.

Theorem 3.3. If (H1), (H2) and (H3) hold, we have the following results.

(1) all roots of Eq (12) have negative real parts for $0\leq\tau < \tau_{pace}^0$, and at least a pair of roots with positive real parts for $\tau\in(\tau_{pace}^0, \tau_{pace}^0+\varepsilon)$, for some $\varepsilon > 0,$

(2) zero equilibrium of system (10) is asymptotically stable for $0\leq\tau < \tau_{pace}^0$, and unstable for $\tau\in(\tau_{pace}^0, \tau_{pace}^0+\varepsilon)$, for some $\varepsilon > 0,$

(3) when $\tau = \tau_{pace}^0$, system (10) undergoes a Hopf bifurcation at zero equilibrium,

where

Remark 3.3. Near the critical value $\tau = \tau_{pace}^0$, the periodic solution of system (10) at the origin accords with pacing gait.

3.4.   Bound

In a bound, legs on the same side (front or hind) as the current leg stimulate the current leg, and the other two legs inhibit the current leg, thus

Eq (1) becomes the following bounding VDP-CPG system.

and the linearization of Eq (13) at the origin is

the characteristic equation of system (14) is

where

Similarly, by theorem 3.1, we have following theorem.

Theorem 3.4. If (H1), (H2) and (H3) hold, we have the following results.

(1) all roots of Eq (15) have negative real parts for $0\leq\tau < \tau_{bound}^0$, and at least a pair of roots with positive real parts for $\tau\in(\tau_{bound}^0, \tau_{bound}^0+\varepsilon)$, for some $\varepsilon > 0,$

(2) zero equilibrium of system (13) is asymptotically stable for $0\leq\tau < \tau_{bound}^0$, and unstable for $\tau\in(\tau_{bound}^0, \tau_{bound}^0+\varepsilon)$, for some $\varepsilon > 0,$

(3) when $\tau = \tau_{bound}^0,$ system (13) undergoes a Hopf bifurcation at zero equilibrium,

where

Remark 3.4. Near the critical value $\tau = \tau_{bound}^0$ , the periodic solution of system (13) at the origin accords with bounding gait.

4.   Numerical simulations

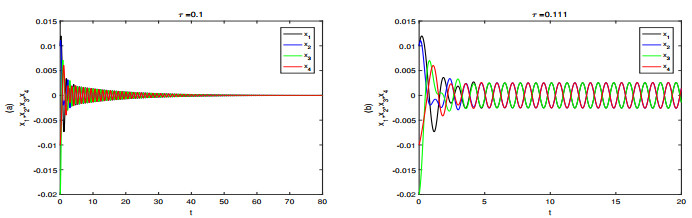
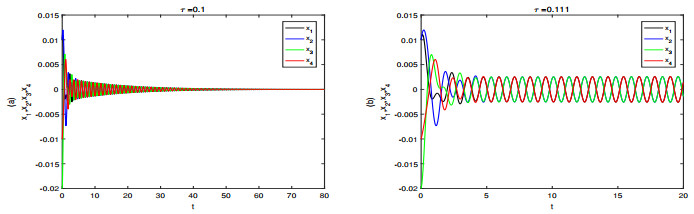
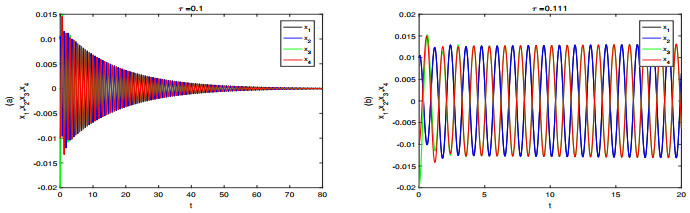
In this section, the numerical simulation of model is carried out to verify the results obtained in the previous sections. Let $\alpha = -1.5$, $\; p = 1, \; w = 4$, $\; K = 0.3$, according to the calculation, we obtain the $h = -1.5, \; s = 16, \; m = 0.1357, \; K^2 = 0.09, \; \frac{1}{9}m = 0.0151$. Thus $2s-h^2 = 29.7500 > 0, \; \frac{1}{9}m < K^2 < \min\{m, \frac{1}{9}\}$ and the critical value $\tau_{walk}^0 = 0.7039$, $\tau_{trot}^0 = \tau_{pace}^0 = \tau_{bound}^0 = 0.1103$ are obtained. Basing on Theorem 3.2, we know the zero equilibrium is asymptotically stable when $\tau < \tau_{trot}^0$ (shown in Figure 2a), when $\tau > \tau_{trot}^0$, the zero equilibrium of system (8) is unstable, and the periodic solution corresponding to the trot gait occurs (see Figure 2b). From theorem 3.3, we know the zero equilibrium is asymptotically stable when $\tau < \tau_{pace}^0$ (shown in Figure 3a), when $\tau > \tau_{pace}^0$, the zero equilibrium of system (10) is unstable, and the periodic solution corresponding to the pace gait occurs (see Figure 3b). From theorem 3.4, we know the zero equilibrium is asymptotically stable when $\tau < \tau_{bound}^0$ (shown in Figure 4a), when $\tau > \tau_{bound}^0$, the zero equilibrium of system (13) is unstable, and the periodic solution corresponding to the bound gait occurs (see Figure 4b).

5.   Conclusions

In this paper, a kind of CPG network system is constructed by using VDP oscillators, and a VDP-CPG network system with four basic gaits (walk, trot, pace and bound) is presented. By studying the corresponding characteristic equations of four gaits systems, it is found that the conditions for the periodic solutions of four gaits systems are $h < 0, \; 2s-h^2 > 0$ and $\frac{1}{9}m < K^2 < \min\{m, \frac{1}{9}\}$ and the critical values $\tau_{walk}^j, \; \tau_{trot}^j, \; \tau_{pace}^j$ and$\; \tau_{bound}^j, \; j = 0, 1, 2\cdots$. Thus, the range of coupling strength between legs in four gaits is $\frac{1}{9}m < K^2 < \min\{m, \frac{1}{9}\}$. Finally, the numerical simulations show that the gait systems (trot, pace and bound) produce corresponding gaits near the corresponding critical value.

Acknowledgements

This research is supported by the Fundamental Research Funds for the Central Universities (No.2572019BC12). The authors wish to express their gratitude to the editors and the reviewers for the helpful comments.

Conflict of interest

The authors declare there is no conflict of interest