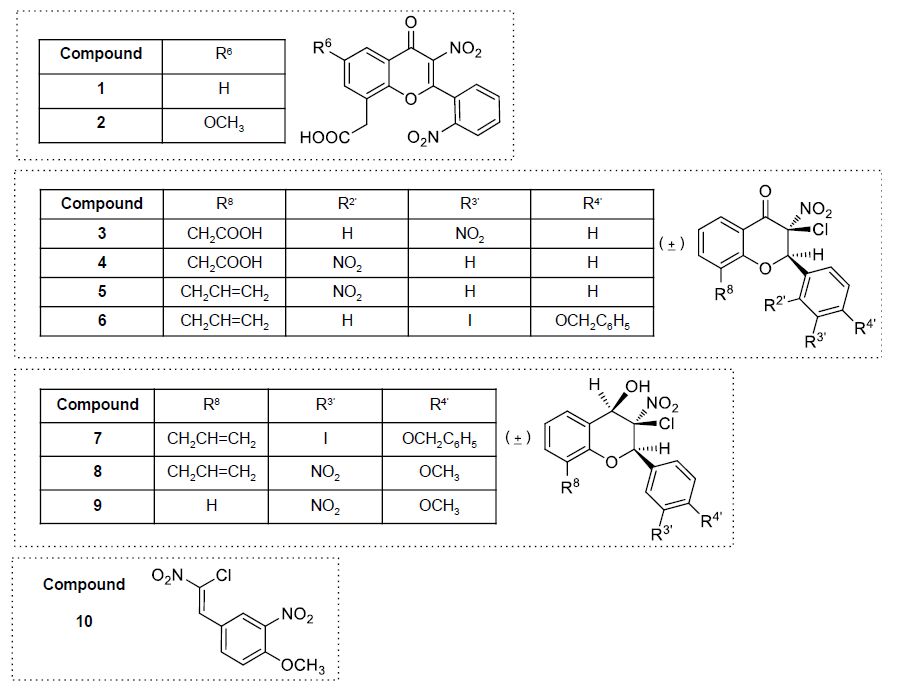
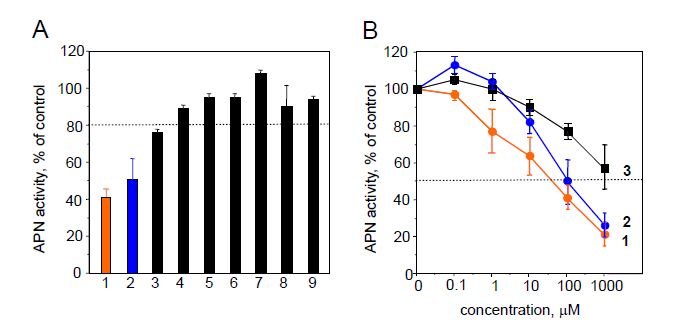
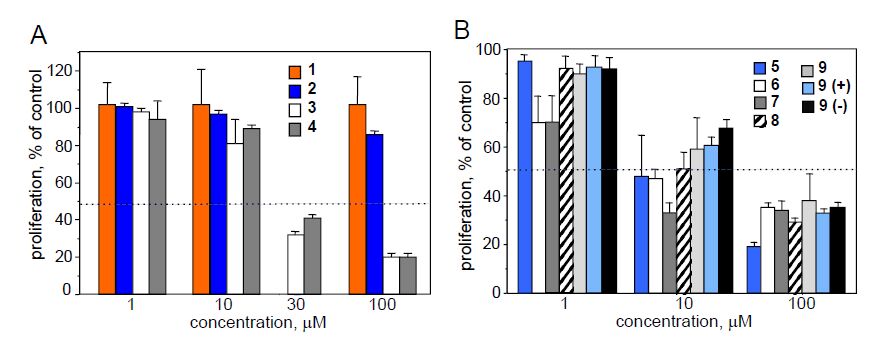
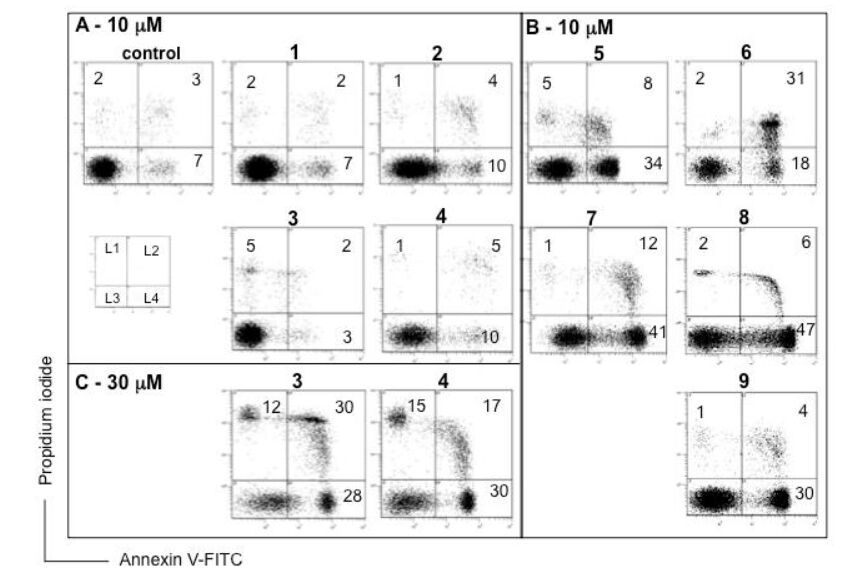
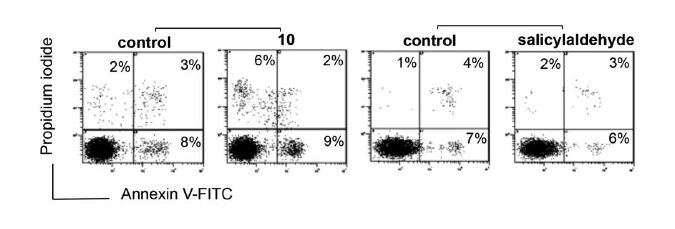
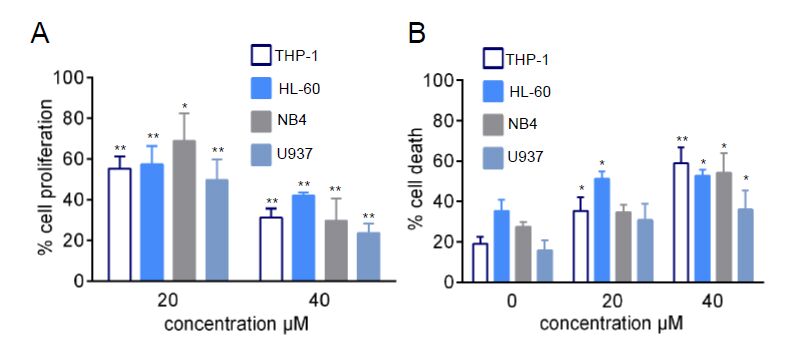
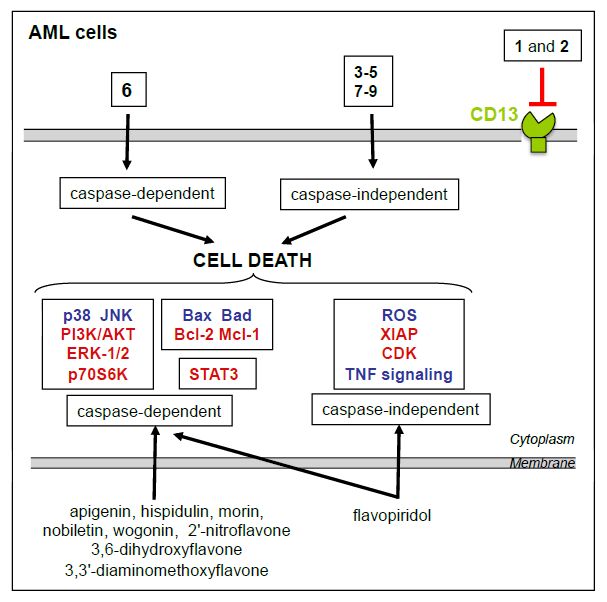
Leukemia cells from patients with acute myeloid leukemia (AML) display high proliferative capacity and are resistant to death. Membrane-anchored aminopeptidase-N/CD13 is a potential drug target in AML. Clinical research efforts are currently focusing on targeted therapies that induce death in AML cells. We previously developed a non-cytotoxic APN/CD13 inhibitor based on flavone-8-acetic acid scaffold, the 2',3-dinitroflavone-8-acetic acid (1). In this context, among the variously substituted 113 compounds further synthesized and tested for evaluation of their effects on APN/CD13 activity, proliferation and survival in human AML U937 cells, eight flavonoid derivatives emerged: 2',3-dinitro-6-methoxy-flavone-8-acetic acid (2), four compounds (3–6) with the 3-chloro-2,3-dihydro-3-nitro-2-phenyl-4H-1-benzopyran-4-one structure, and three (7–9) with the 3-chloro-3,4-dihydro-4-hydroxy-3-nitro-2-phenyl-2H-1-benzopyran framework. Different structure-activity relationships were observed between APN/CD13 activity and growth/survival processes. We showed that compound 2, but not benzopyran derivatives 3–9, inhibited APN activity (although to a less degree than 1). Both 1 and 2 did not affect AML cell proliferation and survival, indicating that CD13’s APN activity is not required for these processes. In contrast, benzopyran compounds 3–9 inhibited in a concentration-dependent manner the growth of U937 cells by inducing death as evidenced by phosphatidylserine externalization. Cell death was associated with the presence of geminal nitro group and chlorine at the 3-position of the 2H-1-benzopyran scaffold. The presence of other substituents such as CH2COOH or CH2CH=CH2 groups at the 8-position, NO2 or I substituents at the 2'- or 3'-position, OCH3 or OCH2C6H5 groups at the 4'-position did not affect cell death. Importantly, the inhibitory effects evidenced with compounds 7–9 were not due to their potential decomposition into the corresponding (Z)-(2chloro-2-nitroethenyl)benzene and salicylaldehyde. Based on these preliminary data, the 3-chloro,3-nitro-2H-1-benzopyran derivatives could be classified as a new group of compounds with promising antitumor properties; this study therefore provides the opportunity to explore their potential efficiency in AML patients’ cells ex vivo.
1.
Introduction
The concept of semiring was firstly introduced by Dedekind in 1894, it had been studied by various researchers using techniques coming from semigroup theory or ring theory. The algebraic theories of semirings were widely applied in automata theory, optimization theory, parallel computation systems and the mathematical modeling of quantum physics, etc. [7]
A semiring (S,+,⋅) is an algebra with two binary operations + and ⋅ such that the additive reduct (S,+) and the multiplicative reduct (S,⋅) are semigroup connected by ring-like distributive laws, that is,
In recent several decades, many authors extended the concepts and results of semigroups to semirings which is one of the development power of semiring theory. For instance, many researchers investigate idempotent semirings in which both additive reduct and multiplicative reduct are bands, which play a role in semirings just as the role of bands in semigroups in many aspects [2,4,17,18,19], etc. Semirings whose additive reduct is a band are also studied by many authors [3,11,25], etc. Karvellas introduced additively inverse semirings whose additive reduct is an inverse semigroup [10]. Zeleznikow studied regular semirings in which both additive and multiplicative semigroups are regular [27]. He also introduced the orthodox semirings firstly [28]. Grillet gave the structure theorem of semirings with a completely simple additive semigroup [6].
Meanwhile, semirings are generalizations of distributive lattices, b-lattices, rings, skew-rings. Sen, Maity, and Shum extended the concept of Clifford semigroup to semiring by defining a class of semiring which is called Clifford semiring and showed that a semiring S is a Clifford semiring if and only if it is a strong distributive lattice of skew-rings [20]. What's more, as a further generalization, they proved that a semiring S is a generalized Clifford semiring if and only if it is a strong b-lattice of skew-rings. Sen and Maity had also extended completely regular semigroups to completely regular semirings by giving a gross structure theorem: A semiring S is completely regular semiring if and only if it is a b-lattice of completely simple semirings [21]. Pastijn and Guo used inspiration for the study of semirings which are disjoint unions of rings in theory developed for completely regular semiring [26]. Maity and Ghosh also extended completely regular semiring to quasi completely regular semirings, and show that S is quasi completely regular semirings if and only if S is an idempotent semiring of quasi skew-rings [13,14]. Since the ideas of transversals are important to study algebraic structures which is useful in the study of semigroups structure [15,16,23,24]. In 2022, Huang et al. introduced some special semiring transversals into semirings and extended the results of completely regular semirings [9].
On the other hand, in the regular semigroups with inverse transversals, split orthodox semigroups are not only special regular semigroups with inverse transversals but also one of the origins of inverse transversals. In [12], D. B. McAlister and T. S. Blyth introduced a kind of semigroups which are called split orthodox semigroups and used a band, an inverse semigroup, and Munn morphism to give a structure theorem for them. El-Qallali studied the split quasi-adequate semigroups whose idempotents are commutative and extended the result of split orthodox semigroups [5]. Li extended split orthodox semigroups to split P-regular semigroups [22].
To develop new ways to study semirings, we will study a kind of semirings called split additively orthodox semirings which have the property like split orthodox semigroups. It is also a class of special semirings with transversals. In this paper, after obtaining some properties theorems of such semirings, we obtain a structure theorem for them by idempotent semirings, additively inverse semirings, and Munn semigroup. Consequently, the corresponding results of Clifford semirings and generalized Clifford semirings in [20], and split orthodox semigroups in [12] are also extended and strengthened.
For the terminology and notions not given in this paper, the reader is referred to [1,8].
2.
Preliminaries
Firstly, we claim that the following theorem will be frequently used without further mention.
Theorem 2.1. (Miller-Clifford theorem) [8]
(1) Let e and f be D-equivalent idempotents of a semigroup S. Then each element a of Re∩Lf has a unique inverse a′ in Rf∩Le, be such that aa′=e and a′a=f.
(2) Let a,b be elements of a semigroup S. Then ab∈Ra∩Lb if and only if Rb∩La contains an idempotent.
In this section, we will list some elementary results of split bands and split orthodox semigroups. The following results are all due to D. B. McAlister and T. S. Blyth. For convenience, throughout this section the letter D will always denote the Green's relation on a band B.
Definition 2.1. (Definition 1.1 [12]) Let B=∪{Bα:α∈Y} be a band with structure semilattice Y and D-classes the rectangular bands Bα. If ♮:B→B/D is the natural morphism then we shall say that B is split if there is a morphism π:B/D→B such that π♮=idB/D. Such a morphism π will be called a splitting morphism.
Definition 2.2. (Definition 1.2 [12]) Let B=∪{Bα:α∈Y} be a band. Then by a skeleton of B shall mean a subset E={xα:α∈Y} such that xα∈Bα for every α∈Y and xαxβ=xαβ=xβxα for all α,β∈Y.
Lemma 2.1. (Lemma 1.3 [12]) A band B is split if and only if it has a skeleton. If π:B/D→B is splitting morphism then \rm{Im} π is a skeleton of B.
We recall that the relation
on an orthodox semigroup T turns out to be the smallest inverse semigroup congruence on T. Moveover, on B the band of idempotents of T, γ is the same to D.
Definition 2.3. (Definition 1.4 [12]) Let T be an orthodox semigroup and let ♮:T→T/γ be natural morphism. Then we shall say that T is split if there is a morphism π:T/γ→T such that π♮=idT/γ.
Definition 2.4. (Definition 1.5 [12]) Let T be an orthodox semigroup with band of idempotents B. Suppose that E is a D-transversal of B in that E meets every D-class only once. Then we define the span of E by
Lemma 2.2. (Lemma 1.6 [12]) Let T be an orthodox semigroup with band of idempotents B. Suppose that E is a D-transversal of B in that E meets every D-class only once. Then Sp (E) meets every γ-class of T exactly once.
We denote the unique inverse of a∈Sp(E) in Sp(E) by a∘. Moreover, note that e=aa∘ and f=a∘a. Then
Theorem 2.2. (Theorem 1.7 [12]) Let T be an orthodox semigroup with band of idempotents B and suppose that B has a skeleton E. Then the following statements are equivalent:
(1) There is an inverse subsemigroup S∘ of T that meets every γ-class of T exactly once and has E as semilattice of idempotents;
(2) aEa∘⊆E for every a∈ Sp (E);
(3) Sp (E) is a subsemigroup of T.
Moreover, if (1) holds, then necessarily S∘= Sp (E).
B is a band with a skeleton E. e∈E. Let θ be a band isomorphism between subbands of B of the form eBe. We say θ is skeleton-preserving if it satisfies that
What is more, as shown in [12], if denote Dom(θ) and Im(θ) by eθBeθ and fθBfθ respectively, then
Now, denote by TB the set of skeleton-preserving isomorphisms θ between subbands of B of the form eBe, where e∈E.
Lemma 2.3. (Lemma 2.1 [12]) Let B be a band with a skeleton E. Then TB is an inverse semigroup.
Lemma 2.4. (Lemma 2.2 [12]) Let B be a band with a skeleton E. For θ∈TB, define ˉθ:B→B as following:
Then ¯θϕ=ˉθˉϕ, ∀θ,ϕ∈TB.
Given θ∈TB, let θ:eθBeθ→fθBfθ. It is clear that E∩Domθ=eθE and E∩Codθ=fθE. Moreover, θ induces an isomorphism ˆθ:eθE→fθE. For every x∈eθE, we have xˆθ=xθ. The assignment ^:θ↦ˆθ is then a morphism from TB to TE (the Munn semigroup of semilattice E).
Suppose now that S is an inverse semigroup with semilattice of idempotents E, let μ:a↦μa be a morphism from S to TE.
If there exists a morphism θ:S→TB making the following diagram commutative,
we call it is a triangulation of μ. Denote aθ=θa, then ˆθa=μa, μa:aa∘E→a∘aE,e↦a∘ea,e∈aa∘E.
Lemma 2.5. (Lemma 2.3 [12]) Let S be an inverse semigroup with semilattice of idempotents E and let B be a band with skeleton E. For every a∈S, let the domain and codomain of μa be eaE (so that ea=aa∘) and faE (so that fa=a∘a). Let θ be a triangulation of μ. Then given a,b∈S and e,f,u,v∈B such that eLea, fRfa, uLeb, vRfb, we have
Corollary 2.1. (Corollary 2.4 [12]) If
then the prescription
defines a binary operation on W.
Theorem 2.3. (Throrem 2.5 [12]) W(B,S,θ) is an orthodox semigroup whose band of idempotents is isomorphic to B.
Theorem 2.4. (Theorem 2.7 [12]) The orthodox semigroup W=W(B,S,θ) is split and W/γ≅S.
Theorem 2.5. (Theorem 2.8 [12]) Let T be a split orthodox semigroup with band B of idempotents. If π:T/γ→T is a splitting morphism then the set E=B∩ Imπ of idempotents of Imπ is a skeleton of B and Sp (E)= Imπ. Moreover, if θ: Im π→TB is given by aθ=θa, where the domain of θa is aa∘Baa∘, the codomain of θa is a∘aBa∘a and bθa=a∘ba, then θ is a triangulation of μ: Im π→TB and
3.
Split adtitively orthodox semirings
Let (S,+,⋅) be a semiring. Then the Green's relation on (S, +) denoted by +R, +L and +H. The set of additive idempotents and the set of multiplicative idempotents of S are denoted by E+(S) and E∙(S) respectively.
We also denote the additive inverse of x∈S by x′, (x′)′ by x″, and all the additive inverses of x by +V(x) respectively.
Lemma 3.1. Let (S,+,⋅) be a semiring. ∀x,y∈S, if x′∈+V(x)≠∅, then (xy)′=x′y and (yx)′=yx′.
Proof: Clearly.
In this section, we introduce the concept of split additively orthodox semirings. For convenience, T is denoted the additively orthodox semiring whose additive idempotents forms an idempotent semiring always. The letter +D will always denote the Green's relation on (+E(S),+). Since +D is congruence on (+E(S),+,⋅) and every +D-class is an idempotent semiring for which the additive reduct is a rectangular band. Such idempotent semiring will be called additive rectangular idempotent semiring in this paper.
T is an additively orthodox semiring, so (T, +) is an orthodox semigroup. Then we have the following corollary.
Corollary 3.1. The relation
is the smallest additively inverse semiring congruence on T.
{Proof: }∀x,y,a∈T,xγy, then +V(x)=+V(y). ∀(ax)′∈+V(ax), (ax)′=ax′. Since x′∈+V(x)=+V(y), then
and
So +V(ax)⊆+V(ay). Similarly, we can show the other side. Hence, γ is the semiring congruence on T.
Moreover, γ is an additively inverse semiring congruence on T, since T/γ is an additively inverse semiring.
Now, let ρ to be a semiring congruence on T such that T/ρ is an additively inverse semiring. For (x,y)∈γ, let a∈+V(x)(=+V(y)). Then both xρ and yρ are inverses of aρ in the additively inverse semiring T/ρ. So xρy which implies that γ⊆ρ.
Therefore, γ is the smallest additively inverse semiring congruence on T.
Moveover, on an idempotent semiring I, γ is the same to +D, i.e. I/γ=I/+D which is b-lattice.
Example 3.1. Let S1={0,a,b} whose additive and multiplicative Cayley tables as following:
Then (S1,+,⋅) forms an additively inverse semiring.
Let I1={p,q} and Λ1={u,v} whose additive and multiplicative Cayley tables as following:
It is easy to verify that (I1,+,⋅) and (Λ1,+,⋅) form idempotent semirings. The additive reduct of (I1,+,⋅) is a left zero band, and its multiplicative reduct is a semilattice. The additive reduct of (Λ1,+,⋅) is a right zero band, and its multiplicative reduct is a semilattice.
Then the direct product T=I1×S1×Λ1 forms an additively regular semiring, and E+(T)=I1×E+(S1)×Λ1 is an idempotent semiring, hence T is an additively orthodox semiring.
∀(i,x,y)∈T,
It implies that
So, T/γ={I1×{x}×Λ1|x∈S1}≅S1. Therefore, γ is the smallest additively inverse semiring congruence on T.
Definition 3.1. Let T be an additively orthodox semiring whose additive idempotents forms an idempotent semiring and ♮:T→T/γ be natural morphism. Then we shall say that T is split if there is a morphism π:T/γ→T such that π♮=idT/γ.
Some additively orthodox semirings are neither completely regular semirings nor split additively orthodox semirings, see the following example.
Example 3.2. Let S1 as shown in Example 1. Then it is also a completely regular semiring. Although the set E+(S1)={0,b} is an ideal of S1, (S1,+,⋅) is not a generalized Clifford semiring [20].
Let I2={p,q} and Λ2={u,v} whose additive and multiplicative Cayley tables as following:
We can verify that (I2,+,⋅) and (Λ2,+,⋅) form semirings. The additive reduct of (I2,+,⋅) is a left zero band, and its multiplicative reduct is a group. The additive reduct of (Λ2,+,⋅) is a right zero band, and its multiplicative reduct is a group.
Then the direct product T=I2×S1×Λ2 forms an additively regular semiring, and E+(T)=I2×E+(S1)×Λ2 forms its subsemiring, hence T is an additively orthodox semiring. But E∙(T)={p}×E+(S1)×{u}, according to Lemma 2.5 in [21], thus (T,+,⋅) is not a completely regular semiring. Since E+(T) is not an idempotent semiring, T is not a split additively orthodox semiring. Moreover, {(p,x,u)|x∈S1} is an additively inverse semiring transversal of T [9].
A split additively orthodox semiring may not be a completely regular semiring, see the following example.
Example 3.3. Let S2={0,i,a,e,f,x,y} whose additive and multiplicative Cayley tables as following:
It is easy to verify that (S2,+,⋅) forms an additively inverse semiring, but +Hx={x} is not a skew-ring, so S2 is not a completely regular semiring or a generalized Clifford semiring.
Let I1 and Λ1 as shown in Example 3.1. Then the direct product T=I1×S2×Λ1 forms a additively regular semiring, and E+(T)=I1×E+(S2)×Λ1 is an idempotent semiring, hence T is an additively orthodox semiring. Additionally, T/γ={I1×{x}×Λ1|x∈S2}. Let π:T/γ→{p}×S2×{u},I1×{x}×Λ1↦(p,x,u). It is easy to verify that π is a split morphism, so T is a split additively orthodox semiring. Moreover, Imπ is an additively inverse semiring transversal of T. But Imπ≅S2 which means that it is not a generalized Clifford semiring transversal of T. In addition, +H(p,x,u)={(p,x,u)} is not a skew-ring, so T is not a completely regular semiring.
A split additively orthodox semiring may be also a completely regular semiring, see the following example.
Example 3.4. Let T as shown in Example 3.1. So T is an additively orthodox semiring, and T/γ={I1×{x}×Λ1|x∈S1}≅S1. Let π:T/γ→{p}×S1×{u},I1×{x}×Λ1↦(p,x,u). It is easy to verify that π is a split morphism, so T is a split additively orthodox semiring. What is more, Imπ={(p,x,u)|x∈S1} is an additively inverse semiring transversal of T. But Imπ≅S1 which means that it is not a generalized Clifford semiring transversal of T. Meanwhile, T is a completely regular semiring.
Theorem 3.1. Let T be an additively orthodox semiring with a generalized Clifford semiring transversal S. Then the following statements are equivalent:
(1) T is a completely regular semiring;
(2) T is a split additively orthodox semiring.
Proof: (1)⇒(2): T is an additively orthodox semiring which means that E+(T) forms a band. Moreover, E+(T)⊆E∙(T), since T is a completely regular semiring. Let π:T/γ→S,γx↦x∘,x∘∈+V(x)∩S. It is easy to verify that π is a split morphism.
(2)⇒(1): By Theorem 4.1 in [9], T is a b-lattice of additively orthodox semirings with skew-ring transversals. For each additively orthodox semiring with skew-ring transversals Sα, Sα is an additively completely simple semiring by Theorem 3.1 in [9]. Moreover, E+(T)⊆E∙(T). Hence, Sα is a completely simple semiring. Therefore, T is a b-lattice of completely simple semiring which means that T is a completely regular semiring.
By Definition 2.1 and Definition 3.1, if there is a split morphism π on the idempotent semiring I, then π is a split morphism on band (I,+).
Definition 3.2. Let I=∪{Iα:α∈Y} be an idempotent semiring, where Y is a b-lattice. Then by a skeleton of I shall mean a subset E={xα:α∈Y} such that xα∈Iα for every α∈Y, and xα+xβ=xα+β=xβ+xα and xαxβ=xαβ for all α,β∈Y.
Example 3.5. Let Y={0,e} whose additive and multiplicative Cayley tables as following:
It is easy to verify that (Y,+,⋅) forms a b-lattice. Let I1 and Λ1 as shown in Example 3.1. Then the direct product I=I1×Y×Λ1 forms an idempotent semiring.
Additionally, I/γ={I1×{x}×Λ1|x∈Y}≅Y. Denote I1×{x}×Λ1 by γx, then I=γ0∪γe.
Let E={(p,0,u),(p,e,u)}. Then (p,0,u)∈γ0 and (p,e,u)∈γe. Moreover,
and
where (p,0,u)∈γ0e
Therefore, E is a skeleton of I.
By Definition 2.2 and Definition 3.2, we easily get that if E is a skeleton of I then (E, +) is a skeleton of (I, +).
Lemma 3.2. An idempotent semiring I is split if and only if it has a skeleton. If π:I/+D→I is splitting morphism then Imπ is a skeleton of I.
Proof: By Lemma 2.1, Definition 3.1, and Definition 3.2, it is clear.
4.
The structure theorem
From now on, we explore the structure of split additively orthodox semirings.
Lemma 4.1. Let T be a split additively orthodox semiring whose additive idempotents forms an idempotent semiring I. Then E=I∩ Imπ is a skeleton of I.
Proof: Imπ is an additively inverse subsemiring of T, and meets every γ-class of T exactly once. As a result, E=I∩Imπ is the set of all the additive idempotents of Imπ forms b-lattice, and E meets every +D-class of I exactly once, hence it is a skeleton of I.
The span of E is also the important set:
By Lemma 2.2, the following lemma is obtained directly.
Lemma 4.2. Let T be a split additively orthodox semiring whose additive idempotents forms an idempotent semiring I. Then Sp (E) meets every γ-class of T exactly once.
Noting that for every a∈Sp(E), exist e,f∈E satisfy that e+Ra+Lf, then +Le∩+Rf contains an additive inverse a′ of a, and a′∈Sp(E). By Lemma 4.2, we get that a′ is the unique inverse of a in Sp(E), which is denoted by a∘ hereafter. Moreover, e=a+a∘ and f=a∘+a. Actually, we can get more from the following theorem.
Theorem 4.1. Let T be an additively orthodox semiring with an idempotent semiring of additive idempotent I and suppose that I has a skeleton E. Then the following statements are equivalent:
(1) There is an additively inverse subsemiring S of T that meets every γ-class of T exactly once and has E as b-lattice of additive idempotents;
(2) a+E+a∘⊆E for every a∈\rm{Sp}(E);
(3) Sp (E) is a subsemiring of T.
Proof: (1)⇒(2): By Theorem 2.2, it is clear.
(2)⇒(3): By Theorem 2.2, Sp(E) is close under addition. Now we show that it is close under multiplication. Given a,b∈Sp(E), there exist ea,eb,fa,fb∈E such that ea+Ra+Lfa, and eb+Ra+Lfb. Since +R and +L are multiplicative congruence on S, then eaeb+Rab+Lfafb. Since eaeb,fafb∈E, it follows that Sp(E) is a subsemiring of T.
(3)⇒(1): If Sp(E) is a subsemiring, by the remarks following Lemma 9, Sp(E) is an additively orthodox subsemiring which meets every γ-class exactly once and has E as its set of additive idempotents.
By Lemma 2.2, the following corollary is obtained directly.
Corollary 4.1. Let T be a split additively orthodox semiring whose additive idempotents forms an idempotent semiring I. Then Sp (E)= Im π.
For every a∈Imπ, let ea=a+a∘, fa=a∘+a. Define θa:ea+I+ea→fa+I+fa by xθa=a∘+x+a. According to the proof of Theorem 2.5 (i.e. Theorem 2.8 in [12]), θa is a skeleton-preserving isomorphism from (ea+I+ea,+) to (fa+I+fa,+) satisfies that
Denote all the skeleton-preserving isomorphisms φ between the subbands such as e+I+e of (I, +) by +TI, where e∈I. Then define the addition on +TI as composition of maps, i.e. e(φ+ϕ)≜(eφ)ϕ. By Lemma 2.3, we get that (+TI,+) is an inverse semigroup.
Lemma 4.3. Let T be a split additively orthodox semiring whose additive idempotents forms an idempotent semiring I. E=I∩ Imπ. TE is the Munn semigroup of (E,+). For μa∈TE, define θ: Imπ→+TI by aθ=θa, where the domain of θa is a+a∘+I+a+a∘, and the codomain is a∘+a+I+a∘+a. Moreover, bθa=a∘+b+a, then θ is a triangulation of μ: Imπ→TE.
Proof: According to the proof of Theorem 2.3 (i.e. Theorem 2.5 in [12]), the mapping θ:Imπ→+TI defined by aθ=θa is a morphism from (Imπ,+) to (+TI,+). By the definition of θa, we obtain that ˆθa=μa, where μa∈TE. TE is the Munn semigroup of (E,+), and define eμa=a∘+e+a which is an isomorphism from (a+a∘+E,+) to (a∘+a+E,+). As a result, θ is a triangulation of μ:Imπ→TE.
Moreover, we can extend each θ∈+TI to a mapping ˉθ:I→I by defining
And define the addition between two maps as composition of maps. By Lemma 4, we get that
Theorem 4.2. Let S be an additively inverse semiring with b-lattice of additive idempotents E and I be an idempotent semiring with skeleton E. For every a∈S, let the domain and codomain of μa∈TE be ea+E (so that ea=a+a∘) and fa+E (so that fa=a∘+a). Let θ be a triangulation of μ. Then given a,b∈S and e,f,u,v∈I such that e+Lea, f+Rfa, u+Leb, v+Rfb, we have
(1) (e+(f+u)ˉθa∘)+Lea+b and ((f+u)ˉθb+v)+Rfa+b;
(2) ab+H(ab)∘ and eab=fab=eafb=faeb=eaeb=fafb;
(3) eu+Leab and fv+Rfab.
Proof: (1) By Lemma 2.5, it is clear.
(2) Since ea+La∘+Rfa and fb+Lb+Reb, then eafb+La∘b+Rfaeb. Similarly, we can get that eafb+Rab∘+Lfaeb. By Lemma 6, a∘b=(ab)∘=ab∘. So eafb+L(ab)∘+Lfaeb and eafb+R(ab)∘+Rfaeb, that is eafb+H(ab)∘+Hfaeb. Similarly, we get that eaeb+Hab+Hfafb. Consequently, ab+H(ab)∘ and eab=fab=eafb=faeb=eaeb=fafb.
(3) Since e+Lea and u+Leb, then eu+Leaeb=eab. Similarly, fv+Rfab.
Theorem 4.3. Let T be a split additively orthodox semiring whose additive idempotents forms an idempotent semiring I. For any a,b∈ Imπ and e,f,u,v∈I such that e+Lea, f+Rfa, u+Leb, v+Rfb, then
Proof: Firstly, on the one hand, since f+L(e+a+f)+Re and v+L(u+b+v)+Ru, then fv+L(e+a+f)(u+b+v)+Reu. On the other hand, since e+Lea, f+Rfa, u+Leb and v+Rfb, then eu+Leab and fv+Rfab, so fv+L(eu+ab+fv)+Reu. Hence, (e+a+f)(u+b+v)+H(eu+ab+fv).
Secondly, since e+Lea+La∘ and f+Rfa+Ra∘, then
and
so a∘∈+V(e+a+f), i.e. a∘ is the unique additive inverse of e+a+f in Imπ. Similarly, (u+b+v)∘=b∘ and (eu+ab+fv)∘=(ab)∘. Thus,
Consequently, (e+a+f)(u+b+v)=eu+ab+fv as required.
Theorem 4.4. Let T be a split additively orthodox semiring whose additive idempotents forms an idempotent semiring I. For any a,b,c∈ Imπ and e,f,u,v,g,h∈I such that e+Lea, f+Rfa, u+Leb, v+Rfb, g+Lec, h+Rfc, then satisfies the following four equations:
and
Proof: For any a,b,c∈Imπ and e,f,u,v,g,h∈I such that e+Lea, f+Rfa, u+Leb, v+Rfb, g+Lec, h+Rfc. On the one hand, by Theorem 4.2, we get that
then
that is
where
and
So,
On the other hand, since +L and +R are multiplicative congruence on T, then
By Theorem 4.2, we get that
that is
where
and
So,
Therefore,
as required. Similarly, we can show the following three equations:
and
Theorem 4.5. Let S be an additively inverse semiring with b-lattice of additive idempotents E and I be an idempotent semiring with skeleton E. For every a∈S, let the domain and codomain of μa∈TE be ea+E (so that ea=a+a∘) and fa+E (so that fa=a∘+a). Let θ be a triangulation of μ. Then given a,b∈S and e,f,u,v∈I such that e+Lea, f+Rfa, u+Leb, v+Rfb, g+Lec, h+Rfc, and satisfies the following four equations:
and
Define two binary operations
and
on
Then W is a split additively orthodox semiring whose additive idempotents form an idempotent semiring which is isomorphic to I, and W/γ≅S.
Conversely, every split additively orthodox semiring is of the form W(I,S,θ).
Proof: By Theorem 2.3, (W,+) is an orthodox semigroup. And the associativity of multiplication is clear. We only need to prove the distributivity of the semiring W. Give (e,a,f),(u,b,v),(g,c,h)∈W, by the four equations,
Thus the distributivity on left is hold. And the distributivity on right can be proved similarly. Hence W is additively orthodox semiring as required.
By the proof of Theorem 2.3 (i.e. Theorem 2.5 in [12]), we get that +E(W)={(e,a,f)∈W:a∈+E(S)}, moreover, the map ϕ defined from +E(W) to I by (e,a,f)ϕ=e+f is bijective and preserves addition. So we need to show it also preserves multiplication well. For any (e,a,f),(u,b,v)∈+E(W), since a,b∈+E(S) then a∘=a and b∘=b, we find that ea=a+a∘=a+a=a=a∘+a=fa and eb=b+b∘=b+b=b=b∘+b=fb, so e+La+Rf and u+Lb+Rv. On the one hand, by Theorem 2.1, we get that e+R(e+f)+Lf and u+R(u+v)+Lv, so eu+R(e+f)(u+v)+Lfv since +R and +L are both multiplicative congruence on I. On the other hand, we get that eu+Lab+Rfv, then eu+R(eu+fv)+Lfv by Theorem 2.1. Therefore, (e+f)(u+v)+H(eu+fv) which means that (e+f)(u+v)=eu+fv. Hence,
Thus ϕ is an isomorphism as require.
By the proof of Theorem 2.3 (i.e. Theorem 2.5 in [12]), we get that
and the mapping π:W/γ→W given by γ(e,a,f)π=(ea,a,fa) preserves addition and satisfies that π♮=idW/γ. Now we will show that it also preserves multiplication:
Finally, it is clear that
the second isomorphism being that given by (ea,a,fa)↔a.
Conversely, let T be a split additively orthodox semiring with the idempotent semiring I of additive idempotents, and mapping π:T/γ→T be a splitting morphism. By Lemma 4.1 and Corollary 4.1, the set E=I∩Imπ of additive idempotents of Imπ is a skeleton of I and Sp(E) = Imπ.
Moreover, define θ: Imπ→TI by aθ=θa, where the domain of θa is a+a∘+I+a+a∘, the codomain of θa is a∘+a+I+a∘+a and bθa=a∘+b+a. By Lemma 4.3, θ is a triangulation of μ:Imπ→TE. By Theorem 4.4, W(I,Imπ,θ) satisfies the four equations. We can therefore construct the split additively orthodox semiring W=W(I,Imπ,θ).
Define the map ψ:W→T by
By the proof shown in [12]. ψ is bijection and preserves addition.
Since for any a,b∈Imπ and e,f,u,v∈I such that e+Lea, f+Rfa, u+Leb, v+Rfb, then
So it also preserves multiplication clearly.
Therefore, ψ is a semiring isomorphism.
As shown in [20], a generalized Clifford semiring S is not only an additively orthodox semiring, but also a strong b-lattice T of skew-rings Rα(α∈T), i.e. S=<T,Rα,ϕα,β>. Hence, S/γ=T. Let π:T/γ→S,α↦x∈Rα. It is easy to verify that π is a split morphism, so S is a split additively orthodox semiring.
Remark 1. From Theorem 4.5, we can see that the class of split additively orthodox semiringsis actually not only a general extension of the class of Clifford semirings and generalized Clifford semirings studied in [20], but also a general extension of the class of split orthodox semigroups in [12].
5.
Conclusions
In this paper, we introduce and explore split additively orthodox semirings. Some property theorems are obtained, and a structure theorem is established by using idempotent semirings, additively inverse semirings, and Munn semigroup. It not only extends and strengthens the corresponding results of Clifford semirings and split orthodox semigroups but also develops a new way to study semirings.
Acknowledgments
This work was supported in part by the Dongguan Science and Technology of Social Development Program (2022), in part by the NNSF of China (11801239, 12171022).
Conflict of interest
All authors declare no conflicts of interest in this paper.



















 DownLoad:
DownLoad: