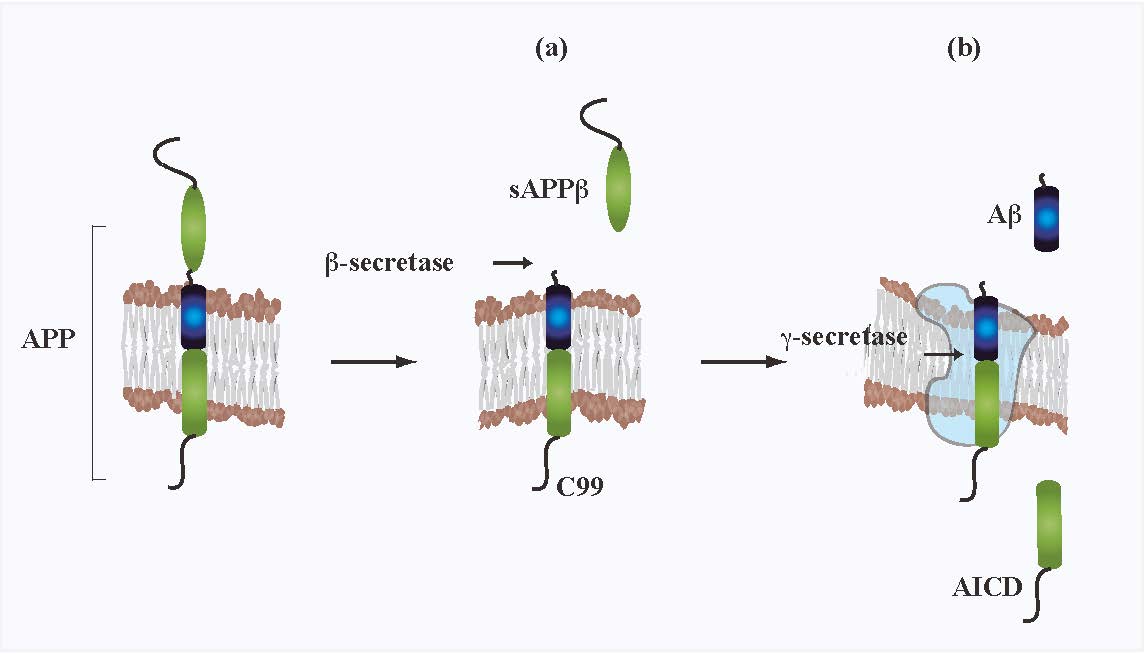
The critical discovery of the presenilins and their association with familial Alzheimer’s disease (AD) prompted an intensive research effort to understand the molecular mechanisms of that disease. The presenilins were subsequently found to be the catalytic component of the multi-protein enzyme complex, γ-secretase, the enzyme that is known to act on the amyloid precursor protein (APP) to generate amyloid beta (Aβ) peptides that comprise the neuritic plaques implicated in AD pathology. Here, we discuss the background of γ-secretase- mediated proteolysis of APP and its association with familial AD. We discuss the association of neuroinflammation with AD, focusing on the link between the innate immune response, the clearance of the Aβ peptides and disease progression. Currently, there are limited treatments for AD that strive to ameliorate the symptoms of the disease but do not address the molecular basis of the disease. The greater understanding of γ- secretase functions has provided new insights into potential therapeutics for AD, a number of which are in clinical trials.
1.
Introduction
For decades, many researchers have studied and established mathematical models describing interactions among species. Initially, most studies primarily focused on various types of interaction mechanisms and models using random dispersal of species. The importance of species dispersal, which is one of the main factors involved in species behavior, led to the establishment of more realistic models for species dispersal, for example, self-cross diffusion [1,2,3,4,5,6,7,8,9,10], advection-diffusion [11,12,13,14,15,16,17,18,19,20], and other types of non-uniform dispersal [21,22,23,24,25,26,27,28] models. For the predator–prey interaction, a popular way of describing the dispersal mechanism of predators is using prey-taxis [29,30,31,32,33,34]. There are some predator dispersal types such as the cross diffusion [2,3,4,5,6] and starvation-driven diffusion [22,25]. However, most models describing the dispersal mechanism of predators were dependent on prey's population density.
In this paper, we examine the predator–prey model describing a situation wherein the predator dispersal depends on other environmental factors rather than prey density. Here, we consider the following model with a directional dispersal of a predator in a spatially heterogeneous environment:
where $ \Omega $ is a bounded convex domain in $ \mathbb{R}^n $. The zero-flux condition is provided on the smooth boundary $ \partial\Omega $, where $ \vec{n} $ is the outward unit normal vector on the boundary. The functions $ u(x, t) $ and $ v(x, t) $ represent the population densities of the prey and predator, respectively. $ m(x) $ is the growth rate of the prey depending on the location $ x\in\Omega $, and $ \mu $ and $ \eta $ are the diffusion rates of the prey and predator, respectively. $ \alpha(x) $ is a positive function representing the capturing rate. $ \beta(x) $ is proportional to $ \alpha(x) $, $ \beta = k\alpha $, where $ k > 0 $ is a conversion efficiency of food into offspring. A positive function $ d(x) $ is a measure of the interference for the predators during hunting the prey. $ c $ and $ \chi $ are positive constants representing the death rate of the predator and taxis sensitivity coefficient, respectively. The reaction term of the predator represents a case wherein the predator is fed only using the prey. To describe the predator–prey interaction, a ratio-dependent functional response is adopted. By considering the spatially heterogeneous environment, we use the predator-dependent form, such as the ratio-dependent form, for the system [35,36,37].
The model (P) represents a situation wherein the predator dispersal is unaffected by the prey density. The evolution of prey's behavior and traits has helped them against the threats of the predators. Consequently, these evolved traits and behaviors, for example, nocturnality [38,39], camouflage and masquerade [40,41], or living underground [42], make it difficult for the predators to chase the prey directly. This implies that the prey density does not affect the predator dispersal anymore. In response to defensive mechanisms of the prey, predators not only memorize the location where the prey was detected before but also learn the locations to hunt the prey in their habitat efficiently. Some studies have investigated the searching mechanism depending on such spatial memory [43,44,45,46]. In [43], the artificial experiments using birds was introduced, which provided some evidence of such animal learning to find better locations (see [43] and references therein). Thus, we assume that the prey has evolved to avoid detection from the predator, and the predator disperses using a spatial memory from experiences about the good locations to forage efficiently.
Such predator dispersal is mathematically described using the taxis term $ -\nabla\cdot(\chi v\nabla \beta) $. An attractant function $ \beta(x) $ includes factors such as an encounter with prey and attack success rates. That is, $ \beta(x) $ indicates which area has high or low hunting efficiency for predators. Thus, the taxis term represents that the predator moves toward locations with high foraging efficiency using the spatial memory about $ \beta $, which is a kind of mnemotaxis [44,45]. The reaction–diffusion system with the taxis term has a property that $ v $ is concentrated around the local maximums of $ \beta $ [15,16]. This implies that the predator gathers near the locations that have a high hunting efficiency. Thus, the predators' directional dispersal toward the location with better hunting efficiency can be described using such type of taxis term.
For the described dispersal mechanism of the predators, two situations can occur. The first situation wherein $ \beta $ is proportional to the resources of prey $ m $ ($ \beta = \kappa m $ for some constant $ \kappa $). This means that the predators move toward locations where the prey is abundant because the prey is distributed along with the distribution of resources. Mathematical and experimental works have been performed on a similar situation that the predators track the prey's resources instead of the prey density [47,48,49]. The second situation in which the distributions of $ \beta $ and $ m $ are different, i.e., $ \beta $ is not proportional to $ m $. This situation can happen because some places are rich with prey but are easy to hide, making it difficult to hunt for predators, or because the predators memorized correctly, but the environment of prey's habitat has changed due to external factors. This situation seems to be disadvantageous to the predators. Thus, this paper aimed to show the effect of the directional movement of predators in both situations.
In our model, we let $ w = e^{ -\chi \beta (x)/\eta }v $. Then, an alternative form of (P) is obtained as follows:
where $ w(x_0) = e^{ -\chi \beta (x)/\eta }v_0 $. Throughout this paper, we give assumptions on $ m $, $ \alpha $ and $ \beta $:
Under the assumption (A), the global existence and uniqueness of the classical solution to (P') follows from the Amann's results [50] for quasilinear parabolic equations. And (P') has one semi-trivial solution $ (\theta, 0) $, where $ \theta $ is a unique positive steady state solution of
In this paper, we first investigate the local stability of the semi-trivial solution $ (\theta, 0) $, which is closely related to the survival of the predator. We also consider the elliptic system of (P'). We show that the elliptic system has a positive solution, called the coexistence steady-state, under the conditions for the instability of $ (\theta, 0) $. We also investigate the nonexistence of the positive solution.
The remaining part of this paper is organized as follows. In Section 2, we state the main theorems and give a biological explanation. The theorems address the stability of $ (\theta, 0) $ and the existence of a coexistence steady-state. Moreover, the effects of taxis sensitivity $ \chi $ are observed. We provide the proofs of stability theorem using the principal eigenvalue analysis in Section 3. The existence of a coexistence steady-state is shown by the fixed-point index theory in Section 4. In Section 5, we present the numerical simulations for some cases. Section 6 summarizes the results obtained and concludes the paper.
2.
Main results
2.1. Stability of $ (\theta, 0) $
First, we introduce the results for the stability of $ (\theta, 0) $. The instability of $ (\theta, 0) $ and the positivity of the prey density imply that the predator can invade the region. This implies that the predator can survive in the environment, even though this is rare. This allows us to examine whether the taxis is beneficial to the survival of the predator. As in [29], we can show the positivity of the prey density and $ \liminf_{t\rightarrow\infty}u(x, t) > 0 $ if $ \int_\Omega{m(x)dx} > \int_\Omega{\alpha(x)dx} $. Therefore, if we assume $ \int_\Omega{m(x)dx} > \int_\Omega{\alpha(x)dx} $, the invasibility of the predator can be determined by the instability of $ (\theta, 0) $.
To study the stability of $ (\theta, 0) $, we consider the following linearized eigenvalue problem of (P') at $ (\theta, 0) $:
We multiply $ e^{\chi\beta/\eta} $ by the second equation of Eq (2.1) and obtain
Equation (2.2) is the weighted eigenvalue problem $ \lambda e^{\chi\beta/\eta}\psi = L\psi $, where $ L\psi = \eta\nabla\cdot(e^{\chi\beta/\eta}\nabla\psi) + (-c+\beta(x))e^{\chi\beta/\eta}\psi $. Since $ L $ is a self-adjoint, we have the following variational form of the principal eigenvalue:
We denote the principal eigenvalue of the operator $ L $ by $ \lambda_1(L, \chi) $. It is well-known that $ \lambda_1(L, \chi) $ and the local stability of $ (\theta, 0) $ have the following relation: If $ \lambda_1(L, \chi) > 0 $, then $ (\theta, 0) $ is locally unstable; if $ \lambda_1(L, \chi) < 0 $, then $ (\theta, 0) $ is locally stable (see [51]).
We define the ecological reproduction number $ \mathcal{R}_0 $ as
Thus, we have the following lemma whose proof is analogous to the proof of Lemma 2, 3 in [52].
Lemma 2.1. $ \mathcal{R}_0 > 1 $ if and only if $ \lambda_1(L, \chi) > 0 $.
Lemma 2.1 implies that $ (\theta, 0) $ is unstable if $ \mathcal{R}_0 > 1 $, and $ (\theta, 0) $ is locally asymptotically stable if $ \mathcal{R}_0 < 1 $. Then, $ \mathcal{R}_0 $ has a similar role as the basic reproduction number in epidemiology. This means that the survival of the predator is determined by the sign of $ \mathcal{R}_0-1 $.
Now, we introduce the results for the local stability of $ (\theta, 0) $ with an assumption on $ \beta $, $ \frac{\partial\beta}{\partial \vec{n}} = 0 $. For a function $ f $, we denote the average of $ f $ in $ \Omega $ by $ \overline{f} $. We first present the stability result about the predator's death rate $ c $ when $ \frac{\partial\beta}{\partial \vec{n}} = 0 $.
Theorem 2.2. Let $ \eta > 0, \chi\geq0 $ be given. If $ \frac{\partial\beta}{\partial \vec{n}} = 0 $, there exists $ \tilde{c}\in \big(\overline{\beta}-\frac{\chi^2}{4\eta}\overline{|\nabla\beta|^2}, \max_{\bar{\Omega}}\beta \big) $ such that $ (\theta, 0) $ is unstable when $ c < \tilde{c} $, and $ (\theta, 0) $ is locally asymptotically stable when $ c > \tilde{c} $.
In Theorem 2.2, the sharp criteria for the local stability of $ (\theta, 0) $ about $ c $ is obtained, which represents invasibility of the predator. Given $ \eta > 0 $ and $ \chi\geq0 $, there exists a threshold value $ \tilde{c} $ such that $ \lambda_1(L, \chi) = 0 $ for $ c = \tilde{c} $ and the sign of $ c-\tilde{c} $ determines the stability of $ (\theta, 0) $. From Theorem 2.2, $ (\theta, 0) $ is unstable for all $ \eta > 0 $ when $ c < \overline{\beta} $ and $ \chi = 0 $, but $ \chi > 0 $ gives a possibility $ (\theta, 0) $ to be stable if $ c\in(\overline{\beta}-\frac{\chi^2}{4\eta}\overline{|\nabla\beta|}, \overline{\beta}) $. This means that the directional dispersal could be disadvantageous.
Next, we give the result for the local stability of $ (\theta, 0) $ about the death rate $ c $ and diffusion rate $ \eta $ of a predator.
Theorem 2.3. Suppose that $ \frac{\partial\beta}{\partial \vec{n}} = 0 $. Let $ \chi > 0 $ and $ \xi > 0 $ be given constants.
(i) If $ c > \max_{\bar{\Omega}}\beta $, then $ (\theta, 0) $ is locally asymptotically stable for all $ \eta > 0 $.
(ii) If $ c < \min_{\bar{\Omega}}\beta $, then $ (\theta, 0) $ is unstable for all $ \eta > 0 $.
(iii) If $ c < \overline{\beta}-\frac{1}{4\xi}\overline{|\nabla\beta|^2} $, then $ (\theta, 0) $ is unstable when $ \eta > \xi\chi^2 $.
(iv) Suppose that $ c\in \big(\overline{\beta}-\frac{1}{4\xi}\overline{|\nabla\beta|^2}, \max_{\bar{\Omega}}\beta \big) $. Then $ \tilde{\eta} > 0 $ exists such that if $ \tilde{\eta} < \xi\chi^2 $ then $ (\theta, 0) $ is locally asymptotically stable for $ \eta\in(\tilde{\eta}, \xi\chi^2) $; and if $ \tilde{\eta} > \xi\chi^2 $ then $ (\theta, 0) $ is unstable for $ \eta\in(\xi\chi^2, \tilde{\eta} $).
Theorem 2.3 gives sufficient conditions of the stability of $ (\theta, 0) $ for the predators' diffusion rate $ \eta $ when $ c $ is in a proper region. A positively given $ \xi $ plays a role for obtaining the sufficient conditions for the stability. For example, we suppose that $ c $ and $ \chi $ such that $ c < \overline{\beta}-\frac{1}{4\xi_1}\overline{|\nabla\beta|^2} $ and $ c\in \big(\overline{\beta}-\frac{1}{4\xi_2}\overline{|\nabla\beta|^2}, \max_{\bar{\Omega}}\beta \big) $ for some $ \xi_1 > \xi_2 $. Then, we obtain from Theorem 2.3 that $ (\theta, 0) $ is unstable for $ \eta > \xi_1\chi^2 $. Moreover, $ (\theta, 0) $ is unstable for $ \eta\in(\xi_2\chi^2, \tilde{\eta}(\xi_2)) $ if $ \tilde{\eta(\xi_2)} > \xi_2\chi^2 $, and $ (\theta, 0) $ is locally asymptotically stable for $ \eta\in(\tilde{\eta}, \xi_2\chi^2) $ if $ \tilde{\eta} < \xi_2\chi^2 $.
Now, we investigate the effect of taxis $ \chi $ for fixed $ c $ and $ \eta $.
Theorem 2.4. Suppose that $ \beta $ has at least one isolated global maximum point and $ \max_{\bar{\Omega}}\beta > c $. For given $ \eta > 0 $, there exists $ \tilde{\chi} > 0 $ such that if $ \chi\geq \tilde{\chi} $ then $ (\theta, 0) $ is unstable.
From Theorem 2.4, we can compare the stability of $ (\theta, 0) $ with or without the predator's directional movement. Without the taxis ($ \chi = 0 $), the predator cannot survive when they are rare for $ (c, \eta)\in (\overline{\beta}, \max_{\bar{\Omega}}\beta)\times (\eta^*, \infty) $ for some $ \eta^* $, which will be immediately shown by lemma in Section 3. However, Theorem 2.4 shows that a large taxis $ \chi > 0 $ makes the predators invade a region. This implies that the strong taxis for predators gives a survival advantage to them compared with a random dispersal.
Next, we give the final result for the stability of $ (\theta, 0) $ when $ \beta(x) = \kappa m(x) $ for $ x\in\Omega $. Consider the following equation $ A\chi^2 + B\chi + C = 0 $, where
If $ B $ is positive and $ B^2-4AC > 0 $, the equation has two real roots $ \chi_1 < \chi_2 $ such that $ \chi_2 $ is positive.
Theorem 2.5. Suppose that $ m $ is positive, $ \beta = \kappa m $ for some constant $ \kappa > 0 $ and $ \max_{\bar{\Omega}}\beta > c $. If $ B^2-4AC > 0 $, $ (\theta, 0) $ is unstable when $ \chi\in(\max\{\chi_1, 0\}, \chi_2) $.
Remark that $ \beta(x) = \kappa m(x) $ implies that the predator moves toward the favorable habitat of the prey. Because the prey has a property to be distributed according to $ m(x) $, such movement of the predator allows them to go to an environment where the prey population is sufficient. Moreover, as the assumption $ \beta(x) = \kappa m(x) $ gives two effects, which are taxis toward the location with an abundance of prey and high hunting efficiency, the fitness of the predator increases. Therefore, a proper taxis sensitivity provides a survival advantage to the predator without the assumption on $ \beta $ in Theorem 2.4 for which predators cannot survive without taxis (Theorem 2.5).
2.2. Coexistence steady-state
Consider the steady-state of the system (P'):
In Eq (2.5), the ratio-dependent functional response is not defined at $ (u, w) = (0, 0) $. Since
we can extend the domain of $ \frac{ud(x)we^{ \chi \beta (x)/\eta }}{u + d(x)we^{ \chi \beta (x)/\eta }} $ to $ \{(u, w) : u\geq 0, w\geq 0\} $, so that $ (0, 0) $ becomes a trivial solution of Eq (2.5).
Let a positive solution of Eq (2.5) be a coexistence steady-state. Then, we have the following results for the existence of the coexistence steady-state of Eq (2.5), which is proven using the fixed-point index theory.
Theorem 2.6. Let $ \eta > 0 $ and $ \chi\geq0 $ be given. If $ \frac{\partial\beta}{\partial \vec{n}} = 0 $, there exists $ \tilde{c}\in \big(\overline{\beta}-\frac{\chi^2}{4\eta}\overline{|\nabla\beta|^2}, \max_{\bar{\Omega}}\beta \big) $ such that Eq (2.5) has at least one coexistence steady state if and only if $ c < \tilde{c} $.
Theorem 2.7. Suppose that $ \frac{\partial\beta}{\partial \vec{n}} = 0 $. Let $ \chi > 0 $ and $ \xi > 0 $ be given constants.
(i) If $ c < \overline{\beta}-\frac{1}{4\xi}\overline{|\nabla\beta|^2} $, then Eq (2.5) has at least one coexistence steady state when $ \eta > \xi\chi^2 $.
(ii) If $ c < \min_{\bar{\Omega}}\beta $, then Eq (2.5) has at least one coexistence steady state for all $ \eta > 0 $.
(iii) Suppose that $ c\in \big(\overline{\beta}-\frac{1}{4\xi}\overline{|\nabla\beta|^2}, \max_{\bar{\Omega}}\beta \big) $. Then $ \tilde{\eta} > 0 $ exists such that if $ \tilde{\eta} < \xi\chi^2 $ then Eq (2.5) has at least one coexistence steady state for $ \eta\in(\xi\chi^2, \tilde{\eta} $).
Theorem 2.8. Suppose that $ \beta $ has at least one isolated global maximum point and $ \max_{\bar{\Omega}}\beta > c $. For given $ \eta > 0 $, there exists $ \tilde{\chi} > 0 $ such that if $ \chi\geq \tilde{\chi} $ then Eq (2.5) has at least one coexistence steady state.
Theorem 2.9. Suppose that $ m $ is positive, $ \beta = \kappa m $ for some constant $ \kappa > 0 $ and $ \max_{\bar{\Omega}}\beta > c $. If $ B^2-4AC > 0 $ for given $ A, B $ and $ C $ as Eq (2.4), then Eq (2.5) has at least one coexistence steady state when $ \chi\in(\max\{\chi_1, 0\}, \chi_2) $.
It is noteworthy that the conditions for the existence of coexistence steady-state are closely related to the sign of $ \lambda_1(L, \chi) $, which will result in the proof of the above theorems. From the results in subsection 2.1, Eq (2.5) has more chance to have the coexistence steady-state when taxis sensitivity $ \chi $ is properly chosen.
3.
Stability of $ (\theta, 0) $
In this section, we prove Theorem 2.2–2.5. Recall that the principal eigenvalue of (2.2) is defined by
We assume that $ \frac{\partial\beta}{\partial\vec{n}} = 0 $ and consider $ \varphi = e^{\chi\beta/2\eta}\psi $. Since $ \psi\in H^1(\Omega) $ and $ \beta\in C^2(\bar{\Omega}) $, $ \varphi $ is also in $ H^1(\Omega) $. In addition, a mapping $ \psi\mapsto e^{\chi\beta/2\eta}\psi $ is bijective. Thus, if we take $ \psi = e^{-\chi\beta/2\eta}\varphi $ and take supremum over $ \varphi\in H^1(\Omega) $, we can rewrite the (3.1) as
Then, by Green's identity and the assumption of $ \beta $, we have
It can be easily shown from (EV2) that $ \lambda_1(L, \chi) $ is the principal eigenvalue of
Let $ \psi_1 $ be the principal eigenfunction with respect to $ \lambda_1(L, \chi) $. From (EV2), we obtain
where $ \varphi_1 = e^{\chi\beta/2\eta}\psi_1 $. Since the principal eigenfunction is unique, $ \varphi_1 $ is the principal eigenfunction with respect to $ \lambda_1\Big(\eta\Delta -\frac{\chi}{2} \Delta \beta -\frac{\chi^2}{4\eta}|\nabla\beta|^2 +\big(\beta(x)-c\big)\Big) $. Therefore, $ \lambda_1(L, \chi) = \lambda_1\Big(\eta\Delta -\frac{\chi}{2} \Delta \beta -\frac{\chi^2}{4\eta}|\nabla\beta|^2 +\big(\beta(x)-c\big)\Big) $. We will utilize the forms (EV1) and (EV2) in proving our results.
Before proving the theorems, we introduce some properties of the principal eigenvalue. The first property is well-known; the proof is omitted here (See [53]).
Lemma 3.1. Let $ \lambda_1(\eta\Delta+g(x)) $ be the principal eigenvalue of
Then,
(i) $ \lambda_1(\eta\Delta+g(x)) $ is monotone decreasing function to $ \eta $;
(ii) $ \lambda_1(\eta\Delta+\tilde{g}(x))\geq\lambda_1(\eta\Delta+g(x)) $ for a function $ \tilde{g}(x)\geq g(x) $;
(iii) $ \lim_{\eta\rightarrow0}\lambda_1(\eta\Delta+g(x)) = \max_{x\in\bar{\Omega}}g(x) $;
(iv) $ \lim_{\eta\rightarrow\infty}\lambda_1(\eta\Delta+g(x)) = \overline{g}. $
Lemma 3.2. Let $ \lambda_1(\eta\Delta+g(x)) $ be the principal eigenvalue of (3.2).
(i) If $ g(x) < 0 $, then $ \lambda_1(\eta\Delta+g(x)) < 0 $.
(ii) If $ \overline{g} > 0 $, then $ \lambda_1(\eta\Delta+g(x)) > 0 $.
(iii) If $ \int_\Omega{g(x)dx} < 0 $ and $ g(x) $ is positive somewhere, then there exists $ \tilde{\eta} > 0 $ such that $ \lambda_1(\eta\Delta+g(x))\geq0 $ if and only if $ \eta\leq\tilde{\eta} $. The equality holds when $ \eta = \tilde{\eta} $.
Proof. (i) is obvious by the definition of the principal eigenvalue.
(ii) Suppose $ \int_\Omega{g(x)dx} > 0 $. From the definition of $ \lambda_1(\eta\Delta + g(x)) $,
(iii) Let $ S: = \{x:g(x) > 0\}\neq \emptyset $. Then, we can choose a test function $ \tilde{\psi} $ with $ ||\tilde{\psi}||_2 = 1 $ whose support is in $ S $. Then, we obtain
for sufficiently small $ \eta $. Since $ \lambda_1(\eta\Delta+g(x)) $ is monotone decreasing function to $ \eta $ and $ \lim_{\eta\rightarrow\infty}\lambda_1(\eta\Delta+g(x)) = \overline{g} < 0 $, there exists $ \tilde{\eta} $ such that if $ \eta > \tilde{\eta} $, then $ \lambda_1(\eta\Delta+g(x)) < 0 $, and if $ \eta < \tilde{\eta} $, then $ \lambda_1(\eta\Delta+g(x)) > 0 $, which is a desired result.
Now, we first give the proof Theorems 2.2 and 2.3.
Proof of Theorem 2.2. From the definition of the principal eigenvalue (3.1), we have
for $ c > \max_{\bar{\Omega}}\beta $.
Next, from (EV2) and $ \frac{\partial\beta}{\partial\vec{n}} = 0 $, we obtain
where $ \varphi_1 $ is the principal eigenfunction with respect to $ \lambda_1\Big(\eta\Delta -\frac{\chi}{2} \Delta \beta -\frac{\chi^2}{4\eta}|\nabla\beta|^2 +\big(\beta(x)-c\big)\Big) $. Also, by the Green's first identity, we have
It follows from Eq (3.3) and Lemma 3.2 that
Also, since Eq (3.1) and (EV2) are equivalent form of the principal eigenvalue,
By Lemma 3.1 (ii), $ \lambda_1\Big(\eta\Delta -\frac{\chi}{2} \Delta \beta -\frac{\chi^2}{4\eta}|\nabla\beta|^2 +\big(\beta(x)-c\big)\Big) $ is monotone decreasing function to $ c $. Then, we can find $ \tilde{c}\in \big(\overline{\beta} -\frac{\chi^2}{4\eta}\overline{|\nabla\beta|^2}, \max_{\bar{\Omega}}\beta \big) $ such that $ \lambda_1\Big(\eta\Delta -\frac{\chi}{2} \Delta \beta -\frac{\chi^2}{4\eta}|\nabla\beta|^2 +\big(\beta(x)-c\big)\Big) = 0 $. By the monotonicity of $ \lambda_1(L, \chi) $ to $ c $, $ (\theta, 0) $ is unstable when $ c < \tilde{c} $, and $ (\theta, 0) $ is locally asymptotically stable when $ c > \tilde{c} $.
Proof of Theorem 2.3. As in the proof of Theorem 2.2, it suffices to check the sign of $ \lambda_1(L, \chi) $. From the form Eq (3.1), (i) and (ii) are immediately obtained.
For (iii), we denote $ \lambda_1\Big(\eta\Delta -\frac{\chi}{2} \Delta \beta -\frac{\chi^2}{4\eta}|\nabla\beta|^2 +\big(\beta(x)-c\big)\Big) $ by $ \tilde{\lambda} $. Consider an eigenvalue problem as follows:
Then, the principal eigenvalue of Eq (3.4) can be written by
From Lemma 3.1 (ii),
Then, the results (iii) follows from Lemma 3.2.
(iv) Assume that $ c\in \big(\overline{\beta}-\frac{1}{4\xi}\overline{|\nabla\beta|^2}, \max_{\bar{\Omega}}\beta \big) $. By Lemma 3.2 (iii), there exists $ \tilde{\eta} > 0 $ depending on $ \xi $ and $ \chi $ such that $ \lambda_1\Big(\eta\Delta -\frac{\chi}{2} \Delta \beta -\frac{1}{4\xi}|\nabla\beta|^2 +\big(\beta(x)-c\big)\Big) < 0 $ if and only if $ \eta > \tilde{\eta} $. For $ \tilde{\eta} < \xi\chi^2 $, $ (\tilde{\eta}, \xi\chi^2) $ is a non-empty interval. Then, it follows form (3.5) that $ \tilde{\lambda} < 0 $ when $ \eta\in(\tilde{\eta}, \xi\chi^2) $, and thus $ (\theta, 0) $ is locally asymptotically stable. Similarly, for $ \tilde{\eta} > \xi\chi^2 $, $ (\theta, 0) $ is unstable when $ \eta\in(\xi\chi^2, \tilde{\eta}) $.
Next, we prove Theorem 2.4.
Proof of Theorem 2.4. It can be proved similarly to Theorem 4.4 in [15]. For reader's convenience, we give the proof here. Since the principal eigenvalue of (2.2) is
we only need to find a function $ \Psi $ with $ \int_\Omega{e^{\chi\beta/\eta}\Psi^2} = 1 $ such that
From the assumption, a point $ x_0\in\bar{\Omega} $ exists satisfying $ \beta(x_0) = \max_{\bar{\Omega}}\beta $ and $ \beta(x_0)-c\geq \delta $ for some $ \delta > 0 $. Let $ R_1 > 0 $ be small such that $ \beta(x)-c\geq \frac{1}{2}\delta $ in $ B_{R_1}(x_0)\cap\Omega $, where $ B_{R_1}(x_0) $ is a ball of radius $ R_1 $ and centered at $ x_0 $. We define $ \beta_1 = \max_{(B_{R_1}(x_0)\setminus B_{R_1/2}(x_0))\cap\Omega}\beta $ and $ \beta_2 = \min_{B_{R_2}(x_0)\cap\Omega}\beta $ for $ R_1, R_2 > 0 $. Since the global maximum point is isolated,
for sufficiently small $ R_2 $ satisfying $ R_2\leq R_1/2 $.
Define a function $ \Phi\in C^1(\bar{\Omega}) $ as
If we put $ \Psi: = \Phi/\big(\int_\Omega{e^{\chi\beta/\eta}\Phi^2}\big)^{1/2} $ in Eq (3.6), the left-hand side becomes
where $ C_1 $ satisfies $ ||\nabla\Psi||_\infty\leq C_1 $. The right-hand side of Eq (3.6) is
for some positive constant $ C_2 $. Since $ C_1 $ and $ C_2 $ is independent of $ \chi $, Eq (3.6) holds if we choose $ \chi $ large enough. Hence, we have a desired result.
Finally, we assume that $ \beta(x) = \kappa m(x) $ for $ x\in\Omega $, which is the assumption in Theorem 2.5. Before proving the theorem, we give a known result in [14].
Lemma 3.3 (Cantrell et al. [14]). The integral $ \int_\Omega{\theta \nabla\theta\cdot\nabla m dx} $ is positive if $ \Omega\subseteq\mathbb{R} $ is an interval or if $ \Omega\subseteq \mathbb{R}^n $ is convex.
Then, we give the proof of Theorem 2.5.
Proof of Theorem 2.5. Let $ \lambda_1(L, \chi) $ be the principal eigenvalue with the form (EV1). Since $ \beta(x) = \kappa m(x) $ for $ x\in\Omega $,
where $ A, B $ and $ C $ are given as Equation (2.4). Since $ B^2-4AC > 0 $, $ A < 0 $ and $ B > 0 $ by Lemma 3.3, the equation has two real roots $ \chi_1 $ and $ \chi_2 $ with at least one positive solution, say $ \chi_2 $. Then, $ A\chi^2 +B\chi +C > 0 $ for $ \chi_1 < \chi < \chi_2 $. which implies $ (\theta, 0) $ is unstable for $ \chi\in(\max\{\chi_1, 0\}, \chi_2) $. We note that $ B^2-4AC $ cannot be positive for $ c > \max_{\bar{\Omega}}\beta $, because $ (\theta, 0) $ is locally asymptotically stable ($ \lambda_1 < 0 $) when $ c > \max_{\bar{\Omega}}\beta $. Hence, Theorem 2.5 is valid for $ c < \max_{\bar{\Omega}}\beta $.
4.
Coexistence steady-state
In this section, we present the proofs of Theorems 2.6–2.8 which are about the existence and non-existence of the coexistence steady-states of Eq (2.5). Before proving the theorems, we introduce the fixed-point index theory.
Fixed-point index theory
Let $ E $ be a real Banach space and $ W \subset E $ a closed convex set. $ W $ is called a total wedge if $ \alpha W \subset W $ for all $ \alpha \geq 0 $ and $ \overline{W\cup (-W)} = E $. A wedge is said to be a cone if $ W \cap (-W) = \{0\} $. For $ y \in W $, we define $ W_y = \{ x \in E\; :\; y + \gamma x \in W \; \; \mbox{for some}\; \; \gamma > 0 \} $ and $ S_y = \{ x \in {\overline W}_y \; :\; -x \in {\overline W}_y\} $. Then, $ {\overline W}_y $ is a wedge containing $ W $, $ y $ and $ -y $, while $ S_y $ is a closed subspace of $ E $ containing $ y $.
Let $ T $ be a compact linear operator on $ E $ satisfying $ T({\overline W}_y) \subset {\overline W}_y $. We say that $ T $ has property $ \alpha $ on $ {\overline W}_y $ if there are $ t \in (0, 1) $ and $ w \in {\overline W}_y \backslash S_y $ such that $ w - tTw \in S_y $. Let $ F : W \rightarrow W $ is a compact operator with a fixed-point $ y \in W $ and $ F $ is Fréchet differentiable at $ y $. Let $ L = F'(y) $ be the Fréchet derivative of $ F $ at $ y $. Then, $ L $ maps $ {\overline W}_y $ into itself. For an open subset $ U \subset W $, define $ \operatorname{index}_W(F, U) = \operatorname{index}(F, U, W) = \operatorname{deg}_W (I-F, U, 0) $, where $ I $ is the identity map. If $ y $ is an isolated fixed-point of $ F $, then the fixed-point index of $ F $ at $ y $ in $ W $ is defined by $ \operatorname{index}_W(F, y) = \operatorname{index}(F, y, W) = \operatorname{index}(F, U(y), W) $, where $ U(y) $ is a small open neighborhood of $ y $ in $ W $.
The following theorem can be obtained from the results of [54,55,56].
Theorem 4.1. Assume that $ I - L $ is invertible on $ {\overline W}_y $.
(i) If $ L $ has property $ \alpha $ on $ { \overline W}_y $, then $ \operatorname{index}_W(F, y) = 0 $.
(ii) If $ L $ does not have property $ \alpha $ on $ { \overline W}_y $, then $ \operatorname{index}_W(F, y) = (-1)^{\sigma} $, where $ \sigma $ is the sum of multiplicities of all the eigenvalues of $ L $ which are greater than 1.
Lemma 4.2. Any coexistence state $ (u, w) $ of system (2.5) has an a priori estimate
where $ Q_{1} = \max_{\bar{\Omega}} m, \; Q_{2} = \dfrac{Q_1\max_{\bar{\Omega}}\beta}{c\min_{\bar{\Omega}}d} $.
Proof. Let $ (u, w) $ be a positive solution of (2.5). Since $ -\mu \Delta u \leq u\Big(m(x) - u \Big) $, we obtain $ u \leq \max_{\bar{\Omega}}{m} $ by maximum principle for elliptic.
Let $ w(x_0) = \max_{\bar{\Omega}} w $ and $ h = \chi / \eta $. Then, by maximum principle for elliptic equation,
Since
it implies that
Notation 4.3.
(i) $ X : = C^{1}_{N} (\bar{\Omega}) \bigoplus C^{1}_{N} (\bar{\Omega}) $ where $ C^{1}_{N} (\bar{\Omega}): = \{ \phi \in C^{1}(\bar{\Omega}) : \frac{\partial\phi}{\partial \vec{n}} = 0 \; \; on\; \; \partial \Omega \} $.
(ii) $ Q : = \max\{ Q_1, Q_2 \} + 1 $.
(iii) $ D : = D_Q \bigoplus D_Q $ where $ D_Q = \{ \phi \in C^{1}_{N}(\bar{\Omega}) : \phi < Q \; \; on\; \; \bar{\Omega} \} $.
(iv) $ W : = D_0 \bigoplus D_0 $ where $ D_0 = \{ \phi \in C^{1}_{N}(\bar{\Omega}) : 0 \leq \phi \; \; on\; \; \bar{\Omega} \} $.
(v) $ D^{\prime} : = D \cap W $.
For $ \tau \in [0, 1] $, define a positive compact operator $ F_{\tau} : X \to X $ by $ F_{\tau}(u, w) = (-D\Delta + P)^{-1}[P\mathcal{I} + \tau G](u, w)^{T} $ where
and $ P $ is a positive constant such that $ (2Q + \frac{\max_{\Omega}\alpha}{\min_{\Omega}d} + \frac{\max_{\Omega} \beta}{{\min_{\Omega}d}} + c)Q + \chi \Vert \nabla \beta \Vert_{\infty}\Vert \nabla w \Vert_{\infty} < P $. $ F_{\tau} $ is positive and compact operator. We denote $ F = F_1 $. Then, (P') has a positive solution if and only if $ F $ has a positive fixed-point.
For the operator $ F $, we first find the result for the index values, $ \operatorname{index}_{W}(F, D^{\prime}) $ and $ \operatorname{index}_{W}(F, (0, 0)) $. The following lemmas can be proved by similar argument to [57]; the proofs are omitted here.
Lemma 4.4. $ \operatorname{index}_{W}(F, D^{\prime}) = 1 $.
Lemma 4.5. $ \operatorname{index}_{W}(F, (0, 0)) = 0 $.
Next, we calculate the $ \operatorname{index}_{W}(F, (\theta, 0)) $. Remark that the principal eigenvalue $ \lambda_1(L, \chi) $ of Eq (2.2) is real, and the corresponding principal eigenfunction $ \Psi $ is positive. Since the principal eigenpair $ (\lambda_1(L, \chi), \Psi) $ satisfies Eq (2.2), $ (\lambda_1(L, \chi), \Psi) $ also satisfies the second equation of Eq (2.1):
Lemma 4.6. If $ \lambda_{1}(L, \chi) > 0 $, then $ \operatorname{index}_{W}(F, (\theta, 0)) = 0 $.
Proof. By calculation, we have
Define
We first claim that $ \mathcal{I}-\mathcal{L} $ is invertible. Let $ \mathcal{L}(\phi, \psi)^{T} = (\phi, \psi)^{T} \in \overline{W}_{(\theta, 0)} $.
For $ \psi \geq 0 $, multiply the second equation of Eq (4.2) by $ e^{\chi\beta / \eta}\Psi $ and integrate over $ \Omega $, where $ \Psi $ is a principal eigenfunction of $ \lambda_{1}(L, \chi) $. Then, we obtain
which implies $ \psi\equiv0 $. The last equality holds from Eq (4.1).
Since $ \lambda_1(\mu\Delta + (m-\theta)) = 0 $ with the corresponding principal eigenfunction $ \theta $, $ \lambda_1(\mu\Delta + (m-2\theta)) < 0 $ by Lemma 3.1 (ii). We multiply the first equation of Eq (4.2) by $ \phi $ and integrate over $ \Omega $. Then, we have
Hence, $ \phi \equiv 0 $ and $ \mathcal{I}-\mathcal{L} $ is invertible.
Next, we show that $ \mathcal{L} $ has a property $ \alpha $. Let $ r $ be $ \mbox{the spectral radius of} \; (-\eta \Delta + P)^{-1}(\chi \nabla \beta \cdot \nabla + \beta - c + P) $. Then, the assumption $ \lambda_{1}(L, \chi) > 0 $ implies that $ r > 1 $. Then, there exist corresponding eigenfunction $ \xi $ exists in $ D_0\setminus\{0\} $. Take $ t = 1 /r \in (0, 1) $, then
Hence, $ \mathcal{L} $ has property $ \alpha $. By Theorem 4.1 (i), we have $ \operatorname{index}_{W}(F, (\theta, 0)) = 0 $.
Now, we give the proofs of Theorems 2.6–2.9. Theorems 2.7–2.9 can be proved in a similarly manner; we only give the proof of Theorem 2.6.
Proof of Theorem 2.6. Suppose that $ \frac{\partial\beta}{\partial \vec{n}} = 0 $. From Theorem 2.2, there exists $ \tilde{c}\in \big(\overline{\beta}-\frac{\chi^2}{4\eta}\overline{|\nabla\beta|^2}, \max_{\bar{\Omega}}\beta \big) $. Then, it follows from Lemma 4.4–4.6 that
Hence, Eq (2.5) has at least one coexistence state for $ c < \tilde{c} $.
Next, we assume that $ c\geq \tilde{c} $. Suppose that $ (u, w) $ be the positive solution of Eq (2.5). Then, $ (u, w) $ satisfies
Let $ \tilde{w}: = w\big/\big(\int_\Omega{e^{\chi\beta/\eta}w^2}\big)^{1/2} $. If we multiply Eq (4.3) by $ e^{\chi\beta/\eta}\tilde{w}/\big(\int_\Omega{e^{\chi\beta/\eta}w^2}\big)^{1/2} $ and integrate over $ \Omega $, we have
The last inequality holds by the definition of the principal eigenvalue $ \lambda_1(L, \chi) $. From Eq (4.4), we obtain
which is a contradiction because $ \lambda_1(L, \chi)\leq0 $ under the assumption $ c\geq\tilde{c} $. Hence, there is no positive solution of Eq (2.5) if $ c\geq \tilde{c} $.
5.
Numerical simulation
In this section, we present some numerical simulations to verify the mathematical results of this paper. Throughout the simulations, the following parameters and functions are used:
We used the upwind scheme with the finite difference method, and the toleration of iteration is selected as $ 10^{-6}. $ The simulation results presented show the important role of directional dispersal with taxis compared to the random dispersal when $ c, \beta $ and $ \eta $ are given.
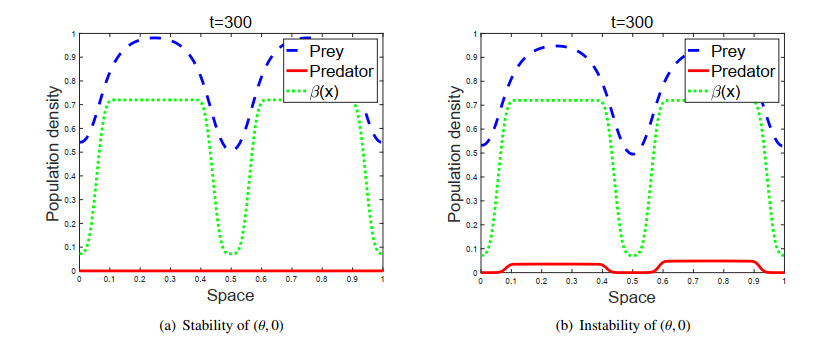
Figure 1 shows that a large $ \chi $ gives the predator with directional dispersal a survival advantage when $ c\in\big(\overline{\beta}, \max_{\bar{\Omega}}\beta\big) $. Theorem 2.4 implies that the $ (\theta, 0) $ is locally asymptotically stable when $ \chi = 0 $ for any given $ c $ and $ \eta $, but a large $ \chi $ allows $ (\theta, 0) $ to be unstable. This means that the strong taxis of predator can make them survive under the condition in which the predator with random dispersal cannot survive. Figure 1 shows that such dispersal makes the predator and prey coexist in the environment. It is noteworthy that, as can be seen in Figure 1, the density of the predator is concentrated on the local maximum of $ \beta $, which is a feature of the species with directional dispersal.
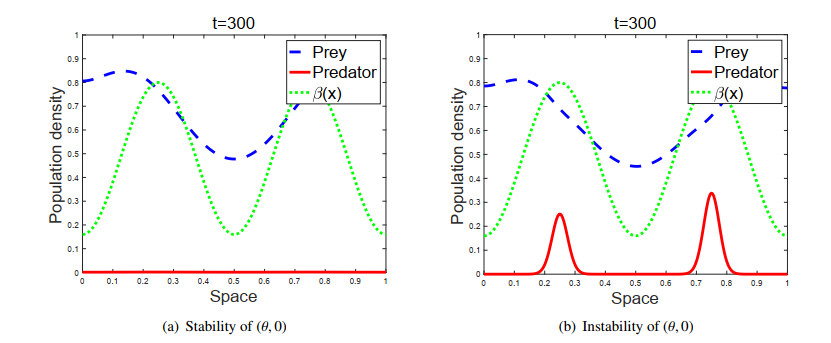
In Figure 2, the case that $ \beta(x) = \kappa m(x) $ is considered. If $ \beta(x) $ has at least one isolated global maximum point, we have a same result in Theorem 2.4 and Figure 1. Thus, we give $ \beta(x) $ as a combination of smoothstep function for Figure 2, which is the case when $ \beta $ has no isolated global maximum point on $ \overline{\Omega} $. Figure 2 shows that the properly chosen taxis sensitivity $ \chi > 0 $ can make the predator survive under the condition when the predator without taxis cannot survive. This represents the result of Theorem 2.5 that the directional dispersal is beneficial for the predator's survival when $ \chi $ is in a proper region regardless of the assumption on $ \beta $. This is a natural ecological result because the taxis of the predators not only makes them move towards the region with high hunting efficiency, but also the prey's favorable habitats where the density of the prey is large.
6.
Conclusion
In this paper, we suggested the predator–prey model describing the phenomena that the predator moves with taxis toward the region with a high hunting efficiency. For the predator–prey model, most of the studies dealing with taxis have considered the prey-taxis [29,30,31,32,33,34]. Authors in [29] adopted the ratio-dependent functional responses with a spatially heterogeneous environment, which are the same as our model, and they showed that the prey taxis is always beneficial for the predator's survival. However, the predators cannot chase the prey directly because the model we established describes the situation that prey has evolved to avoid detection from the predator. Thus, we considered other type of predators' dispersal mechanism with taxis toward the location where the hunting efficiency is high using the spatial memory [43,44,45,46]. There are two cases of the rate at which predators capture the prey: proportional ($ \beta = \kappa m $) or not proportional ($ \beta\neq \kappa m $) to the resources of prey. For the first case, a similar idea is introduced in [47,48,49] that the predators move in the direction of high prey's resources instead of tracking the prey directly, and [47] established the mathematical model of such dispersal and obtained some mathematical results. The other case can be followed from the prey's defensive mechanisms or environmental change from other external factors. This could make the predators go to a region with low prey density, which seems not helpful for the predators. In this paper, we investigated whether the defensive mechanism of the predators is advantageous to them for both cases.
Through this article, we determined the criteria and sufficient conditions for the local stability of the semi-trivial solution, which is closely related to the survival of the predators. Furthermore, the conditions for the existence of coexistence steady-state were obtained. We studied the stability and coexistence conditions for the three parameters: the death rate, diffusion, and taxis sensitivity. Finally, the obtained results were verified by using numerical simulations. From a biological perspective, the results for stability indicate that, when the predators have the spatial memory where the location is good to forage efficiently, the taxis toward the location could give a greater chance of invasion than when they disperse randomly (Theorems 2.2, 2.4 and 2.5). This implies that the directional movement toward the region with high foraging efficiency increases the fitness of predators. Consequently, such dispersal helps the predators to invade a region. If $ \beta $ has at least one isolated global maximum point, the dispersal is advantageous to the predator's survival when taxis is strong even though $ \beta $ is not proportional to $ m $ (Theorem 2.4). This represents that the dispersal mechanism also affects to the predators fitness regardless the distributions of $ \beta $ and $ m $. When $ \beta $ has no isolated global maximum, the proper taxis sensitivity gives survival advantage to the predators (Theorem 2.5). This means that the properly chosen taxis sensitivity helps predators survive regardless of assumption on $ \beta $ when the predators have directional movement toward the location with abundant prey and high hunting efficiency ($ \beta $ is proportional to $ m $). Moreover, as a dictum in ecology that "invasibility implies coexistence, " the taxis influences on the coexistence of predator and prey. This dispersal of predators could give them a greater possibility to coexist in the ecosystem than random dispersal (Theorems 2.6, 2.8 and 2.9). Thus, we conclude that the dispersal considered in this work plays a vital role in the survival of the predator and the coexistence in the predator–prey system.
Acknowledgments
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (NRF-2015R1A2A2A01007013; NRF-2018R1C1B5039938).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: