Fibonacci signals with timing jitter

1.   Introduction

In the field of mathematical epidemiology, the SIR epidemic model is known as one of the most basic epidemic models, in which the host population is divided into three classes called susceptible, infective and removed ^[1]. In the study of epidemic models, the basic reproduction number ${\cal R}_0$ is one of the key concepts, and it is defined by the expected value of secondary cases produced by a typical infective individual in a totally susceptible population ^[2]. Mathematically, ${\cal R}_0$ is defined by the spectral radius of the next generation operator, and the method of numerical computation of ${\cal R}_0$ has been studied for structured epidemic models ^[3]. In a simple SIR epidemic model given by a system of ordinary differential equations, ${\cal R}_0$ completely determines the model dynamics in the sense of global stability of each equilibrium: If ${\cal R}_0 \leq 1$, then the disease-free equilibrium is globally asymptotically stable, whereas if ${\cal R}_0 > 1$, then the endemic equilibrium is globally asymptotically stable [4, Section 5.5.2]. On the other hand, in some more complicated epidemic models, a stable endemic equilibrium can exist even if ${\cal R}_0 < 1$ due to a backward bifurcation ^[5]. Also, an endemic equilibrium can be destabilized, and a stable periodic solution can arise for ${\cal R}_0 > 1$ due to a Hopf bifurcation ^[6]. Periodic solutions in epidemic models have attracted much attention because they can describe non-seasonal oscillations of epidemics. Some of the known causes of the periodicity in epidemic models are periodic coefficients, time delay, nonlinear incidence and age structure ^[7,8,9,10]. In this study, we consider the periodicity in an age-structured SIR epidemic model. Age-structured epidemic models have been widely applied for epidemiological considerations in the era of COVID-19 ^[11].

In the field of mathematical epidemiology, the time elapsed since the infection is called the infection age, whereas the time elapsed since the birth is called the chronological age. For an infection age-structured SIR epidemic model, a complete threshold property of ${\cal R}_0$ in the sense of the global stability of each equilibrium was shown by constructing a suitable Lyapunov function ^[12]. In contrast, for a chronological age-structured SIR epidemic model, the complete threshold property of ${\cal R}_0$ does not hold in general. More precisely, although the global stability of the disease-free equilibrium for ${\cal R}_0 < 1$ was proved in ^[13], some additional conditions were needed to guarantee the local or global asymptotic stability of the endemic equilibrium for ${\cal R}_0 > 1$ ^[13,14], and the possibility of the instability of the endemic equilibrium for ${\cal R}_0 > 1$ was studied in ^{[15,16,17,18]}.

In ^[15], Thieme showed that the unique endemic equilibrium can be unstable for ${\cal R}_0 > 1$ in a chronological age-structured SIR epidemic model with age-dependent infectivity. However, the existence of periodic solutions and the occurrence of Hopf bifurcation have not yet been proved for this model. The purpose of this study is to tackle this problem when the transmission rate has a specific form. More precisely, we assume that the transmission rate is a shifted exponential function (see (A5) in the next section) and perform a Hopf bifurcation analysis regarding the infimum of the support of the function as a bifurcation parameter. Epidemiologically, such a shifted exponential function represents the case where infected people do not have infectivity until a certain critical age, and the infectivity decreases in an exponential sense after the critical age. This function enables us to consider a special case studied in ^[15], where the product of the transmission rate and the stable age distribution is highly concentrated in a particular age class. In this paper, we obtain concrete sufficient conditions for a Hopf bifurcation.

This paper is organized as follows: In Section 2, we introduce the model in this study. In Section 3, we give some preliminaries for the analysis, including the existence and uniqueness of the endemic equilibrium for ${\cal R}_0 > 1$. In Section 4, we perform a Hopf bifurcation analysis for a special case where the force of infection in the steady state is equal to the removal rate. We show that there always exists a critical value such that a Hopf bifurcation occurs when the bifurcation parameter reaches it. In Section 5, we perform a more general analysis for the case where the force of infection in the steady state is not equal to the removal rate. We obtain a similar Hopf bifurcation result as in Section 4 when the distance between the force of infection and the removal rate is sufficiently small. Moreover, we numerically confirm a special case where the stability switch of the endemic equilibrium occurs more than once. Finally, Section 6 is devoted to a discussion.

2.   Model

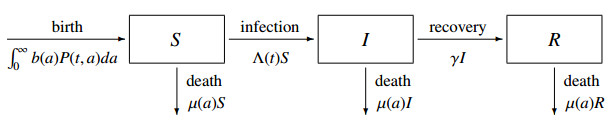
Let $S(t, a)$, $I(t, a)$ and $R(t, a)$ be the susceptible, infective and removed populations of age $a$ at time $t$, respectively. In this paper, we consider the following SIR epidemic model with chronological age structure:

where $\mu(a)$ is the mortality rate, $\gamma$ is the removal rate, $b(a)$ is the birth rate, $P(t, a) : = S(t, a)+I(t, a)+R(t, a)$ is the population age density, and

is the force of infection with the transmission rate $\beta(a)$. We assume $\gamma > 0$, and the following

(A1) $\mu \in L_{+, \text{loc}}^1(0, \infty)$, and $\int_0^\infty \mu(a)da = \infty$.

(A2) $\int_0^\infty b(a) \ell(a) da = 1$, where $\ell(a) : = e^{-\int_0^a \mu(\sigma)d\sigma}$ is the survival probability.

(A3) The population has attained the stable age distribution, that is, $P(t, a) = P^*(a) : = N\ell(a)/L$ for all $t > 0$ and $a > 0$, where $N > 0$ is the stationary population size, and $L : = \int_0^\infty \ell(a) da$ is the life expectancy.

Let

For notational simplicity, dropping the tildes on $\tilde{S}$ and $\tilde{I}$, we obtain the following normalized SI system:

where

Note that these $S$ and $I$ are the normalized age-densities satisfying $0\leq S, I \leq 1$, and we can omit the equation of $R$ as it does not affect the dynamics of system (2.2).

In ^[15], Thieme investigated the stability of the endemic equilibrium of system (2.2) when it uniquely exists. He analytically showed that it can be destabilized if $\beta(a)P^*(a)$ is highly concentrated in a particular age class. However, the problem of the existence of periodic solutions when the endemic equilibrium is unstable was unsettled. In this paper, we deal with this problem by applying the method of local Hopf bifurcation theory. In ^[15], it was assumed that there exist constants $c_1, c_2 > 0$ such that $\beta(a) \ell(a) \leq c_1 e^{-c_2 a}$ for all $a > 0$. In this paper, we make the following additional assumptions:

(A4) $\mu(a) = \mu > 0$ for all $a > 0$.

(A5) There exist $\beta_0 > 0$ and $\tau, k \geq 0$ such that

In other words, the transmission rate $\beta(a)$ is a shifted exponential function. One can then see that $\beta(a) \ell(a) \leq c_1 e^{-c_2 a}$ for all $a > 0$ holds for $c_1 = \beta_0$ and $c_2 = \mu+k$. If both $\beta_0$ and $k$ are large, we can say that $\beta(a)P^*(a)$ is highly concentrated in a particular age $\tau$ as in the case studied in ^[15]. Here, we remark that we can consider a different situation where $\beta(a)P^*(a)$ is exponentially distributed for $a \geq \tau$. Regarding $\tau$ as a bifurcation parameter, we investigate the existence of a critical value $\tau_c > 0$ such that a Hopf bifurcation occurs, and a periodic solution bifurcates from the endemic equilibrium when $\tau = \tau_c$.

3.   Preliminaries

Let $X : = L^1(0, a_\dagger)$ and $X_+ : = L^1_+(0, a_\dagger)$. It is easy to see that system (2.2) always has the disease-free equilibrium $E^0 = (1, 0) \in X_+ \times X_+$. Let $E^* = (S^*, I^*)$ denote an endemic equilibrium of system (2.2). It then holds

where the endemic force of infection obeys

Solving (3.1), we obtain

Substituting the equation of $I^*$ into the right-hand side of (3.2) and dividing both sides by $\Lambda^*$, we obtain

Since the right-hand side of (3.4) is monotone decreasing for $\Lambda^*$, we see that a unique $\Lambda^* > 0$ satisfying (3.4) exists if and only if ${\cal R}_0 > 1$, where

is the basic reproduction number ^[2] for system (2.2). More precisely, we obtain the following proposition.

Proposition 3.1. If ${\cal R}_0 > 1$, then system (2.2) has a unique endemic equilibrium $E^* = (S^*, I^*) \in X_+ \times (X_+ \setminus \{ 0 \})$.

Proof. As explained above, if ${\cal R}_0 > 1$, then there exists a unique $\Lambda^* > 0$ such that (3.4) is satisfied. We then obtain $S^*(a)$ and $I^*(a)$ from (3.3). This completes the proof. □

In what follows, we assume ${\cal R}_0 > 1$ and investigate the local stability of the endemic equilibrium $E^*$. Let

be the perturbation from $E^*$. We then have the following linearized system.

Substituting $U(t, a) = e^{\lambda t}u(a)$ and $V(t, a) = e^{\lambda t}v(a) \; (\lambda \in \mathbb{C})$ into (3.5) and dividing each equation by $e^{\lambda t}$, we have

We first show that $\lambda = 0$ is not an eigenvalue.

Lemma 3.1. If $\lambda = 0$, then there exists no $(u, v) \neq (0, 0)$ satisfying (3.6).

Proof. For $\lambda = 0$, recalling that $S^*(a) = e^{-\Lambda^* a}$, we obtain

Substituting the equation of $v(a)$ into $w = N^{-1} \int_0^\infty \beta(a)P^*(a)v(a) da$ and dividing both sides by $w$, we have

However, by (3.4), we have

which is a contradiction. This completes the proof. □

By Lemma 3.1, we can focus on $\lambda \neq 0$. Recalling that $S^*(a) = e^{-\Lambda^* a}$, we obtain

Substituting the equation of $v(a)$ into $w = \int_0^\infty \beta(a)P^*(a) v(a) da$ and dividing both sides by $w$, we have

Under assumptions (A4) and (A5), this equation can be rewritten as

where $\beta_1 : = \beta_0/L$ and $p: = k+\mu+\gamma$. Eq (3.7) is the starting point of our Hopf bifurcation analysis.

4.   Hopf bifurcation analysis ($\Lambda^*=\gamma$)

We now consider a special case where $\Lambda^* = \gamma$. In this case, Eq (3.7) can be rewritten as

Since we are interested in a Hopf bifurcation at which $\mathrm{Re} \lambda = 0$, we restrict our attention to $\lambda$ such that $\mathrm{Re} \lambda > - p$. We can then rewrite (4.1) as

On the other hand, from Eq (3.4), we have

and thus,

Substituting (4.3) into (4.2), we obtain

which is equivalent to

Hence, we obtain the following characteristic equation:

where

Note that although $\lambda = 0$ satisfies (4.4), we can disregard it by virtue of Lemma 3.1. We now prove the following lemma.

Lemma 4.1. If $\tau = 0$, then all nonzero roots $\lambda$ of the characteristic Eq (4.4) have negative real parts.

Proof. If $\tau = 0$, Eq (4.4) can be rewritten as $\lambda^4 + p \lambda^3 + \gamma p \lambda^2 = 0$. As $\lambda \neq 0$, dividing both sides by $\lambda^2$, we have $\lambda^2+p\lambda + \gamma p = 0$. We then easily see that all $\lambda$ have negative real parts because $p$ and $\gamma p$ are strictly positive. This completes the proof. □

Lemmas 3.1 and 4.1 imply that the endemic equilibrium $E^*$, which uniquely exists under ${\cal R}_0 > 1$, is locally asymptotically stable if $\tau = 0$. By the continuity, $E^*$ is locally asymptotically stable for small $\tau > 0$. In what follows, we investigate the existence of a $\tau_c > 0$ such that $E^*$ is locally asymptotically stable for $\tau \in [0, \tau_c)$ and destabilized at $\tau = \tau_c$.

4.1.   Existence of a pair of simple pure imaginary roots

We now seek a pair of simple pure imaginary roots $\lambda = \pm i \omega \ (\omega > 0)$ of the characteristic Eq (4.4). Since all coefficients in (4.4) are real, if $\lambda = i \omega$ satisfies (4.4), then $\lambda = -i \omega$ also satisfies (4.4). Therefore, we focus on $\lambda = i \omega$. Substituting $\lambda = i \omega$ into (4.4), we have

As $e^{-i\omega \tau} = \cos \omega \tau - i \sin \omega \tau$, we obtain the following two equations for real and imaginary parts, respectively:

Taking squares of both sides in the two equations of (4.5) and adding them, we obtain

Rearranging this equation, we obtain

(note that $a_0^2-b_0^2 = 0$), where

As we can rule out $\omega = 0$ by Lemma 3.1, dividing both sides of (4.6) by $\omega^2$, we obtain

On the existence of a positive $\omega > 0$ satisfying (4.7), we prove the following lemma:

Lemma 4.2. The Eq (4.7) has a unique nonzero positive root $\omega > 0$.

Proof. Let $h(x) = c_3x^3+c_2x^2+c_1x+c_0$. It suffices to show that $h(x) = 0$ has a unique positive root $x^* > 0$, for which $\omega = \sqrt{x^*} > 0$ is the desired root of (4.7). It is obvious that $c_3 = (p\tau + 1)^2 > 0$. Moreover, we have, using $p = k+\mu+\gamma > \gamma$,

and, using $b_0 = -a_0$ and $b_1 = -\gamma p^3 \tau - a_1$,

$c_0 < 0$ and $c_2, c_3 > 0$ imply that $h(x) = 0$ has a unique positive root $x^* > 0$. This completes the proof. □

The following corollary will be used in the proof of the transversality:

Corollary 4.1. Let $h(x)$ and $x^*$ be as defined in the proof of Lemma 4.2. Then, $h'(x^*) > 0$.

Proof. The assertion immediately follows from $c_0 < 0$ and $c_2, c_3 > 0$. □

Note that since $a_2, a_3, a_4, b_1$ and $b_2$ in (4.4) depend on $\tau$, the root $\omega$ also depends on $\tau$: $\omega = \omega(\tau)$. Since (4.7) is a necessary condition for $\lambda = i\omega$ to be a root of (4.4), we have to find a $\tau_c > 0$ such that $\omega(\tau_c)$ satisfies not only (4.7) but also (4.5). By (4.5), we have

We define $\theta \in (0, 2\pi]$ by

It then follows from (4.8) that $\omega \tau = \theta$, and thus,

Note that $\varphi$, $\psi$ and $\theta$ also depend on $\tau$. Let $f(\tau) : = \theta(\tau)/\omega(\tau)$. Then, the desired $\tau_c$ is a positive fixed point of $f$: $\tau_c = f(\tau_c)$. Before proving the existence of such $\tau_c$, we give the following lemma:

Lemma 4.3. For coefficients $c_0, c_1, c_2$ and $c_3$, it holds that

Proof. The convergence of $c_i/(p\tau)^2 \ (i = 0, 2, 3)$ can be easily checked by using the expressions of $c_0, c_2$ and $c_3$ given in the proof of Lemma 4.2. For $c_1$, we have

and hence, $\lim_{\tau \to \infty} c_1/(p\tau)^2 = p^2(p^2-\gamma^2)$. This completes the proof. □

We now prove the following proposition:

Proposition 4.1. There exists a $\tau_c > 0$ such that $\lambda = \pm i \omega(\tau_c)$ is a pair of simple pure imaginary roots of the characteristic Eq (4.4).

Proof. By Lemma 4.2 and its proof, one can see that $\omega(\tau)$ is continuous and finite for all $\tau \geq 0$. Thus, $\theta(\tau)$ and $f(\tau)$ are also continuous and finite for all $\tau \geq 0$. Moreover, it follows that $f(0) = \theta(0)/\omega(0) > 0$. Hence, by the continuity, if $\lim_{\tau \to \infty}f(\tau) < \infty$, then we can conclude that there exists a $\tau_c > 0$ such that $\tau_c = f(\tau_c)$.

Let $\{ \tau_n \}_{n = 1}^\infty$ be an increasing sequence in $(0, \infty)$, and let $\omega_n : = \omega(\tau_n)$. By dividing both sides of (4.7) by $(p\tau_n)^2$, we have

By Lemma 4.3, we see that $\{ \omega_n \}_{n = 1}^\infty$ converges to $\omega_\infty$, which is the unique positive root of the following equation:

Thus, we have $\lim_{\tau \to \infty}f(\tau) \leq 2\pi/\omega_\infty < \infty$. This completes the proof. □

Proposition 4.1 guarantees the existence of a pair of pure imaginary roots at $\tau = \tau_c > 0$.

4.2.   Transversality condition

We next investigate the transversality condition at $\tau = \tau_c$, that is,

where $\omega_c : = \omega(\tau_c)$. Following a general result given by ^[19], we define $g(\tau) : = \tau - f(\tau)$. Now, we have the following proposition.

Proposition 4.2. If $g'(\tau_c) > 0$, then (4.9) holds.

Proof. Let $y (\omega)$ be the left-hand side of (4.6):

Following a calculation in [19, Proof of Theorem 2.2] for a general characteristic equation, we can obtain a similar result as in [19, Theorem 2.2]:

Note that from Lemma 4.2 and Corollary 4.1, it follows that $h(\omega_c^2) = 0$ and $h'(\omega_c^2) > 0$. We then have that

Hence, we have

This completes the proof. □

As shown in the proof of Proposition 4.1, we have $f(0) > 0$ and $\lim_{\tau \to \infty}f(\tau) < \infty$. This implies that there exists at least one $\tau_c > 0$ such that $g(\tau_c) = \tau_c-f(\tau_c) = 0$ and $g'(\tau_c) > 0$. That is, a Hopf bifurcation is always possible in model (2.2) with ${\cal R}_0 > 1$ and $\Lambda^* = \gamma$. More precisely, we obtain the following main result:

Proposition 4.3. Suppose that $\beta_1$ depends on $\tau$ as for (4.3). Then, ${\cal R}_0 > 1$ and $\Lambda^* = \gamma$ hold for all $\tau \geq 0$, and there exists a $\tau_c > 0$ such that a pair of simple pure imaginary roots $\pm i \omega(\tau_c)$ ( = $\pm i \omega_c$) satisfies the characteristic Eq (4.4) and crosses the imaginary axis from left to right as $\tau$ increases over $\tau_c$.

Under the condition in Proposition 4.3, there always exists a critical value $\tau_c > 0$ such that a Hopf bifurcation occurs, and a periodic solution arises when the infimum $\tau$ of the support of function $\beta(a)$ reaches $\tau = \tau_c$. In the next subsection, we numerically confirm this result.

4.3.   Numerical experiments

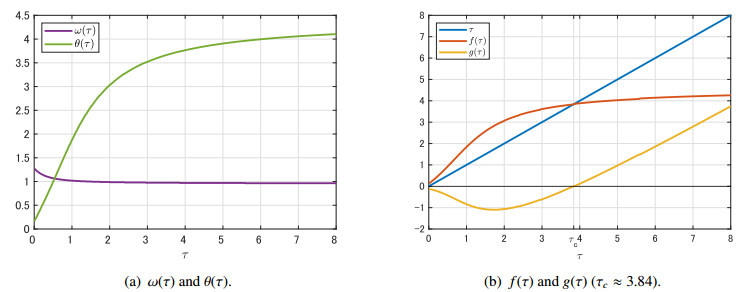
For simplicity, we fix $\mu = \gamma = k = 1$. Note that these parameters are technically chosen in order to confirm the validity of Proposition 4.3, and thus, there is no biological reason for this choice. In this case, $p = 3$, and we can numerically calculate functions $\omega(\tau)$, $\theta(\tau)$, $f(\tau)$ and $g(\tau)$, and $\tau_c \approx 3.84$ as shown in Figure 2. Note that $L = 1/\mu = 1$, and the force of infection is

It then follows from (4.3) that $\beta_0 = \beta_1 = p^2 e^{p\tau}/(p\tau + 1)$. For the normalized system (2.2), we choose the initial condition as $S(0, a) = 0.99$ and $I(0, a) = 0.01$ for all $a > 0$.

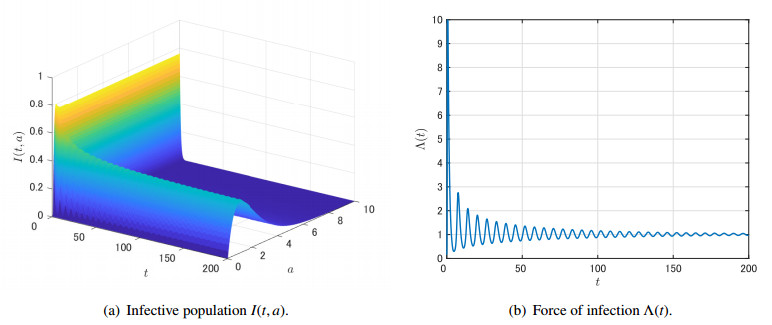
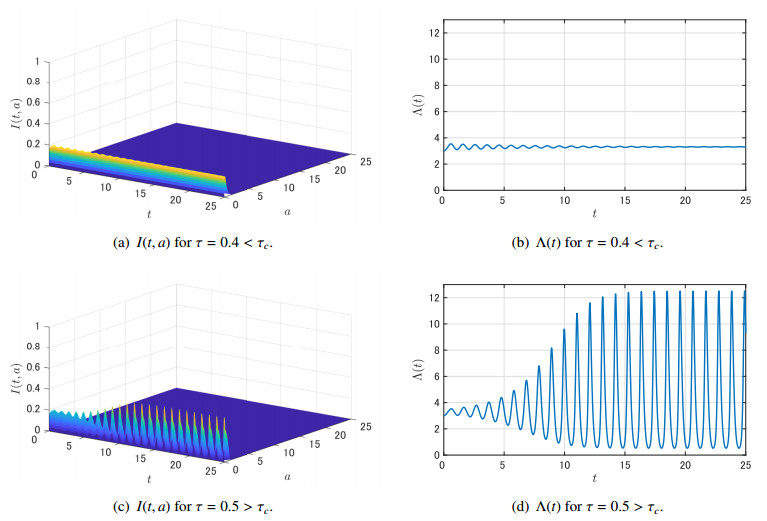
For $\tau = 3.7 < \tau_c$, we see in Figure 3 that the numerical solutions of $I(t, a)$ and $\Lambda(t)$ converge to the positive steady states $I^*(a)$ and $\Lambda^*$, respectively. In particular, we can confirm that $\Lambda^* = \gamma = 1$ in Figure 3 (b).

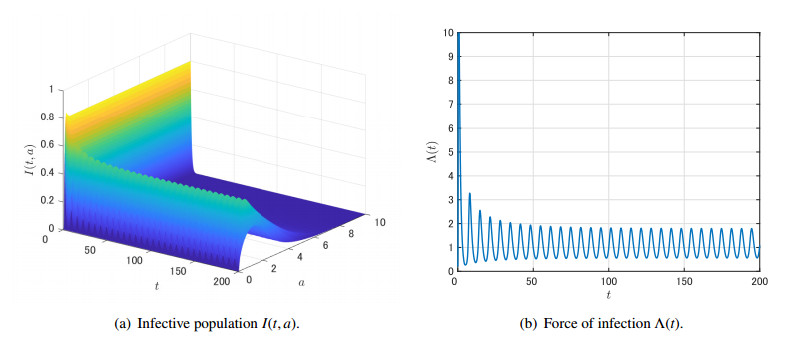
For $\tau = 4 > \tau_c$, we see in Figure 4 that the numerical solutions of $I(t, a)$ and $\Lambda(t)$ do not converge to the positive steady states but to positive periodic solutions.

Thus, we can conclude that a Hopf bifurcation occurs at $\tau = \tau_c$. In this case, the outbreaks occur periodically if the length $\tau$ of the period with no infectivity is sufficiently large.

5.   Hopf bifurcation analysis ($\Lambda^* \neq \gamma$)

We next consider the case where $\Lambda^* \neq \gamma$. Let $q: = \gamma - \Lambda^* \neq 0$. Note that $p-q = k+\mu+\Lambda^* > 0$. As in the previous section, since we are interested in a Hopf bifurcation at which $\mathrm{Re} \lambda = 0$, we restrict our attention to $\lambda$ such that $\mathrm{Re} \lambda > \max (-p, -(p-q))$ and $\lambda \neq - q$. Equation (3.7) can then be rewritten as

On the other hand, Eq (3.4) can be rewritten as

Thus, we have

Let $Q = Q(q, \tau) : = (e^{q\tau}-1)/q$. Note that $Q(q, \tau) > 0$ for all $q \in \mathbb{R} \setminus \{ 0 \}$ and $\tau > 0$, and

(5.2) can then be rewritten as

Substituting this $\beta_1$ into (5.1) and rearranging it, we obtain

We then have

Multiplying by $(\lambda+p)(\lambda+q) (\lambda + p-q)$ on both sides, we obtain

Note that $e^{q\tau} = qQ+1$. We then have

It can be rewritten as

where

We can check that (5.4) is equivalent to (4.4) if $q \to 0$. In fact, we have the following lemma:

Lemma 5.1. For each fixed $\tau > 0$, it holds that

Proof. For each fixed $\tau > 0$, recalling that $\lim_{q\to 0}(Q, \Lambda^*) = (\tau, \gamma)$, we obtain

This completes the proof. □

By Proposition 4.3 and Lemma 5.1, regarding $\tau$ as a bifurcation parameter, we see that a Hopf bifurcation can occur as in Section 4 if $|q|$ is sufficiently small. More precisely, we obtain the following corollary:

Corollary 5.1. Suppose that $q\neq 0$, $|q|$ is sufficiently small, and $\beta_1$ depends on $\tau$ as for (5.3). Then, ${\cal R}_0 > 1$ and $\Lambda^* = \gamma-q > 0$ hold for all $\tau \geq 0$, and there exists a $\tau_c > 0$ such that a pair of simple pure imaginary roots $\pm i \Omega(\tau_c) \left( = \pm i \Omega_c \right)$ satisfies the characteristic Eq (5.4) and crosses the imaginary axis from left to right as $\tau$ increases over $\tau_c$.

We next proceed to a more general case where $|q|$ is not small. We can prove the following lemma, which corresponds to Lemma 4.1.

Lemma 5.2. If $\tau = 0$, then all roots $\lambda$ except $0$ and $-q$ of the characteristic Eq (5.4) have negative real parts.

Proof. If $\tau = 0$, then $Q = 0$, and the characteristic Eq (5.4) can be rewritten as

This equation is equivalent to

If $\lambda \neq 0, -q$, then we have

We then see that all roots $\lambda$ have negative real parts because $p-q > 0$ and $\Lambda^* p > 0$. This completes the proof. □

Using Lemma 5.2, we prove the following proposition on the local asymptotic stability of $E^*$ for $\tau = 0$:

Proposition 5.1. If ${\cal R}_0 > 1$, $q\neq 0$ and $\tau = 0$, then the endemic equilibrium $E^*$ of system (2.2) is locally asymptotically stable.

Proof. By Lemma 5.2, it suffices to show that $\lambda = 0$ and $-q$ do not affect the stability of $E^*$. In fact, by Lemma 3.1, $\lambda = 0$ cannot be a characteristic eigenvalue. If $q > 0$, then $\lambda = -q$ does not affect the stability of the endemic equilibrium $E^*$. If $q < 0$, substituting $\lambda = -q$ into the first equation in (5.1), we obtain, for $\tau = 0$,

Since $\beta_1 = p (p-q)$ for $\tau = 0$, we have

which is a contradiction (note that $p < p-2q$ as $q < 0$). Hence, $\lambda \neq -q$. This completes the proof. □

5.1.   Existence of a pair of simple pure imaginary roots

As in Section 4.1, substituting $\lambda = i\Omega \ (\Omega > 0)$ into (5.4), we obtain

Dividing this equation into real and imaginary parts, we have

Taking squares of both sides in the two equations and adding them, we obtain

Rearranging this equation, we have

(note that $A_0^2-B_0^2 = 0$), where

By Lemma 3.1, we can rule out $\Omega = 0$. Hence, we obtain

As in Section 4.1, we define $H(x): = C_3x^3+C_2x^2+C_1x+C_0$. If $H(x) = 0$ has a positive root $x^* > 0$, then $\Omega = \sqrt{x^*}$ satisfies (5.7). To find such $x^*$, we investigate the signs of coefficients in (5.8). We prove the following lemma:

Lemma 5.3. $C_2 > 0$ and $C_3 > 0$ for all $\tau \geq 0$.

Proof. It is obvious that $C_3 = (pQ+1)^2 \geq 1 > 0$ for all $\tau \geq 0$. On $C_2$, we have

Recalling that $p-q = k + \mu + \Lambda^* > \Lambda^*$ and $qQ+1 = e^{q\tau } > 0$, we obtain

for all $\tau \geq 0$. This completes the proof. □

By Lemma 5.3, if $C_0 < 0$ for all $\tau \geq 0$, then a similar argument as in the proof of Lemma 4.2 gives the existence of the unique $\Omega > 0$ satisfying (5.8). However, unlike the case of $\Lambda^* = \gamma$ in Section 4, $C_0 < 0$ for all $\tau \geq 0$ does not hold in general. To clarify this point, we investigate a special case where the following additional condition is satisfied:

(A6) $\gamma \gg k + \mu$.

For example, if the reduction rate $k$ of infectivity is small, then (A6) is not so unrealistic because, in many human infectious diseases, the infection period is much shorter than the average life span (that is, $\gamma \gg \mu$). Under assumption (A6), $p \approx \gamma$, and coefficients in (5.4) can be rewritten as

(note that $\Lambda^* = \gamma-q > 0$). We next prove the following lemma on the sign of $C_0$:

Lemma 5.4. Suppose that (A6) holds. Then, the following properties hold:

(ⅰ) If $|q| < \gamma/\sqrt{2}$, then $C_0 < 0$ for all $\tau \geq 0$. In particular, $C_0$ is monotone decreasing for $\tau \geq 0$.

(ⅱ) If $q > (\sqrt{3}-1) \gamma$ or $q < -(\sqrt{3}+1) \gamma$, then $C_0 > 0$ for all $\tau \geq 0$. In particular, $C_0$ is monotone increasing for $\tau \geq 0$.

Proof. Under assumption (A6), $C_0$ can be calculated as

If $|q| < \gamma/\sqrt{2}$, then $2q^2-\gamma^2 < 0$, and thus,

for all $\tau \geq 0$ (note that $\sqrt{3}+1 > \sqrt{3}-1 > 1/\sqrt{2}$). The second assertion follows from (5.11) and the fact that $\partial Q/\partial \tau = e^{q\tau} > 0$. This proves (ⅰ).

If $q > (\sqrt{3}-1)\gamma$ or $q < -(\sqrt{3}+1)\gamma$, then $2q^2-\gamma^2 > 0$ (note that $\sqrt{3}-1 > 1/\sqrt{2}$), and thus,

for all $\tau \geq 0$. The second assertion follows in a similar way as in (ⅰ). This proves (ⅱ). □

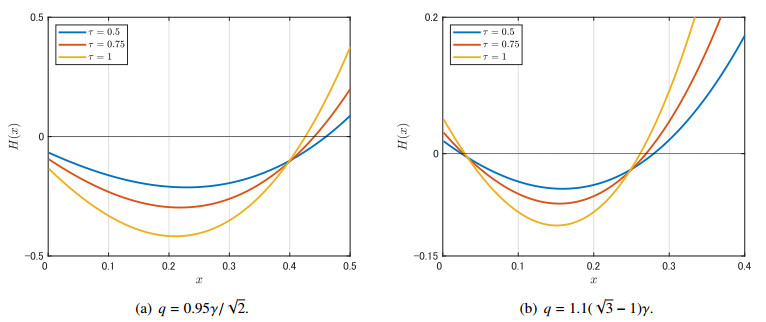
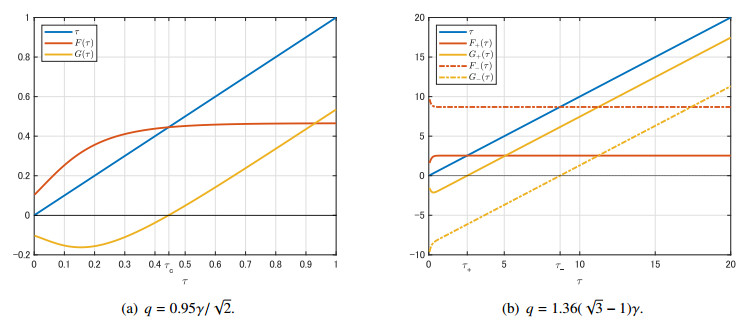
Figure 5 shows an example of each case in Lemma 5.4. $(k, \mu, \gamma) = (0.01, 0.01, 1)$ is fixed so that $\gamma \gg k+\mu$. In Figure 5(a), $q = 0.95\gamma/\sqrt{2}$, and hence, $|q| < \gamma/\sqrt{2}$ holds. In this case, as stated in Lemma 5.4 (ⅰ), we can check that $C_0 = H(0)$ is negative and monotone decreasing for each $\tau \geq 0$. By Lemma 5.3, as in Lemma 4.2, there always exists a unique $x^* > 0$ such that $H(x^*) = 0$, and hence, $\Omega = \sqrt{x^*}$ satisfies (5.8). In addition, one can see that $H'(x^*) > 0$.

On the other hand, in Figure 5(b), $q = 1.1(\sqrt{3}-1) \gamma > (\sqrt{3}-1) \gamma$. As stated in Lemma 5.4 (ⅱ), we can check that $C_0 = H(0)$ is positive and monotone increasing for each $\tau \geq 0$. As shown in this figure, there can exist two positive numbers $x_+^* > 0$ and $x_-^* > 0$ ($x_+^* > x_-^*$) such that $H(x_\pm^*) = 0$. In this case, (5.8) has two positive solutions $\Omega = \sqrt{x_\pm^*}$. In addition, one can see that $H'(x_+^*) > 0$ and $H'(x_-^*) < 0$.

Note that, as in Section 4, (5.8) is a necessary condition for $\lambda = \pm i\Omega$ to be a pair of simple pure imaginary roots of the characteristic Eq (5.4). From (5.6), we have

and define $\Theta \in (0, 2\pi]$ by

It then follows from (5.12) that $\Omega \tau = \Theta$. For each $\tau \geq 0$, let $F(\tau): = \Theta(\tau)/\Omega(\tau)$. Our aim is then to show the existence of a positive fixed point $F(\tau_c) = \tau_c > 0$, which implies that $\lambda = \pm i \Omega(\tau_c)$ is a pair of simple pure imaginary roots of the characteristic Eq (5.4). To this end, we now show the following lemma:

Lemma 5.5. Suppose that (A6) holds. For coefficients $C_0, C_1, C_2$ and $C_3$, it holds that

Proof. Note that $\lim_{\tau \to \infty} Q = \infty$. It then follows that

From (5.11), it follows that

Moreover, replacing $p$ and $\Lambda^*$ in (5.9) by $\gamma$ and $\gamma-q$, respectively, we can perform a similar calculation as in (5.10) and obtain

For $C_1$, we have

We then have $\lim_{\tau \to \infty} C_1/ (\gamma Q)^2 = -2(\gamma -q) [(\gamma-q) \gamma q + q^3]$. This completes the proof. □

Using Lemmas 5.3–5.5, we prove the following proposition on the existence of a pair of simple pure imaginary roots for $|q| < \gamma/\sqrt{2}$:

Proposition 5.2. Suppose that (A6) holds, and $|q| < \gamma/\sqrt{2}$. Then, there exists a $\tau_c > 0$ such that $\lambda = \pm i \Omega(\tau_c)$ is a pair of simple pure imaginary roots of the characteristic Eq (5.4).

Proof. By Lemmas 5.3 and 5.4, for each $\tau \geq 0$, the positive $\Omega(\tau) > 0$ uniquely exists. Hence, we have $F(0) = \Theta(0)/\Omega(0) > 0$. As in the proof of Proposition 4.1, by the continuity, it suffices to show that $\lim_{\tau \to \infty}F(\tau) < \infty$.

Let $\{ \tau_n \}_{n = 1}^\infty$ be an increasing sequence in $(0, \infty)$, and let $\Omega_n : = \Omega(\tau_n)$ and $Q_n : = Q(\cdot, \tau_n)$. By dividing both sides of (5.8) by $(\gamma Q_n)^2$, we have

By Lemma 5.5, we see that $\{ \Omega_n \}_{n = 1}^\infty$ converges to $\Omega_\infty$, which is the unique positive root of the following equation:

Thus, we have $\lim_{\tau \to \infty}F(\tau) \leq 2\pi/\Omega_\infty < \infty$. This completes the proof. □

For $q > (\sqrt{3}-1) \gamma$ or $q < -(\sqrt{3}+1)\gamma$, by Lemma 5.4 (ⅱ), $C_0 > 0$ for all $\tau \geq 0$, and hence, $H(x) = 0$ may have multiple positive roots $x_\pm^* > 0$ such that $H'(x_+^*) > 0$ and $H'(x_-^*) < 0$ (see Figure 5(b)). In this case, it seems difficult to show analytically the existence of a pair of simple pure imaginary roots. Instead, we will investigate it numerically in Section 5.3.

5.2.   Transversality condition

As in Section 4.2, we investigate the transversality condition of a Hopf bifurcation. Let $G(\tau) : = \tau - F(\tau)$.

Lemma 5.6. Suppose that there exists a $\tau_c > 0$ such that $G(\tau_c) = 0$. Then, the characteristic Eq (5.4) has a pair of simple pure imaginary roots $\lambda = \pm i \Omega(\tau_c) = \pm i \Omega_c$, and

Proof. As in the proof of Proposition 4.2, we have

where $Y(\Omega)$ is defined by the left-hand side of (5.7):

Now, we have

(note that $H(\Omega_c^2) = 0$). As $\Omega_c^3 > 0$, we then have

and hence, (5.13) follows from (5.14). This completes the proof. □

In the case of Lemma 5.4 (ⅰ), $H(x) = 0$ has only one positive root $x^* > 0$ such that $H'(x^*) > 0$ (see Figure 5(a)). Therefore, by Lemma 5.6, we see that if $\lambda = \pm i \Omega_c = \pm i \sqrt{x^*}$ is a pair of simple pure imaginary roots of (5.4), then it crosses the imaginary axis from left to right. This together with Lemma 5.4 (ⅰ) and Proposition 5.2 gives the following main theorem:

Theorem 5.1. Suppose that (A6) holds, $q\neq 0$, and $|q| < \gamma/\sqrt{2}$. If $\beta_1$ depends on $\tau$ as for (5.3), then ${\cal R}_0 > 1$ and $\Lambda^* = \gamma-q > 0$ hold for all $\tau \geq 0$, and there exists a $\tau_c > 0$ such that a pair of simple pure imaginary roots $\pm i \Omega(\tau_c) \left( = \pm i \Omega_c \right)$ satisfies the characteristic Eq (5.4) and crosses the imaginary axis from left to right as $\tau$ increases over $\tau_c$.

Under the condition in Theorem 5.1, there always exists a critical value $\tau_c > 0$ such that a Hopf bifurcation occurs, and a periodic solution arises at $\tau = \tau_c$. Note that, under assumption (A6), "sufficiently small $|q|$" in Corollary 5.1 is improved to the inequality $|q| < \gamma/\sqrt{2}$ in Theorem 5.1. For the case of Lemma 5.4 (ⅱ), we have the following remark:

Remark 5.1. In the case of Lemma 5.4 (ii), $H(x) = 0$ may have two positive roots $x_+^* > x_-^* > 0$ such that $H'(x_+^*) > 0 > H'(x_-^*)$ (see Figure 5(b)). Therefore, by Lemma 5.6, we see that if $\lambda = \pm i \Omega_c = \pm i \sqrt{x_+^*}$ (resp. $\pm i\sqrt{x_-^*}$) is a pair of simple pure imaginary roots of (5.4), then it crosses the imaginary axis from left to right (resp. from right to left). In other words, $\lambda = \pm i \sqrt{x_+^*}$ (resp. $\pm i \sqrt{x_-^*}$) can lead to the destabilization (resp. stabilization) of the endemic equilibrium $E^*$.

In other words, in the case of Lemma 5.4 (ⅱ), the stability switch of the endemic equilibrium $E^*$ can occur more than once. We numerically confirm this point in the next subsection.

5.3.   Numerical experiments

Fix the following parameters:

Note that they are chosen for a technical reason to confirm the validity of Theorem 5.1 and Remark 5.1, and there is no biological justification. We can regard $\gamma \gg k + \mu$, and thus, assumption (A6) holds. For each $q \in (-\infty, 0) \cup (0, \gamma)$ and $\tau \geq 0$, set $\beta_1$ as (5.3). Then, ${\cal R}_0 > 1$, and $\Lambda^* = \gamma - q > 0$ holds. To investigate the stability of the endemic equilibrium $E^*$, set the initial condition as

First, set $q = 0.95 \gamma/\sqrt{2} \approx 6.7175$. In this case, by Theorem 5.1, there exists a $\tau_c > 0$ such that a Hopf bifurcation occurs. In fact, we can calculate $\tau_c \approx 0.446$ (see Figure 6(a)).

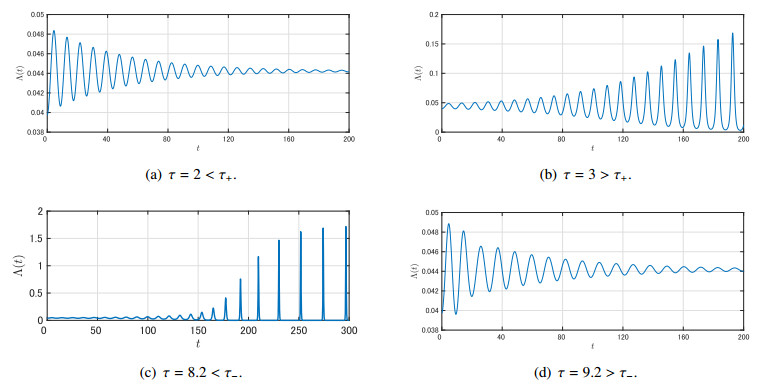
Figure 7(a) and (b) show that, for $\tau = 0.4 < \tau_c$, $I(t, a)$ and $\Lambda(t)$ converge to the steady states $I^*(a)$ and $\Lambda^* = \gamma -q \approx 3.2825$, respectively.

On the other hand, Figure 7(c) and (d) show that, for $\tau = 0.5 > \tau_c$, $I(t, a)$ and $\Lambda(t)$ converge to positive periodic solutions. This indicates that a Hopf bifurcation occurs at $\tau = \tau_c$.

Next, set $q = 1.36(\sqrt{3}-1) \gamma \approx 9.9559$. In this case, by Lemma 5.4 (ⅱ), $C_0 > 0$ for all $\tau \geq 0$, and hence, $H(x) = 0$ may have two positive roots $x_+^* > x_-^* > 0$ such that $H'(x^*_+) > 0 > H'(x_-^*)$. As stated in Remark 5.1, $\lambda = \pm i \sqrt{x^*_+}$ (resp. $\pm i \sqrt{x_-^*}$) can lead to the destabilization (resp. stabilization) of the endemic equilibrium $E^*$. To clarify this point, let $F_+(\tau)$ and $G_+(\tau)$ (resp. $F_-(\tau)$ and $G_-(\tau)$) be $F(\tau)$ and $G(\tau)$ corresponding to $\Omega(\tau) = \sqrt{x_+^* (\tau)}$ (resp. $\sqrt{x_-^*(\tau)}$), respectively. If there exists a $\tau_+ > 0$ (resp. $\tau_- > 0$) such that $G_+ (\tau_+) = 0$ (resp. $G_- (\tau_-) = 0$), then the destabilization (resp. stabilization) of the endemic equilibrium $E^*$ can occur at $\tau = \tau_+$ (resp. $\tau_-$). In fact, we can compute $F_\pm (\tau)$ and $G_\pm (\tau)$ as shown in Figure 6(b) and obtain $\tau_+ \approx 2.55$ and $\tau_- \approx 8.7$. That is, we can predict that the endemic equilibrium $E^*$ is stable for $\tau \in [0, \tau_+)$, is unstable for $\tau \in (\tau_+, \tau_-)$ and becomes stable again when $\tau$ increases over $\tau_-$. Indeed, in Figure 8(a), the force of infection $\Lambda(t)$ converges to the positive steady state $\Lambda^* = \gamma-q \approx 0.0441$ for $\tau = 2 < \tau_+$, whereas in Figure 8(b), $\tau = 3 > \tau_+$, and $\Lambda(t)$ converges to a periodic solution.

In Figure 8(c), for $\tau = 8.2 < \tau_-$, $\Lambda(t)$ converges to a periodic solution, whereas in Figure 8(d), for $\tau = 9.2 > \tau_-$, $\Lambda(t)$ converges to the positive steady state. That is, the stability switch of the endemic equilibrium $E^*$ occurs twice at $\tau = \tau_+$ and $\tau_-$.

6.   Discussion

In this paper, we have studied the local stability of the endemic equilibrium in a chronological age-structured SIR epidemic model with age-dependent infectivity. We assumed that the transmission rate is a shifted exponential function and investigated the possibility of a Hopf bifurcation regarding the infimum of the support of the transmission rate as a bifurcation parameter. We have shown that, if the distance between the force of infection at the endemic equilibrium and the removal rate is zero or sufficiently small ($|q| \ll 1$), then there always exists a critical value of the bifurcation parameter at which a Hopf bifurcation occurs. Furthermore, in a special case where the removal rate is sufficiently larger than the sum of the mortality rate and the reduction rate of infectivity, we have obtained a specific inequality ($|q| < \gamma/\sqrt{2}$) for which a similar critical value for a Hopf bifurcation always exists. We have performed numerical simulations and observed bifurcations of a stable periodic solution from the endemic equilibrium. On the other hand, for the case where $q > (\sqrt{3}-1)\gamma$, we have numerically confirmed that the stability switch of the endemic equilibrium can occur multiple times.

Our results have given a partial answer to a question of the possibility of a Hopf bifurcation in a chronological age-structured SIR epidemic model with age-dependent infectivity, which was raised in ^[15]. As our results are restricted to a special case where the transmission rate is a shifted exponential function, the study of other cases would be interesting future work. In particular, although we disregarded the age-dependent susceptibility for the sake of simplicity in the analysis, it would make the model more realistic because the assumption of the shifted exponential function could be suitable for some sexually transmitted diseases for which people under a certain age do not have the infectivity and susceptibility. It is an open problem whether a Hopf bifurcation still occurs if we introduce the age-dependent susceptibility to our model. Although it might be easily checked by numerical simulations, the analytical proof may be a more challenging task because it may be difficult to obtain a concrete characteristic equation like (4.4) when the force of infection depends on the age of the susceptible population.

Although our work in this paper was motivated by the mathematical analysis, periodic solutions in autonomous systems like our model could help in understanding the mechanism of the non-seasonal recurrent outbreaks which have been observed in many diseases such as measles. The application of our results to epidemiological considerations would also be important future work.

Acknowledgments

We deeply appreciate the editor and the anonymous referees for their valuable and constructive comments that helped us to improve the manuscript. T. Kuniya was supported by the Japan Society for the Promotion of Science (JSPS) [grant numbers 19K14594, 23K03214]. H. Inaba was supported by the Japan Society for the Promotion of Science (JSPS) [grant number 22K03433].

Conflict of interest

The authors declare there is no conflict of interest.