1.
Introduction
The method of monitoring physiological condition by means of bioimpedance remains a novel technique for more than 50 years or so. The non-destructive method of bioimpedance measurement for fruits and vegetables is extensively used for various purposes such as to access health conditions [1],[2], effect of storage conditions [3], physiological changes including assessing the quality of fruits and vegetables [4]–[8]. On the other hand, investigations are also carried out to understand the science behind the characteristics of bioimpedance of plant tissues [9]–[17]
The necessity of invariability of bioimpedance parameters is extremely important in practical application of Cole model for discriminating fruits (or vegetables) from a reference fruit (or vegetable). Say for example someone wants to compare the Cole parameters for two different species of a given fruit. In such cases, the parameters can be compared if the parameters are not dependent on position (of a given fruit or sample). If the position (of measurement) dependent variability is high, one cannot distinguish two different samples under investigation. Thus, the measurement method should be robust enough to establish invariability of bioimpedance parameters which can be treated as reference parameters for comparison purpose.
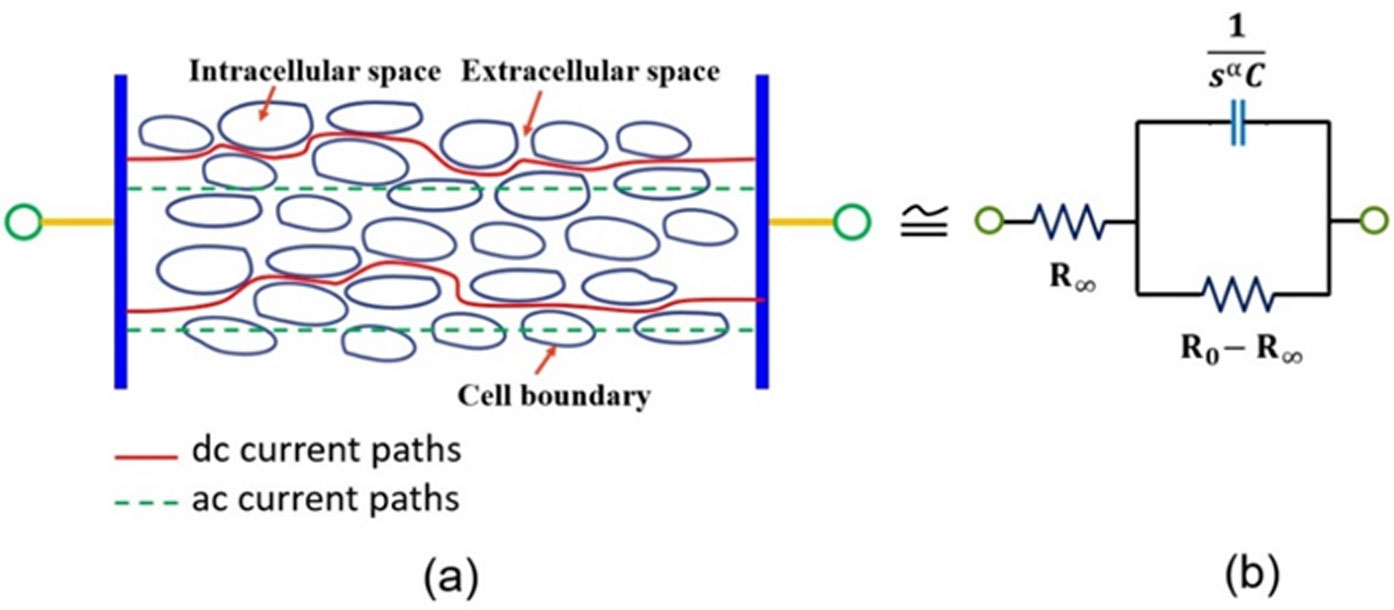
Cole model is widely applied for living biological tissue [15],[18]–[21]. In general, lump tissue is represented by Cole equivalent circuit and single dispersion model is accepted for its simplicity [7],[14] (Figure 1). Among the various method of bioimpedance measurements, direct measurement (i.e. using LCR meter) with two-electrode configuration is the most generic one due to its high degree of reliability [5],[20]. The electrical current paths inside a tissue is schematically shown in Figure 1 (a). It is intuitive from this figure, that if impedance is measured for the same tissue at other position, keeping the distance between the electrode invariant, one should obtain the same results (within the limits of experimental error for living tissue). On the other hand, if the distance between the electrodes is not kept same for measuring impedance at two different positions, the variability in measured parameters are clearly observed [14],[15],[22]. Thus, in order to obtain the comparable results among the samples, it is quite obvious to keep the distance between the electrode invariant. The reasons of choosing apple and potato are as follows. First of all, apple is a fruit whereas potato is a vegetable (tuber) and both of them are extensively used as food materials and therefore have importance in agriculture sector. Further, apple grows in open atmosphere whereas potato grows under soil. Not only these, the tissue of apple will have a natural tendency towards ripen (or to be eaten) so that seed can be dispersed. On the other hand, potato tissue will have tendency to fight against external environment to sustain so as to produce the next generation potato. The porosity (fraction of empty space) of apple is highly different than that of potato.
In this work, a specific electrode-pair is designed and is used to measure bioimpedance of apple and potato tissues. It is needless to mention that, though apple is a fruit, potato is a vegetable and providing us two different kind of living tissue to be investigated under this study. Applying single dispersion Cole model, impedance parameters are extracted by curve fitting. It is established here that the tissue of apple and potato can be specified in terms of bioimpedance parameters which in turn can be used to discriminate similar tissue of different species with 98% confidence. Further, with 99% confidence, it is evidently shown here that the position of measurement of bioimpedance of a given fruit or vegetable is not a factor of variability. Thus, our process of measurement can directly be applied in assessing quality (or condition) of fruits or vegetables. In addition to this, our method can be applied to monitor the ripening of fruits similar to citrus fruit like orange [8].
2.
Single dispersion Cole bioimpedance model
Single dispersion Cole bioimpedance model is a widely accepted model is extensively used for various kinds of biological tissue [5]–[8],[10]–[21]. The single dispersion Cole equivalent circuit for lump biological tissue is shown in Figure 1(b). The equivalent circuit consists of a constant phase element (CPE) comprising of a fractional capacitor (C) with a parallel resistance (R0 - R∞) and a series resistance R∞. The CPE maintains the phase invariancy by the dispersion parameter α. In the equivalent circuit, R0 is the dc resistance (or low frequency resistance of the tissue); R∞ is the ac resistance of tissue at high frequency. The impedance of single dispersion equivalent circuit (Cole equivalent circuit) is usually expressed as
where, j=√−1 . The symbol τ in Eq. (1) is known as the characteristics time constant of the tissue and is expressed as
Separation of Z into real and imaginary parts is not straight forward due to the non-integer value of α (0 < α ≤1), which turns the Eq. (1) into the category of fractional calculus. Nevertheless, analytically it is possible to express the impedance Z in terms of real and imaginary part using jα=(jsinαπ2+cosαπ2) and after simplifying we obtain
where,
X=R∞+(R0−R∞)(1+ωαταcosαπ2)(1+ωαταcosαπ2)2+(ωαταsinαπ2)2 and
Y=−(R0−R∞)(ωαταsinαπ2)(1+ωαταcosαπ2)2+(ωαταsinαπ2)2.
Thus, the modulus of Z becomes
Experimentally, Eq. (4) |Z| is obtained as a function of frequency f (= ω/2π). The experimental data is then fitted (non-linear curve fitting) and values of R0, R∞, C, α are obtained. From these parameters, the relaxation time τ is calculated using Eq. (2).
3.
Specially designed electrode-pair
In general, the physiological parameters are non-repetitive and standard deviation is large. For example, if at identical condition, the cell size is measured for a given tissue, the variation of more than 20% is not uncommon while the grain size of a metallic conductor is measured, the result is found to be within the tolerance level (about 5% or so). The variation in cell size would therefore lead to a large variation in the tissue related parameters. Thus, it is extremely important to specify the tissue by means of Cole model parameters as well as relaxation time. On the other hand, it is essential to keep the distance (or gap) between the electrode-pair invariant. Intuitively, this is due to the fact that the Cole parameters (except α) are highly dependent on the gap between the electrodes. Hence, to discriminate tissues from one another, it is essential to obtain the invariability of impedance irrespective of measuring position (of tissue) of fruits or vegetable.
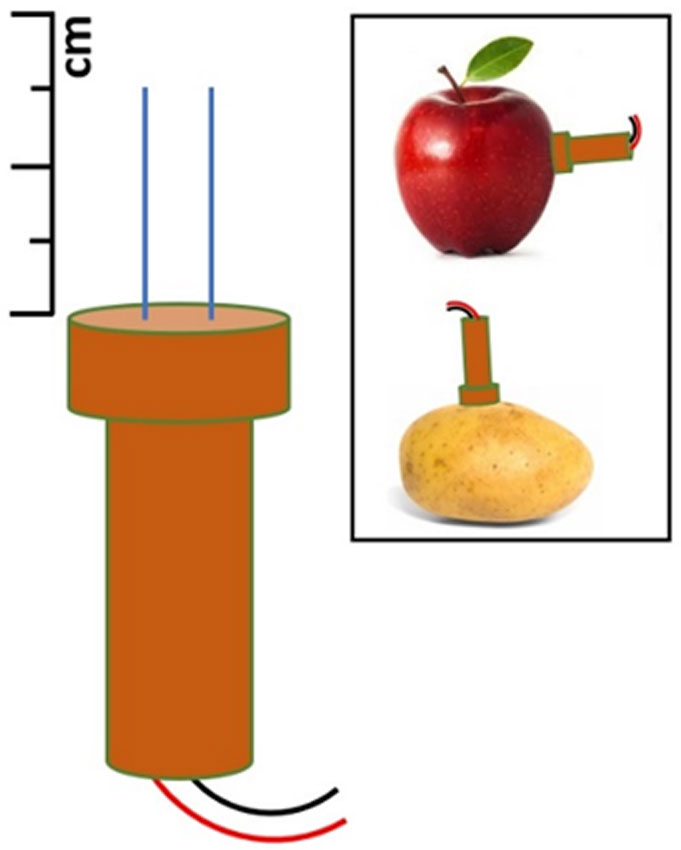
An electrode-pair is designed and fabricated for the purpose of bioimpedance measurement of fruit or vegetable. A schematic of the fabricated electrode-pair is shown in Figure 2. The depth of penetration and diameter of the electrodes are 1.5 cm and 0.28 mm respectively and these are maintained throughout this work unless otherwise stated. The electrodes are separated by plastic material (of negligibly low leakage current). The plastic holder of the electrode-pair is made by cutting a disposable syringe. The gap between the electrode is kept at 3 mm. For electrode material, stain-less steel is chosen for its inertness of reacting with any other materials and retain sufficient strength at low wire diameter.
4.
Experiments
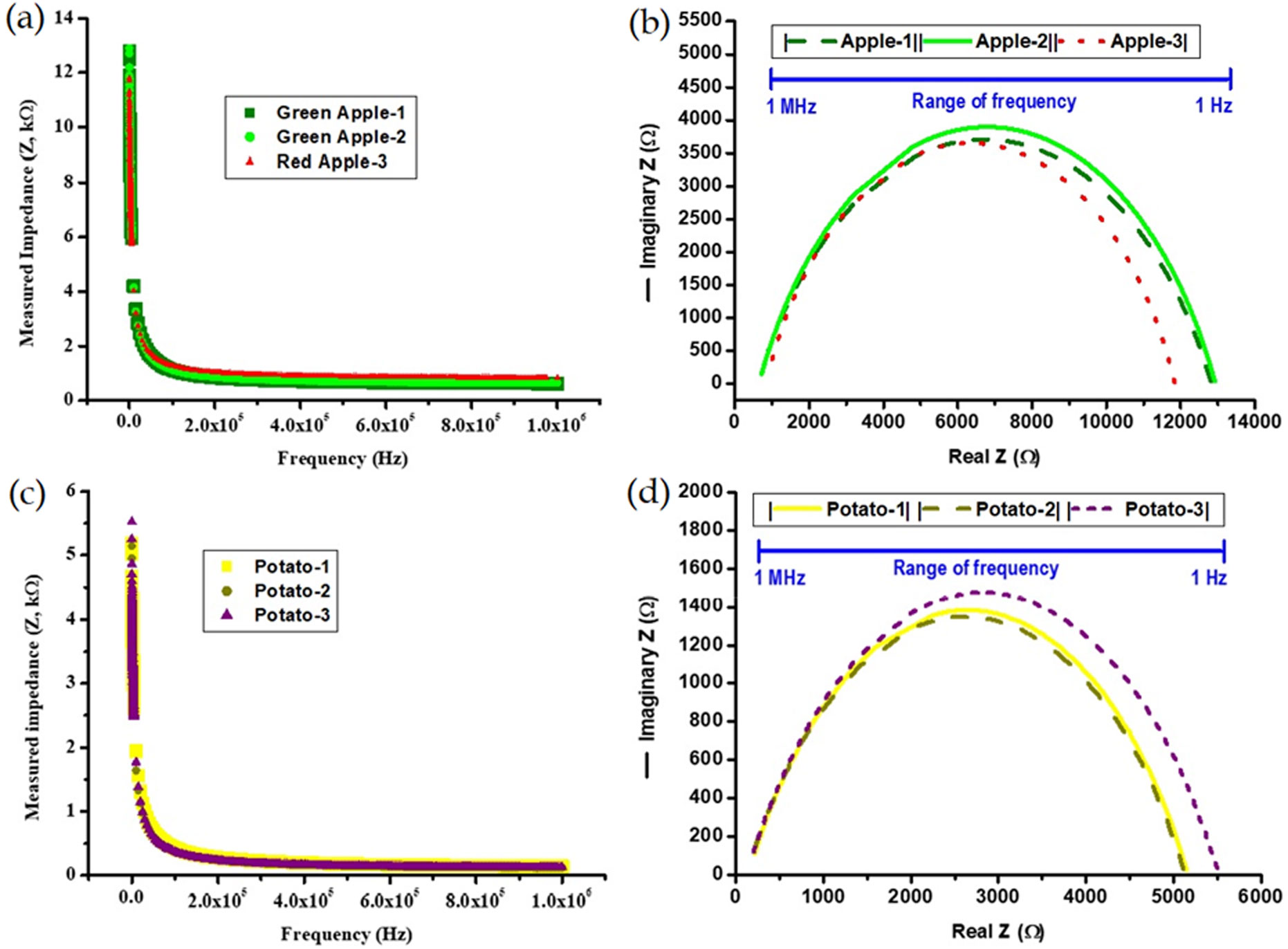
The sample matrix is shown Table 1. In order to remove any parasitic effect that may arise from electrodes and probes, the LCR meter (Model: 8101G, Make: Gw Instek) is calibrated before taking any measurement data. Each time electrodes are cleaned by medicated sprit and dried properly before inserting into fruit or vegetable. By inserting the electrode-pair at desired position of the sample, impedance is measured in the frequency range of 1 Hz to 1 MHz with amplitude of 1 V (peak to peak). All measurements are conducted at identical condition. In order to avoid any physical damage in the tissue due to high electric field, small signal is chosen for measurement. The impedance is found to decrease with the increase in frequency and becomes sufficiently flat around the frequency of 1 MHz and thus restricts the choice of upper limit on the frequency of interest. For each sample, five measurements are done at five different positions and each measurement contains four hundred data points. Typical measurement data are plotted as a function of frequency and is shown in Figure 3.
5.
Results and discussions
Experimentally |Z| is obtained as a function of frequency for different samples and for different position of a given sample as mentioned in Table 1. The non-linear curve fitting is performed by commercial MS Excel 2016 package. As a common practice, in the curve fitting process, the value of R0 and R∞ is considered to be the measured values R0 and R∞. Hence in this work, the measured impedances at 1 Hz and 1 MHz are considered to be R0 and R∞ respectively. The value of α and C are estimated by fitting the experimental curve with the Eq. (4). The characteristic time constant τ is then estimated using Eq. (2) for each set of data.
From the experimental plots of |Z| as a function of frequency (see Figure 3) it is not possible to distinguish the species of a given fruit or vegetable and this is because the plots of different species almost overlap on each other when plotted simultaneously in a single graph. On the other hand, the important parameters related to equivalent circuit of these plots may differ significantly.
The fitted Cole plots are shown in Figure 3(b) and Figure 3(d) for apple and potato respectively. Since, the sample Apple-1 and Apple-2 are from same species, the Cole plots of these do not differ and follow one another for the entire span of frequency range. While the Cole plot for the sample Apple-3 slightly differ from the other two, especially at the low frequency range. This is probably due to the fact that the species of sample Apple-3 is different from that of sample Apple-1 or Apple-2. Exactly similar observation is found for potato samples (Figure 3. (d)). From the fitted Cole plots, it is noticed that the distinguishable capability of bioimpedance method is better at the low frequency range for apple as well for potato. This fact suggests that the bioimpedance study of apple and potato can be limited to 3 kHz. By reducing the frequency range while keeping the number data point same, we can obtain better experimental results.
5.1. ANOVA on apple and potato samples
In this study, all ANOVA are performed using commercial MS Excel 2016 package. The Cole parameters for apple samples are shown in Table 2. ANOVA on τ is performed considering position and sample as two factors. The first factor is considered to understand whether position of measurement is a factor or not. On the other hand, the second factor is considered to understand the discriminating capability of the bioimpedance measurement.
To test these hypotheses, two apples of same species (Green Granny Smith in this case) are taken from a local shop and thus the biological differences between the apples are minimized. Then for each apple, impedance is measured at five different positions. The measured and calculated data is shown in Table 2. Result of ANOVA for tissue of apple is shown in Table 3. Interestingly it is found that none of the factors are significant (since, Fcritical > F-value) at the confidence level as high as 99% when ANOVA is performed among the sample Apple-1 and Apple-2. This means that one the Cole parameters i.e. the relaxation time are indistinguishable as far position is concerned. The two samples (Apple-1/Apple-2) are also found to be indistinguishable. Or in other words, the tissues of Apple-1 and Apple-2 are statistically same. Thus, with respect to our electrode system, the relaxation time is invariable and it is does depend on the position of measurement and remains same for biologically same samples.
On the other hand, though the position is found be indistinguishable in Apple-1 and Apple-3 (or Apple-2 and Apple-3), they are found to be disguisable (Fcritical < F-value) when ANOVA is performed for these two pair of samples. Thus, again as before, the position of measurement is not found to be a factor. However, in the present two cases, the sample is found to be a factor and is discriminated by respective relaxation time. This means the tissues of Apple-1 and Apple-3 are different. This fact proves that the relaxation time of apple tissue can be used to discriminate different species of apple.
The various Cole parameters for potato samples are tabulated in Table 4. Similar to apple samples, ANOVA is performed on τ for potato samples and the result of the ANOVA is shown in Table 5. Based on the ANOVA, we have obtained similar conclusion as in apples. That is position of measurement is not a factor and different tissue of potato samples can be distinguished based on the relaxation time.
In order to gain confidence on our discrimination method described above, the entire experiment is repeated by taking another two specimens of each type using the same electrode-pair. When data is analyzed similar outcome is resulted. Thus, our method is found to be repetitive and robust.
5.2. Physiological difference between apple and potato
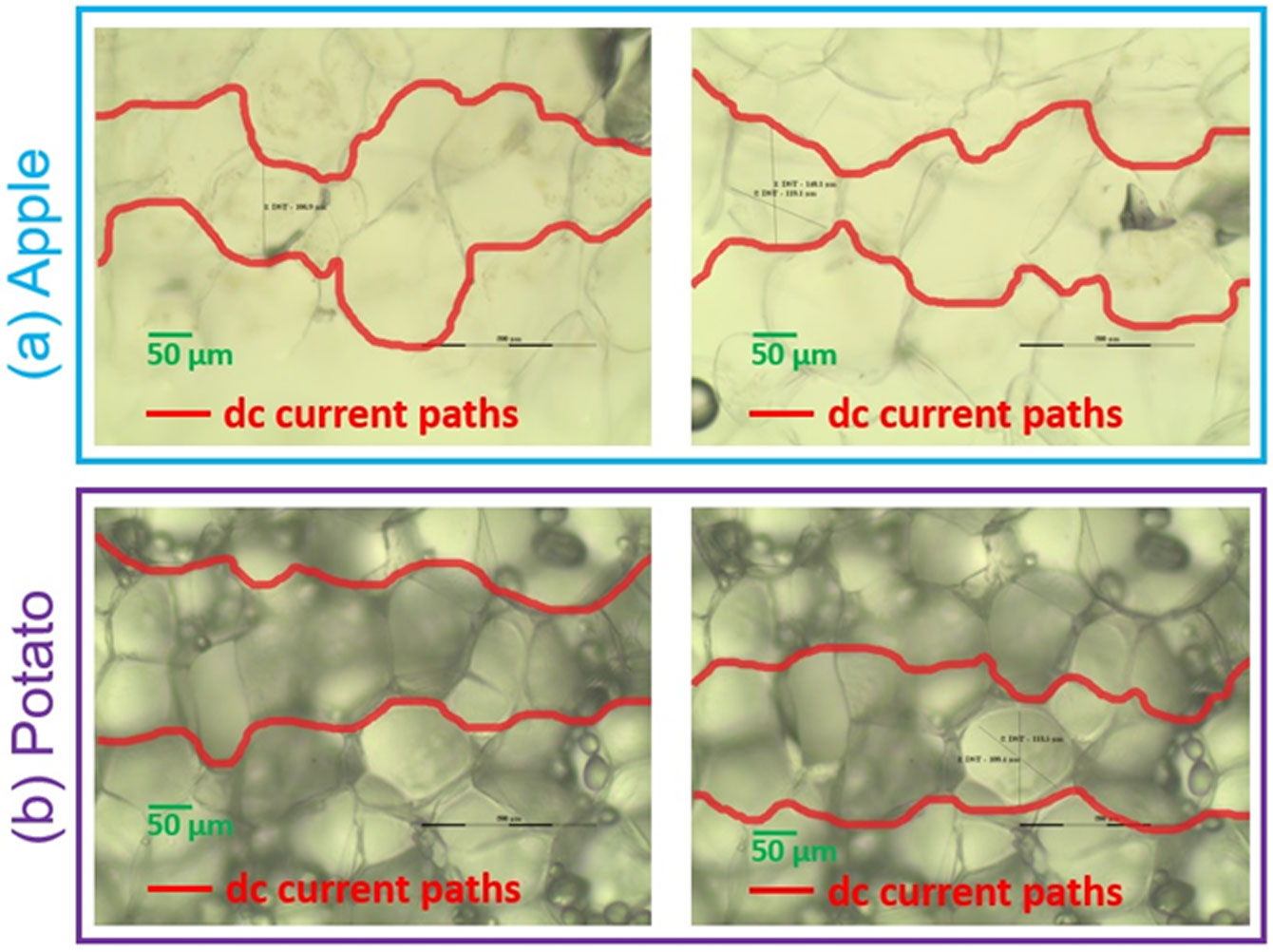
It is intuitive from the Figure 1(a), that the values of the Cole parameters are highly dependent on (a) cell size, (b) porosity, (c) constituents etc. In order to assess the cell size, extensive analysis is performed on the cellular images obtained using a confocal microscope (Olympus CX41). The average cell size of apple and potato (of typical species used in bioimpedance measurement) are estimated to be (10–12) × 103 µm2 and (18–20) × 103 µm2 respectively. The measured cell areas agree well with the similar measurement presented in published references [23],[24]. Thus, the cell size of potato is about 1.8 times larger than that of apple.
On the other hand, the porosity of the apple and potato are in the range of 0.15–0.22 and 0.03–0.08 respectively [25]. Hence, apple tissue contains much more extracellular space than that of the potato. The estimated cell size and porosity in the tissues under investigation can be used to explain the capacitance obtained experimentally. The capacitance of potato tissue is found larger than that of apple tissue (see Table II and Table IV). In the cellular structure, two nearby cells and extracellular space between cells behave like the plates and dielectric material respectively of a parallel plate capacitor. As the capacitance of a parallel plate capacitor is proportional to the plate area and is inversely proportional to the separation between the plates (the extracellular space), the capacitance (C) is found larger in potato tissue as its cell size is larger and extracellular space (porosity) is smaller.
The dc resistance on the other hand depends on the length the dc current path. Longer the dc current path, larger is the dc resistance R0. Typical dc current paths are drawn manually (based on the principle that dc current flows through the extracellular space) and are shown in Figure 4. It is clear from this figure that the detouring of dc current path of apple tissue is greater than that of potato tissue and as a result apple shows larger R0 which is indeed found experimentally (see Table 2 and Table 4). Thus, the orientation of cells in the tissue highly affects the dc resistance. More the misorientation among the cells, longer is the dc current path and yields larger dc resistance. Another factor that may affect the dc resistance is the resistivity of the constituents of the extracellular space in tissues and such investigation is beyond the scope of this work. Therefore, the comparison of Cole parameters of the tissues of Apple and Potato from the biophysical point of view is tentative.
6.
Conclusions
An experimental method is established here to distinguish different species of fruits or vegetable by means of measuring Cole parameters. Cole parameters are extracted for apple and potato tissue by specially designed electrode-pair using direct measurement technique. Among the various Cole parameters, the relaxation time τ is found to be most promising tissue characterizing parameter, since it contains all other Cole parameters of a given tissue. With statistical relevance, it is shown that tissues of different species of apple as well as potato can be distinguished by our experimental method. Our method can have wide application to distinguish unhealthy (or treated) fruits or vegetables from healthy one. The method is not costly and therefore this method has potential application in accessing plant tissue.









 DownLoad:
DownLoad: