Asymptotic approximations to travelling waves in the diatomic Fermi-Pasta-Ulam lattice

1.   Introduction

In this paper, we consider the effects that variations in the masses of nodes in the FPU lattice has on travelling waves by considering a diatomic FPU system in which lighter and heavier masses alternate. The original monatomic version of this lattice was simulated numerically simulated by Fermi, Pasta and Ulam ^[7], who discovered recurrence of the initial data. Similar recurrence behaviour was found in the Korteweg-de-Vries system and explained, by Zabusky and Kruskal ^[28], using solitons, which prompted investigations into solitary travelling waves in FPU ^[8].

The Klein-Gordon lattice (KG), nearest-neighbour interactions are linear and the nonlinearity is due introduced via an onsite potential, for example

Travelling waves solutions have been studied in diatomic KG lattices for some time, often in the presence of second neighbour interactions ^[22,26]. In contrast, the FPU lattice has no onsite potential, instead, each node experiences nonlinear interactions with its nearest neighbours via the Hamiltonian

which gives rise to the equations of motion

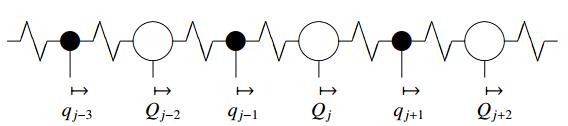
The standard monatomic case is given by $m_j = m$ for all $j$; however, here we consider the case where $m_j = m$ for odd $j$ and $m_j = M$ for even $j$ with $M > m$, giving a mass ratio $\mu = m/M < 1$. The distinction between the two masses is indicated in the notation of $Q_j$ for the larger particles' displacements, and $q_j$ for the smaller, as shown in Figure 1. Here, we retain the restriction to nearest-neighbour interactions, acknowledging that many diatomic systems will have second-neighbour interactions, which significantly complicate the permitted dynamics ^[23].

Early interest in the behaviour of diatomic lattices was initiated by the work of Collins ^[5], who extended his earlier improved quasi-continuum expansions from standard FPU lattice ^[3,4] to the diatomic FPU case, again finding solitary waves which have the characteristic sech$^2$ profile at leading order. Pnevmatikos et al. ^[15] studied a generalised FPU-type lattice which had second-neighbour (SNI) as well as nearest-neighbour interactions (NNI). They used an ad hoc decoupling ansatz to reduce the system of coupled equations to a single generalised Boussinesq equation for the leading-order behaviour of the travelling solitary wave solution. One effect of SNI is that for certain parameter values, subsonic solitary travelling waves are predicted ^[25]. Pnevmatikos et al. ^[15] also obtain breather solutions of the FPU system with SNI.

Huang ^[11] investigated the diatomic FPU-KG system with symmetric nonlinearities, that is, only cubic nonlinearities in both the onsite potential and the NNI. They found breather modes in both optical and acoustic cases with forms governed by the NLS equation and travelling waves whose shape was determined by mKdV. A diatomic FPU system with no quadratic nonlinearity has been studied by Qin ^[18], who sought periodic travelling waves, and obtained the form of the wave for the lighter and heavier masses. Periodic travelling wave solutions of the diatomic FPU have been constructed by Betti and Pelinovsky ^[1] using analytic continuation from the limit of zero mass ratio. They also show that the larger wavelength solutions are stable. Vainchtein et al. ^[23] consider the case of highly different masses in the diatomic FPU finding a bifurcation from the simple single-humped sech$^2$-like profile seen in monatomic FPU to a broader wave which supports multiple oscillations on its peak, which may be of small amplitude, and may have an amplitude similar to that of the wave itself. Faver and Wright ^[6] investigate the form of travelling wave solutions of a diatomic FPU lattice, and find that the underlying problem is singularly perturbed, leading to the presence of background small amplitude periodic wave upon which the solitary wave is superimposed. This system is studied further by Hoffman and Wright ^[10], in the limit of small mass ratios. They only find solutions when the mass ratio lies within certain ranges. Ponson et al. ^[16] analyse the propagation and scattering of waves in disordered diatomic FPU systems, as a model of granular crystals. They find that in disordered systems, the wave amplitude undergoes power law decay. Porubov and Andrianov ^[17] consider diatomic FPU lattice with both quadratic and cubic nonlinearities and derive generalised coupled Boussinesq equations for the mean displacements and differences in displacements, which describe a single system in which waves can travel in either direction.

Rigorous results on the FPU system with (periodically-arranged) polyatomic masses have been derived by Chirilus-Bruckner et al. ^[2] and Gaison et al. ^[9]. In the former work, the authors establish that the leading order asymptotic solution is valid for extremely long time intervals; the leading order solutions being those generated by the KdV approximation for travelling waves and for breather solutions, the NLS. Similar results are derived by Gaison et al. ^[9] who note that for arbitrary initial data, the solution decomposes into waves travelling in both directions. In both papers, corrections terms are shown to be small but are not determined.

To approximate travelling waves in this diatomic FPU system we assume separate profiles for the displacements of the heavy and light particles. The amplitude of the displacement is used as a small parameter; at each order of magnitude we find a pair of governing equations which are simplified using asymptotic expansions and solved at each order of magnitude in sequence using the Fredholm alternative.

The travelling waves discussed in this work are approximations and the system may not support exact moving solutions. Previous work, such as ^{[2,5,9,11,15]} has focused primarily on determining the form of the leading-order term; here, we aim to find the first correction terms as well, with the aim of explaining the oscillations observed in the numerical work of Vainchtein et al. ^[23]. A beyond-all-orders asymptotic expansion, akin to the analysis of Segur and Kruskal ^[21], may show that no such exact solutions exist. However, numerical solutions of discrete systems suggest that these solutions decay extremely slowly and hence are relevant in understanding energy transport in applications. An analysis of this type has been carried out in the case of a diatomic Toda lattice with an asymptotically small mass ratio. Lustri and Porter ^[13] find 'nanoptera', that is oscillations in the tail away of the solitary wave, which are finite in amplitude but exponentially small.

In Section 2 we formulate the problem, defining variables for the masses, their displacements and interaction potentials, before reformulating the system in terms of differences in displacements, in which the system of differential equations has a form more closer to the classical travelling wave PDE. Further transformations of variables are introduced in Section 3, where the problem of seeking travelling waves is posed as a system of coupled differential-delay equations. The two cases of quadratic and cubic nonlinear forces are analysed in detail in Sections 4 and 5. Finally, in Section 6, we compare the results of the two cases with each other and draw comparisons with the results of other authors.

2.   Formulation of problem

The Hamiltonian of our diatomic FPU chain is given by

where $V(\cdot)$ is the potential due to interactions between nearest neighbour particles via nonlinear springs. The light particles all have mass $m$, whilst the heavy particles have mass $M$; we assume that $m < M$ and define $\mu = m/M$. The quantities $P_{2j}$ and $p_{2j+1}$ denote the momenta conjugate to the displacements $Q_{2j}$ and $q_{2j+1}$ respectively. Using Hamilton's equations, we obtain

Here, we assume the potential function and interparticle forces are given by

where in this case the argument $\phi$ will be the difference of the displacements $q_{j+1}$ and $Q_{j}$ (or vice versa).

Analysis of the monatomic system (1.3) is simplified by using the difference in displacements $\phi_j(t) = q_{j+1}(t)-q_j(t)$ rather than the displacements ($q_j$) themselves, since this leads to a governing equation which is more clearly a discrete nonlinear wave equation, namely $\partial_t^2 \phi_j = V'(\phi_{j+1})-2V'(\phi_j) + V'(\phi_{j-1})$. We follow this procedure in the diatomic system, introducing

where $\phi_{j}$ and $\psi_{j}$ now describe the difference displacements between neighbouring light and heavy particles, (and heavy and light particles, respectively). We assume that even nodes are occupied by the heavier masses, so that $Q_j$ and $\phi_j$ are defined for even $j$, and the odd nodes host the lighter masses (that is, $q_j$ and $\psi_j$ correspond to odd $j$). Under the reformation (2.5), the governing equations (2.2)–(2.3) become

with the interaction potential $V(\cdot)$ being given by (2.4).

3.   Travelling solitary waves

To investigate travelling waves, we introduce the spatial shift operator ${{\rm{e}}}^{\pm\partial}$, where ${{\rm{e}}}^{\pm \partial} f(j) = f(j\pm1)$. We also define the mass ratio $\mu = m/M$ with $0 < \mu < 1$, rescale time via $t = \tilde{t}\sqrt{\mu M}$ and drop the tilde, so the system of equations (2.6)–(2.7) are rewritten as

We define

so that $\xi = \mbox{ $\frac{1}{2}$ } (\phi+\psi)$ and $\zeta = \mbox{ $\frac{1}{2}$ } (\phi-\psi)$. Since both $\phi$ and $\psi$ are differences in displacement, $\xi$ is formally a mean difference in displacements and $\zeta$ is a second difference. By adding and subtracting (3.1)–(3.2) we obtain

To proceed further, we need to scale both independent ($j, t$) and dependent ($\xi, \zeta$) variables, and these scalings differ, depending on whether $a = 0$ or $a\neq0$, so we consider each case separately. We start with the quadratic case $a\neq0$ and, for simplicity, assume $b = 0$. Later we consider the cubic case $a = 0$, $b\neq0$.

4.   Quadratic case: $a\neq0$, $b=0$

Following the standard method for deriving a KdV equation from the FPU lattice equations, we introduce $h\ll1$ and write

At leading order, we expect $\phi = \psi = {\mathcal O}(h^2)$, and hence the scaling for the second difference in displacement, $\zeta$, needs to be smaller than that of the mean displacement, $\xi$. To ensure as many terms as possibly balance in the equation for $v$, $\zeta$ has to be just one power of $h$ smaller than $\xi$.

We assume that the functions $\xi$ and $\zeta$ are slowly-varying in $j$, and noting that $\partial = \partial/\partial j$ and $\partial_y = \partial/\partial y$, we replace the discrete differences by their continuum limits

The governing equations (3.4)–(3.5) thus become

From the leading order terms in (4.5) we have $v = \mbox{ $\frac{1}{2}$ } u_y (1-\mu)/(1+\mu)$, and from (4.4) we have $C_1 u_{\tau\tau} = C_2 u_{yy} + C_3 v_y$ for suitable constants $C_j$. Thus the system has the form of a travelling wave equation.

Transforming to a moving wave frame, via

implies $\partial_y = \partial_z$ and $\partial_\tau = h^2 \partial_T -c_0\partial_z$. After expanding terms, integrating the equation for $u$ (4.4) once with respect to $z$, moving all ${\mathcal O}(1)$ terms to the LHS, and ${\mathcal O}(h^2)$ to the right, and neglecting higher order terms, we find

where

Equations (4.7)–(4.8) have the form ${\bf A w} = h^2{\bf g}$ where $h\ll1$ and we are seeking an ${\mathcal O}(1)$ solution for ${\bf w}$. At leading order, the problem reduces to ${\bf A w} = {\bf 0}$, which only has an ${\mathcal O}(1)$ solution for ${\bf w}$ if ${\bf A}$ is singular. Hence a condition for a solution to exist is that we choose the currently undetermined speed $c_0$ so that det$({\bf A}) = 0$. This requirement means that

is the speed of sound in the $(y, \tau)$ coordinate system, which corresponds to the speed of sound in the original lattice being

in $(j, t)$ coordinates. To obtain expressions for $u(z, T)$ and $v(z, T)$ we need to consider the next order terms, which requires more careful analysis, including an application of the Fredholm alternative ^[14].

4.1.   Leading-order analysis—the quadratic case

The singular matrix, ${\bf A}$, has a kernel, $\mbox{span}\{{\bf k}\}$, range, $\mbox{span}\{{\bf r}\}$, and normal to the range, ${\bf n}$, given by

Hence the solution of ${\bf Aw} = {\bf 0}$ is ${\bf w} = w(z, T){\bf k}$ for any function, $w(z, T)$.

In order for there to be a solution of the perturbed problem ${\bf A w} = h^2{\bf g} \neq {\bf 0}$ we have an additional consistency condition, this time on the RHS vector, ${\bf g}$. Since ${\bf A}$ maps all ${\mathbb R}^2$ onto the line $\lambda {\bf r}$ the RHS vector, ${\bf g}$ must lie on this line, hence in (4.8) we require $g_2 = 2 g_1 (1+\mu)/(1-\mu)$. As the vector ${\bf n}$ (4.11) is normal to the range, the condition can be written as ${\bf n}\cdot {\bf g} = 0$ or, from (4.8)

Since the problem (4.7) has two components, the ${\mathcal O}(h^2)$ correction term should also have two components, which we write as coefficients of the two independent vectors ${\bf r}$ and ${\bf k}$. For $0 < \mu < 1$, the vectors ${\bf r}$ and ${\bf k}$ are never parallel (or antiparallel) so, in general, we can write the solution of ${\bf A w} = h^2{\bf g}$ as

and since ${\bf w} = (u_z, v)^T$, we have

A component of the correction term in the ${\bf k}$ direction can simply be absorbed into the leading order solution, which we have already discussed. So, here, we only consider the rôle of the component $\tilde w_z$ in the ${\bf r}$ direction.

Using the leading order expressions $u = 2(1+\mu) w$, $v = (1-\mu)w_z$ and (4.9), simplifying (4.12) yields

which is a KdV equation, with solitary wave solution

This gives the leading order description of $u$, and hence also $\xi$, and $\phi, \psi$.

4.2.   Higher-order analysis–the quadratic case

Inserting (4.13) into ${\bf Aw} = h^2 {\bf g}$, we now aim to solve $\tilde w_z {\bf Ar} = {\bf g}$, and so find the higher-order correction terms $\tilde{w}$. We have

so substituting the solution (4.14) into (4.7)–(4.8), yields

Inverting the transformations (4.14), (4.1), and (2.5), we obtain

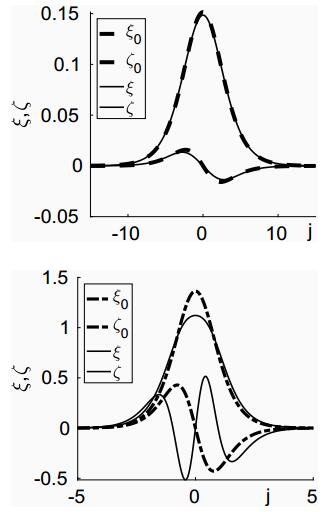
The functions $\xi, \zeta$ are illustrated in Figure 2, which shows both the leading-order solution $(\xi_0, \zeta_0)$ arising from ${\bf w} = w_z{\bf k}$ in (4.13), and the solution ${\bf w} = w_z {\bf k}+ h^2 \tilde w_z{\bf r}$ which includes the first corrections terms, leading to $(\xi, \zeta)$. We note that when $h = 0.1$, the curves for $\zeta_0$ and $\zeta$ are almost identical, as are the profiles of $\xi$ and $\xi_0$. Furthermore, $\zeta$ is small and has the same shape as $\xi'$, thus the combinations $\xi(y, \tau) \pm \zeta(y, \tau)$ will be well-approximated by $\xi(y\pm s, \tau)$ for some shift, $s$. However, at larger values of $h$, as illustrated in the lower panel of Figure 2, the more accurate approximation introduces a more complicated oscillation into the shape of $\zeta$ as shown by the lower solid line. The generation of such internal oscillations in the peak of the travelling wave has been observed in the numerical work of Vainchtein et al. ^[23], who consider the Toda lattice, $V(\phi) = (\alpha/\beta) ({{\rm{e}}}^{-\beta\phi}-1) + \alpha \phi$ which corresponds to $V'(\phi) = \alpha (1- {{\rm{e}}}^{-\beta\phi})$. Expanding this for small $\phi$ leads to $V' (\phi) \approx \alpha \beta (\phi - \mbox{ $\frac{1}{2}$ } \beta \phi^2)$, which gives the quadratic FPU system, and we note that no choice of $\alpha, \beta$ is approximated by the cubic FPU system. Small amplitude travelling waves in this diatomic Toda lattice are thus well-approximated by the quadratic diatomic FPU system.

The amplitude of the main pulse $\xi_0$, given by the leading order $\mbox{sech}^2$ solution (4.16), and the perturbations due to $\zeta$ and $\tilde{w}$ waves all depend on the mass ratio, $\mu$. By introducing a shift ($z = \tilde z - h \delta$ with $\delta = \mbox{ $\frac{1}{2}$ } (1-\mu)/(1+\mu)$) into (4.19) we obtain

From the solution (4.19)–(4.20) we determine a speed-amplitude relationship for the kink: In terms of the original $(j, t)$ variables the speed is given by $c = (\tilde c_0 + h^2C)/\sqrt{m}$, and the amplitude of the kink is

So, in this system, the only slowly-varying travelling waves are supersonic. Equation (4.10) again gives the relationship between $\tilde{c}_0$ and $c$ (4.9). Note that in the limit $\mu\rightarrow0^+$, (4.22) gives large amplitude kinks.

5.   Cubic case: $a=0$, $b\neq0$

In the case, where there is no quadratic nonlinearity in the system, but there is a cubic term, that is, $a = 0$ and $b\neq0$, we need to use a different scaling: In place of (4.1), we define

so that (3.4)–(3.5) become

We still have the second difference of displacements, $\zeta$, being smaller than the mean difference of displacements, $\xi$, by one order of magnitude in $h$, since we expect $\phi = \psi$ to leading order, but now $\phi, \psi = {\mathcal O}(h)$, in place of ${\mathcal O}(h^2)$ in the quadratic case, compare (5.1) with (4.1).

5.1.   Leading-order analysis–the cubic case

At leading order, from (5.3), we again have $v = \mbox{ $\frac{1}{2}$ } u_y (1-\mu)/(1+\mu)$, and from (5.2), $2u_{\tau\tau} = (1+\mu) u_{yy} - 2(1-\mu)v_y$, so the leading order terms have the form of a travelling wave equation. Transforming to a moving wave frame, via (4.6) leads to (5.2)–(5.3) being replaced by

Here, we have integrated the upper equation with respect to $z$; and in both equations, collected the leading order terms onto the LHS are leading order, leaving the ${\mathcal O}(h^2)$ first correction terms on the right. The matrix ${\bf A}$ on the LHS of (5.4) is the same as that in (4.7), and we follow the same strategy as in §4.1, that is, we write the solution as (4.13).

5.2.   Higher-order analysis—cubic case

We write (5.4)–(5.5) as ${\bf Aw} = h^2{\bf g}$ where ${\bf A}$ is singular and has kernel, range and normal to the range, $\mbox{span}\{{\bf k}\}$, $\mbox{span}\{{\bf r}\}$, ${\bf n}$ given by (4.11) respectively. We again write the solution as (4.14) and require that the RHS vector ${\bf g}$ satisfies ${\bf n\cdot g} = 0$. At leading order in $h$, this consistency condition, together with the substitutions (4.14) implies

which is an mKdV equation, rather than the KdV equation (4.15), which occurs for the quadratic case. Equation (5.6) has a solitary wave solution given by

Converting this back to the original variables ($j, t$), we find the speed of the wave is $c = (c_0+h^2C)/\sqrt{m}$: since we require $C > 0$, these waves are supersonic. The amplitude of the resulting kink is

which has no dependence on the speed $c$ (at leading order). A similar cancellation occurs with the standard continuum approximation of the monatomic FPU problem, where the dependence of amplitude on speed can be recovered by use of quasicontinuum approximations ^[19,20,24].

We can also determine the correction term, $\tilde{w}_z$: from the assumed form (4.14) we have ${\bf A w} = h^2 \tilde w_z \lambda {\bf r}$; and from the last line of (5.4)–(5.5), we obtain

hence the first correction term in (4.13) is given by

where $w$ is given by (5.7). Note that while the same ansatz (4.14) is used in both quadratic and cubic cases, the expressions for $w$, (4.16) and (5.7), and $\tilde{w}$, (4.18) and (5.10), differ. Inverting the changes of variables, the spring extensions $\phi, \psi$ are given by

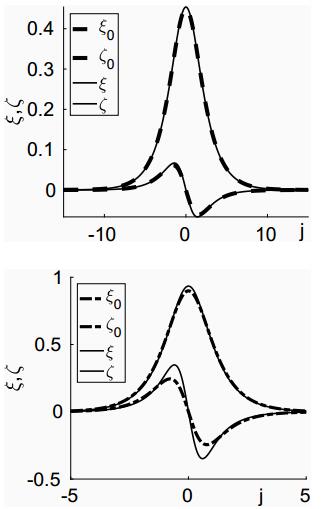
In figure 4 we plot the solutions for $\xi, \zeta$ for the case $h = 0.1$ and $h = 0.2$ with $C = 1$. We show both the leading order solution, $\xi_0, \zeta_0$ which only includes the terms arising from ${\bf w} = w_z{\bf k}$, and the solution $(\xi, \zeta)$ which includes both terms on the right hand side of (4.13), that is, it includes the effect of $\tilde{w}$. This correction term is seen to increase slightly the amplitude of the oscillation in $\zeta$, but not make a significant change in wave form as was observed in the quadratic case (Figure 2).

The first correction term in (5.11) can be removed by applying a phase shift $z\rightarrow \tilde z+\delta$ with $\delta = \mbox{ $\frac{1}{2}$ } h (1-\mu)/(1+\mu)$, following which, we obtain

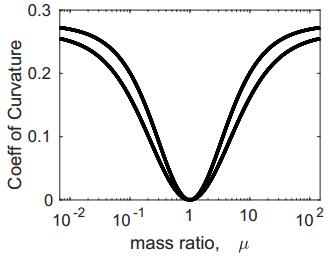
The quantity $\kappa$ is the upper curve plotted in Figure 3, for both the quadratic (4.21) and cubic cases (5.13). We note that in both cases, $\kappa$ takes the value zero at $\mu = 1$ (the monatomic case), and increases away from $\mu = 1$, and is symmetric under the transformation $\mu\mapsto1/\mu$. The limiting values as $\mu\rightarrow0^+$ are $\kappa_{2lim} = 19/72\approx0.264$ and $\kappa_{3lim} = 5/18\approx0.278$. Note, however, that the definitions of $\phi$ in the two cases (4.21) and (5.13) have different signs in the coefficient of $\kappa w_{\tilde z\tilde z}$ due to the differing signs in (4.18) and (5.10).

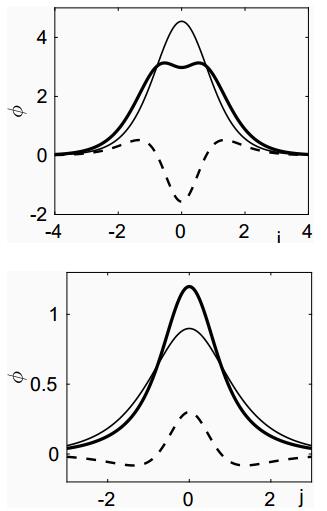
In Figure 5 we show the effect of the higher-order perturbative terms on the travelling wave, after the effects of a shift in the Goldstone mode is accounted for. In both panels we plot $\phi$, which is identical to $\psi$ once the phase shift has been accounted for. We see that in the quadratic case (upper panel), there is the development of an oscillation on the peak of the travelling pulse, whereas in the cubic case, (lower panel) the effect of the perturbation is to 'sharpen' the pulse, increasing the amplitude and reducing the half-height width.

6.   Conclusions

We have investigated the properties of travelling waves in a one-dimensional diatomic FPU lattice with a polynomial interaction potential. To do this, we have derived continuum limit equations in multi-component systems, and used small amplitude asymptotic expansions to convert the governing equations to a system of coupled PDEs. Whilst many authors consider the diatomic system in the limit of asymptotically small mass ratio, for example ^[1,10], our results, in contrast, are valid for any mass ratio. We solve the equations at each order of the asymptotic expansion by application of the Fredholm alternative. This is similar to the approach based on Bloch waves used by Chirilus-Bruckner et al. ^[2] in that it removes the requirement of an ad hoc ansatz that was used by Pnevmatikos et al. ^[15] to reduce the coupled two-component system to a single equation.

In our formulation, the leading order problem is singular, giving the wave speed–amplitude relationship. At next order we have a singular forced equation, which is subject to a consistency condition. The leading-order solution gives rise to the usual sech$^2$ or sech—type solutions, which have been found by many authors previously, for example, ^[5,15,11], and proven to be accurate approximations ^[2,9] for long periods of time. At next order, the correction terms that we have found here correspond to simple phase shifts and, at the following order, we find terms which give rise changes in the shape of the solitary waves. We believe these last results to be new.

Comparing the equations (4.21) for the quadratic nonlinearity with the cubic case (5.13), we note a difference in the sign of the correction term: $\phi = 2h(1+\mu) [w \pm \kappa h^2 w_{\tilde z\tilde z}]$, (both $\kappa_2$ and $\kappa_3$ are positive, as shown in Figure 3). In the case of a quadratic nonlinearity, the '$+$' sign causes the emergence of an oscillation in the peak of the solitary wave; whilst in the cubic system, the '$-$' sign causes a 'sharpening' of the peak and possibly the development of an oscillation in the tail of the solitary wave. All the calculations presented herein are based on small amplitude asymptotic approximations. At larger amplitudes, we expect the oscillations to grow, both in amplitude and in number—as shown in the numerical results of Vainchtein et al. ^[23] who investigate the diatomic Toda chain. With the Toda potential, there is typically a combination of quadratic, cubic and higher-order nonlinearities involved. Also, we note from Figure 3 that extremely small or large mass ratios will exhibit a greater effect than mass ratios close to unity—the almost monatomic case.

In future work, we hope to apply these methods to find properties of travelling waves in mass-in-mass FPU systems ^[12], which is an alternative generalisation of the FPU system with two components in each unit cell.

Acknowledgments

We thank the referees for their helpful comments.

Conflict of interest

The author declares no conflict of interest.