DlncRNALoc: A discrete wavelet transform-based model for predicting lncRNA subcellular localization

1.   Introduction

The sudden outbreak of coronavirus disease 2019 (COVID-19) has had a major impact on the economy, society and daily life ^[1,2,3,4,5]. Long non-coding RNAs (lncRNAs) have significant research implications for the prevention and treatment of viral epidemics. For instance, lncRNAs can serve as emerging regulators of COVID-19 ^[6].

LncRNA was once thought to be a transcriptional "noise" of genes with no biological function. Recently many important functions of lncRNAs, including the regulation of gene expression and the modulation of protein activity have been discovered. These functions are closely related to life activities such as cell structural integrity, cell differentiation, cell cycle, and immune response ^[7], which has caused lncRNAs to receive an increasing amount of attention in the field of life sciences. However, due to the complexity of the molecular mechanisms and functions themselves, lncRNA-related research has largely lagged behind the research on other types of non-coding RNAs (ncRNAs) and proteins.

The function of lncRNAs also depends on the cellular compartment in which they are located, which is similar to that of proteins; thus, localizing their information plays a vital role in understanding their function ^[8]. The computational prediction of subcellular localization (SL) has been an important topic in bioinformatics due to the fact that SL prediction is difficult to realize through biological experiments ^[9]. Consequently, there is an immediate necessity to adopt computational approaches in order to accelerate the research on lncRNAs, such as the research on the identification of drug targets ^{[10,11,12,13]}, enhancers ^[14,15], interactions between ncRNAs and proteins ^[16,17], circular RNAs ^[18,19], miRNAs ^{[20,21,22,23]} and reducing dimensionality ^{[24,25,26,27]}. However, most prediction tools are constructed for proteins ^{[28,29,30,31,32,33,34,35]}. Sequence-based methods for predicting the SL of proteins can be generally categorized into statistical machine learning-based and homologous transfer. Homologous transfer attempts to determine annotated homologous proteins for query sequences from a large database, but failure may be predicted when no homologous proteins are found ^[36]. The relative slowness of lncRNA annotation and its sequence diversity is due to the difficulty in obtaining lncRNA sequences with definitive homology annotations. Therefore, the machine learning-based approach is suitable for the development of SL predictors for lncRNA at the current stage.

However, the machine learning-based method for predicting lncRNA subcellular localization (LSL) face several challenges. First, traditionally, it was assumed that most lncRNAs are primarily located only in the nucleus and regulate nuclear gene regulators ^[37]. Recent studies using fluorescence in situ hybridization techniques have revealed that lncRNAs exhibit diverse SLs, with many being found in the cytoplasm ^[38]. Some lncRNAs are also evenly distributed between the nucleus and cytoplasm. Second, the prediction of LSL via machine learning methods encounters difficulties due to insufficient relevant data.

With the deepening of LSL research, lncRNA subcellular-related databases and tools are constantly being proposed, providing a strong support for the study of LSL based on machine learning. Zhang et al. ^[39] constructed the RNALocate database, which collected more than 37,700 LSL data entries. Afterward, Mas-Ponte et al. ^[40] created the LncATLAS database, which is a specialized database for storing LSL data. Chen and Carmichael ^[37] systematically analyzed the distribution of LSL in gastric cancer, thus revealing its relationship with the existence of cancer development. Feng et al. ^[41] collected ncRNAs from mitochondrial, kinetoplast, and chloroplast genomes and proposed a model for predicting the location of ncRNA organelles. Cao et al. ^[8] developed a lncLocator predictor to predict LSLs based on the k-mer frequency feature, and a deep learning model was proposed to allow the lncLocator predictor to predict LSL. Su et al. ^[42] proposed the model iLoc-lncRNAL for predicting LSL; it is based on lncRNA sequence octamers and demonstrated good prediction performance.

As mentioned above, although developing the calculation methods for LSL is very important, there are still relatively few studies on it, and there are three main problems: (ⅰ) data imbalance, the LSL dataset shows serious unbalanced distribution; for example, recently, some of the proposed methods have not considered the problem of data imbalance ^[42,43]; (ⅱ) feature extraction of lncRNA sequences, unlike other short ncRNA sequences, due to the specificity of lncRNAs, it is more difficult to capture their feature information; (ⅲ) the prediction accuracy is generally low. For instance, Cao et al. ^[8] proposed the lncLocator method, which addresses the issue of data imbalance. However, the method achieves an overall accuracy (OA) of only 0.59, suggesting that there is significant room for improvement.

To address those problems, we propose a novel discrete wavelet transform (DWT)-based predictive method, DlncRNALoc, to identify the LSL. Firstly, we introduce aDWT-based representation of lncRNA sequence features. Recently, the application of wavelet analysis in bioinformatics research has received much attention ^[44,45]. The Fourier coefficients contain only global information about the time domain name; therefore, there is a loss of characteristic information of the signal in the bit domain ^[46]. The decomposition of lncRNA sequence signals via DWT can remove the redundant information of features and yield the characteristic signals of each type of lncRNA. This is important for improving the prediction performance. Next, we employ the local Fisher discriminant analysis (LFDA) ^[47] to reduce the noisy information and feature dimensions and combine it with the synthetic minority over-sampling technique (SMOTE) ^[48] to mitigate the effects of data imbalance. Finally, we construct a support vector machine (SVM) to construct models to predict the LSL. Extensive experiments show that the DlncRNALoc model has excellent performance. The main highlights are as follows.

1) We propose the LP matrix, which converts an lncRNA sequence into an L*6-dimensional matrix by considering its 2-tuple physical structure's properties. The LP matrix can also be applied in other lncRNA research domains.

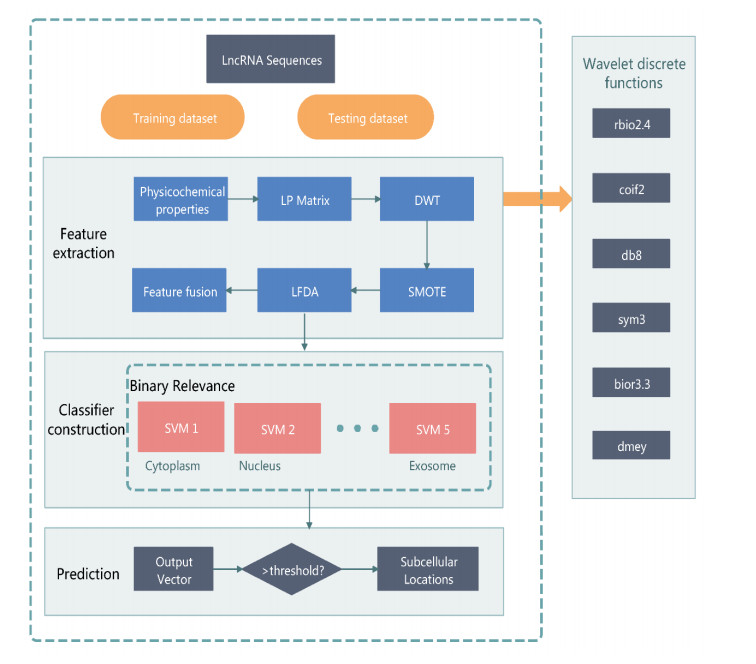
2) We introduce the DWT feature extraction method by combining the LP matrix with DWT. We utilize six discrete wavelet functions (WFs) (rbio2.4, coif2, db8, sym3, bior3.3, and dmey) for this purpose.

3) We employ the SMOTE to address the data imbalance caused by uneven distribution of lncRNA samples across different subcellular locations.

4) Extensive experimental results demonstrate that DlncRNALoc outperforms several state-of-the-art approaches in the area of LSL.

2.   Materials and methods

2.1.   Framework of the DlncRNALoc model

This study has yielded a DWT-based LSL prediction model termed DlncRNALoc. The DlncRNALoc consists of two major parts: feature extraction and model construction. We obtain the LP matrix of lncRNA based on its physicochemical properties. From this LP matrix, we extract the DWT characteristics of each lncRNA. A total of six discrete WFs were used: rbio2.4, coif2, db8, sym3, bior3.3, dmey. Additionally, we use the SMOTE technology to synthesize new samples and the LFDA to mitigate the effects of the high-dimensional features. Furthermore, we adopt the one-to-one (OVO) strategy to construct the SVM classifier. The feature information is fed into the SVM to predict the LSL. Finally, extensive experimental analyses were performed to evaluate the performance of the DlncRNALoc model. Figure 1 shows the overall framework of the DlncRNALoc model.

2.2.   Datasets

We used two sets of ​lncRNA sequence benchmark datasets for SL experiments derived from the RNALocate database. This database serves as a repository for localization information on various ​RNA molecules, including mRNA, miRNA, and lncRNA molecules. The latest version of RNALocate encompasses over 37,700 manually-planned SL entries and experimental evidence for RNA molecules, and it covers more than 21,800 encoded and non-coding RNAs in 65 species ^[39]. Table 1 presents the two benchmark datasets for the SL of lncRNA sequences.

Dataset 1 was created by Cao et al. ^[8] using the RNALocate database. Dataset 1 consists of 612 lncRNA sequences that are categorized into five subcellular loci: cytoplasm (301), cytosol (91), exosome (25), nucleus (152), and ribosome (43).

Dataset 2 was established by Su et al. ^[42], and it contains 655 lncRNA sequences divided into four subcellular loci: cytoplasm (426), ribosome (43), exosome (30) and nucleus (156).

Dataset 3 was established by Li et al. ^[49], and it contains 769 lncRNA sequences divided into four subcellular loci: cytoplasm (328), ribosome (8), exosome (28) and nucleus (325).

To mitigate bias caused by redundant sequences, Datasets 1, 2 and 3 were constructed by using the cd-hit method ^[50,51] to remove redundant lncRNA sequences with a cutoff value of 80%. Detailed information about Datasets 1, 2 and 3 can be found in Table 1.

2.3.   LP matrix

The LP matrix represents the physicochemical property matrix of the 16 2-tuples bases of the lncRNA sequence. The lncRNA sequence contains 16 2-tuples formed by combining the four bases: A, T, C, and G. These 2-tuples include AA, AC, AG, and so on, up to TT. Previous studies ^[52] have shown that each pair of 2-tuple bases contains six physicochemical properties: twist, tilt, slide, roll, shift and rise. The values for these six physicochemical properties corresponding to the 16 2-tuple bases were obtained from the literature ^[52], and they are presented in Table 2. For the sake of convenience, we represent the 16 2-tuple as ${N}_{1}$, …, ${N}_{16}$ in Table 2.

Let S = ${s}_{1}$, …, ${s}_{L}$ represent a lncRNA base sequence of length L. Then, the sequence S can be described as Eq (1):

Here, ${p}_{i}$ represents any adjacent 2-tuples in the sequence S. Therefore, based on Table 1 and Eq (1), the given sequence can be transformed into an LP matrix of $(L-1)\times 6$, as given by Eq (2):

where ${p}_{i, \mathrm{j}}$ represents the jth (j = {1, 2, 3, 4, 5, 6}) physicochemical properties of the ith 2-tuple of the sequence S. For example, if S = "ACAGA", then ${p}_{\mathrm{1, 1}}$ represents the first physicochemical property "twist" of the first 2-tuple "AC". Using Table 1, we can determine that ${p}_{\mathrm{1, 1}}$ = 0.036. Similarly, ${p}_{\mathrm{2, 2}}$ represents the second physicochemical property "tilt" of the second 2-tuple "CA" of the sequence, and its value from Table 1 is ${p}_{\mathrm{2, 2}}$ = 0.025. These computations can be extended to derive the physicochemical properties for other 2-tuples in the sequence. The collection of all of these 2-tuple forms the LP matrix.

2.4.   DWT

DWT ^[34] is a transformation that captures the discrete sampling of wavelets. It provides significant frequency and positional information for sequences. DWT is the decomposition of the physicochemical properties of lncRNA sequences into coefficients of different resolutions, as achieved by projecting the signal onto a wave function (WF). DWT effectively filters out noise from the high-pass curve. In our approach, we consider the LP matrix of each lncRNA sequence as a two-dimensional signal and utilize DWT for denoising purposes.

Mathematically, WT is the projection of the signal $f(t)$ onto a WF:

In this equation, $a$($a>0$) is the scale factor and $b$ is the translation factor, both of which are real numbers. $\Psi\left(\frac{t-b}{a}\right)$ represents the analyzing WF, whereas $T(a, b)$ corresponds to the WT coefficient of the signal at a position ($t = b$) and a particular wavelet period defined by the scale factor $a$. By using the DWT, lncRNA sequences can be decomposed into various dilation coefficients, facilitating the elimination of noise components. Nanni et al. ^[53,54] devised a strategy that utilizes the DWT. If we assume that $f(t)$ is a discrete signal represented by $x[n]$, it can be defined by the following equations.

The length of the discrete signal is denoted by N. $y_{\text {high }}[n]$ indicates the detailed coefficient, representing its high-frequency component. The approximation coefficients of the signal are denoted by $y_{\text {low }}[n]$, which represents the low-frequency component of the signal. The low-pass filter is denoted by $g$, while the high-pass filter is denoted by $\mathrm{h}$. As the level of decomposition increases, more intricate signal characteristics become discernible. Figure 2 depicts four filters that are compatible with the "dmey" WF. These filters include the decomposition and reconstruction of the low-pass and high-pass filters.

DWT is visually represented in Figure 3 across four distinct levels. At each stage, the data are divided between noisy information in the higher frequency bands and valuable signals in the lower frequency bands. These bands must undergo additional transformations in subsequent steps.

The high-frequency and low-frequency signals are separated at each level of the DWT. We calculated the standard deviation, minimum, maximum, and average values of the bands at each level to derive four features for the high-frequency and low-frequency bands, generating a total of eight features. Furthermore, since these first five elements encapsulate vital information regarding the sequence in the compressed low band, we obtained the initial five discrete cosine coefficients from the approximation coefficients.

Consequently, 52 features are obtained from each level of the DWT, comprising four features each in the high-frequency and low-frequency bands, and five features from the discrete cosine coefficients. By utilizing the 5-level DWT method, it is possible to extract 52 features for each attribute in the LP matrix. As a result, all six physical and chemical properties collectively provide a total of 390 features.

2.5.   SMOTE

Table 1 shows noticeable disparities in the data distribution of lncRNAs across different subcellular locations. Since machine learning algorithms often tend to categorize new samples into the majority class, the presence of an unbalanced data distribution can adversely affect the classification performance of the minority class. This problem becomes more pronounced when dealing with multiple classification tasks. The SMOTE method mitigates the effects of data imbalance by generating synthetic samples and oversampling a few classes of samples. SMOTE technology achieves data balance by synthesizing new samples for the minority class.

The imbalance levels and sampling rates can be derived based on different samples in each category. The number of SLs is denoted by the symbol $\mathrm{C}$, and ${num}_{i}(1\le i\le \mathrm{C})$ is the number of samples in the $i$th subcellular of the benchmark dataset. The imbalance level in the $i$th category can be calculated using the following formula:

Here, the number of samples in the largest category in the dataset is denoted by $num\_ma$. The sampling rate ${n}_{i}$ is calculated by rounding the imbalance level ${IL}_{i}$, as defined below in the following equation:

For each subcellular class with a non-maximum number of lncRNAs, find the nearest K samples for each sample in the class and randomly extract ${n}_{i}$ samples from the K samples (${n}_{i}$ is the sampling magnification, $K > {n}_{i}$), denoted as ${y}_{1}$, ${y}_{2}$, ..., ${y}_{{n}_{i}}$. Therefore, a random interpolation operation between X and ${y}_{j}$ is performed to obtain an interpolated sample ${syn}_{j}$. The interpolation equation is defined as follows:

Here, ${rond}(0, 1)$ indicates a number that is randomly generated in the interval (0, 1), and ${y}_{j}$ represents a neighboring sample of a few subcellular samples.

2.6.   LFDA

Here, we describe our use of a supervised dimensionality reduction technique called LFDA ^[47]. LFDA offers an embedded transformation with an analytical form and it can be efficiently solved by addressing generalized eigenvalue problems. The LP matrix of the lncRNA base is defined as LP = [${x}_{1}, {x}_{2}, \dots, {x}_{i}, \dots, {x}_{n}$], ${x}_{i}\in {R}^{d}$, where $n$ is the number of lncRNA sequence samples, the symbol $d$ denotes the dimension of the eigenvector, ${y}_{i}\in \{\mathrm{1, 2}, \dots, \mathrm{c}\}$ indicates the category label and ${n}_{\mathcal{l}}$ is the total number of lncRNAs of a subcellular $\mathcal{l}$; then, we have

The local intraclass scattering matrix ${S}^{\left(w\right)}$ and the local interclass scattering matrix ${S}^{\left(b\right)}$ are respectively defined as follows:

where,

Here, $A$ is an affinity matrix, and ${A}_{i, j}\in A$ is the affinity of ${x}_{i}$ and ${x}_{j}$. In this paper, we use the affinity matrix ${A}_{i, j} = \mathrm{e}\mathrm{x}\mathrm{p}(-‖{x}_{i}-{x}_{j}‖/{\sigma }_{i}{\sigma }_{j}$) defined in ^[55], ${\sigma }_{i} = ‖{x}_{i}-{x}_{i}^{K}‖$ denotes a local scaling of the samples surrounding ${x}_{i}$ and ${x}_{i}^{K}$ is the kth nearest neighbor of ${x}_{i}$. Solve the LFDA transformation matrix ${T}_{LFDA}$ as follows:

The resulting dimensionally reduced matrix is described as follows:

2.7.   SVM

We implement the SVM module by using the LIBSVM package proposed by Chang and Lin ^[56], which adopts a one-to-one (OVO) strategy for multi-classification problems. We apply a dataset $\mathrm{D} = \left\{\left({x}_{1}, {y}_{1}\right), \left({x}_{2}, {y}_{2}\right), \dots, \left({x}_{n}, {y}_{n}\right)\right\}, {y}_{i}\in \{{C}_{1}, {C}_{2}, \dots, {C}_{k}\}$, where ${y}_{i}$ is the category label corresponding to ${x}_{i}$. The OVO method involves designing a classifier between the categories of each pair, which requires an aggregate of k(k-1)/2 classifiers for k categories. During the testing phase, the test sample is evaluated by all classifiers, producing k(k-1)/2 classification results. The final prediction is determined via a voting process, where the category receiving the most votes is selected. In cases where two categories have the same number of votes, the category that appeared first during voting is assigned as the final prediction category.

2.8.   Evaluation criteria

For a well-established classification prediction model, there must be a test method and some indicators to evaluate the model. We choose to use 5-fold cross-validation and independent validation methods to evaluate the performance of LSL prediction models and apply the Matthew's correlation coefficient (MCC), OA, sensitivity (SE), specificity (SP), recall, and ${F}_{1}$-score (${F}_{1}$) as the evaluation metrics. The equations to calculate these metrics are as follows:

where ${ Practsion }^{(i)}$ indicates the precision of the ith class. TP, FP, TN and FN denote the numbers of true positive, true negative, false positive and false negative instances, respectively.

3.   Results

3.1.   Selection of WF

The concept of WT involves transforming a signal into a representation composed of wavelet basis functions. Different families of WFs generate distinct wavelet basis functions, each offering unique signal processing capabilities and outcomes ^[57,58]. The effectiveness of feature extraction from a sequence is enhanced when the characteristics of the WF align well with the structure of the analyzed signal. It is widely acknowledged that WFs possess several desirable features, including compact support, symmetry, orthogonality, smoothness, and high-order vanishing moments. However, the choice of WF involves certain conflicting constraints as no single one possesses all of these characteristics simultaneously. In order to select the characteristic information that can effectively extract the LSL, in this study, six WFs were mainly investigated: discrete meyer (dmey), daubechies of number 8 (Db8), biorthogonals of number 3.3 (Bior3.3), coiflet of number 2 (Coif2), symlets of number 3 (Sym3) and rbio2.4. The results of applying the LSL prediction models using the above six WFs on the benchmark datasets, Datasets 1 and 2 are shown in Tables 3 and 4, respectively. We used jackknife cross-validation as the evaluation method and selected sensitivity (SE) and overall accuracy as the evaluation indicators.

Based on Table 3, the dmey WF yields the highest OA, i.e., 87.07%, and the OA of the coif2 function is the smallest among the five WFs, i.e., rbio2.4, coif2, db8, sym3, and bior3.3; the OA of the rbio2.4 function is 86.53%, which is very close to that of the dmey function.According to the dmey WF, except for a lower sensitivity in predicting lncRNA subcellular localization in the nucleus (MCC = 0.655) compared to the rbio2.4 function, the prediction accuracies of lncRNA for the other three subcellular compartments (cytoplasm, ribosome, and exosome) are 0.714, 0.960, and 0.966, respectively, which are the highest values.

As shown in Table 4, the dmey WF achieves the maximum OA of 91.28%. Among the five WFs, rbio 2.4, coif2, db8, sym3 and bior 3.3, the OA of the sym3 function is the smallest (OA = 88.24%). The OA of the bior 3.3 function is 90.06%, which is very close to that of the dmey function.

In the case of the dmey WF, the MCC values of lncRNA predicted for the cytosol and nucleus are 0.962 and 0.757, respectively, which are the best among several methods. Although the MCC values for the exosome (MCC = 0.994) and nucleus (MCC = 0.996) are not the best, they are very close to the best. Note that the OA of the db8 WF is found to be 89.93%. Although this is not very prominent, the MCC values for the cytoplasm and ribosome are 0.774 and 0.998, respectively. These values are better than those for the other WFs.

Figures 4 and 5 show the sensitivity and specificity of the six WFs on Datasets 1 and 2, respectively, where each sub-cell is mapped with a different color across a radar chart.

It can be seen in Figure 4 that the sensitivity of the six WFs is ranked as follows: nucleus, cytoplasm, ribosome, and exosome for the four sub-cells; also, the cytoplasm, nucleus, exosome, and ribosome have been sorted from small to large. Similarly, as shown in Figure 5(A), the exosome and ribosome curves almost coincide, indicating that the six WFs are almost identical in sensitivity to the exosome and ribosome; the sensitivity of the other three sub-cells has been ordered from small to large: nucleus, cytoplasm and cytosol. In Figure 5(B), the subcellular curve is divided into two groups: cytoplasm and nucleus curves, and exosome, cytosol and exosome curves.

Based on the above analysis, different WFs are used to predict the performance on different sub-cells, indicating that different WFs can capture different types of characteristic information of lncRNA sequences. The predicted overall performance of the dmey WF is found to be optimal. Therefore, we applied the dmey WF to construct the prediction model.

3.2.   Comparison with state-of-the-art methods

In order to objectively assess the performance of the DlncRNALoc model in terms of predicting LSLs, we introduced three benchmark datasets. We compared their use with different existing methods on each benchmark dataset.

Table 5 presents the results of iLoc-lncRNA, lncLocator, and DlncRNALoc on Dataset 1, respectively, using SE, SP, MCC and OA as the evaluation criteria. Table 5 shows that the OAs for the three LSL prediction methods are 86.72%, 66.50%, and 87.41%, respectively. Obviously, the OA of the DlncRNALoc model is the largest, and the OA of the lncLocator model is the lowest, at only 66.50%. The DcncRNALoc model predicted MCC values for lncRNA for the four sub-cells of nucleus, cytoplasm, ribosome and exosome: 0.666, 0.722, 0.960 and 0.966, respectively. Among them, the MCC values for the ribosome and exosome are the best, and at least 30% higher than the second-ranked iLoc-lncRNA prediction model; additionally, the MCCs for the nucleus and cytoplasm sub-cells are ranked second, but the value of the MCC for the first-ranked iLoc-lncRNA is very close.

Table 6 indicates the experimental results of the DlncRNALoc prediction model, LoR ensemble, average ensemble, and lncLocator prediction model on Dataset 2, and in terms of the OA, recall, and ${F}_{1}$ as evaluation indicators. Among them, the LoR ensemble, average ensemble, and lncLocator methods' experimental results were taken from the literature ^[8]. The values ​​of OA, ${F}_{1}$ and recall for the DlncRNALoc model are 91.08%, 91.19% and 91.22%, respectively, which are larger than those for the other prediction methods.

In order to compare ​advanced deep learning methods, we have utilized a dataset from ​the literature ^[49] called ​Dataset 3. We selected three ​baseline methods, namely, the ​convolutional neural network (CNN), long short-term memory (LSTM), and GraphLncLoc ^[49]. The results were verified via a five-fold cross-validation experiment, and they are shown in Table 7. The experimental results of the CNN and LSTM methods were obtained from the literature ^[49]. As depicted in Table 7, the DlncRNALoc method yields performance metrics of 69.44% for OA, 57.56% for the ${F}_{1}$ score and 55.00% for recall. These results are superior to those obtained via the other evaluated methods.

To comprehensively assess the efficacy of ​DlncRNALoc in predicting the LSL, we evaluate it alongside existing methods for comparison. We employed an independent test set—furnished by ​GraphLncLoc—comprising sequences from the cytoplasm (20), ribosome (10), nucleus (20), and exosome (7). Our chosen baseline methods included ​lncLocator ^[8], ​iLoc-lncRNA ^[42], ​Locate-R ^[59], DeepLncLoc ^[60], and GraphLncLoc ^[49]. Table 8 shows the results of this independent test. The DlncRNALoc method outperforms other methods, as evidenced by an OA of 59.65%, an ${F}_{1}$ score of 63.16%, and a recall of 61.43%.

The main reasons for the superior performance of DlncRNALoc compared to deep learning methods can be attributed to the following factors: 1) Deep learning models achieve high prediction accuracy by leveraging large-scale datasets and increasingly complex models. Consequently, training these models becomes progressively challenging, often leading to suboptimal performance. 2) lncRNA sequences vary significantly in length, such as in Dataset 3, where the sequence length ranged from 126 to 551,120. Deep learning models often adopt a fixed sequence length and employ rules to handle shorter or longer sequences. However, this approach leads to inevitable information loss or wasted space. It is to be noted that the experimental results featured in Tables 7 and 8 were obtained without the utilization of SMOTE for data processing. To summarize, The DlncRNALoc model has good predictive performance and effectiveness in LSL prediction.

4.   Conclusions

The role of SL in understanding the intricate biological functions of lncRNAs underscores its importance in research, particularly in predicting LSL. We developed a DlncRNALoc approach for predicting LSL. This approach incorporates various features, encoding techniques, and machine learning methodologies to improve prediction performance and provide insight into the mechanisms that govern LSL.

The initial step involved the construction of the ​LP matrix, utilizing a 2-tuple of physicochemical properties of the bases in the lncRNA sequence. This was followed by the implementation of a DWT-based feature extraction, which employed the LP matrix. The ​SMOTE was then incorporated for sample generation, and the ​LFDA algorithm was implemented for optimal feature extraction through information dimensionality reduction. Finally, the LSL was predicted by using SVM algorithm. Evaluation of the DlncRNALoc predictions on two benchmark datasets yielded overall accuracies of 87.41% and 91.08%, respectively. Comparison with existing approaches revealed significant improvement of the performance for LSL, signifying the potential of the proposed method to predict other lncRNA properties and functions.

This study focuses on exploring the representation of ​lncRNA sequences. In the future, it is recommended to fuse structural information and physicochemical property information to further enhance the accuracy of LSL prediction. Additionally, conducting extensive benchmarking and comparative evaluations of ​DlncRNALoc with other computational methods on diverse datasets is necessary to evaluate their performance and identify their strengths and weaknesses. Moreover, it is essential to investigate methods for interpretable DlncRNALoc predictions that provide insights into the specific features or characteristics contributing to the LSL. Such an investigation can improve model transparency and facilitate biological interpretation. By addressing these future research directions, this study can significantly advance our understanding and prediction of LSL, ultimately contributing to our knowledge of lncRNA function and cellular regulation.

Use of AI tools declaration

The authors declare that they have not used artificial intelligence tools in the creation of this article.

Acknowledgments

The work was supported in part by the National Natural Science Foundation of China (Nos. 62002111, 62372158), the Natural Science Foundation of Hunan Province (No. 2022JJ40090). And it was also supported by a grant from the 'Macao Young Scholars Program' (Project code: AM2021025).

The authors would also like to express their gratitude to Prof. Yao Xiaojun from Macao Polytechnic University for his invaluable suggestions and enlightening discussions, which significantly improved the clarity and overall presentation of this manuscript.

Conflict of interest

The authors declare that there is no conflict of interest.