1.
Introduction
Tumourigenesis is a complex, multi-step process which leads to the formation of solid malignancies. A critical step in this process is angiogenesis in which tumours develop their own vasculature and blood supply. In normal tissues, angiogenesis is carefully self-regulated and tightly controlled, whereas in tumours, the vessels are structurally and functionally abnormal. Accordingly, they are often characterized by defective endothelia, basement membranes, and pericyte coverage leading to inefficient nutrient delivery to tumour cells despite a high global blood flow in the environment [1]. In particular, the poor delivery of oxygen results in regions of severe hypoxia—a trait observed in nearly all solid malignancies [2,3]. Tumour hypoxia has been linked to the increase of many cancerous behaviors such as genomic instability, malignant progression, and metastasis formation [4,5].
The clinical implications of hypoxia for cancer therapy are also of great importance, most evidently in the context of radiation and chemotherapy. It has been established that resistance to radiation is conferred by hypoxia, and the mechanism by which this is achieved is well understood [4,6]. The radioresistance arises in the hypoxic regions because of the relatively fewer oxygen-derived free radicals generated by ionizing radiation that compromise the cytotoxic effects of radiotherapy. In the case of chemotherapy, hypoxia has also been shown to elicit an overall decrease in efficacy in vivo. This is likely related to inefficient drug delivery due to the abnormal tumour vasculature, though the underlying mechanisms dictating this are less well understood [4,7].
On the other hand, hypoxia is a theoretically ideal target for guided drug delivery. To overcome hypoxia-induced treatment resistance, hypoxia-activated prodrugs (HAPs) have been developed that are nontoxic under physiological oxygen concentrations but are activated through a bioreduction specifically in hypoxic tumour regions. Once HAPs become activated at hypoxic sites, some of them are able to diffuse back out of hypoxic areas allowing them to attack nearby, non-hypoxic cells as well—a phenomenon called the bystander effect. These bystander effects play a vital role in the overall cytotoxic effectiveness of HAPs. Furthermore, the failure of several recent clinical studies involving HAPs suggests that one of the several factors contributing to this failure is insufficient classification of patients based on their hypoxia and nitroreductase expression statuses [8,9]. Hence, not only the presence of hypoxia, but also its spatial distribution, might significantly influence the efficacy of treatments involving HAPs. Preclinical studies have examined the effect of HAPs, administered singly or in combination with conventional treatments such as chemotherapy and radiotherapy, resulting in very promising outcomes in the control of tumour growth [10,11,12]*. Despite the theoretical and preclinical results, several HAPs have recently failed to demonstrate efficacy in clinical trials. The disconnect between theory and practice is hypothesized to be mainly due to sub-optimal patient selection and heterogeneities in distributions of hypoxia, in addition to other issues common to chemotherapies such as poor delivery due to the insufficient blood supply and high interstitial fluid pressures [9,13]. A better understanding of these therapies and their interactions with tumour cells and the surrounding micro-environment for individual patients is required before they can be successfully translated into clinical practice.
*https://www.youtube.com/watch?v=LjbfbQ_OON8&t=s
Mathematical modelling approaches have been used to study the interaction between hypoxia and external beam radiation therapy [14,15,16,17] as well as the action of HAPs [18,19,20,21,22]. Here, we developed an experimentally motivated mathematical model to predict the effect of HAPs by incorporating the amount of tumour hypoxia and the action of the prodrug as well as the sensitivity of activated metabolites. Once the model is calibrated and validated with appropriate experimental data, it can be used to determine the efficient administration of HAPs for a given tumour and to predict the outcome of a combination of HAPs and radiotherapy. Moreover, the developed mathematical model can be further used to analyse and generate testable hypotheses that can be further studied experimentally.
2.
Mathematical model
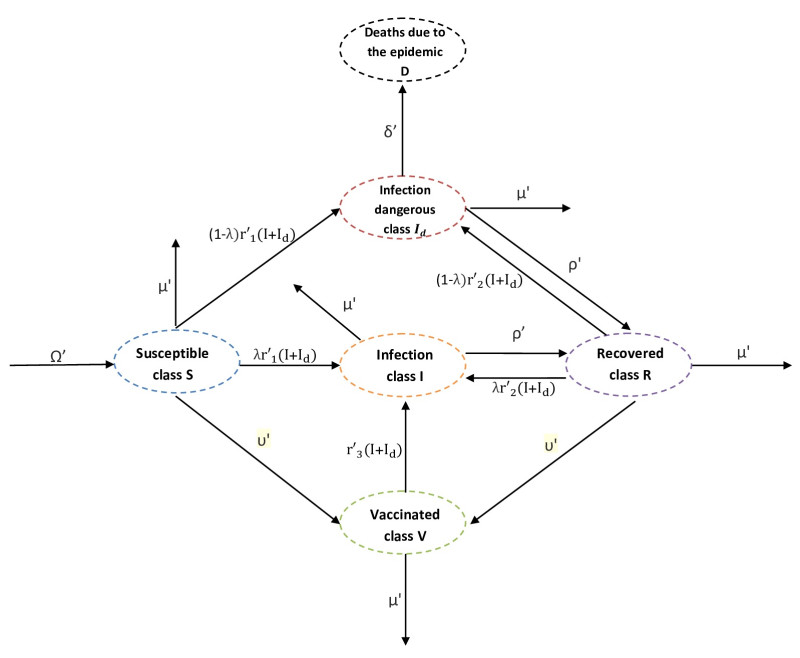
Our mathematical model is developed based on the experimental observations of TH-302 administration by Peeters et al. [11]. In this study, Rhabdomyosarcoma R1 and H460 NSCLC xenografts were treated with TH-302 and external beam radiation therapy, and the effects on tumour size and hypoxic fraction were examined. Furthermore, the TH-302 efficacy based on initial hypoxia level was assessed as well as efficacy of its combination with radiation as well as order of treatment administration. In order to study the effect of HAPs and their bystander effects on tumour cells— particularly hypoxic tumour cells—we consider the spatio-temporal evolution of tumour cell concentration, oxygen distribution, inactive HAP distribution and active metabolite distribution. If we denote n(x,t),k(x,t),c(x,t) and ca(x,t) as the concentrations of tumour cells, oxygen, HAP (inactive) and active metabolite at the location x and time t, we can write the model equations as given below.
Cancer cells
Oxygen
Hypoxia activated prodrugs (HAPs)
Activated HAP (AHAPs)
The description of the relevant parameters and corresponding values are given in Table 1. Here, we assume that cancer cells (n(x,t)) follow an oxygen-dependent, exponential growth law and are treated with HAPs alone or in combination with external beam radiation therapy. The oxygen-dependent growth is incorporated to account for the well-known phenomenon of cancer cells altering their growth pathway in the absence of oxygen [23]. Mathematically, this is incorporated by the use of a Hill function, which is commonly used to model the dependence of a rate on a specific quantity. Notice that as the oxygen concentration increases, the Hill function in the oxygen-dependent growth term approaches r (its maximum growth rate) and that as oxygen decreases, the growth rate approaches zero. The parameter δa, the rate of HAP induced cell death, is assumed to be cell-specific and reflects the death rate of the cancer cells to the activated HAPs (sensitivity to warhead). The radiation induced cell kill is incorporated into the model using a linear term with a radiosensitivity parameter αk and dose rate dt. While αk is a constant dependent on the tissue of interest, we employ an oxygen enhancement ratio to show the decreased effect of radiation in hypoxic areas of tumours. This is common in modelling the interaction of radiation with hypoxia and is shown above in Eq (2) where oxygen concentration is incorporated into the equation for αk [19]. When modelling external beam radiation therapy, the linear-quadratic (LQ) model is often used to describe tumour survival. Here, we make the simplification that the linear term is dominant and exclusion of the quadratic term does not impact the qualitative results (as done in [14] for example). Radiation schedule is incorporated with the model using the function, f(t), where f(t)=1, when the radiation is given.
Oxygen and drug distributions follow reaction diffusion equations and are assumed to be in quasi-steady state with respect to the computational time-step length used in numerical simulations. Specifically, their distributions are time-dependent over the course of the simulation, but achieve equilibrium within the span of a single computational time step of 0.001 days. Moreover, oxygen and HAP are assumed to be delivered from the blood vessels. Here, v(x,t) stands for the density of the blood vessels and v(x,t)=1 for the presence of the blood vessel and zero otherwise. Notice that a Hill function is again utilized for modelling the dependence of the oxygen consumption on the oxygen concentration. The function g(t), controls the delivery of HAP and when HAP is delivered, g(t)=1. The inactive HAPs (c(x,t)) supplied by the vessels are activated at the presence of hypoxia and nitroreductases to produce activated HAPs (ca(x,t)). Once again a Hill function is used to mathematically show the dependence of the HAP activation rate on oxygen concentration. The parameter qa accounts for the rate by which HAPs are activated by nitroreductases. Here, for simplicity, we consider a uniform decay for both HAP and AHAP as we are not incorporating the details of drug dynamics. This could be improved with further experimental details and information. The active metabolites diffuse farther to produce a bystander effect affecting both hypoxic and oxygenated tumour cells. The formulation of the model is then completed by prescribing no-flux boundary conditions and an initial condition on the tumour cell density [16].
2.1. Computational domain and parameters
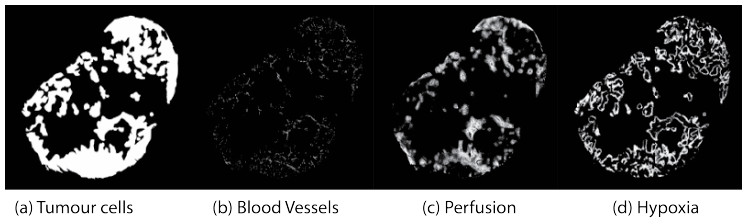
The simulations are performed using the images (Figure 1) obtained with the help of immunofluorescence staining techniques on a H460 xenograft to obtain vascularity, perfusion, and hypoxia using CD31 (endothelial marker), Hoechst 33342, and pimonidazole respectively, as described previously [11]. The stained tumour sections were then scanned and a threshold was applied to generate the corresponding binary masks.
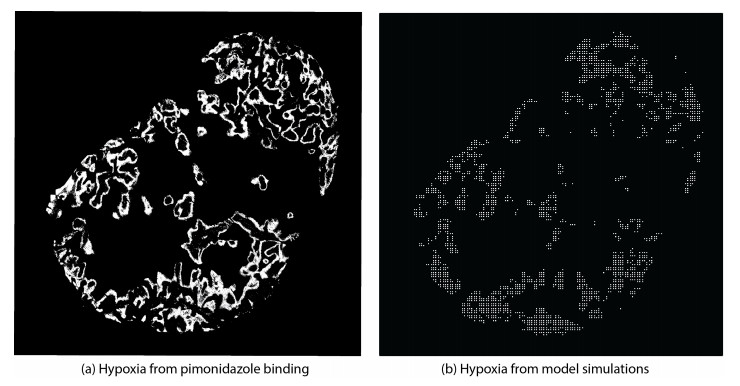
Following Powathil et al. [16], we assume that the perfused vascular network is the source of oxygen and drug supply, and thus gives the initial spatial distribution of concentrations. The perfused vasculature (at a fixed time) is obtained by combining the images of perfused areas (Hoechst 33342) and vascular structures (CD31) using the logical ``AND'' operation. The images of hypoxic regions (pimonidozole positive) are then used to compare the simulated hypoxic area and thus to calibrate/validate the mathematical model (Figure 1). The simulation is carried out over the image of the tumour cross-section (tumour mask). Note that for the in vitro case, we may assume a uniform distribution of oxygen and drug concentrations (when given). Further details can be found in [16].
The parameters for the model are listed in the Table 1. When available, we have used suitable parameters from previous studies [14,16]. The parameter values for oxygen dynamics have been calibrated to match the experimental results as shown in Figure 2. The experimental findings [24,25,26], suggest that HAPs have the ability to diffuse into hypoxic areas and exert their effect. Importantly, the diffusion parameters used in our model are estimates based on experimental observations and therefore are reflective of both the diffusive properties of the substances as well as their interactions with cells near the blood vessel. Production or supply rate of the drug is assumed to be (around 1.6 times) lower than that of oxygen and the decay rates of HAPs and AHAPs are assumed to be 0.023 (1/s). Moreover, we assume that HAPs are activated when the oxygen concentration is less than 5 mmHg [27]. We have further analyzed the effects of estimated parameter values using a sensitivity analysis, the results of which are reported in the relevant sections below. The initial spatial distribution of oxygen as determined from the vascular distribution is assumed to be constant with maximum value. Furthermore, we assume a uniform cell distribution as our initial condition, since we are considering a two dimensional cross section of in vivo xenografts.
To our best of knowledge, most of the parameter values related to the evolution of HAPs and AHAPs are generally unknown or not clear and hence, these parameters are assumed phenomenologically based on the experimental observations and information. The clinical and experimental investigation into the effects and efficacy of HAPs alone or in combination with other treatment modalities is still in its infancy and consequently, modelling studies can play a vital role in providing a better overall qualitative or quantitative understanding. However, since these experimental and clinical studies are ongoing, the limited information available may not always help to accurately estimate all the necessary parameters needed for any modelling approaches. Nevertheless, they may help to give some qualitative, phenomenological estimates of the parameters that eventually help to provide qualitative inferences. Moreover, these modelling approaches can further inform experimental studies on accurately estimating appropriate parameters to provide quantitative insights. There are existing modelling works in this direction but each are focused on different compounds and settings and similarly use assumed values when accurate estimates are unavailable [15]. However, these assumed values can be modified or refined when accurate values of these parameters are estimated. For the values that are assumed in the current study, a sensitivity analysis is given to illustrate the sensitivity of the model results on the parameter values. We believe that unavailability of such data should not hinder modelling studies that might inform and motivate related experimental research; although, one should consider these results with some reservations until accurate parameters are available.
The partial differential equations governing each of the concentrations are numerically solved by using Finite Difference Method (FDM) over the tumour cross-section and the model is implemented using Matlab [28]. In addition, an iterative scheme is used to solve the equations for Oxygen, HAPs and AHAPs. Here, we assume that the growth is restricted within the cell-map obtained from images and the aim is to understand the effects of various treatment within this tumour cross section. Hence, for computational implementation, the tissue cross sections are embedded on a square domain with boundary conditions prescribed on the square domain. The dynamics of various distributions are only active where the cellmap (Figure 1a) is non-zero. A uniform distribution is used for the initial condition of tumour cells across the mask and the other equations are solved in the steady state, so an initial condition is not necessary. The tumour cross-section is considered to be a 200 × 200 grid and is treated over 5 days with the simulation consisting of 5000 time steps each of size 0.001 days. The time step length remains constant throughout the treatment and particularly during the treatment times. The perfused vasculature network is read into the MATLAB script through the imread function.
3.
Results and discussions
The identification of hypoxia in many types of tumours and its role in treatment resistance, especially in radiation therapy, prompted the exploration of other treatment options—in particular, HAPs [9]. However, as discussed earlier, recent clinical studies have failed to demonstrate the success of various HAP-based treatments. One possible reason for this failure could be lack of detailed information about the hypoxia levels of each patient and how that affects the success of the therapy [9]. In this section, following Powathil et al. [16], we discuss a theoretical, non-invasive approach to predict the spatial and temporal distribution of hypoxia (oxygen concentration) and analyze the effects of HAPs—alone and in combination with radiation.
In earlier work, Powathil et al. [16] discussed a computational approach to simulate and explore the spectrum of spatial hypoxia distributions at a snapshot in time that will result from a given vascular distribution. We used two-dimensional binary images of tumour cross-sections together with a vascular distribution as a computational domain on which a model for the oxygen distribution and tumour cell density was solved. The resulting hypoxic area was quantified and compared against the hypoxic proportions determined from images [16]. Here, since we are only considering viable tumour mass (tumour mask), necrotic regions are not included in the analysis. The methodology and results were discussed in detail in Powathil et al. [16]. Here, we use a similar approach to estimate the hypoxia on a xenograft sample and use it to study the effects of HAPs under varying hypoxic conditions. Figure 2 compares the binary images of hypoxia estimated using the mathematical model simulations and experiments (immunohistochemical analysis) and re-illustrates the usefulness of mathematical and theoretical approaches to predict hypoxic distributions. While the experimental and in silico tumours are not identical in their images, the model predicts hypoxic area to within 3.06% accuracy. As mathematical models are idealized by their nature, small discrepancies are expected. Furthermore, the model is still able to predict phenomena shown in experiments like efficacy based on hypoxic level and differences in sequencing.
3.1. HAPs and hypoxic levels
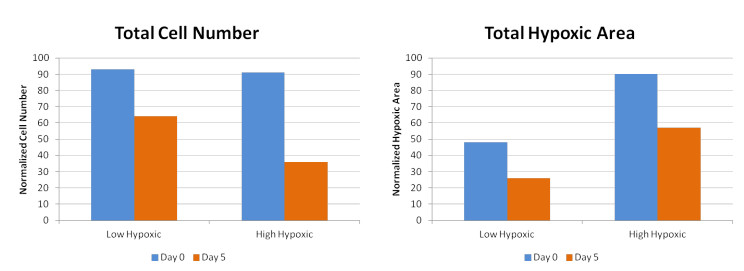
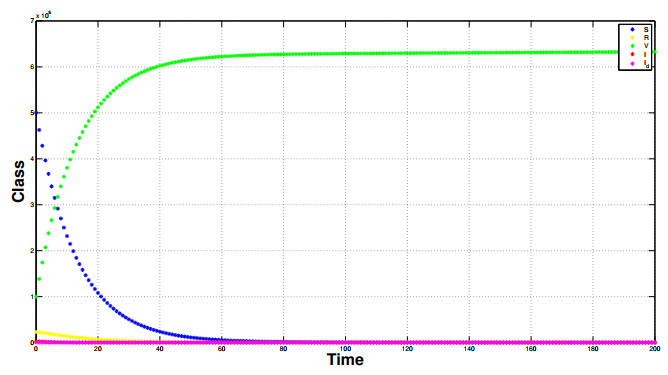
To study the role of spatial hypoxia distributions on HAP effectiveness, we used the above-described mathematical model to simulate the HAP response under two different hypoxic levels—low and high. In the low hypoxic case, we used all the perfused vessels obtained via image analysis of xenograft images [16] and in the high hypoxic case, we used a hypothetical scenario with only 50% of the perfused vessels. Figure 3 shows the comparison of total cell number and corresponding hypoxic area before and after 5 days of HAP treatment. In both cases, HAPs are given as daily doses over 5 days. We assume that in each dose, the drug is active in the system (delivered via vessels) for up to 3 hours. This can be changed or adapted appropriately depending on the given drug or mode of delivery. Since the primary aim of this study is to qualitatively study the effects of HAPs, we believe this schedule to be sufficient.
The simulation results shown in Figure 3 are qualitatively in agreement with experimental results [11]. The plots show that HAPs are more effective in reducing the number of cells under high hypoxic conditions: HAP treatment reduces cell number by 60.4% in the high hypoxic case and only by 31.1% in the low hypoxic case. Note that one possible reason for a relatively higher hypoxic area after treatment in simulation results might be due to the fact that experimental results account only for hypoxic area with viable cells (as binding is required), while simulation hypoxic area accounts for the hypoxic area within the entire domain (including regions with low cell density due to the cytotoxic effect of the released drug). This clearly indicates that information about hypoxic area can be a vital factor in determining the successfulness of treatments involving HAPs.
3.2. Combining HAPs with radiation
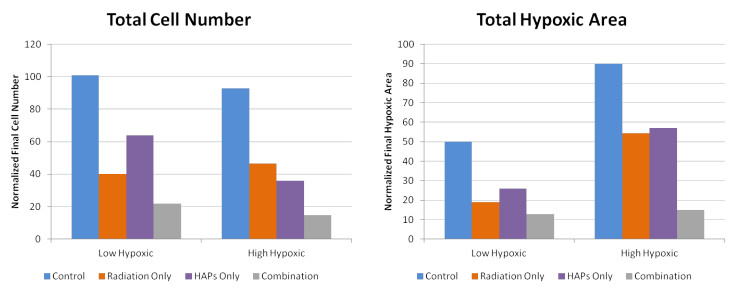
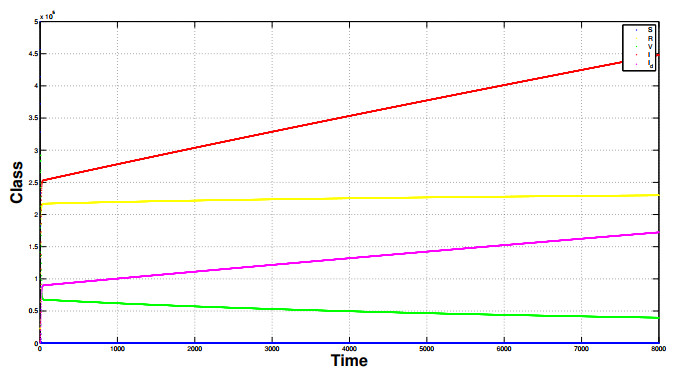
Radiation therapy is widely known to be very effective at targeting well-oxygenated tumour cells while hypoxic cells often show a degree of radiation resistance. Therefore, the biological rationale in combining radiation with HAPs is very promising as HAPs target hypoxic cells, leaving radio-sensitive tumour cells to be killed by radiation. Furthermore, recent preclinical experimental studies [8,29,11] suggest that the antitumour effectiveness of HAPs is enhanced by combining HAPs with radiotherapy. Here, we use the formulated mathematical model to study the effects of HAPs alone and in combination with radiation in low- and high-hypoxic tumours. Figure 4 shows the number of cells (Figure 4a) and hypoxic area (Figure 4b) before and after treatment under low- and high-hypoxic conditions. These results show that depending on the tumour type (hypoxia level), a combination treatment of radiation combined with HAPs can be very effective (compared to radiation alone).
3.3. Effects of treatment scheduling
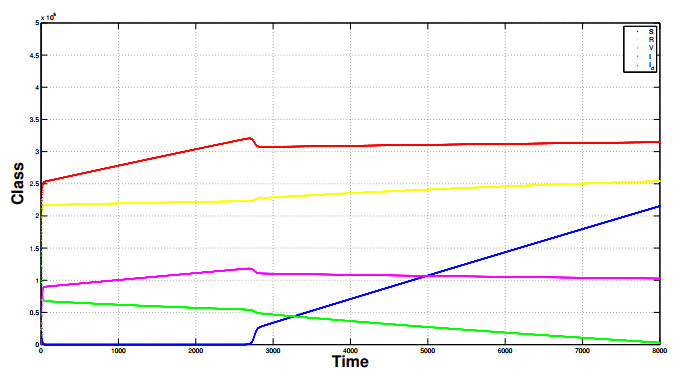
Although combination therapies with HAPs have shown promising results in controlling a growing tumour, the positive response of this combination treatment often depends on the treatment sequencing and scheduling parameters. For example, Liu et al. showed in xenograft models that TH-302 in combination with a conventional chemotherapeutic achieved the greatest tumour inhibition when TH-302 was administered 2–8 hours prior to its companion (either cisplatin, docetaxel, gemcitabine, or doxorubicin) [10]. This work hypothesized that administration of the conventional therapeutic prior to TH-302 caused a reoxygenation of the tumour microenvironment, therefore decreasing the activation rate of the HAP and leading to decreased efficacy. Conversely, HAP-first treatment was thought to lead to a reoxygenation allowing further penetration of the accompanying drug. Peeters et al. examined the combination of TH-302 with radiotherapy applying TH-302 in different schedules with a single 8 Gy dose of radiation (as done in our simulations) [11]. They showed that TH-302 combined with radiation therapy increased tumour control from the radiation monotherapy case. Furthermore, it was shown that pretreatment with TH-302 prior to radiation lead to optimal efficacy. They speculated that HAP treatment reduced the hypoxic fraction which enhanced the radiation effectiveness. Nytko et al. showed the same qualitative results experimentally by combining radiation and HAP therapy, determining that a neoadjuvant (HAP-first) was the optimal treatment schedule [29].
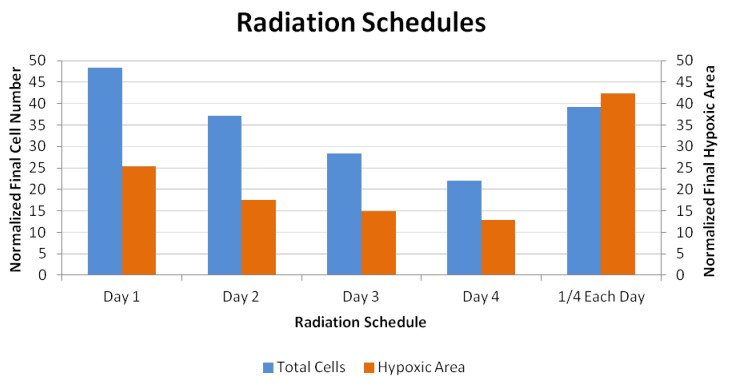
Determining the optimal plan for administration of HAPs and radiation in a combination therapy is clearly an important goal. To help answer this question, the model was used to see the resulting tumour cell population and hypoxic area at the end of treatment for 5 different radiation schedules. In each schedule, HAPs are given on days 1 through 5 and the results are calculated at the end of the 5th day. An 8 Gy fraction of radiation is also given over a 3 minute interval on one of the first 4 days. Additionally, the case of splitting the dose into 4 fractions with 2 Gy/day was also included.
The analysis shows that the best option is to apply radiation on the 4th day of treatment, both in considering tumour cell population and hypoxic area. Though we only carried out this analysis for the 5-day treatment plan, we expect that this result would generalize to the best option simply being to apply radiation as late as possible. This is because the radiation has its highest effectiveness when hypoxic area is lowest: So naturally, the way to have the lowest hypoxic area is to apply the highest amount of HAPs before radiation. Similarly, the further fractionated 2 Gy/day schedule lies at a medium effectiveness. However this may not be the case for rapidly growing tumours where the turnover rate of hypoxic cells is very high. The results of this analysis are shown in Figure 5.
4.
Parameter sensitivity analysis
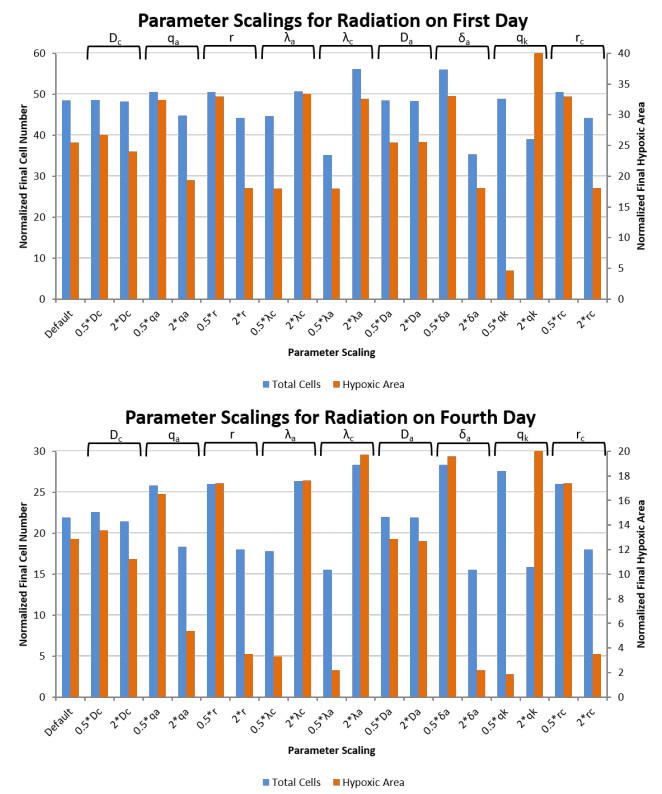
Here, we use a simple sensitivity analysis to study the influence of assumed/chosen parameters by comparing the results (cell number and hypoxia) obtained by halving and doubling the chosen values (default) of the parameters for two treatment scenarios.
The effectiveness of HAPs is also influenced by other relevant measurable parameters. For example, the diffusivity of the inactive HAPs, Dc, impacts the delivery the drug to the hypoxic zones. To see this, we simulated the mathematical model with the drug diffusivity scaled by factors of 0.5 and 2 (0.5Dc and 2Dc) and study the effect on resulting tumour cell population and hypoxic area. This was done in combination with radiation therapy for radiation given either on day 1 or day 4. The results show that the larger diffusivity results in a decrease in tumour cells and hypoxic area while the smaller diffusivity results in an increase in tumour cells and hypoxic area. However, the overall effect due to either change in diffusivity is low.
Another parameter which can be examined is the activation rate of the HAPs, qa. While this activation rate can't easily be pharmacologically altered, it is potentially alterable through the expression of nitroreductases in the tumour cells. With measurements of the levels of these enzymes, this activation rate could be theoretically estimated. Like for the diffusivity, we simulated the model for the activation rate scaled by factors of 0.5 and 2 for radiation given on either day 1 or day 4. The results show that the higher activation rate leads to a decrease in cell number and hypoxic area and a decrease in activation rate leads to the opposite. The overall effect of the change in activation rate is more significant than the effect of changing the diffusivity.
The effectiveness of the HAP also depends on the sensitivity of the activated HAPs in inducing cytotoxic effects to hypoxic and surrounding cells. For example, if it is an alkylating agent, the DNA repair status will be an important factor to consider while studying the effectiveness. DNA crosslinker such as the drug evofosfamide TH-302, pose strong replication blocks and cellular survival requires the concerted action of nucleotide excision, Fanconi anemia (FA) and homologous recombination (HR) driven DNA repair pathways [30,31]. The sensitivity to the drug is included into the model using the parameter δa and we have further explored its effects by varying this parameter. The results are reported in the Figure 5. The results show that increased sensitivity improves final outcome (higher cell-kill and lower hypoxic area), as expected.
A similar analysis was performed to study the sensitivity of each of the parameters related to the HAPs including: rc,λc,Da, and λa in addition to Dc and qa as mentioned above. This analysis consisted of simulating the model with each of the parameters sequentially scaled by a factor of either 0.5 or 2 for radiation given on either the first or the fourth day. The parameters are scaled one at a time to assess to which parameters the model is most dependent. Looking at Figure 5, we can see that qa,rc,λc, and λa are the parameters which have the largest impact on tumour cell number and hypoxic area. Though this method is not a rigorous sensitivity analysis, it nonetheless is a good indicator of the stability and robustness of our model since scales of parameters do not lead to drastic changes in the overall results. As precise measurements of the parameter values are not reliably known, especially since they can very patient-to-patient, we seek only to make qualitative predictions rather than quantitative ones. Accordingly, the goal of testing simple parameter scalings is to establish that the model is robust to changes of parameter values within a reasonable range. When precise measurements are able to be obtained, they can be used with the model to make more accurate predictions. The next step is thus to carefully design experimental studies to obtain relevant data such as HAP (drug specific) diffusivity and half-life to better understand and parameterize the mathematical model.
5.
Conclusion
We have developed here a spatio-temporal mathematical model to describe the effects of HAPs, alone and in combination with radiation, on a growing tumour. The model incorporates cell number, oxygen concentration, inactive HAPs, and activated metabolites. The system was solved on a domain obtained through imaging of perfused areas and vascular structures.
The model was solved for a low-hypoxia and high-hypoxia tumour to see which was more susceptible to treatment using HAPs. The model results showed a significant improvement in overall cell kill for tumours with high levels of hypoxia which was in agreement with experimental results [11]. This was extended to include a combination with radiation therapy which again predicted that the combination therapy is more effective for high-hypoxic tumours. Treatment sequencing was also altered to attempt to determine the optimal schedule of treatment methods. For our model, the best case scenario was to administer HAPs before radiation, which resulted in the highest cell kill and lowest hypoxic area. Additionally, scaling key model parameters can have an effect on the treatment efficacy. Simulating the results for different parameter scalings shows that increasing the diffusivity and activation rate of HAPs also improves the treatment efficacy, although the degree of change due to diffusivity scaling is relatively small.
Presently, the model is developed only using one cross-section of xenograft experimental image, showing its potential strength in studying the effects of HAPs in combination with radiation within a realistic microenvironmental setting. Further calibration and validation of the computational model using multiple images can help the model for further generalization. Also note that currently the model assumes a static vasculature over the treatment. Since the focus of this work is to study the effects of HAPs alone/in combination with radiation at a snapshot of the time with given spatial distribution of hypoxia resulted from a particular distribution of vasculature, the use of static vessels may be justified accordingly in a two dimensional settings. However, it would be ideal to simulate this in a three dimensional scenario, provided such spatial maps are available to implement the model. Furthermore, as the simulations take place over a maximum length of 5 days, the tumour vasculature is unlikely to change significantly over the course of treatment. For an in vivo tumour growing over a longer period of time, we would expect the vasculature to change throughout the treatment, thereby altering the transport of oxygen and drugs and effecting the treatment efficacy. This is another direction we hope to examine in the future. Another future direction is to incorporate a detailed pharmacodynamics of considered drug to improve the predictive ability of the model, moving a step closer to personalised therapeutic delivery. For example, for a drug such as PR-104, the intermediate molecules along its activation path may play a significant role as they too can have cytotoxic effects [13]. However, for a drug such as TH-302, as we considered here, bromo-isophosphoramide mustard (Br-IPM) is the lone dominant cytotoxic form (though the Cl-IPM metabolite also appears) [32]. Similarly, the simplified model that we used here to study radiation effects can be modified further to include multiple effects of radiation such as delayed cell death, indirect effects, cell-cycle sensitivity and so on, depending on the availability of the data and required complexity of the model. Spatial effects are also not examined to their full extent. Analysis of treatment efficacy as it relates to distance from vessels is an interesting question which we hope to examine in future works. As we use only one experimental image to generate the hypoxia distribution, the conclusions we can draw here are limited.
Although, current predictions from the model are qualitative in nature, we have shown that the model can be used to understand the combined effects of radiation and HAPs in general. Moreover, the results from the model are in good agreement with experimental observations and the inferences from the model results such as optimal combinations and sequencing, can be further analyzed and validated using appropriate experimental studies. Once the model is carefully calibrated with HAP specific experimental data, it can be used for quantitative predictions and treatment optimizations. Furthermore, this model can be adapted for clinical applications by using relevant hypoxic data obtained from biopsies and novel imaging techniques such as perfusion CT imaging to spatially reconstruct tumour hypoxia map for the model.
Acknowledgements
Financial supports by the ERC advanced grant (ERC-ADG-2015, n 694812 Hypoximmuno) and Kankeronderzoekfonds Limburg from the Health Foundation Limburg (AY, LJD, and PL), and the Natural Sciences and Engineering Research Council of Canada (NSERC) (MK) are gratefully acknowledged.
Conflicts of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: