An improved arithmetic optimization algorithm with forced switching mechanism for global optimization problems

1.   Introduction

The spreading of communicable diseases is affected by many factors including infectious agents, modes of contact, and latent periods. Since different diseases may have distinctive features of infection, it is necessary to model the evolutionary of various diseases by different mathematical models. Following the pioneer work of Kermack and McKendrick ^[1], the total population is often classified into the susceptible (S), the infective (I), and the recovered (R), and the corresponding models are called SIR models. The contact pattern between the susceptible and the infective is often described by the incidence function. Nonlinear incidence functions have been utilized in many epidemic systems including the following SIR model ^[2]

in which all the parameters are positive and $h, g:\mathbb R^+ \to \mathbb R^+$ describe the contact pattern, $\mu$ represents the constant death ratio and death rate and the constant recruitment rate. Here, the nonlinear incidence is partly due to the effect of media, government behavior. For some typical examples of $h, g$ and their biological backgrounds, we may refer to ^[2]. Clearly, some properties of this system can be obtained by only investigating $S, I.$

In epidemic models, time delay may reflect that a susceptible individual was attacked by the pathogen (by contacting an infective) at an earlier time but becomes infective after several days, which may be reflected by delayed effect of the infective. Since an ostensible susceptible may be infected one that may transmit the pathogen to other true susceptible, the delayed effect must be involved in some cases. When the delayed effect on latent periods is concerned in (1.1), Huang et al. ^[3] studied the following model

in which all the parameters are positive, $\tau$ reflects the latent period. By comparing ^[2,3], time delay may be harmless to the stability of the system but decrease the basic reproduction ratio, which indicates the nontrivial role of time delay. Moreover, the latent periods may be different, and distributed delays may be useful, see a model of hematopoiesis by Adimy et al. ^[4]. In particular, by assuming that each individual of the susceptible class has the same probability being infected, $h(u)$ is in proportion to $u$ in many models in the above works.

Over a period of time there has been a growing awareness of the importance that includes a spatial aspect in constructing realistic models of biological systems, with a consequent development of both approximate and mathematically rigorous methods of analysis ^[5]. It is important to characterize the speed of spatial expansion of diseases ^[6,7,8], and the expansion speed may be a constant [9,Chapter 13]. In literature, many reaction-diffusion systems have been established to reflect the process ^[5]. Due to the deficiency of monotone semiflows in many epidemic models, the long time behavior of the initial value problems of epidemic models can not be studied by the theory of monotone semiflows ^[10], we may refer to Ducrot ^[11,12].

When both the spatial factor and delayed effect are involved in mathematical epidemiology, one important factor is the effect of nonlocal delays ^[13,14]. Here the nonlocal delay may reflect the history movement ability of the infective, which includes the cases of discrete delays and distributed delays ^[15,16]. De Mottoni et al. ^[17] studied the following model with spatial nonlocality

in which all the parameters are positive, $\Omega$ is the spatial domain, $K$ is a nonnegative function. For more epidemic models with nonlocal delays, we refer to Ruan ^[16]. The purpose of this paper is to study diffusive epidemic models with nonlocal delays, nonlinear incidence rate and constant recruitment rate, during which the effect of time delay and spatial nonlocality will be also presented.

For simplicity, we firstly consider the initial value problem after scaling

with

where $x\in\mathbb R, t > 0, s\in (-\infty, 0].$ In model (1.2), $S(x, t)$, $I(x, t)$ denote the densities of susceptible and infective individuals at time $t$ and location $x$, respectively, $d > 0$ is a constant describing the spatial diffusive motility of the susceptible, $\sigma > 0$ represents the entering flux as well as the death rate of the individuals, $\mu$ is the death rates of infective, $\beta > 0$ reflects the infection rate, $\gamma > 0$ is the recovery rate of the infective individuals, and the positive constant $\alpha$ measures the saturation level, $\phi(x, s)\ge 0$ is a continuous bounded function. The nonlocal delayed term $\frac{\beta S(x, t)(J*I)(x, t)}{1+\alpha (J*I)(x, t)}$ describes the interaction between the infected individuals at an earlier time $t-s$ at location $y$ and susceptible individuals at location $x$ at time $t,$ which implies that only the susceptible individuals at location $x$ at the present time $t$ affect the change rate of the susceptible class although the contact leading to infection maybe occurred at location $y$ at an earlier time $t-s.$

Clearly, model (1.2) is a subsystem of the following SIR model

where $R$ denotes the removed individuals, $d_3 > 0, \mu_1 > 0$ are constants on spatial diffusion ratio and death rate of the removed, respectively. Clearly, after investigating (1.2), some properties of the class $R$ can be obtained (see. e.g., Li et al. [18,Section 5]) since

for any $t > 0, x\in\mathbb R,$ and we only study system (1.2) in this paper. These systems may model the evolutionary of the epidemic with nonlinear incidence rate and constant recruitment rate. For the dynamics in the corresponding functional differential equations with discrete or distribute delay, we may refer to Enatsu et al. ^[19], Huang et al. ^[3], in which the persistence and the extinction of $I$ were studied. In particular, by ^[3], we may find that the so-called basic reproduction ratio is $\frac{\beta}{\mu +\gamma}.$

Recently, traveling wave solutions of different versions for (1.2) have been studied ^[18,20,21], in which these solutions take the form

for some $c > 0$ and $S, I$ satisfy

By letting $\xi = x+ct$, such a solution indicates that at any fixed location $x\in\mathbb R$, there was no infective long time ago ($\xi\to -\infty$ iff $t\to-\infty$) while the infective and susceptible will coexist eventually ($\xi\to \infty$ iff $t\to \infty$). However, from the viewpoint of initial value problems, these traveling wave solutions formulate that the infective individuals live in a habitat of infinite size at any fixed time. This contradicts to the outbreak of many diseases, during which the initial habitat of the infective individuals is finite, see a similar process in biological invasion by ^[22,23,24]. Motivated by this, we will study the corresponding initial value problem of (1.2) by the following index ^[25].

Definition 1.1. Assume that $u(x, t)$ is a nonnegative function for $x\in \mathbb{R}, t > 0$. Then $c'$ is called the spreading speed of $u(x, t)$ if

a) $\lim_{t\rightarrow \infty} \sup_{|x| > (c'+\epsilon)t}u(x, t) = 0$ for any given $\epsilon > 0$;

b) $\liminf_{t\rightarrow \infty} \inf_{|x| < (c'-\epsilon)t}u(x, t) > 0$ for any given $\epsilon \in (0, c')$.

The spreading speeds of unknown functions governed by reaction-diffusion equations and other parabolic type systems have been widely studied since ^[25], and there are some important results for monotone semiflows ^{[10,26,27,28,29]} and nonmonotone scalar equations ^[30,31,32]. For noncooperative systems, Ducrot ^[11] estimated the asymptotic spreading in a predator-prey system of Holling-Tanner type, Ducrot ^[12] considered the spatial propagation of an epidemic model with recruitment rate and bilinear incidence rate, Lin et al. ^[33,34] studied the spreading speeds of two competitive invaders in competitive systems, Lin and Wang ^[35] and Pan ^[36] investigated the invasion speed of predators in a predator-prey system of Lotka-Volterra type. For coupled systems in ^{[11,12,33,34,35,36]}, the comparison principle plays the crucial role.

In this paper, to focus on our main idea, we first study (1.2) by estimating the limit behavior of $I(x, t)$ motivated by ^[35,36]. With the uniform boundedness of $S, I$, we try to estimate $S,$ by which we may obtain an auxiliary equation on $I(x, t)$. However, this equation involves the nonlocal delay ^{[14,15,16,37]} and does not generate monotone semiflows. Further by the smoothness of $I(x, t),$ we obtain an auxiliary equation with quasimonotonicity, of which the spreading speed has been established. Then we obtain the spreading speed of $I(x, t).$ Here, the spreading speed is coincident with the minimal wave speed of traveling wave solutions in some well studied cases. For example, when it just involves discrete delays, the spreading speed in this paper equals the minimal wave speed of traveling wave solutions in Li et al. ^[18].

Subsequently, we study the general model

where $x\in \mathbb R, t > 0, s\in (-\infty, 0], f:[0, +\infty) \to [0, +\infty)$ is Lipscitz continuous. We also obtain the spreading speed of $I(x, t)$ even if $f$ is not monotone, and the convergence of $(S, I)$ is established from the viewpoint of asymptotic spreading. Furthermore, to show the effect of time delay and spatial nonlocality and estimate the spreading speeds, we present some numerical examples.

The rest of this paper is organized as follows. In Section 2, we show some necessary preliminaries on reaction-diffusion systems with nonlocal delays. Section 3 is concerned with the spreading speed of $I(x, t)$ in (1.2). We then consider the spreading speed in the general model (1.3) in Section 4, and show the convergence result of $I(x, t)$. To further illustrate our analysis results, we present some numerical results in Section 5. Finally, we provide a discussion on the epidemic backgrounds and mathematical conclusions.

2.   Preliminaries

In this section, we introduce some concepts and review some relevant results. Firstly, when a partial order in $\mathbb R ^2$ is concerned, it is the standard partial order in $\mathbb R ^2.$ That is, if

then $u\le v$ iff $u_1\le v_1, u_2\le v_2.$ For the kernel function $J$ that is integrable, we make the following assumptions.

(J1) $J(y, s) = J(-y, s)\ge 0, \int_{0}^{\infty }\int_{\mathbb{R} }J(y, s)dyds = 1, y\in \mathbb{R}, s\geq 0;$

(J2) for each fixed $c > 0,$ there exists $\lambda_c \in (0, \infty]$ such that

For $f,$ we make the following assumptions.

(f) There exists $I' > 0$ such that $f(I) < (\mu + \gamma) I, I > I'. f:[0, \infty)\to \mathbb R^+$ is $C^1$. $f'(0) > \mu + \gamma,$ and there exist positive constants $L, \alpha$ such that

Besides by taking

as in (1.2), there are also many other functions satisfying (f), e.g., the following function

where $\gamma > 0.$ By taking different parameters, it may be nonmonotone, the corresponding kinetic model was proposed and analyzed by Liu et al. ^[38], Xiao and Ruan ^[39]. By the above assumptions, we define

for each fixed $c > 0$ with $\lambda \in [0, \lambda_c).$ From (J1)-(J2) and (f), $\Lambda (\lambda, c)$ satisfies the following property.

Lemma 2.1. There exists a constant $c^* > 0$ such that

(R1) $\Lambda (\lambda, c) = 0$ has no real roots if $c < c^*,$

(R2) if $c\ge c^*,$ then $\Lambda (\lambda, c) = 0$ has positive real roots.

Evidently, we see that time delay and spatial nonlocality may affect the threshold $c^*,$ a similar conclusion was reported by Li et al. ^[40] (we may refer to a recent paper by Li and Pan ^[41] and references cited therein for the traveling wave solutions of delayed models). To further quantificationally illustrate the role, we first consider the case of discrete delay such that

and

in which $\tau > 0.$ Let $c^*(\tau)$ be the threshold depending on $\tau,$ then we have

and

That is, the time delay may decrease the threshold, we also refer to Zou ^[42]. On the other hand, to quantificationally show the effect of spatial nonlocality, we consider a simple nonlocal case with

and so

Let $c^*(l)$ be the threshold depending on $l > 0,$ then

and

For this type of kernels, we say the nonlocality is stronger if $l > 0$ is larger, so the spatial nonlocality may increase the threshold, which will be further illustrated by numerical simulations.

Let

for any bounded and continuous function $v(x, t), x\in \mathbb R, t > 0.$ Then by the theory of abstract functional differential equations with application to delayed reaction-diffusion systems ^{[43,44,45,46]}, we have the following existence and uniqueness of mild solutions.

Lemma 2.2. (1.3) admits a mild solution $(S(x, t), I(x, t)), x\in\mathbb R, t > 0$ such that

and $(S(x, t), I(x, t))$ takes the form

for $x\in\mathbb R$ and any given $r\in [0, t).$ If $t > 1,$ then $S(x, t), I(x, t)$ are uniformly continuous in $x\in \mathbb R, t > 1.$ In particular, if $\phi (x, 0)$ admits nonempty compact support in (1.2), then

Moreover, if $\tau > 0$ such that

then $t > \tau$ implies that $(S, I)$ is the classical solution of (1.3) in the sense of partial derivatives.

The local existence of mild solutions is ensured by the theory of analytic semigroups as well as abstract functional differential equations ^[43,47], and the global existence is guaranteed due to the existence of positive invariant regions because of the existence of $I'$.

In addition, the proof depends on the comparison principle and asymptotic spreading of the following equation with nonlocal delays

where $\epsilon \ge 0,$ all the other parameters are the same as those in (f) and $\varphi(x, s)$ is a positive continuous function satisfying

for some $L > 0.$ By results in Martin and Smith ^[47], Ruan and Wu ^[43], (2.1) satisfies the following comparison principle.

Lemma 2.3. Let $T\le \infty$ hold and $f$ be nondecreasing. Assume that a continuous function $\overline{u}(x, t): \mathbb R \times (-\infty, T)\to \mathbb R^+$ satisfies

and

for $x\in \mathbb R$ and any given $r\in [0, t).$ Then

Furthermore, results by Liang and Zhao ^[10], Yi et al. ^[48] imply the following spreading property even if $f(u)$ is not monotone for all $u > 0$.

Lemma 2.4. Let $u(x, t)$ be the unique mild solution of (2.1) with $\varphi (x, 0) > 0$ for some $x\in\mathbb R$. Then for any given $c > c^*, u(x, t)$ satisfies $\lim_{t\to\infty, |x| > ct} u(x, t) = 0,$ and for any given $c\in (0, c^*), u(x, t)$ satisfies $\liminf_{t\to\infty}\inf_{ |x| < ct} u(x, t) > 0.$

3.   Spreading speed of (1.2)

In this section, we establish the main results of (1.2). In particular, we take $f'(0) = \beta$ in this section, $\phi(x, 0)$ admits nonempty compact support and

with some $L > 0.$ The following is the main result of this section.

Theorem 3.1. Assume that $I(x, t)$ is defined by (1.2). Then for any given $c > c^*, I(x, t)$ satisfies

and for any given $c\in (0, c^*), I(x, t)$ satisfies

Proof. By Lemma 2.2, we have

which implies that

for all $x\in \mathbb{R}, r\in \lbrack 0, t).$ Further by Lemmas 2.3 and 2.4, we obtain (3.2).

We now prove (3.3) for any fixed $c\in (0, c^*)$. Since it involves long time behavior, we assume that $t > 1$ is large and $(S(x, t), I(x, t))$ is uniformly continuous in $x\in\mathbb R, t > 1$. Define $\mathbb S (x, t) = 1-S(x, t),$ then Lemma 2.2 indicates that

Therefore, if $\mathbb S$ is smooth enough, then it satisfies

and similarly, we can verify that

where

for any bounded and continuous function $v(x, r), x\in \mathbb{R}, r > 0.$

Returning to the equation of $I(x, t),$ we have

with

In what follows, we prove the following claim.

(C) For any $\epsilon \in (0, \beta),$ there exists $M(\epsilon) > 0$ such that

if $t > 1$ is large.

From Lemmas 2.3 and 2.4, (C) implies that

by selecting and fixing $\epsilon > 0$ small enough, which implies what we wanted.

Subsequently, we verify (3.5) for any fixed $\epsilon > 0$. If

then (3.5) is true. Otherwise, let $x\in\mathbb R$ and $t > 1$ be large enough such that

Firstly, we fix $T > 1$ such that

For such a fixed $T > 1,$ we further select $N > 0$ such that

which is admissible since

Further choose sufficiently small $\delta > 0$ such that

So we obtain

for any $t > T+ \delta+1,$ and (3.6) implies

The left side of (3.7) is

for any $\tau > 0, K > 0.$ By the convergence in (J1) and (J2), if $\tau > 0, K > 0$ (independent on $x, t$) are large enough, then

and we now fix constants $\tau, K.$

Note that $\frac{e^{-\sigma (t-r)}}{\sqrt{4\pi d(t-r)}}, e^{\frac{-y^{2}}{ 4d(t-r)}}$ are uniformly continuous and uniformly bounded for $r\in \lbrack t-T, t-\delta], y\in \lbrack -N, N],$ then (3.8) implies that we can choose constants

such that

here $\lambda '$ depends on $\epsilon$ and is independent of $x\in \mathbb{R}, t\geq T+1 +\tau.$ Again by the uniform continuity of $I(x, t)$ and convergence of $J,$ we fix $\lambda, \iota$ depending on $\lambda '$ such that

for some

and the uniform continuity further implies that

From the equation of $I(x, t),$ we see that

for any $0\leq r < t.$ By the property of semigroup, we also have

for any $s\in \lbrack 0, t).$ So for any given $s_0\geq 0,$ if

then we have

By what we have done, $x, t$ satisfying (3.6) lead to

where $\underline{I}$ is uniform for any $x\in \mathbb{R}, t\geq T+\tau +1$ such that (3.6) holds. Again by the uniform boundedness of $I(x, t)$ and

we obtain the existence of $M,$ which is also independent on $x, t$ once (3.7) is true and $t\geq T+\tau + 1.$ The proof is complete.

Remark 3.2. From (3.4) and Lemma 2.4, we see that

implies

That is, the sign of $f'(0) -(\mu + \gamma)$ determines the persistence and extinction of $I,$ which is similar to the case in the corresponding functional differential systems. Therefore, the basic reproduction ratio of the corresponding functional differential systems may determine the failure or propagation of the disease, and also may affect the spreading speed if the ratio is larger than 1.

4.   Asymptotic spreading of (1.3)

In this section, we first study the spreading speed and then estimate the convergence of $(S, I)$ in (1.3), in which $f$ satisfies (f). The first result on spreading speed is formulated as follows.

Theorem 4.1. $c^*$ is the spreading speed of $I(x, t)$ if $I(x, s)$ satisfies (3.1).

Proof. Due to the proof of Theorem 3.1, we just give a sketch. Firstly, we define

then there exists $\underline{v}_1 > 0$ such that

and $\overline{f}(u)$ is nondecreasing such that

Therefore, $I(x, t)$ satisfies

for any $r\in [0, t).$ So for any given $c > c^*, I(x, t)$ satisfies

Further define

then there exists $\underline{v}_2 > 0$ such that

and

So $I(x, t)$ satisfies

for any $r\in [0, t).$ Similar to that in Section 3, we obtain

for any given $c\in (0, c^*).$ The proof is complete.

Theorems 3.1 and 4.1 imply that the infective individuals successfully invade the habitat of the susceptible. We now estimate the limit behavior of $S(x, t), I(x, t).$ Firstly, we consider (1.3) when $S(x, 0), I(x, s)$ satisfies

and make the following assumption.

(C) Assume that (4.1) holds. Then

where $(S^*, I^*)$ is the unique positive spatially homogeneous steady state of (1.3).

Remark 4.2. In some cases, (C) is true. For example, if $f$ is monotone such that $f'(0) > \mu +\gamma$ and (1.3) with (4.1) is persistent, further define

then the persistence implies that

By dominated convergence theorem, we have

If these inequalities imply $\overline{S} = \underline{S}, \overline{I} = \underline{I}$, then (C) is true by applying the dominated convergence theorem in the corresponding integral equations ^[18].

Now, we formulate the limit behavior of $S(x, t), I(x, t)$ defined by (1.3) if $I(x, 0)$ satisfies (3.1).

Theorem 4.3. Assume that there exist $\tau \ge 0, K > 0$ such that

and if $\tau > 0,$ then

for any $\tau ' \in (0, \tau).$ If (C) holds, then

which holds for any given $c\in (0, c^*).$

Proof. We prove that for any given $c\in (0, c^*), \epsilon > 0,$ there exists $T > 0$ such that

by the idea in ^[49]. Firstly, by Theorem 4.1, there exist $\delta > 0, T_1 > 0$ such that

Then (4.2) is true if we can prove that for any $T_2 > T_1$ large enough, there exists $T_3 > 0$ independent on $T_2$ such that

since

when $t(>T_2)$ is large enough.

Let $\mathbb S, \mathbb I$ be the solution of (1.3) with initial value satisfying

Then (C) implies that there exists $T_3 > 0$ such that

Let

then the boundedness indicates that there exists $L > 0$ satisfying

for any $r\in \lbrack 0, t).$ Then $s(x, t), i(x, t)$ satisfy

where $(X(x, t), Y(x, t))$ is defined by

with

Let $N > 0$ be a fixed constant (clarified later) such that

and

Let $C > 0$ be large and $\lambda > 0$ be small such that

of which the admissibility is clear by the existence of $\tau, K.$ Define a continuous function

for $t\ge -\tau, x\in\mathbb R,$ which implies that

Then we have

for any $0\leq r < t < \infty, x\in \mathbb R,$ and so

Then we fix $N = N(T_3) > 0$ such that

and for any $T_2 > 0$ such that

we have (4.3), so for (4.2). The proof is complete.

5.   Numerical simulations

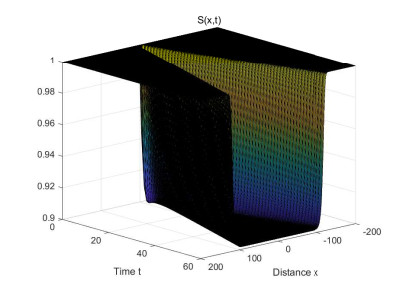
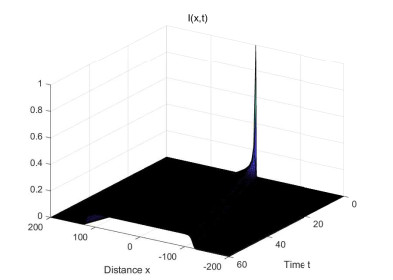
In this section, we shall illustrate the analytic conclusion by some numerical examples. Due to Theorem 3.1, we simulate the dynamics in a large spatial interval $[-N, N]$ and take the following boundary conditions

Moreover, $I(x, 0)$ is defined by

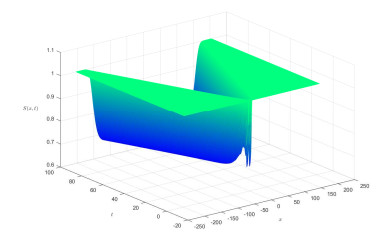
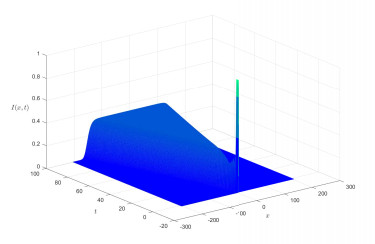
Firstly, we consider (1.2) without nonlocal delay and taking

With these parameters, we see that

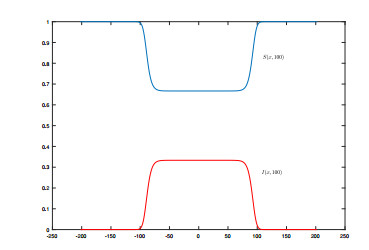
and $c^* = 2.$ We now show the numerical results as follows.

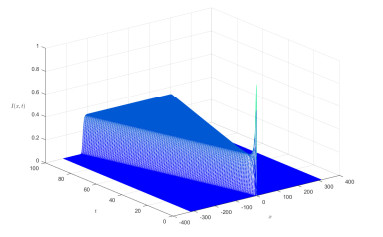
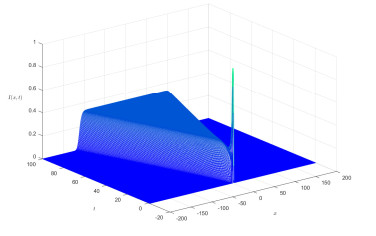
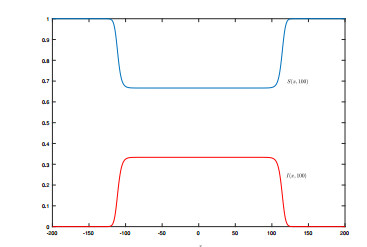
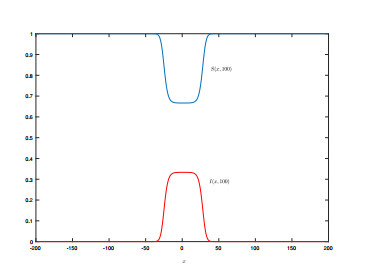
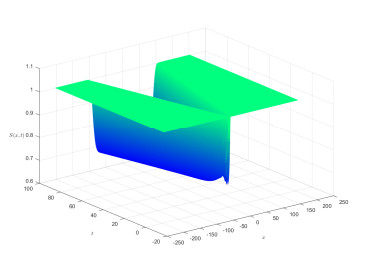
From Figures 1 and 2, we see that $I$ almost invades and $S$ almost decreases at a constant speed. To further show the invasion speed of $I$, we present the following Figure 3 on the distribution at $t = 100,$ by which we see that the invasion speed is close to $c^* = 2.$

We now consider the effect of time delay in the following model

such that

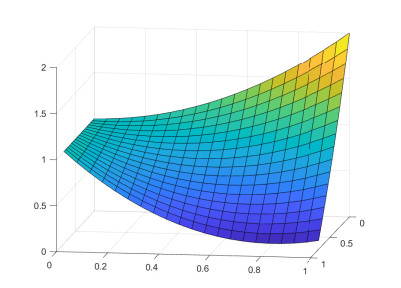
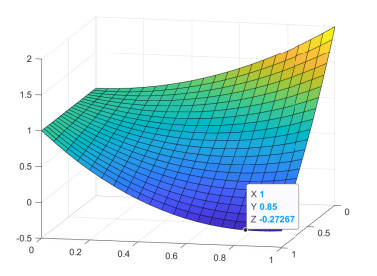
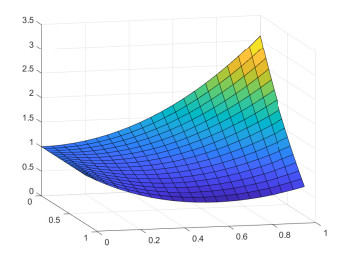
When $\tau = 1,$ we show the graphs of $\Lambda (\lambda, c)$ by the following Figures 4 and 5, from which we see that $c^*$ is close to 1.

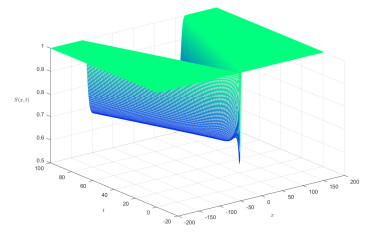
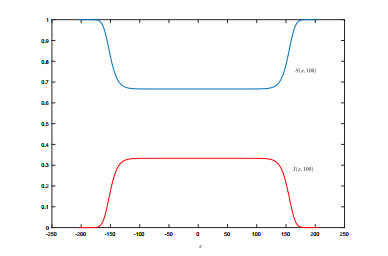
The evolution of $S, I$ with $\tau = 1$ is presented by Figures 6 and 7.

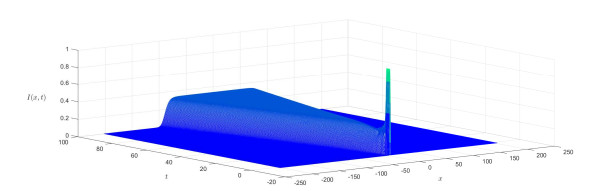
To estimate the invasion speed with different $\tau$, we give the distribution of $t = 100$ by Figures 8 and 9, by which we see the role of time delay.

To show the effect of nonlocality, we consider

and

We first show the graph of $\Lambda (\lambda, c)$ as follows when $\tau = 1, l = 1$ by Figures 10 and 11.

Comparing Figures 4 and 5 with Figures 10-11, we see that the nonlocality increases the invasion speed. We $\tau = l = 2,$ we see that $c^*$ is close to $1$ from the following Figure 12.

Although $\tau = 2 > 1, c^*$ is close to $1$ due to the role of spatial nonlocality. The evolution of $S, I$ with $\tau = l = 2$ is presented as follows.

To further show the effect of spatial nonlocality, we also simulate $S, I$ by $l = 4, \tau = 2$ by the following Figures 15 and 16.

Clearly, although $\tau = 2 > 1$ in Figures 6 and 7, the spreading speed is close to that in Figures 6 and 7, which indicates the role of spatial nonlocality.

To show the role of spatial nonlocality, we fix $\tau = 2$ and take $l = 2, l = 4$ and compare the distribution. From the following Figures 17 and 18, we see that the stronger nonlocality implies larger spreading threshold.

Finally, different from that in the monotone model (5.1), we consider the following system without comparison principle

Clearly, the spreading speed of (5.4) is the same as that in (5.1), and the following figures imply the spreading speed of $I$ is close to 2.

6.   Discussion

The spatial spreading of epidemic models attracts much attention since it greatly affects the human behavior in modern days. In population dynamics, there are many works on the study of spatial dynamics of epidemic models. Since the interesting works of ^[7,8], the threshold of spatial spreading of epidemic models has been widely studied. Thus the analysis of parameters dependence of propagation threshold may show the factors on disease spreading and control. In this paper, we have shown the effect of time delay and spatial nonlocality by theoretical analysis and numerical simulations. But it is difficult to change the latent periods in many cases. Due to our analysis, the spatial movement of the infective in history may increase the spreading speed of the disease, and it is reasonable to restrain the spatial movement of potential infective individuals to control some diseases. The recipe has been utilized in controlling many disease including SARS.

As we have mentioned in Section 1, the traveling wave solutions can not well illustrate the outbreak of some diseases, of which the initial prevalent district is small. To model the feature, asymptotic spreading is a suitable index. Comparing with the traveling wave solutions, there are a few results on the asymptotic spreading of nonmonotone epidemic models. In this paper, we obtained the spreading speed in a class of epidemic models. In fact, the methodology in this work can be extended to more general systems. For example,

in which $f_1\neq f_2$ is admissible and kernel functions $J_1, J_2$ may be different, $f$ may be a function including $f(u) = ru(1-u).$ Under proper assumptions, we could estimate the spreading speed of $I.$

The spreading speed in this paper equals the minimal wave speed of traveling wave solutions in some known results. For some models similar to (2.1), it has been proven that the traveling wave solutions with minimal wave speed is stable in the sense of weighted functional spaces, see ^[51,52] and references cited therein. Therefore, it is possible to understand the dynamics of the corresponding initial value problems by traveling wave solutions. In this paper, we show a rough speed on the branch $I(x, t).$ Very likely, the shape of spreading of $I$ governed by (1.2) can be approximated by the shape of traveling wave solutions with minimal wave speed in proper weighted functional spaces.

Acknowledgments

We are grateful to three referees and Professor Shigui Ruan for their valuable comments. Lin was supported by NSF of China (11731005) and Fundamental Research Funds for the Central Universities (lzujbky-2018-113), Yan was supported by NSF of China (61763024) and Foundation of a Hundred Youth Talents Training Program of Lanzhou Jiaotong University (152022).

Conflict of interest

The authors declare no conflict of interest in this paper.