1.
Introduction
The recent spreading of the COVID-19 epidemic led the central governments to introduce restrictions such as social distancing and lockdown policies. These non-pharmaceutical containment measures were adopted with the aim of reducing the epidemic peak, in order to guarantee public health and the efficiency of the national health system in periods of strong increase in the number of infected. The effects of the restrictions were recently tested by resorting to mathematical models of compartmental epidemiology [1,2], namely models in which the population is divided into compartments in order to simulate the epidemic evolution. In the Italian case, the actual evolution of the number of registered infected people immediately appeared subject to unavoidable incompleteness of the data during the entire emergency. It has therefore proved necessary to develop forecasting techniques to understand the impact of uncertain quantities during a health emergency. Furthermore, the necessary easing of lockdown measures has raised new questions about how to preserve production capacity while guaranteeing public health.
Such non-pharmaceutical measures, however, necessarily entail significant social and economic costs, which can only be incurred over limited time horizons. Therefore, to optimize containment strategies which save at possible these costs, it results necessary to adopt a new approaches to mathematical modeling combining both clinical information of the disease and a realistic social structure of the population.
The study of mathematical models to understand the spread of an epidemic represents a consolidated scientific field of applied mathematics. A fundamental step is furnished by the pioneering work of Kermark and McKendrick on compartmental epidemiology [3], which has given rise to a widely used model in which the initial population is divided into susceptible (S), who can contract the disease, infected (I), who have already contracted it and can transmit it, and recovered (R), who are immune or cured of the disease. This model is often mentioned as the SIR model, using the acronym of the categories just introduced.
The hypothesis made by Kermack and McKendrick is that of homogeneous mixing: it is assumed that every individual has the same probability of contacting any other individual in the population. It is understandable that this hypothesis is unrealistic since the intensity and nature of contact with people from our family, our workplace, school class, or a group of friends are very different, and on the other hand we rarely come into contact with those who live in different social realities.
For these reasons, starting from the original SIR model, more articulated models have been examined, capable of representing the population more realistically, dividing it in more detail. Several models are currently able to consider characteristics related to the mobility or age of the subjects, together with further sociological factors that determine the social interactions that can favor the transmission of the infection [1,2,4,5,6].
Nevertheless, the accuracy of a predictive model, at least in the first phase of the spread of a pandemic, is very difficult to assess. A problem that cannot be ignored is the uncertainty present in the official data provided by different countries in relation to the number of infected people. The heterogeneity of the procedures used to carry out the tests of positivity to the disease, the delays in recording and communicating the results and the high percentage of asymptomatic patients make the construction of predictive scenarios affected by high uncertainty. In general, the actual number of infected and recovered people is typically underestimated, causing delays in the implementation of public health policies in the face of the spread of epidemic fronts.
A few months after the outbreak of the COVID-19 epidemic, and in the face of containment policies operated by governments, we now have a lot of data available [7,8], which allow us to understand how much and in how the measures of social distancing have succeeded in the containment. Starting from these data, an essential aspect for the development of a predictive mathematical model is to build it in such a way as to accurately take into account the influence of social contacts in the contagion mechanism, and which, tested on the various measures of containment operated by different countries, can provide a correct answer in different situations.
Contacts between individuals occur according to interaction matrices that depend on the age of the individuals in the social activity considered (for example, school, work, family). Extensive studies have been carried out on this aspect. Among these, the recent works [9,10] provided an updated and complete picture of the statistical distribution of the daily social contacts of the population by age, sex, profession and more in various countries. The social contact matrices are very similar for European and non-European countries. These matrices show a peak of contacts in correspondence to people of school age, and of working age. Furthermore, two contact strips are highlighted between people of different ages, corresponding to the interactions between family members.
Taking into account the homogeneity of the social contact matrices with respect to different countries [10], a statistical model in which the populations of susceptible (S), infected (I) and recovered (R) are characterized by the number of daily social contacts has been proposed [11]. The resulting SIR-type model (in brief S-SIR or Social SIR) is in this case characterized by an inhomogeneous mixing. Unlike the classical model, the probability of contagion is considered proportional to the average of the contacts of the individuals in the population, and the increase of the infected is directly proportional to the product between the average of the daily contacts of the populations of infected and susceptible. The probability of contact is now characterized by a function that takes into account memory effects linked to the percentage of infected over a limited time span.
The model is further based on the hypothesis that the time scale that controls social contacts is much faster than the time scale on which the pandemic develops, a very reasonable hypothesis on which, among other things, the government provisions aimed at changing social contacts via lockdown policies. The characteristic parameters of the model are obtained starting from the statistical distribution of contacts observed in [9].
In [11], the output of the new model has been tested resorting on public data made available on the web, which allowed to evaluate accurately the key function characterizing the evolution of the epidemic in terms of the amount of social contacts of infectious people. These experiments showed a good agreement in the evolution of compartments predicted by the model with the data relative to the containment of the epidemic consequent to the lockdown policies in various countries.
These first results encouraged further study. This has been made possible by a joint effort of two groups, one from the University of Pavia, the other from the the Health Protection Agency (ATS) of the province area of Pavia, who analyzed the data relative to the COVID-19 infection starting from the early appearance, in February 2020, to extract from them the correct values of the parameters to be inserted into the S-SIR model developed in [11]. These data are relative to a population of about half a million of people in Northern Italy, a population which is sufficiently large to give stable statistics about diffusion and recovery rates in terms of age and sex.
By means of this joint work, it has been possible to improve the original model developed in [11], and to use the new version to follow at best the numbers of the compartments in the pandemic. A better adherence of the model to real situations, and a prediction in the short term of the availability of places for people to be hospitalized, has been obtained by resorting to the available detailed data. This allowed a statistical but coherent knowledge both of the percentage of people to be hospitalized in relation to the population of infectious, and of the recovery time of hospitalized people.
2.
The Social SIR model
One of the main goal of the mathematical models of infectious diseases is the possibility to evaluate control and prevention strategies by comparing their cost with effectiveness, and to support public health decisions [12,13]. With the sudden spreading of COVID-19 epidemic, and the consequent containment measures adopted to limit its diffusion, special attention was paid by the scientific community to previous researches devoted to estimate the distribution of contacts between individuals (cf. [9,14,15,16] and the references therein).
Starting from the analysis of [9], a mathematical framework to connect the distribution of social contacts with the spreading of a disease in a multi agent system was recently developed in [11]. The new model has been obtained by integrating the epidemiological dynamics given by the classical SIR compartmental model [5,17,18] with an approach based on kinetic equations, which furnish a detailed mechanism for the formation of social contacts at a rapid scale.
Since this model will be the starting point of the forthcoming analysis, let us briefly recall it with some details. Given a population of individuals, we denote by fS(x,t), fI(x,t) and fR(x,t) the distributions at time t>0 of the number x≥0 of social contacts of susceptible (S), infected (I), and recovered (R) individuals, respectively. The distribution of contacts of the whole population is then recovered as the sum of the three distributions
Assuming for simplicity that the population in the system remains constant, the total distribution of social contacts is assumed to be a probability density for all times t≥0
The knowledge of the functions fJ(x,t), J∈{S,I,R} allows to compute all relevant observable quantities. The integrals
denote the fractions at time t≥0 of the three sub-populations. Analogously we can compute moments, defined, for any given constant α>0 by
The mean values, corresponding to α=1, are denoted by mJ(t), J∈{S,I,R}.
The evolution of the densities is built in [11] by assuming that the various classes in the model could act differently in the social process constituting the contact dynamics. The kinetic model then follows combining the epidemic process with the contact dynamics, as modeled in [19]. This gives the system
where τ≫1 is a relaxation time, γ>0 is the recovery rate while the transmission of the infection is governed by the function K(fS,fI), the local incidence rate, expressed by
According to the literature on the subject [5], in Eq (2.3) the contact function κ(x,y) is a nonnegative function growing with respect to the number of contacts y of the population of infected, and such that κ(x,0)=0, which expresses the fact that the epidemic can not spreading in absence of infected people. Thus, the evolution of the epidemic depends heavily on the shape of the function κ(⋅,⋅) used to quantify the rate of possible contagion in terms of the number of social contacts between the classes of susceptible and infected.
Note that the evolution of the mass fractions J(t), J∈{S,I,R} then obeys to the classical SIR model by choosing κ(x,y)≡β>0 [5], thus considering the spreading of the disease independent of the intensity of social contacts. In [11] the contact function has been considered of the form κ(x,y)=βxy, leading to an incidence rate of the form
which implies an incidence of the contagion proportional to the product of the mean values of the populations of infectious and susceptible.
In system (2.2) the operators QJ, J∈{S,I,R} describe the formation of the social contacts of the populations, and are constructed to rapidly push the densities fJ(x,t), J∈{S,I,R} towards the equilibrium densities of daily contacts, which are given by suitable Gamma density functions. This choice is consistent with the results of empirical studies based on a precise analysis of a heterogeneous sample of French population, which established that Gamma densities are the most suitable to describe the daily number of contacts in the pre-pandemic scenario [9]. Further, a theoretical basis to the formation of this equilibrium profile has been recently done in the recent paper [11]. A simple choice for the relaxation operators is given by the linear BGK-type model [20]
where the Gamma-like equilibrium density is given by
where ν>0 is a parameter measuring the heterogeneity of the population, and
We remark that the equilibrium density is built to have the same mass and mean value of the function fJ(x,t), J∈{S,J,R}. Another choice is given by relaxation operators in the form of Fokker-Planck-type operators. We point the interested reader to [11] for a detailed discussion.
Integrating the equations of the system (2.2) with respect to the contact variable x leads to the system for the evolution of the proportions J(t) defined in Eq (2.1), J∈{S,I,R}
Unlike the classical SIR model, system (2.5) is not closed, since the evolution of the mass fractions J(t), J∈{S,I,R} depends on the mean values mJ(t).
Hence, fixing the mass of the large time contact distribution of infectious individuals equal to I(t), its momentum is given by
Analogously, if the mass of the large time contact distribution of susceptible individuals is S(t), its momentum is given by
In Eq (2.6) the constant ˉxI denotes the mean number of social contacts of infectious, while the function H captures the actual intensity of social contacts, in dependence of the amount, at time t≥0, of infected people. Proceeding as in classical dynamics of fluids, we obtain the closure
In system (2.7) we defined ˉβ=βˉxIˉxS. This identifies the classical transmission parameter of the SIR model, where however now the difference is that this quantities are not postulated but instead derived starting from microscopic considerations.
The key point in [11] was to quantify in a proper way the function H, describing the action of the variation of the intensity of social contacts on the evolution of the epidemic. For a given constant N≫1, the function H was assumed to be the decreasing function
which describes a possible way in which, in presence of the spread of the disease, the susceptible and the infected population tend to reduce the mean number of daily social contacts ˉxJ, J∈{S,I}. This choice produces a SIR model with global incidence rate
that fulfils all the properties required by the non-linear incidence rates considered in [3].
In addition to the form in Eq (2.8), the following function was considered in [11]
This function satisfies the same properties of Eq (2.8) in terms of the incidence rate requests detailed in [3] and takes into account memory effects on the population's behavior. In fact, it is reasonable to assume that both the restrictions operated by governments and the individual behavior are based not only in terms of the daily contacts to answer to the actual pandemic situation as expressed by Eq (2.8), but considering the evolution of the epidemic over a certain period of time.
The spreading of the COVID-19 pandemic in presence of lockdown measures has been tested in [11] through system (2.7), where both the form of the function H and the values of the parameters ˉβ and γ have been computed by resorting to public available data. As we shall see, the possibility to have at disposal more detailed data, will lead to an improvement of the Social SIR, and to and its better adherence to epidemic reality. Analogous results have been obtained through an experimental approach in [21] in the region of Wuhan and Shanghai.
3.
Dataset description
The Social SIR model has been fitted and tested on the accurate dataset collected by the ATS, representative of a local but extensive territory such as the province of Pavia. The dataset collects all the confirmed COVID-19 cases from February 20, 2020, to November 15, 2020, covering a wide period characterized by different behaviors in the spreading of the disease. For each confirmed case, all the relevant dates related to the personal evolution of the disease are reported: date of the first positive swab test, recovery date, death date, admission and discharge date in case of hospitalization. Age and sex of each COVID-19 patient recorded in the dataset are also available. This information proved essential to make the best estimate of the parameters of the Social SIR model leading to an accurate picture of the spread of COVID-19 infection in the province of Pavia.
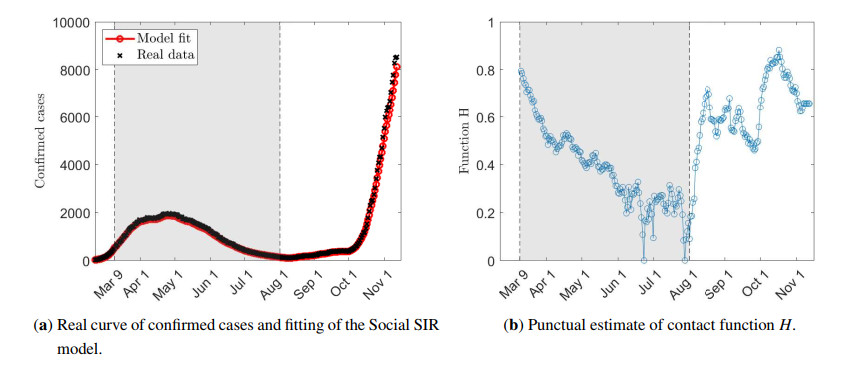
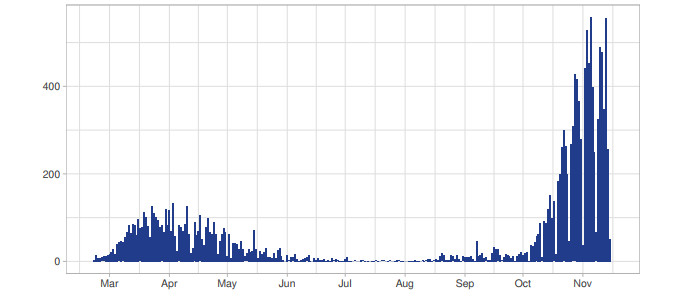
In Figure 1 the number of confirmed COVID-19 cases per day is displayed, for a total of 15,768 infectious individuals and 1415 cumulative deaths during the considered period. Figure 1 clearly shows two different crucial periods: the first one represents the initial outbreak of the disease, and the second one, with the restart of the activities.
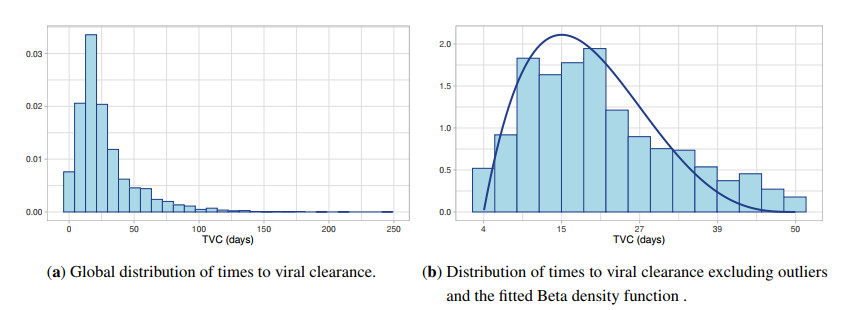
The detailed information collected in the ATS dataset allows to extrapolate the time to viral clearance (TVC), corresponding to the time from the first positive test to the second negative test before October 12nd or the first negative test after October 12nd, in agreement with the policies of the Ministry of Health. Furthermore, since we considered in the recovered compartment also deceased patients, the computation of the TVC considers in this case the date of the patient's death. Figure 2a shows the global distribution of TVC computed in days with a minimum value of 0 and a maximum value of 250. The values 0 and greater to 100 may be due to anomalies in the registration of swab tests in the period of first emergency. To deeper study the type of distribution of the TVC we focus the analysis on the interval between 4 and 50 days, as reports in Figure 2b. This interval includes the 82% of the recovered patients. The corresponding distribution has been estimated by testing a Beta density function on the empirical distribution of the available data on the bounded interval [4,50]. The method of Maximum Likelihood Estimation has been implemented to estimate the relevant parameters, and to realize that B(2,4) is the Beta distribution capable to best approximate the registered times to viral clearance.
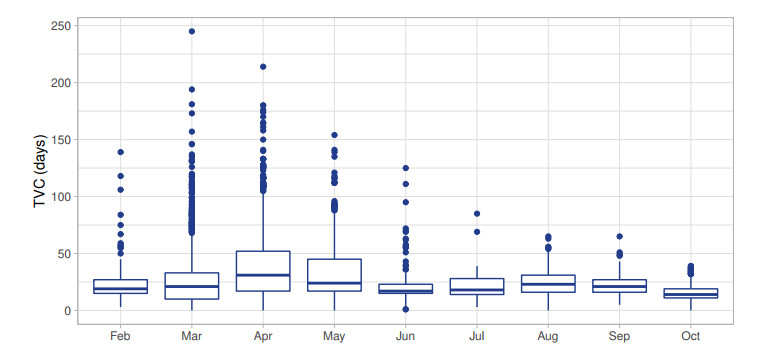
According to several studies, the TVC during the early phase of the epidemic can approximately span from 10 to 24 days (cf. [2,22,23] for further discussions). The present analysis, based on the data of the province of Pavia, is substantially in agreement with the aforementioned works. In Figure 3 we present the boxplots for TVC by month. We may observe how the presence of outliers appears strongly reduced after July 2020, whereas the median TVC remains stable in the considered period.
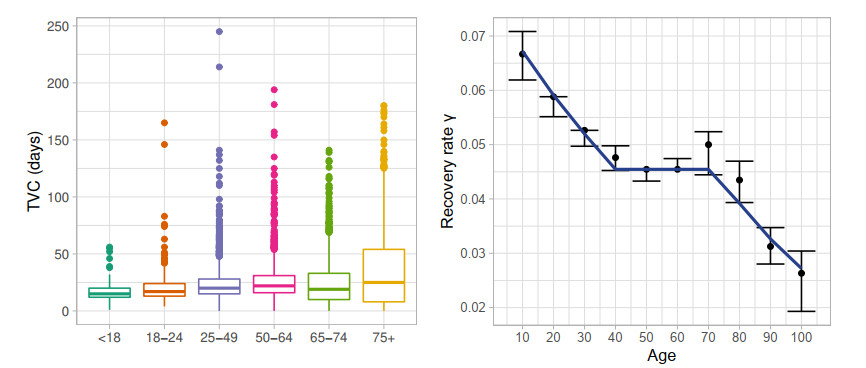
Since the age component influences significantly the morbidity and mortality of COVID-19 patients [24], we have preliminarily investigated the dependency of the recovery of patients from the age variable a∈[0,100]. Figure 4a shows that heterogeneities in registered time to viral clearance with respect to age exist in terms both of range values and median value. In particular, the median time to viral clearance in days increases with the age of patients, from a minimum value of 15 days if a≤18 till a value of 25 days if a≥75.
This difference is presented in Figure 4b where the bootstrap confidence intervals (confidence level equal to 95%) for the median values of the recovery rates are estimated for each value of age reported on x axis. The analysis on median values has been preferred with respect to the mean values since recovery distributions for each group age are strongly positive skewed, as displayed in Figure 4a, and the median value is a more robust statistic with respect to outliers.
Resorting to these results the constant recovery rate γ of the original continuous model (2.7) can be substantially improved. An age-dependent recovery rates γ(a) in the form of the following piecewise function
is depicted in Figure 4b. The parameters p1, p2, p3 and q1, q2, q3 can be obtained by solving a least square optimization problem in the three introduced subcategories. The results of the optimization problem are reported in Table 1.
Recovery distribution has been also analyzed comparing different months of the considered period in order to understand if significant changes have occurred during the evolution of the epidemic. Figure 3 displays a particular trend in the first months of the outbreak (March, April, May and June) characterized by a right-skewed distribution and a wide range of times to viral clearance. From July to September the distributions become more and more stable around the median value of 25 days.
This significant difference, between the first months of the epidemic and the following ones, can be explained considering that collections of data of first period have been affected by lot of imprecisions due to the overwhelming activities which have involved the ATS of Pavia because of this new emergency.
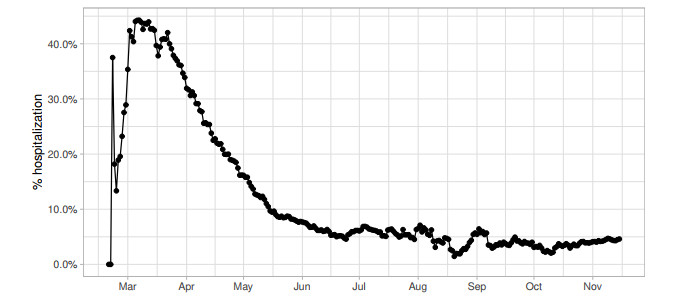
Finally, we consider the number of hospitalizations in terms of admission and discharge dates in the hospitals of Pavia. This allows to estimate the daily percentage of hospitalized patients over all the daily confirmed cases. The percentage trend is represented in Figure 5. This value shows a peak during the first outbreak of the epidemic, between March and April, achieving 50% and becomes more and more constant starting from the beginning of June, with an average value equal to 4.7%. It is reasonable to consider this last one as a more accurate estimate of the real hospitalization rate, since data collected from March to May are altered by the low number of swab tests performed during this period.
4.
Calibration of S-SIR model and forcastings
In this section we perform the estimation of epidemiological parameters of the introduced S-SIR model taking into account the ATS dataset. It is worth to mention that the estimation of such parameters for compartmental models is generally a difficult task and is strongly related on the assumptions of the adopted model. A comparison between several available models and methods has been recently presented in [25]. Furthermore, available epidemiological data represent typically a lower bound of the real diffusion of the epidemic since according to recent results of the serological campaigns promoted in Italy around 80% of infected are asymptomatic [26]. Another source of uncertainty is given by the limited testing capacity which is particularly evident at the beginning of the epidemic. Therefore data are partial and heterogeneous with respect to their assimilation making the fitting problem challenging. We mention in this direction the detailed discussions in [27,28,29,30].
Several approaches have been developed to infer the time-course of infections of COVID-19 in Italy from available agammaegated data through specific compartmental analysis of the population. In particular, a common trait in existing literature relies in considering the compartment of hospitalized or infected acutely symptomatic whose evolution depends on specific choice of parameters [1,2,31]. Nevertheless, we have observed in Figure 5 how the percentage of hospitalizations in the Province of Pavia remain quite stable from June 2020 up to November 15 around the 5% of the current cases. Interestingly enough, from February to April 2020 the registered hospitalizations increased a lot in the reference area with a peak of more than 40% of the current cases. Hence, the hospitalizations decreased constantly from April to June 2020. This fact may be explained by the limited testing capacity in the early phases of the epidemic. In agreement with [26] the real number of infected has been largely underestimated.
We will predict the number of hospitalized patients using the percentage of hospitalizations estimated from the last available month before the time interval considered for the prediction. As already pointed out, we will show that this percentage appears stable from July to October.
4.1. Extrapolation of the contact function
In the following, we present a calibration approach which is based on a strategy with two main optimization horizons related to the pre-lockdown and lockdown time spans. We consider first the time interval t∈[t0,tℓ], being tℓ the day in which lockdown started in Italy and t0 the day in which reported cases hit 30 units. The lower bound has been imposed to reduce the limited testing capacity in the early phase of the infection.
We estimate the recovery rate γ>0 from data by computing the median value of the empirical recovery rates distribution, γ=0.0476 corresponding approximatively to a median time to viral clearance of 21 days. Hence, to determine β, we solve a least square problem based on the minimization of a cost functional J which takes into account the sum of two relative L2([t1,t2]) norms over the time horizon [t1,t2]. In particular, we consider a cost functional taking into account the difference between the reported number of infected and the reported total cases, i.e., ˆI(t) and ˆI(t)+ˆR(t), and the evolution of I(t) and I(t)+R(t) given by the S-SIR model (2.7) with H≡1 and t∈[t1,t2]. In details, we solve the constrained optimization problem
subject to the dynamics in Eq (2.7). In Eq (4.1) the cost functional J is a convex combination between two relative L2 norms
with μ=10−2. We solved the introduced optimization problem confronting different integration methods and we obtained β=0.218.
Once the epidemiological parameters have been estimated in the pre-lockdown time interval we can proceed with the estimation of the shape of the contact function H in the time span [tℓ,T]. In order to reduce the fluctuations due to possible delays in the registration procedure, we solve the corresponding least square problems for a sequence of time steps ti in [ti+κr,ti+κℓ] where κr,κr≥1 are integers chosen to cover a window of seven days. We considered κr=2 and κℓ=5 for regularization along one week of available data. To this end, we considered a second optimization problem
where the parameters β,γ have been determined as a result of the optimization problem in Eq (4.1). These optimization problems have been solved testing different optimization methods in combination with RK4 integration method of the system of ODEs.
The available data start on February 20, 2020, when moderate social restrictions were already enforced by the national government, and the lockdown started on March 9, 2020. In Figure 6 we present the evolution of the current confirmed cases together with the result of the described fitting procedure. The punctual evolution of the contact function H(t), t∈[tℓ,T], is presented in the left column. We highlighted a shaded gray zone to indicate the first wave of the infection for which we can clearly observe that the contact function can be coherently approximated through a decreasing function.
On the other hand, the beginning of the second wave of infections can be detected in the first days of August since the function H returned rapidly to its early pandemic values remaining quite stable till November 15th.
4.2. Forecasts of hospitalizations
In this Section we present the prediction results furnished by the improved S-SIR model for expected hospitalizations due to COVID-19 acute symptoms. In particular, we will take into account the information on the times to viral clearance presented in Section 3 where we have observed that the experimental data are well approximated with a Beta distribution p(z) of the form
and h0=46, h1=4. In the following we will indicate the support of z with Γ=[4,50].
The S-SIR model with stochastic recovery rate can be obtained in the same theoretical setting described in Section 2 and reads
In order to handle efficiently the introduced stochasticity in the dynamics we will adopt a stochastic collocation approach based on stochastic Galerkin methods (see [32] for an introduction and [27,30] for their application to epidemiological dynamics). These methods allow to handle efficiently the stochasticities of a system when information on the uncertainties distribution are available thanks to the fast convergence properties holding under suitable regularity assumptions.
We construct the sample {γ0,…,γM} from γ(z). The samples are obtained in a collocation approach using Gauss-Jacobi polynomials with M=10. For each fixed value γj, j=0,…,M, we solve the optimization problem (4.1) subject to the dynamics in Eq (2.7) to obtain the value βj>0. Hence, we estimate the contact function Hj(t), j=0,…,M, in time by solving the subsequent optimization problem (4.2) in the time interval [ti+kℓ,ti+kr], with κr=2 and κℓ=5, and where γ=γj, β=βj are fixed.
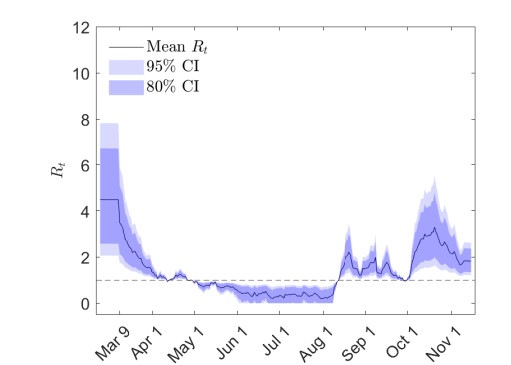
In Figure 7 we report the expected value of Rt together with the 95% and 80% confidence intervals with respect to the stochastic parameter z. The results show that, in presence of the marked reduction of social contacts enforced by the lockdown measures of the government, the reproduction number Rt has been drastically reduced and its expected value fell below one in the first week of April. Then, the observed Rt remains stably below unity from May to the first week of August.
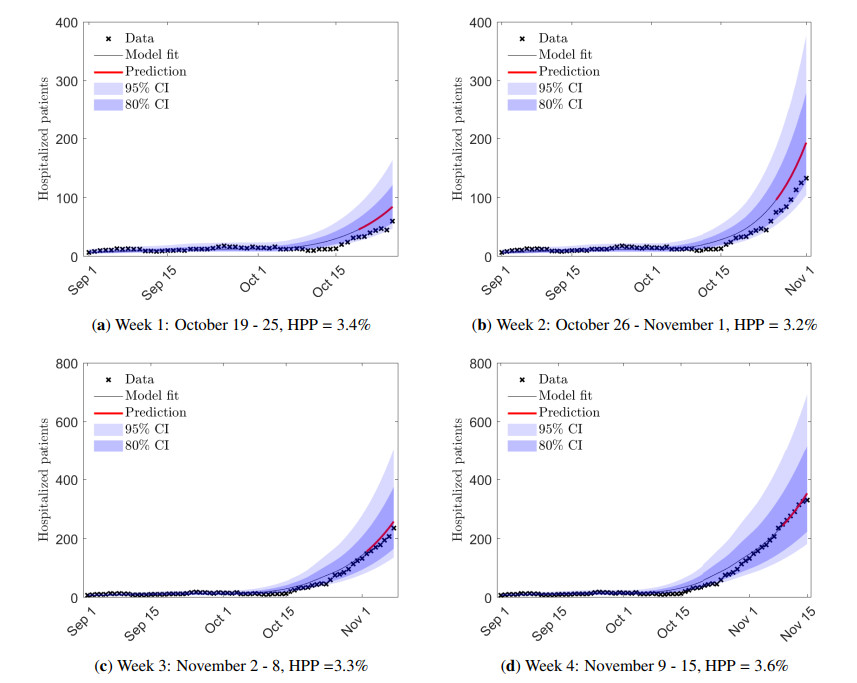
In Figure 8 we present the dynamics of the confirmed cases with respect to the available data in four successive weeks from October 15, 2020 to November 15, 2020. In particular, we performed the fitting procedure of the model up to the week of prediction. We fixed for the whole prediction horizon Hj(t)=Hj(T), t∈[T,T+7]. We highlight in red the expected value of the predicted cases, i.e., E[I(z,t)]=∫ΓI(z,t)p(z)dz. Together with the expected trends we plot the confidence intervals (CI) that are obtained by imposing
and c=0.05 for the 95% CI and c=0.2 for the 80% CI. For any given week of interest, the previous seven days have been neglected in the fitting procedure, and then plotted together with predictions to establish the performance of the modelling setting. We can observe how through S-SIR model with stochastic recovery rate we are capable to catch the epidemic dynamics with a good level of accuracy.
Once a sufficiently precise evolution of the infections has been obtained, we can infer the expected hospitalizations thanks to the preliminary statistical results introduced in Section 3. In details, for each prediction week, we computed the percentage of hospitalized patients (HPP) taking into account the previous 30 days of observations. Hence, the prediction is obtained by multiplying the predicted cases with HPP. In Figure 9 we present the obtained predictions of hospitalized patients from the S-SIR model with stochastic recovery rate (4.3). As before, we neglected the previous seven days of observations for each week of interest to estimate the parameters of the model. The performance of the model are compatible with the expected hospitalized patients E[I(z,t)].
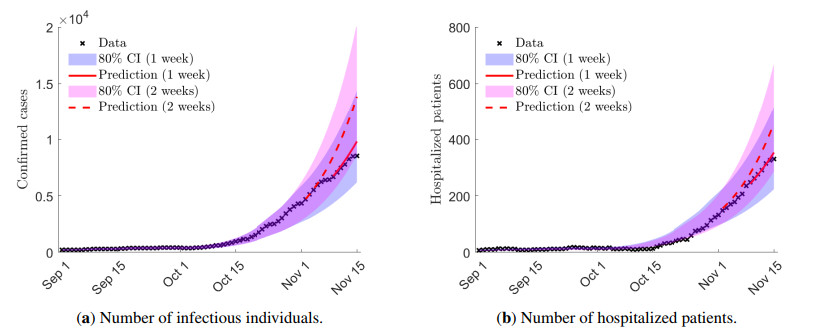
We considered a prediction horizon of one week, since a complex phenomenon like the COVID-19 diffusion in Italy embed a huge number of hidden uncertainties and variable factors. We briefly discussed some of them in the previous paragraphs. In Figure 10 we present a comparison between a 1 week prediction horizon, i.e., the S-SIR model is calibrated taking into account data until November 8th 2020, and a 2 weeks prediction horizon, where the calibration is based only on data until November 1st 2020. For the left figure we also used the HPP relative to the week November 2-8, i.e., HPP=3.3%. We may observe how we lose some accuracy in a longer prediction horizon even if we are qualitatively able to catch the observed trends.
5.
Conclusions
The recent spreading of the COVID-19 epidemic led the scientific community to improve the existing mathematical models of infections spreading by adding to them the possible effects of social contacts about individuals. In this direction, the social S-SIR model introduced in [11] aimed to quantify the effects of the lockdown policies operated by governments to limit the spreading of COVID-19 epidemic in terms of a computable reduction of the contacts. Months after the early phase of the epidemic, the huge amount of data at disposal of the authorities can be fruitfully used to calibrate the parameters of the epidemic mathematical models to furnish a better knowledge of the evolution of infections. In the present paper, by resorting to the ATS dataset relative to the province of Pavia, we were able to correctly evaluate the key parameters of the S-SIR model. In particular, the knowledge of data relative to the recovery rate of infectious allowed to substitute in the S-SIR model the constant recovery rate parameter with a Beta distributed random variable, thus providing a better adherence to real data. Further, a critical inspection of the dataset outlined the importance of considering a novel mathematical model in which, in addition to the social contacts, one has to take into account in a proper way the age variable, mainly responsible of the expected number of hospitalized, and consequently of the possible critical situations in the health system. Nevertheless, in absence of this new type of refined mathematical model, the merging of the evolution of spreading obtained by means of the S-SIR model with a reasoned use of the dataset, led to an accurate output on a one-week time horizon, with a uniform goodness in a period of four weeks, ranging from the middle of October, 2020 to the middle of November, 2020. Based on the prediction performance of this modeling approach, this joint research represents a first step towards a easy-to-handle fruitful numerical approach to the mechanism of control of a local health system during the period of epidemic spreading.
Acknowledgments
This work has been written within the activities of the Agreement 60/2020, Protocol number 154,768 of December 21, 2020, between the Department of Political and Social Sciences of the University of Pavia and the Health Protection Agency (ATS) of the province area of Pavia, with object "Mathematical modeling and statistics for the forecast of the COVID-19 epidemic in the territory of the Province of Pavia". M. Z. and G. T. acknowledge support from the GNFM group of INdAM (National Institute of High Mathematics), from MIUR project "Optimal mass transportation, geometrical and functional inequalities with applications", and by the Italian Ministry of Education, University and Research (MIUR): Dipartimenti di Eccellenza Program (2018–2022)–Dept. of Mathematics "F. Casorati", University of Pavia.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: