1. Introduction

Mathematical models in epidemiology often make the assumption that successful control of epidemics is only determined by the availability and effective deployment of control measures such as vaccination and isolation, whose success largely depends on factors such as quantity of vaccine and logistical constraints. In recent years, some mathematical models are focusing on endogenously incorporating the impact of human behavioral patterns on the regulation of communicable diseases. Upon gaining awareness about an infectious disease outbreak, susceptible individuals may decrease their infection risk by isolating themselves or reducing interactions with their friends, colleagues, etc, through staying at home and avoiding social contacts. This practice is known as social distancing [16,22]. Along with social distancing, hand-washing, use of masks, and other respiratory etiquette are further examples of so-called 'non-pharmaceutical interventions' (NPIs) that can reduce infection spread [31]. While healthcare providers often advise the public on appropriate NPIs, behavioral choices of individual members of the host population partially determine the dynamics and feasibility to control an infectious disease outbreak.

Social distancing and other NPIs have assisted the control of infections such as flu, severe acute respiratory syndrome (SARS) and plague [6,12,40,23,14,36,15,38,21,2]. However despite the availability of a large amount of information about the dangers and risks of sexually transmitted infections (STIs), actions like unsafe sexual behavior and needle sharing during intravenous drug use have been linked to the pandemic-scale dissemination of STIs such as HIV/AIDS [26,24,39,25]. Generally, negligence or relaxation of precautionary measures is brought about by factors such as lack of awareness and engaging in infection-enhancing social practices such as handshakes, hug, kisses, sharing of food and concurrent sexual partner, as well as some cultural practices. The 2014 epidemic outbreak of Ebola in West Africa is an example of how cultural or religious practices, such as engaging in risky rituals and inappropriate handling of the sick or deceased, also influence the dynamics of infectious diseases [28].

Human behavior also plays a role in the regulation of some animal infectious diseases. For instance, the use of dogs in hunting and grazing cattle in countries such as Kenya and Botswana, influences transmission of canine diseases between domestic dogs and the African wild dog [1]. Although culling (slaughtering of infectious or at-risk animals) has been found to effectively control foot and mouth disease, farmers' resistance towards this intervention measure (because of fear of loss of livestock) often makes it difficult to bring the disease under control.

In [12] the authors explore the impact of social distancing on the spread of an infection by incorporating health status-based contact behavior patterns into a mean-field equations epidemic model. Thus, the transmission dynamics are governed by differing contact levels between individuals of different health types. For example, due to the perceived risk of infection, susceptible individuals are likely to avoid contact with infected individuals, while maintenance contact with recovered individuals may have a less significant impact.

In [15] the authors explore the idea that the adoption of social distancing or other NPIs is driven by the level of information individuals have, such that members of the host population who possess first hand information become more cautious and therefore less susceptible than those who have second hand information. Similarly, individuals who have second hand information are less susceptible than those who posses third hand information, etc. This study was carried out by modeling information transmission and spread of an infection using mean-field equations and individual-based epidemic models. The research also discusses the significance of repeated re-generation of awareness into the population to ensure that most individuals have access to primary, or close-to-primary, information, which increases the number of individuals who exercise contact precautions and/or NPIs.

In [14] the authors capture the dynamic nature of individuals' decisions leading to adoption or non-practice of social distancing, by assuming that the network geometry within which the host population resides (particularly the neighborhood size) changes over time, depending on individuals' perceived risk of infection. Thus, adjustment of individuals' perceptions about the disease over time results in variation of contact pattens and, therefore, it affects the infection dynamics. Other researchers have explored game-theoretical [33] or rule-based simulation models [35,37] of social distancing.

The spatial dimension of social distancing has been explored in some of this previous work [15,14,35,37]. Spatial dynamics can be analytically intractable, hence the frequent decision to employ agent-based models. However, one method for implicitly capturing spatial dynamics that often permits analysis is moment closure approximation (MCA). MCAs employ pairs, triples, quadruples, etc., of connected individuals, as model state variables, such that transmission takes place only between connected susceptible and infectious individuals on the network. MCAs are usually comprised by a system of differential equations, where each equation describes time evolution of second order, third order, fourth order, etc., spatial correlations between individual members of the host population. Equations of motion for pairs involve terms in triples, equations of motion for triples involves terms in quadruples, etc. Therefore in order to obtain a closed system of equations, this hierarchy is truncated by techniques referred to as moment closures. Carrying out the closure at the level of pairs produces a pair approximation model [34,8,7,5,29,30,32,13,9,19,11,17].

Here our objective is to demonstrate how pair approximations and analytical expressions for the basic reproduction number can be developed for spatially-structured socio-epidemiological systems. We develop and analyze a pair approximation model and explore the impacts of NPIs on the spread of an infectious disease. We incorporate impacts of NPIs by dividing the susceptible population into susceptible individuals who protect $(S_p)$ (i.e., those who practice NPIs) and individuals who do not $(S)$. State $S$ individuals learn from state $S_p$ and/or infectious (state $I$) individuals in their network neighborhood, and then decide whether or not to adopt NPIs. The dichotomy between adopting NPIs due to being next to an infectious person, versus learning NPIs from other individuals who adopt NPIs, captures the distinction between practicing NPIs reactively because of an immediate threat due to an infectious neighbour versus changing one's habits pre-emptively based on observing the actions of other individuals, and forming new habits (such as using hand sanitizers, or using a paper towel to open a bathroom door). We refer to learning NPIs from other state $S_p$ contacts as "social learning", versus "exposure learning" that occurs from reacting to infection in an immediate network neighbour. Because social learning cannot occur without individuals who have first adopted NPIs through exposure learning in the early stages of the outbreak, exposure learning can be viewed as a first order effect, while social learning can be viewed as a second order effect. We also derive the basic reproduction number and analyze the pair approximation equations to understand how control success depends on epidemiological and behavioral change parameters. The model is described in the following section.

---

2. Model

A state $S$ individual who is neighbouring a state $S_p$ individual transitions to the $S_p$ state at a per capita rate $\xi$. Similarly, a state $S$ individual neighbouring a state $I$ individual transitions to the $S_p$ state at a per capita rate $\rho$. These interactions thereby result in susceptible individuals adopting NPIs. Switching from state $S_p$ back to state $S$ occurs at a per capita rate $\kappa$, representing forgetting, or complacency.

The rate of infection transmission from an infectious individual to a neighbouring state $S_p$ individual is $\tau_p$, whereas transmission to a neighbouring state $S$ individual occurs at a rate $\tau > \tau_p$. Infected individuals recover at per capita rate $\sigma$. Thus, the state variables of the pair approximation model are numbers of susceptible, protective, infectious and recovered individuals denoted by $[S]$, $[S_p]$, $[I]$ and $[R]$, respectively, and numbers of paired individuals, $[XY]$ where, for instance $[S_pI]$ represents the number of edges comprising of susceptible protective and infectious individuals. We derive equations of motion for our model in the Appendix. We assume that the disease spreads on a regular network in which all nodes have the same degree $n$, in a population of size $N$, and we use the binomial ordinary pair approximation (Equation (14)), to approximate triples in terms of pairs and singletons, resulting in:

$\begin{align*} \frac{d[S]}{dt}&=-\tau[SI]-\xi[S_pS]+\kappa[S_p]-\rho[SI] \\ \frac{d[S_p]}{dt}&=-\tau_p[S_pI]+\xi[S_pS]-\kappa[S_p]+\rho[SI] \\ \frac{d[I]}{dt}&=\tau[SI]+\tau_p[S_pI]-\sigma[I] \\ \frac{d[R]}{dt}&=\sigma[I] \\ \frac{d[SS]}{dt}&=-2\frac{n-1}{n}\frac{[SS]}{[S]}\bigg((\tau+\rho)[SI]+\xi[S_pS]\bigg)+2\kappa[SS_p] \\ \frac{d[SS_p]}{dt}&=-\frac{n-1}{n}\bigg((\tau+\rho)\frac{[SI][SS_p]}{[S]}+\tau_p\frac{[SS_p][S_pI]}{[S_p]}-\xi\frac{[SS_p][SS]}{[S]}-\rho\frac{[SI][SS]}{[S]}\bigg) \\&-\:\xi[SS_p]+\kappa([S_pS_p]-[SS_p]) \\ \frac{d[S_pS_p]}{dt}&=-2\frac{n-1}{n}\bigg(\tau_p\frac{[S_pI][S_pS_p]}{[S_p]}-\rho\frac{[SI][SS_p]}{[S]}\bigg)+2\xi[SS_p]-2\kappa[S_pS_p] \\ \frac{d[SI]}{dt}&=\frac{n-1}{n}\Bigg(\frac{[SI]}{[S]}\bigg(\tau[SS]-(\tau+\rho)[SI]-\xi[SS_p]\bigg)+\tau_p\frac{[SS_p][S_pI]}{[S_p]}\Bigg) \\&-\:(\tau+\sigma+\rho)[SI]+\kappa[S_pI] \\ \frac{d[S_pI]}{dt}&=\frac{n-1}{n}\Bigg(\frac{[SI]}{[S]}\bigg((\tau+\xi)[SS_p]+\rho[SI]\bigg)+\frac{[S_pI]}{[S_p]}\tau_p\bigg([S_pS_p]-[S_pI]\bigg)\Bigg) \\&-\:(\tau_p+\sigma+\kappa)[S_pI]+\rho[SI] \\ \frac{d[SR]}{dt}&=-\frac{n-1}{n}\frac{[SR]}{[S]}\bigg((\tau+\rho)[SI]+\xi[SS_p]\bigg)+\sigma[SI]+\kappa[S_pR] \\ \frac{d[S_pR]}{dt}&=-\frac{n-1}{n}\bigg(\tau_p\frac{[S_pI][S_pR]}{[S_p]}-\frac{[SR]}{[S]}(\rho[SI]+\xi[S_pS])\bigg)+\sigma[S_pI]-\kappa[S_pR] \\ \frac{d[II]}{dt}&=2\frac{n-1}{n}\bigg(\tau\frac{[SI]^2}{[S]}+\tau_p\frac{[S_pI]^2}{[S_p]}\bigg)+2\tau[SI]+2\tau_p[S_pI]-2\sigma[II] \\ \frac{d[IR]}{dt}&=\frac{n-1}{n}\bigg(\tau\frac{[SI][SR]}{[S]}+\tau_p\frac{[S_pI][S_pR]}{[S_p]}\bigg)+\sigma([II]-[IR]) \\ \frac{d[RR]}{dt}&= 2\sigma[IR].\end{align*}$

(1)

---

2.1. The basic reproduction number

The basic reproduction number $R_0$ is the expected number of secondary infection cases produced by a single infectious individual upon introduction into a wholly susceptible population [10,5,3,20,27]. An epidemic may occur if $R_0>1$, but the infection will die out if $R_0 \leq 1$. Therefore, effective disease control reduces $R_0$ below 1.

Here we use the pair approximation model above to derive an expression for $R_0$ that incorporates some effects of spatiality and allows us to study the impact of adoption of NPIs on the dynamics of the disease at the initial stage of an outbreak. For simplicity, we derive $R_0$ for a scenario where individuals start to learn and practice contact precautions during an outbreak ($S_p(0) \ll N$).

The condition under which the infection will spread is

$\frac{d[I]}{dt}> 0 \Rightarrow \tau[SI]+\tau_p[S_pI]-\sigma[I]> 0,$

(2)

which can be rearranged to yield

$\frac{\tau[SI]+\tau_p[S_pI]}{\sigma[I]}> 1.$

(3)

Therefore, we write $R_0$ in terms of (ⅰ) susceptibility of individuals who do not protect (captured by a high transmission parameter $\tau$), (ⅱ) susceptibility of individuals who practice NPIs (captured by a low transmission rate $\tau_p$), (ⅲ) the rate of recovery $\sigma$, and (ⅳ) the numbers of S-I and $S_p$-I pairs as well as the overall number of infections individuals $[I]$:

$R_0=\frac{\tau[SI]}{\sigma[I]}+\frac{\tau_p[S_pI]}{\sigma[I]}.$

(4)

Next we express pairs $[SI]$ and $[S_pI]$ in terms of the correlations between state $S$ individuals and their infectious neighbors, and state $S_p$ individuals and their infectious contacts, respectively. The correlation between individuals with status $X$ and $Y$ is given by

$C_{XY}=\frac{N}{n}\frac{[XY]}{[X][Y]},$

(5)

where $n$ and $N$ are the number of contacts each individual has and the total population size, respectively. $C_{XY}< 1$ implies avoidance of interaction between state $X$ and state $Y$ individuals, $C_{XY}=1$ assumes homogeneous mixing, while $C_{XY}> 1$ implies strong correlation between state $X$ and state $Y$ individuals. Note that Equation (5) can be re-written as

$[XY]=\frac{[n]}{N}[X][Y]C_{XY},$

(6)

therefore,

$R_0=\frac{n}{\sigma N}(\tau[S]C_{SI}+\tau_p[S_p]C_{S_pI}).$

(7)

At the initial stage of an epidemic, we assume that the population is comprised mainly by susceptible individuals, only a few of whom practice NPIs:

$[S]+[S_p]\approx N, \text{where } [S_p]<<[S]$

(8)

We define $s_p \equiv [S_p]/N$, thus the proportion of state $S$ individuals at the beginning of the epidemic is $1-s_p$, and $R_0$ becomes:

$R_0=\frac{n}{\sigma }\bigg(\tau (1-s_p) C_{SI}+\tau_p s_p C_{S_pI}\bigg).$

(9)

To estimate the values for $C_{SI}$ and $C_{S_pI}$, we use biologically reasonable assumptions about disease spread, as follows. There is a very small number of infectious individuals at the beginning of an outbreak, so $C_{SI}\approx1$. However as the infection spreads, $C_{SI}$ decreases and the clustering of infected individuals leads to a decrease in the rate of spread, and the disease may die out if there are not enough susceptible individuals in the vicinity of the infected cluster to transmit the disease to. The dynamics of the disease at this point (referred to as the local minimum and denoted by $C_{SI}^{min}$) determine whether an epidemic will succeed or fail to take off. Thus, we need to evaluate $C_{SI}^{min}$ [18]. Similar reasoning applies to $C_{S_pI}^{min}$. Hence

$R_0=\frac{n}{\sigma }\bigg(\tau (1-s_p) C_{SI}^{min}+\tau_p s_p C_{S_pI}^{min}\bigg).$

(10)

The quantities $C_{SI}^{min}$ and $C_{S_pI}^{min}$ are the solutions of $\frac{d}{dt}C_{SI}=0$ and $\frac{d}{dt}C_{S_pI}=0$, respectively.

The derivation of these quantities as well as the full expression of $R_0$ are presented in the Appendix. The full expression of $R_0$, Equation (17), is unwieldy but it depends on epidemiological parameters $\tau,\tau_p$ and $\sigma$, NPIs-based parameters $\xi,\rho$ and $\kappa$, as well as initial network configuration-dependent correlations $C_{S_pS}$ and $C_{S_pS_p}$. It is clear from Equation (17) that a higher rate of recovery $\sigma$, reduces $R_0$, but the equation is too complicated to directly infer the impacts of other model components. Hence, numerical computations will be used to explore dependence of $R_0$ on model parameters and initial network configurations (Section 3).

We derive reduced versions of $R_0$ by considering special cases where individuals adopt NPIs through (a) social learning only (i.e. $\xi>0$ $day^{-1}$ and $\rho=0$ $day^{-1}$) and (b) exposure learning only (i.e. $\xi=0$ $day^{-1}$ and $\rho>0$ $day^{-1}$). For both of these scenarios we assumed that protective individuals consistently practice NPIs throughout the outbreak so that state $S_p$ individuals do not switch back to state $S$ (i.e. $\kappa=0$ $day^{-1}$). Furthermore, we assumed that the initial network configuration constitutes one infectious (state $I$) individual with one protective (state $S_p$) neighbor who also has one state $S_p$ contact, and the rest of the population is completely susceptible (i.e. state $S$) such that at the initial stage of the outbreak $[S]\approx N$, where the population size $N$ is very large.

---

2.1.1. High efficacy NPIs adopted through social learning only

In the Appendix we simplified Equation (17) to derive the expression for the basic reproduction number for dynamics in which adoption of NPIs results from social learning only (case (a) above), and that NPIs are highly effective as a control measure ($\tau_p<<\tau$), and for typical model parameters ($N=40000$, $s_p=2/N$, $n=4$, $\tau=1$ $day^{-1}$, $\tau_p=0.0025$ $day^{-1}$, $\sigma=0.25$ $day^{-1}$ and $\xi=0.25$ $day^{-1}$), to obtain

$R_0\approx\frac{\tau n\chi -\xi+\sqrt{\tau^2n^2\chi^2+\xi(\xi+2\tau n\chi)}}{2\sigma},$

(11)

where

$\chi\approx\frac{\tau(n-2)+\sqrt{\tau^2(n-2)^2+4\tau \tau_p(n-1)}}{2\tau n}.\nonumber$

Equation (11) confirms that social learning ($\xi$) reduces the initial spread of the infection. As expected, a highly transmissible infection (large $\tau$) will increase $R_0$. We note that $R_0$ increases with $\chi$. We discuss in the Appendix that $\chi$ approximates the minimum of the correlation function $C_{SI}^{min}$ between susceptible and infectious individuals. Therefore, factors that increase $\chi$ should also increase $R_0$. The quantity $\chi$ increases with the transmission rate to protective susceptible neighbours ($\tau_p$), as well as the number of neighbours per individual ($n$), confirming the mitigating effects of spatially localized transmission.

---

2.1.2. High efficacy NPIs adopted through exposure learning only

For comparison to Equation (11), in the Appendix we also simplified Equation (17) to derive the expression for the basic reproduction number for dynamics in which adoption of NPIs results from exposure learning only (case (b) above), and that NPIs are highly effective as a control measure ($\tau_p<<\tau$), and for typical model parameters ($N=40000$, $s_p=2/N$, $n=4$, $\tau=1$ $day^{-1}$, $\tau_p=0.0025$ $day^{-1}$, $\sigma=0.25$ $day^{-1}$ and $\xi=0.25$ $day^{-1}$), to obtain

$R_0\approx\frac{\tau n\chi+\sqrt{\bigg(\tau^2n^2\chi+4\tau_p\rho n \bigg)\chi}}{2\sigma},$

(12)

where

$\chi\approx\frac{\tau(n-2)-\rho+\sqrt{\tau^2(n-2)^2-2\tau\rho(n-2)+\rho^2+4\tau \tau_p(n-1)}}{2\tau n}.\nonumber$

Hence, more rapid adoption of NPIs due exposure learning ($\rho$) decreases $\chi$, and therefore also decreases $R_0$. Spatial structure has a mitigating effect in this case as well.

In the Appendix we show that when adopted NPIs are not strict (such that $\tau_p<<\tau$ does not hold), then the corresponding expressions of $R_0$ for cases where individuals practice cautious behavior due to social learning only and exposure learning only are given by Equations (18) and (21), respectively.

---

3. Results

---

3.1. Dependence of $R_0$ on model parameters and network configuration

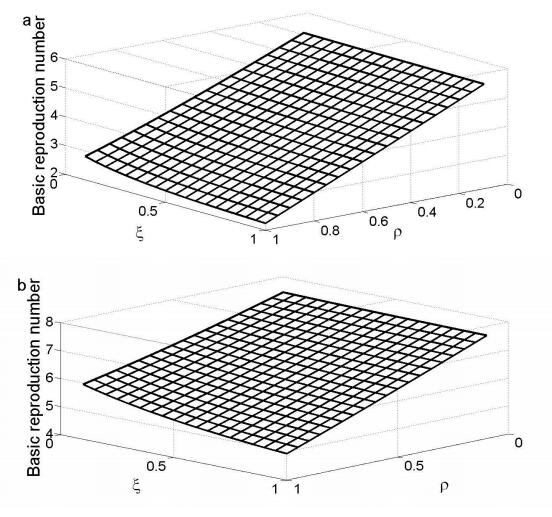
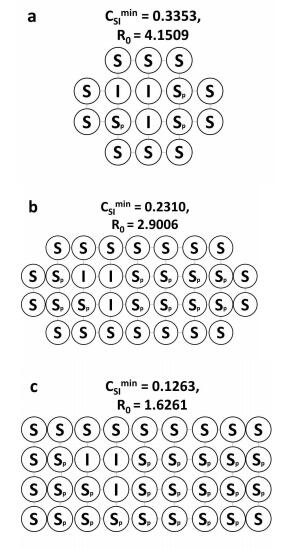
The spatial distribution of susceptible individuals ($S$) and individuals who practice NPIs ($S_p$) around the infection source at the initial stage of an epidemic have a strong influence on $R_0$, as computed from the full expression appearing in the Appendix, Equation (17) (Figure 1).

As expected, $R_0$ decreases with the proportion of protective individuals around the infection source cluster and in the entire population (Figures 1a versus 1c). This finding implies that upon inception of an outbreak it is crucial to identify the infection source promptly, and sensitize members of the host population about the disease and prevention measures, so that they can propagate awareness further through interactions with their spatial neighbours. We note that associating $R_0$ (and the overall disease dynamics) with specific network configurations in which diseases and social interactions disseminate would not be possible under a mean-field equations approach, which ignores spatial structure altogether. Spatial processes such as transmission of most infectious diseases and dessemintion of information can be understood better by the study of spatially oriented models such as pair approximation models.

Increasing the rate of adopting NPIs, either through exposure learning ($\rho$) or through social learning ($\xi$), decreases $R_0$. However, increasing the rate of adoption via infectious neighbours reduces $R_0$ more effectively than increasing the rate of adoption via protective susceptible neighbours (Figure 2a, b). This occurs because being next to infectious neighbors results in prompt adoption of preventative measures and avoidance of infection from that infectious neighbor, and hence it reduces $R_0$ better than a scenario where adoption of NPIs results from interaction with protective neighbors only, which may leave some infectious individuals in a part of the network with no protective individuals, while other parts of the network may have significant populations of protective individuals, but no infections. However, we note that this only applies when social learning can only begin at the start of an outbreak, and not beforehand as a pre-emptive measure.

---

3.2. Numerical analysis of pair approximation differential equations

---

3.2.1. Social and exposure learning during an outbreak

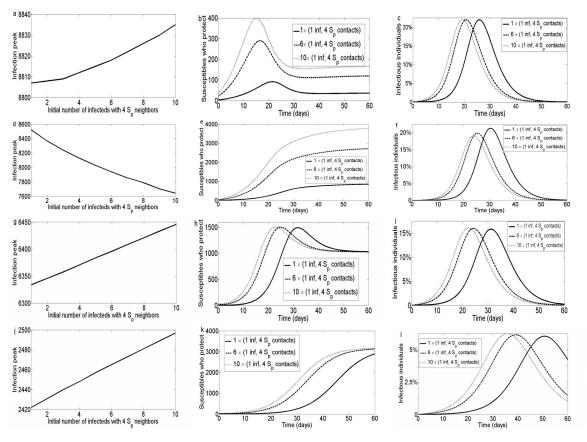
Numerical analysis of our model was carried out in MATLAB using the ode45 solver Similar to the results from the $R_0$ derivation, numerical simulation of Equation (1) shows that if both forms of learning can begin only during an outbreak, then NPIs adopted due to exposure learning ($\rho$) have a much larger impact on the size of the epidemic peak, than NPIs adopted due to social learning ($\xi$) (Figure 3i, l versus 3c, f). We also find that, adoption of NPIs stimulated by neighbouring infectious individuals leads to a higher number of protective individuals throughout and at the end of the epidemic, than practice of NPIs due to social learning (Figures 3h, k versus Figures 3b, e). This occurs because in this situation, learning from a neighbouring protective susceptible contact may not reach the parts of the network that need to be protected, resulting in those parts of the network being infected before they can adopt NPIs.

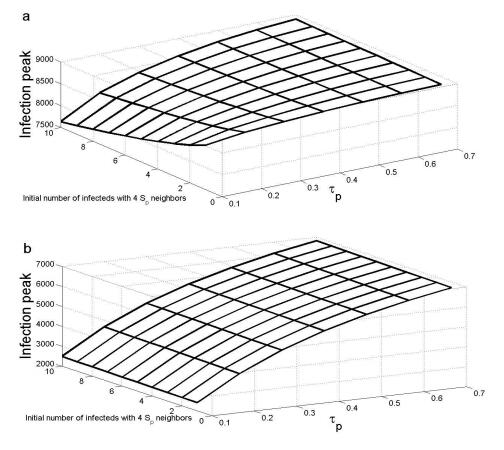
Increasing the initial number of infection source points with $n$ protective neighbours (i.e. completely surrounded by individuals who practice NPIs) generally increases the infection peak (Figures 3a, g, j). This confirms intuition. However, contrary to phenomena normally observed in homogeneous-mixing models, increasing the number of infection source points who are surrounded by highly protective individuals can actually decrease the infection peak in other parameter regimes ($\tau_p=0.1$ $day^{-1}$, see Figures 3d and 3f). On the other hand, when NPIs are not strictly practiced (leading to a relatively high value of $\tau_p$), increasing the number of infection source points will increase the infection peak, as usual, even when each of the initial infection sources are surrounded by a large proportion of protective contacts (see Figure 4a).

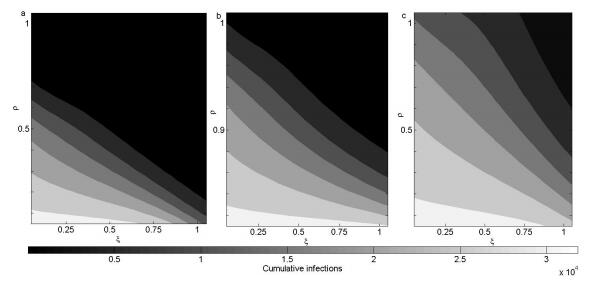
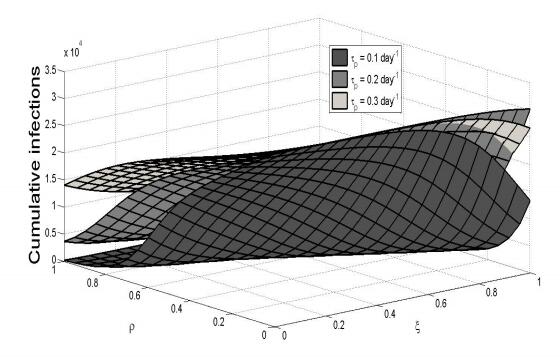
Cumulative infections over a period of two months decrease with adoption of precautionary behavior due to social learning at a rate $\xi$, and exposure learning at a rate $\rho$, but, also as observed in Figures 2 and 3, the decrease in cumulative infections is more profound when individuals use exposure learning than social learning (Figure 5). Furthermore, adoption of NPIs only moderately decreases cumulative infections if upon learning about the disease and becoming protective, the new state $S_p$ individuals practice less effective precautionary measures, resulting in an increased rate of transmission to state $S_p$ individuals, $\tau_p$ (Figure 5a versus Figure 5b versus Figure 5c). The asymmetry between effects of $\xi$ and $\rho$, and the impact of complacency, on cumulative infections, shown in Figure 5, are even more obvious in the corresponding surface plot of the same model outcomes (see Figure 6).

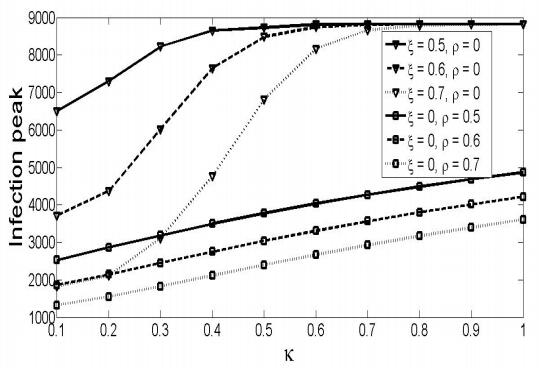
If individuals who practice NPIs lose this habit (captured by conversion from state $S_p$ to state $S$ at a 'forgetting' rate $\kappa$) then the population susceptibility increases, leading to a large number of infection cases and occurrence of large epidemic outbreaks, which are characterized by high infection peaks (Figure 7). However, with respect to the governing model equations used in this paper, the response of infection peaks to changes in the rates of forgetting is qualitatively different for the two types of learning: $\kappa$ scales linearly or logistically with infection peak, depending on whether only $\rho$ or only $\xi$, respectively, is active. This stems from the fact that per capita success of exposure learning--which operates only in immediate neighbours of an infected node--depends less on population prevalence than social learning. In particular, when the rate of forgetting is low, then the infection peak is roughly the same for both types of learning. However, when the rate of forgetting is high, then infection peaks are very high under social learning, but only moderately high under exposure learning. This occurs because effective social learning requires large parts of the network to be 'ready' for any infections which may enter the area by having high and stable populations of protective susceptible individuals, and large rates of forgetting prevent this from happening.

---

3.2.2. Social learning before and during an outbreak, and exposure learning during an outbreak

Many of the behaviours that fall under the rubric of NPIs, such as hand-washing and respiratory etiquette, are learned preventively and are practiced in a population even before an epidemic. This builds up the proportion of protective individuals before introduction of the disease. Thus, the effectiveness of social learning may thus be considerably improved, although it is not clear how far in advance social learning must begin for it to be useful. In this subsection we consider scenarios where social learning can occur both prior to and after the introduction of an infection. In particular, we contrast a scenario where only social learning is practiced (but social learning begins to spread before the epidemic starts), to a scenario where only exposure learning takes place, and we compare their performance.

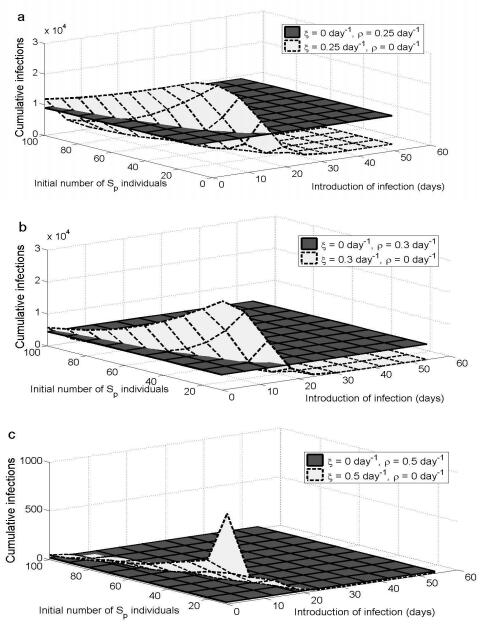
In the absence of exposure learning ($\rho=0$), model simulations confirm how social learning before an epidemic creates large pools of protective individuals before the epidemic begins, leading to a decreased epidemic final size (Figure 8). At baseline parameter values, introducing social learning as early as possible is a highly effective way of decreasing the epidemic final size; increasing the initial number of protective individuals, $S_p$, also works but is less effective than stimulating social learning as early as possible (Figure 8a-c). Either of these measures is made more effective when social learning is more rapid (large $\xi$, Figure 8c versus b and a).

In contrast to observations made in most of the simulations in the previous subsections, social learning reduces the epidemic final size more effectively than exposure learning, except when social learning is not introduced soon enough before the epidemic, or when there are not enough initial protective individuals (Figure 8 a-c). In either of these two exceptional cases, there is an insufficient pool of protective susceptible individuals in the population at the beginning of the epidemic, for social learning to be effective.

---

4. Discussion

NPIs partly determine the feasibility of infection control for many infectious diseases, especially ones where pharmaceutical interventions are not yet available. Here, we constructed a pair approximation model of a self-limiting infectious disease where individuals can choose to adopt NPIs either in response to learning it from other susceptible individuals, or having been stimulated to learn it from neighbouring an infectious person. Our objective was to demonstrate how pair approximation methods might be useful for studying socio-epidemiological processes in spatially structured populations.

We found that the impact of NPIs depends on the structure of the initial network configuration, particularly, the number and the neighborhood distribution of infectious, susceptible and individuals who practice NPIs, at the beginning of an outbreak. Both social learning and exposure learning lead to a decrease in the final size. At baseline parameter values, exposure learning is much more effective than social learning if social learning can only begin during the outbreak. However, social learning can outperform exposure learning if social learning begins early enough before the epidemic (although the initial number of protective individuals is not as important). While peak disease prevalence increases with the rate at which protective susceptible individuals stop the habit of practicing NPIs, the response of the infection peak to the rate of forgetting is qualitatively different for the two types of learning. We also found that, under certain parameter regimes, if infection source points are initially surrounded by protective individuals, increasing the number of infection source points at the beginning of an outbreak actually decreases the infection peak. This phenomena would not be revealed by the non-spatial, mean-field equations models.

Our model makes several simplifying assumptions. The model is based on the assumption that disease propagation and spatially localized learning take place only between connected neighbors on a regular network. In real life, networks within which infections spread are more complex, and mean-field effects (such as mass media) may be important. Future work could extend the pair approximation model to account for these effects. On the other hand, the importance of higher-order spatial correlations in many spatial systems is known. In spatially-structured epidemic systems in particular it may be necessary to use triple approximations instead of just pair approximations in order to capture dynamics of the full spatially explicit model with a high degree of accuracy [4]. Our paper did not evaluate the importance of higher-order correlations in spatial socio-epidemiological dynamics, and this aspect is left for future research as well.

In Section 3.2.2 we found that social learning is more effective in reducing cumulative infections than exposure learning, provided there is a sufficient pool of protective susceptible individuals in the population at the beginning of the epidemic. Future work could include derivation of the threshold for the initial population size of protective susceptible individuals, above which social learning will be more effective than exposure learning. Also, in general, social networks are structurally different from networks in which infections spread. Thus, future work could also develop pair approximations for dual-level networks consisting of both a social network and a disease spread network.

In conclusion, we have shown how pair approximation models that incorporate both spatial transmission of diseases and impacts of NPI decision-making can be developed and analyzed. Future research using this methodology might yield insights regarding infection control in spatially-structured socio-epidemiological systems.

---

Appendix

Derivation of the equation of motion for $[SI]$. Here we demonstrate the construction of equations of motion for pair approximation models by deriving $\frac{d[SI]}{dt}$.

In moment closure approximations the equation of motion for a state variable $g(t)$, is determined by expressing $\frac{dg(t)}{dt}$ as a function of the sum of all events that affect the state variable. That is

$\frac{dg(t)}{dt}=\sum\limits_{\epsilon\in events} r(\epsilon)\Delta g(\epsilon),$

(13)

where $r(\epsilon)$ is the rate of event $\epsilon$ and $\Delta g(\epsilon)$ is the change this event causes in $g(t)$. Equation (13) is referred to as the master equation. As illustrated below, at each node on the network the rates $r(\epsilon)$ and change $\Delta g(\epsilon)$ are expressed in terms of their population-averaged values and the deviations of those values from the expected means at a given node. The summation over each node is carried out in such a way that any significant stochasticity is incorporated in the evaluation of a state variable while the remaining stochasticity can be treated as random noise and may be discarded. We illustrate this concept below.

The time evolution of the number of S-I pairs is determined by the following events.

Infection at a rate $\tau$ of a susceptible, $S$ individual by their infectious, $I$ neighbour (in a S-I pair) converts S into I, i.e. $SI\mapsto II$, where $\mapsto$ means 'transformed to'. This process destroys a S-I pair. Similarly, infection at a rate $\tau$ of a susceptible individual 'from the left' in a triple I-S-I, i.e. $I\leftrightarrow SI$ also destroys a S-I pair. However a S-I pair is created as a susceptible individual is infected at the same rate, $\tau$, in a triple I-S-S.

Transmission of the disease from an infectious, $I$ individual to their protective contact, $S_p$ at a rate $\tau_p$ in a triple S-$S_p$-I transforms $S_p$ to $I$, and therefore create a S-I pair.

Recovery of the infectious individual at a rate, $\sigma$ in a pair S-I implies $SI\mapsto SR$. Therefore the process destroys S-I.

Adoption of NPIs at a rate $\xi$, by a state $S$ individual as a result of social learning from their state $S_p$ neighbor in a triple $S_p$-S-I converts $S$ to $S_p$, and therefore it destroys a S-I link.

Adoption of NPIs at a rate $\rho$, by a state $S$ individual due to being in the neighborhood of a state $I$ individual in a pair S-I or a triple I-S-I converts $S$ to $S_p$, and therefore it destroys a S-I link.

Stopping the use of NPIs by a protective individual at a rate $\kappa$ in a $S_p$-I pair increases their susceptibility, i.e. $S_p$ converts to $S$, and the process creates a S-I pair.

To demonstrate the next steps of the derivation of the equation of motion for $[SI]$, the following notations will be useful:

$n_x(i)$: number of state $i$ neighbours of a node $x$;

$n_{xy}(i)$: number of state $i$ neighbours of a node $x$, which has node $y$ as a neighbour;

$\zeta_{x}$: disease state of node $x$;

$\zeta_{xy}$: disease state of an edge involving $x$ and $y$.

Using this notation, the master equation for the dynamics of $[SI]$ can now be represented as the sum of all the events (listed above) as $\frac{d[SI]}{dt}=\sum\limits_{\zeta_{xy}=SS} \tau(n_{xy}(I))(+1)+\sum\limits_{\zeta_{xy}=SI} \tau(n_{xy}(I))(-1)+\sum\limits_{\zeta_{xy}=SS_p} \tau_p(n_{xy}(I))(+1)+$ $\sum\limits_{\zeta_x=S} \sigma(n_x(I))(-1)+ \sum\limits_{\zeta_{xy}=SI} \psi(n_{xy}(I))(-1)+\sum\limits_{\zeta_{xy}=SI} \xi(n_{xy}(S_p))(-1)+$ $\sum\limits_{\zeta_{xy}=SI} \rho(n_{xy}(I))(-1)+\sum\limits_{\zeta_{x}=I} \kappa(n_x(S_p))(+1).$

The positive ($+$) and negative ($-$) signs in the master equation above indicate that the corresponding events create or destroy S-I pairs, respectively.

Next we replace quantities such as $n_x(I)$ and $n_{xy}(I)$ by their population-averaged values (means) plus the stochastic deviations of those quantities from the means at nodes $x$ and pairs $xy$. Let $n(i|j)$ be the population-averaged value of $n_x(i)$ when $\zeta_{x}=j$ and let $n(i|jk)$ be the population-averaged value of $n_{xy}(i)$ when $\zeta_{xy}=jk$. Then at each node we replace $n_{xy}(I)$ by $n(I|SI)+\theta_{xy}(I|SI)$ where $\theta_{xy}(I|SI)$ represents the stochastic fluctuation from the mean. The resulting expression is then simplified by taking out constants such as $n(I|SI)$ and the model parameters out of the sums and further noting that terms such as $\sum\limits_{\zeta_x=S}\theta_x(I|S)$ that represent fluctuations are zero by definition. Furthermore the following identities (which apply to all network types):

$n(i|jk)= \frac{[ijk]}{[jk]}$; $n(i|ji)= 1+\frac{[iji]}{[ji]}$; $n(i|j)= \frac{[ij]}{[j}$ and $n(i|i)= 1+\frac{[ii]}{[i]}$,

enable us to write the equation of motion for $[SI]$ as

$\frac{d[SI]}{dt}=\tau([ISS]-[ISI]-[SI])+\tau_p[SS_pI]-\sigma[SI]-\xi[S_pSI]+\kappa[S_pI]-\rho([ISI]+[SI])$.

We assume the disease spreads a regular network where neighbors of an individual are themselves conditionally independent, therefore, third order correlations take the form

$n(i|jk)=\frac{(n-1)}{n}n(i|j)$ and $n(i|ji)=1+\frac{(n-1)}{n}n(i|j)$.

That is, to close the system (i.e. approximate higher-order moments by lower-order moments) of equations we use the binomial ordinary pair approximation (OPA):

$[ijk]=\frac{(n-1)}{n}\frac{[ij][jk]}{[j]}.$

(14)

The binomial OPA is based on the idea that the disease state of a node $j$ is directly influenced by the states of two of its indirectly connected neighbors $i$ and $k$. That is, there are no triangles in the network.

Derivation of the basic reproduction number. Here we derive the expressions for $C_{SI}^{min}$ and $C_{S_pI}^{min}$, and present expressions of the basic reproduction number resulting from a number of disease scenarios.

$C_{SI}=\frac{N}{n}\frac{[SI]}{[S][I]}$, therefore the equation of motion for $C_{SI}$ is given by

$\frac{d}{dt}C_{SI}=\frac{N}{n}\bigg(\frac{1}{[S][I]}\frac{d}{dt}[SI]+\frac{[SI]}{[S][I]}(-\frac{1}{[I]}\frac{d}{dt}[I]-\frac{1}{[S]}\frac{d}{dt}[S])\bigg)$.

We substitute the equations of motion for the number of susceptible-infectious pairs, $[SI]$, the number of infectious individuals, $[I]$, and the number of susceptible individuals, $[S]$ from Equation (1) into the equation above, and approximate triples by the OPA to show that

$\frac{d}{dt}C_{SI}=\tau(n-1)\frac{[S]}{[N]}C_{SS} C_{SI}-\tau(n-1)\frac{[I]}{N}C_{SI}^2-\tau C_{SI}+$$\tau_p(n-1)\frac{[S_p]}{N}C_{S_pS}C_{S_pI}-\sigma C_{SI}-\xi(n-1)\frac{[S_p]}{N}C_{S_pS} C_{SI}+\kappa\frac{[S_p]}{[S]}C_{S_pI}$$-\rho(n-1)\frac{[I]}{N}C_{SI}^2-\rho C_{SI}-\tau n\frac{[S]}{N}C_{SI}^2-\tau_p n\frac{[S_p]}{N}C_{S_pI}C_{SI}+\sigma C_{SI}+\tau n\frac{[I]}{N}C_{SI}^2$$+\xi n\frac{[S_p]}{N}C_{S_pS} C_{SI}-\kappa\frac{[S_p]}{[S]}C_{SI}+\rho n\frac{[I]}{N}C_{SI}^2.$

Similarly, the equation of motion for the correlation between susceptible individuals who protect and infectious individuals can be written as

$\frac{d}{dt}C_{S_pI}=\tau(n-1)\frac{[S]}{[N]}C_{SS_p} C_{SI}+\tau_p(n-1)\frac{[S_p]}{N}C_{S_pS_p}C_{S_pI}$$-\tau_p(n-1)\frac{[I]}{N}C_{S_pI}^2-\tau_p C_{S_pI}-\sigma C_{S_pI}+\xi(n-1)\frac{[S]}{N}C_{S_pS} C_{SI}-\kappa C_{S_pI}+$$\rho \frac{[S]}{[S_p]}C_{SI}-\tau_p n\frac{[S_p]}{N}C_{S_pI}^2-\tau n\frac{[S]}{N}C_{S_pI}C_{SI}+\sigma C_{S_pI}+\tau_p n\frac{[I]}{N}C_{S_pI}^2-$$\xi n\frac{[S]}{N}C_{S_pS} C_{S_pI}+\kappa C_{S_pI}$.

We make biologically reasonable assumptions about the disease to simplify the equations above as follows. At the beginning of the epidemic there are very few infectious individuals (initial inoculation: $[I]=1$) such that the entire population, $N$ comprises almost only of susceptible individuals who protect, $[S_p]$ and those who do not protect, $[S]$ i.e. $[I]<<N$ (where total population $N$ is very large) and $[S_p]+[S]\approx N$. We remind the reader that our derivation of $R_0$ is based on the idea that both social and exposure learning take place only after the disease has been introduced. Therefore, we assume that at the initial stage of an outbreak the public has little information about the disease and only a small proportion of the population is aware and can decide to practice NPIs. Thus, at the beginning of an outbreak $[S_p]/N=s_p$, $[S]/N=1-s_p$, where $0<s_p<<1$. Therefore, we can simplify further the equations of motion for $C_{SI}$ and $C_{S_pI}$ above by equating to zero all terms in which the denominator is large and $[I]$ is the numerator.

Although it may be necessary to also derive the equations of motion for three other correlation functions (for $C_{SS},C_{S_pS}$ and $C_{S_pS_p}$) that appear in the equations of motion for $C_{SI}$ and $C_{S_pI}$ above, we estimate them from the network configuration of the disease at the beginning of an outbreak. This step will help explore the relationship between the initial network configuration of the population with respect to the disease, and the evolution of the epidemic outbreak. We assume that at the beginning of the outbreak susceptible neighboring individuals mix homogeneously. That is, $C_{SS}\approx1$. This value remains constant throughout calculations of the basic reproduction number for the initial network configurations considered in this paper, but the same does not hold for $C_{S_pS}$ and $C_{S_pS_p}$, since the latter take different values depending on various initial distributions of state $S$ and state $S_p$ individuals around the infection source. Since at the beginning of the outbreak $s_p$ is very small, it is reasonable to assume that $[S]\approx N$. Therefore, at the initial stage of an infection $C_{S_pS}=\frac{N}{n}\frac{[S_pS]}{[S_p][S]}\approx \frac{1}{n}\frac{[S_pS]}{[S_p]}$ while $C_{S_pS_p}=\frac{N}{n}\frac{[S_pS_p]}{[S_p][S_p]}$. These values are calculated from actual initial network configurations as shown in Figure 1. We proceed with the derivation of $C_{SI}^{min}$ and $C_{S_pI}^{min}$.

Note that now

$\frac{d}{dt}C_{SI}=\tau(n-1)(1-s_p) C_{SI}-\tau C_{SI}+\tau_p(n-1)s_pC_{S_pS}C_{S_pI}+$$\xi s_p C_{S_pS}C_{SI}+\kappa s_pC_{S_pI}-\rho C_{SI}-\tau n(1-s_p)C_{SI}^2-\tau_p ns_pC_{S_pI}C_{SI}-\kappa s_pC_{SI}$.

and

$\frac{d}{dt}C_{S_pI}=\tau(n-1)(1-s_p) C_{S_pS}C_{SI}+\tau_p(n-1)s_pC_{S_pS_p}C_{S_pI}-\tau_p C_{S_pI}+\xi(n-1)$$(1-s_p)C_{S_pS} C_{SI}+\rho \frac{1-s_p}{s_p}C_{SI}-\tau_p ns_pC_{S_pI}^2-\tau n(1-s_p)C_{S_pI}C_{SI}-\xi n(1-s_p) C_{S_pS}C_{S_pI}$

Solving $\frac{d}{dt}C_{SI}=0$ and $\frac{d}{dt}C_{S_pI}=0$ yields:

$C_{SI}^{min}=\frac{R-\tau_pns_pC_{S_pI}^{min}+\sqrt{(R-\tau_pns_pC_{S_pI}^{min})^2+4\tau n s_p(1-s_p)\bigg(\tau_p(n-1)C_{S_pS}+\kappa\bigg) C_{S_pI}^{min}}}{2\tau n(1-s_p)},$

(15)

$C_{S_pI}^{min}=\frac{Q+\sqrt{\bigg(T-\tau n(1-s_p)C_{SI}^{min}\bigg)^2+4\tau_p n s_p(1-s_p)\bigg((n-1)(\tau+\xi)C_{S_pS}+\rho/s_p\bigg) C_{SI}^{min}}}{2\tau_p ns_p},$

(16)

where

$Q=T-\tau n(1-s_p)C_{SI}^{min}$, $R=\tau(n-1)(1-s_p)-\tau -\rho -\kappa s_p+\xi s_pC_{S_pS}$ and $T=\tau_p(n-1)s_pC_{S_pS_p}-\tau_p -\xi n(1-s_p)C_{S_pS}$.

Simplifying assumptions

Note that at the beginning of an outbreak the initial network configuration constitutes very few susceptible individuals who practice NPIs, so that while $s_p\approx O(1/N)$ (for a network where the infection source has at least 1 protective contact), $C_{S_pI}$ is large (i.e. $C_{S_pI}^{min}=O(N)$). Therefore we can simplify Equation (15) by assuming that $s_pC_{S_pI}^{min}\approx 1$, so that $C_{SI}^{min}\approx\frac{R-\tau_pn+\sqrt{(R-\tau_pn)^2+4\tau n (1-s_p)\bigg(\tau_p(n-1)C_{S_pS}+\kappa\bigg) }}{2\tau n(1-s_p)}=\chi$ is a constant determined by the initial proportion of susceptible individuals who protect, $s_p$, the model parameters $\tau,\tau_p,\sigma,\rho,\xi$ and $\kappa$, as well as the initial network configuration-specific values of correlation functions $C_{S_pS}$ and $C_{S_pS_p}$. Substituting $\chi$ and the resulting expression of $C_{S_pI}^{min}$ into Equation (10) yields

$R_0\approx\frac{T+n\tau(1-s_p)\chi+\sqrt{\bigg(T-\tau n(1-s_p)\chi\bigg)^2+4\tau_p n s_p(1-s_p)\bigg((n-1)(\tau+\xi)C_{S_pS}+\rho/s_p\bigg)\chi}}{2\sigma},$

(17)

where $T=\tau_p(n-1)s_pC_{S_pS_p}-\tau_p -\xi n(1-s_p)C_{S_pS}$,

$\chi\approx\frac{R-\tau_pn+\sqrt{(R-\tau_pn)^2+4\tau n (1-s_p)\bigg(\tau_p(n-1)C_{S_pS}+\kappa\bigg) }}{2\tau n(1-s_p)}$ and $R=\tau(n-1)(1-s_p)-\tau -\rho -\kappa s_p+\xi s_pC_{S_pS}$.

Simulation results involving the basic reproduction number (in the Results section) are based on Equation (17).

Below we explore other scenarios of the disease to present simpler expressions of $R_0$. We consider cases where protective susceptible individuals are assumed to maintain the habit of practicing NPIs throughout the epidemic outbreak (i.e. $\kappa=0$). Also let the initial network configuration constitute 1 infectious individual with 1 state $S_p$ neighbor (who also has 1 state $S_p$ contact) and let the rest of the population be state $S$ individuals so that for a large population size, initially $[S]\approx N$. Thus, the properties of the network at the initial stage of an outbreak are $s_p=2/N, C_{S_pS}=5/2n,C_{S_pS_p}=N/4n$.

(a) Adoption of NPIs through social learning only

Here individuals are assumed to learn about the disease, and therefore adopt NPIs, from their contacts who already practice preventative behavior, and not from their infectious neighbors. That is we let $\xi> 0$, and $\rho=0$.

If the population size, $N$ is very large, and there are very few state $S_p$ individuals at the beginning of the outbreak, so that $s_p=\frac{[S_p]}{N}\approx 0$, then we can simplify $R$ by noting that $1-s_p\approx 1$ and $\xi s_pC_{S_pS}\approx 0$ (since $0\leq\xi\leq 1$ and $C_{S_pS}=O(1)$). Therefore

$R\approx\tau(n-2)$.

Also, we simplify $T$ by further noting that $s_pC_{S_pS_p}\approx O(1)$ and $nC_{S_pS}\approx O(1)$, so that

$T\approx\tau_p(n-2) -\xi$.

Thus, the expression of the basic reproduction number can be written as

$R_0\approx\frac{\tau_p(n-2) -\xi+\tau n\chi+\sqrt{\bigg(\tau_p(n-2) -\xi-\tau n\chi\bigg)^2+4\tau_p s_p(n-1)(\tau+\xi)\chi}}{2\sigma},$

(18)

where $\chi\approx\frac{\tau(n-2)-\tau_pn+\sqrt{\bigg(\tau(n-2)-\tau_pn\bigg)^2+4\tau \tau_p(n-1)}}{2\tau n}$.

High efficacy case

Here we estimate the expression of $R_0$ for a case where individuals acquire preventive behavior through interaction with contacts who practice NPIs only, and the adopted NPIs are highly effective (i.e. $\tau_p$ is small so that $\tau_p^2\approx 0$). Therefore,

$\bigg(\tau_p(n-2) -\xi-\tau n\chi\bigg)^2=\tau^2n^2\chi^2-2\tau_p(n-2)(\xi+\tau n\chi)+\xi(\xi+2\tau n\chi)+\tau_p^2(n-2)^2\approx \tau^2n^2\chi^2-2\tau_p(n-2)(\xi+\tau n\chi)+\xi(\xi+2\tau n\chi)$

and

$\bigg(\tau(n-2)-\tau_pn\bigg)^2=\tau^2(n-2)^2-2\tau\tau_pn(n-2)+\tau_p^2n^2\approx \tau^2(n-2)^2-2\tau\tau_pn(n-2)=\tau(n-2)\bigg(\tau(n-2)-2\tau_pn\bigg)$.

The resulting expression of the basic reproduction number is

$R_0\approx\frac{\tau_p(n-2) -\xi+\tau n\chi+\sqrt{\tau^2n^2\chi^2-2\tau_p(n-2)(\xi+\tau n\chi)+\xi(\xi+2\tau n\chi)+4\tau_p s_p(n-1)(\tau+\xi)\chi}}{2\sigma},$

(19)

where

$\chi\approx\frac{\tau(n-2)-\tau_pn+\sqrt{\tau(n-2)\bigg(\tau(n-2)-2\tau_pn\bigg)+4\tau \tau_p(n-1)}}{2\tau n}$.

Model parameter-based $R_0$ for high efficacy case

We simplify Equation (19) further by prescribing a reasonable model parameter regime. Let $N=40000,s_p=2/N,n=4$, $\tau=1$ $day^{-1}$, $\tau_p=0.0025$ $day^{-1}$, $\sigma=0.25$ $day^{-1}$ and $\xi=0.25$ $day^{-1}$. Then the following features of Equation (19) become apparent:

$\tau(n-2)>>\tau_pn$;

$\tau(n-2)>>2\tau_pn$;

$\xi>>\tau_p(n-2)$;

$\tau n\chi>>\tau_p(n-2)$;

$\tau^2n^2\chi^2>>4\tau_p s_p(n-1)(\tau+\xi)\chi$;

$\tau^2n^2\chi^2>>2\tau_p(n-2)(\xi+\tau n\chi)$;

$\xi(\xi+2\tau n\chi)>>4\tau_p s_p(n-1)(\tau+\xi)\chi$;

$\xi(\xi+2\tau n\chi)>>2\tau_p(n-2)(\xi+\tau n\chi)$.

We use these observations to cancel terms of Equation (19) that are insignificant (as per the prescribed parameter regime) to write the expression of the basic reproduction number as

$R_0\approx\frac{\tau n\chi -\xi+\sqrt{\tau^2n^2\chi^2+\xi(\xi+2\tau n\chi)}}{2\sigma},$

(20)

where

$\chi\approx\frac{\tau(n-2)+\sqrt{\tau^2(n-2)^2+4\tau \tau_p(n-1)}}{2\tau n}$.

(b) Adoption of NPIs due to exposure learning only

Here we consider a scenario where individual members of the population gain awareness about the disease, and in turn adopt NPIs, due to being next to infectious contacts only. Thus, we assume $\rho>0$ and $\xi=0$.

Applying similar arguments as in part (a) above, we simplify the original values of $R$, $T$ and $\chi$ so that $R\approx\tau(n-2)-\rho$, $T\approx \tau_p(n-2)$ and

$R_0\approx\frac{\tau_p(n-2) +\tau n\chi+\sqrt{\bigg(\tau_p(n-2) -\tau n\chi\bigg)^2+4\tau_p n s_p\bigg(\tau(n-1)C_{S_pS}+\rho/s_p\bigg)\chi}}{2\sigma},$

(21)

where

$\chi\approx\frac{\tau(n-2)-\rho-\tau_pn+\sqrt{\bigg(\tau(n-2)-\rho-\tau_pn\bigg)^2+4\tau \tau_p(n-1)}}{2\tau n}$.

High efficacy case

Applying the condition for a high efficacy case (i.e. $\tau_p<<\tau$) and simplifying assumptions also applied in part (a) to a scenario where susceptible individuals adopt positive behavior through exposure learning only, transforms Equation (21) to

$R_0\approx\frac{\tau_p(n-2) +\tau n\chi+\sqrt{\bigg[\tau^2n^2\chi-2\tau\tau_pn(n-2)+4\tau\tau_p s_p(n-1)+4\tau_p\rho n \bigg]\chi}}{2\sigma},$

(22)

where

$\chi\approx\frac{\tau(n-2)-\rho-\tau_pn+\sqrt{\tau^2(n-2)^2-2\tau(n-2)(\rho+\tau_pn)+\rho(\rho+2\tau_pn)+4\tau \tau_p(n-1)}}{2\tau n}.\nonumber$

Model parameter-based $R_0$ for high efficacy case

We prescribe the same parameter regime used in part (a) above, but note that here $\xi=0$. Thus, $N=40000,s_p=2/N,n=4$, $\tau=1$ $day^{-1}$, $\tau_p=0.0025$ $day^{-1}$, $\sigma=0.25$ $day^{-1}$ and $\rho=0.25$ $day^{-1}$. We cancel out parts of Equation (22) that are numerically less significant so that the expression of the basic reproduction number becomes

$R_0\approx\frac{\tau n\chi+\sqrt{\bigg(\tau^2n^2\chi+4\tau_p\rho n \bigg)\chi}}{2\sigma},$

(23)

where

$\chi\approx\frac{\tau(n-2)-\rho+\sqrt{\tau^2(n-2)^2-2\tau\rho(n-2)+\rho^2+4\tau \tau_p(n-1)}}{2\tau n}.\nonumber$

Scenarios considered for the development of the above expressions of the basic reproduction number, are summarized in Table 1.

---