A review of the applications of ultra-high performance concrete in flat components and the associated fire-induced spalling risk

1.   Introduction

The missile target allocation (MTA) problem is an essential expression of the weapon target assignment (WTA) problem in the field of military operations research ^[1]. In essence, the MTA problem belongs to the resource allocation problem, which also widely exists in other real-world fields ^[2,3,4]. The issue addressed in this paper is that limited missiles need to intercept and strike targets, satisfying the expectations of minimizing the survivability of targets and minimizing the cost consumption of missiles. Recent studies of scholars ^[5,6] have reported that the WTA problem is NP-complete, which belongs to the typical constrained combinational optimization problem. Specifically, the WTA problem has been divided into two versions in more detail, static WTA (SWTA) problems and dynamic WTA (DWTA) problems ^[7]. Furthermore, scholars have focused on the research of DWTA and derived multi-stage WTA (MWTA) problems ^[8], and multi-objective WTA (MOWTA) problems ^[9] in order to describe the battlefield situation. In this paper, we further investigate a multi-stage MTA (M-MTA) problem of a multi-objective optimization version by combining MWTA and MOWTA problems.

The cooperation of multiple missiles can ensure the accomplishment of striking targets, where these missiles must be strictly independent of each other during this progress. What is more, more complex constraints should be taken into account in real-world problems. Meanwhile, using missiles during the allocation is another primary concern in practical applications. Therefore, MTA belongs to the multi-objective optimization problem (MOP) with constraints in real-world applications, whose general mathematical formulation is stated as follows.

where $\textbf{x} = (x_1, x_2, \ldots, x_N)$ denotes the candidate solutions, which belongs to the decision space $\Omega$. $\boldsymbol{F}\textbf{(x)}$ is the conflicting objective function, where $M$ means the number of the objective function. $g_i(\textbf{x})$ and $h_e(\textbf{x})$ express inequality constraints and equality constraints, respectively.

Thus, obtaining the optimal allocation of limited missiles to targets cooperatively is challenging. In the past decades, several attempts have been made to develop various efficient algorithms to optimize the WTA problem, which contains many proposed exact methods ^[1,10], and heuristic algorithms ^[11,12]. In terms of exact methods, many technologies have sprung up, such as the branch-and-bound, the maximum marginal return ^[13], dynamic programming, and so on. However, rapid changes in the computational scale have significantly affected applying heuristic algorithms to solve WTA problems. The swarm optimization algorithm ^[14,15] and genetic algorithm with the greedy mechanism ^[16] are the breakthrough in solving the SWTA problem. Improved artificial bee colony algorithm ^[17] has also made remarkable achievements in DWTA problems. In terms of the research of MOWTA problems, scholars ^[18,19] have successfully applied and improved based on multi-objective optimization evolutionary algorithms (MOEAs) ^[20,21] to solve the problem.

Significantly, a fast and elitist multiobjective genetic algorithm (NSGA-II) ^[20] on the basis of NSGA ^[22] is an excellent multi-objective optimization algorithm, which is mainly composed of fast non-dominated sorting (fast-NS), crowding distance (CD), and the elite strategy. The operations of NSGA-II are driven by genetic mechanisms. The sorting method is designed to divide several subspaces containing feasible solutions. The advantage of fast-NS is that each solution $\gamma$ is compared with all solutions in order by using two defined parameters: 1) $n_{\gamma}$: domination count, 2) $S_{\gamma}$: a set of $\alpha$ dominates other solutions, and filed into the corresponding dominant front finally. The CD is proposed to replace the traditional shared function for density estimation, and the elite strategy is combined with crowding distance to ensure the distribution of solutions. In the same dominant front, the CD of each solution $\gamma$ is defined as the Manhattan distance of solution $\gamma+1$ and solution $\gamma-1$ in the objective space. In order to make NSGA-II more generalized for complex combinatorial optimization problems, many scholars ^[23,24,25] have improved the algorithm from the perspective of feasibility solution generation and density estimation approach. As a basic framework, NSGA-II has been successfully involved in many complex optimization problems in science and engineering.

In this paper, a multi-objective mathematical model of M-MTA is formulated. Then, we propose a novel NSGA-II framework (NSGA-MTA) for solving this problem. The framework mainly constitutes the rule-based initialization, the hybrid encoding mechanism, an efficient non-dominated sorting ^[26] (efficient-NS), and genetic operators with the greedy mechanism and random repair strategy. Furthermore, the Taguchi method is adopted to verify the effectiveness of the proposed strategy. There are some main innovations and contributions in this article as follows:

$1)$ A multi-objective mathematical model of M-MTA is formulated to describe the survivability of targets and the cost consumption of missiles simultaneously. Meanwhile, the constraints that can reflect the characteristics of multi-stage and combat are proposed.

$2)$ NSGA-MTA derived from NSGA-II is proposed for solving the M-MTA, and it is further demonstrated that the performance is superior to that of other excellent algorithms.

a) A hybrid encoding mechanism is built to express the allocation scheme, which combines integer coding with binary coding to involve the algorithm.

b) A rule-based initialization is designed to generate feasible solutions in advance according to prior knowledge.

b) Genetic operators with greedy mechanisms and random repair strategies are constructed to maintain the trade-off between exploration and exploitation and further handle the constraints.

The remainder of this paper is organized as follows. Section 2 defines the detailed mathematical model of the M-MTA. The proposed NSGA-MTA is presented in detail in Section 3. Preliminary numerical experiments are implemented in Section 4. Section 5 gives the experimental results and the discussion based on obtained results. Finally, Section 6 provides the conclusion of this paper.

2.   Problem description and formulation

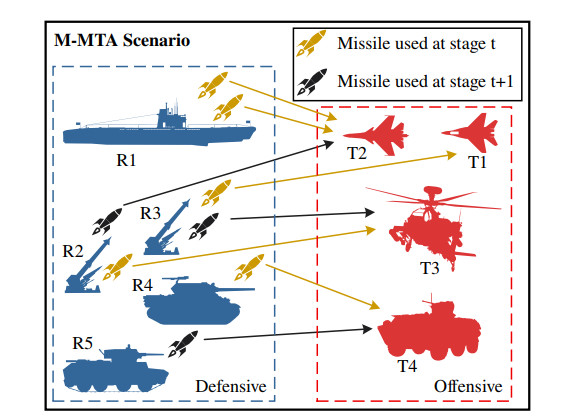
In this paper, the multi-stage MTA (M-MTA) occurs in this scenario ^[27] wherein $R_n$ different defensive missile types are allocated to strike $T_n$ offensive targets in $S_n$ stages cooperatively, depicted in Figure 1. Meanwhile, we assume there will be cost consumption after the allocation, and each target has its threat value $v_t$. Without a doubt, each missile has a corresponding capability to destroy targets at each stage, wherein the capability is defined as the kill probability. In this paper, the kill probability is determined as a probability value $p_{rt}(s)(r \in [1, R_n], t \in [1, T_n], s\in [1, S_n])$, which is stochastic and independent. Last but not least, each target must match at least one missile for a successful interception.

The allocation scheme of M-MTA intuitively is expressed as mapping by $\boldsymbol{X} = [[x_{rt}(s)]_{R_n \times T_n}]_{1 \times S_n}$. Furthermore, $x_{rt}(s)$ is the decision variable, which means that $r$ th missile is allocated to $t$ target at $s$ stage. This variable is defined as a binary variable. That is, if the allocation is determined, it will be 1. Otherwise, it is 0. Specifically, the notations adopted in this formulation will briefly be described in Table 1. Therefore, the objective function $F_1$, $F_2$ of M-MTA is established as follows.

Specifically, ${\prod\limits_{s = h}^{{S_n}}{\prod\limits_{r = 1}^{{R_n}(h)} {{{\left({1 - {p_{rt}}(s)} \right)}^{{x_{rt}}(s)}}} } }$ denotes the survive expectation of $t$ th target after $S_n$ stages. Thus, $F_1$ expresses the total survival expectation of targets after all stages. Meanwhile, $F_2$ represents the cost consumption of missiles during the allocation. Finally, it is also necessary to design reasonable constraints to solve the above problem. From the perspective of reliability and feasibility, the following constraints are built.

Constraints (2.2) mean that each target is strictly allocated to at least one missile type in terms of reliability. Constraints (2.3) indicate the maximum amount of each missile that can be allocated to strike the target. The same type of missile can destroy one target in all stages. Then the type can be regarded as several independent same missiles. What is more, this constraint also limits the cost of missiles. Constraints (2.4) represent the multi-stage feature, which reflects that the actual allocation of each stage must obey the feasibility allocation. Preliminary data and decision-makers often obtain feasibility allocation to achieve the expected allocation in the corresponding stage.

Furthermore, the definition of feasibility variables is similar to the decision variable. If the allocation is feasible, the variable ${z_{rt}(s)}$ is 1. Otherwise, it is 0, where the formulation is ${z_{rt}(s)} = \left\{ {\begin{array}{*{20}{l}} {1, \text{if the allocation is feasible at } s \text{ stage}, }\\ {0, \text{otherwise.}} \end{array}} \right.$. Therefore, we can transform the M-MTA into a multi-objective optimization model as follows.

3.   Algorithm framework for M-MTA

This paper focuses on determining the optimal allocation scheme of M-MTA. Hence, we proposed a problem-specific framework (NSGA-MTA) based on the NSGA-II, shown in Algorithm 1. In the beginning, an initial population with feasible solutions will be obtained by the designed rule-based initialization. Then, the population will be selected through the binary tournament and genetic operators with the greedy mechanism and random repair strategy iteratively. Next, a novel Efficient-NS with low complexity provides a search strategy for non-dominated solutions, and CD plays a role in density estimation.

Meanwhile, the proposed hybrid encoding mechanism will transform the best individuals into the expected binary decision matrix. Finally, the corresponding objective function will also be evaluated. The detailed contributions of NSGA-MTA are depicted in the following subsections.

3.1.   Hybrid encoding

The hybrid encoding mechanism that expresses integer encoding and binary encoding is developed for M-MTA in this paper. Binary encoding is a very intuitive representation of the problem and algorithm construction. However, a large number of redundant 0s and 1s will cause dimension explosion, especially when $R_n$, $T_n$, and $S_n$ increase with the complexity of the problem. Therefore, integer encoding is implemented to express feasible solutions at runtime, and binary encoding is adopted to speed up the calculation at function evaluation. Moreover, integer encoding can effectively guarantee the Constraints (2.2) of the proposed M-MTA, and it is more suitable than permutation encoding in terms of repeatable expression.

The encoding proposed in this subsection constructs a mapping relationship of decision variables, taking Figure 2 as an example. The value of each individual represents the target number that the index number weapon strikes at a particular stage. As shown in Figure 2, the value of the first position representing missile 1 is assigned to damage target 4 in the first stage.

In general, the beginning will generate a population of N individuals ($I_i, i \in [1, N]$) with $S_n$ subspaces, each of which represents an allocation scheme of the proposed problem. Precisely, each element of individuals in each subspace corresponds to the mapping of missile type r allocated to target t at stage s. $R_n$ and $S_n$ determine the length of individuals. Then, each mapping relationship will be transformed into a straightforward binary matrix $\boldsymbol{X}$ for function evaluation. Besides, the repeatable expression mentioned above is ubiquitous in the M-MTA. The execution process of this encoding with $S_n$ stages is described in detail in Algorithm 2.

Appropriate encoding can provide the basis for evolution, but enhancing the diversity and convergence of the population also needs to design proper heuristic initialization and match genetic operators.

3.2.   Rule-based initialization

In general, the initialization method of MOEAs usually adopts the random generation mechanism. Although this is effective for some benchmark problems, it is also necessary to design a rule-based initialization to construct feasible solutions for real-world problems. In other words, the search space exploration will only be efficient if we continue to apply the random generation mechanism. When a reasonable rule-based method is taken into account in the mechanism, this phenomenon will be alleviated to a great extent. Significantly, the whole evolutionary process will be accelerated toward the global optimal or near-optimal solutions. However, suppose the initial population is full of many rule-based solutions. In that case, the algorithm will fall into the local optimum, and the population also will need more diversity. Therefore, a rule-based initialization with priority is developed to generate the initial population in this paper.

The rule-based initialization for M-MTA is inspired by design in the DWTA problem ^[17] to generate solutions. The proposed initialization not only adopts the heuristic of missile choice priority and sequence calculation to increase feasible solutions but also applies the random generation to ensure diversity. The proposed method aims to get the allocation scheme by maximizing the expected damage effectiveness of missiles to targets based on prior knowledge. The prior damage effectiveness $p_{rt}^{prior}(s)$ of missile $r$ to target $t$ at the stage $s$ is calculated as follows.

where definitions of $p_{rt}(s)$ and $v_t$ have been given in Table 1.

The main framework of the proposed rule-based initialization with priority is described in Algorithm 3. Firstly, the random population $\boldsymbol{Pop}_{rnd}$ is constructed according to population size N and decision variable D. Meanwhile, prior knowledge $\boldsymbol{P}_{rt}^{prior}$ can also be obtained via Eq (3.1). Next, we assume that the heuristic mainly follows the rule of missile choice priority, which means that missiles can choose the most threat target based on damage ability. Although feasible solutions are generated under the given data, we also pay attention to the lack of diversity in the population. Synthetically, the sequence calculation is involved in constructing more heuristic solutions, whose purpose is to disorderly sort the given data and obtain more feasible solutions. Finally, the rule-based solutions replace $\boldsymbol{Pop}_{rnd}$ in the proportion of $\rho$ in order to get the population H, where $\rho$ is defined as a dimensionless constant ($\rho \in (0, 1)$).

3.3.   Efficient-NS

The non-dominated sorting method is essential in determining non-dominated fronts as a search strategy. The outstanding advantage of NSGA-II lies in the design of fast-NS, but there are still some redundant comparisons in finding non-dominated solutions. In brief, fast-NS shows that each solution needs to be compared with all solutions in the population to determine the non-dominated front. Then, there will inevitably be many redundant comparisons to aggravate the complexity of the whole algorithm. Hence, a novel efficient-NS is implemented to the improved framework in this paper, which has been proved to have lower complexity and higher efficiency than fast-NS ^[26]. The critical characteristic of efficient-NS is that the solution only needs to be compared once. A new front will be created when the compared solution belongs to something other than the existing non-dominated fronts. This operation only terminates once all the dominant fronts are determined.

The M-MTA has been transformed into a constrained optimization problem above, so we made some problem-specific improvements. Infeasible solutions are repaired by combining the results of heuristic factors and the constraints. Meanwhile, any objective function can be sorted in ascending order. The efficient-NS is expressed in Algorithm 4 in detail.

3.4.   Offspring Generation with random repair strategy

The genetic algorithm drives the main framework of NSGA-II, so selection, crossover, and mutation operations must occur during the offspring generation. The selection operator is a significant element in the whole generation, directly determining the parent individuals participating in the next step. Hence, we adopt the binary tournament select approach with low complexity and adjustable selection pressure to generate parent individuals. This approach aims at selecting two individuals randomly from the population and defining the winner with a better objective function value as the parent individual.

Furthermore, the crossover operator and the mutation operator are involved in Algorithm 5 (Variation) in this paper, both necessary conditions for evolution in maintaining diversity. Recently, various crossover and mutation operators have been conducted by many scholars, such as single-point crossover, order crossover, uniform crossover and simulated binary crossover (SBX), simple mutation, uniform mutation, and Gaussian mutation. Nevertheless, it is worth noting that the proposed encoding contains repeatable integer encoding, and the M-MTA belongs to the combinational optimization problem. Therefore, we design the greedy mechanism and the random repair strategy to add the partially mapped crossover (PMX) and inverse mutation in this paper, respectively.

3.4.1.   The design of greedy mechanism

Moreover, the greedy mechanism is vital in preserving better genes during the crossover. When the parents have the same gene in the same position, Eq (3.1) is applied to judge whether the current gene is good. If the selected genes are good, they will inherit from the parents to offspring. Finally, two positions are randomly selected for a crossover at other positions where good genes are removed. In particular, if no good genes exist, the crossover will be done according to the PMX operator. The primary process can be illustrated in Algorithm 6 (Crossover with greedy mechanism).

3.4.2.   The design of random repair strategy

Last but not least, the random repair strategy is introduced in mutation, which will randomly select the generated offspring and repair the infeasible individuals via handling the Constraints (2.3) and (2.4). In detail, the strategy aims at querying unassigned targets, randomly reassigning them according to the damage capacity of missiles, and simultaneously repairing the assigned results according to the feasibility constraints. Finally, the repaired individuals rejoin the offspring to participate in the next evolution. Notably, the mutation follows the inverse mutation for individuals satisfying the constraints. The detailed process is described in Algorithm 7 (Random repair strategy).

3.5.   Complexity analysis

In this subsection, we further complete the complexity analysis on the proposed NSGA-MTA, where m is denoted as the number of objectives. Firstly, the time complexity of initialization is $O(m \cdot N \cdot \rho)$. Then, the process of Efficient-NS is $O(m \cdot N \cdot \sqrt{N})$. Next, generating solutions based on proposed strategies is $O(m \cdot N)$. Finally, $O(m \cdot N \cdot \log N \cdot Iter)$. So, the time complexity of NSGA-MTA is $O[m \cdot N \cdot (1 + \rho + \sqrt{N} + \log N \cdot Iter)]$.

4.   Preliminary numerical experiments

This section is devoted to evaluating and comparing the proposed NSGA-MTA. Firstly, a test-case generator for the M-MTA is constructed to provide 15 different problems with various scenarios. Then, four prevailing MOEAs were selected for the performance comparison, and some parameters were determined from the relevant literature. Meanwhile, we introduce four metrics to measure performance.

4.1.   Test-case generator

In this subsection, we design the test-case generator to provide 15 different M-MTA scenarios, and each represents the corresponding problem scale to evaluate the algorithm's performance. Moreover, we refer to the settings in ^[9,28] to construct the essential parameters in the model, which will be further generated within the interval based on the following rules.

$1)$ Generation of $v_t$. The threat value of target t ($\forall t \in [1, T_n]$) is defined as a random value in a range between 1 and 100.

$2)$ Generation of $p_{rt}(s)$, and $c_{rt}(s)$. The damage capability and cost of missile r to target t at s stage are described as follows, respectively.

where $\forall r \in [1, R_n]$, $\forall t \in [1, T_n]$, and $\forall s \in [1, S_n]$; rand denotes a uniformly distributed number between 0 and 1; $p_h$ and $p_l$ are the constants with $0 < p_l < p_h < 1$ which represent the limitation of damage capability; Similarly, $c_h$ and $c_l$ are the constants with $0 < c_l < c_h < 1$ which mean the available cost consumption.

The parameters can be referenced as $p_h = \{0.9, 0.95, 0.99\}$, $p_l = \{0.55, 0.6, 0.65\}$, $c_h = \{8, 10, 12\}$ and $c_l = \{5, 6, 7\}$, referred to the settings in ^[6,9,28]. Therefore, we further apply the Taguchi method to tune these parameters as follows, where the main effect plot for tuning parameters is shown in Figure 3. Referring to the data under the maximum SN ratios in Figure 3, the parameters are determined as $p_l = 0.55, p_h = 0.95, c_l = 5$, and $c_h = 10$. $3)$ Generation of $Num_r$. The available number of missile r ($\forall r \in [1, R_n]$) will be discussed in line with different scenarios.

4.2.   Comparison algorithm and Performance metrics

4.2.1.   Comparison algorithm

In order to verify the effectiveness of the improvements, we compare NSGA-MTA with four algorithms that have shown excellent performance in the constrained optimization problem. These algorithms include Pareto-based algorithm (NSGA-II ^[20], NSGA-III ^[29], C-TAEA ^[30]), and decomposition-based algorithm (C-MOEA/D ^[31]). More importantly, these algorithms had shown superior performance in solving the allocation problem ^[12,32,33] discussed in this paper.

4.2.2.   Performance metrics

Furthermore, this paper introduces four state-and-art metrics to compare the performance among different algorithms.

Inverted generational distance (IGD) ^[34] The IGD metric can express the diversity and convergence of solutions simultaneously, whose characteristic is to obtain the average distance between known PF ($P$) and true PF ($P^*$). The algorithm with smaller $IGD(P, P^*)$ shows that the obtained $P$ is closer to $P^*$, so the performance of this algorithm will be better. The detailed formulation is as follows.

Generally, $P^*$ means a set of points distributed along the true PF or nearly true PF in the objective space. $d(\textbf{k}, P)$ denotes the minimum Euclidean distance between k in $P^*$ and elements in $P$. In this paper, the discussed problem belongs to a real-world problem, so its true PF is hard to obtain. We run different algorithms independently 31 times and sort all the obtained fronts via non-dominate sorting. Finally, the first front is determined to be nearly true PF ($P^*$).

Inverted generational distance plus (IGD+) ^[35] The IGD+ metric further measures the diversity and convergence by slightly improving the distance calculation of IGD. The improved distance $d^{+}(\textbf{k}, \textbf{a})$ between $\textbf{k} = (k_1, k_2, \dots, k_m)$ in $P^{*}$ and the solution $\textbf{a} = (a_1, a_2, \dots, a_m)$ in the dominated region is defined as follows, where $k_m$ and $a_m$ denote the component of $\textbf{k}$ and $\textbf{a}$ in m-th objective space, respectively.

Therefore, the detailed formulation of IGD+ is defined as follows.

where the main form of $IGD+$ is similar to $IGD$, the difference lies in the distance calculation. The nearly true PF ($P^{*}$) is also obtained in the same way as in $IGD$.

Hypervolume (HV) ^[36] The HV metric mainly determines the volume of the objective space that PF weakly dominates to evaluate the performance of algorithms. The detailed definition is shown as follows.

where VOL means the Lebesgue method for measuring volume, and $[b_1^w, b_2^w, \dots, b_n^w]$ denotes the worse points in the hyper-volume and is also defined as the reference point. It can be seen from Eq (15) that the larger HV formed by the reference point and the points in PF, the better the performance of the algorithm.

Therefore, the reference point is of great significance in measuring performance. In this paper, we obtain the worst point from the true PF evaluated above and define the value expanded by 1.1 times as the reference point.

Metric for diversity (DM) ^[37] The metric for diversity (DM) mainly measures the spread of non-dominated solutions on the Pareto front. The detailed formulation is as follows.

where $f^1_i$ and $f^2_i$ means the first and second objective values of the i-th non-dominated solution, respectively.

4.3.   Experiment environment and parameters settings

All the experiments were implemented using Python 3.8.5 and run on a PC with a 5.0 GHz Core i7-12700KF CPU and 32.00 GB RAM, mainly conducted on the Pycharm and Minitab software platforms. Moreover, numerical results are derived from 31 independent runs of each algorithm on the 15 scenarios.

Firstly, 15 different M-MTA scenarios built by the proposed test-case generator are shown in Table 2, where the value in brackets in the $R_n$ column denotes the number of available missiles at each stage. Besides, we divide the problem scale into small ($0 < R_n < 50$), medium ($50\leq R_n < 100$), and large ($R_n\geq100$) according to the number of decision variables ($R_n$). Based on the definition of multi-stage, we also divide the scenarios into two and more than two stages.

Significantly, the population size (PopNum) and the number of iterations (Iter) need to be consistent for each algorithm during the process. According to preliminary experiments ^[9], the effect of PopNum was negligible. Furthermore, we define Iter based on the number of decision variables ($R_n$) as follows, where $NE = PopNum \times Iter$.

The other parameters mainly include the crossover rate ($p_c$), mutation rate ($p_m$), and the ratio of rule-based individuals to initial individuals ($\rho$). Their settings adopted mainly refer to those claimed in ^{[6,17,19,32,38,39]}, shown in Table 3.

5.   Results and discussion

5.1.   Results

Experimental results on the 15 scenarios are involved in this section, which mainly consists of two parts. Regarding the multi-stage nature, we group experiments into scenarios with $S_n = 2$ and $S_n \geq 2$. Besides, the effect of the proposed strategies is further verified by the Taguchi method.

The statistical results (the median and IQR of IGD, IGD+, HV, and DM) about the 31 independent runs are provided in Tables 4 and 5, wherein the best results are highlighted in bold, and IQR is revealed in the corresponding brackets. Furthermore, the Wilcoxon rank-sum test results are added to the table.

5.1.1.   Experiments on effect of proposed NSGA-MTA

A. Results of the scenarios with $S_n = 2$. Table 4 expresses the median and IQR of metrics for each algorithm under the scenarios with $S_n = 2$. The table shows that the proposed NSGA-MTA is statistically better than other algorithms in all metrics. It is worth mentioning that the results obtained by NSGA-MTA under IGD and IGD+ have more significant advantages than other algorithms, significantly as the scale of the problem increases, and the numerical difference is even more significant. However, in Scenario 1, C-MOEA/D is statistically equal to NSGA-MTA in DM by about 7.2%, which means that C-MOEA/D also has certain advantages in obtaining better diversity of PF distribution in small-scale problems.

B. Results of the scenarios with $S_n \geq 2$. In this group, scenarios with $S_n \geq 2$ are experimentally demonstrated individually, whose results are shown in Table 5. Intuitively, it can be argued that the overall performance of MTA is statistically slightly better than other algorithms. In particular, C-TAEA performs better and slightly equal to NSGA-MTA on IGD for Scenarios 8 and 15, respectively. Furthermore, in Scenario 8, NSGA-MTA fails to show the superiority in IGD so that it is only statistically equal to NSGA-II and NSGA-III by about 2%, and 5.2%, and worse than C-TAEA by about 14.2%.

C. Results of all scenarios. The PF of each algorithm in all scenarios under the best IGD+ is visually shown in Figure 4. In each subfigure, the true PF is composed of points (solutions) in the shape of red squares, the first non-dominated layer obtained by all algorithms. Moreover, the PF made of green is obtained by NSGA-MTA, which is the closest to the true PF in all scenarios. Combined with the comprehensive metrics (IGD, IGD+, and HV) in Tables 4 and 5, the results in Figure 4 further prove that the PF obtained by MTA has better convergence and diversity in distribution than others.

5.1.2.   Experiments on effect of proposed strategies

Last but not least, the Taguchi method is adopted to verify the effect of the novel strategies in NSGA-MTA. The detailed descriptions of the levels and the factors in the Taguchi method are shown in Table 6. We select the $L8(2^3)$ orthogonal table for the number of factors and levels. The signal-to-noise (SN) ratio is the measure of robustness, where the larger SN ratio means better algorithm performance.

where Y and $N_o$ represent the response value and the number of rows in the orthogonal table, respectively. Meanwhile, Y is the combination of HV and IGD, where $\frac{HV}{IGD}$ expresses that the larger value is better, and $HV$ and $IGD$ are the medians for 31 independent runs about the $i$th test scenario. Y represents the mean of this ratio under ${N_t}$ test scenarios. All scenarios are chosen to perform the sensitivity verification, so the value of $N_t$ equals 15. Therefore, the results of the orthogonal table are shown in Table 7, and the main effects plot of SN ratios is shown in Figure 5. The SN of No. 6–8 in Table 7 and results in Figure 5 denote that the proposed strategies all significantly contribute to the algorithm's performance and efficiency.

5.2.   Discussion

The numerical results have revealed some significant findings. The first finding is that for multi-stage in the M-MTA problem, the performance exhibited by the NSGA-MTA is enormous compared to those of the algorithms proposed in the literature ^[6,39]. Tables 4 and 5 can intuitively reflect that IGD, IGD+, and HV of NSGA-MTA are statistically improved by about 55, 73, and 36% compared with NSGA-II, respectively. Besides, it is worth noting that NSGA-MTA is prominently superior to C-MOEA/D in IGD+ and HV by about 77% and 45%. These results may indicate that the improvements of NSGA-MTA are practical and have a considerable impact on overall performance.

Further analysis, the second finding is that convergence and diversity of NSGA-MTA are well documented via different experimental groups. In the first group ($S_n = 2$), NSGA-MTA is tested for all scale problems, whose metrics and obtained PF show that the proposed greedy mechanism and random repair strategy can play an essential role in obtaining better convergence and diversity of PF. Due to the small search space, rule-based initialization fails to show benefit. However, the initialization has gradually demonstrated its ability to solve large search spaces, with the increasing number of stages in the second group ($S_n \geq 2$). The conclusions from this group found are similar to the literature ^[15].

In particular, it can be found that the PF obtained by NSGA-MTA in all scenarios has the characteristics of uniform distribution, good convergence, and guaranteed solution diversity compared with others in Figure 4. However, C-TAEA still has a better effect in dealing with medium-scale scenarios, which benefits from the dual archiving mechanism. Besides, C-MOEA/D has a slight advantage in small-scale scenarios depending on the decomposition mechanism.

Therefore, another finding combined with the Taguchi method is that the proposed strategies have meaningful contributions to solving 15 scenarios and are superior to traditional mechanisms. In detail, the proposed initialization mechanism and the random repair strategy provide the direction for maintaining the diversity of the population in medium and large-scale scenarios. This kind of verification has also been applied in the literature ^[28], and similar results are obtained in this paper.

Lastly, this paper still has some technical areas for improvement. Although some parameters have been fine-tuned, there will still be a phenomenon in which parameter perturbation affects the algorithm's robustness. With the development of data-driven techniques, surrogate models ^[40] and deep-learning ^[41] have been successfully applied to real-world combinatorial optimization problems. The limitation is that the M-MTA studied in this paper is challenging to combine with these technologies in terms of coding form and multiple constraints. Therefore, we will work on the fusion of new technologies to solve the constrained M-MTA in the future.

6.   Conclusions

In order to describe the conflict between minimizing the survival of targets and minimizing the cost consumption of missiles, a constrained multi-objective optimization version of the M-MTA model is formulated. Furthermore, a multi-objective optimization framework (NSGA-MTA) is proposed to solve this model based on NSGA-II. Specifically, rule-based initialization is developed to provide feasible solutions in advance through prior knowledge to enhance the ability to search for solutions. Based on the characteristics of the M-MTA, genetic operators with the greedy mechanism and random repair strategy not only guarantee the constraints but also maintain the balance between exploration and exploitation in the whole algorithm. Besides, a hybrid encoding mechanism is built as the expression between the model and the algorithm, ensuring that generated solutions meet the proposed constraints. The results of numerical experiments under the Wilcoxon rank-sum test demonstrate that the proposed NSGA-MTA can determine a better optimal allocation scheme than other excellent algorithms to ensure convergence and diversity. Moreover, the results of the Taguchi method further show that the proposed strategies have a promoting and influential role in improving the algorithm's performance.

In this paper, the built model of M-MTA still needs to take the uncertainty into account, resulting in the need for a complete representation of the actual combat environment. Besides, there are still too many parameter settings in the algorithm, which dramatically affects the robustness algorithm. In future work, reinforcement learning based on deep Q-network will be further used to replace the excessive parameter settings in the algorithm to enhance the algorithm's generalization ability. Besides, uncertainty will also be added in building the model.

Acknowledgments

This work was supported by the Major Program of Natural Science Foundation of China (61690210).

Conflict of interest

The authors declare that they have no conflict of interest.

Supplementary

The data generated in the experiment can be available at https://github.com/shiqi0404/M-MTA.