Micelle formation, structures, and metrology of functional metal nanoparticle compositions

1.   Background

1.1.   Surfactants

Surfactants have been an essential tool for emulsion applications, especially in the petroleum industry. Colloid-stabilized emulsions are often encountered in crude oil production and can be problematic. A couple of examples of such problematic emulsions include intractable emulsions in crude oil-brine during oil recovery processes, and emulsions in oil spills ^[1]. The application of surfactants has been found to be a solution to these problems. Surfactants are amphiphilic molecules that typically contain both hydrophobic and hydrophilic entities in the molecule's chain and head-group, respectively. Amphiphilicity enables the surfactants to interact with both polar and non-polar groups, and in high enough concentrations, the surfactants self-assemble to create well-defined aggregates called micelles ^[2]. The formation of micelles is dependent on the surfactant concentration along with the originating solution's chemical properties including the presence of nanoparticles (NPs). The concentration at which small consistent aggregates form is referred to as the critical micelle concentration (CMC).

It is useful to distinguish three distinct classes of critical micelle concentrations: the CMC, the second CMC (2cc = 3*CMC) and the third CMC (3cc = 7*CMC) concentrations. At each CMC, chemical and physical properties of the composition change. These properties vary, but can be osmotic coefficients, ionic bonding, structure, viscosity, solubilization, and partial molar volume ^[3]. It is important to note that these changes are not solely morphological, but can also be thermodynamic in nature. In other words, these changes can be measured and/or calculated, with the first and second CMC observed as a break in the measured physical property ^[4]. However, most research groups focus on the first CMC, which will be what is referred to throughout this review as 'the CMC' unless stated otherwise.

The CMC is calculated as the intersection of two straight lines of solution properties above and below some micelle concentration ^[5]. Phillips defined it as "the maximum change in gradient in an ideal property-concentration (φ against Tc) relationship" ^[6] represented mathematically by the inflection point:

where φ, Eq 2, is:

and α and β are constants of proportionality, [S] is the monomeric surfactant concentration and [M] is the micelle concentration ^[5]. Philips' method is the most widely used one in literature due to it being dependent upon an inflection point in the rate of change of surfactant and micelle concentrations ^[7,8]. This makes it measurable with a variety of techniques.

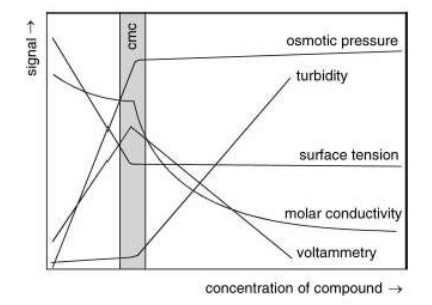
There are two major types of methods employed to measure the CMC; each makes use of either changes in the interfacial properties (not addressed in this review), or of micelle formation. The first type, and most commonly used, is a direct measurement of the CMC; as the concentration of the micelle-forming surfactant is increased in the solution, a significant change in physical property is observed. This can be an inflection point, change in slope, or discontinuity in the physical property ^[4]. Example plots of changes in specific physical properties, such as osmotic pressure, surface tension, etc., as a function of concentration can be seen in Figure 1 where the CMC is shown in gray. The second type of measuring the CMC is by indirect means; e.g. this can be by observing a change in a substance other than the micelle-forming compound (i.e. measuring probe) present in the solution. Spectrometric methods are amongst the most common in this type ^[4].

1.2.   Purpose of this review

The CMC can be measured in a multitude of ways, and it would therefore be convenient to collate all such techniques into a review and layout the advantages and disadvantages of each technique, allowing future researchers easy access to find techniques that are best suited to their study. In this context, this review will cover the formation of micelles and the metrology involved, especially concerning the CMC (which is dependent on the solvent, surfactant(s), and NPs used), and finally propose a new method that could potentially lead to in situ measurements of the CMC. It is possible that some of the methods, i.e. probed methods, can be done in situ, but has yet to be utilized in such a way. By understanding the mechanisms of the CMC formation and discerning and evaluating measurement methods, a strong knowledge foundation can be built that can help further research and technology in this area.

The first two sections of this review give a background on micelles including applications and their uses, as well as the micellar formation and structures. The succeeding sections are the bulk of the review and discuss the CMC metrology methods, with the final section evaluating the various metrology used for measuring the CMC. The review concludes by discussing where research is lacking and recommending what steps need to be taken to overcome these deficiencies. This review is intended to help understand micelle formation, stability, and the CMC metrology, thereby providing future research teams an easy way to figure out the appropriate surfactant/NP/solvent system that is required to produce the necessary micelle variety for either synthesis or stabilization of metal NPs. In this review we focus on solutions that contain metallic NPs, emphasizing silver NPs (AgNPs), since they have been extensively studied especially with regard to forming printable conductive ink solutions.

2.   Micelle background

2.1.   Micelle formation

The Gibbs free energy change for micellization per mole is calculated using Eq 3.

where X_cmc is the mole fraction at the CMC, R is the universal gas constant, and T is the temperature given in Kelvin ^[9,10]. The enthalpy change is calculated through Eq 4, with dln(X_cmc)/dT calculated through the slope of the line of X_cmc vs. temperature ^[11].

Finally, the entropy change (ΔS_m), Eq 5, can be calculated from the change in enthalpy and energy ^[12,13,14]:

To understand how micelles form, it is first convenient to look at a simplified model of parallel plates inserted into a polymer solution and visualize what happens as the plates are brought together (Figure 2). In the initial stage, the plates are sufficiently far apart that the polymer density in the middle, i.e. at half the distance between the plates, will be equal to the bulk density (Figure 2a). Further, as Asakura and Oosawa noted, the polymer density will be less than that in bulk near a single surface ^[15]. The density depletion results because conformal polymer molecules that would otherwise cross the depletion interface are excluded. The exclusion results because of two principles:

1.No molecular center of mass of width W (i.e. radius of gyration of polymer chain) may approach closer to any interface than a distance of W/2.

2.All molecular centers of mass will be distributed uniformly across all accessible regions.

As the plates approach, the lower polymer density near the plates is unchanged and so there is no change in the free energy. However, as the plates continue to approach, a second stage will occur, as seen in Figure 2b, where the parallel plates are close enough that the polymer density cannot increase to bulk density. As the distance continues to decrease, the maximum polymer density (located at half the distance between the plates) will decrease monotonically from the bulk value. This causes a less uniform distribution of polymer molecules thereby raising the free energy. Finally, in the third stage, the distance between the plates is less than the width of the polymer molecules and results with no polymer between the plates (Figure 2c). All of the polymer is outside the plates at this stage, and therefore solvated with the solvent outside. This results in a fall in free energy because the free energy of dilution is negative ^[16].

With the above model in mind, it should be noted that there is a minimum and maximum free energy of solvation, with the maximum occurring when the distance between the two plates is equal to the width of the polymer molecules (W = D). For electrostatic stabilization, as the limit goes to 0 for D, the free energy decreases and goes through a sign change reaching a minimum at D = ~0. For steric stabilization there is no maximum free energy and the free energy increases monotonically as the distance decreases ^[16].

The repulsion in the second stage allows for particulates to clump, but the magnitude of Gmin is not large enough to cause aggregation itself. However, increasing polymer concentration will increase Gmax and |Gmin|, and at some critical concentration of the surfactant, aggregation will occur resulting in micelles. This critical concentration can be changed by additions to the solution such as NPs, or a change in temperature. Further increasing concentrations will increase the repulsive maximum and eventually give rise to stability of the micelles ^[16].

2.2.   Micelle self-assembly and NP surface assembly

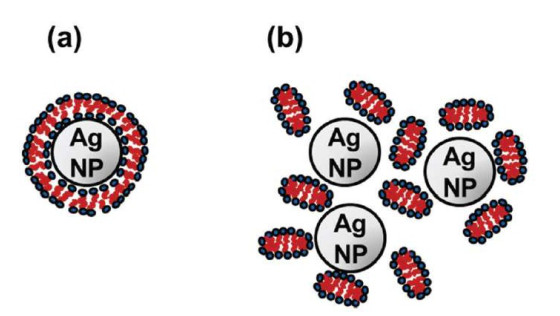
Micelles can form with several structures: as a self-assembled entity, formed on the surface of the NP, formed as a bilayer, or formed into worm-like structures. Specific micelle structures include spherical micelles, cylindrical micelles, bilayer vesicles, lamellar phases, and inverse micelles ^[17,18,19]. Inverse micelles are useful in synthesizing NPs with a variety of morphologies and sizes depending on the formation conditions. Expectedly, characterizing the structure of any micelle is not straightforward. For instance, Skoglund et al. wanted to study the dynamics of enhancement in AgNPs' dispersability in the presence of micelles ^[20]. They initially speculated that dodecyl trimethylammonium chloride (DTAC) micelles would form a bilayer (a structure that micelles can form when fully coating an NP) directly onto the surface of silver NPs. However, in a follow-up study the authors found that small-angle neutron scattering (SANS) data did not corroborate this speculation. The oscillating pattern that is indicative of a bilayer shell or micellar patches (see section small angle neutron scattering for more details) was absent in the SANS scans. This led them to conclude that the micelles formed clusters amongst themselves which then surrounded, but not actually coated the AgNPs, as in agreement with the obtained SANS data ^[20]. A schematic of the predicted micelle bilayer structure is shown in Figure 3a, along with the clustered micelle structure, Figure 3b.

However, depending on the NP loading if micelles end up forming on the NP, not every NP can form a micelle core-shell as shown in Figure 3a. This is obviously due to the availability of a limited mass of the surfactant which can be established by several different techniques (see section evaluation of techniques). Instead, it is possible that micelles get randomly absorbed onto the surface of the NPs in what Lugo et al. describes as "micelle decorated" NPs ^[21]. This is different from the above Figure 3b, because these spheres formed on the surface of the NP (see Figure 4b), while in the previous example, the surfactant formed agglomerates amongst themselves around, not on. It should also be noted that this is not necessarily always the case. The micelles could form different shapes, however micelle spheres were observed in the case of Lugo et al. ^[21].

2.3.   NP stabilization

Micelles, as discussed at the outset, began to be first utilized in emulsions employed by oil and gas companies early on in the twentieth century, but have since been used to synthesize and stabilize NPs ^{[19,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]}. Stabilization of NPs via micelles is extremely significant due to the important ability that it affords to enhance the consistency of the suspension or dispersion properties of such NPs as a function of time. In other words, when micelles are produced with the studied NPs, if the properties of the resultant system do not change over time, including whether or not the particles stay in suspension, it is then considered to be stable. For instance, Kocak and Bütün synthesized platinum NPs using micelles and observed consistency in dispersability over six months at room temperature of the micelle/NP dispersion in aqueous solution, thereby concluding that the NPs and micelles were stable ^[38].

There are generally three mechanisms recognized for stabilization of colloids when polymers are present in solution (note: colloids being the suspension of any particles in solution, which may or may not contain micelles). The first mechanism is steric stabilization, which was originally coined by Heller and Pugh due to repulsion of electron-electron or electron-nuclei interactions resulting in thermodynamic stabilization ^[39,40]. Non-ionic and surface active agents are quintessential examples of entities that exert the repulsion forces necessary for steric stabilization, due to the ability to be absorbed at the particle surface. Stabilization will be achieved once the repulsive and attractive forces are equilibrated within the thickness of the absorbed layer ^[22]. The second mechanism is electrostatic repulsion, which is thermodynamically metastable ^[16]. In this case, stabilization is achieved via repulsive forces applied from increased surface charge of the dispersed particles ^[22]. The third mechanism was established by Feigin and Napper, who called it depletion stabilization. Depletion stabilization results close to or on the surface of the colloidal particles, and is due to the reduction in free polymer in that surface area ^[16].

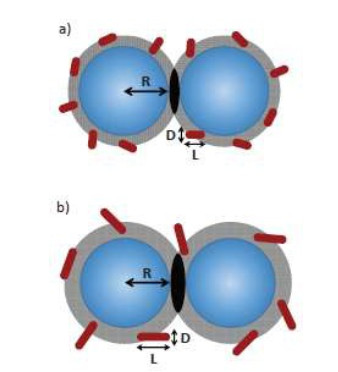
The above discussed concept of depletion stabilization was developed after Asakura and Oosawa first noted that the bulk free polymer density was higher than that on the surface of a single particle ^[15] and derives from an attraction force that develops between large colloidal particles when small non-adsorbing particles, i.e. micelles, are added to the solution ^[41]. The non-adsorbing micelles, when used in this manner, are called depletants; hence depletion stabilization. Figure 5 is a schematic of how depletion stabilization works. The grey areas represent the exclusion zones where the center of the rods of length L cannot fit. When the exclusion zones of two spheres overlap, represented by the black regions, an attractive force arises because the rod entropy increases proportionally to the overlap volume (Figure 5a). This force can be increased by increasing L while keeping all other variables constant (i.e., the colloidal particle cross-sectional diameter D, center-to-center distance between colloidal particles r, radius of the large colloid particle R, and micelle volume fraction) due to an increase of overlap volume ^[41].

It has been shown that the depletion stabilization can be manipulated ^{[15,41,42,43]}. For instance, Gratale et al. increased the depletion interaction of rod-like micelles by increasing solution temperature ^[41]. This resulted in rod-like micelles increasing in shape anisotropy which led to a stronger depletion interaction between particles in the colloid suspension ^[41].

Acids can also have an effect on the system, such as micelle size ^[44,45,46] and stabilization ^[33,47,48]. Sidorov et al. for instance ^[33], saw an increase of stabilization of Pt compounds (H₂PtCl₆·6H₂O, Na₂PtCl₄·H₂O) with an increase of pH, i.e. at more basic conditions. With chloroplatinic acid (H₂PtCl₆) it was found that a positively charged stabilizing polymer would interfere with positively charged compounds, thereby increasing sedimentation of the colloid. In Sidorov's case, the acid reduces the Pt compound thereby increasing its tendency to sediment out of solution ^[33]. However, care should be taken when changing pH because at the isoelectric point (IEP) of a molecule, i.e., the pH where a molecule has a net charge of zero, the prevalent conditions can result in its precipitation ^{[47,49,50,51]}. In the case of casein (a protein that makes up 80% of protein found in milk) micelles, it was shown that at the IEP, i.e. pH 4.6, the electrostatic and steric repulsions were diminished causing aggregation and precipitation of the casein micelles ^[47,51]. Therefore understanding the surface charge characteristics of the micelles can lead to better understanding of their stability. A way to test for the charging of the surface is through zeta potential measurements ^[52,53]. For instance, Li et al. measured bare and paclitaxel (a chemotherapeutic drug)- loaded methoxy polyethylene glycol based deoxycholic acid and N-acetyl-L-cysteine modified hyaluronic acid (mPEG-HA(DCA)-NAC) micelles to have zeta potential values of −35.5 mV and −38.3 mV, respectively. With the increase in negative charge on the micelles, an increase in electrostatic repulsion yielded their increased stability ^[53].

2.4.   NP synthesis

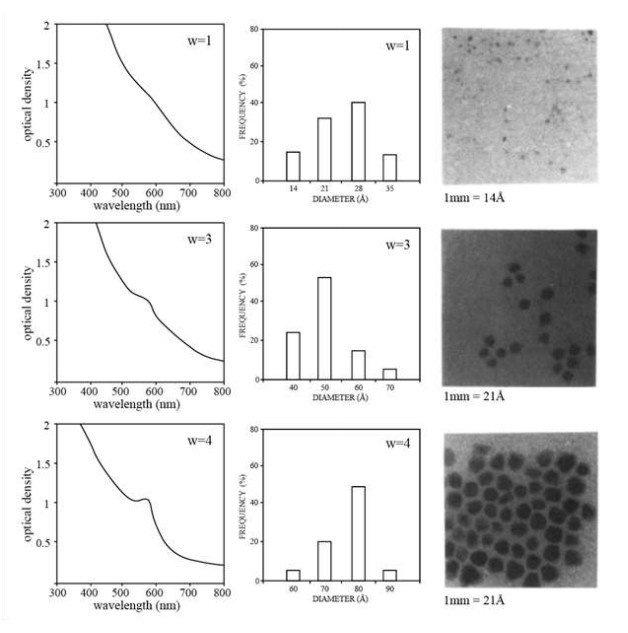
Micelles have been adapted to synthesize metal NPs of different sizes and structures, including that of gold ^[23,24], silver ^{[25,26,35,54,55,56,57]}, platinum^[27], palladium ^[28,58], copper ^[30], and ferrous material compounds ^[29,59] using a wet method called the reverse micelle method ^[28]. In this method, surfactant gets dissolved in an organic solvent producing spheroid aggregates called micelles. The polar core of the micelles will readily solubilize with water, producing "water-pools" within. If the molar ratio of water to surfactant (w) is below 15, then the aggregates are called reverse micelles, but when w > 15 then the aggregates are designated microemulsions with droplets containing a large amount of water ^[30]. The inner-core of the reverse micelle is considered to be a nanoreactor where nanocrystals can be grown and are controlled by the state of the water molecules within its core ^[28]. By controlling w, the size of the NP itself can be controlled. This was demonstrated by Pileni in 1993 where the author looked at the absorption spectra, SEM, and histogram of particle size of metallic copper with varying w (Figure 6) ^[30]. It can be seen that as w increases, so does the NP size. The top row for Figure 6 shows the results of NPs synthesized with w = 1 resulting in NPs sized around 2.0 nm. As w increases, the size of the NPs and reverse micelles increase, as shown in the subsequent rows in Figure 6. Thus in increasing w to 3, the diameter of the NPs increased to around 5.0 nm and w = 4 yielded NPs of diameter 8.0 nm.

However, by changing the reducing agent used in the system, Pelini was able to reduce the NP size with increasing w, showing that NP size in the synthesis is not only related to w, but also that the size dependence changes as a function of surfactant, reactants, and solvents ^[30]. As w is a very simple ratio to manipulate, it is a convenient parameter to control the NP size. Shah et al. got similar results when looking at the synthesis of AgNPs in the presence of sodium dodecyl sulfate (SDS) ^[22]. Shah et al. found that below the CMC, i.e. at lower w, AgNPs formed a larger and broader distribution of sizes than NPs formed at or above the CMC, i.e. at larger w. It was postulated that larger AgNPs formed because there was not enough surfactant or micelles present to retard the nucleation of AgNPs ^[22].

As seen above in the section on micelle formation, introducing NPs to the system changes the Gibbs free energy. This leads to an interesting question that has yet to be answered: how much do NPs affect the CMC? By measuring the CMC of a surfactant in a given solution with and without NPs, a predictive model of the shift in Gibbs free energy could be developed. This model would provide a more thorough understanding of micelle development such as how NP type, size, polarity, charge, morphology, etc. effects micelle growth, structure, and the CMC.

3.   Metrology

The CMC is the concentration at which the formation of micelles becomes appreciable. Above this concentration the surfactant solution will undergo changes in both physical and chemical properties ^[2]. Rosen concluded that the CMC of a composition can be found by plotting a physical property of that composition such as absorbance, surface tension, fluorescence, etc., as a function of surfactant concentration, with the concentration where a discontinuity in such a measured physical property is observed being coined as the CMC ^[60]. Many research teams have measured the CMC in many different ways. This section will not cover every method used to measure the CMC; just the most common techniques reported in literature.

3.1.   Surface plasmon resonance

Surface plasmon resonance (SPR)-based measurement is an indirect method of measuring the CMC of solutions containing metal NPs. It entails comparing measured absorbance over a range of given wavelengths as a function of surfactant concentration, and was first demonstrated by Karimi et al. in ^[61]. Figure 7 shows the results of Karimi et al.'s study, and it can be seen that there are clearly two distinct segments in the plot with associated distinct slopes. By inserting linear fits and calculating their point of intersection, the CMC was determined. An interesting aspect of SPR is that it relies on the charge density oscillations between the metal layer and its environment; in this case with the surfactant/solvent solution. The signal, or peak of the absorbance, is proportional to the mass of the absorbing material, and therefore, from its value, the mass and thickness of the absorbing layers can be estimated.

3.2.   Raman

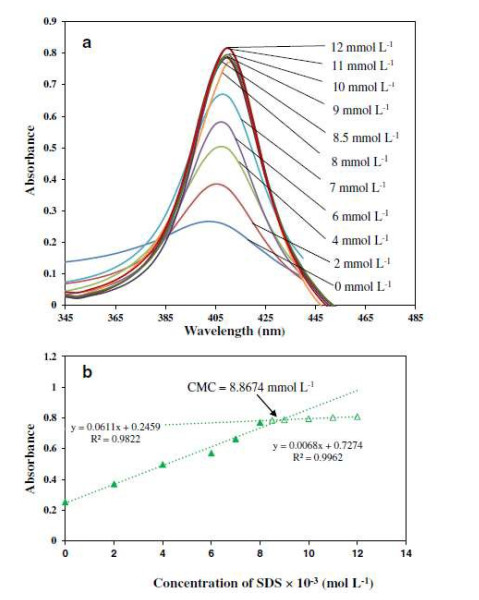
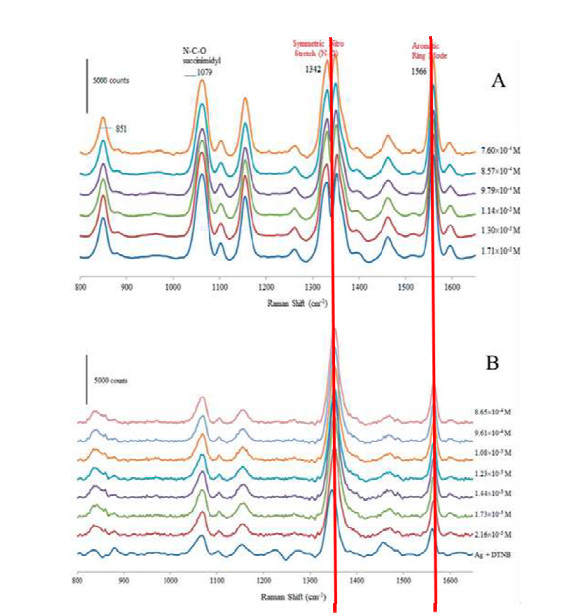
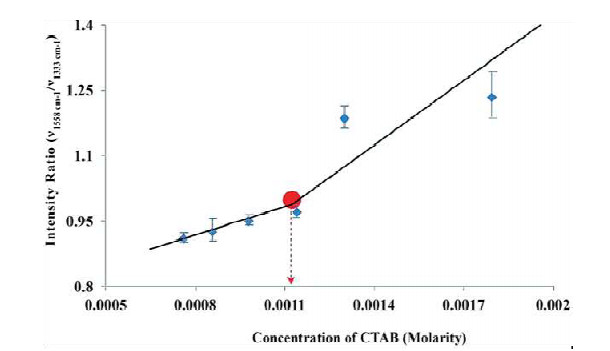
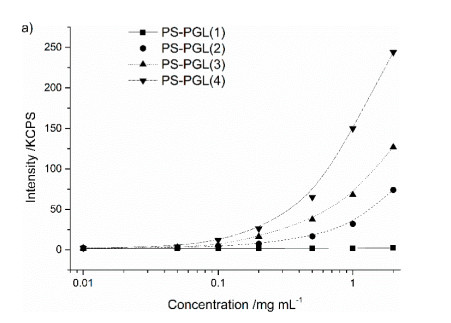
Surface-Enhanced Raman Scattering (SERS) technique has become a powerful tool for characterization when multiple analytes are present. For this reason, Shrestha and Yan first proposed using SERS to measure the CMC ^[62]. This technique measures the shift in the relative intensity of the signal, and like with SPR, the mass of the absorbing material can be estimated. This is an indirect method, and Shrestha and Yan used a Raman-active molecule: Ellman's reagent, 5, 5'-dithiobis-(2-nirtobenzoic acid) (DTNB), to measure the perturbations in its Raman spectra. With increasing surfactant concentration, the vibrational bands of DTNB changed and the CMC could be measured. More specifically, the symmetric vibrations, 1333 cm⁻¹ and 1558 cm⁻¹, of nitro groups in DTNB's aromatic ring, change independently and allowed for an accurate determination of the CMC of cetyl trimethyl ammonium bromide (CTAB) seen in Figure 8. Figure 9 is another example of calculating the CMC as the point of intersection of two linear lines displaying a discontinuous change in the ratio of the said two symmetric vibrations of DTNB. It should be noted here that the study also included SDS as a surfactant, but this method was more sensitive to CTAB.

3.3.   Surface tension

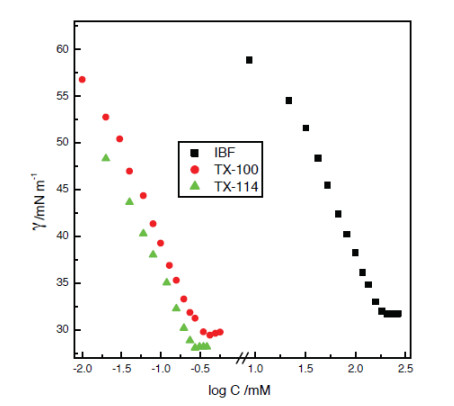
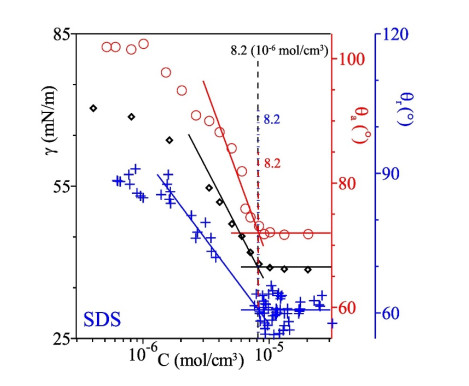
One of the most commonly used ways to determine the CMC is through surface tension measurements. As the concentration of the surfactant increases, there is an observed change in surface tension of the surfactant-containing solution. At some specific concentration, the change in surface tension becomes asymptotic, and this concentration at which such an inflection occurs is denoted as the CMC. This can be seen in Figure 10 in which the surface tension is displayed as a function of the amphiphile concentration in an aqueous solution. Rub et al. made the observation that the CMC can be manipulated with the addition of urea ^[63]. In the presence of water, urea changes the structural organization of water only around the solutes ^[64], into what Frank and Evans describe as an "iceberg structure" (the water organization becomes more ordered and crystalline) that organizes around the hydrocarbon portion of the amphiphile molecule ^[64]. Urea changes such water organization without lowering the chemical potential, thereby leaving the micellar state unchanged ^[63]. It should be noted that the manipulation of the CMC was expected and predicted by thermodynamics, as previously described in the section, micelle formation.

3.4.   Fluorescence

Fluorescence is an example of an indirect method for determining the CMC. This method uses a fluorescent probe molecule that changes its fluorescence behavior when micelles are formed. Pyrene is one of the most commonly used fluorescent probe molecules for measuring the CMC. However, Salem et al. have reasoned that the CMC determination using pyrene has limitations when used with surfactants that also absorb in the same region where pyrene fluoresces, therefore interfering with the fluorescent signal ^[65]. In addition, the authors pointed out that a complex ratio of excitations is necessary to calculate the CMC limiting pyrene's usefulness. Instead, the authors used the fluorescence probe, fluorescein, for the aforementioned reasons, and measured the change in fluorescence in the range of 400–650 nm. Salem et al. saw that as the concentration of the surfactant increased, the peaks became redshifted due to the fluorescein interacting more and more with the micelles, which was then used to determine the CMC ^[65].

3.5.   Light scattering

Dynamic Light Scattering, or DLS, is another technique in which intensities of a scattering vector (q), such as light, are used for measurement of the CMC. The intensity of q will begin to change as a function of the concentration of micelles. At some micelle concentration, the intensity will start to increase dramatically. Again, the CMC can be determined by fitting a linear curve to each portion of a plot of intensity as a function of concentration, and taking their intersection point, Figure 11 ^[66]. DLS is not only used to measure the CMC, but it also used to measure the particle size of the micelles ^[22,66,67].

Static Light Scattering (SLS), is similar to DLS, but is used to help discern the structure of the micelle by using a regularization method developed by Glatter and Schnablegger ^[68,69]. The SLS data is fitted with a volume-weighted pair-distance distribution that has a distinct aspect ratio based on geometry (a more thorough description of the process is described elsewhere by Glatter and Schnablegger ^[68,69]). Although not reported in literature yet, it stands to reason that by using SLS in conjunction with DLS, a thorough characterization of micelle size and structure can be ascertained.

3.6.   Conductivity

Testing the conductivity of the micelle solution can be done in many different ways, as long as either the conductive particles (e.g. AgNPs) are present and percolation has been achieved, or the solution by itself is conductive. Determination of the CMC is done similarly to other techniques, such as by using the Philips' method described in section surfactants. After conductivity measurements are made, mathematical models/procedures such as the ones listed below, can be employed:

(1) Plotting the differential conductivity vs. the square-root of the compound concentration.

(2) Directly integrating the Boltzmann-type sigmoidal function to fit experimental raw data.

(3) Applying local polynomial regression functions ^[4].

The simplest measurement, although, is plotting specific conductivity as a function of concentration of surfactant. Another relatively easy measurement can be made using potentiometry. This method entails the use of ion-selective electrodes to measure the dissolved species, and can be tailored to select either the counter-ion, the organic part of the surfactant, or the surfactant as a whole. As stated earlier, voltammetric methods are indirect measurements that allow the determination of the CMC. If the solution contains an electroactive specie (i.e. the probe), micelle formation can be measured based off the change in limiting current of that species, associated with an effect caused by the change in diffusion coefficient. These techniques include: tensammetry, polarography, and voltammetry. Lastly, electromigration methods can be used to measure the CMC via several rounds of electrophoresis runs. The specifics of the techniques are listed below:

(1) Measuring capacitance k' as a function of the surfactant concentration. The CMC is when capacitance is equal to 0 (usually found by applying curve fitting and then extrapolating to k' = 0).

(2) Effective electrophoretic mobility of the probe as a function of the surfactant concentration.

(3) If using an electrolyte micelle forming compound, current can be measured as a function of the surfactant concentration.

(4) Zeta potential as a function of the surfactant concentration ^[4].

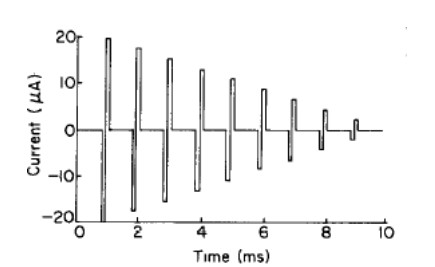
A new and emerging conductivity technique is the bipolar pulse conductance (BICON) method that measures cell current after the application of two fast pulses of equal magnitude and duration of opposite polarity ^[70]. Such an example as a function of time can be seen in Figure 12. The method was developed by Johnson and Enke ^[71], and it was first used to measure the CMC by Baxter-Hammond ^[70]. An interesting aspect of the Baxter-Hammond method was to look at the equilibrium time for the conductance measurement after adding deionized water to the surfactant ^[70]. This is interesting because it suggests that the research team was able to conduct such measurements in situ. Thus, it should have been possible to measure conductance while adding surfactant to the solution while determining the CMC in situ. Equilibrium time of the conductance of course will need to be taken into account, but this could potentially make measurements in the future easier and faster. It should be noted however that, as of this paper, the authors are unaware of this method being used in such a way in any other instance. In measuring the CMC in situ, it is possible that more information may be gained, such as how fast micelles form as a function of equilibrium time. This method, however, would be limited by the type of solvent used and/or micelle formed, as specific individual characteristics of the surfactant play a significant role in sustaining conductance.

3.7.   Small angle neutron scattering

As opposed to most methods discussed in this review, small angle neutron scattering (SANS) is not used to measure the CMC, but gives insight into the mechanisms of how the NPs are stabilized ^[73]. AgNPs can have a low scattering contrast compared to cationic surfactants, especially such as CTAB. Skoglund et al. demonstrated this, and concluded that high intensities from the SANS, especially at low q-values must be from larger structures that the surfactant has produced ^[20]. Since the AgNPs used in the study were hydrophilic, there was no particular driving force for the micelles to form a monolayer or even hemi-micelles on the surface of the AgNPs ^[20].

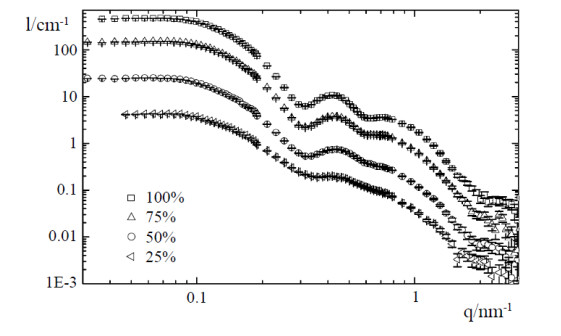
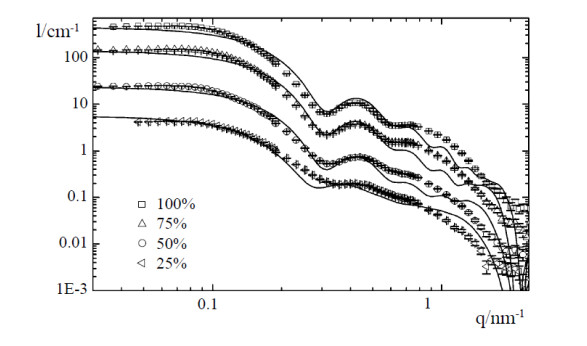
Oscillations found on SANS plots (see Figure 13) are indicative of either a core-shell structure ^[21], or structures that have formed at larger length scales than traditionally observed with micelles. This implies that a bilayer has formed, or micelles have been absorbed directly onto the surface of the NP ^[74]. The smearing of the oscillations increases with more polydisperse micelles, and the reciprocal of the size of the micelles determines the width and position of the oscillations ^[75].

Scattering at high q (scattering wave vector) values can give insight into the geometry of the micelles absorbed onto the surface of the NP. For core-shell micelles with a constant thickness on the surface of the NP, scattering will fall off at high q values as there is a more uniform surface, and hence a lower degree of scattering. However, if the surface is undulated or inconsistent, scattering at high q values will be present, as the lower intensities will have more chances to be scattered away. This is especially the case with decorated-micelles. Lugo et al. predicted the coherent scattering cross-section for spherically symmetric silica nanoparticles using Eq 6 (below), but it stands to reason that Eq 6 may also be applied to other spherically symmetric NPs that are not silica ^[21]. Although, examples of this have not been found in literature at the time of this review's submission, the application of Eq 6 can give insight into how much surface area is available for scattering. Lugo et al. used it to calculate the thickness of the core-shell and found that a uniform thickness model significantly underestimated the amount of surface area of the micelles. However, assuming the decorated-micelle model, this approach proved to accurately produce the high q values of the SANS signal as seen in Figure 14 ^[21].

where the volume fraction of particles is denoted by φ, the difference between the scattering length densities of the matrix (in this case the solvent) and the particle is denoted by Δρ, Vb is particle volume, F(q) is the form factor, and S(q) is the structure factor. S(q) is the correlation of interactions between particles and can be either attractive or repulsive but does not include volume or electrostatic repulsion parameters ^[21]. It can be seen from Eq 6, then, that if all variables besides the surface area of the micelle on an NP (taken into account in F(q)) are constant, a larger F(q) will increase I(q), resulting with oscillations at higher intensities.

3.8.   Implementation of contact angle

As seen in the section surface tension, surface tension can be used to determine the CMC, which in turn affects the contact angle. Research teams have looked at the wettability above and below the CMC ^[76,77,78], as well as measured the CMC via contact angle measurements ^[79,80] (Figure 15).

To measure contact angle, a liquid solution must be delivered onto a surface in a controlled manner. This means that the solution can be manipulated in real time producing in situ measurements of, in this case, the change in contact angle as a function of surfactant concentration, and ultimately the CMC. By adding surfactant to the delivery mechanism, each succeeding droplet and measurement would be that of a new surfactant concentration.

Generally speaking, contact angle measurements require a droplet with a given volume to be delivered onto a surface or substrate. This means that surfactant can be added to the solvent in the delivery pipette between dispensations of droplets and the change in contact angle can be observed in real time. Between each succeeding droplet, solvent will be lost and consequently the amount of surfactant will be enhanced, therefore care must be taken when calculating concentrations. It should be noted that this method may be substrate-sensitive. It would be interesting to find if the CMC concentration stays consistent across different substrates. Since surfactants alter the surface tension and, therefore, the surface energy, this will in turn affect contact angle. Therefore, it would be interesting to see how surfactant solutions with different hydrophobic or hydrophilic characteristics may change the CMC. This information is of use because it could give insights into how the micellized solvents interact with a given substrate or material.

This method can also be used in conjunction with other techniques to get a full profile of the evolution of micelles in real time. For instance, used in conjunction with DLS, the size of the micelles can be tracked as they develop in real time, as well as how the surfactant solution interacts with the material surface that the contact angle is measured on. We want to emphasize here that the utilization of contact angle measurement as a means for the in situ determination of the CMC is an original contribution of ours and has not been previously reported in the literature.

3.9.   Molecular dynamics simulations

In the last couple of decades, molecular dynamics simulations (MDS) have emerged as a powerful tool to study atomistic and mesoscale dynamics of a multitude of systems ^[81]. This tool has been used to explore the dynamics of micelle systems. For instance, Chen et al. modeled each individual atom of a micelle in water using GROMACS ^[81]. However, modeling each individual atom restricts the size of the unit cell that can be modeled and therefore of the micelle, because with increasing number of atoms the number of calculations and computations increases exponentially. Due to this Chen et al. even while using 20000 water molecules in the simulation, could only reach a size of 6 nm in diameter for the largest micelle formed due to computational limitations ^[81]. Through MDS, Chen et al. found that the amount of sulfonates exposed to a water phase could be reduced due to larger uniform micelles forming at oil/water interfaces. Luo et al. also used an atomistic approach to study the interactions of small surfactant molecules and large block copolymers ^[82] and discovered that the introduction of phenolic hydroxyl groups impacted the micellar morphology. Other research teams have also employed such atomistic approaches ^[83].

Modeling individual atoms is not the only option. Other effective approaches consist of the united-atom (UA) ^{[84,85,86,87]}, or coarse graining (CG) (for further reading on coarse graining MDS see ^{[88,89,90,91]}). The latter represents molecular groups as one individual sphere or "atom" through a specific force field, and the former uses one "atom" to represent an entire molecular unit. These options allow researchers to model much larger systems by replacing tens to hundreds of atoms within one unit.

Regardless of the modeling method, MDS can elucidate fundamental dynamics of studied systems and provide valuable information. Sambasivam et al. used MDS to understand how NPs in their micellar systems were stabilized ^[92]. Modeling showed that the NPs were stabilized electrostatically due to a NP-micelle junction. The micelle end-caps open up and bridge with the surfactant functionalized-NP through a surfactant exchange process that is diffusion-limited. The team was also able to learn rheological characteristics and structure of their micelle system ^[92]. A large part of micelle MDS is understanding how the molecules aggregate. This can include such investigations as the effect of surface morphology and hydrophobicity on contact angle, how the surfactant aggregates into micelles ^[83], how surfactants aggregate at the air/water interface ^[84], or how physical properties of polymer chains effect aggregation as in the study by Jesher and Likos ^[93]. The authors modeled the aggregation of semi-flexible and flexible polymers chains in a ring (circular) shape. The goal was to understand how the chains would aggregate if there was varying degrees of amphiphilicity and ring flexibility, and it was found that as the amphiphilicity increased, clustering of the ring-shaped micelles increased ^[93].

MDS helps to elucidate how micelles are formed, and the structures in which they form. A limitation to such experiment and measurement is the lack of accounting of the side groups due to an averaging over all groups. Pires et al. demonstrated this by modeling the spontaneous formation of SDS micelles. In the study they showed that at the end of the simulation (with a duration of 1000 ns), there are three distinct micelle agglomerate sizes based on the amount of monomers available for agglomeration ^[83]. The agglomerates were formed through the exchange and fusion of monomers, and changed in shape over time. Small micelles formed spheres, medium-sized micelles morphed into ellipsoids, and the large micelles transformed into worm-like structures. The simulation also showed that the presence of salt was essential to form bridges between aggregates of monomers during fusion to create new micelles ^[83].

3.10.   Evaluation of techniques

Depending on the type of the technique used to determine the CMC, it is possible that different values of the CMC may be obtained because of the intricacies and sensitivities of such techniques. It is therefore important to evaluate the techniques that have been discussed here and understand their inherent sensitivities. For instance, the surface tension method is sensitive to impurities leading to inaccuracies ^[62]. This is especially true when considering Phillips' method as it relies on the intersection of two linear lines above and below some concentration where the change in slope is derived from a change in physical property. If that property undergoes a slow gradual change, it can become quite hard to derive two distinct/different curves. That is not to say that gradual changes do not provide any information, just that the CMC may be obscured in such cases. Kale et al. revealed that a gradual change in the slope of the curve is an indication that there is dimerization, or early and gradual micelle formation instead of a sudden and rapid formation ^[94]. They explain that assuming that micelles form due to chemical equilibria, the concentrations of anions and cations will follow the growth rate of micelles ^[94]. Another consideration to be taken into account is the fact that the presence of NPs can affect Gmax and |Gmin| which affects the CMC. An example of this is from the Skoglund et al.'s study that showed the appearance of aggregates far below the CMC, leading to the conclusion that the presence of AgNPs affects the micellar aggregates ^[20].

SERS is a technique that gives insight into whether the micelles are formed on the surface of an NP or not. As Shrestha and Yan explain, the electrostatic forces of a cationic micelle will get "adsorbed" onto the surface of an anionic AgNP ^[62]. According to the authors, such adsorption is strongly correlated with the aggregation extent of micelles which shows up in the form of a relative intensity shift in the Raman spectra ^[62]. Thus, SERS has the advantage of being able to corroborate and complement the CMC determinations along with other techniques. However, SERS does require the use of specific Raman active molecules.

SANS requires the use of specific structural model for the measured micelles, e.g. ellipsoidal, spherical, cylindrical, etc. The accuracy in the selection of this model can impact the obtained data's accuracy. While SANS may not specifically yield the CMC, it gives insight into what mechanism is responsible for stabilizing the NP during its incorporation into a CMC. A case in point is as follows: Skoglund et al., in a study without using SANS, concluded that the micelles were forming a bilayer on AgNP ^[31]. However, in a subsequent study of the same system using SANS, Skoglund et al. found that the characteristic oscillations to be expected from SANS if micelle bilayers were indeed being formed were absent. A more thorough investigation revealed that the micelles were actually self-assembling in the vicinity of the AgNP and not on them ^[20].

Conductivity testing is a simple and effective way to measure the CMC. Experimentally it is simple, and the measurements can be made using inexpensive equipment. It does, however, have many drawbacks. The use of AC bridge techniques require capacitance-bridge balancing which can be tedious. Other drawbacks can be skewing of the results due to frequency dependence, temperature changes resulting from high power outputs, and susceptibility to double layer effects. Further drawbacks of conductivity testing also include the requirement of post processing of the data, which requires extensive analysis. Also, the resulting curves may reveal a gradual change, which makes finding the inflection point difficult. This can add uncertainty to the result based on the level of accuracy of the model, which can only be improved with more data points necessitating more time and resources for the measurement. On the other hand, many of these problems can be mitigated by using the bipolar pulse conductance method, which has the advantage that a lot of measurements can be made in a short period of time. With pulses lasting only µs, hundreds of measurements can be made in minutes. Caution in general should be taken when making conductivity measurements, because current produces heat, and as described in section micelle formation, the CMC can be sensitive to heat.

Techniques such as fluorescence, dynamic light scattering and contact angle measurements can prove to be powerful tools for measuring the CMC when they are simultaneously used to examine valuable structural information during the onset of the CMC. Especially with fluorescence measurements, appropriate probes need to be developed that can produce discernible changes in their absorption spectra when present as a component of a micelle at the CMC in comparison to their non-aggregated states. Such absorption information can provide fundamental insight into the dispersive forces that evolve among the surfactant molecules, which are harder to be distinguished by other techniques. As suggested by us, a combined use of static and dynamic light scattering measurements can yield a fundamental insight into the associative steps that molecules undertake on their path to the CMC. Such information is invaluable as it should provide a means to steer the fate of micelles to desired outcomes. Further, as also suggested by us, the contact angle measurement techniques method can be used in conjunction with techniques such as fluorescence and light scattering methods to get a full profile of the evolution of micelles in real time. Thus, there is an immediate need to advance the state of techniques that can provide information in real time or on the in situ molecular transformations on the path to the CMC.

It should be noted that most research involving the CMC only refers to stability in passing, and does not show corresponding data as a function of time. For instance, Kocak and Bütün claimed that their Pt NP dispersions "were stable for more than 6 months", yet provided no data to support that claim. This is a common occurrence and should really be addressed. This may be due to the lack of knowledge or understanding of the mechanics and dynamics that keep the micelles and NPs in suspension, but this can be addressed and illuminated via MDS.

4.   Conclusions and perspectives

Micelles are a versatile tool that have many applications spanning many different industries. The critical property involving them, i.e., the CMC, can be measured in a multitude of ways. However, with such versatility there also exists associated drawbacks. Since the CMC measured with such multitude of ways can cause uncertainty in its correct value, this necessitates that more than one technique should be used to make trustworthy conclusions.

New powerful methods such as contact angle in conjunction with other methods such as DLS can fully elucidate the temporal development of micelles in real time. Coupled with computational modeling such as molecular dynamics, specific metrological methods can give a full picture of the micelle development in any solvent leading to deeper understandings, which in turn can lead to better predictions of systems for use in a given application. This information then can be collated and used in machine learning algorithms that would be able to predict the characteristics of the micelle systems much faster and more efficiently than by trial and error. For example, when using micelles for drug delivery, data gathered from in situ measurements can be input into machine learning algorithms to rapidly predict which micelles, and micelle structure, should be used to deliver a particular drug, or deliver the same drug in different conditions such as according to the blood type or blood pressure of a patient. Alternatively, if the NPs' effect on micelles is characterized as suggested in section 3.0, new machine learning algorithms could be used to predict what the effect of changing the type of NPs in a given system is on the micelle size, structure, and the CMC.

Acknowledgements

This work was supported by the American Chemical Society of Engineering Education (J. Middleton), Joint Fuze Technology Program (J. Middleton, R. Siefert, A. Schrand and M. Kolel- Veetil) and the Washington Center for Internships and Academic Seminars (M. James) and the financial support is hereby gratefully acknowledged.

Conflict of interest

There is no conflict of interests with the authors and the publication of this paper.