Finite element model updating of metallic and composite structures-A state of the art review

1.   Introduction

The finite element (FE) method has a very wide variety of applications in engineering practice such as structural analysis and structural damage detection. It is not necessary that the numerical model of any engineering structure will represent all the actual physical and geometrical aspects of the actually built structure. Due to which, a significant difference may exist between the results obtained by the constructed FE model and the results obtained from the modal testing on the actual structure. In order to improve the correlation between the numerical predictions and measured data, there is a need to update or correct the developed FE model so that these discrepancies/uncertainties may be reduced. This can be achieved by using the various methods available for the finite element model updating. The existing model updating methods using vibration measurements generally can be classified into two categories, first is response-based methods and second is modal based methods ^[1]. In response-based methods, for the updating of the finite element numerical models, the measured frequency response function (FRF) data are directly employed. By minimizing the error between FE numerical and experimental input forces or output responses, structural parameters such as stiffness and mass can be easily obtained. The response-based methods provide more accurate results in low frequency range but these methods are not suitable for higher frequency range.

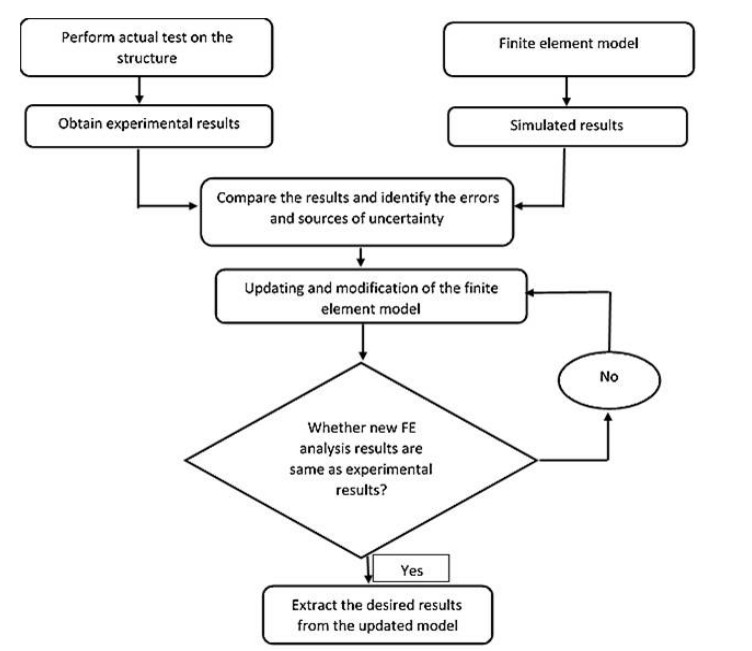
Second category of FE model updating methods includes modal-based methods. In modal-based methods modal data, such as natural frequencies and mode shapes are utilized in the structural parameter updating process. To update the structural parameters of the FE model often by modal based methods, an optimization process will be required. For this analysis the Eigen solutions and associated sensitivity matrices of the FE model will be used. Performance of the modal based methods affected by the selections of an objective function and constraints, structural updating parameters and optimization techniques. These methods require significant computational efforts in the model updating process. However, in this regard, the main objective of this paper is to present a review on the application of different methods of finite element model updating on various metallic and composite structures. Figure 1 represents the methodology that can be used to update or correct the analytical FE model through updating techniques. First the test is performed on the actual structure then its FE model is constructed. Then results will be compared and the errors and source of uncertainties will be identified. In next step updating of FE model is done and we continue until our results don't match with the experimental results.

2.   Literature review on finite element model updating of metallic structures

In this section, the detailed literature survey regarding finite element model updating of metallic structures is carried out first. Chen et al. ^[2] proposed a direct identification procedure by using the test measured eigenvalues and eigenvectors so that mass and stiffness matrices can be obtained. This method is quite simple so one can use it in real time operation during the structural testing quite easily. Cornwell et al. ^[3] studied the application of the strain energy damage detection method to plate like structures. Stubbs et al. ^[4] proposed an extension of this method. Authors proposed utilization of the mode shapes before and after damage. The original formulation presented can only be used for structures characterized by one-dimensional curvature. The method is applied and generalized for plate-like structures also. To analyze the limitations of the method, it is applied to several sets of simulated data and comparisons are drawn between the original formulation on a series of slices of the structure and the true two-dimensional formulation. Modak et al. ^[5] proposed the use of an updated finite element model for dynamic design. Authors applied FE model updating on F-shape structure. An updated model is obtained by employing a method of model updating based on constrained optimization proposed recently ^[6]. The model updating method using constrained optimization is based on minimizing an objective function representing a norm-based error between the measured and the analytical versions of the natural frequencies and the mode shapes. This objective function subjected to constraints is minimized using non-linear optimization. With this purpose the structural modifications in the form of mass and beam modifications have been considered. Modak et al. ^[7] carried out the comparative study of model updating methods using simulated experimental data. The inverse eigensensitivity method (IEM) and the response function method (RFM) are relatively more popular and successful methods for improving analytical model. The objective was to study the convergence of these methods and the accuracy with which they predict the corrections required in a finite element model. The test cases of complete, incomplete and noisy experimental data along with the effect of the amount of experimental data used on the quality of an updated model is studied. The updated models are compared using some error indices that are developed to quantify error in the predicted natural frequencies, mode shapes and response functions.

Lee and Kim ^[8] proposed a method based on identification of damping matrices from measured frequency response functions. In this paper, a new theoretical procedure for the damping identification is discussed. Hybrid modeling has been used in this analysis. In hybrid modeling for the formulation of mass and stiffness matrices finite element method is used but for damping matrices experimental method is preferred. A simple three degree-of-freedom lumped parameter system has been used for the experiment. The effect of the noise in the measured FRFs is also studied using this example. To confirm its effectiveness in real engineering problems this method is then applied on a thin beam with clamped boundary condition with two damping configurations. Bais et al. ^[9] proposed a method to study the dynamic design of drilling machine by constructing updated FE models and using analytical and experimental results. Consequences of the structural dynamic modifications on vibration characteristics of the drilling machine can be predicted by using the updated FE models. Two studies have been carried out on the machine wherein the first study involved modal tests performed on a drilling machine in which an impact hammer has been used for the excitation. Also, method of modal identification has been used. A computer program has been developed for the FE modeling of the machine. Then a comparison has been made among the results obtained by FEM and the experimental studies by using mode shapes and modal assurance criterion (MAC) values. Analytical FE model has been updated by using direct methods of model updating. In the second study, modal testing has been performed by using random noise generator and modal exciter. Analytical FE modeling has been done using I-DEAS software. FEM software has been used for the prediction of correlation of FE results with the experimental ones.

Steenackers and Guillaume ^[10] studied FEMU by taking into account the uncertainty on the modal parameters estimates. The focus of this paper is on statistically derived response surface models. These methods can be used for both linear and nonlinear problems. In the case of response surface meta-models, design of experiments methods (often called response surface methods) are employed using which one can determine the location of the sampling points. There are several versions for design of experiments available in literature ^[11,12]. After choosing the data points carefully, meta-models then can be fitted by using the standard multiple regression methods to get polynomial model. This polynomial model will relate the input parameters to output features. These models are empirical in nature but the efficient use of these models depend on the expertise of the experimenter i.e. how accurately he assigns the model input parameters and choice of appropriate output features. In this analysis the influence of the mesh also has been discussed briefly. For the measurement of Frequency response function (FRF), an aluminum test plate has been used. A FE model has been developed for the test plate and used as a function of one or more modeling parameters.

Lin and Zhu ^[13] studied the FEMU using vibration test data under base excitation. Frequency response function (FRF) data is used to update analytical models. The proposed method involved the developing of mathematical formulations to identify mass and stiffness modeling errors. The method presented was applied on a cantilever beam as well as a practical GARTEUR structure. The method was observed to have noise-resisting ability when the measured response function data are contaminated by certain level measurement noise. Arora et al. ^[14] studied the FEMU with damping identification. For accurate prediction of complex FRFs, it is necessary to employ the damping matrices also during the FEMU. Finite element model updating procedure is proposed which also include the effect of damping on the structures. The proposed FEMU procedure with damping basically consists of two steps. In the first step, mass and stiffness matrices are updated using FRF data. Second step involves the use of updated mass and stiffness matrices obtained in last step so that we can estimate the updated damping matrix. Study was carried on a fixed-fixed beam and F shape test structure. Collins et al. ^[15] studied the eigen-data sensitivity for analytical model updating in an iterative framework. Lin and Ewins ^[16] proposed a method in which measured FRF data has been used to update an analytical model.

Pradhan and Modak ^[17] proposed a method for damping matrix identification using frequency response data. Authors proposed a method which allows us to separate updating of the damping matrix from that of updating of the stiffness and the mass matrix. The concept of normal frequency response functions (FRFs) has been used during this updating method. The method is formulated in such a way so that the difference between the complex FRFs can be reduced. Then from the measurement of complex FRFs we can estimate the normal FRFs. The proposed method is applied on a beam structure. Effect of noise is also investigated during this analysis. Yuan ^[18] proposed proximal-point method for finite element model updating problem. The problem of finding the optimal approximation to analytical stiffness matrix modeled by the finite element method is considered in this paper. Desired matrix properties, symmetry, positive semi definiteness and physical connectivity are the constraints which have been used in this minimization problem. Partial Lagrangian multipliers technique is used to convert the optimization problem into a matrix linear variation inequality. The results of numerical examples show that this method can also be used for incomplete measured data. The analysis has been carried on a spring mass system and then on two sides fixed plate.

Seifi and Abbasi ^[19] proposed a method for Friction coefficient estimation in shaft/bush interference using FEMU. The model updating method is applied on the interference joint of a shaft and bush. Model updating is used to estimate and update the friction coefficient in the contact surface of interference shaft and bush joints. Dongying et al. ^[20] studied the safety evaluation of marine derrick steel structures based on dynamic measurement and updated finite element model. This method can be used for forecasting the safety loading capacity of marine derrick steel structures. Modal parameters identified from vibration measurement and updated FE model with optimization are two important bases of this method. For judgment criterion the safety assessment theory has been used. In first step the analysis of the design feature and the shock excitation mode of marine derrick steel structures have been carried out so that the formulas can be obtained for identifying modal parameters. In second step the dynamic model for the updating finite element model theory is established with optimization. The frequency and modal shape are the two important indicators used in this step. In third step, safety judgment criterion is obtained which depends on the specifications. In last step, safety evaluation of the marine derrick steel structures has been carried out.

Fu et al. ^[21] studied damage identification in plate using FEMU in time domain. For identifying the local damages in isotropic plate structures, response sensitivity based approach is used by measuring the structural dynamic responses. The local damage has been simulated by reduction in the Young's modulus of the plate. For the identification of the damage, a penalty function method with Tikhonov regularization has been used. For the detection of damages, a mathematical model of the structure along with the experimental modal parameters of the structure has to be used. Changes in the natural frequencies ^{[22,23,24,25]}, mode shapes and their derivatives ^{[26,27,28,29]}, measured dynamic flexibility ^[30,31,32] or frequency response function ^{[33,34,35,36]}, these three are the basis for the identification approach. It is easy to measure the natural frequency with great precision, and it is also the most common used dynamic parameter for damage detection. But to avoid the problem of non-uniqueness in the solution of damage identification due to the structural symmetry, mode shapes are used. Li et al. ^[37] presented a strain mode technique for damage identification in plate-like structures. Yam et al. ^[38] conducted a sensitivity analysis on static and dynamic response parameters used for damage identification in plate-like structures. Wu and Law ^[39] showed damage identification in plate structures based on changes in uniform load surface. For the formation of the FE model of plate structures, Reissner-Mindlin plate element is used. The effect of transverse shear deformation is also considered during this analysis. During this analysis the effects of simulated measurement noise, measurement point and measurement time duration on the results have also been observed. This indicates that the proposed method could be applied for the practical applications.

Chen and Maung ^[40] proposed a method based on Regularized FEMU using measured incomplete modal data. This method can directly adopt measured incomplete modal data. Hence, the proposed methods do not require the sensitivity analysis and development of an objective function. The structural parameters which we want to update are properly chosen so that they can characterize the modifications of structural parameters i.e. differences in stiffness and mass matrices between the finite element model and tested structure, at element or critical point level. To determine the chosen structural updating parameters in the least squares sense, without the use of any optimization technique, iterative solution method along with simplified direct method has been used. Min et al. ^[41] used Sensitivity-based FEMU with natural frequencies and zero frequencies for damped beam structures. Adhikari and Woodhouse ^[42] studied a viscous damping system for which they analyzed that only the complex natural frequencies and complex mode shapes were needed to obtain a damping matrix. An identification method was suggested which was based on the constrained error minimization approach. Ozgen and Kim ^[43] proposed the theory of direct experimental identification of damping matrix by using the dynamic stiffness matrix method and also introduced the concept of hybrid modeling. The proposed method has been applied on a real cantilever beam attached damping material on one side. Modak ^[44] proposed a method which was based on model updating using uncorrelated modes. There may be various situations in which not all of the modes identified through an experiment can be correlated with certainty with those predicted by the FE model and some experimental modes may be left uncorrelated. Author proposes a new method of FE model updating which includes both correlated as well as uncorrelated modes for updating. To check the effectiveness of this method, it is applied on a beam structure and a more complex F shape structure. The robustness of the method in the presence of simulated noise is also studied.

Sehgal and Kumar ^[45] presented a review of structural dynamic model updating techniques. To remove the uncertainties, present in the analytical FE model, FEMU techniques have been used. These techniques may be classified as direct updating techniques and Iterative updating techniques. Direct updating techniques provides the solution in single step by updating the incorrect FE model. There is no problem of divergence and it reproduces the measured data accurately. In iterative techniques the difference between the experimental results and FE results are reduced in all iterations. These techniques are also called as gradient based techniques. Iterative techniques provide symmetric and positive definite updated system matrices, which can be easily understood on a physical basis but this is not possible in case of direct updating techniques. The basic experimental setup for the modal testing is shown in Figure 2.

This input force is applied by using a shaker, or an impulse hammer. Excitation may be random, sinusoidal or impulse depending upon the applications. Output of the experimental set-up is based upon their characteristics such as mass, sensitivity, frequency range, operating temperature range and temperature sensitivity, and power supply. Signal from accelerometer is then conditioned using a signal conditioner. Most commonly used accelerometer is piezoelectric accelerometer. Conditioned signal is then sent to Fast Fourier Transform analyzers. FFT will convert the time domain signal to frequency domain so that we can extract more information easily. Park et al. ^[46] studied FEMU considering boundary conditions using neural networks. Author proposed a technique based on the concept of neural networks which is used to evaluate the bridge boundary condition. Consideration of the behaviors of boundary conditions allows us to predict more accurate finite element model. In the proposed method for the representation of the aging and constraining effect of the boundary conditions, an artificial rotational spring at each support is used. The proposed method was verified through laboratory and field tests that were performed on a steel girder bridge. This analysis allows us to estimate the bridge boundary conditions directly from the actual behaviors of bridge supports. Kang et al. ^[47] studied the model updating for rotor-discs system and its application in dynamic coefficients identification of journal bearings. Particle swarm optimization (PSO) algorithm is used to update the system mass and stiffness matrices. For the selection of appropriate variables to be optimized, sensitivity analysis is carried out. The FE model of a dual rotor-discs system was updated to check the validity of the method. An experiment was conducted on the flexible rotor test rig for the validation of updated model and to identify the dynamic coefficients. The results obtained shows that the updated model has higher accuracy than the original model, especially for the system under critical speed.

3.   Finite element model updating of a three degree of freedom spring-mass system

Finite element model updating of the three degree of freedom spring-mass system, 1-D beam, 2-D plate and a composite laminate is carried out. A method known as a direct updating method (DUM) has been developed to update the mass and the stiffness matrices of the structures by using the measured Eigen values and the eigenvectors of the structures ^[48]. The direct updating method is used to remove the error present in the simulated FE model. There are two approaches of direct updating of mass and stiffness matrices of any structure. One is to modify the mass matrix and then modify the stiffness matrix based on the modified mass matrix. This method satisfies the orthogonality constraints. Eq 1 gives the updated mass matrix:

Where, [M_u] is an updated mass matrix, [M_a] is an analytical mass matrix, [ϕ_e] is an experimental mode shape matrix and [I] is an identity matrix. Also: $\left[\overline{\bf{M}_{\mathrm{a}}}\right] = \left[{\mathrm{\phi}}_{\mathrm{e}}\right]^{\mathrm{T}}\left[\mathrm{M}_{\mathrm{a}}\right]\left[{\mathrm{\phi}}_{\mathrm{e}}\right]$.

An updated stiffness matrix is presented in Eq 2 as below:

where [K_u] is an updated stiffness matrix, [K_a] is an analytical mass matrix, [ϕ_e] is an experimental mode shape matrix, [M_u] is an updated mass matrix and [$\lambda$_e] represents experimental eigen values, Second approach is to modify the stiffness matrix and then modify the mass matrix based on the modified stiffness matrix and is given as below.

Eq 3 presents an updated stiffness matrix:

where [K_u] is an updated stiffness matrix, [K_a] is an analytical stiffness matrix, [$\varphi$_e] is an experimental mode shape matrix and $[\lambda$_e] represents experimental eigen values.

An updated mass matrix will be given according to Eq 4 as below:

where [M_u] is an updated mass matrix, [M_a] is an analytical mass matrix, [ϕ_e] is an experimental mode shape matrix, [$\lambda$_e] represents experimental eigen values and [K_u] is an updated stiffness matrix.

The simplest problem of a three degree of freedom spring-mass system is carried out first to remove the uncertainties present in the elastic properties of the spring stiffness's. Figure 3 shows the three degree of freedom spring-mass system.

For simulated model:

M₁ = 5 Kg, M₂ = 5 Kg, M₃ = 5 Kg, K₁ = 1500 N/m, K₂ = 3000 N/m and K₃ = 3000 N/m.

For simulated-experimental model:

M₁ = 5 Kg, M₂ = 5 Kg, M₃ = 5 Kg, K₁ = 3000 N/m, K₂ = 3000 N/m and K₃ = 3000 N/m.

It is assumed that the error is present in the simulated model, a spring that is connected to the boundary. The percentage of the error is 50. Table 1 represents the comparison of the natural frequencies between simulated and simulated-experimental model. It is observed that there is an error between the natural frequencies predicted from the simulated model. The maximum error is 20.0% due to the variation in the spring stiffness. So, there is a need to correct or update the simulated model. Now, the algorithm of direct updating method is used to remove the error between both the models. Table 2 presents the natural frequencies of updated simulated model and simulated-experimental model. It is observed that after applying the direct updating method on this three degree of freedom spring-mass system, the error becomes zero.

Figure 4 shows the frequency response function (FRF) curve among the simulated model, simulated-experimental model and updated simulated model. It is a point frequency response function curve. It is clearly visible from the figure that there is a considerable difference between the natural frequencies predicted by the simulated model and the simulated-experimental model. However, after doing the updating using the direct updating method, the updated simulated FRF curve overlaps the simulated-experimental model response. It is also observed that the updated-simulated FRF completely follows the simulated-experimental model FRF at resonance as well as at anti-resonant frequencies. Figure 5 shows the modal assurance criterion (MAC) values. It represents the correlation between the mode shapes predicted from the updated-simulated and simulated-experimental model. The maximum value of the MAC is 1.0. It means that there is a good correlation between the eigenvectors of the updated simulated and simulated-experimental model. It is concluded from the above results that the direct updating method can be used successfully on multi-degree of freedom system. It not only removes the error but also improves the simulated model.

4.   Finite element model updating of metallic structures

In this section, the finite element model updating of the aluminum material beam (1-D) and plate (2-D) is carried out. The direct updating method (DUM) has been compared with the response function method (RFM) in the past to accurate the FE model of the F-shape structure ^[49]. It was found that the RFM updating method is more accurate as compared to the DUM. The regularized algorithms have been used effectively to improve the effectiveness of the direct updating method. Authors found that the proposed method gave the accurate prediction of the relationship between the perturbation of structural parameters such as the stiffness and the modal properties of the actual tested dynamic structure. The direct updating method is used to improve the FE model of a steel plate backed by a 3-D acoustic cavity. It was found that the application of the direct updating method accurately updates the FE model of the vibro-acoustic cavity in the frequency range of interest.

4.1.   One dimensional beam

In this section, the finite element model updating of an isotropic cantilever beam is carried out by using direct updating method. Figure 6 represents the cantilever beam that is taken in this numerical study. The length (L), width (W) and the thickness (t) of the beam is 0.5 m × 0.02 m × 0.005 m respectively.

A 1-D beam element is used to make the finite element model of the beam. The elemental mass and stiffness matrices are written as below ^[50]. Eq 5 presents the elemental mass matrix of the beam:

where [M_e] is an elemental mass matrix of beam, L_e is length of beam element, A_e is cross-sectional area of beam and ρ is density of beam material. The elemental stiffness matrix of the beam is decribed as given in Eq 6 below:

where [K_e] is elemental stiffness matrix of beam, E is Young's modulus of elasticity, I is moment of inertia and L_e is length of beam element.

For simulated FE model, the material of the beam is aluminum, the young's modulus of elasticity is 65 GPa, the density of the beam is 2700 kg/m³, the beam is divided into 10 finite number of elements. For simulated-experimental FE model, the material of the beam is aluminum, the young's modulus of elasticity is 71 GPa, the density of the beam is 2700 kg/m³, the beam is divided into 10 finite number of elements. It is assumed that the error is present in the simulated FE model. The size (dimensions), the mass (weight, density) of the aluminum beam can be measured accurately. So, the chances of uncertainty in the dimensions as well as in the density of the beam are less. However, it is very difficult to measure the exact value of the young's modulus of elasticity of the beam. In this regard, the uncertainty is assumed in the elastic properties of the beam that are used to develop the simulated FE model. The elastic properties used in the simulated-experimental FE model are assumed to be correct and represents the actual elastic values. The global mass and global stiffness matrices are developed by assembling the elemental matrices.

Table 3 presents the comparison between the natural frequencies predicted from the simulated and simulated-experimental FE model. It is observed that due to uncertainty present in the simulated FE model there is an error between the natural frequencies. The predicted natural frequencies from the simulated model are not matching with the simulated-experimental FE model. The maximum percentage error is 5.88. So, there is a need to correct the simulated FE model.

Now, the direct updating method is used to correct or update the simulated FE model. The global mass and global stiffness matrices of the cantilever beam are updated and then eigenvalue problem is solved to predict the natural frequencies of the beam. Table 4 shows the comparison of the natural frequencies predicted from the updated simulated FE model and simulated-experimental model. It is clearly visible that after using the direct updating method the error between the natural frequencies is zero. It means that the updated simulated FE model exactly represents the simulated-experimental FE model. In this regard, the updated simulated model can be used to predict the dynamics of the real structure.

Figures 7 and 8 present the overlay of the point and transfer frequency response function (FRFs) curves. In the case of point FRF (${\propto }_{11}$), the excitation is applied at node number 1 (x = 0.05 m) and the response is predicted at the same node (x = 0.05 m) from the fixed end of the beam. However, in the case of transfer FRF (${\propto }_{15}$), the excitation is applied at node number 5 (x = 0.2 m), but response is recored at node number 1 (x = 0.05 m).

It is clearly visible that there is a significant gap between the simulated response and simulated-experimental response. This is due to the error present in the young's modulus of elasticity of the beam in the simulated FE model. But, after applying the direct updating algorithm on the simulated FE model, the response of the updated simulated FE model overlaps with the simulated-experimental model. The overlap between them is at resonance, anti-resonance as well as at minima of the FRF curve. It is concluded from the above results that the direct updating method can be used to correct the uncertain simulated FE model of the metallic beam.

4.2.   Two-dimensional isotropic plate

In this section, the finite element model updating of an isotropic rectangular aluminum plate is carried out (Figure 9). A four nodded rectangular bending element with straight edges is used to make the finite element model of the plate. The elemental mass matrix of the plate is given according to Eq 7, however Eq 8 presents the elemental stiffness maytrix of the plate as below ^[51]:

where [M_e] is an elemental mass matrix of plate, ρ is density of plate material, h is thickness of the plate, $a$ is Length of the plate, $b$ is width of the plate, ξ & η are dimensionless coordinates, [K_e] is an elemental stiffness matrix of plate, I_z is moment of inertia of the plate and [D] is a material property matrix.

For simulated FE model, the material of the plate is aluminum, the young's modulus of the elasticity is 65 GPa, the density of the plate is 2700 kg/m³, the size of the plate is 0.414 m × 0.314 m × 0.001 m respectively, the plate is fixed at all the edges and divided into 16 × 16 finite number of elements, and the Poisson's ratio is 0.35. For simulated-experimental FE model, the material of the plate is aluminum, the young's modulus of the elasticity is 71 GPa, the density of the plate is 2700 kg/m³, the size of the plate is 0.414 m × 0.314 m × 0.001 m respectively, the plate is clamped-clamped and divided into 16 × 16 finite number of elements, and the Poisson's ratio is 0.35.

It is assumed that the error is present in the simulated FE model of the plate. The size (dimensions), the mass (weight, density) of the aluminum plate can be measured accurately. The uncertainty is assumed in the elastic properties of the plate that are used to develop the simulated FE model. The elastic properties used in the simulated-experimental FE model are assumed to be correct and represents the actual elastic values. The natural frequencies predicted by simulated-experimental FE model by solving eigenvalue problem using MATLAB software exactly matches with the natural frequencies as reported in the past ^[51]. Table 5 represents the comparison between the natural frequencies predicted from the simulated and simulated-experimental FE model of the clamped-clamped plate. It is observed that due to uncertainty present in the simulated FE model there is an error between the predicted natural frequencies. The predicted natural frequencies from the simulated model do not exactly match with the simulated-experimental FE model. The maximum percentage error is 4.83. So, there is a need to correct the simulated FE model.

Now, the direct updating method is used to correct or update the simulated FE model of the aluminum plate. The global mass and global stiffness matrices of the plate are updated and then eigenvalue problem (EVP) is solved to predict the natural frequencies of the clamped-clamped plate. Table 6 shows the comparison of the natural frequencies predicted from the updated-simulated FE model and simulated-experimental model. It is clearly visible that after using the direct updating method the error between the natural frequencies is zero. It means that the updated-simulated FE model exactly represents the simulated-experimental FE model. In this regard, the updated simulated model can be used to predict the dynamics of the real plate like structures.

Figure 10 presents the overlay of the point frequency response function (FRF) curve. In the case of point FRF, the excitation is applied at node number 73 (x = 0.103 m, y = 0.0785 m) and the response is predicted at the same node from the origin of the plate (x = 0.00 m, y = 0.00 m). It is clearly visible that there is a significant gap between the simulated response and simulated-experimental response. This is due to the error present in the young's modulus of elasticity of the plate in the simulated FE model. But, after applying the direct updating algorithm on the simulated FE model, the response of the updated-simulated FE model overlaps with the simulated-experimental model at resonant and anti-resonant frequencies.

5.   Finite element model updating of composite structures

Composite materials are mainly used in aerospace, automotive, construction, mining and marine industry etc. In this regard, the experimental modal analysis of the composite materials at different loadings is required to measure its spatial-model (mass and stiffness matrices), modal-model (natural frequencies, mode shapes and damping coefficients), and response model (time and frequency response functions). To overcome the complexity of the experimental modal testing of the complex structures, mostly, the numerical or simulated models are developed to predict the mechanical or vibrational behavior of the materials. FE modeling is an important numerical tool that is mostly used for this purpose ^{[52,53,54,55,56,57,58]}. During the process to develop the FE model of the composite structures the various parameters are assumed. The parameters may be the in-plane material properties, fiber orientation, dimensions and the boundary conditions of the composite structure. Due to these uncertain parameters or assumptions in the simulated FE model, the developed model is unable to predict the exact or real behavior of the composite structure at different loadings or excitations. So, there is a need to correct or update the simulated FE model of the composite structures. In this regard, the FEMU is an important numerical tool that can be used to identify and estimate the uncertain parameters of the simulated finite element model by taking the advantage of the experimental testing outputs such as Eigen values and Eigen-vectors of the real structure ^[59]. Then, the updated simulated FE model can be used to predict the response or behavior of the real structures. The application of the finite element model updating on the composite structures has been presented in past ^[60]. FEMU technique such as inverse Eigen-sensitivity method (IESM) can be used to predict the stiffness properties of the composite materials. The important parameters such as generalized mass errors, optimal location of the transducers and approximate reanalysis of Eigen-solutions are addressed while doing model updating of the composite structures.

A multi-model updating technique is used to predict the stiffness properties of the individual layers of the layered composite materials ^[61]. The main purpose to use the multi-model updating technique is to update the developed FE model from the experimental testing so that the in-plane elastic properties of the individual layers of the laminated plate can be predicted analytically. The three important steps on which the success of the implementation of the FEMU for the structures depends has been investigated in past ^[62]. Those are a correct objective function, the correct selection of the updating parameters and the selection of the robust optimization algorithm. They proposed to use a multi-objective optimization technique in the FEMU procedure. Regularized model updating technique has been developed to accurately identify the mechanical properties of the various constituents of the composite materials ^[63]. It was found that the developed Regularized model updating (RMU) technique can handle the random noise present in the measurements very well as compared to the conventional FEMU technique. Inverse Eigen-sensitivity algorithm (IEM) is used to update the developed FE model of the composite plate so that at the constituent level the fiber and matrix elastic properties can be identified accurately ^[64]. A new gradient based step size controlled inverse Eigen-sensitivity method is developed to estimate the material properties and boundary conditions of isotropic and orthotropic composite plates ^[65]. They found that the proposed method is capable to converge the iterations fast as compared to no-step size controlled IEM.

A FEMU based inverse identification technique is developed to accurately estimate the constituent level mechanical properties of fiber reinforced plastic composite panels ^[66]. The error present in the boundary conditions of the FRP composite panel is removed by using the developed technique. The weighted sensitivity-based FEMU technique has been proposed to accurately identify the degree of composite behavior of operational bridge decks with uncertain installation of shear connectors ^[67]. The proposed model is limited only to predict the stiffness of the bridge deck. Kriging metamodel is introduced in the optimization process of the frequency response function (FRF) based model updating technique to attenuate the solving time as well as to facilitate the application of intelligent algorithms in the FEMU of the honeycomb composite sandwich beam ^[68]. A new approach named double connective layer has been developed in combination with FEMU for bolted joints interfaces in hybrid aluminum/composite structures to predict its dynamic properties ^[69]. A sensitivity based inverse Eigen-sensitivity method (IEM) was used on "I" shape fiber reinforced plastic (FRP) composite material to estimate the in-plane material elastic properties ^[70]. The experimental modal analysis (EMA) was carried out on a free-free and simply supported FRP beam. Then the experimentally measured eigenvalues are used to update the finite element model that can be used to accurately estimate the most uncertain mechanical properties of FRP beam. They concluded that the updated finite element model of the 'I' shapes FRP composite can be used for health monitoring application as well as it can successfully stand along with the actual dynamic loading conditions.

A brief review about the FEMU techniques has been presented that can be used for the composite materials ^[71]. The main objective of the authors to present this review is to represent the importance of different uncertainties present in the simulated finite element model of the composite structures. However, the important issues such as parameterization and regularization are also highlighted. IESM has been used in past to reduce the error in between the experimental modal analysis (EMA) and finite element analysis (FEA) results of a composite plate ^[72]. They suggested that the error in between the EMA and FEA of the composite structures are mainly due to the various discrepancies present such as different material properties, thickness of the lamina and laminates, fiber orientations and boundary conditions etc. However, the authors have successfully reduced the error in between the natural frequencies of composite plate measured from EMA and FEA models by selecting the optimum parameters in the IESM optimization algorithm.

It is observed from the above literature review that mostly the sensitivity based such as inverse Eigen-sensitivity method (IEM) is used to remove the uncertainties present in the simulated finite element model of the composite structures. The main principle of the IEM is to minimize the objective function and iteratively predict the uncertain parameters of the composite structures. However, there are few drawbacks of the IEM. The initial estimate of the uncertain parameters and the time taken to solve the iterations in the IEM algorithm is quite cumbersome. In this regard, there is a strong need of a simple and faster algorithm that can be successfully implemented on the composite structures to improve its simulated finite element model. Direct updating method (DUM) is a quick method and that can be used to remove the uncertainties present in the simulated finite element model. Also, this method is very helpful to predict the spatial-model, modal-model and response model of the composite structures at different excitations.

5.1.   Finite element model updating of a graphite- epoxy composite material laminate

In this section, the FEMU of a graphite-epoxy composite material laminate is carried out. Figure 11 shows the four layer cantilever square laminated plate. A four nodded rectangular bending element with straight edges is used to make the finite element model of the composite laminate. The elemental mass matrix is presented in Eq 9 and the elemental stiffness matrix is given according to the Eq 10 as below ^[73].

where M_e is an elemental mass matrix, J_s is Jacobian determinant of the transformation, N is an interpolation or shape function matrix, I is a composite inertia matrix, ξ & η are dimensionless coordinates, K_e is an elemental stiffness matrix, B is strain displacement matrix and C is an elasticity matrix of the composite,

Table 7 represents the material properties that are used to develop the FE model of the graphite epoxy composite laminate. It is assumed that material properties such as in-plane elastic modulus, out of plane elastic modulus etc. are correct for the simulated-experimental FE model and represents the actual values. However, in the case of simulated FE model, it is assumed that the error present in the in-plane elastic modulus. The present percentage error is 9.35%. Also, the fiber orientation is assumed in-correct in the simulated FE model.

It is found that the presence of uncertainty in the fiber orientation directly affects the eigenvalues and eigenvectors of the laminate structures. Therefore, it is considered as an uncertainty in the simulated FE model. So, the prime objective of this study is to apply the direct updating technique on a graphite-epoxy composite laminate to remove the error in the simulated FE model.

Table 8 represents the comparison of the natural frequencies predicted by the simulated and simulated-experimental FE model. It is found that the maximum percentage error present is 18.18%. This clearly represents the mismatch between the spatial and modal-model of both the FE models. So, it is required to correct the spatial and modal-model of the simulated FE model. In literature, as already discussed, the IESM is mostly used to update the simulated FE model of the composite structures. In this paper, the direct updating method is applied on the simulated FE model to correct it. After updating the simulated FE model, it is observed that the error between both the models has been reduced. The percentage error now is 0.00% between both the models. It reflects that the direct updating method is also very effective on the composite laminate structures to update its modal analysis characteristics.

It is clearly visible from the above results that the direct updating method can be successfully implemented on the composite structures. The application of the direct updating method to remove the error in the FE models of isotropic structures is extensively used in the past. However, this study definitely motivates to the researchers to successfully apply the direct updating method on the anisotropic structures like composite materials.

6.   Conclusions

Finite element modeling is a numerical tool that is mostly used to predict the dynamic characteristics of the different materials at different excitations. The material properties, fiber orientations, dimensions and boundary conditions are assumed in the FE model of the different structures. Due to these assumptions or uncertainties, there is an error between the predictions of FE model and real experimentation. However, the developed FE models should be reliable enough so that they can be directly used to predict the actual behavior of the materials. In this regard, to remove the error between the simulated FE model outputs and measured data, the finite element model updating based updating algorithms can be used to accurate the simulated FE model. It is observed from this numerical study that the direct updating method (DUM) can be used to update the spatial-model, modal-model and response model of the different structures. The main achievement of this work is to review and successfully apply the direct updating method on the metals as well as on the graphite-epoxy composite material laminate. The iteration and direct method can be used for the isotropic structures (metals) and also for the composite material structures. The composite materials are anisotropic materials; in this regard the successful application of updating methods is having a great importance. Without consuming a large amount of time, updating methods are quick and fast so that they can be used to update or correct the simulated FE model. Updating methods directly updates the spatial-model (mass matrix and the stiffness matrix) of the simulated models. This prediction directly influences the modal-model (eigenvalues and eigenvectors) of the structure. If the eigenvalues and eigenvectors are predicted accurately then it is possible to estimate the actual behavior of the system in-terms of time and frequency response functions (FRFs).

Acknowledgments

The authors received no financial support for the research, authorship and/or publication of this article.

Conflict of interest

The authors do not mention any conflict of interest regarding this article.