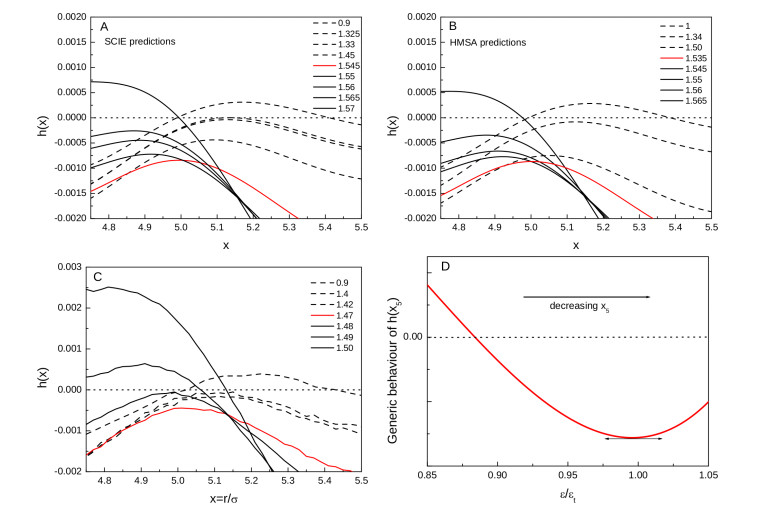
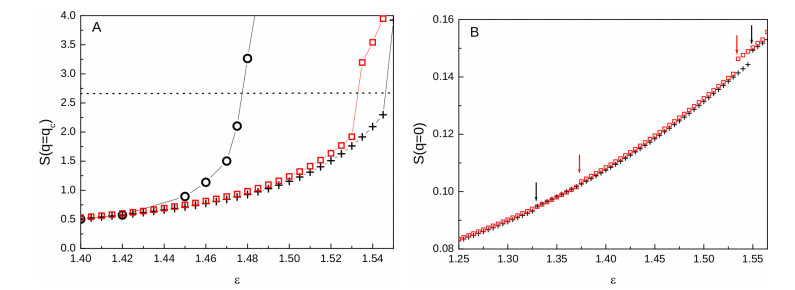
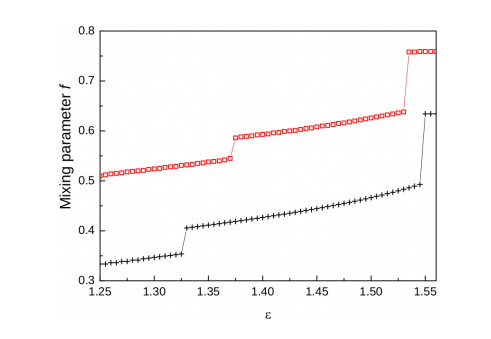
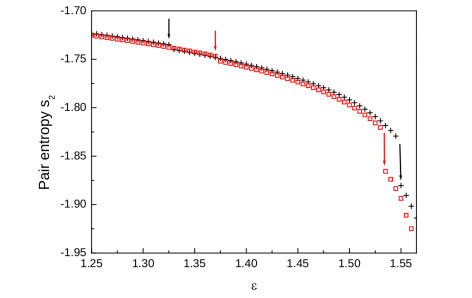
The formation of aggregates is commonly observed in soft matter such as globular protein solutions and colloidal suspensions. A lively debated issue concerns the possibility to discriminate between a generic intermediate-range order taking place in the fluid, as contrasted with the more specific presence of a clustered state. Recently, we have predicted by Monte Carlo simulations of a standard colloidal model — spherical particles interacting via a short-range attraction followed by a screened electrostatic repulsion at larger distances — the existence of a tiny structural change occurring in the pair structure. This change consists in a reversal of trend affecting a portion of the local density as the attractive strength increases, that is shown to take place precisely at the clustering threshold. Here, we address the same issue by refined thermodynamically self-consistent integral equation theories of the liquid state. We document how such theoretical schemes positively account for the observed phenomenology, highlighting their accuracy to finely describe the aggregation processes in model fluids with microscopic competing interactions.
1.
Introduction
The noticeable accomplishment of any research study is its ability to be put to use in real-world situations by incorporating all cutting-edge ideas into contemporary applications. Therefore, all categories of decision-making are considered to be hot and trendy research areas for researchers. These decision-making techniques are designed to facilitate people from different professions making critical decisions. In this regard, a number of multi-criteria decision-making (MCDM) and multi-criteria group decision-making (MCGDM) techniques have been created for choosing the best option out of several options in this ambiguous and uncertain environment.
To account for uncertain propositions and measurements, Zadeh's fuzzy sets [1] came forward as a ground-breaking model whose structure was able to express uncertainty with the help of the unit interval [0, 1]. To rank the alternatives according to their possession of various attributes or features, Fatimah et al. [2] incorporated N-grading to crisp soft set theory [3], hence inaugurating N-soft set (NSS) theory. Its semantical content has been investigated recently [4]. Particularly, two possible interpretations of the grades are applicable, namely, rates (the interpretation presumed so far) and values of truth (which hints at connections with multi-valued logic, much like fuzzy set theory owes to fuzzy logic). Also recently, aggregation and multi-agent decisions with NSSs have been first achieved with the aid of ordered weighted averaging operators [5].
In order to add a touch of fuzziness to crisp soft set theory, Maji et al. [6,7] put forward fuzzy soft set theory. Valuation fuzzy soft sets [8] enhanced their model with an applicable variation that was tested with real estate data. Sayed et al. [9] worked on decision-making soft pre-rough sets. Likewise, Akram et al. [10] incorporated fuzziness into N-soft grading and proposed fuzzy N-soft set (FNSS) theory. The attractiveness of the NSS model can be demonstrated by the emergence of further hybrid models, to name but a few: hesitant FNSS [11], N-soft rough sets [12] and NSSs approach to rough sets [13], multi-fuzzy NSS [14], complex FNSS [15] and picture FNSS [16].
Let us now throw some light on the remarkable success of various MCDM and MCGDM techniques. Many methodologies have been developed in order to break the shackles of decision making hurdles with crisp values [17,18,19,20]. In the context of ambiguous information, the first step was taken by Bellman and Zadeh [21] who recommended different versions of fuzzy decision making techniques. To make adequate these approaches for the needs of vague and uncertain human nature, which is often expressed by N-grading, many fuzzy MCGDM techniques have been developed [22,23,24,25]. They quickly became popular for their multiple applications. Among these techniques, the PROMETHEE technique has proven to be a most appropriate decision making method, either to choose the best alternative or to order the alternatives (subject to the required conditions and circumstances). PROMETHEE (an acronym for preference ranking organization method for enrichment of evaluations) was introduced by Brans and Vincke [19]. It works on the principle of pairwise comparison of the alternatives with respect to their conflicting criteria. Partial and complete rankings of the alternatives deduced by the PROMETHEE I and PROMETHEE II strategies, respectively. The background of the PROMETHEE method was expanded by Goumas and Lygerou [26], who adapted it to a fuzzy scenario. Lolli et al. [27] and Chen et al. [28] also worked to develop the PROMETHEE-based decision-making techniques within the fuzzy context. Krishankumar et al. [29] came up with an intuitionistic fuzzy PROMETHEE method to tackle the belongingness and non-belongingness of data with the help of linguistic values. Further, Wu et al. [30] and Sun et al. [31] developed more decision-making techniques to evaluate uncertain data properly. Ziemba [32] introduced a new MCDM technique by suggesting the NEAT F-PROMETHEE strategy, where trapezoidal fuzzy numbers [33] are used to extract the conclusion. These methods have a variety of applications. For example, Abdullah et al. [34] and Brans et al. [35] applied both PROMETHEE I and II for ranking suppliers and project ranking, respectively. Zhao et al. [36] reevaluated PROMETHEE II for enhancing proficiency in emergency response. Ozsahin et al. [37] used the fuzzy PROMETHEE technique in the evaluation of a nuclear medicine imaging device. Behzadian et al. [38] have performed a profound examination of various frameworks and applications of the PROMETHEE method. Govindan et al. [39] used a PROMETHEE-based strategy in supply chain management to achieve appropriate green supplier ordering. Evaluation of solid state detectors in medical imaging with fuzzy PROMETHEE was achieved by Ozsahin et al. [40]. Maisaini et al. [41] evaluate lung cancer treatment techniques by using a fuzzy PROMETHEE approach. Gul et al. [42] employed a fuzzy logic based PROMETHEE method for material selection problems. The PROMETHEE II technique has been used in an emergency department for the management of hospital resources [43]. Molla et al. [44] extended the PROMETHEE technique with Pythagorean fuzzy sets for medical diagnosis problems. A fuzzy AHP-PROMETHEE II approach for evaluation of solar power plant location alternatives in Turkey was deployed by Samanlioglu and Ayag [45].
To summarize, various MCGDM techniques have been developed to bring ease in the decision making process, either to opt for a most preferable alternative or to order all the alternatives (e.g., from most to least preferable). Particularly, the various PROMETHEE methods have a distinctive importance for their exceptional performance in decision making processes, and also for their notable ability to completely rank the set of alternatives.
Therefore, the following factors embolden us to propose a novel MCGDM technique, within this remarkable family, that we call FNS PROMETHEE, because it operates in FNSS environment:
● Undoubtedly, Zadeh's fuzzy sets [1] achieved a breakthrough in dealing with the ambiguity and uncertainty present in everyday life. However, when one is restricted to giving the alternatives predetermined ratings, other notions are required.
● Fuzzy soft sets [6] already incorporate fuzziness with a parameterized family of the alternatives, but they still lack the ability of capturing N-grading.
● The FNS PROMETHEE technique not only handles the uncertainty of attributes, but it also provides the ease of ranking the alternatives according to the family of the attributes.
The proposed methodology, FNS PROMETHEE, is based on the principle of comparison between any pair of alternatives by calculating the deviation of the alternatives by formulating score degrees, defining a suitable preference function, computing multiple criteria preference indexes and the outgoing and incoming flows of the alternatives. The following are the key contributions of this article:
● A step-by-step procedure of the FNS PROMETHEE technique, along with the flow chart, is included. It that deals with fuzziness of the attributes and helps us to assign N-ordered grading to the alternatives.
● Prior to the procedure of the FNS PROMETHEE technique, an AHP technique is used for normalization of weights that helps us to get more refined results and apply the techniques on the numerical example of the selection of best robot butler.
● The FNS PROMETHEE technique is compared with fuzzy ELECTRE [24], and the outcome of the same best alternative from both of the techniques proved it's rationality and credibility.
The remainder2 includes the procedure of AHP technique [20]. Section 2 comprises the methodology of the FNS PROMETHEE technique. Section 3 incorporates the application of selection of best robot butler using FNS PROMETHEE. Section 4 includes the comparative analysis and discussion of FNS PROMETHEE (using various criteria preference functions) with FNS PROMETHEE (using usual criteria preference function) and FNS PROMETHEE technique with fuzzy ELECTRE [24]. Section 5 concludes this paper.
2.
Structure of FNS PROMETHEE methods
In this section, the paradigms of fuzzy set theory and the N-grading principle are integrated within the PROMETHEE technique to propose new outranking techniques. First, we review a basic definition:
Definition 2.1. [10] Let GN={0,1,2,⋯,N−1} be a set of N ordered grades, where N>1 is a natural number. A triplet (Γ,A,N) is said to be a fuzzy N-soft set on U, where F(U) consists of the set of all fuzzy sets on U, and A is a set of attributes, if Γ:A→2F(U)×GN satisfies the condition for each a∈A and u∈F(U), and there exists a unique r∈GN such that (u,r)∈F(a).
The FNS PROMETHEE technique that stems from this combination is based on the principle of incoming and outgoing flows of the alternatives with the selection of the generalized preference function according to the nature and type of the criteria. The step-by-step algorithm of the FNS PROMETHEE technique can be expressed by the following actions:
1. Construction of independent decision matrices by each expert:
FNS PROMETHEE, an MCGDM technique, is concerned with a group of decision making experts who after examining the alternatives on the basis of the criteria allocate membership degrees and ordered grades to the alternatives under the FNS environment. Therefore, we consider a set of 'q' experts, E={et},t=1,2,⋯,q, who thoroughly analyze a set of 'r' alternatives, A={al},l=1,2,⋯,r, with respect to the 'p' criteria under consideration as C={cs},s=1,2,⋯,p. After a careful survey of the alternatives, each tth expert, from the panel of experts, assigns the independent membership degrees to the lth alternative with respect to the sth criterion in the form of fuzzy N-soft values (FNSV) as (dls,μls). These grades and membership degrees are represented in the form of the FNS decision matrix as follows:
2. Construction of aggregated fuzzy N-soft decision matrix:
In practical situations, the appointed experts do not necessarily have equal importance in the decision making process (because every expert has his/her own expertise, relationship with the issue under decision, et cetera). Therefore, the individual independent decisions of each expert, in the forms of grades and membership degrees, must be accumulated to form a combined decision having the impacts of each decision made by a single expert. A fuzzy N-soft averaging (FNSA) operator is used to merge the decisions of all the experts in a single persuasive decision as follows:
3. Construct the score matrix:
The score degrees of the aggregated values of the aggregated decision matrix are evaluated to estimate the deviation of an alternative with respect to the other one. The score degree is always calculated to determine the supremacy of an alternative over the others. By using the score degree, a score matrix S=[˜sls]r×p, the score degree of the aggregated membership degree and the aggregated ordering is calculated by using Eq (2.4) as follows:
4. Calculation of the deviation of the alternatives with respect to the score degrees:
The main principle of the PROMETHEE method is to evaluate the pairwise deviation of the alternatives with respect to the difference between their score degrees. Therefore, to calculate the deviation between the alternatives hl and hm with respect to the criteria ck, we use Eq (2.5):
5. Define the suitable preference function for the alternatives:
Since every alternative has its own worth and value, the decision making process depends upon the nature and type of the criteria of that alternative. To maintain the eminence of each alternative, decision makers define a suitable preference function for each alternative according to the nature of the criteria. The value of preference function ξk(hl,hm) varies from 0 to 1. The preference function with value exactly 1 indicates the strong preference of an alternative, while the preference function with value 0 is indifferent for the decision makers to the alternative.
6. Evaluation of criteria weights:
In this step, the subjective weights of the criteria are determined using the preferences of the decision-making panel. For this purpose, Saaty's AHP technique [20] is applied to determine the normalized weights of criteria.
7. Determination of the multiple criteria preference index:
In the FNS PROMETHEE method, we calculate the incoming and outgoing flows of the alternatives, for which purpose we evaluate the multiple criteria preference index based on the preference function defined by the decision makers according to the nature of the criteria and the criteria weights calculated by utilizing the AHP technique [20]. The multiple criteria preference index put forward the outranking relation among the alternatives, based on which an outranking graph is made to estimate the superiority and inferiority of an alternative over the other. The multiple criteria preference index can be calculated by using Eq (2.6), as follows:
Since the criteria weights calculated by the AHP technique are normalized, p∑k=1v(k)=1. Therefore, Eq (2.6) reduces to Eq (2.7) as follows:
This preference index indicates the potential of the preference of the decision makers of an alternative over another with respect to all alternatives. This preference index has values that lie between 0 and 1, such that
● τ(hl,hm)≈1 indicates the strong preference of alternative hl over hm with respect to all criteria. It shows the supremacy of hl over hm.
● τ(hl,hm)≈0 indicates the weak preference of alternative hl over hm with respect to all criteria. It shows the inferiority of hl to hm.
8. Deduce the partial and complete preference ranking:
Now, the preference ranking of the alternatives is obtained by utilizing the multiple criteria preference index. The preference raking of the alternatives shows the dominance and subjugation of an alternative over the other with respect to the all criteria. The partial outranking is obtained by using the PROMETHEE I technique, and the complete outranking is obtained by using the PROMETHEE II technique. The working principles of PROMETHEE I and PROMETHEE II techniques are explained as follows:
● The partial outranking flow of the alternatives (PROMETHEE I):
This technique surrounds with the outgoing and incoming flows of the alternatives that decide the supremacy or inferiority of an alternative compared to others. The outgoing flow of the alternatives is calculated by using Eq (2.8) as follows:
The outgoing flow is also known as leaving flow or positive flow and measures the dominant behavior of an alternative over all other alternatives. It is actually the average of all outgoing arcs drawn from hl as shown in Figure 1.
On the other hand, the incoming flow of the alternatives is calculated by using Eq (2.9) as follows:
This incoming flow is also known as negative flow and measures the submissive behavior of an alternative compared to all other alternatives. It is actually the average of all incoming arcs towards hl as shown in Figure 2.
The alternative with larger outgoing flow and smaller incoming flow is the preferable one or dominant over all other alternatives. The preferences of the alternatives based on the outgoing and incoming flows can be computed by using Eqs (2.10) and (2.11):
The intersection of these preference rankings facilitates us with the partial outranking (˜F,˜G,˜K) of PROMETHEE I by using Eq (2.12):
In Eq (2.12), hl˜Fhm indicates that hl outranks hm, and hl˜Ghm indicates that hl is indifferent to hm, that is, both the alternatives are at the same position while hl˜Khm indicates that hl is incomparable with hm. Therefore, PROMETHEE I gives us the partial outranking, as some of the alternatives remain incomparable.
● The complete outranking flow of the alternatives (PROMETHEE II):
In order to get the complete outranking of the alternatives with respect to the incoming and outgoing flows, PROMETHEE II comes up with spectacular features for providing us the complete outranking of the alternatives. The net outranking of the alternatives is formulated with the help of Eq (2.13):
Eq (2.13) shows the difference between outgoing and incoming flows of the alternatives that provides us the complete outranking (P∗,I∗) in PROMETHEE II of the alternatives with the help of Eq (2.14):
In Eq (2.14), hlF∗hm indicates that hl outranks hm, and hlG∗hm indicates that hl and hm both are at the same position and indifferent to each other. Hence, the alternative with greatest outranking flow is considered as the most suitable choice. In this way, PROMETHEE II works out with the complete outranking of the alternatives and plays a requisite role in the multi-criteria decision making process.
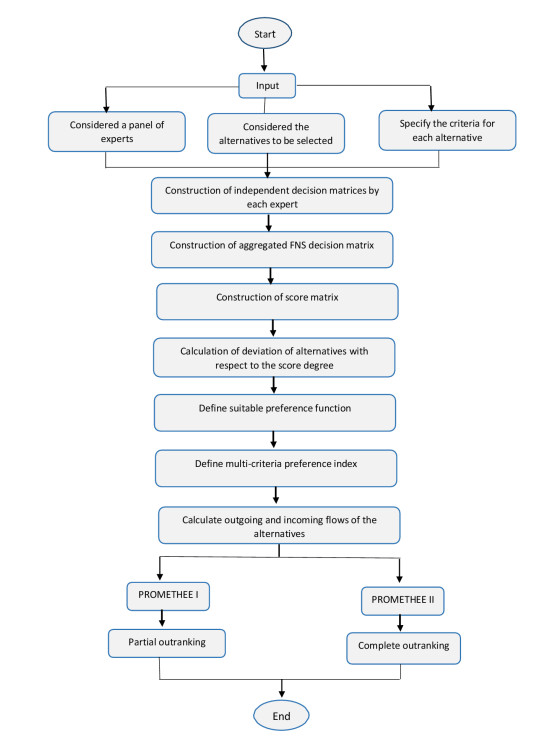
This detailed step-by-step procedure of FNS PROMETHEE is summarized in a flowchart, as shown in Figure 3.
The choice of preference function for each criterion of alternatives is a difficult task. Brans et al. [19,35] specified the general preference function according to the nature and type of the criteria. These preference functions cover most of the aspects of the nature of the criteria. The definitions of these preference functions are as follows:
Definition 2.2. The usual criterion preference function (Type I) is defined as
where x is the difference between any two alternatives. This preference function does not possess any parameter and under this function a criterion can be used in its usual way.
Definition 2.3. The usual Quasi-criterion preference function (Type II) is defined as
where t is the indifference threshold value between any two alternatives. The two alternatives remain the same unless their difference does not exceed value of t. If their difference gets larger than value of t, a strict preference relation is developed.
Definition 2.4. The criterion with linear preference function (Type III) is defined as :
where p∈[0,1] is the preference threshold assigned by the decision maker, where the preference of the decision maker increases linearly with x until the difference of alternatives is lower than p. When x is greater than p, a strict preference of an alternative is obtained with respect to that criterion.
Definition 2.5. The level criterion preference function (Type IV) is defined as :
where l and m represent the priority and indifference thresholds, respectively, given by the decision maker, and can be selected from interval [0, 1]. In such functions, two alternatives behave similarly only if the difference between two alternatives lies in the interval [-l, l].
Definition 2.6. The criterion with linear preference having indifference area (Type V) is defined as :
where v and w represent threshold values that lie in [0, 1]. Under such functions, two alternatives have entirely same behavior unless their deviation does not exceed value of u. The preference increases linearly as long as the deviation equals to u + v, and after that value, a strict preference is achieved.
Definition 2.7. The preference function for the Gaussian criteria (Type VI) is defined as
where the value of θ∈[0,1] is assigned by decision maker and represents the distance between the origin and the point of inflexion.
3.
Applications
This section is summed up with the application of the remarkable MCGDM technique, FNS PROMETHEE, that facilitates us in making the best suitable decisions in the FNS environment according to the terms and conditions. This section is entailed with two real life applications of decision making techniques. The first one is related to the field of artificial intelligence, that is, selection of the best robot butler for household chores. The second one is concerned with the medical field, that is, the selection of the most suitable emergency unit in a hospital for the treatment of the patients who come in critical condition.
3.1. Selection of the best robot butler for household chores
This subsection provides a detailed explanation of the problem statement to describe the background. Unquestionably, artificial intelligence has gained remarkable popularity by inventing different devices that have made our life much easier and quicker. The miracles of artificial intelligence are revered by several researchers, and their remarkable achievements in most branches of science, medical, media, engineering, industry or mechanics are acknowledged. Everything that has been made possible from the development of smart Android phones and to the Astrobee robot (which was sent to the space station; see https://www.nasa.gov/astrobee), is a blessing of artificial intelligence. Now, scientists are interested in inventing robot butlers that can do all household chores more smoothly, quickly and efficiently and can save some time for a man in his busy routine. Many scientists have created humanoid robots with the help of artificial intelligence, such as a 6-foot 3-inch radio-controlled robot that could do some ironing at its inventor Peter Holland's home in Hertfordshire. Engineer Boris Grishin built a robot secretary capable of answering the phone, waking up the family in the morning, controlling the temperature, and turning on and off the lights, Toshiba introduced a prototype housekeeping robot called ApriAttenda that can open the door of a fridge and picking a bottle. The robot's designers want to employ these tremendous machines in a variety of ways. (https://www.huffpost.com).
Consider a scenario where a robotics company wants to introduce a robot butler in the market that fulfils the needs of people and can share the burden of household chores with them. To provide its customers the best service, suppose the company has five alternatives (robots) Φ={φ1,φ2,φ3,φ4,φ5} to be selected and a panel of experts ζ={ς1,ς2,ς3,ς4} who have expertise in various fields to analyze all the aspects of these selected alternatives. The panel of experts consists of the following professionals:
● Information technology (IT) expert (ς1):
An information technology expert will monitor and manage computer hardware, software and networks within the machinery of the alternatives. The IT specialist will maintain and improve the technical system of the robot to ensure implementation, monitoring, and maintenance of IT systems installed in the selected robots. He will keep track of the system functionality.
● Logistics expert (ς2):
The logistics expert will be responsible for the life cycle of the products, including preparation, shipping and receiving. He will develop reports showing transportation costs on this precise project and moves, support the maintenance of logistics policies, administer, maintain inventory control program systems and work within the logistical department of the company that hires him.
● Coding expert (ς3):
Code is the main instructions or programm installed in any system to run it. A coding expert will analyze the alternatives based on the software programming installed in them, as an expert in the development of computer technology. A coding expert will perform the following tasks: system conception, design, system development, writing code, testing, debugging, implementation and maintenance.
● Roboticist (ς4):
Roboticists are generally involved in the design, programming, construction, and testing of robots. They can work on any stage of development, from creating software to building hardware and troubleshooting the finished product. Robotics engineers spend the majority of their time designing the plans and processes needed to not only build robots, but to have them work effectively. Some robotics engineers also design the machines that actually assemble the robots.
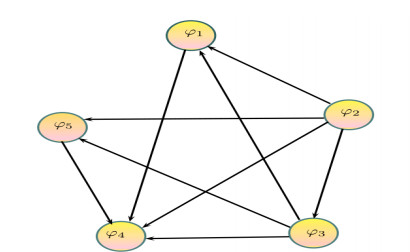
The above mentioned experts make the decision after a thorough analysis of the considered criteria ξ={η1,η2,η3,η4} that are displayed in Figure 5 and explained as follows:
● Adaptive to the environment (η1):
As robots operate in the real world experiencing a range of different environments and tasks, it is essential for the robot to have the ability to adapt to its surroundings to work efficiently in changing conditions and circumstances by allowing adaptation to internal, as well as external factors.
● Fast learner (η2):
Robots should not only work with the pre-defined programming but also be able to learn things with time. Robots can perform efficiently in all the tasks and hurdles for which they are already programmed, but humanoid robots mast have this unique feature of humans, as they must be fast learners of different new things and tasks.
● Biometric technology (η3):
Robots must be equipped with biometric technology that enables them to differentiate between family members, strangers, physical spaces and household items. This feature is very essential for the robot so that it would recognize any stranger coming into the house, place the household items in their specific place and also detect the temperature of the other people.
● Prepared for emergency (η4):
Robots must be prepared for emergency situations as they must sense that something is going wrong and not in the usual way, such as having a fire in a house, robbers robbing the house, gas leakage, water leakage or water overflow. They must avoid harmful situations to people, property and themselves.
3.2. Steps for the selection of a best robot butler by using FNS PROMETHEE technique
This subsection describes the complete solution of the described decision-making problem. As our proposed MCGDM methodology, FNS PROMETHEE is a pre-eminent tool for the selection of the best robot butler to be launched in the market by a certain company. The main principle of this technique is the comparison between any pair of alternatives based on the incoming and outgoing flows of the alternatives. This methodology comprises the deviations of the alternatives with respect to the score degree, general preference function, multi criteria preference function, and partial and complete rankings of the alternatives. The initial evaluations considered in this specific numerical example are the sample data. The detailed step-by-step procedure of the FNS PROMETHEE technique for the selection of the best robot butler is as follows:
1). Each expert in the designated panel of experts, after thorough analysis of the alternatives based on the considered criteria, assigns the grades and membership degrees, in the form of fuzzy N-soft values (FNSV), to the alternatives separately. These individual assessments are arranged in Tables 1–4, respectively.
2). This discrete assessment from each decision maker is assembled in one matrix that has the collective effect of the decisions of the experts by using the mFNSA operator, given in Eqs (2.2) and (2.3), represented as AF6SDM in Table 5.
3). Calculate the score degrees of the aggregated values in the aggregated decision matrix by using Eq (2.4) to construct a score matrix, displayed in Table (6), that will be used to calculate deviations of the alternatives.
4). Calculate the deviations of the alternatives with respect to the score degree by using Eq (2.5), which shows the difference between the score degrees of any pair of alternatives. These deviations of the alternatives are arranged in Table 7.
5). To maintain the eminence of each alternative, define a suitable preference function among the six types of preference functions formulated by Brans [19,35] on the basis of indifference and preference thresholds. Here, we have considered preference functions of Types I–III for the sake of simplicity and to deal with preferences and indifference between the alternatives. The types of criteria are specified by the generalized preference functions given in Table 8.
6). In this step, the weights of the criteria are calculated by using the AHP technique. The comparison table is displayed in Table 9 based on the Saaty preference scale. The comparative scale, assigned by the experts to the attributes, depends on the comparative importance of the attributes over one another according to their nature and the circumstances under which those attributes are being considered. In this specific example of selection of best robot butler, the initial evaluations are being taken as test data.
After multiplication of comparison table of criteria and criteria weights, the Bϱ matrix is shown in Eq (3.1):
The maximum eigenvalue is calculated as follows:
The consistency index is calculated as S=0.026. The consistency index near zero shows that the comparative values are consistent. After evaluating the consistency index, we calculate the consistency ratio by dividing the consistency index by the random index. Here, we have considered n=4 and T=0.90. The consistency ratio is calculated as Y=0.0289. As 0.0289<0.10, it is acceptable. The normalized weights are displayed in Table 10. The obtained weight vector is shown in Table 11.
7). The preference degrees of every pair of alternatives with respect to each of the criteria are calculated by using generalized criteria preference function by Brans [19,35], as displayed in Table 12.
8). Based on the preference function and the criteria weights calculated by AHP technique 11, determine the multi-criteria preference index by using Eq (2.7), indicating the potential of the preference of experts of an alternative over another. The multi-criteria preference index is shown in Table 13.
9). The next step is to deduce the partial and complete outranking of the alternatives. The partial outranking of the alternatives is estimated with FNS PROMETHEE I and by the formulation of outgoing and incoming flows of the alternatives by using Eqs (2.8) and (2.9), respectively. The outgoing and incoming flows of an alternative with respect to another alternative are deduced by Eqs (2.10) and (2.11), respectively, and displayed in Table 14. The intersection of these flows facilitates the partial outranking of the alternatives, which can be estimated by Eq (2.12) as follows:
φ1ˆPφ4, φ2ˆPφ1, φ2ˆPφ3, φ2ˆPφ4, φ2ˆPφ5, φ3ˆPφ1, φ3ˆPφ4, φ3ˆPφ5, φ5ˆPφ4.
However, φ1 and φ5 are incomparable. This partial relation of PROMETHEE I is shown in Figure 6.
10). For the complete outranking of the alternatives with FNS PROMETHEE II, the net outranking of the alternatives is formulated by Eq (2.13). Now, by using Eq (2.14), we can get the complete outranking of the alternatives, as shown in Table 15.
11). After performing all the calculations, we evaluate the net flows of the alternatives in Table 15, which shows that greater the net flows more suitable an alternative is, according to which the ordering of the alternatives is as follows:
φ2>φ3>φ1>φ5>φ4. Here, Table 15 seems to show that φ2 has the highest net flow (most favorable), and φ4 has least value of net flow (least preferable).
4.
Comparative analysis
In this section, a comparative study of the proposed technique with the existing approaches is carried out to manifest the authenticity and accuracy of the proposed technique. Further, this section includes a thorough discussion to highlight the dominance of the proposed approaches.
4.1. Comparison of the proposed method with existing technique [24]
In this subsection, we perform the fuzzy ELECTRE technique [24] on the application of the selection of the beset robot butler to be launched in the market to compare this technique with our proposed MCGDM technique, FNS PROMETHEE. For the sake of convenience, we have considered a fuzzy ELECTRE environment, and after performing the calculations, we will come to know that the same best alternative is selected under both techniques. Now, the steps of the fuzzy ELECTRE technique [24] are as follows:
1). First of all, the aggregated fuzzy importance weights for each criteria are calculated, as shown in Table 16.
2). After analyzing all the criteria for each alternative, all the experts (ς1,ς2,ς3,ς4) assigned fuzzy weights to the considered alternatives, and the decision matrix is presented in Table 17.
3). Construct a normalized decision matrix, as shown in Table 18, after applying the normalization on the decision matrix.
4). The weighted normalized decision matrix shown in Table 19 is formed by multiplying the normalized decision matrix with the aggregated fuzzy importance weights.
5). The concordance and discordance indices are calculated for each of the criteria (wj1,wj2,wj3). The concordance indices are calculated to check the levels of superiority of the alternatives over the others. The concordance set (CS) and concordance index (CI) with respect to the criteria wj1, wj2 and wj3 are shown in Tables 20, 21 and 22, respectively.
6). The discordance index (DI) is used to determine of the level of inferiority of an alternative compared to another according to the selected criteria. Therefore, the fuzzy DI is formulated to check the level of inferiority. The discordance set (DS) and discordance index (DI) with respect to the criteria wj1, wj2 and wj3 are shown in Tables 23, 24 and 25, respectively.
7). The final concordance and discordance indices are computed, where the larger values of CI and smaller values of DI indicate the strong and preferable relation among the alternatives. The final CI and DI values are displayed in Tables 26 and 27.
8). The average concordance index is 0.44, and the average discordance index is 0.49. The alternative φ2 has the concordance greater than the average concordance and the discordance lesser than the average discordance index. Therefore, alternative φ2 is selected as the best robot butler to be launched in the market.
9). The comparison between the proposed FNS PROMETHEE technique and the fuzzy ELECTRE I [24] shows us the selection of same best alternative. The comparison is shown in Table 28.
Table 28 shows that the same best robot butler (φ2) is chosen for the household chores by applying both of the techniques on the same example. {Thus, the results of this comparison are consistent with our proposed technique and verify its competency.
4.2. Theoretical comparison
Both the FNS PROMETHEE technique and fuzzy ELECTRE method fall in the category of outranking approaches, but the proposed technique performs more brilliantly owing to the operational and theoretical backgrounds of the PROMETHEE methods. Moreover, the proposed techniques prevails due to the tendency of establishing the ranking list from the most favorable to least favorable one with respect to their net flows, while the other existing outranking techniques may lose this feature due to incomparability. The proposed variants of the PROMETHEE method have the edge to incorporate the grading in addition to inexact information due to the prevalent structure of FNSS. Oppositely, the fuzzy ELECTRE approach lacks representation of the grading information. Thus, the proposed technique, working on the background of soft and fuzzy set theory, is more compatible and adaptable to manipulate decision-making problems.
4.3. Merits and demerits.
This subsection is dedicated to a precise discussion on the advantages and drawbacks of the proposed strategies.
● The most visible achievement is the extension of the applicability of a remarkable MCGDM technique, namely, PROMETHEE, to a novel knowledge structure. It had already been extended to fuzzy data. Here, we have adapted PROMETHEE so that we can apply its spirit even in the case of fuzzy N-soft data. With this further extension, one can incorporate the vagueness of the human expressions that are often put across through an N-grading of the parameterized family of alternatives.
● In agreement with this road map, the FNS PROMETHEE technique focuses mainly on the incoming and outgoing flows of the alternatives based on their deviations, by constructing the score degree and multi-criteria preference index.
● FNS PROMETHEE I gives a partial outranking of the alternatives, while FNS PROMETHEE II produces a complete out ranking of the alternatives. Both outrankings of the alternatives can be shown by the corresponding outranking graphs.
● Despite all these distinctions, the proposed techniques is still inept in accommodating multi-polar information due to the inherent structure of FNSS.
5.
Conclusions, limitations and future research
Multiple MCGDM techniques have revolutionized the operational approach to decision-making. Even though human nature is intrinsically imprecise, various approaches to uncertainty are compatible to interpret the fuzziness of real life scenarios. Further, the grading approach of the FNSS, relatable to the trendy opinion expression of the modern world, makes it highly adaptable and suitable to carry the imprecision as well as the grading of the particular object within the specified range. This model is designed by merging the many-valued logics with fuzzy expressions to deal with parametric families associated with attributes by dint of both "ratings" and "values of truth".
The core aim of this article is to employ the well suited structure of FNSS to address a real life problem to look for a more appropriate decision. Noticing the impressive decision-making aptitude of the PROMETHEE technique, we have produced, applied and discussed a novel FNS PROMETHEE approach. We have given a detailed step-by-step description of the proposed methodology, and a comprehensive flowchart has been included to convey the concise summary of this strategy. Then, a specific example concerning the selection of the best robotic butler and a comparative study have been presented to manifest its competency with strong arguments.
The proposed strategy allows the expression of a parameterized family of the alternatives (in terms of the attributes) with nice characteristics (fuzziness plus graded expressions). The main advantages of the FNS PROMETHEE technique is its ability to deal with uncertainty and N-ordered grading at the same time, where fuzzy sets or fuzzy soft sets used to fail, and these circumstances occur in many practical field, like science and management, departments of information and technology, business administration, artificial intelligence, computational mathematics, and industrial management. Despite the numerous benefits of the proposed technique, the aptitude of the proposed technique is limited to dealing with only one aspect (single pole) of the information. Another drawback of this study is its malfunctioning in dealing with periodic information. Thus, to overcome these limitations, we are planing to extend the family of PROMETHEE techniques in different domains with the grading feature of N-SS, including m-polar FNSS and complex m-polar FNSS.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through General Research Project under grant number (R.G.P.2/48/43). Alcantud is grateful to the Junta de Castilla y León and the European Regional Development Fund (Grant CLU-2019-03) for the financial support to the Research Unit of Excellence "Economic Management for Sustainability" (GECOS).









 DownLoad:
DownLoad: