Discrete-element model of electrophoretic deposition in systems with small Debye length: effective charge, lubrication force, characteristic scales, and early-stage transport

Abbreviations: κ: inverse of Debye length, m⁻¹; h: interparticle gap, m; m_p: mass of the particle (incl. immobile Stern layer), kg; m_a: added mass for the particle, kg; F_field: force on particle due to electric field, N; F_hydro: force on particle due to hydrodynamic interaction (incl. viscous drag and resultant interparticle hydrodynamic force), N; F_{interparticle}: force on particle due to resultant interparticle interaction (sum of van der Waals forces, interparticle electric repulsion, and direct mechanical contact forces), N; F_gravity: force on particle due to gravity, N; F_buoyancy: force on particle due to buoyancy, N; F_d: viscous drag force on particle, N; F_lub: lubrication force on particle, N; F_el: electric repulsive force between two particles, N; F_gb: sum of gravity and buoyancy forces on particle, N; F_c: force caused by a direct mechanical contact between two particles, N; r: particle position vector, m; v: particle velocity, m/s; R: effective radius of the particle, m; q_eff: effective charge of the particle, C; E: electric field, N/C; v_∞: terminal velocity of the particle, m/s; μ: dynamic viscosity of interstitial fluid, Pa∙s; ε₀: electric constant, F/m; ε: relative permittivity; ζ: zeta-potential, V; A_H: Hamaker constant, J; V_el: Yukawa potential, V; ξ₁: ratio of external electric force to viscous drag force; ξ₂: ratio of electric repulsive force (Yukawa potential) to viscous drag force; ξ₃: ratio of van der Waals force to viscous drag force; ξ₄: ratio of lubrication force to viscous drag force; ξ₅: ratio of gravity + buoyancy force to viscous drag force; ξ₆: ratio of electric repulsive force (Coulomb potential) to viscous drag force; ρ_p: density of particle, kg/m³; ρ_f: density of interstitial fluid, kg/m³; ρ: sum of particle density and half of fluid density, kg/m³; i, j: particle indices (used as subscripts or superscripts in the equations); R_r: reduced particle radius, m; n: wall’s unit normal vector; h_cutoff: cut off gap for lubrication wall, m; x: particle coordinate in 1D treatment, m; x₀: initial particle coordinate in 1D treatment, m; τ₀: characteristic speed-up time of the particle, s; t: time, s.

1.   Introduction

Electrophoretic deposition (EPD) refers to deposition of particles from a suspension by application of electric field ^[1,2]. This technology, used e.g. in manufacturing of ceramic coatings, is based on the effect known as electrophoresis: suspended particles carrying electric charge are set in motion when electric field is applied. The strength of this effect is determined, amongst other factors, by the ζ-potential of the particles, i.e. the electric potential at the slip surface (the boundary between the Stern layer and the diffuse layer) ^[3,4]. The characteristic length scale of the diffuse layer is given by the Debye length, usually denoted as κ⁻¹.

Electrophoresis of cement slurry was recently proposed as a new method for controlling properties and structure of the interface between cement and steel, in particular in well construction ^[5,6]. A variety of additives are usually used in well cements, in order to facilitate the pumping of the slurry down the hole, to improve the downhole properties of the slurry, to optimize the setting time, etc ^[7,8]. Some of these additives may have a significant effect on the zeta-potential and electrokinetic properties of cement particles ^[9,10,11]. On account of large variety in cement compositions, it is necessary to supplement the ongoing experimental campaigns with numerical modelling of electrophoretic deposition of cement on steel surfaces. One of the methods that can be used to model electrophoretic deposition is the discrete-element method (DEM) ^{[12,13,14,15,16]}. In this method, particles are represented explicitly, as spheres or agammaegates of spheres ^[17]. At each timestep, forces acting on each particle are calculated, and the particle accelerations are evaluated. The latter are then used to integrate the particle velocity and position. In its most basic implementation, DEM is thereby an explicit, fully Lagrangian numerical method.

An (incomplete) list of forces acting on an individual particle in electrophoretic deposition is as follows:

1) Hydrodynamic forces (incl. the added-mass effect);

2) External electric force;

3) Gravity and buoyancy forces;

4) Interparticle van der Waals forces (typically attractive);

5) Interparticle electrical double-layer forces (repulsive);

6) Brownian force;

7) Direct interparticle contact force (if particles ever come into direct mechanical contact, with the interparticle gap, h, reduced to zero or a negative value, i.e. overlap);

8) Others (electrophoretic relaxation etc).

Of the above, only hydrodynamic forces, external electric force, and interparticle forces (van der Waals forces, double-layer forces and possibly direct mechanical contact forces) are significant for cement slurries as long as the slurry is in liquid state (before hydration of cement starts). The Brownian force is only relevant for submicron particles ^[18]. The relative magnitude of other forces will be discussed in section 2.3. The resultant force acting on a charged particle moving in a quiescent fluid is thus given by ^[15]:

where m_p is the mass of the particle (incl. the immobile Stern layer); m_a is the added mass for the particle (which is equal to half of the mass of the displaced fluid); and the five force terms on the right-hand side stand for the force due to the electric field, hydrodynamic interaction (incl. viscous drag and resultant interparticle hydrodynamic force), resultant interparticle interaction (sum of van der Waals forces, interparticle electric repulsion, and direct mechanical contact forces), gravity and buoyancy.

The first term on the r.h.s. of Eq 1, the force due to the electric field, is usually calculated as:

where E is the electric field and q_eff is the so-called “effective charge” of the particle ^[15]. In order to apply Eq 1, an effective particle charge must thus be assigned to each particle. Since F_field is the primary driving force for electrophoresis, it is of utmost importance to have a valid expression for q_eff in order to have a satisfactory discrete-element model of EPD. Assuming spherical particles, as is often done in DEM, q_eff is expected to be a function of particle’s radius (R) and ζ-potential. R is understood here as the effective radius of the particle, i.e. the distance from the centre of the particle to the slip boundary (interface between the Stern layer and the diffuse layer). Another characteristic scale of a charged particle is the Debye screening length, κ⁻¹. The Debye length is the characteristic size (thickness) of the diffuse layer. With regard to these characteristic lengths, cement slurries have two important features:

● The particle size distribution is quite wide, with the order of magnitude of particle diameter from a 1 μm up to 100 μm ^[19].

● The Debye length is typically quite small, on the order of 1 nm ^[20].

The product κR is thus on the order of 10³…10⁵ for cement slurries. We always assume therefore that κR >> 1 in this study (small-Debye-length approximation). The first objective of this study was to choose a reasonably accurate expression for q_eff that could be used in a DEM model of EDP in systems with κR >> 1.

Besides F_field, another term that has a pronounced effect on particle motion is F_hydro. This term is usually assumed to be given by the Stokes law, possibly with some adjustments for the particle shape, hindered motion, etc. This might be sufficient for modelling electrophoresis pure. In deposition modelling, however, we are interested not only in free motion of single particles, but also in hydrodynamic forces that appear when particles approach each other (and the electrode) while being deposited. When two particles are approaching each other, viscous fluid needs to be squeezed out of the interparticle gap. Part of the kinetic energy of the particles is used to overcome the viscous forces during this process. This is perceived as an extra force acting on the particles (or on the particle, if the particle is moving near a wall). This indirect hydrodynamic force, or “lubrication force”, is singular at h→0. This force is often neglected in EPD models. The second objective of this paper was to take a closer look at the role and significance of the lubrication force in EPD modelling.

Due to the multitude of forces acting on particles in EPD, the number of input parameters in a model may quickly become so large that the practical value of modelling becomes negligible. The number of particle forces could be reduced, and the significance of input parameters could be better understood, if a set of non-dimensional parameters is constructed that describes the relative significance of the forces. The third objective of this paper was thus to construct several non-dimensional parameters that may be useful in evaluating the significance of different forces in a discrete-element model of EPD.

2.   Materials and methods

2.1.   Effective charge on particle

In order to set up a DEM model, one needs to assign an effective charge to each particle. This parameter should be chosen in such way that, at least, it leads to some reasonable predictions in certain limiting cases. As one such case, we consider motion of a single particle far away from the walls in a constant and uniform electric field. When electric field is turned on, a particle (initially at rest) is accelerated to its terminal velocity (the issue of particle acceleration at early stage of transport will be discussed in section 3.2). After the initial acceleration time, the particle will be moving with a constant terminal velocity, v_∞, which, in the case of κR >> 1, is commonly approximated by the Smoluchowski Eq^{1 [21,22]}:

¹ In the case of κR << 1, the terminal velocity would be given by the Debye–Hückel equation: $v_{\infty} = 2 \varepsilon_{0} \varepsilon_{r} \zeta E / 3 \mu$.

where μ is the dynamic viscosity of the interstitial fluid. The terminal velocity given by Eq 3 is independent of the particle radius. A more accurate approximation is given by ^[23]:

We now require that the effective charge of the particle in DEM be assigned in such way that Eq 4 is recovered if we perform a DEM simulation of a single particle’s motion in constant uniform electric field.

When a particle is moving with a constant terminal velocity, there are two forces acting on it: the external electric field and the viscous drag force. The former is given by Eq 2. The viscous drag force is usually approximated by the Stokes law in DEM models ^[15]:

It follows then that, in order to recover Eq 4 in DEM at κR >> 1, we could assign the effective charge as follows:

In EPD from a cement slurry, κR = 10³…10⁵, and we can set

2.2.   Lubrication force

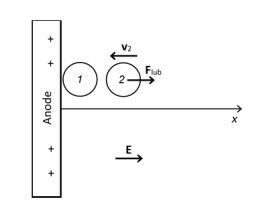
Lubrication force is a viscous force acting on particles in a suspension and caused by relative motion of adjacent particles. This force is often neglected in DEM simulations of EDP. Let particle 1 be at rest (for instance, particle 1 has been deposited earlier) and let particle 2 be moving towards particle 1 along the line connecting the particles’ centres (head-on collision, Figure 1). The lubrication force on particle 2 is given in this case by ^[24,25]:

Figure 1.  Lubrication force acting on particle 2 in a head-on collision of two particles. Particle 2 is approaching particle 1. Particle 1 is at rest (deposited). Both particles carry negative electric charge. Equal force, but in the opposite direction, is acting on particle 1.

DownLoad: Full-Size Img PowerPoint

For simplicity, all particles are assumed to have the same radius, R, here. The total hydrodynamic force on particle 2 is a sum of the viscous drag force and the lubrication force:

From Eqs 5 and 8, the ratio of the lubrication force to the Stokes drag force on particle 2 is given by R/4h.

Two factors govern the magnitude of the interparticle lubrication force: (ⅰ) the relative velocity of the particles and (ⅱ) the width of the interparticle gap. As particles in the bulk suspension are moving towards the electrode, the lubrication force is of little significance because (ⅰ) particles are moving with similar velocities (electrophoretic mobility coefficient, v_∞/E, is the same for all particles) and (ⅱ) interparticle distance is relatively large in the bulk suspension. Particles’ velocities still can differ, e.g., if particles have experienced collisions during the acceleration phase and therefore have velocity components normal to the applied field. However, viscous forces are likely to smooth out such differences soon after the particles are set in motion.

As particles come closer to the deposit, lubrication force will play a significant role in particles' slowing down because the force is singular at h→0. This force will act so as to prevent particles from directly contacting each other and the electrode ^[26,27]. For a particle of 40 μm in diameter, the lubrication force becomes the same order of magnitude as the Stokes drag force when the interparticle gap decreases to 5 μm. This gap, however small it is, is still three orders of magnitude larger than the typical thickness of the double layer for cement particles. Thus, it is necessary to include the lubrication force in a DEM model of EPD, at least for particles approaching the deposit, in order to represent the deposition process correctly. The implementation of lubrication force requires a pairwise search for adjacent particles and is therefore computationally expensive. Switching on the lubrication force only in the vicinity of the deposit may somewhat alleviate the computational extra burden that lubrication force is to impose on the DEM.

2.3.   Non-dimensional parameters and relative magnitude of forces on particle

When setting up Eq 1, only external electric, interparticle, hydrodynamic and gravity/buoyancy forces were included. We will now estimate the relative magnitude of these forces by constructing several non-dimensional ratios². One such parameter, R/4h, was already introduced in the previous Section in order to estimate the relative significance of hydrodynamic forces (direct and indirect). Other non-dimensional parameters are summarized in Table 1. While constructing Table 1, it was assumed that the forces, to the order of magnitude, can be evaluated as follows:

Table 1.  Non-dimensional parameters describing relative magnitude of forces on particle in EDP with κR >> 1.

Force ratio	Expression
External electric/viscous drag	$\xi_{1}=\frac{\varepsilon_{0} \varepsilon_{r} \zeta E}{\mu v_{\infty}}$
Electric repulsive/viscous drag	$\xi_{2}=\frac{3 \zeta e^{-\kappa h}}{2 E \kappa R(h+2 R)}$
Van det Waals/viscous drag	$\xi_{3}=\frac{16 A_{H} R^{5}}{3 \pi \varepsilon_{0} \varepsilon_{r} \zeta E h^{2}(h+4 R)^{2}(h+2 R)^{3}}$
Lubrication/viscous drag	$\xi_{4}=R / 4 h$
Gravity + buoyancy/viscous drag	$\xi_{5}=\frac{2 R^{2} g\left(\rho_{p}-\rho_{f}\right)}{9 \varepsilon_{0} \varepsilon_{r} \zeta E}$

---

 | Show Table

DownLoad: CSV

The van der Waals force between two particles, assuming both particles have the same radius, is given, in a first approximation, by ^[28]:

²As before, all particles are assumed to have the same radius, R, in this Section.

where A_H is the Hamaker constant.

The electric repulsive force (the “double layer force”) can be estimated assuming the Yukawa-type potential ^[29,30]:

Then, for κR >> 1, the electric repulsive force between two particles is given by:

The gravity and buoyancy force:

where ρ_p and ρ_f are densities of the particle and the fluid, respectively. Other forces used when constructing Table 1 are given by Eqs 5 (viscous drag) and 8 (lubrication force).

Non-dimensional (relative) magnitudes of the forces were computed for 36 combinations of the particle radius (R), Debye length (κ⁻¹) and interparticle gap (h). The velocity was assumed on the order of v∞ and thus given by Eq 3. We also assumed the following values for the EDP settings: electric field 100 V/m, ζ-potential 1 mV, viscosity of the fluid 1 cP, relative permittivity of the fluid ε_r = 78, densities ρ_p = 2500 kg/m³ and ρ_f = 1000 kg/m³, the Hamaker constant A_H = 5.0 × 10⁻²⁰ J. A similar exercise was performed with ζ = 10 mV. The results od these computations can be summarized as follows:

1. The lubrication force (ξ₄) appears to be the strongest force on the particle at small gaps. In reality, during deposition, the particle velocity would decrease (because of the lubrication force) as the particles approach each other, and the lubrication force would not be able to rise indefinitely. Both the viscous drag force and the lubrication force would approach zero as the particle is put to a halt. It should, however, be noted, that, in our force calculations, we assumed that the particle velocity is on the order of v_∞. In reality, as particles approach each other, the lubrication force will be smaller.

2. The electric repulsive force, ξ₂, is negligible at all separations, h. This is due to the large size of the particles and the form of Yukawa potential used herein. If we switch to Coulomb’s potential, the ratio of electric repulsive to viscous force becomes

Numerical calculations indicate that, even with the Coulomb potential, the electric repulsive force is relatively weak. The reason is, again, the large size of the particles.

Based on the above results, the following forces should be included in a DEM model of electrophoretic deposition from a suspension of particles with κR >> 1 and particle size from 1 to 100 μm: viscous drag force (Stokes law), force due to the external electric field, gravity + buoyancy force, direct mechanical force (as a safeguard in case of numerical overshooting), lubrication force, and van der Waals force. The latter two may be turned on within a certain cut-off distance, in order to reduce the computational load.

3.   Results

3.1.   DEM simulation of EPD

In our DEM simulations of EPD, particles have different diameters, sampled from a uniform distribution. It was established in the previous Section that, in a system with κR >> 1, the following forces should be included in DEM: viscous drag force (Stokes law), force due to the external electric field, gravity + buoyancy force, lubrication force, van der Waals force, and direct mechanical contact force. Hydrodynamic forces caused by particle rotation are neglected. The equation of motion of the i-th particle is hence given by:

where ${\bf{r}}^{i}$ is the position vector of particle i; ${\bf{F}}_{\text {fied }}^{i}, {\bf{F}}_{\mathrm{d}}^{i}, {\bf{F}}_{\mathrm{gb}}^{i}$ are the external electric force, the viscous drag force, and the gravity + buoyancy force on particle i, respectively (${{\bf{F}}}_{{\rm{gb}}}^i$ was deactivated in the simulation presented in this Section); $m_{p}^{i}$ and $m_{a}^{i}$ are the mass of the particle and half of the mass of the displaced fluid; ${\bf{F}}_{\mathrm{lub}}^{i j}$ is the lubrication force on particle i caused by its interaction with particle j; ${\bf{F}}_{\mathrm{vdW}}^{i j}$ is the van der Waals force on particle i caused by its interaction with particle j; ${\bf{F}}_{\mathrm{lub}}^{i}$ is the lubrication force caused by the interaction with the wall (the electrode); ${\bf{F}}_{\mathrm{c}}^{i j}$ is the force caused by a direct mechanical interaction of particle i with particle j. The latter includes shear and normal components. Summations over j are over particles located within the cut-off radii for the lubrication force (the first sum in Eq 15) and the van der Waals force (the second sum in Eq 15). The effective charge on the particle is assigned based on Eq 7. External electric force, viscous drag force, gravity force and buoyancy force are given by Eqs 2, 5 and 13, respectively. The van der Waals force on particle i of radius R_i caused by its interaction with particle j of radius R_j is given by ^[13]:

When R_i = R_j, Eq 10 is recovered from Eq 16. The lubrication force on particle i is given, in the first approximation, by ^[24]

where the reduced radius, R_r, is given by

Only lubrication force components caused by the centerline component of particles’ relative velocity are included in the DEM model since these components dominate in particle-particle collisions. The lubrication force on particle i caused by its interaction with the wall is given, in the first approximation, by ^[24]

where n is the unit vector normal to wall.

Only the component of the particle-wall lubrication force caused by the component of particle’s velocity normal to wall is included in the DEM model because (ⅰ) this component dominates in particle-wall collisions and (ⅱ) the particle motion in EPD is predominantly towards the wall.

Cut-off distance must be set for van der Waals and lubrication forces. Numerical force calculations discussed in section 2.3 suggest that the same cut-off distance can be set for both. We turn on these two forces when the interparticle gap becomes equal to or smaller than

The lubrication force between the particle and the electrode is turned on when the gap becomes equal to or smaller than the particle radius, i.e. for ${\bf{F}}_{\mathrm{lub}}^{i}$ we set

The DEM model described herein was implemented using FISH-calls in the commercial DEM code PFC^3D (Itasca). The direct mechanical contact force is available in the standard implementation of DEM in PFC^3D and therefore is not described here. Due to the singularity of lubrication force at zero gap, direct mechanical contact between particles should, in theory, never happen. However, it may happen due to the finite size of the timestep in a DEM simulation. In such case, the resulting contact interaction would be handled by the standard implementation.

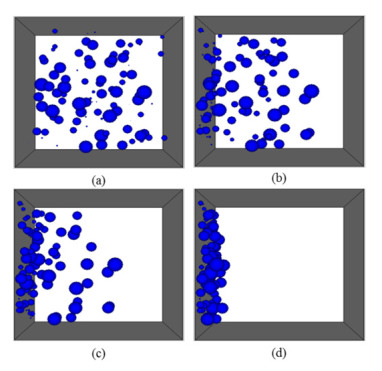
An example simulation of EPD from a dilute suspension was set up as follows. One hundred particles were generated in a 1 mm × 1 mm × 1 mm box. The applied external electric field was E = (−100, 0, 0) V/m. The particle radius was uniformly distributed between 1 μm and 50 μm. Densities of the particles and the fluid were equal to 2500 and 1000 kg/m³, respectively. The fluid viscosity was equal to 1 cP. The ζ-potential and the Hamaker constant were equal to −1 mV and 5 × 10⁻²⁰ J, respectively (for all particles). The relative permittivity of the fluid was 78. The initial positions of particles are shown in Figure 2a. Particle positions at three subsequent times (two in the middle of EPD and the last after all the particles have been deposited) are shown in Figure 2b-d.

Figure 2.  Particle configurations at the beginning of DEM simulation (a), during deposition (b, c), and at the end of deposition (d). The left-hand wall of the model is the electrode.

DownLoad: Full-Size Img PowerPoint

3.2.   Early-stage transport in EPD

It is evident from Figure 2 that smaller particles are deposited first. This might look surprising because electrophoretic mobility does not depend on the particle radius, and hence the terminal velocity, v∞, should not either. However, the particle dynamics is determined not only by the terminal velocity but also by the particle speed-up at the early stage of transport, immediately after the electric field is applied. Let us examine the characteristic speed-up time.

Consider a single particle of radius R moving in a dilute suspension, so that the distance to the closest neighbors is greater than the cut-off distance for both lubrication and van der Waals forces. From Eqs 5, 7 and 15, the equation of motion in this case is given by

where ρ_p, and ρ_p and ρ_f are the densities of the particle and the fluid, respectively. Without loss of generality, we can assume that particles carry negative charge (ζ < 0) and the electric field is such that E_x > 0 (Figure 1). Solving Eq 22 yields:

Or

where x₀ is the initial position of the particle along the x-axis, and τ₀ is the characteristic speed-up time of the particle given by

Thus, for a particle initially located at x = x₀, the travel time to the electrode can be found from the equation:

Thus, the acceleration time and the travel time from x = x₀ to x = 0 (location of the electrode) do depend on the particle's radius. This is due to the inertial term in Eq 22 being proportional to R³ with the other two terms being proportional to R. Since we are interested only in the early stage of EPD here, we neglect possible effects of deposit build-up, solution depletion and resistivity change on the travel distance and on the particle transport, the effects discussed e.g. in ^{[31,32,33,34]}. The electric field, E_x, is assumed constant throughout the early stage of EPD.

From Eqs 25 and 26, it will take longer time for larger particles to arrive at the electrode, at the early stage of EPD. Thus, finer particles will be deposited first, followed by coarser particles being deposited on the finer substrate. Let us estimate the duration of the early stage, i.e. the time during which the particle speed-up takes place.

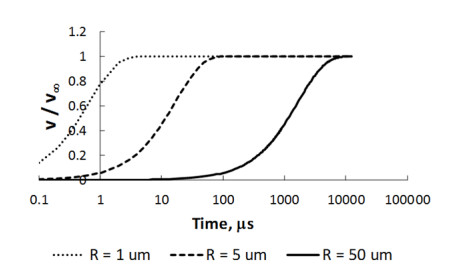
Assuming ρ_p = 2500 kg/m³, ρ_f = 1000 kg/m³, μ = 1 cP, the characteristic speed-up times for particles of different radii are given in Table 2. Table 2 suggests that “early stage” refers to the very first micro- or milliseconds after the electric field is turned on. This is the timescale it takes for a particle to approach the terminal velocity. Velocity (normalized by v_∞) vs. time is plotted in Figure 3, for the three values of the particle radius. It takes less than 10 μs for the smallest particle and ca. 10 ms for the largest one to approach the terminal velocity. This very short duration is the reason why the speed-up phase is usually neglected in EDP kinetic models, and particles are assumed to be moving with their terminal velocity at once.

Table 2.  Characteristic speed-up time for particles of different radius in a fluid with ρ_f = 1000 kg/m³, μ = 1 cP. Particle density ρ_p = 2500 kg/m³.

R	τ0
1 μm	0.67 μs
5 μm	16.7 μs
50 μm	1.67 ms

---

 | Show Table

DownLoad: CSV

Figure 3.  Normalized particle velocity vs. time in a dilute suspension for three values of particle radius (based on Eq 27).

DownLoad: Full-Size Img PowerPoint

4.   Conclusions

The relative magnitude of different forces in suspensions of polydisperse particles with small Debye length (such as a Portland cement slurry) has been examined. It was shown that the following forces need to be included in a discrete-element model of electrophoretic deposition in such systems: viscous drag force (Stokes law), force due to the external electric field, gravity + buoyancy force, lubrication force, van der Waals force, and direct mechanical contact force. The recommended cut-off gaps for van der Waals and lubrication forces in discrete-element simulations are equal to the radius of the larger particle participating in the interaction. An example DEM simulation has demonstrated that deposition starts with depositing finer particles. This is due to the larger speed-up time for larger particles. The observed effect may lead to some size segregation at the early stage of deposition, even though the particle mobility coefficient is independent of the particle size. The duration of the early stage is on the order of 10 μs (for 1 μm-particles) to 10 ms (for 100 μm-particles). The setup of DEM model developed herein can be further used to study electrophoresis in systems with small Debye length. In particular, the model enables some insight into the processes that take place during the earlier stage of EPD that are difficult to capture and analyze in laboratory experiments.

This article presents a DEM model that can be used to investigate the effect of different parameters on the electrophoresis and to optimize the electrophoresis regimes. This will be the subject of the future study, along with model validation against experiments. The latter can be achieved only indirectly because the model provides insight into micromechanical aspects of electrophoresis that cannot be directly investigated in an experiment.

Acknowledgements

This publication has been produced in the project “Voltage on casing for improved well cement quality” (267651/E20) funded by the Research Council of Norway through the PETROMAKS2 programs.

Conflict of interest

The author is not aware of any conflicts of interest regarding this paper.