Development of measurement system of cutting load response in nipper blade, and estimation of wedge angle effect on cutting characteristics and shear edge trace of polystyrene bars

1.   Introduction

Nowadays, cutting nippers and pliers are widely used in various cutting process, e.g. resin parts of miniature model connected by branches (bars) for splitting them into small parts, general purpose splitting such as resin ribbon, electronic copper wire, semi-hard steel wire and shaving after rough cutting by a large angle wedge. The basic design (ISO 5742) of nippers and pliers consists of three major sections: jaws, fulcrum, and handles. The jaws are a part of the tool in front of the pivot bolt (fulcrum), and they are used to grip and cut a wire-like material. The cutting edges are implemented onto the tips of the jaws. The cutting edges are applied to the jaws as a double sharp design (a pair of side wedge or symmetric wedge for upper/lower jaw) or can have a knife and anvil design. The fulcrum connects the two halves of the tool together and acts as the pivot point between the handles and the jaws. They have many similarities with the cutting mechanism. Many types of pliers and nippers have been used mainly for cutting electrical wires, tying different parts together, holding materials during assembly, fastening and unfastening components ^[1]. They are used in many occupational areas such as tying works of constructions ^[2,3,4,5], working of electrical assembly ^[6] and wiring of telecommunications ^[7]. The blade of a nipper is made of a pair of side wedge blade for making a rectangular shape in one side, while the plier's blade is made of a pair of symmetric wedge blade. Nipper and pliers are made from a high-grade tool steel, and have a slim head for greater accessibility in tight or hard-to-reach areas ^[8]. They are processed as forging and polished on the cutting edges of jaws.

When considering to cut a bar-like polymer material, one side of a split bar/ribbon is expected to be a smart rectangular shape when using the nipper. It is generally difficult for novices to cut a small specimen of bar or ribbon off for having a nice trace at the sheared edge. The specimen sometimes doesn't split well from the connecting rods. Many makers of nippers try to manufacture a new model of nipper blade that can cut a specimen off with a low resistant load and a smooth sheared profile. However, before launching such the new product, the makers of nippers need to examine the invented nipper by using appropriate measurement system. Empirically, when pushing the outside top position of nipper handle using a loading system, the corresponded peak maximum force during a cutting process of a work material was often evaluated as a performance factor.

However, such the load response that be gotten from any prototype loading system was insufficient to check for consistency and openness. Therefore, appropriate measurement system of cutting load of a developed nipper should be designed and verified through a specified condition based experiment. In this work, firstly, a rotational-linked fixture JIG was designed and prepared for loading the nipper handle. Through this development of fixture JIG, the repeatability and reliability of cutting load response and the easiness of set-up working were discussed.

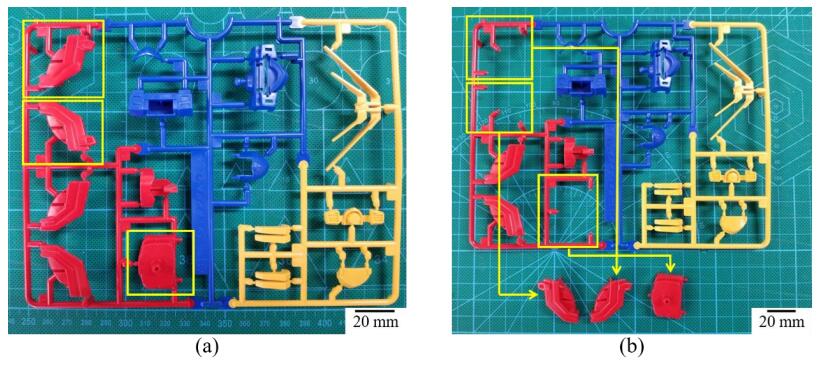
As mentioned above, the peak maximum force of cutting nipper is empirically evaluated as the industrial needs. In other words, a certain level of low load response in cutting process and also a smooth cutting trace are desired as the performance of cutting nipper. For an example, in assembling model kits such as GUNPLA (Gundam Plastic Model) ^[9], the model parts of God Gundam as shown in Figure 1(a) were attached with sprue which must be cut off before assembling (Figure 1(b)).

Figure 1.  An example of GUNPLA model kit. (a) Before cutting model parts which were attached with sprue. (b) After cutting the model parts off.

DownLoad: Full-Size Img PowerPoint

Since the edge profile of split parts often has a protuberance and an inclined angle shape as shown in Figure 2(a), additional shaving of the edge profile is necessary. If the edge profile is cut off with a smooth trace as shown in Figure 2(b), any additional machining process (e.g., shaving) can be skipped.

Figure 2.  An example of model parts after cutting off. (a) A rough split state with inclined protuberance on the split portion, (b) A shaved trace of protuberance.

DownLoad: Full-Size Img PowerPoint

Regarding the relationship between the cutting load (or the cutting moment) and the displacement at the pushing point of nipper handle, appropriate theoretical estimation of cutting characteristics of the nipper is necessary for understanding the effects of mechanical parameters such as the apex angle of blade, the asymmetric attitude of upper/lower blade (or anvil).

As for the wedge cutting resistance, since there are several fundamental theories ^[10,11,12], the cutting resistance is characterized with the apex angle of wedge and the indentation depth against the thickness of worksheet. One of primary mechanical factors that characterize the cutting resistance is the shear stress. Canakci et al. reported that the shear stress increased with the compressed density of modified expanded polystyrene ^[13]. Nagasawa et al. reported about the effects of two-line wedge blade on the cutting characteristics of several resin materials ^{[14,15,16,17]}. The cutting line force and deformation of specimens were affected by the geometry of the blade edge such as the tip radius, the primary height of wedge and the apex angle of blade.

Murayama et al. ^[18,19] and Chaijit et al. ^[20] have reported the cutting mechanism of a 42° wedge indentation into a 0.4 mm thickness aluminum sheet by using a trapezoidal cutting blade imitated as a crushed tip. In that study, a couple of separation modes were estimated with the ratio of blade tip thickness w by the worksheet thickness t. In case of w/t > 0.23, the second mode necking occurred and the string-like burrs were generated beneath the blade tip.

Mitsomwang et al. ^[21] used the elasto-plastic large deformation model based Finite Element Method (FEM) Code for simulating the wedge indentation process of lead alloy sheet until the final splitting stage when varying the apex angle of wedge blade. It revealed that the maximum cutting load response increased with the apex angle of blade and the simulated necking process matched to the experimental results. Not only the edge shape of blade but also the stiffness of underlay affected to the load response and deformation profile of work sheet ^[22]. Another problem of wedge cutting is to generate unstable (multiple deformation modes) shear edge trace (sheared profile) of resin specimen. The multiple deformation modes of shear edge trace were appeared to be caused by the frictional instability or adhesion of wedge surface when choosing a Polycarbonate (PC) and a Polyethylene terephthalate (PET) sheet ^[23,24,25]. That provides unstable cracking, bent up necking, large inclination and burred of lower zone.

Several shaped (bar, ribbon and plate) polystyrene (PS) are widely used for producing small parts of miniature models connected by branches (bars). However, a wedge cut of PS material seems to be not yet discussed when using a nipper mechanism for cutting a 3 dimensional bar or ribbon. In order to predict the cutting resistance and deformation behavior of a PS square bar, some features of this material are necessary. PS material can be distilled an oily liquid named styrol from the resin of Turkish sweet gum trees. The thermoplastic resin has generally the higher resistance of compressive deformation than that of tensile deformation. Polystyrene (PS) is also such a brittle resin in a tensile mode, while it has ductile behavior in the compressive mode ^[26]. PS is the most employed aromatic thermoplastic polymer due to the hardness, stiffness, and chemical stability over a wide pH range, and also it is a brilliantly transparent synthetic resin produced by polymerization of styrene. It has a wide range of application such as a food packaging product and an insulator in buildings due to some advantages as the versatility, dimensional stability and low cost ^[27,28]. Therefore, in this research, in order to reveal the wedge angle effect on the cutting characteristics of a PS bar material, the rotational-linked fixture JIG system was provided for the use of three kinds of nippers.

The first two nippers (the big nipper: the upper/lower asymmetric two-line wedge composed of α = 90–72°, α' = 85–72° and the medium nipper: the upper/lower asymmetric two-line wedge composed of α = 49–55°, α' = 42–50°) were used for comparing the effects of blade angle on the cutting characteristics. Here, α was the apex angle and α' was the back angle of two-line wedge. The big nipper is normally used for cutting a metallic wire and classified as a strong type, while the medium nipper is empirically used for cutting a various plastic and a small metallic wire. The third nipper (the small nipper: 13° single apex, side wedge) seems to be used for the precision-cut of small plastic model parts. Since the small nipper has a keen apex and then difficult to make alignment of the upper and lower blades fine, it empirically consists of a keen wedge and a narrow anvil. The three kinds of nippers were compared with the load response and cutting trace of a 3 mm square PS bar, in order to reveal the cutting characteristics of PS bar for splitting and trimming plastics model kits.

2.   Materials and experiments

2.1.   Specifications of fixture JIG of nipper handle and PS specimens

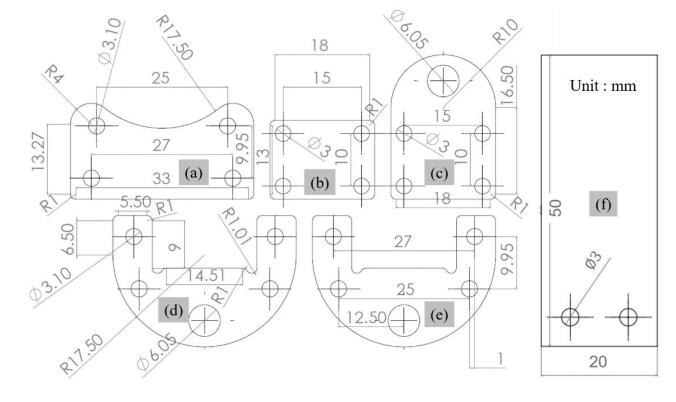
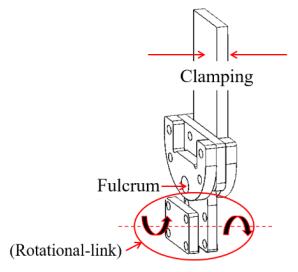
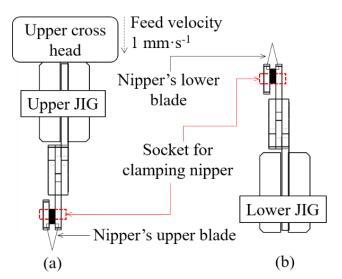
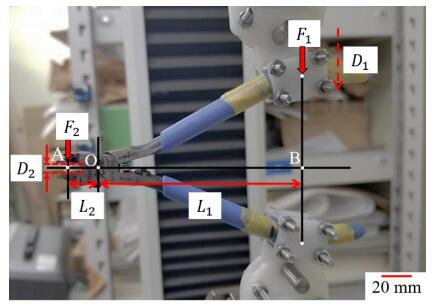
Dimensions of each component of fixture JIG were shown in Figure 3 and the thickness of all the components were 3.5 mm. They were made of polyoxymethylene (Polyacetar resin) plate and machined by a rapid-prototype milling machine. When assembling the components, the structure of fixture JIG was shown in Figure 4. In this structure, the upper parts (a), (d), (e), (f) were fasten by M3 bolts and nuts, while the lower parts (b), (c) were assembled with M3 bolts and nuts as a set of fixture plates (socket), which were used for fixing the upper or lower handle of nipper. The upper assembly and lower assembly was loosely jointed by a M6 bolt and nut. On the experimental apparatus of cutting test, the same two sets of the assembly were prepared as the upper and lower fixture JIG. The upper JIG was mounted on the upper cross head which had a load cell with the maximum load 10 kN. The lower JIG was mounted on the lower cross head. The upper and lower arm (handle) of the nipper were inserted into the upper/lower socket for clamping respectively, as shown in Figure 5. The attitude of the blade was arranged to be vertical against the PS bar. Because the bar specimen was set up across to the nipper blade in the horizontal attitude. Since there is the fulcrum of M6 bolt as shown in Figure 4, the assembly parts (b), and (c) of JIG can rotate with a small friction in the clockwise and/or counter clockwise, against the assembly parts (a), (d), (e), and (f). When the upper fixture JIG (mounted on the upper cross head) moves downward, the assembly parts (b), and (c) of the lower fixture JIG (mounted on the lower cross head) rotates in the opposite wise.

Figure 3.  Dimensions of components of fixture JIG.

DownLoad: Full-Size Img PowerPoint

Figure 4.  Assemble structure of fixture.

DownLoad: Full-Size Img PowerPoint

Figure 5.  Side view of schematics of fixture by (a) is Upper JIG and (b) is lower JIG.

DownLoad: Full-Size Img PowerPoint

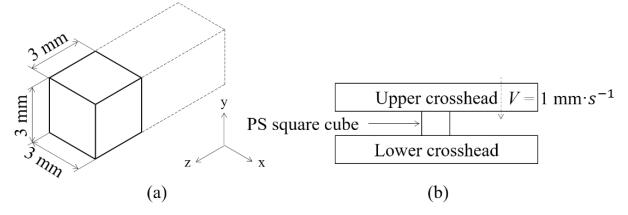
A 3 mm square polystyrene (PS) bar TAMIYA Item 70130-360, which had a longitudinal length of l = 40 mm, was used for the cutting test. All the specimens of PS bars were sufficiently cleaned before cutting. The tensile stress-strain relationship in machine direction (MD) (longitudinal direction of bar) of the 3 mm polystyrene square bar was examined with the feed velocity V = 5 mm·s⁻¹. Here, the bar specimen, the longitudinal length of which was chosen as 110 mm, was prepared and the both sides of 30 mm were clamped by upper and lower holders, while the central part of 50 mm length was evaluated as an elongated zone. The mechanical properties of the 3 mm square bar specimen were shown in Table 1.

Table 1.  In-plane tensile mechanical properties of polystyrene (PS) in longitudinal direction (the strain rate: 0.1 s⁻¹ with the span of 50 mm).

Symbol	Thickness t/mm	Young's modulus E/GPa	Yield strength σY/MPa	Tensile strength σB/MPa	Breaking strain 𝜺B
Tensile mode	3.0	1.88	30.18	41.65	0.32
		(1.80–1.97)	(28.05–35.73)	(39.83–43.60)	(0.28–0.34)
Average (Maximum-Minimum measured)

---

 | Show Table

DownLoad: CSV

The compressive test of 3 mm square polystyrene bars was measured for 𝜺 ≈ 0.65 with V = 1 mm·s⁻¹. Here, the 𝜺 is the true strain in TD. Figure 6 shows a specimen and the setup of apparatus for compressive test. Through this compressive test, the results were that the compressive Young's modulus E_C in the y direction (cutting direction) and the yield strength σ_YC in the y direction (cutting direction) were shown in Table 2. Here, it was noted that this compressive σ_YC included a sort of frictional restriction.

Figure 6.  Schematics of compressive test of 3 mm square Polystyrene (PS) bars. (a) Sizes of PS specimen and (b) Experimental setup for compressive test.

DownLoad: Full-Size Img PowerPoint

Table 2.  Out of plane compressive mechanical properties of polystyrene (PS) in the cutting direction (the y direction). The strain rate: 0.33 s⁻¹.

Symbol	Thickness t/mm	Young's modulus EC/GPa	Yield strength σYC/MPa
Compressive mode	3.0	5.04	85.63

---

 | Show Table

DownLoad: CSV

The experiment for finding the friction coefficient of PS bars and a steel blade was carried out, as the horizontal method based on JIS K7125. The average dynamic friction coefficient was estimated as 0.31. Here, since it was difficult to use the real blade surface of nippers, a body surface of Thomson knife (Material: SK5, the surface hardness was 747VHN) was examined with the horizontal method under the applied pressure of 1.35 kPa and the value of surface roughness of R_a = 3.7 µm.

2.2.   Measuring principle and calibration procedure of cutting force and displacement

After assembling a cutting nipper in the fixture JIG on the cutting test apparatus based on ISO 5744, the applied pushing force at the clamped-top position of nipper handle F₁ was measured by the load cell when cutting a 3 mm square PS bar. The cutting force at the blade biting position F₂ was calculated by Eq 1 and f₂ ( = the ratio of F₂ by the width of 3 mm) N/mm was the cutting line force. Putting the indentation displacement of the nipper handle (arm) D₁, that of the blade biting position D₂ is principally calculated by Eq 2. Here, since the full stroke value of D₂ is equal to the height of specimen, namely D_{2 (full stroke)} ≈ 3 mm in this work. When F₁ was measured during the cutting test, D₁ was measured as the upper crosshead displacement as shown in Figure 7 and the arm span length (L_1, L₂) were shown in Table 3, for each nipper. Here, the variation (dispersion) of maximum and minimum value of L₂ was fairly large due to a slip of the specimen at the inclined biting state.

Figure 7.  Zoomed up view of a nipper and each measured arm span length.

DownLoad: Full-Size Img PowerPoint

Table 3.  Arm span lengths among the emphasis (biting), fulcrum and action points, used in experiment.

	L1 (mm)	L2 (mm)
Big nipper	87.58	16.29
Medium nipper	78.28	13.73
Small nipper	66.78	9.65

---

 | Show Table

DownLoad: CSV

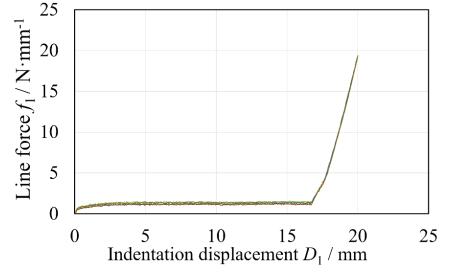
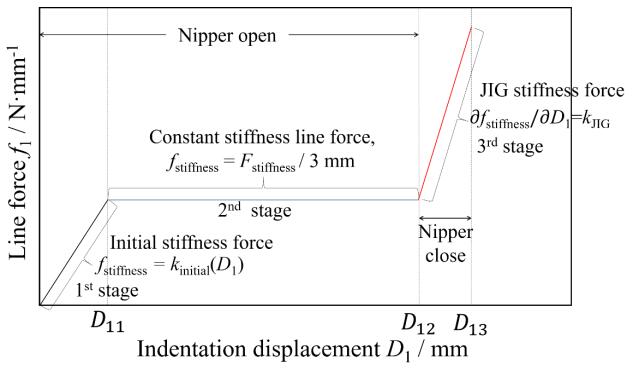
The effective pushing force at the clamped-top position F₁' (N), that excludes the inside-spring force of nipper from the raw force F₁ measured by the load cell, is estimated using an idle cut calibration test without any work material. Similarly, the effective upper crosshead displacement D₁', that excludes the elastic deformation of fixture JIG, is calibrated from the measured raw displacement D₁ using the idle cut calibration test without any work material. Figure 8 was an example of real loading response when using the fixture JIG assembled with the medium nipper, while Figure 9 illustrated the idle cut load response with a specified nipper using the fixture JIG. Here, the vertical axis was denoted as the line force (N·mm⁻¹), as the pushing force divided by the width of specimen 3 mm.

Figure 8.  Example of relationship of real cut line force and pushing displacement real response with medium nipper.

DownLoad: Full-Size Img PowerPoint

Figure 9.  Relationship of idle cut line force and pushing displacement.

DownLoad: Full-Size Img PowerPoint

The idle cut loading response consisted of three stages of the mechanical loading condition as shown in Figure 9. In the first stage (D₁ < D₁₁: a saturated position), the line force increased with the upper crosshead displacement D₁. In the second stage (D₁₁ < D₁ < D₁₂: a middle zone), the line force was almost constant. The upper/lower nipper blades were shut and collided with each other at D₁ = D₁₂. In the third stage (D₁ > D₁₂), the line force remarkably increased as the upper and lower blades collided with each other. The values of D₁₁ of the big/medium/small nipper were 1.07, 0.8 and 3.01 mm, respectively and the values of D₁₂ of the big/medium/small nipper were 15.48, 17.0 and 20.47 mm, respectively. In order to use the fixture JIG in safe from the damage, the upper limit D₁₃ is required for investigating the third stage gradient k_JIG. The values of D₁₃ of the big/medium/small nipper were empirically 19, 20, 24 mm, respectively. The first stage gradient k_initial, the second stage constant f_stiffness and the third stage gradient k_JIG were shown in Table 4.

Table 4.  Values of idle cut parameters k_initial, f_stiffness, k_JIG for three stages.

	kinitial/N·mm−2	fstiffness/N·mm−1	kJIG/N·mm−2
Big nipper	1.317	1.39	12.04
Medium nipper	1.73	1.53	5.64
Small nipper	0.4	1.2	5.36

---

 | Show Table

DownLoad: CSV

The effective pushing line force at the clamped-top position f₁^' (N·mm⁻¹) in the first stage for each nipper was calculated by using Eq 3.

Since the second stage had a constant line force resistance, the effective pushing line force f₁^' in this stage was calculated by using Eq 4.

In the third stage, the nipper blade was shut in the case of idle cut. The k_JIG was gotten in this stage and Eq 5 was used for calibrating the displacement of nipper arm from the raw displacement D₁.

Using Eqs 3–5, the relationship between the effective pushing line force f₁^' and the indentation displacement of nipper arm D₁^' is estimated in the following sections. The experiments were carried out under the following conditions: a room temperature of 297 K, and a room humidity of 50%RH.

2.3.   Specifications of three nippers and these profile parameters on cutting process

The cutting experiment of the 3 mm square bar was carried out using the three kinds of nippers. Figure 10 shows a big nipper which has the upper two-line wedge composed of apex angle α = 90° and the back angle α' = 72°, and the lower two-line wedge composed of α = 85° and α' = 72°. Figure 11 shows a medium nipper which has the upper two-line wedge composed of the apex angle α = 49° and the back angle α' = 42°, and the lower two-line wedge composed of α = 55° and α' = 50°, Figure 12 shows a small nipper which has a side wedge of apex angle α = 13° against an anvil of 0.35 mm width. In case of the small nipper, the blade structure didn't consist of symmetric wedges with the upper and lower. It was composed of a side-wedge blade against a narrow anvil.

Figure 10.  Setup of big nipper. (a) General view, (b) Front view of blade.

DownLoad: Full-Size Img PowerPoint

Figure 11.  Setup of medium nipper. (a) General view, (b) Front view of blade.

DownLoad: Full-Size Img PowerPoint

Figure 12.  Setup of small nipper. (a) General view, (b) Front view of blade.

DownLoad: Full-Size Img PowerPoint

3.   Results and discussions

3.1.   Calibration of cutting force with device stiffness at clamped-top position of nipper handle

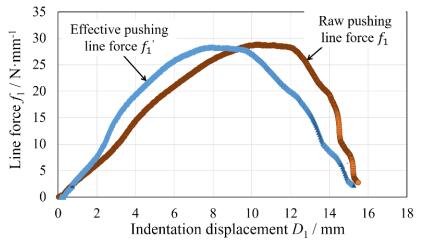
Regarding the cutting load diagram using the nipper, the indentation velocity of blade V = dD₁/dt was chosen as 1 mm·s⁻¹ at the clamped-top position. The raw cutting load response (f₁-D₁) was calibrated using Eq 3–5, and the effective cutting load response (f₁^'-D₁^') was generated. Figure 13 showed an example of comparison of raw load response and calibrated load response with respect to the big nipper.

Figure 13.  Comparison of a representative raw pushing response f₁-D₁ and its effective pushing response f₁'-D₁', in case of the big nipper.

DownLoad: Full-Size Img PowerPoint

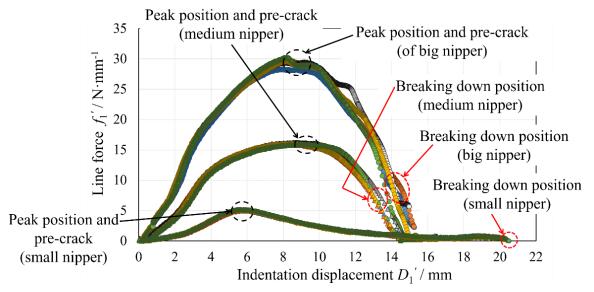
Seeing Figure 13, it was found that the peak maximum position of raw data was about 73% while that of calibrated data was about 53% of the full stroke. Using Eqs 3–5, all the cutting response of five specimens were calibrated with respect to the three kinds of nippers. The relationship between the effective pushing line force f₁^' and the indentation displacement of nipper arm at the clamped-top position D₁^' was shown in Figure 14.

Figure 14.  Relationship of the effective pushing line force f₁^' and indentation displacement of nipper arm D₁^' under the indentation velocity V = 1 mm·s⁻¹. Sample numbers were five for each nipper.

DownLoad: Full-Size Img PowerPoint

Figure 14 revealed that the cutting force response f₁^'-D₁^' was stable and the reproducibility was sufficient in the early stage for each nipper. Here, the stability of load response was especially high in the range of D₁^' < 50% of 15 mm for the big nipper, in that of D₁^' < 67% of 15 mm for the medium nipper and in that of D₁^' < 75% of 20 mm for the small nipper, respectively. This means that the proposed rotary-linked fixture JIG is good enough for examining the cutting performance of various nippers.

Seeing the last breaking stage, there was a certain dispersion in the cases of big and medium nippers, whereas the breaking down was quite stable in the case of small nipper. Because the wedge opening rate is relatively small and the frictional restriction by the anvil underlay fastens any unstable crack generation. The small nipper needs more displacement to finish the cutting process due to its low sensitivity ratio L₂/L₁. As the theoretical displacement D₁^' is estimated from the Eq 2: D₂ ( = 3 mm)·L₁/L₂, the stroke difference is principally calculated as 3.7 mm (or 4.6 mm) between the small nipper and the medium (or large) nipper. Namely, the estimated D₁^' of medium nipper must be 0.9 mm larger than that of the big nipper. However, seeing Figure 14, the measured displacement D₁^' of the medium nipper was a little smaller than that of the big nipper. This difference seems to be caused by the effect of apex angle on the frictional restriction. The apex angle of big nipper was α = 85–90° while that of medium nipper was α = 49–55°.

The pushed line force f₁^' was monotony increased with D₁^' for the first half (less than 30%). This tendency was common for the three nippers. However, in the latter half (larger than 50%), the big and medium nippers had a saturated load response and had a breaking point in the range D₁' > 50–67% of 15 mm, while the small nipper had stably a reducing load response in the latter half (larger than 30% of 20 mm).

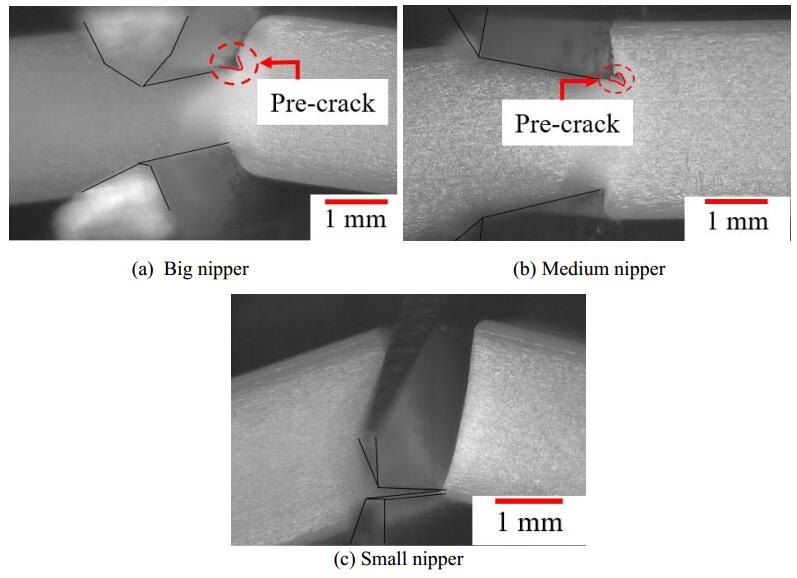
Figure 15 shows a scene of pre-cracks generation for the three nippers. As shown in Figure 15, the small nipper had a static wedging without any large crack due to the frictional restrain of lower anvil. The big and medium nippers showed a sort of unstable crack in the cutting process. In the big nipper, the initial crack generated at D₁^'≈8.76 mm, while the initial crack generated at D₁^'≈8.81 mm in the medium nipper.

Figure 15.  Generation of pre-cracks in specimen. (a) Big nipper (D₁'≈8.76 mm, D₂≈1.6 mm), (b) Medium nipper (D₁'≈8.39 mm, D₂≈1.5 mm) and (c) Small nipper (D₁'≈20.5 mm, D₂≈2.95 mm).

DownLoad: Full-Size Img PowerPoint

3.2.   Cutting resistance response at biting position

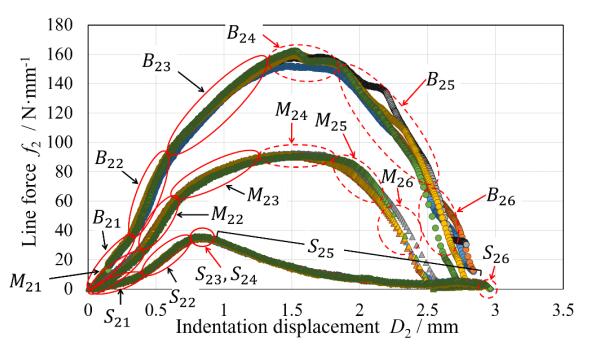
The relationship between the blade biting line force f₂ and the blade displacement at the biting position D₂ was shown in Figure 16. The horizontal axis of D₂ (mm) was converted from D₁' by using Eq 2, while the vertical axis of f₂ (N·mm⁻¹) was converted from f₁' by using Eq 1.

Figure 16.  Relationship of the blade biting line force f₂ and blade displacement at the biting position D₂ under the constant indentation velocity of V = 1 mm·s⁻¹ (See Table 5).

DownLoad: Full-Size Img PowerPoint

Table 5.  Classification of cutting load response f₂-D₂.

	Stage	Description
Big nipper	B21	Pushed early stage.
	B22	Pushed middle stage.
	B23	Penetrated stage, bending due to asymmetric indentation of upper/lower
	B24	Necked stage, Peak maximum point and Pre-crack.
	B25	Propagation of cracks
	B26	Cut off (Breaking down).
Medium nipper	M21	Pushed early stage.
	M22	Pushed middle stage.
	M23	Penetrated stage.
	M24	Necked stage, Peak maximum point and Pre-crack.
	M25	Propagation of cracks
	M26	Cut off (Breaking down).
Small nipper	S21	Pushed early stage.
	S22	Pushed middle stage.
	S23, S24	Penetrated and necked stage, Peak maximum point
	S25	Propagation of cracks plus bending
	S26	Static cut off.

---

 | Show Table

DownLoad: CSV

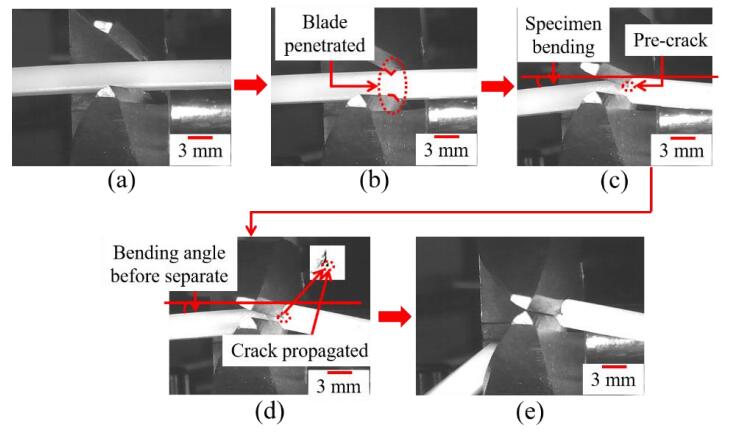
All the parameters described in Figure 16 were shown in Table 5. The representative cutting states were classified in 6 stages in Figure 16. In the case of the small nipper, since the penetrated and necked stage appeared to be merged, the table contents were arranged in 5 groups. The first half of wedge cutting was classified as the pushed (early and middle) stage and the penetrated stage, which included a slight bending due to asymmetric indentation of upper/lower blades. The early pushed stage was a state that the blade edge slightly indented to the surface of specimen. The middle pushed stage has the larger gradient than the early pushed stage and appeared to be under high pressure contact. Here, the yielding resistance and the friction coefficient seemed to increase with the strain increment. In the penetrated stage, since the blade indentation was about 20–50%, the central layer also slightly affected by the wedge thrust force. In the cases of big and medium nippers, meanwhile, the specimen was bent due to asymmetric indentation of upper/lower blades. This penetrated stage was not clearly observed, but as a sort of crack collapse occurred at this timing by the small nipper, the peak maximum point ocuured at near D₂ = 27% of the height of specimen. After the penetrated stage, the cutting reaches the peak maximum load point. Since this peak point was generally observed at near the balance state of force variance by the sectional reducing of uncut area (necking) and the increment of wedge contact area ^[29], the deformation of this peak point is classified as the necked stage. In the latter half of big and mediate nippers, a pre-crack was observed at the necked stage. Then, the crack was dynamically propagated into the uncut area, and finally the specimen was separated under having the biting collision of upper/lower blades. Seeing Figure 15(a) and Figure 16, the indentation of the upper blade was larger than that of the lower blade in the early stage when choosing the big nipper, and a pre-crack was detected on the upper side.

Figure 17, 18 and 19 show the intermediate deformation states of PS bar specimen in each stage refered from Figure 16. These figures show 4 or 5 stages of deformation, owing that the video movies by the CCD camera couldn't detect any difference between the pushed early stage and pushed middle stage.

Figure 17.  Deformation states of PS bar specimen indented by big nipper. (a) Early pushed stage at D₂ ≈ 0.07 mm, (b) Penetrated stage at D₂ ≈ 0.35 mm, (c) Necked stage with bending and pre-crack at D₂ ≈ 1.33 mm, (d) Crack propagated at D₂ ≈ 1.89 mm, and (e) Cut off at D₂ ≈ 2.71 mm.

DownLoad: Full-Size Img PowerPoint

Figure 18.  Deformation states of PS bar specimen indented by medium nipper. (a) Early pushed stage at D₂ ≈ 0.07 mm, (b) Penetrated stage at D₂ ≈ 0.71 mm, (c) Necked stage with pre-crack at D₂ ≈ 1.31 mm, (d) Crack propagated at D₂ ≈ 1.85 mm and (e) Cut off at D₂ ≈ 2.25 mm.

DownLoad: Full-Size Img PowerPoint

Figure 19.  Deformation states of PS bar specimen indented by small nipper. (a) Early pushed stage at D₂ ≈ 0.17 mm, (b) Penetrated stage at D₂ ≈ 0.41 mm, (c) Crack propagated plus bending at D₂ ≈ 0.76 mm and (d) Static cut off at D₂ ≈ 2.94 mm.

DownLoad: Full-Size Img PowerPoint

Using the sliding field theory ^{[10,11,12,30]}, the gradient $\partial {f_2}/\partial {D_2}$ is estimated with Eq 6 as a function of apex angle of cutting blade and the friction coefficient in a shallow indentation stage.

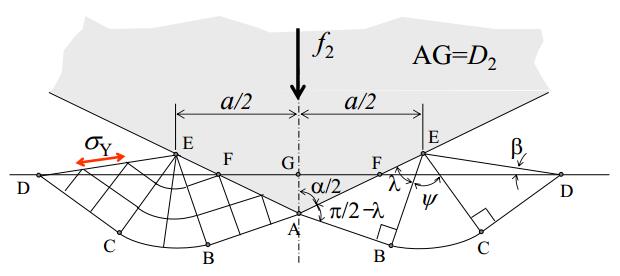
Here, $\beta = {\rm{}}\left({\check{\alpha} /2} \right) - \psi + \left({\pi /4} \right) - \lambda, {\rm{cos}}\left({\check{\alpha} /2} \right){\rm{sin}}\left({\check{\alpha} /2} \right) = \sqrt 2$sinβcosλ$\left({\sqrt 2 {\rm{cos}}\lambda {\rm{cos}}\beta + 2{\rm{sin}}\left({\check{\alpha} /2} \right)} \right)$ and cos(2λ) = µ(1 + 2ψ + sin(2λ)) are restricted. When $\check{\mathsf{ α}}$ and µ are large, since any arbitrary positive λ does not exist, then λ = 0 is assumed. The friction coefficient µ was assumed to be 0.31. The apex angle $\check{\mathsf{ α}}$ of big nipper, medium nipper and small nipper was representatively evaluated as 72°, 42° and 13° respectively. Therefore, the initial cutting resistance of PS bars by the big nipper, medium nipper and small nipper was estimated as Eqs 7–9 respectively, using the deformation diagram Figure 20 which was used in the sliding field theory of a shallow indentation of a wedge ^[30]. Here, $\check{\mathsf{ α}}$ = α was the apex angle of wedge blade, while the three angles λ, ψ and β were used for analyzing the stream line in Figure 20.

Figure 20.  Slip line field diagram of shallow indentation of wedge against plastic surface (Ref. ^[30] Nagasawa, S. et al. 2016, p.81).

DownLoad: Full-Size Img PowerPoint

In the case of $\check{\mathsf{ α}}$ = 72°, since the surface of wedge appeared to be adhered to the work material, the angle of λ was assumed to be zero (a special restricted condition).

The ratios of gradient c₇₂/c₁₃ and c₄₂/c₁₃ were 1.47 and 1.05, respectively. If the cutting resistance of the big and medium nipper is not symmetric with respect to the upper and lower blade, the resistance of the wedge indentation seems to be similar to one side wedge indentation. Since this seems to occur at the initial shallow indentation stage, the ratios of gradient appeared to increse up to two times of the symmetric condition. Namely, the ratios of gradient c₇₂/c₁₃ and c₄₂/c₁₃ appear to increase up to 2.94 and 2.1, respectively when the upper/lower blade indentation is not symmetric.

Seeing Figure 16, the secant gradient k = $\Delta {f_2}/\Delta {D_2}$ was observed as k₇₂ = 124.0, k₄₂ = 78.3 and k₁₃ = 29.9 N·mm⁻¹ for the big, medium and small nipper respectively in the early stage (D₂ = 0~0.33 mm). In the case of small nipper, the equivalent yielding stress was reversely estimated as 24.6 MPa by using Eq 9.

Seeing the compressive and tensile strength of PS (Table 1 and 2), the compressive yield stress σ_Y = 85.6 MPa was larger than the tensile yield stress σ_Y = 30.2 MPa, although the compressive yield stress included the frictional restriction. Therefore, it was found that the cutting resistance as the equivalent yield stress was fairly closed to the tensile yielding stress. Regarding the gradient of cutting resistance, the ratios of secant gradient k₇₂/k₁₃ and k₄₂/k₁₃ were 4.15 and 2.62, respectively. They were relatively close to the theoretical resistance of non-symmetric cutting with the big and medium nipper. The corresponded yielding stresses of the big and medium nipper were reversely estimated as 124.0/4.79 = 25.9 MPa, and 78.3/2.568 = 30.5 MPa, respectively. So far, it was found that the equivalent yielding stress of the PS bar material was close to the tensile yielding stress when cutting the PS bar material using the three nippers. This result means that the sliding field theory using the apex angle, the yielding stress and the friction coefficient is useful for estimating the initial-cutting resistance of the three kinds of nippers.

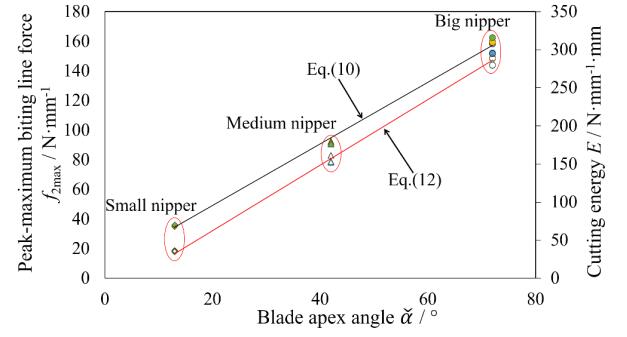
The relationship between the apex angle of wedge $\check{\mathsf{ α}}$ (°) and the maximum blade biting force f_2max was approximated as Eq 10. Here, $\check{\mathsf{ α}}$ = 72, 42 and 13° was chosen as the representative angle of wedge, and the Pearson's correlation coefficient of Eq 10 was 0.997. The peak maximum biting force f_2max was linearly estimated with the blade apex angle. This scatter relation is plotted in the section 3.3.

Regarding to the peak maximum biting force, the ratios of maximum biting force f_2max of the big and medium nipper with the small nipper were 4.48 and 2.58, respectively. These values were almost same as that of secant gradient. Hence, the peak maximum biting force f_2max appeared to be linearly related to the secant gradient k = $\Delta {f_2}/\Delta {D_2}$.

3.3.   Relationship between the cutting force and cutting energy

The cutting energy is principally calculated by Eq 11. Using the relationship of the line force at the biting position f₂ and the corresponded displacement D₂ in Figure 16, the trapezoidal rule was applied to estimate the cutting energy. Here, the range of integration was up to D_{2 (full stroke)} ≈ 3 mm.

After finding the numerical integration of Eq 11 from Figure 16, the results of average cutting energy were shown in Table 6.

Table 6.  Average cutting energy of three kinds of nipper at the indentation velocity V = 1 mm·s⁻¹ (Maximum-Minimum measured).

Cutting energy/N·mm·mm−1
Big nipper	Medium nipper	Small nipper
286.47 (279.69–295.1)	154.50 (152.23–161.04)	35.55 (34.41–36.39)

---

 | Show Table

DownLoad: CSV

The relationship between the representative apex angle of wedge $\check{\mathsf{ α}}$(°) and the cutting energy was approximated as Eq 12. Here, the Pearson's correlation coefficient of Eq 12 was 1.0.

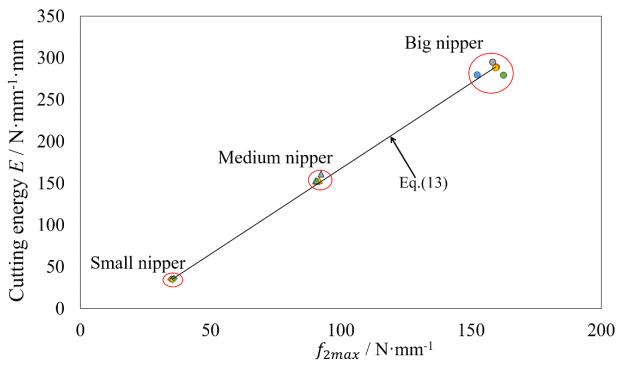
Figure 21 shows the peak maximum biting line force f₂ and the cutting energy E with respect to the representative apex angle of wedge $\check{\mathsf{ α}}$. Seeing Eq 10, 12 and Figure 21, as the variation of cutting energy was similar to that of peak maximum line force, the relationship between the peak maximum line force f_2max (N·mm⁻¹) and the cutting energy E (N·mm·mm⁻¹) was plotted in Figure 22, and its relation was linearly approximated by Eq 13. Since the cutting energy increased with the peak maximum line force and the apex angle of balde, that seemed to be mainly caused by the wedging plastic flow work.

Figure 21.  The dependency of the peak maximum line force at the biting position f_2max and the cutting energy on the representative apex angle of wedge $\check{\mathsf{ α}}$ (°).

DownLoad: Full-Size Img PowerPoint

Figure 22.  Relationship between the cutting energy and the peak maximum line force f_2max.

DownLoad: Full-Size Img PowerPoint

From these graphs, it was found that the big nipper had the largest dispersion of f_2max and E, while the small nipper had the fewest dispersion of them. It appeared that the larger dispersion they are, the farther spread unsteady cracks are. Regarding the cutting energy performance, the ratios of cutting energy of the big and medium nipper with the small nipper were 8.06 and 4.35, respectively.

3.4.   Effects of blade structure on sheared profile

After cutting PS bar specimens at V = 1 mm·s⁻¹, the sheared profile of the specimens was observed by a microscope CCD camera. Figures 23 shows the representative side views of sheared zone of PS bar specimen using the three kinds of nipper. Here, the right side of specimen was located in the front side of Figures 10, 11 (the big, medium nippers) and in the rear side of Figure 12 (the small nipper). The profile parameters of the left sheared edge were defined as h₁(mm), h₂(mm), h₃(mm), θ₁(°), and θ₂(°). That of the right sheared edge were defined as t₁(mm), t₂(mm), t₃(mm), w and Ø(°). The parameters of sheared edge profile were measured from the photographs of a microscope CCD camera. The values of the left sheared edge parameters were shown in Table 7 and the values of the right sheared edge parameters were shown in Table 8. Seeing Figure 23(a), (b), and Table 7 and 8, the wedged profile was asymmetric with the thickness direction. This means that the indentation depths of upper/lower blades were asymmetric and then a certain extent of bent attitude occurred in the cutting process. The existence of the torn zone h₂ seemed to correspond to the stages of B₂₄-B₂₅ and M₂₄-M₂₅.

Figure 23.  Representative sheared profile of PS bar specimen that was cut off by using (a) Big nipper, (b) Medium nipper and (c) Small nipper.

DownLoad: Full-Size Img PowerPoint

Table 7.  Values of left sheared edge parameters (Maximum-Minimum measured).

	h1/mm	h2/mm	h3/mm	θ1/°	θ2/°
Big nipper	1.23 (0.96–1.42)	0.70 (0.53–0.87)	1.18 (0.92–1.40)	46 (36–59)	61 (55–67)
Medium nipper	1.13 (1.05–1.20)	0.96 (0.84–1.09)	0.82 (0.72–0.91)	30 (27–33)	45 (41–48)
Small nipper	-	-	-	9 (8–10)	-

---

 | Show Table

DownLoad: CSV

Table 8.  Values of right sheared edge parameters (Maximum-Minimum measured).

	t1/mm	t2/mm	t3/mm	w/mm	Ø/°
Big nipper	0.68 (0.53–0.87)	0.86 (0.61–1.17)	1.51 (1.16–1.89)	-	12 (8–19)
Medium nipper	0.97 (0.87–1.06)	1.22 (1.12–1.37)	0.75 (0.68–0.83)	0.24 (0.19–0.31)	-
Small nipper	-	-	-	0.14 (0.13–0.15)	-

---

 | Show Table

DownLoad: CSV

The sheared surfaces of specimens cut by the three kinds of nippers were captured by a Scanning Electron Microscope (SEM) and shown in Figure 24, 25 and 26. In these figures, the symbol (a) denoted the left side and the symbol (b) denoted the right side of PS bar specimen in Figure 23.

Figure 24.  SEM micrographs of sheared surfaces of PS bar specimen cut by big nipper. (a) Front view of left side of sheared specimen, (b) Front view of right side of sheared specimen shown in Figure 23(a).

DownLoad: Full-Size Img PowerPoint

Figure 25.  SEM micrographs of sheared surfaces of PS bar specimen cut by medium nipper. (a) Front view of left side of sheared specimen, (b) Front view of right side of sheared specimen shown in Figure 23(b).

DownLoad: Full-Size Img PowerPoint

Figure 26.  SEM micrographs of sheared surfaces of PS bar specimen cut by small nipper. (a) Front view of left side of sheared specimen, (b) Front view of right side of sheared specimen shown in Figure 23(c).

DownLoad: Full-Size Img PowerPoint

When choosing the small nipper, any large pre-crack was not detected during the full stroke and there were not any variation (dispersion) of force drop for D₂ > 30% of 3 mm in Figure 16. Therefore, the small nipper's wedge cutting of PS bar seemed to be kept in a certain restricted condition in the longitudinal (in-plane) direction by the friction of the lower anvil at the final cutting stage. This frictional restriction of wedging made the sheared profile smoother than that of other nippers, as shown in Figure 26. Due to the geometrical feature of side wedge form, the left side sheared surface was stably compressed by the inclined line of the blade while the right side sheared surface was weakly touched with the perpendicular line of the blade. In this case, the compressive force for wedging the left side work material makes a thrust force to the blade. As the result, the blade was a little inclined to the right side direction and then the sheared surface was slightly curved as shown in Figure 23(c). This asymmetric cutting condition seems to make the difference of surface roughness with the right and left side surface of the work material as shown in Figure 26. Seeing this situation, the contact pressure of wedge seemed to make the sheared surface in smooth.

Since the big and medium nippers had the force drop after passing the peak position D₂ ≈ 50% of bar height in Figure 16, the size of final breakage had almost a half of bar height. The final process of the big, medium nippers generated a torn zone in the sheared PS bar as shown in Figure 24 and 25, then a collision of upper/lower bites occurred after the force drop. Regarding the surface roughness of sheared surface, several features were detected from Figure 24 and 25.

In the case of medium nipper, the upper and lower zones of the left side sheared surface were smoother than that of the right side sheared surface. However, in the case of big nipper, that of the left side and the right side sheared surface were evenly smooth. The difference of surface roughness seemed to be caused by the pressure level on the wedge. Namely, the contact pressure of wedge seemed to make the sheared surface in smooth.

Seeing the middle (final breakage) zone of sheared surface of the work material, the both side sheared surfaces by the medium nipper were smoother than that by the big nipper. This difference of surface roughness seemed to be caused by the in-plane tensile stress level. Since the right side inclined angle of wedge was quite small in the case of the medium nipper, compared to the big nipper, the final breakage of the middle zone appeared to be weakly tensile. Therefore, the in-plane tensile force by the wedge ought to be relatively small for making the sheared surface in smooth.

4.   Conclusion

In order to reveal performance of JIG fixture and the effect of blade edge profile to the cutting line force and the sheared edge profile of 3 mm square Polystyrene(PS) bars, three kinds of nippers: a big nipper (the upper/lower asymmetric two-line wedge of angles: α = 85–90°, α' = 72°), a medium nipper (the upper/lower asymmetric two-line wedge of angles: α = 49–55°, α' = 42–50°) and a small nipper (the side wedge of angle α = 13° against the anvil of 0.35 mm width) were experimentally investigated. The results were as follow:

(1) In order to perform a certain extent of reproducibility in the cutting test of a handheld nipper under a constant indentation velocity, the prototype JIG fixture was appropriate when considering the discussed calibration method of idle cutting response.

(2) When comparing the three nippers in cutting process, the load response was varied with the blade apex angle. By evaluating the force and blade displacement at the biting position, the cutting load response was commonly analyzed using the sliding line field theory, and the cutting resistance was characterized as a function of the yielding strength of work material and the friction resistance. Through the discussion of yielding stress of work material based on the sliding line field theory, a certain extent of asymmetric wedge indentation became obvious, and also the effect of bending attitude by the asymmetric wedge indentation was revealed through a CCD camera observation.

(3) Regarding the cutting behavior of PS bar material, the correlation between the cutting energy and the peak maximum line force was revealed. The larger angle of blade the nipper has, the more cutting energy and larger force the nipper handle needs.

(4) When comparing the sheared edge trace with the three nippers, the small nipper generated a smooth sheared surface without any dynamic large force drop. When the apex angle was 13 degrees (small nipper), the pre-crack at the necked stage did not occurred, and also the frictional restriction by the counter anvil appeared to fasten the force drop and the dynamic crack propagation.

(5) Synthetically, the difference of apex angle effect of nipper can be characterized using the cutting load response based on the prototype cutting test system.

Acknowledgements

The authors thank Kazuo Hatari and Reo Chiba, who were the undergraduate students of NUT, for their assistance with preliminary experiment and a design of JIG elements.

Conflict of interest

All authors declare there is no conflict in this paper.