Heterogeneous Stefan problem and permafrost models with P0-P0 finite elements and fully implicit monolithic solver

1.   Introduction

In this paper we are interested in numerical approximation of heat conduction with phase change in heterogeneous and composite materials. We are motivated by important applications in modeling permafrost, human tissue, and phase change materials (PCM) for thermal energy storage, smart textiles and buildings. These applications involve materials with drastically different thermal properties separated by an interface, thus require conservative algorithms. While we focus on mathematical and computational challenges rather than on practical engineering or geophysics scenarios, we aim to develop robust and accurate yet simple algorithms adequate for low regularity of solutions and easily extendable to future multiphysics simulators. Challenges similar to those discussed here occur in simulation of multiphase flow in fractures or rocks of different type ^[1,2], as well as in other applications which we give in what follows.

Overview. We focus on two phases: solid and liquid, separated by a free boundary, or by a region in which these phases coexist. In a single material we consider the following nonlinear parabolic equation

to be supplemented by appropriate boundary and initial conditions. The model is solved for the temperature $\theta$, the internal energy (enthalpy) density $w$ and the heat flux $q$. Here $f$ represents heat sources, $k$ is the heat conductivity. The definition of $w$ closes the model. For this definition, we consider one of the following equilibrium relationships

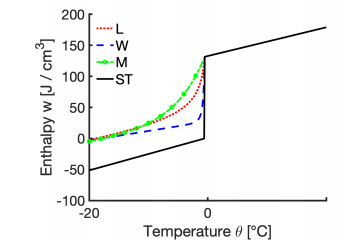
In particular, in the Stefan problem denoted by (ST), $w\in \alpha^{ST}(\theta) = c\theta +L\chi$. Here $c$ is the heat capacity, $L$ is the latent heat, and the water fraction $\chi \in \mathcal{H}(\theta)$ (where $\mathcal{H}$ is the Heaviside graph) "translates" the well known Stefan condition prescribing the velocity of the free boundary $S$ between the liquid and solid regions to (1.1) defined over both solid and liquid regions. Its approximation is (ST)$_{\epsilon}$, in which $\alpha ^{ST_{\epsilon}}(\theta)$ is some $\epsilon$-dependent single-valued piecewise smooth approximation to $\alpha ^{ST}$ with Lipschitz constant $L_{\alpha ^{ST_{\epsilon}}}\sim \epsilon^{-1}$; see Section 2 for details. In turn, in permafrost models (P) $w = \alpha^{P}(\theta)$ is given by a monotone piecewise smooth Lipschitz function $\alpha^P(\cdot)$, with some large Lipschitz constant $L_{\alpha^{P}}$; we give details in Section 5. See also a summary of notation in Table 1.

Known work. Even in a single material the models (1.1) and (1.2) does not have classical solutions and features challenges to the analysis and approximation due to the nonlinear multi-valued or only piecewise smooth character of $\alpha(\cdot)$. Typically, (1.1) is posed in the sense of distributions, and its solutions $(\theta, w)$ have low regularity.

The majority of numerical analysis for (1.1), under homogeneous Dirichlet boundary conditions, is carried out for (ST)$_{\epsilon}$ after so-called Kirchhoff transformation which renders (ST) or (ST)$_{\epsilon}$ in the equivalent form, and with a new variable $u$ instead of $\theta$

Since $u$ (as well as $\theta$) are expected to be continuous, it appears natural to seek their continuous piecewise linear (P1) finite element approximations. In turn, $w_h$ is either also piecewise linear (P1) ^[3] or piecewise constant (P0) ^[4,5]. We denote these approaches, respectively, as P1-P1 or P1-P0. For the permafrost (P) problem, the literature reports on the node-centered finite difference or piecewise linear finite element implementations, but without theoretical analysis or studies of convergence; see, e.g., in ^{[6,7,8,9,10,11]}. These also fall in the category of P1-based approximations. In turn, it is common to use cell-centered finite differences (CCFD) or finite volumes (FV) for a variety of fluid flow problems including those in subsurface ^[12].

Heterogeneous materials and conservative approximations. It is well-known that the P1-based approximations due to their poor approximation of fluxes are not well suited for computational modeling of problems with large heterogeneity of coefficients such as Darcy flow in porous media coupled to transport; see, e.g., discussions in ^[12,13]. For computational models of (1.1) and (1.2) alone in single material, this would not be an issue.

However, our goals in this paper are to study (1.1) and (1.2) in heterogeneous domains; additionally, we seek robust algorithms suitable for coupled multiphysics system such as THM ^{[14,15,16,17]}, and, simultaneously, for multiphase multicomponent systems at complicated geometries such as at pore-scale based on voxel grids ^{[18,19,20,21]}. Therefore, we draw from literature on conservative approximations using mixed finite element methods for multiphase flow in porous media and specifically on problems with nonlinearities similar to (1.2) ^[22,23,24]. These feature conservative fluxes and piecewise constant (P0) approximations to scalar unknowns. In this paper we approximate both $\theta$ and $w$ with piecewise constants (P0), thus we refer to these algorithms as P0-P0. Finally, when fluxes are approximated in the space $RT_{[0]}$ (discussed below), the algorithms can be conveniently implemented as cell-centered finite differences (CCFD); this gives a robust easily extendable structure towards more complex physics across many scales. Although these algorithms feature lower order approximation error, this is not an issue given low regularity of solutions to (1.1). Unfortunately, the approximation of fluxes features a technical gap since the normal fluxes for (ST) feature a jump; we defer the associated theoretical issues to future work.

Our results. (i) We first evaluate the feasibility of P0-P0 approximations with fully implicit in time approximations for (1.1) with (1.2) for a single material such as bulk water. We show our approach compares well to P1-based schemes, and that the solvers are robust, even if there are some theoretical concerns. (ii) Second, we develop P0-P0 algorithms for the heterogeneous case $k = k(x; \theta)$ and $\alpha = \alpha(x; \theta)$ in multiple materials, when the data features the realistic but most challenging case of piecewise constant $k(x; \cdot)$ and $\alpha(x; \cdot)$. Another challenge is that $\theta$ may not be continuous across material interfaces with high thermal resistivity. We prove various results and show robustness of our P0-P0 and monolithic CCFD algorithm which is conservative. Finally, we apply P0-P0 scheme to permafrost modeling including in heterogeneous materials, tie the theoretical framework for $\alpha^{P}$ to that developed for other $\alpha ^{ST}$ and $\alpha ^{ST_{\epsilon}}$, and confirm convergence.

Overall, we find that P0-P0 algorithm is robust for heterogeneous extensions of (1.1) with any of (1.2) we considered. The order of convergence in the scalar variables $(\theta, w)$ is, for the most part, about $O(h)$ and, $O(\sqrt{h})$ whenever time step $\tau = O(h)$ is used. The nonlinear solver performs also well, even though it might need improvements for strongly heterogeneous nonlinearities.

Outline: We give details on the phase change problems modeled by (1.1) with (1.2a) and (1.2b) in Section 2. In Section 2.4 we overview, compare, and illustrate traditional piecewise linear approximations to (ST) and (ST)$_{\epsilon}$ which we call P1-P1 or P1-P0. In Section 3 we define our P0-P0 approximations to (ST) and (ST)$_{\epsilon}$, prove some auxiliary results, and compare convergence and robustness of the scheme to P1-based approaches. In Section 4 we address heterogeneous (ST) such as in (1.3), and prove properties of the P0-P0 scheme for the solutions that feature a jump across the material interfaces. In Section 5 we provide details on the permafrost model (P) (1.2c), along with convergence results for P0-P0 scheme, and illustrate with simulations for both homogeneous and heterogeneous problem. We close in Section 6, with auxiliary results given in Appendix 7.

1.1.   Notation

The problem (1.1) is posed in $\mathcal{Q} = \Omega \times (0, T)$ where $\Omega \subset \mathbb{R}^d$ is an open bounded spatial domain with a smooth boundary $\partial \Omega$. In heterogeneous case, we partition $\overline{\Omega} = \bigcup_{j = 1}^{ N_{MAT}} \overline{\Omega^{(j)}}$ into subdomains $\Omega^{(j)}$, corresponding to $j = 1, \ldots N_{MAT}$ materials, with the material interfaces $\Gamma = \bigcup_{ij} \Gamma^{(ij)}, \Gamma^{(ij)} = \partial \Omega^{(i)} \cap \partial \Omega^{(j)}$. Thermal properties of a region depend on the material in that region. We assume that in material $j$ the heat conduction and phase transition parameters are known fixed constants. For example, at a point $x \in \Omega^{(j)}$, the freezing temperature is fixed for this material so that $\theta_{fr}(x) = \theta_{fr}^{(j)}$. In turn, the thermal conductivity $k(x; \theta) = k^{(j)}(\theta)$ depends on the temperature in a fixed way specific to material $j$. We denote this dependence of thermal properties as follows

The notation $\mathcal{Q}^{(j)}_p$ indicate the portion of $\mathcal{Q}$ in domain $(j)$ and phase $p$.

We assume that the subdomains and interfaces are smooth enough so that standard notation and results using the spaces $C^k(\Omega)$, and Lebesque and Sobolev spaces such as $L^p(\Omega)$ and $H^k\Omega)$ make sense. For a Lipschitz continuous function $f$ we denote its Lipschitz constant by $L_f$. We denote by $V = H_0^1(\Omega)$ for the primal variational formulation, and by $X = H_{\mathrm{div}}(\Omega)$ and $M = L^2(\Omega)$ the spaces for fluxes and scalars, respectively, needed in the mixed setting. By $(u, v) = \int_{\Omega}uv$ we denote the inner product of scalar functions on $L^2$ as well as that for vector valued functions on $(L^2)^d$. The norms $||{f}||_{{G}}$ of functions in space $G$ are as indicated with a subscript $G$ which is dropped if $G = L^2(\Omega)$ or $G$ can be inferred from context. For time-dependent problems when $t \in (0, T)$ and, e.g., $u \in L^2(0, T;V)$ we use the shorthand notation $L^2(V)$. For discrete formulations, we recall the spaces $V_h \subset V$ of piecewise linear finite elements based on a triangular grid. We will also use $X_h \subset X$ some approximations to the vector valued functions such as heat flux, and $M_h \subset M$ the space of piecewise constant approximations.

By ${\bf{1}}_U(x)$ we denote the characteristic function of set $U \subset \mathbb{R}^d \ni x$. For two sets $\Omega^-$ and $\Omega^+$ separated by an interface $\partial \Omega^+ \cap \partial \Omega^-$, by $[r(x)] = (r\vert_{\Omega^+}-r\vert_{\Omega^-})\vert_x$ we denote the jump of quantity $r$ at some interface point $x \in \partial \Omega^+ \cap \partial \Omega^-$. These two domains correspond to two materials, or to two phases of one material. When the sign of the jump is important, we make it precise on which side of the interface the limits are taken.

Next, consider real functions $u, w$ defined on $\mathcal{Q}$, and a function $\beta: \mathbb{R} \to \mathbb{R}$. The statement $u = \beta(w)$ means that $u(x, t) = \beta(w(x, t))$ a.e. on $\mathcal{Q}$. Similarly, consider a graph of a relation $\alpha \subset \mathbb{R} \times \mathbb{R}$ for which $\alpha^{-1} = \beta$ is a non-injective function, but $\alpha(\cdot)$ is multi-valued. In this case $\upsilon \in \alpha(r)$ is equivalent to $(r, \upsilon) \in \alpha$, and, for functions $u, w$ on $\mathcal{Q}$, the statement $w \in \alpha(u)$ means that $w(x, t) \in \alpha(u(x, t))$ a.e. $(x, t) \in \mathcal{Q}$.

In time-discrete formulations we use uniform time stepping with time step $\tau > 0$ and $0 = t^0 < t^1, \dots$ and $t^n = n\tau$. For an unknown $u(\cdot, t^n)$, we denote by $u^n(\cdot)$ its time approximation, and by $u_h^n(\cdot)$ its fully discrete approximation, which may be identified by the set of values such as $U^n_i$. For a known function $f(\cdot, t)$, we denote $f^n$ to be the value $f(\cdot, t^n)$ or its integral average $\tfrac{1}{\tau}\int_{t^{n-1}}^{t^n}f(\cdot, \upsilon)d\upsilon$, made precise in the context.

Finally, when using physical data and units, we use SI units or state otherwise; see Table 1.

In addition, we make some assumptions on the data. Assumption 1.1 is a standard assumption for data of heat conduction problems.

Assumption 1.1. We assume that the latent heat coefficients $L^{(j)}\geq 0$, and that heat capacity and conductivity coefficients are $c_{max}\geq c_p^{(j)}\geq c_{min} > 0; k_{max} \geq k_p^{(j)}\geq k_{min} > 0$ for all phases $p = s, l$, and domains $j = 1, \ldots N_{MAT}$.

For simplicity of notation when reviewing literature as well as in the proofs of some results we assume the following. (More realistic cases are given in examples.)

Assumption 1.2. Let $\theta$ satisfy homogeneous Dirichlet b.c. $\theta\vert_{\partial \Omega} = 0$. We also assume that some initial value $w_{init}\in L^2(\Omega)$ is given.

Last but not least, our focus in this paper is on the nonlinear relationship $\alpha$ given as one of the three specific choices $\alpha^{(ST)}$, $\alpha^{(ST)_{\epsilon}}$, $\alpha^{(P)}$ defined in (1.2) which come from phase change problems. However, our results apply to other possible $\alpha(\cdot)$ with properties summarized in Assumption 1.3. These properties are well known for $\alpha^{(ST)}$, $\alpha^{(ST)_{\epsilon}}$; see, e.g., ^[25]. For $\alpha^{(P)}$ in the permafrost problem, these properties follow from the algebraic formulas discussed in Section 5.

Assumption 1.3. We assume that $\alpha$ satisfies one of the following properties (a)–(c), similar to (ST), (ST)$_{\epsilon}$, (P), respectively: (a) $\alpha$ is a maximal monotone graph with a non-injective Lipschitz inverse $\beta = \alpha^{-1}$, similarly to $\alpha ^{ST}$, (b) $\alpha$ is a monotone strictly increasing function which is piecewise smooth and globally Lipschitz, with an injective Lipschitz inverse, similarly to $\alpha ^{ST_{\epsilon}}$, (c) $\alpha$ is a smooth strictly increasing globally Lipschitz function which has one point of non-differentiability (similar to $\alpha^P$).

2.   Formulations and approximation of Stefan problem in a single material

In this section we provide details on (ST) and (ST)$_{\epsilon}$. We suppress these superscripts now. A description of the variables used in this paper is given in Table 1.

2.1.   Stefan problem

We follow closely ^[27] as well as the applications literature ^[28] for thermodynamics of multiple phases. We consider the temperature field $\theta(x, t), x \in \Omega, t > 0$ and define $\Omega_l = \{x\in \Omega: \theta > 0\}$, $\Omega_s = \{x\in \Omega: \theta < 0\}$, with $\mathcal{Q}_l, \mathcal{Q}_s$ defined analogously. We also consider the phase interface $S = \partial \mathcal{Q}_l \cap \partial \mathcal{Q}_s$, and $S_t$ its instance at time $t$. The motion of $S_t$ is described by its velocity $v$, with the normal component $v \cdot \nu$. In turn, the normal $n$ to $S$ is oriented towards $\mathcal{Q}_l$, with components $(n_x, n_t)$ with $n_x$ parallel to $\nu$, so that we have $n_t = -v \cdot n_x$.

We recall first the so-called strong (classical) formulation of Stefan problem: we seek the temperature $\theta$ in each region $\Omega_p, p = s, l$ which satisfies the heat equation

The first part of (2.1a) is the energy conservation involving heat flux $q$, external source $f$, and the internal energy $c\theta$ dependent on the temperature. The second part is the Fourier heat conduction law.

The coefficients of volumetric heat capacity $c$ and heat conductivity $k$ depend on the phase of a material; see Table 2 for typical values. In this paper we consider the simplest realistic case in which $c, k$ are piecewise constant in each $\Omega_s, \Omega_l$, respectively.

One can extend (2.1b) to $\theta = 0$ using arithmetic averages ^[27](Ⅳ.4.1); see also Section 3.2.3.

2.1.1.   Free boundary

Finding the free boundary $S = \partial \mathcal{Q}_l \cap \partial \mathcal{Q}_s$, is part of the problem, with $S(x, t): \theta(x, t) = 0$. Additionally, the Stefan condition governs the velocity of $S_t$ as follows

where $\nu$ is the unit normal to $S_t = S \cap \Omega \times \{t\}$.

The strong (classical) form of the Stefan problem seeks $\{S, \theta\}$, with $\theta$ is expected to have continuous derivatives to all the relevant order in $\mathcal{Q} \setminus S$. As is well known, such a solution may not exist ^[27] (v)Section Ⅳ.1. Hence, there is need to define weak solutions of (2.1).

2.2.   Weak formulation

The weak form of (2.1) is derived upon integration by parts using test functions from $D(\mathcal{Q})$ and assuming that $\theta \in C(\overline{ \mathcal{Q}})$ but that its derivatives need only be in $L^1(\mathcal{Q}\setminus S)$. The energy conservation (2.1a) is written in all of $\mathcal{Q}$, and the weak form, in the sense of distributions, reads

The definition of enthalpy $w$ follows by integration of parts of (2.2a) written in the sense of distributions, the use of (2.1a)–(2.1c) along with the assumption that $S$ is smooth and $\theta$ continuous across $S$; see, e.g., ^[27](Ⅳ.1p.101) ^[25](A1 p244). This definition "translates" the Stefan condition (2.1c) as follows, in one of the many variants

Here $\phi$ is the order (phase) parameter and $\chi = \frac{\phi+1}{2}$ is the water fraction. In equilibrium, these are set to $\phi = 1, \chi = 1$ in $\Omega_l$ and $\phi = -1, \chi = 0$ in $\Omega_s$. On $S$ where $\theta = 0$, $\phi$ and $\chi$ are independent variables determined uniquely by the heat content $w$; in particular, $0 \leq \chi = \frac{w}{L} \leq 1$ when $\theta = 0$. However, when written in terms of temperature, the relationships $(\theta, \chi)$ or $(\theta, \phi)$ appear multi-valued

This only appears when the fact that $\chi$ (and $\phi$) are independent variables is ignored.

The definition (2.2b) can be also explained from thermodynamic principles: here we have $dw = c(\theta, \chi) d\theta+L d\chi$ which expresses a general dependence of $c$ on $\theta$ in (2.1b) as a weighted fraction of the heat capacities $c_l$ in the liquid and $c_s$ in solid phases

with a possibly variable $c_p = c_p(\theta)$. Then one integrates $dw = c d\theta+L d\chi$ to yield

This formula implies (2.1b) and has a nice nontrivial counterpart in permafrost; see Section 5.

In relaxation or in phase field models, i.e., away from equilibrium, $\phi$ is not given by (2.3), but is governed by its own dynamics, with its range possibly outside $[-1, 1]$. We describe and illustrate such models in Section 2.4.1.

2.2.1.   Kirchhoff transformation

The analysis of (2.2) proceeds after we change variables and write

The variable $u$ is called the "Kirchhoff temperature" and is distinguished from the true temperature $\theta$. To transform (2.2) to (2.6) we replace $k \nabla \theta = k(\theta)\nabla\theta = \nabla u$ with $u(\theta) = \int_0^{\theta} k(r)dr$, which, with (2.1b), gives

Next, from (2.2b) with (2.1b) we have the relationships for $(\theta, w)$

Finally, we combine (2.8) with (2.7) and see that $u = u(\theta) = u(\beta(w)) = \beta_{\rm{K}}(w)$ with

We see that $\beta$ and $\beta_{\rm{K}}$ are non-injective functions, while $\alpha$ and $\alpha_{\rm{K}}$ are maximal monotone graphs, i.e., the range of identity plus the graph is $\mathbb{R}$, and they are monotone. The functions $\beta_{\rm{K}}, \beta$ are Lipschitz, with Lipschitz constants

The functions $\beta_{\rm{K}}, \beta$ along with the graphs $\alpha_{\rm{K}}, \alpha$ are affine bounded, i.e., there are constants $C_{\beta} = max\{c_s^{-1}, c_l^{-1}, Lc_l^{-1} \}, C_{ \beta_{\rm{K}}} = max\{k_s c_s^{-1}, k_l c_l^{-1}, L k_l c_l^{-1} \}$ and $C_{\alpha} = max\{c_s, c_l, L\}, C_{ \alpha_{\rm{K}}} = max\{c_s k_s^{-1}, c_l k_l^{-1}, L \}$ with which

2.2.2.   Approximations of (ST)

There are many ways to approximate a multi-valued graph $\alpha$ (or $\alpha_{\rm{K}}$, ${\mathrm{sgn}}$ or $\mathcal{H}$) by a single-valued Lipschitz function so that its inverse is injective. One very specific (one-sided) approximation is the Yosida approximation

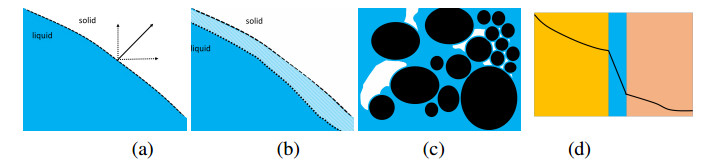
We see that $L_{\alpha_\lambda} = O(\lambda^{-1})$ which blows up as $\lambda \downarrow 0$. For this and other similar approximations of $\alpha ^{ST}$ by $\alpha ^{ST_{\epsilon}}$ there is no jump of $q \cdot n$ or of $w$ across the free boundary $S$. Rather, these variables vary sharply in the region

See, e.g., illustration in Figure 1(c).

2.3.   Well-posedness

The models (1.1) with (1.2) and in particular (2.2) and (2.6) are nonlinear monotone evolution equations with maximal monotone graphs $\alpha$. Theory for such equations in Banach spaces is given in ^[25]; the specific case of Stefan problem is discussed in ^[27] in an abstract Hilbert space setting; see also ^[3].

We recall only the case of Dirichlet homogeneous boundary conditions, in the Hilbert space case with $V = H_0^1(\Omega)$. We seek $w \in L^{\infty}(L^2) \cap H^1(H^{-1})$, $u \in L^2(V)$ such that $u = \beta_{\rm{K}}(w), \ w(\cdot, 0) = w_{init} \in L^2(\Omega)$ and (see, e.g., ^[4])

Assuming some smooth enough $w_{init}$ is given, the maximal monotonicity of $\alpha_{\rm{K}}$ and the fact that both $\alpha_{\rm{K}}$ and $\alpha_{\rm{K}}^{-1}$ are affine bounded are sufficient for ^[27](1.20, p34; Thm.Ⅱ.5.1, p59). In particular, with $f \in L^1(L^2) \cap L^2(V')$, and $w_{init} \in L^2(\Omega)$, one obtains that there exists a unique solution $\int_0^T u \in L^{\infty}(V) \cap H^1(L^2)$ (note that this implies $u \in L^2(L^2)$). Further refinement of the theory ^[27](Prop.Ⅱ.1.3 and Thm.Ⅱ.1.4))^[27] gives $u, w\in L^{\infty}(L^2)$, with uniqueness in ^[27](Thm 5.2). Further regularity ^[27](Thm 2.5) indicates $u\in H^1(L^2) \cap L^{\infty}(V)$. Since $\theta$ can be found from (2.7) which is continuous, one generally obtains similar qualitative properties of $\theta$ as those of $u$.

These results indicate quite low regularity of $w$ in contrast to the case when $\alpha_{\epsilon}$ is single valued and Lipschitz continuous, since then $w_{\epsilon}$ has the same regularity as $u_{\epsilon}$ ^[27](Thm 2.6). Further results hold for in-homogeneous Dirichlet data as long as it is smooth enough; these results elucidate the connection between weak and strong formulations ^[27](Ⅳ.6). Under nonlinear Neumann boundary conditions ^[29] for $N_{MAT} = 1$ one obtains $\theta \in L^2(H^1), w \in L^2(L^2)$.

2.4.   Approximation of solutions to Stefan problem in a single material: review

In this section we review several approaches towards the numerical approximation of (2.2) and the Kirchhoff transformed version (2.6) which combine time-stepping with some spatial discretization such as finite elements or finite differences. We focus on the traditional mesh-based PDE discretization; other approaches include explicit tracking of the free boundary, but without solving for $(\theta, w)$ on a mesh; see, e.g., ^[30] for review. These latter approaches do not apply very well to the simulation at pore-scale, permafrost, or heterogeneous materials.

In Section 2.4.1 we recall and illustrate time stepping schemes. Next in Section 2.4.2 we review spatial discretization approaches focusing on piecewise linear approximations $u_h \in V_h \subset V$; the methods differ by how $w_h$ is approximated and how (ST)$_{\epsilon}$ is selected.

2.4.1.   Time stepping for an ODE

Consider some $f = f(t)$, and $A > 0$ in

We illustrate several time discrete schemes which approximate the relationship of $(\theta, w)$ either by regularization, Chernoff formula, or by relaxation.

The backward Euler scheme is

and the solution for every $n\geq 1$ is guaranteed from Lemma 7.1; in practice, we use Newton's iteration substituting $\theta^n = \beta(w^n)$.

The solution to (2.15) can be also computed using so-called Chernoff formula ^[4]

where $\mu$ is the relaxation parameter, a constant approximation to $\frac{1}{\beta'}$, which satisfies $0 < \mu \leq L_{\beta}^{-1}$, with $L_\beta$ from (2.10). The Chernoff formula offers a way to linearize the non-linear relationship $\beta$. Chernoff formula does not require any nonlinear iteration, since it solves a linear problem for $\theta$ followed by an update of $w^n$. However, it produces consistency errors growing with $\mu^{-1}$.

We also consider the phase-relaxation approach: we replace the equilibrium relationship (2.8) $w = c\theta+L\chi = c\theta+\frac{L}{2}(\phi+1)$ in which $\phi\in {\mathrm{sgn}}(\theta)$ by a coupled problem which allows $\phi = \phi(t)$ to evolve towards this equilibrium written as ${\mathrm{sgn}}^{-1}(\phi) \ni \theta$. ^[27](Ⅴ.1). This relaxation is another form of approximation to the equilibrium problem; see ^[31] for the PDE (2.2). In a more general phase-field approach, one can consider an additional dissipative term similar to $A\phi$, plus a coarsening term proportional to $\phi$ which acts to counteract $A\phi$; these together moderate the evolution of $\phi$ coupled to the PDE (2.2).

Let $\varepsilon > 0$ and $\gamma > 0$. The phase-relaxation approach to (2.15) is given as

Here $g$ is one of two possible choices which approximate ${\mathrm{sgn}}^{-1}(\cdot)$ and contain the linear destabilisation term. We consider $g_\circ(\phi) = \phi^3-\phi$ similar to that in Allen-Cahn equation, ^[32] which we call "smooth". The other is $g(\phi) = g_\square(\phi) = {\mathrm{sgn}}^{-1}(\phi)-\phi$ which we call "non-smooth" ^[27](Section Ⅵ.5) ^[33,34]. We discretize (2.18) fully implicitly and solve by Newton's iteration

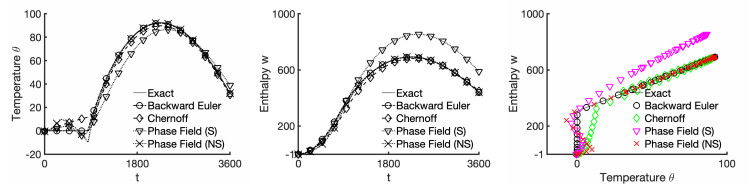
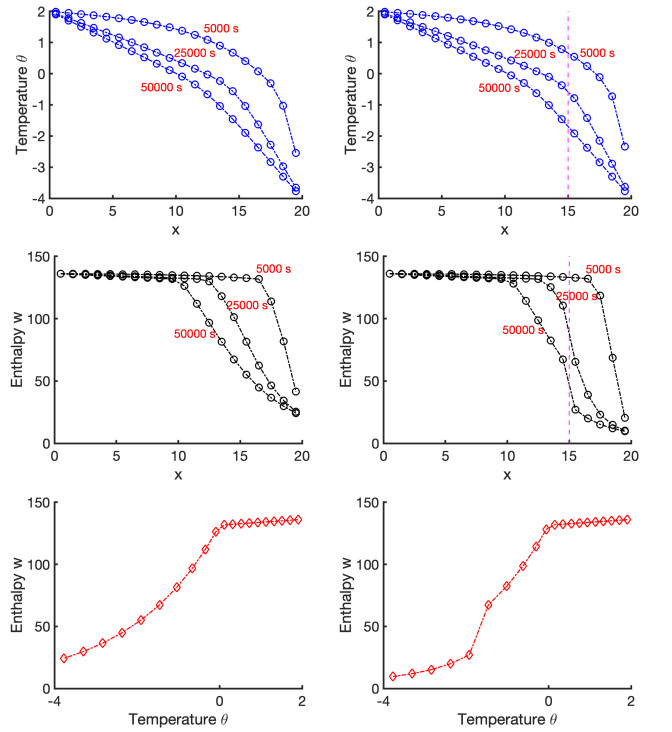
Example 2.1. We solve (2.15) with $\alpha = \alpha ^{ST}$ given by (2.8) with parameters in Table 2 (W). We choose $A = 10^{-2}, w_{init} = -1,$ and a forcing term $f(t) = \sin{\left(\frac{\pi t}{3600} \right)}$ for $t\in [0, 3600]$. We derive the exact solution given in Section 7.1.

In Figure 2 we plot numerical solutions using $\tau = 40$ and one of the three schemes: fully implicit, Chernoff formula, and phase relaxation with (2.18). For Chernoff formula, we choose $\mu = 1.5$ so that $\mu \leq L_{\beta}^{-1} = c_s = 1.90$. For phase relaxation, the key challenge here is a choice of the parameters $\varepsilon = 1/10, \ \gamma = 1$, so that the time-relaxed dynamics resembles that of (2.15).

In the end we see that the fully implicit solution (2.16) trails the exact solutions $\theta(t)$ and $w(t)$ fairly well. The Chernoff formula and phase relaxation approaches seem to have less close agreement, especially in $w(t)$. While they offer other advantages, this experiment informs our subsequent choice to focus on the fully implicit time stepping.

2.4.2.   Spatial approximations

Early approaches to numerical solution to (ST) include the nodal finite difference approach in ^[42] for which convergence (but no specific order) is proven, independently of $\epsilon$ in the regularization (ST)$_{\epsilon}$ of (ST) problem. In ^[26] some time error analysis is provided.

The majority of rigorous work is on nodal piecewise linear approximations $V_h \ni u_h \approx u \in V$ in (2.14); we call these P1-based. The approaches differ in time stepping (as in Section 2.4.1), in how the original problem (ST) is approximated by some (ST)$_{\epsilon}$, and in how $w_h^n$ is defined. In particular, ^[43] prove $L^2(L^2)$ order of convergence close to $O(h)$ for fully implicit approximations for (ST)$_{\epsilon}$, when $\epsilon = O(h^2), \tau = O(h^2)$ but require $\partial_t w_{\epsilon}$ to be bounded, and refer actually to simulations with the (P) problem discussed in ^[7] instead of (ST)$_{\epsilon}$. In turn, ^[4,5,44] approximate solutions for some (ST)$_{\epsilon}$ rather than (ST); ^[4,5] make use of the Chernoff formula similar to (2.17), while ^[44] and ^[31] use phase relaxation; these are closely related as shown in Figure 2.

The main difference between the individual approaches is in the treatment of spatial integrals $\int_{\Omega} w \psi$ and $\int_{\Omega} u \psi$ with $\ \psi \in V_h$, and in adjustments to how $w_h$ is found. In some schemes the numerical integration, or one of projection operators such as $P_h^0, P_h^1, \Pi_h$ are used. In some, piecewise constants and $w^n_h\in M_h$ are used, this is similar to our P0-P0 schemes to be defined in Section 3.

The theoretically estimated convergence error depends, as usual, on $h, \tau$ and $\epsilon$. Generally, $\theta$ is predicted to be approximated well, qualitatively and quantitatively, by all the P1-based schemes, with the order about $O(h)$, in the weaker norms. However, the errors $w-w_h$ are, as expected, higher, and $w_h$ appears "smeared" near the free boundary $S_t$.

We set up detailed experiments and provide illustrations as part of our subsequent studies of P0-P0 schemes for (ST) problem in comparison to P1-based schemes. Our tests given in detail in Section 7.3 along with fine details on the schemes show somewhat better rates than those predicted and tested in ^[26,31,44]. Of the schemes studied, ^[5] produces the best approximation and convergence rates. We acknowledge the limitations of our study only in $d = 1$, but believe these provide good starting point for subsequent comparisons with P0-P0 schemes.

3.   Approximation to Stefan problem using P0-P0 finite elements and CCFD for a single material

In this section we propose P0-P0 spatial discretization for (1.1) combined with any one of (1.2) combined with fully implicit in time scheme. We start with a mixed finite element formulation for (1.1), using $M = L^2(\Omega)$ for scalar unknowns such as $\theta$ and $w$, and $q \in X = H_{\mathrm{div}}(\Omega)$ which features continuous normal components across any smooth surface. Next we choose P0-P0 approximations $\theta_h, w_h \in M_h \subset M$. We also seek fluxes $q_h \in X_h = RT_{[0]}$ on a rectangular grid as in ^[22,45]. The pair $(X_h, M_h)$ is a stable pair for the Darcy problem satisfying the Banach-Neĉas-Babuŝka conditions ^[46]. For linear problems they approximate the fluxes and scalar unknowns to the same order $O(h)$, with superconvergence for smooth solutions and some norms ^{[45,46,47,48]}.

Remark 3.1. For nonlinear relationship represented by (1.2) we encounter here the major challenge. The choice $X = H_{\mathrm{div}}$ works for the (ST)$_{\epsilon}$ and (P) problems when $\alpha(\cdot)$ in (1.2b) and (1.2c) is single-valued. However, in the Stefan problem (ST) with (1.2a), the fluxes $q \not \in H_{\mathrm{div}}(\Omega)$ since their normal takes a jump across $S_t$, which ties to the multivalued character of $\alpha(\cdot)$. This raises concerns on the approximability of $q\not \in X$ by $q_h \in X_h$. We acknowledge this difficulty and formally develop the theory only for the single-valued $\alpha$ such as for (ST)$_{\epsilon}$ and (P) problems, but we extend the algorithms in $X_h \times M_h$ to the (ST) problem. We defer further study to future considerations.

The P0-P0 algorithm has several attractive features. 1) First, the normal fluxes of $q_h \in X_h$ are continuous, which leads to conservative schemes across element and material interfaces; to support this, we work in the $(\theta, w)$ formulation instead with Kirchhoff variables $(u, w)$. 2) Second, if $\theta_h$ is piecewise constant, it is natural to define $w_h = \alpha(\theta_h) \in M_h$ in a consistent fashion so that (2.8) is enforced at every degree of freedom. 3) Third, the P0-P0 equivalent to the mixed framework features approximation properties known from the literature; in particular, the results in ^[22] are most relevant for the present nonlinear case of (ST)$_{\epsilon}$ and (P) problems. In fact, we demonstrate that the convergence in $(\theta, w)$ is not inferior to that for P1-based schemes from Section 2.4 even for (ST) problem; this is done in Section 3.4. 4) Last, the approximations, up to quadrature, are equivalent to a CCFD scheme for $\theta_h \in M_h$ from which the fluxes $q_h \in X_h$ follow post-processing; these features, recalled in Section 3.2, make implementation easy and allow its extensions to more complex nonlinear problems and multiple materials.

Below we first set-up the notation and recall main results on the mixed finite element discretization leading to P0-P0 algorithm. For simplicity of notation we consider $\Omega \subset \mathbb{R}^d, d = 2$ and assume that it is well covered by a rectangular grid $\mathcal{T}^{h} = (\omega_{ij})_{ij}$ so that $\overline{\Omega} = \bigcup_{ij} \omega_{ij}$, with $\max_{ij}|{\omega_{ij}}| = \max_{ij} h_{x, i} h_{y, j} = h^2$. Each cell $\omega_{ij} \in \mathcal{T}^h$ has a center at some $(x_{ij}, y_{ij})$ and edges $\gamma_{i-1/2, j}, \gamma_{i, j-1/2}, \gamma_{i+1/2, j}, \gamma_{i, j+1/2}$, when listed clockwise from the left edge. Throughout this section we use Assumption 1.2.

3.1.   P0-P0 scheme from discrete mixed formulation for linear parabolic problems

We recall the mixed formulation for the linear case of (1.1) and (1.2b) with $L = 0$ but allowing $k = k(x), c = c(x)$, with some given initial condition $w(x, 0) = w_{init}(x)$. We have then $k^{-1}q = -\nabla \theta; \partial_t w + \nabla \cdot q = f; w = \alpha(\theta) = c\theta$. Its weak formulation follows after we multiply each of the equations in (1.1) by test functions $\psi \in X$, $\eta \in M$, integrate by parts, respectively, and apply the boundary conditions. We seek $(q, \theta) \in X \times M$ which satisfy

(In these equations the symbols $(a, b)$ mean inner product $\int_{\Omega}ab$ in $L^2(\Omega)$ as given in Section 1.1). The approximations $q^n_h, \theta^n_h$ with $w_h = \alpha(\theta_h)$ are formulated after (3.1) is discretized in time, and when at each time step $t^n$ we seek $(q^n_h, \theta^n_h) \in X_h \times M_h$ which satisfy a system similar to (3.1). We make these precise now.

We consider the well known spaces $(X_h \times M_h)$ built on $\mathcal{T}^h$ with $X_h = RT_{[0]}$, the lowest order Raviart-Thomas space on rectangles ^[22,45,48]. The space $M_h$ contains piecewise constants on $\mathcal{T}^h$; the basis functions spanning $M_h$ are simply ${\bf{1}}_{\omega_{ij}}$, and $\theta_h\vert_{\omega_{ij}} = \Theta_{ij}$ associated with the cell centers of each $\omega_{ij}$. The vector valued functions in $X_h$ are tensor products of piecewise linears in one coordinate with piecewise constants in the other. In particular, $(q_h)_1$ is identified by their edge values at the left and right edges $(i\pm 1/2, j)$ so we have, e.g., $(q_h)_1 \vert_{\gamma_{i+1/2, j}} = q_{i+1/2, j}$; analogously $(q_h)_2$ is identified by values at the bottom and top edges $i, j \pm 1/2$, respectively, $(q_h)_2 \vert_{\gamma_{i, j-1/2}} = q_{i, j-1/2}$. The basis functions for the vector valued functions in $X_h$ are $\psi_{i\pm 1/2, j}$ for $(q_h)_1$ and $\psi_{i, j\pm 1/2}$ for $(q_h)_2$. Let $(Q^n, \Theta^n)$ denote the degrees of freedom for $q_h^n, \theta_h^n$ in their bases.

We define the fully implicit approximations $(q_h^n, \theta_h^n) \in X_h \times M_h$ to (3.1) as those that satisfy

We applied here numerical integration to the first integral in (3.2a) and replaced $({k}^{-1} q^n_h, \psi)$ by its approximation $({k}^{-1} q^n_h, \psi)_h$. Specifically, the following numerical integration is used: on every $\omega_{ij} = (x_{i-1/2}, x_{i+1/2}) \times (x_{j-1/2}, x_{j+1/2})$, the trapezoidal (T) scheme over $(x_{i-1/2}, x_{i+1/2})$ and (M) midpoint scheme on $(x_{j-1/2}, x_{j+1/2})$ for the first component of $q_h \cdot \psi_h$, and $M \times T$ scheme for the second component. This leads to some useful simplifications, very well known and described in ^[49]. In particular, $({k}^{-1} q^n_h, \psi)_h$ gives $\mathcal{K} Q$ with a diagonal matrix $\mathcal{K}$ of positive edge factors $\mathcal{T}_{i \pm 1/2, j}$ and $\mathcal{T}_{i, j\pm 1/2}$ involving $k^{-1}$; see Section 7.5 for more details. We also get $(\nabla \cdot q_h^n, \eta) = - \mathcal{B} Q^n$ while $-(\theta_h^n, \nabla \cdot \psi)$ becomes $\mathcal{B}^T \Theta^n$. The linear system reads

with $G^n = F^n+\tfrac{1}{\tau}W^{n-1}$. Note that $\mathcal{C}$ is the diagonal matrix of positive coefficients $c\vert_{\omega_{ij}}$.

Remark 3.2. After we multiply the second equation in (3.3) by $(-1)$, the system (3.3) has a saddle-point structure. Thus it is well-posed, i.e., the operator $\mathcal{N} = \left[ \begin{array}{cc}{ \mathcal{K}} & \mathcal{B}^T\\ \mathcal{B} & - \mathcal{C}\end{array} \right]$ is an isomorphism ^[45](Prop.3.3.1 and Thm 3.6.2), because ${ \mathcal{K}}$ is coercive (positive definite) on the kernel of $\mathcal{B}$, $\mathcal{C}$ is positive definite. and $\mathcal{B}$ is surjective from $X_h \to M_h$.

Remark 3.3. The system (3.3) can be easily modified to account for non-homogeneous Dirichlet boundary conditions; see Section 7.5 for details.

Connection to CCFD. Since $\mathcal{K}$ is diagonal, every degree of freedom of $Q^n$ has an easy discrete interpretation, thus one can eliminate $Q^n$, and (3.3) is equivalent to

This system is known as the cell-centered finite difference (CCFD) formulation. Now $\mathcal{B} \mathcal{K}^{-1} \mathcal{B}^T$ is symmetric and at least nonnegative definite for Neumann boundary conditions, and positive definite for Dirichlet conditions. Since $\mathcal{C}$ is positive definite, we have a unique solution $\Theta$ from which $Q$ follows.

3.1.1.   Literature notes

For linear problems such as (3.1), mixed FE solution $(q_h, \theta_h)$ features optimal first order convergence of the errors $||{q-q_h}||_{{X}}$ and $||{\theta-\theta_h}||_{{M}}$ for the choice of $RT_{[0]} \times M_h$ ^[46]. For Darcy and potential flow problems the quadrature error is lower order, and the mixed approach provides formal interpretation of the CCFD algorithm ^[49]. For parabolic problems under Neumann boundary conditions and strong assumptions on the smoothness of $\theta$ and $q$, ^[48] shows that

This order, is, in general, not featured for nonlinear problems such as (1.1).

3.2.   P0-P0 scheme for nonlinear heat equation with single-valued nonlinearity

Now we consider (1.1) or Kirchhoff-transformed problem (2.6) with (1.2b) or (1.2c) in the mixed formulation. We seek $(q, \theta)$ or $(q, u)\in X \times M$ and replace $w = c\theta$ by $w = \alpha(\theta)$ or $w = \alpha_{\rm{K}}(u)$ in (3.1b) to get the weak mixed and discrete mixed formulations similar to that for (3.1).

3.2.1.   Literature for nonlinear problems in mixed form

The challenge, well described in ^[22] is that one must respect the regularity of the unknowns $(q, \theta, w)$ which is usually inferior to that for the linear case when $\partial_t w \in L^2(\Omega)$. In particular, when $\beta_{\rm{K}}(\cdot)$ has derivative vanishing pointwise, it may happen that $\partial_t w \not \in L^2(\Omega)$. This difficulty is partially overcome with a Kirchhoff transformation and upon integration in time, and/or discretization in time; we refer to e.g., ^[22,46,50] for thorough discussion. The approach of taking finite differences in time is also known as the Rothe or Crandall-Ligget or Hille-Yosida framework ^[25,29].

For nonlinear problems which are Kirchhoff-transformed the mixed framework is set-up for the solutions $(w^n_h, u^n_h, q^n_h)$ in ^[22,23,51]. However, the error estimates depend on the smoothness of $w$ and $u$. Disregarding the error in the fluxes, these results, when applied to (1.1) state that, as in e.g., ^[22]

with $C, \overline{C} \downarrow 0$ as $h \downarrow 0$ depending on the smoothness of $u$, but with the order not specified directly. The work ^[22] does not directly address existence and uniqueness of the solutions. Overall, the results in ^[22,23,51] are well-suited for problems such as Richards equation, with $\alpha$ which features somewhat different challenges than those for (ST), (ST)$_{\epsilon}$, (P) problems listed in Assumption 1.3.

3.2.2.   P0-P0 algorithm for nonlinear single-valued function

We extend now (3.3) to the nonlinear case when $k = k(\theta)$ and $w = \alpha(\theta)$, working with $(\theta, w)$ as scalar unknowns. We define some approximations $\tilde{c}^n \approx c(\theta^n)$ and $\tilde{k}^n \approx k(\theta^n)$, and take some $\tilde{\alpha} \approx \alpha$; we make these precise in Section 3.2.3. The fully discrete problem reads

This nonlinear system uses $\tilde{ \mathcal{K}}$ based on $\tilde{k}$. We prove first that the system has a unique solution; this is needed since Remark 3.2 does not apply to this nonlinear case. We complete details on the algorithm in Section 3.2.3.

Lemma 3.1. Let Assumption 1.1 hold on $\tilde{k}$, and let $\tilde{ \mathcal{K}}$ and $\mathcal{B}$ be computed as in Section 3.1; in particular, let $\tilde{ \mathcal{K}}$ be positive definite. Then there exists a unique solution $(Q, \Theta, W)$ to (3.6) and its generalization

Proof. We discuss only (3.7) since the result for (3.6) follows as its special single-valued case. We proceed in one of two alternative ways which are each worthwhile discussing. One is that we rewrite (3.7) eliminating $Q$ as in (3.8)

We set $A = \mathcal{B} \tilde{ \mathcal{K}}^{-1} \mathcal{B}^T$ which is at least nonnegative definite as discussed earlier. The system is as in Lemma 7.1, thus the existence of a unique solution $(\Theta, W)$ follows, with $Q$ found by postprocessing from (3.6a).

Yet another proof follows ideas in ^[50](Thm 3.2), and is worthwhile mentioning because it extends to the abstract weak formulation of (1.1) in $(X, M)$ for the case when $q \in X$. We note that the system (3.7) can be written as $\mathcal{M} ([Q, \Theta]^T) = [0, G]^T$; the nonlinear operator $\mathcal{M}$ a sum of diagonal matrix of maximal monotone operators $\left[ \begin{array}{cc}\tilde{ \mathcal{K}} & 0\\0 & \partial \Phi_{\alpha}\end{array} \right]$ (we define $\Phi_{\alpha}$ as in Lemma 7.1), and the accretive linear thus Lipschitz operator $\left[ \begin{array}{cc}0 & \mathcal{B}^T\\- \mathcal{B} & 0\end{array} \right]$. This means that $\mathcal{M}$ is maximal monotone, and that there exists a unique solution to (3.7).

3.2.3.   Details

Now we need to define $\tilde{k}, \tilde{c}$ and $\tilde{\alpha}$. These are needed since we extend (3.3) to the nonlinear case when $k = k(\theta)$ and $w = \alpha(\theta)$. Typically, we assign these cell-wise based on the $\Theta = (\Theta_{ij})_{ij} \equiv \theta_h$

(The value $k^*, c^*$ can be one of many including $\frac{k_l+k_s}{2}$ and $\frac{c_l+c_s}{2}$, respectively ^[27](Ⅳ.4.1)). Also,

(In practice, the set $\Omega_0^{h}$ is empty). From these the formula for $\tilde{\alpha}$ follows by (2.8).

Lastly, we need to make precise which $\Theta$ we use in (3.10). When entering a new time step $t^n$, we have the previous time step value $\Theta^{n-1}$. When iterating on (3.6), in iteration $m$, we have $\Theta^{n, (m-1)}$ to denote the iteration-lagged value, while we seek the new $\Theta^{n, (m)}$. We must therefore make precise in (3.10) whether it depends on the old $\Theta^{n-1}$, or on iteration-lagged value $\Theta^{n, (m-1)}$. Adopting the notation for the sets in (3.10) from that for $\Theta$ we get, e.g., ${\Omega}_l^{h, n-1}$ or ${\Omega}_l^{h, n, (m-1)}$. In other words, we can calculate $\tilde{k}_{ij}$ from (3.9) as either ${k}_{ij}^{n-1}$ or ${k}_{ij}^{n, (m-1)}$. These choices give the matrix $\tilde{ \mathcal{K}} = \mathcal{K}^{n-1}$ or $\tilde{ \mathcal{K}} = \mathcal{K}^{n, (m-1)}$, respectively. Thanks to Assumption 1.1 these have positive entries; see also Section 7.5. Therefore Lemma 3.1 applies to (3.6).

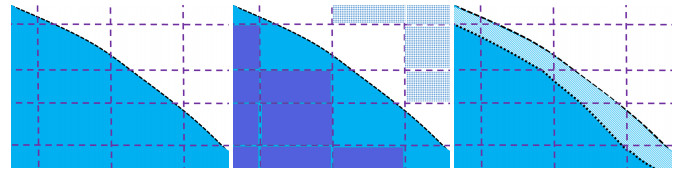
Remark 3.4. The sets in (3.10) are not the same as

If neither of $\Omega_l(t), \Omega_s(t)$ is empty, $\Omega \setminus (\overline{\Omega_l^h}(t^n) \cup \overline{\Omega_s^h}(t^n)) \neq \emptyset$, as illustrated in Figure 3.

3.2.4.   Nonlinear solver

Next we discuss the nonlinear solver for (3.7). The solution to (3.7) exists and is unique according to Lemma 3.1, but the proof makes a reference to some (iterative) optimisation algorithm to find the desired minimizer $\Theta^{n}$.

In practice, the use of such a minimisation algorithm may be tedious and is unnecessary. Instead, we solve the problem using Newton's method: we rewrite (3.8) from the proof of Lemma 3.1 in residual form using the single-valued inverse $\beta$ of $\alpha$.

In each iteration $m = 1, 2, \ldots$, given $W^{n, (m-1)}$, $\Theta^{n, (m-1)}$ we solve

This scheme means we are solving (3.12) simultaneously for two variables $\Theta^{n}, W^{n}$. However, the second part of (3.12) is diagonal, thus we can, instead, eliminate $\Theta^{n, (m)}$ and solve the problem in terms of $W^{n, (m)}$.

It is known that Newton's iteration is not guaranteed to converge for an arbitrary initial guess even for smooth $F = (F_1, F_2)$. Now the nonlinear function $\beta$ in (3.12) is only piecewise differentiable, but such case is covered by the theory and practice of semi-smooth Newton methods in ^[52]. In our tests the Newton solver is robust and essentially grid-independent as long as the time step $\tau$ is not too large. We discuss performance of this iteration in Section 3.4.

3.3.   Addressing multivalued (ST) problem with P0-P0

As we showed in Section 3.2, there is no difficulty formulating P0-P0 algorithm and solving the fully discrete case of (1.1) with multi-valued $\alpha$ (1.2a).

In fact, given $\Theta^n$ we get $Q^n$ from (3.6a); this gives $q^n_h \in X_h$. However, the true $q \not \in H_{\mathrm{div}}$. Thus any attempts to quantify the approximation error for $q_h-q$ must take into account this important discrepancy expressed already in Remark 3.1. Thus there is a question whether the use of $q_h \in X_h$ is appropriate for the (ST) problem. This challenge is somewhat more complex than the pointwise degeneracy with $\beta' = 0$ pointwise handled, e.g., in ^[22], which still keeps $q \in X$.

At this time we see various avenues to address this challenge. One is to solve (ST)$_{\epsilon}$ formally, and create a sequence $q_h^{\epsilon} \in X_h$ for a collection of $\epsilon > 0$ adjusted to $h$, and defining $\tilde{q}_h^n$ as their limit. The fluxes $q_h^{\epsilon}$ would be reasonably accurate approximations to $q^{\epsilon} \in X$, and their limit $\tilde{q}_h^n$ to $q \not \in X$. One other is to find some approximation $\tilde{q_h^n}$ to $q$ by postprocessing $q_h^n$. One can also consider projecting $q$ to $X_h$. We defer further analyses of possible improvements to $q-q_h^n$ to future work.

3.4.   Results of P0-P0 algorithm

Now we present examples and study the convergence of P0-P0 approximation for (ST) problem. We focus on the scalar unknowns $(\theta, w)$, and defer the study of the error $q-q_h$ to future work. We study the approximation error $\theta_{err} = \theta-\theta_h$ and $w_{err} = w-w_h$. We choose only those norms that are easy to use when analytical solution is not available, and are easy to compare to the theoretical results on P1-based schemes. For completeness, the definitions of these norms are given in Section 7.4.1.

In convergence studies we use uniform spatial and temporal discretization. We also note that when using fine grid, the error rates, especially those for $w$, are sensitive to interpolation and machine precision; thus, some care in grid refinement is needed to obtain consistent rates.

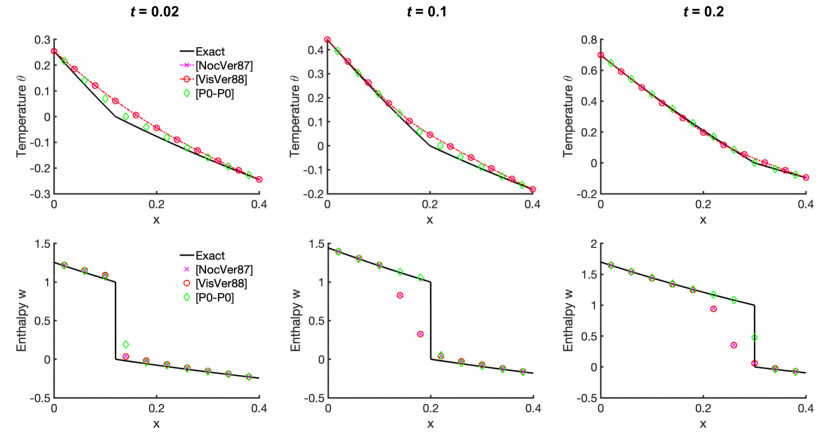
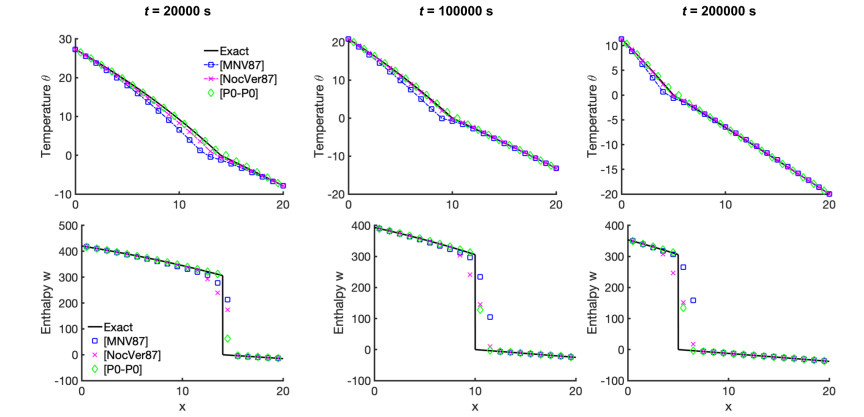
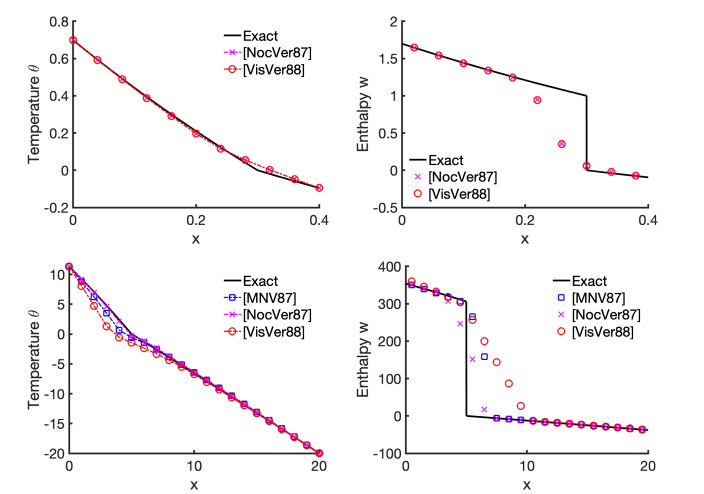
The goal now is to compare the performance of our P0-P0 scheme with the P1-based schemes from Section 2.4. These results provide confidence in our work on multiple materials, as well as guide the choice of time step $\tau$ depending on $h$. We use two test cases which we call (RBC) from ^[26] and another called (VV) from ^[44]. These examples feature an assumed free boundary $S$ moving with some given prescribed velocity, $w_{init}$ and time-dependent Dirichlet boundary conditions found from the exact solution. For illustration, the plots of the solutions and their approximations are given in Figure 4 and Figure 5.

Example 3.1. (VV) This example from ^[44] is not connected to any particular physical scenario, but results in very simple mathematical calculations. Let $\Omega = (0, 0.4)$ and $T = 0.2$, $f = 0$ and $L = c = k = 1$. Note that since the data is not physical, no particular units are used, even if our code assumes units such as those in Table 1. We have the free boundary for (2.2) $S:\psi(x, t) = 0$, with $\psi (x, t) = -x+t+0.1$, and

In experiments we stop the simulation at $T = 0.2$, a time at which the free boundary position is still inside $\Omega$. This choice helps to analyse how well the free boundary is approximated by the different numerical schemes.

Example 3.2. (RBC) example uses realistic physically meaningful data from ^[26]. We have $\Omega = (0, 20)$[cm], $L = 306$[J cm$^{-3}$], $c_s = 1.90$ and $c_l = 4.19$ [J cm$^{-3}$ $^\circ$C $^{-1}$], $k_s = 0.023$ and $k_l = 0.0058$ [J sec$^{-1}$ cm$^{-1}$ $^\circ$C $^{-1} ]$. The free boundary $s(t) = s_0 + v_st$, and

where $\alpha_l = v_s c_l/k_l$ and $\alpha_s = v_s c_s/k_s$, and data as in Table 2. We also use the parameters in Table 3.

3.4.1.   Convergence tests

Convergence results for P0-P0 algorithm and (VV) example are given in Table 4, with $\tau = h/10$. We also provide the fine grid-study with $h_{fine} = 6.4 \times 10^{-5}$ in Table 5; these results are very similar to those in Table 4, thus they validate our process for using $\theta_{h_{fine}}$ as a proxy for $\theta$.

The convergence results for (RBC) using the fine grid solution and exact solution are shown in Tables 6 and 7 respectively. We also tabulate the comparison to P1-based methods in Section 7.4.2 in Table 13.

Summary of convergence of P0-P0 schemes: Generally, we see that our P0-P0 schemes converge roughly with first order in $\theta$ and half order in $w$. These rates are similar to those for P1-P0 schemes from Section 2.4. However, our P0-P0 schemes seem to improve on P1-based schemes qualitatively and quantitatively; in particular, we see improvement in the quality of approximations to the enthalpy, which seems due to the lack of consistency errors such as those for Chernoff formulas or phase relaxation.

We acknowledge that this might be due to only testing in $d$ = $1$; nevertheless, these results are promising.

3.5.   Robustness of nonlinear solver

Last but not least we discuss performance of the nonlinear solver for (3.7) since it works without regularization for (ST) problem, and we have not found a discussion for (ST) problem in the literature.

The maximum number of iterations required for each case to converge is listed in Table 8. The solver uses for stopping criterium a combination of absolute tolerance of $10^{-12}$ and a relative tolerance of $10^{-6}$ and $\tau = h/10$, relative to the first iteration.

Overall, the solver performs reliably under a variety of circumstances, including with uniform coefficients used in Example 3.1 (VV), realistic thermal properties used in Example 3.2 (RBC) and in the presence of multiple materials in Example 4.2 to be discussed below. It is also important that the performance seems to be mesh independent.

Though not illustrated in Table 8, we see in practice that the number of Newton iterations may increase with larger discrepancies between parameters and larger latent heat $L$ values. We add the notes on the specifics of the heterogeneous permafrost case in Section 5.

3.6.   Summary

More work on the theoretical underpinnings of P0-P0 algorithm is needed for Stefan problem, but overall our P0-P0 (CCFD) algorithm seems well suited to all the choices of $\alpha$ in (1.2) including even the most challenging case of $\alpha ^{ST}(\cdot)$.

4.   Stefan problem with heterogeneity, and its P0-P0 approximation allowing for thermal resistivity of interface

We consider now the main challenge addressed in this paper, that of simulation of phase change problem in a heterogeneous domain, a generalization of (2.2) to the case when the region $\Omega$ is occupied by $N_{MAT}$ materials, each in $\Omega^{(j)}, j = 1, \ldots N_{MAT}$, with interfaces denoted by $\Gamma_{ij} = \partial \Omega^{(i)} \cap \partial \Omega^{(j)}$, and $\Gamma = \bigcup_{ij} \Gamma_{ij}$. We also have $\Sigma = \Gamma \times (0, T)$. See Figures 1 and 6 for illustration. The data corresponding to material $(j)$ are denoted by $c^{(j)}_l, c^{(j)}_s, k^{(j)}_l, k^{(j)}_s, \theta_{fr}^{(j)}, L^{(j)}$. With these we formulate $\alpha^{(j)}$ as in (2.8), and assume that the data satisfies Assumption 1.1, and that $\Gamma$ is at least as smooth as $\partial \Omega$. We denote the appropriate functional spaces local to $\Omega^{(j)}$ with superscript $^{(j)}$, e.g., in $X^{(j)}$, and so on.

Let (2.2) hold in each $\Omega^{(j)}$. Denote by $w^{(j)}, \theta^{(j)}$ the restriction of $w, \theta$ to $\Omega^{(j)}$, so we have

This problem requires some initial conditions and some boundary conditions on $\partial \Omega$.

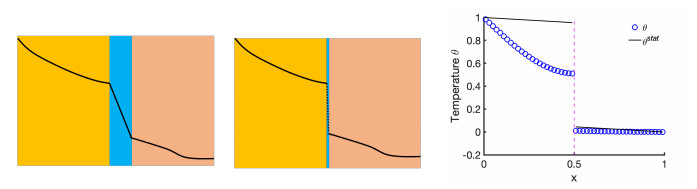
We also need some interface conditions on each $\Gamma_{ij}$. For these, it is natural to assume (i) continuity of fluxes, and (ii) of the temperatures across each $\Gamma_{ij}$. However, in some applications including PCM, the condition (ii) must be relaxed to model the heat conduction across a very thin region of very low heat conductivity. When the width of that layer is very small compared to the width of the regions surrounding this layer, and if the interface region is approximated by a lower dimensional interface $\Gamma_{ij}$, the temperature appears to take a jump, since the limits of temperature from both sides of $\Gamma_{ij}$ are quite distinct, while the flux is preserved ^[37]. See Figure 6 for illustration.

This jump condition is formulated, e.g., in ^[29,53,54]

where $\rho_{R}\geq0$ is called "thermal resisitivity" and where the orientation of the unit normal $\nu$ to $\Gamma_{ij}$ is from $\mathcal{Q}_i$ to $\mathcal{Q}_j$. (More generally, one can consider $\rho_{R}$ to be specific to an interface).

If $\rho_{R} = 0$ or the fluxes $q^{(j)}$ vanish, we have continuity of temperatures $\theta$ across $\Gamma_{ij}$ (but not necessarily of $u$). If $\rho_{R} > 0$, the condition (4.1c) is a Robin condition which slows down the process of reaching thermal equilibrium across the interface. This latter case is important for applications. However, its mathematical and computational challenges have not been well studied. We address some of the challenges that (4.1) brings from theoretical and algorithmic point of view when $\rho_{R} > 0$.

The mixed formulation is particularly convenient for problems involving interfaces and multiple materials. In particular, the condition (4.1b) prescribes the continuity of normal fluxes across $\Gamma$ which is naturally preserved for the fluxes $q \in X$. The condition also prescribes a possible jump of the scalar unknowns, but this is not an issue when extending $\theta \in M$. Therefore, if the problems on each $\Omega^{(j)}$ are well posed in $X^{(j)} \times M^{(j)}$ for each $j$, then the global problem can be well studied in $X \times M$; see, e.g., ^[55,56]. Similarly, one can easily define the P0-P0 (CCFD) algorithms on each subdomain coupled to the discrete counterparts of (4.1b)–(4.1c).

As concerns the overall solution algorithm based on CCFD for (4.1a), in principle, some domain decomposition approach iteration is required to satisfy (4.1b)–(4.1c). However, one of our contributions in this paper is that we are able to formulate a monolithic P0-P0 algorithm on $\Omega$. We also formulate various theoretical results and estimates for $q_h \in X_h$. We note however that even though we do not state approximation properties in this paper, these may involve $\theta$ considered in some broken spaces such as $\mathcal{H}(\Omega) = H^1(\Omega^{(1)}) \times H^1(\Omega^{(2)})$ rather than $H^1(\Omega)$ due to the discontinuity of $\theta$ across $\Gamma$.

After some literature review in Section 4.1, we formulate and illustrate our algorithms in Sections 4.2 for linear and nonlinear problems when $q \in X$. We extend these to (ST) problem and apply the same scheme, even if some of the theoretical results do not apply when $q \not \in X$. We provide examples and study convergence in Section 4.3.2.

4.1.   Literature on heterogeneous Stefan pbm

The mathematical literature on (4.1) is not abundant, but we review what is available. The problem is a special case of more general heterogeneous nonlinear parabolic problem in which

When the data (4.2) vary smoothly as functions of its first argument, it is possible to apply Kirchhoff transformation on $\Omega$ but this introduces various lower order terms in the PDE. This approach considered, e.g., in ^[57,58], allows some well-posedness analysis.

Another class of approaches in ^[59,60,61] study a problem similar to Stefan problem via minimization of a collection of normal convex integrands, and assumes smoothness of $\alpha(x; \theta)$ in $x$, for an application with phase change of a different type where the multivalued graph $\alpha(x; \cdot)$ representing the solubility constraint depends smoothly on $x$. At the same time, the challenges discussed here are similar to those revealed by simulations in ^[61] when applied to piecewise constant data.

The piecewise constant case (1.3) of interest in this paper does not allow Kirchhoff transformation but is also most realistic. The well-posedness of the case $\rho_{R} > 0$ is studied in the primal setting in ^[29] under external Neumann boundary conditions on $\partial \Omega$ and with some initial data. Existence of solutions is proven for $\rho_{R} > 0$, with estimates which allow the limiting case $\rho_{R} \downarrow 0$. Uniqueness is also proven ^[29]. For $\rho_{R} > 0$, the paper predicts $w\in L^{\infty}(Q)$, $\theta\in L^2(\mathcal{H})$, and that the jump is

We note that as as $\rho_{R} \downarrow 0$, the estimates (4.3) suggest continuity of the temperature across $\Gamma$ but also predict the blowup of $\partial_t w$.

As concerns numerical approximation, ^[54] describes the approximation in $(V^{(j)}_h)_j$ similar to the P1-P1 schemes described in Section 2.4. A-priori bounds for $(\theta^n_h, w^n_h)$ including those similar to (4.3) are proved in ^[53] for $\rho_{R} > 0$. Finally, a time discrete approximation to $\partial_t w_h$ is measured in some seminorms which involve $\frac{h^2}{\tau^2}$, $\frac{1}{\sqrt{ \rho_{R}}}$; these suggest to use $\frac{h}{\tau}$ bounded as $h \to 0, \tau \to 0$, and $\rho_{R}$ such that $\frac{\tau^2}{ \rho_{R}} \to 0$. Based on these a-priori bounds, convergence to the solution corresponding to $\rho_{R} = 0$ is established. However, no rate of convergence for the approximation errors $\theta-\theta_h$ is given.

Last but not least we mention other problems and applications which feature jumps of the primary unknowns and fluxes. These works fit in the framework of heterogeneous domain decomposition ^[56] and inform our results, but are not closely related. The closest is our prior work on the domain decomposition approach for semiconductor modeling of heterogeneous junctions in ^[62,63,64]. Further, there is closely related substantial work on multiphase flow and multiple rock types in, e.g., ^[1,2] as well as the abundant literature on Beavers-Joseph conditions on the Stokes-Darcy interfaces, e.g. in ^[65] and other heterogenous domain decomposition settings.

4.2.   P0-P0 scheme

We approximate (4.1) with P0-P0 discrete scheme from Section 3. We recall that even though the formal approximation with $X \ni q \approx q_h \in X_h$ is appropriate only for the single-valued setting $w = \alpha(\theta)$ (as in Remark 3.1), the P0-P0 algorithm produces discrete conservative fluxes $q_h \in X_h$ also for the multivalued case $w \in \alpha(\theta)$.

We start with P0-P0 (or CCFD) algorithm on each material domain, a counterpart of (3.7), which we couple with discrete counterparts of (4.1b)–(4.1c). Then we show that this domain decomposition formulation can be handled by a monolithic solver. With this, the theoretical results including convergence analyses available for single domain formulations in $X^{(j)}_h \times M^{(j)}_h$ extend to that on $X_h \times M_h$ (as long as $q \in X$). Moreover, the problem does not require any iteration on the interface.

We explain the details first for the linear heat equation with the notation from Section 3.2; the generalization to the nonlinear problem is straightforward. For simplicity, we focus on only two materials $N_{MAT} = 2$ which occupy the domains $\Omega^{(1)}, \Omega^{(2)}$ separated by an interface $\Gamma = \Gamma_{12}$.

4.2.1.   P0-P0 formulation with mixed finite elements

We rewrite (4.1) in a time-discrete mixed form, with subdomain problems (4.4a)–(4.4b) to be solved by $(\theta^{n, (j)}, q^{n, (j)})_{j}$. We also make precise the initial, external, and coupling boundary conditions (4.4c) and coupling via (4.4d)

We approximate (4.4) with P0-P0 algorithm for (4.4a)–(4.4c) on each $\Omega^{(j)}$ as in Section 3, each implemented as CCFD, and corresponding to a block linear system similar to (3.3) is solved, with off-diagonal coupling terms expressing (4.4d).

This coupling could be solved by iteration; we refer to ^[56] for a discussion of domain decomposition iterative algorithms. In contrast, we propose to satisfy (4.4d) without an iteration which simplifies the implementation substantially. We explain the ideas briefly for $d = 1$ in Section 4.2.2.

4.2.2.   Monolithic scheme

Let $\Omega = (a, b)$ and $\Omega^{(1)} = (a, x^*)$ and $\Omega^{(2)} = (x^*, b)$, with a grid $(\omega_i)_i$ covering $\Omega^{(1)} \cup \Omega^{(2)}$ so that $\Gamma = x^*$ is one of the cell edges. With global numbering of the cells $\omega_i$ in $\Omega$, we have $i = 1, \ldots j^*, j^*+1, \ldots M$, where $\Gamma = x^* = x_{i*+1/2} = \gamma_{i*+1/2}$ is between some cells $\omega_{i*}$ and $\omega_{i*+1}$. Now the problem is discretized as in Section 3.2 with $q^{(1)}_h$ and $q^{(2)}_h$ identified by the edge values $Q^{(1)} = (Q_{1/2}, Q_{3/2}, \ldots Q_{i*+1/2}^-)$ and $Q^{(2)} = (Q_{i*+1/2}^+, Q_{i^*+3/2}, \ldots Q_{M+1/2})$, respectively. We note the double value of the flux $Q_{i*+1/2}^-, Q_{i*+1/2}^+$ to be set equal due to (4.4d). The temperatures $\theta^{(1)}_h \in M_h^{(1)}$ and $\theta^{(2)}_h \in M_h^{(2)}$, respectively, are identified by the cell values $\Theta^{(1)} = (\Theta_1, \Theta_2, \ldots \Theta_{i*})$, and $\Theta^{(2)} = (\Theta_{i*+1} \ldots \Theta_{M})$. Finally, the Dirichlet conditions at the external boundaries are with $\Theta^*_{1/2} = \theta_D(x_{1/2})$, and $\Theta^*_{M+1/2} = \theta_D(x_{M+1/2})$. These enter (3.3) as in Remark 3.3.

The approximation to the first part of the interface condition (4.4d) equates the fluxes $Q_{i*+1/2}^- = Q_{i*+1/2}^+$. We also require Dirichlet values $\Theta_{\ast}^-$ and $\Theta_{\ast}+$ to be used by each subdomain problem at $x^*$ so that the second part of (4.4d) holds. Finding these is part of the problem. In summary, the approximation to (4.4) is as follows.

where we find $Q_{i*+1/2, j}^-$ and $Q_{i*+1/2, j}^+$ from the solutions on $\Omega^{(1)}$ and $\Omega^{(2)}$ defined as follows.

The solution to (4.5) requires formulation of appropriate matrices $\mathcal{K}^{(1)}$, $\mathcal{K}^{(2)}$ to solve (4.5b) and (4.5c), respectively. These come from the transmissivities $(\mathcal{T}_{i\pm1/2})_i$ on every $\gamma_{i+1/2} \in \Omega^{(j)}$ and are given as in Section 7.5 by (7.11). We also have two boundary edge factors $\mathcal{T}_{i*+1/2}^{-}$ and $\mathcal{T}_{i*+1/2}^{+}$ given by (7.13) independently on $\Omega^{(1)}$ and $\Omega^{(2)}$, respectively.

The problem (4.5) could be solved by iteration. However, our idea is that (4.5) can be solved by a much simpler monolithic CCFD solver on $\Omega$ for $\Theta = (\Theta^{(1)}, \Theta^{(2)})$ and $Q = (Q^{(1)}, Q^{(2)})$ for which $Q_{j*+1/2}^- = Q_{j*+1/2}^+$. The system takes the form

The definition of $\mathcal{B}$ is a straightforward extension of $\mathcal{B}^{(j)}$, but $\mathcal{K}^{ \rho_{R}}$ involves $\mathcal{K}^{(j)}$ as well as an appropriately chosen transmissibility $\mathcal{T}_{i*+1/2}^{\rho}$ to guarantee (4.4d).

Lemma 4.1. Solution to (4.5) exists and is unique; it is equivalent to that of (4.6) provided

where we use the shorthand notation $\mathcal{T}^- = \mathcal{T}_{i*+1/2, j}^-$ and $\mathcal{T}^+ = \mathcal{T}_{i*+1/2, j}^+$.

Proof. The proof is purely algebraic. Assume (4.5) is satisfied. Denote $Q^- = Q_{j*+1/2}^-$, $Q^+ = Q_{j*+1/2}^+$, so (4.5a) holds for some $\Theta_{\ast}^-, \Theta_{\ast}^+$, $Q^-, Q^+$. We know also $\Theta_{i*}, \Theta_{i*+1}$ from (4.5b) and (4.5c).

1. Recall $Q^{-} = \mathcal{T}^-(\Theta_{i*}- \Theta_{\ast}^-)$ and $Q^{+} = \mathcal{T}^+(\Theta_{\ast}^+-\Theta_{i*+1})$. Setting these equal from the first condition in (4.5a), and expressing $Q^-$ from the second part of (4.5a), we work to eliminate $Q^+$ and get a formula for $\Theta^-$ in terms of $\Theta_{i*}$ and $\Theta_{i*+1}$. After some lengthy calculations we get

2. Next we recalculate $Q^{-} = \mathcal{T}^-(\Theta_{\ast}^–\Theta^-_{i*})$. After some algebra we get

3. Now the expression on the right hand side can be written as

This provides the definition of (4.7), i.e., of $\mathcal{K}^{ \rho_{R}}$ for the monolithic formulation. Existence and uniqueness of the solutions to (4.6) follows directly from that for (3.3) with the special definition of $\mathcal{T}^{\rho}_{i*+1/2, j}$ which satisfies the same properties as all other $\mathcal{T}_{i \pm 1/2}$.

Remark 4.1. When $\rho_{R} = 0$, (4.7) reduces to give $\mathcal{T}_{i*+1/2}$ as the usual weighted harmonic average of $k_{i*}$ and $k_{i^*+1}$ in (7.11), and provides the interface value of $\Theta_{\ast} = \Theta_{\ast}^- = \Theta_{\ast}^+$

In other words, a monolithic CCFD approach on matching grids is equivalent to the domain decomposition approach. This observation is perhaps not new, but is nevertheless very useful.

Corollary 4.1. The results in Lemma 4.1 easily extend to $d = 2$ when $\Gamma$ is aligned with cell interfaces. In addition, these results extend to nonlinear problems such as (3.6) and (3.7) with

Here in each time step $n$ and iteration $(m)$ one updates the transmissibilities $\mathcal{T}_{i\pm 1/2}^{n, (m)}$ based on the current guess of $W^{n, (m)}$. This system uses special interface transmissivities involving $\rho_{R}$ resulting in the dependence of matrix $\tilde{ \mathcal{K}}^{n, (m)}_{ \rho_{R}}$ on $\rho_{R}$.

Remark 4.2. Convergence of the solutions $(q_h, \theta_h)$ to $(q, \theta)$ for the linear problem is expected to be qualitatively similar to the case without jump, since, upon Lemma 4.1, it follows from those for CCFD on each domain, e.g., in ^[48]. At the same time, the solution $\theta\in M$ is not globally smooth enough, thus broken norms must be used when referring to the approximation error's dependence on higher order norms.

We provide an example with a numerical approximation in Section 4.3. We also prove theoretical estimates on the jump $[\theta]_{\Gamma}$.

4.2.3.   Estimates of the jump on the interface

We aim to derive results similar to (4.3) in the mixed setting. We write the fully discrete mixed form of (4.4), and work with the discrete counterparts of $\theta^{(j)}, w^{(j)}, q^{(j)}$, with $w^{(j)}\in \alpha^{(j)}(\theta^{(j)})$. As explained for (4.6), we use $\tilde{k}$ which can be $k(\theta^n)$, or $k(\theta^{n-1})$ or $k(\theta^{n, (m)})$, formed, respectively, either in a fully implicit, time-lagging or iteration lagging fashion.

Lemma 4.2. Let $\theta_D = 0$. Then the numerical solution of (4.1) satisfies, at every $t^n$

Proof. We suppress $h$ and $n$. The weak mixed formulation of (4.1a) after integrating and adding the equations over $(j)$ reads: find $(q, \theta) \in X_h \times M_h$ such that for every $\psi \in X_h, \eta \in M_h$ we have the following

To derive the estimates we now choose $\psi = q$ and $\eta = \theta$. Adding the two equations and cancelling the skew-symmetric terms we obtain, after rearranging

The right hand side now involves the boundary and the right hand side $g$. We have control over the boundary term since $\theta_D = 0$. The first term on the left hand side is nonnegative. The second term can be bounded from below for $\alpha ^{ST}$, as well as for $\alpha ^{ST_{\epsilon}}$ and $\alpha^{(P)}$

In fact, for (ST) problem we have $c_{\alpha} = \min_j((c^{(j)}_l), (c^{(j)}_s))$. For (ST)$_{\epsilon}$, we have $c_{\alpha} = \min_j((c^{(j)}_l), (c^{(j)}_s), \epsilon^{-1})$, with a similar calculation for $\alpha^{(P)}$ from Section 5. Then we apply Cauchy-Schwarz inequality to the integral $\int_{\Omega}g\theta \leq ||{g}||_{{L^2}} ||{\theta}||_{{L^2}}$ and follow up with the inequality $|{a}||{b}| \leq \tfrac{a^2}{2s}+\tfrac{sb^2}{2}$. With sufficiently large $s$ we can now move the term $\tfrac{||{\theta}||_{{L^2}}^2}{2s}$ to the left hand side to balance it with $c_{\alpha}||{\theta}||_{{L^2}}$. We conclude that $\int_{\Gamma} (\theta^{(1)}-\theta^{(2)}) q \cdot n \leq \tfrac{s||{g}||_{{L^2}}^2}{2} = C$ thus, upon (4.4d) we finally obtain

from which (4.8) follows.

This result is similar to that predicted in (4.3) ^[29] in the primal formulation. With more work, we can also cover the case $\theta_D \neq 0$.

Corollary 4.2. The estimate in Lemma 4.2 extends to the solutions $(q, \theta)$ for (ST)$_{\epsilon}$ or (P) problems with single-valued $\alpha$ when $q \in X$.

4.3.   Numerical examples of P0-P0 for heterogeneous domain with two materials

Now we illustrate the problem (4.1) with simulations using our P0-P0 solver.

4.3.1.   Linear heat equation with a jump

We consider first an example in $d = 1$ for which we study the dependence of the jump of $\theta$ on $\rho$.

Example 4.1. Let $\Omega = (a, b)$ with some $a < x^* < b$. Let some $\rho\geq 0$ be given, as well as $L = 0$, $k^{(1)}(x) = k_1; k^{(2)}(x) = k_2$, and $c^{(1)} = c^{(2)} = 1$ so that $w = \theta$. We also impose boundary conditions $\theta(a) = \theta_a, \theta(b) = \theta_b$, The numerical solutions are computed with $M = 50$, and $\tau = 0.0.001$. We consider different ratios $k_2/k_1$, and $\rho_{R}$.

We plot the solutions to Example 4.1 found numerically with our monolithic P0-P0 solver. We also consider the corresponding stationary limit $\theta^{stat}(x)$ of (4.1); see the details in (7.15) and (7.14) in Section 7.6.

The numerical solution to the stationary problem in this simple case essentially coincides with the exact solution; this is typical for P0-P0 solution. The non-stationary solutions evolve towards this stationary solution. The qualitative nature is consistent with the imposed interface jump condition.

In the end we also test the scaling of the jump $[\theta]_{\Gamma}$ predicted by (4.8) given what we found for the stationary solution in Section 7.6; we check how it behaves over time. The details in Section 7.6 predict that the jump of $\theta^{stat}(x)$ scales linearly with $\rho_{R}$ as $\rho_{R}\downarrow 0$, unlike $O(\sqrt{ \rho_{R}})$ predicted for the evolution problem in (4.3). For large ratio $\tfrac{k^{(2)}}{k^{(1)}}$ and small $\rho_{R} < 1$ we find that the jump behaves similarly to that for the stationary problem. For small $\tfrac{k^{(2)}}{k^{(1)}}$, and before the solutions are close to the stationary limit, we see that the size of the jump $[\theta_h]_{\Gamma}$ depends significantly on the grid discretization $h$. This behavior correlates with the large magnitude of $\partial_t w$ when $t$ is small. In fact, it also correlates with the estimates of $\partial_t w$ in (4.3) (see also subsequent discussion in Example 4.3). We defer further study of these features to the future.

4.3.2.   Examples for Stefan problem for heterogeneous domain with two materials

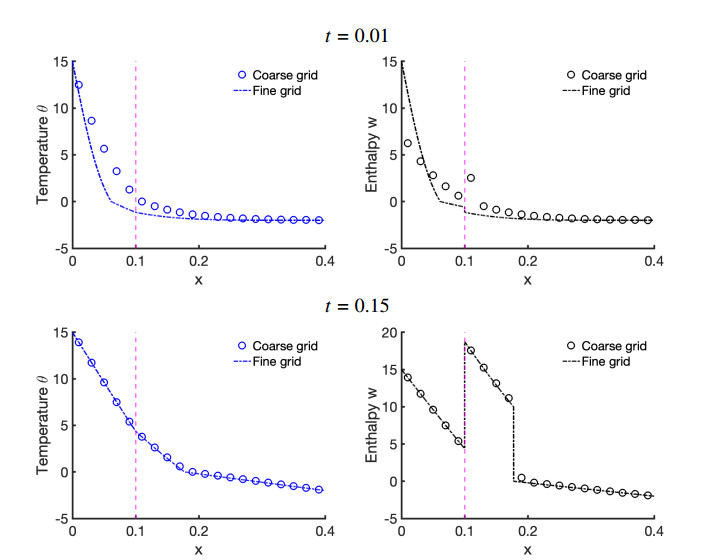
Now we consider (ST) problem, and start by checking convergence of our P0-P0 scheme for the case of heterogeneous materials. To this end, we modify Example 3.2.

Example 4.2. We let $\Omega = (0, 0.4)$ with ${\bar{\Omega} = \bar{\Omega}^{(1)} \cup \bar{\Omega}^{(2)}}$ with parameters given in Table 9. Note that the material within $\Omega^{(2)}$ has $L\neq 0$ while $\Omega^{(1)}$ has $L = 0$; the freezing temperature $\theta_{fr} = 0$ for both.

The initial conditions are $w_{init}(x) = c_s(x)\theta_{init}(x)$ which corresponds to $\theta_{init}(x) = -2$ for all $x \in \Omega$. Boundary conditions are $\theta(0.4, t) = -2$ and $\theta(0, t) = 15$ for $t \in (0, T]$. Figure 8 shows the temperature increase throughout the domain due to the heat transfer through the left boundary.

We do not have an exact solution, thus we must use fine grid solution for convergence studies. The coarse grid solution for $M_x = 20$, is compared with that for the fine grid, $M_x = 2500$ at the first fine grid time step of $t = 0.005$ and the time $t = 0.15$. In convergence study we disregard the initial time period $t \in [0, 0.005]$ in which the solution has very steep $w_t$ due to the discrepancy between the initial and boundary data. The convergence of the solution is of lower order during that time and pollutes the rest of the error analysis.

Convergence results, calculated for $t \in [0.01, 0.15]$ are shown in Table 10. We see similar rates of convergence for this heterogeneous example as for the homogeneous Example 3.2.

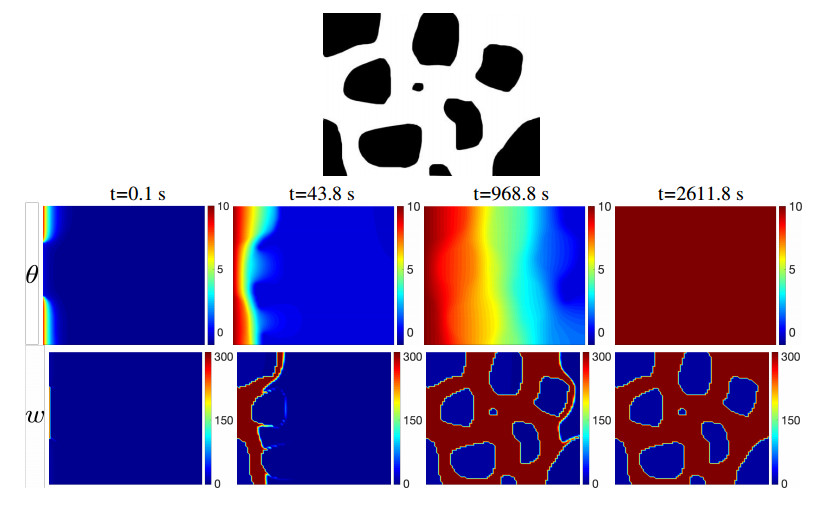
Next we illustrate the need for multiple materials by simulating heat flow at the pore-scale. We proceed to the simulation in $d = 2$ at the pore-scale which is motivated by our interest in permafrost. We use our P0-P0 solver with $\rho_{R} = 0$, since there is no interface with high resistivity between the mineral and water components.

Example 4.3. Let ${\Omega = (0, 1) \times (0, 1)}\mathrm{[{cm^2}]}$ with ${\bar{\Omega} = \bar{\Omega}^{(1)} \cup \bar{\Omega}^{(2)}}$, with water saturated pore space $\bar{\Omega}^{(1)}$, and the rock grains $\bar{\Omega}^{(2)}$; see Figure 9. The material parameters are those of water for $\Omega^{(1)}$ and inferred from those for silica for $\Omega^{(2)}$ as given in Table 2. We start from thermal equilibrium, with constant temperature $\theta_{init} = -1 {{\mathrm{[{^\circ C}]}}}$ with which we calculate $w_{init}(x) = c_s(x)\theta_{init}(x)$.

The heat in $\Omega$ increases due to the boundary condition at $\partial \Omega_{\text{left}} = \{0\} \times [0, 1]$ where we set $\theta_D(x, t)|_{\partial \Omega_{\text{left}}} = 10$. We also assume insulated boundary conditions elsewhere $q \cdot \nu|_{\partial \Omega \setminus \partial \Omega_{\text{left} }} = 0$ for $t \in (0, T]$.

In Figure 9 we show temperature profiles of four time steps. The melting front moves from left to right with a phase change in the void space $\Omega^{(1)}$, but the grains do not undergo phase change. The heat flux moves faster through the areas with more grains, since this change requires less energy required for phase change than the heat conduction in the water component.

4.4.   Summary

More work on testing the heterogeneous Stefan problem and even the linear heat equation is needed, but overall we believe our monolithic P0-P0 scheme performs well for multiple materials. While not reported here, we tested the simulation cases of different freezing temperatures, and drastically different parameter $L$ between domains, and see that the algorithms perform in a robust way across these scenarios, even if a decrease of the time step is needed in the most challenging cases.

5.   Permafrost models

Permafrost is defined as the ground that remains frozen for two or more years ^[41,66,67]. Temperatures in permafrost respond to the changes in ambient temperatures at the soil-atmosphere interface, possibly including the effects of precipitation and vegetation. In the upper portion of permafrost called active layer the temperatures increase in the summer and decrease in other parts of the year. The bottom of the active layer is isothermal but the depth of this layer is changing due to the increase of ambient temperatures, and this causes the thawing of some portions of permafrost, with further environmental consequences. The importance and impact of coupled phenomena within permafrost models is of current interest. Modeling of the coupled phenomena in permafrost regions is complex, and requires careful conservative approximations across the scales ^{[10,14,15,67,68,69]}.

5.1.   Energy conservation in permafrost

We recall now the (ST) problem discussed in Section 2 for conservation of energy in any volume $\Omega$ occupied only by water component in one of two phases: liquid or solid. For any small sub-volume $\omega \subset \Omega$ centered at some $x \in \Omega$ we can calculate the water fraction $\chi(x) = \frac{|\Omega_l \cap \omega|}{|\Omega \cap \omega|}$. In equilibrium, $\chi$ it equals 1 whenever $\theta > 0$ in the entire $\omega$. On the other hand, if $\theta < 0$ on $\omega$, then $\chi(x) = 0$. In the case $\theta = 0$, we have $0 \leq \chi(x) \leq 1$, and $\chi$ can be considered as an independent thermodynamic variable at constant volume; see ^[27]. In other words, the water fraction can be considered a pointwise or a volumetric quantity, and in (ST) problem we assumed (2.3) and $\chi = \chi(\theta)$.

The model for conservation of energy in permafrost must extend this formulation to account for the presence of rock grains which do not change phase. We assume here that the soil rock grains have a constant heat capacity $c_r$ and a constant thermal conductivity $k_r$.

The presence of rock grains has several consequences. The first consequence is that in the energy balance we have to account for the rock as a separate material; we discuss this in Section 5.1.2. Second, the presence of rocks affect the local energy landscape at the fluid-rock interfaces; in particular, it causes depression of freezing temperatures in small pores, as well as premelting, the presence of a thin film of water around rock grains ^[70,71]. Both phenomena have significant effects on the qualitative behavior of phase transitions in permafrost.

In modeling, one must consider the scale at which we wish to consider the phenomena. At the pore-scale of $\mathrm{[{mm}]}$ to $\mathrm{[{nm}]}$ scale, the rock grains and water occupied domains should be treated as separate materials such as in Example 4.3. In practice, modeling large scale changes in permafrost in response to the temperature in the environment must occur at larger scale such as that of $\mathrm{[{m}]}$, i.e., at the so-called Darcy scale. Typically, models at Darcy scale take advantage of constitutive relationships measured experimentally in a laboratory. Thanks to modern computational science the pore-scale modeling can be connected to Darcy scale such as in our work and in particular ^{[18,19,20,21]}, but a thorough discussion is outside our present scope.

5.1.1.   Permafrost as a porous medium

We introduce notation which helps to explain the difference and connections between Stefan problem and permafrost models.

As mentioned earlier, porous medium is made of rock grains and non-rock "void space" occupied by fluids such as water and air. In this paper we consider only the water component. The rock grains occupy a fixed portion $\Omega_r$ of $\Omega$, and the water component in $\Omega_w$ occupies the remainder so that $\overline{\Omega} = \overline{\Omega_w} \cup \overline{\Omega_r}$. The void (non-rock) proportion $\eta = \frac{|\Omega_w|}{|\Omega|}$ is called porosity, and $0 < \eta\leq 1$. The water component can be in liquid or solid phases so that $\overline{\Omega_w} = \overline{\Omega_l} \cup \overline{\Omega_s}$, and we have $\chi = \tfrac{|\Omega_l|}{|\Omega|} = \tfrac{|\Omega_l|}{|\Omega_w|} \tfrac{|\Omega_w|}{|\Omega|} = \eta \chi_w, \text{ with } \chi_w = \tfrac{|\Omega_l|}{|\Omega_w|}$

The quantity $\chi_w$ is called "unfrozen water content" in permafrost and is determined experimentally for a particular soil type depending on the temperature.

5.1.2.   Energy balance in permafrost

The presence of rock grains influences the energy balance. In permafrost the balance of energy must account for the energy content in $\Omega_r$ and $\Omega_w$, thus the heat capacity is a weighted fraction of that in rock grains and in fluid space,

which can be also written, after rearranging, as

where $c_u$ is the (constant) heat capacity of the "unfrozen soil" and $c_f$ is the (constant) heat capacity of the "frozen soil". In the end, we get ^[8]

Remark 5.1. We can now compare the formulas for $w$ in the classical Stefan problem (2.5) and in the permafrost model (5.4). The former sees the change between "solid" and "liquid", but the latter (5.4) presents the phase change problem between the "frozen soil" and the "unfrozen soil", where the amount of each is controlled by the unfrozen water content $\chi_w$.

5.1.3.   Experimental models

One of important features of permafrost is the presence of unfrozen water at low temperatures i.e. $\chi(x, t) > 0$ even when $\theta(x, t) < \theta_{fr}$. This phenomenon is not fully explained, and is accompanied by the depression of the freezing temperatures in small pores. The permafrost models take advantage of the empirical data which fits one of the parametric relationships for $\chi_w(\theta)$ such as (5.1), where $\chi_w$ is the unfrozen water content determined experimentally and dependent on soil type. We follow a formulation based on ^[14]: here $\chi_w(\theta)$ is parametrized with some soil-type dependent parameters $b > 0$, as well as with $\chi_{res} \in (0, 1) \mathrm{[{-}]}$ which denotes the residual unfrozen water content at some really low reference temperature

Now $\theta_{fr}$ is the threshold temperature called freezing point depression such that for $\theta > \theta_{fr}$, only liquid water is present. Unlike in bulk water, typically $\theta_{fr} < 0$. Parameter $b \mathrm{[{1/^\circ C}]}$ depends on the soil type. For example, for coarse-grained soils such as sand, the value of $b$ is large, but for fine-grained soils such as clay $b$ is small. For a particular soil type, we assume $b$ to be a constant.

Remark 5.2. A variety of algebraic models for $\chi_w (\cdot; \theta)$ other than (5.5) are given in applications literature; see Table 11 for expressions adapted so that they fit (5.1). The models are qualitatively similar to each other. For a particular expression for $\chi_w(\theta)$ plugged in (5.4) they produce $w = \alpha^P(\theta)$ which is a monotone increasing injective Lipschitz function. In particular, with (5.5) we get, after some rearranging

For comparison, we plot $\alpha^P$ corresponding to the the different models in Figure 10. Here we use the parameters ^[16] $c_r = 0.9$, $k_r = 0.0195$, $\theta_{fr} = -0.5, \chi_{res} = 0.2035$ and $\eta = 0.43$ along with the thermal properties of water as given in Table 2.

We see that each $\alpha^P$ can be seen as an approximation to the monotone graph $\alpha ^{ST}$, and each is a strictly monotone smooth increasing function of $\theta$, differentiable everywhere except at $\theta_{fr}$ (as we stated in Assumption 1.3 for $\alpha^P$).

5.1.4.   Thermal conductivity in permafrost

To complete the permafrost model, we need to define the thermal conductivity of the porous medium which is made of $\Omega_r$ and $\Omega_w$, with the latter partitioned between $\Omega_l$ and $\Omega_s$.

It is well known that, unlike capacity given in (5.3), conductivity $k$ of composite materials depends not just on the values of $k_r, k_l, k_s$, as well as on the fractions $\eta, \chi_w$, but also on the geometry of how the phases are arranged. Still, some authors consider straightforward weighting with volumetric fractions as in (5.3) which gives, e.g., in ^[16]

where $k_u = \eta k_l + (1-\eta)k_r$ is the thermal conductivity of the "unfrozen soil" and $k_f = \eta k_s + (1-\eta)k_r$ is the thermal conductivity of the "frozen soil". While (5.7) is a good first order approximation, it does not take into account the geometry of the rock grains; more accurate expressions based on data are considered in ^{[10,14,15] [41]}(.) Other general approaches can be considered and involve upscaling or homogenization; see, e.g., ^[18,74]. More work is needed on more accurate expression for $k(x, t)$.

For the needs of this paper we use (5.7), combined with some selected model for $\chi_w = \chi_w(\theta(x, t))$. This completes the permafrost model, once boundary and initial conditions are specified. To construct these for realistic scenarios, care is needed. The former depend on environmental conditions, while the latter must be found carefully since thermal equilibrium might not be always realistic to assume.

5.2.   Approximation of permafrost model with P0-P0

We recall now the P0-P0 (equivalent to CCFD) approximation to (1.1) with (1.2) given in Section 3. The function $\alpha^P$ described in Section 5.1.3 features a piecewise smooth nonlinearity, thus fits the general class of problems that Section 3 applies to, and we expect that the scheme P0-P0 will work well.

In fact, the fluxes $q$ permafrost problem feature continuous normal components since there is no jump prescribed. Therefore, we expect that $\theta$ is approximated to at least to first order accuracy, similarly to what we encountered for the (harder) (ST) problem.

To put our P0-P0 approach in perspective, we first briefly review relevant literature; see Section 5.2.1. Then we follow up with the test of convergence of P0-P0 in Section 5.2.2 along with examples in Section 5.2.3.

5.2.1.   Approaches in literature

The work ^[6] uses a variational formulation, implicitly discretized in time, to generate a set of nonlinear algebraic equations which are solved using the Newton's method; they test their algorithm on $2D$ examples; see also discussion in ^[11]. Next, ^[8] use a fixed grid finite element method further employing Picard's method to deal with the consequential nonlinearity in the mass and stiffness matrix. In turn, ^[9] use a node-centered finite difference scheme and solve the nonlinear equations using Newton's methods, and ^[15] implement their finite element model within the commercially available solver ABAQUS.

We adopt the fully discrete formulation for P0-P0 as given in Section 3 and extended to heterogeneous media in Section 4.

5.2.2.   Convergence of P0-P0 scheme for permafrost model

Example 5.1. For convergence studies, we choose an example based on ^[26]. We consider the scenario as in Example 3.2, but with $\alpha^P(\cdot)$ instead of $\alpha ^{ST}$, and with the following initial and boundary conditions

The soil properties are chosen to be $\eta = 0.43, \ b = 0.9$. We run the simulation over a time period of $(0, 50000)\mathrm{[{s}]}$. Since the exact solution is unknown, the convergence rates are calculated using a fine grid solution $(\theta^n_{h_{fine}}, w^n_{h_{fine}})_n$ computed on a mesh with $M = 4000$ cells and time step $\tau = 25 \mathrm{[{s}]}$.

The results are given in Table 12. We see a modest improvement in the present case with $\alpha^P$ over the rates obtained for $\alpha ^{ST}$ in the Stefan problem, with order robustly $\approx 1$ for $\theta$ and $\approx 0.5$ for $w$. Further, we also observe that the order of convergence seems independent of small variations in the soil type, or in the parameter $b$ in (5.5). These results are for $\tau \approx O(h)$ as in (ST) problem.

Next we attempt $\tau \approx O(h^2)$ which is optimal in linear and mildly nonlinear parabolic problems. We attempt the latter since the graph $\alpha^P$ is much smoother than any of $\alpha ^{ST_{\epsilon}}$, hence, we hope to have better than first order convergence. However, there is only mild improvement in the convergence rate when using $\tau \approx O(h^2)$ compared to $\tau = O(h)$; specifically, the order of convergence is roughly $\approx 1.3$–$1.5$. In the end, this improvement may or may not justify the extra computational effort of using $\tau = O(h^2)$.

5.2.3.   Simulation of realistic examples

Next we apply our P0-P0 algorithm to physical examples pertaining to permafrost thawing. The goal of these examples is to test the robustness of our scheme and to illustrate the modeling aspects of permafrost. Since most of the interesting dynamics in permafrost occurs due to the varying surface boundary conditions and along the depth, we confine ourselves to the $d = 1$ case.

We use the expression (5.5) for the unfrozen water content $\chi_w(\theta)$.

Example 5.2. Homogeneous case. Consider a small column of soil $\Omega = (0, 20) \mathrm{[{cm}]}$ with physical parameters as in Table 2 along with $\eta = 0.43, \chi_{res} = 0.1$, $b = 0.5 \mathrm{[{1/^\circ C}]}$. We use the following initial and boundary conditions

and run the simulation over a time period of $(0, 50000)\mathrm{[{s}]}$. The solution at different times is shown in Figure 11.

We see the temperature profile trending slowly towards the stationary distribution. When the simulation is run over a time period of at least $4.5$ hours, steady state is achieved in which the temperature qualitatively has an almost linear profile.

Example 5.3. Heterogeneous case. We extend Example 5.2 to a heterogeneous case. We consider $\Omega = (0, 20) \mathrm{[{cm}]}$ be composed of two different soil types: $\Omega^{fine} = (0, 15)$ and $\Omega^{coarse} = (15, 20)$. Thermal properties of water are as in Table 2, and we use $\eta = 0.43, \chi_{res} = 0.1$. The difference in the properties of coarse and fine soil is in parameter $b$ in (5.5). We choose $b_{fine} = 0.5 \mathrm{[{1/^\circ C}]}$ and $b_{coarse} = 1 \mathrm{[{1/^\circ C}]}$. We start with the initial and boundary conditions

and run the simulation over a time period of $(0, 50000)\mathrm{[{s}]}$. The solution at different times is shown in Figure 11.

The difference between Examples 5.2 and 5.3 is apparent from Figure 11. At $t \geq 25000 \mathrm{[{s}]}$ a prominent jump in enthalpy appears near $x \approx 15 \mathrm{[{cm}]}$; this effect is due to the soil heterogeneity.

Next we aim to simulate the effect of permafrost warming due to variable temperature at the top boundary, and a possible effect of climate warming.

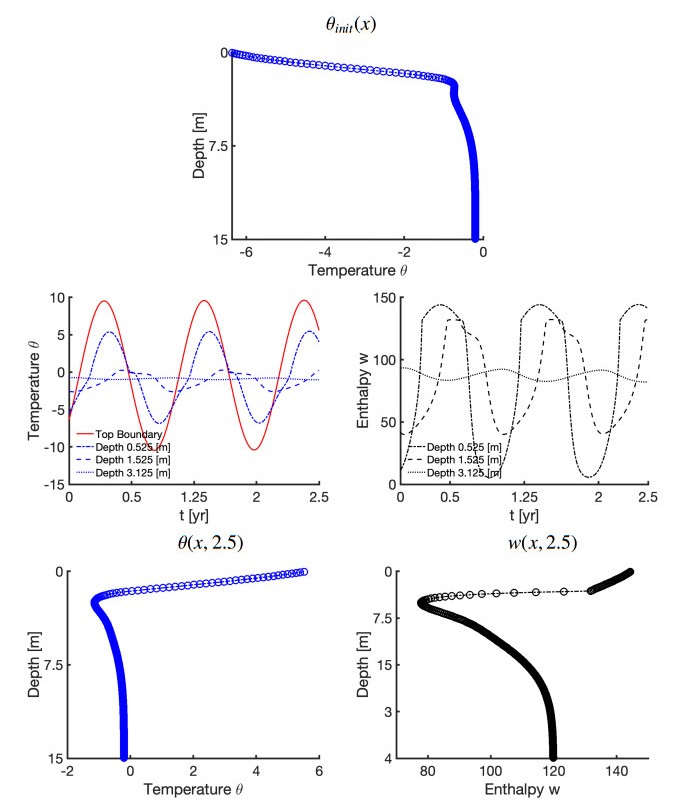
Example 5.4. Homogeneous case with time dependent boundary condition. Let $\Omega = (0, 15) \mathrm{[{m}]}$ represent a column of soil of porosity $\eta = 0.43$, with the top boundary subject to time-varying temperature boundary conditions representing typical environmental change; see, e.g., ^[41](Figures 3–5) and ^[75] where the effect of climate warming is considered. At the bottom we apply fixed Dirichlet condition representing fixed temperature below the active layer. For simulation we use thermal properties of water from Table 2, along with $\chi_{res} = 0.1$, $b = 0.5$. Our goal is to simulate the temperature and enthalpy profile during the time period of $[0, 2.5]$ years following an earlier period of time $[-10, 0]$, initiated with

We use the simulated $w(x, 0)$ (shown in the top row of Figure 12) as the initial data for the new time period $[0, 2.5]$, with

The simulation results are shown in Figure 12. The temperature at a depth $x\approx 0.5, 1.5$ and $3.5$ as a function of time is plotted along with the temperature and enthalpy at the end of $2.5$ years. We use the simulation results to get a rough estimate of the active layer thickness to be $\sim 4 \mathrm{[{m}]}$.

5.3.   Solver challenges and open questions

The P0-P0 approximation scheme and the solver behaves similarly for permafrost problem (P) as for (ST) problem. For single material problems, the model is robust and features essentially mesh independent number of iterations under reasonable time steps.

However, simulation in heterogeneous domains pose difficulties. The performance of Newton's method can be rather rugged, and is a (well-known) challenge ^[76]. For permafrost, the solver performance deteriorates in the case of highly disparate data, and/or and large time steps. Specifically, the former is an issue if there is a big difference, e.g., in the soil parameters $b$ (or $a$) in Section 5.1.

One way to overcome this challenge is to use adaptive time stepping through which the time step is reduced if Newton iteration struggles to converge. Generally, reducing the time step leads to smoother convergence of residuals to zero. For very difficult cases related to high degree of heterogeneity, we regularize the problem by introducing an artificial "intermediate" layer in the region close to the interface $\Gamma$ in which the soil parameters vary more smoothly. Such a strategy can be used to find an initial guess for Newton step, or be used as the solution for a few initial time steps.

5.4.   Summary

More work on the solver and schemes is needed, but overall we believe our P0-P0 scheme performs well for the permafrost problem (P). We see that its behavior is smoother and the challenges are somewhat milder than those for the (ST) problem, except in heterogeneous domains.

6.   Summary and future works

In this paper we consider a collection of models motivated by the applications to the phase change problems dubbed (ST), their (ST)$_{\epsilon}$ modeling approximation, and the models (P) in permafrost.

For approximation, we consider the technique well known for its conservative properties, mixed finite element method on rectangular elements. Because the solutions are expected to have low regularity, we choose to use only lowest order finite elements, with piecewise constant approximations to the scalar unknowns $(\theta, w)$ which we call P0-P0, and which are similar to finite volume or cell-centered finite difference approaches. For time discretization we employ a first order fully implicit scheme. We show that our P0-P0 approach works well for (ST) as well as (ST)$_{\epsilon}$ and (P) permafrost, and that they compare well to the P1-based approaches that were primarily formulated for (ST)$_{\epsilon}$. We extend the P0-P0 approach to heterogeneous case of multiple materials, and showed that a monolithic P0-P0 discretization we construct is robust and easy to implement. We set up theoretical framework relating to known literature results, proved several results, and point out the challenges and open questions.

More work is underway. In particular, due to the challenges we acknowledged above, rigorous convergence analysis of P0-P0 is inaccessible at this time, even if it can be inferred in the limit of that for (ST)$_{\epsilon}$. The main challenge is that that the use of $X = H_{\mathrm{div}}(\Omega)$ for the heat flux $q$ is not directly possible for (ST). At the same time, our algorithms are robust even if they do not address this formal difficulty, but require more work which we defer to the future.

On modeling side, in permafrost, or more generally, in freezing soils, there are additional micro-scale physical effects which contribute to the complex physics of phase change. These include freezing temperature depression, presence of air which acts as an insulator, configuration (geometry) of the pore space, as well as the chemical composition of liquid and mineral phases. While these are not fully explained, we aim to connect the computational models of multi-material pore-scale to the macro-scale experimental models such as those in Section 5.

For (P) models in permafrost, in the paper we neglect convection and other physical phenomena which can potentially contribute to the temperature changes such as flow and mechanical behavior; these, along with other physical and environmental effects including those of radiation, vegetation and snow cover, and more, will be studied in forthcoming paper.

7.   Appendix

7.1.   Exact solution for Example 2.1

The exact solution to (2.15) with data as in Example 2.1 is given by

where $t_1 = 44.2658 \mathrm{[{s}]}$ is when phase change begins, $t_2 = 858.5458 \mathrm{[{s}]}$ is when all the solid has changed into liquid, and $w_{init} = -1$ is the initial enthalpy.

7.2.   Auxiliary finite dimensional result

We consider a useful ODE system on $R^k$ with a matrix $A \in \mathbb{R}^{k \times k}$ and right hand side $F(t)\in \mathbb{R}^k$

We define the solutions $W(t)$ as limits of the solutions $W^n$ to the time-discrete problem

The result below will be used many times in this paper.

Lemma 7.1. Let $\alpha(\cdot)$ be maximal monotone and $A$ symmetric nonnegative definite. Then there exists a unique solution $(U^n, W^n)$ to (7.2).

Proof. We find $U^n$ as the minimizer of

where we set $\Phi_{\alpha}(U) = \sum_{i = 1}^k \phi_{\alpha}(U_i)$, with $\phi_{\alpha}(r)$ the (strictly convex) primitive of $\alpha(r)$ (i.e., $\phi_{\alpha}'(r) = \alpha(r)$, and the subgradient $\partial \Phi_{\alpha}(U) = \sum_k \phi_{\alpha}(U_i)$). The functional $J(U)$ is strictly convex due to the convexity of $U^TAU$ and strict convexity of $\Phi_{\alpha}$, and thus it has a unique minimizer $U$, and we set $U^n = U$. With known $U^n$, we find $W^n$ from $W^n+\tau AU^n = W^{n-1}+\tau F^{n}$, which follows from (7.2).

7.3.   Detailed comparison of P1-based formulations

Now we provide a detailed comparison of the P1-based formulations recalled in Section 2.4. We do so, for simplicity, for $d = 1$ and a grid covering $\Omega = [a, b]$ with $M$ cells $\omega_i = [x_{i-1/2}, x_{i+1/2}]$ with centers $x_i$ so that $\bar{\Omega} = \cup_{i = 1}^{M} \omega_i$ and $x_{\frac{1}{2}} = a, \ x_{M + \frac{1}{2}} = b$. Other results not reviewed here include grid adaptive schemes in ^[77].

We recalling that $u^n_h \in V_h$ is identified by its nodal values $(U_{j\pm 1/2^n})_j$. In turn, in P1-P0 approaches $w_h^n \in M_h$ are identified by $(W_j^n)_j$.

We denote by $\Pi_h^0 u_h^n$ the $L^2$ projection onto constants $\Pi_h^0: L^2(\Omega) \rightarrow M_h$, by $P_h^0$ the $L^2$ projection onto $V_h$, and by $P_h^1$ the Ritz projection onto $V_h$.

P1-P0 approximations: In ^[4]: one seeks $w_h^n \in M_h$ such that

Here we require $\mu \leq L_{ \beta_{\text{K}}}^{-1}$, since (7.3b) implements the Chernoff formula. Note that the advantage of (7.3) is that (7.3a) is linear in $u_h^n$. However, a consistency error arises since $\mu \neq { \beta_{\text{K}}'(W^{n-1}_j)}^{-1}$ and $u^n_h(x_j) = \tfrac{{U^n}_{j-\frac{1}{2}} + {U^n}_{j + \frac{1}{2}}}{2} \neq \beta_{\text{K}}({W}^{n}_j)$, and

Next, ^[5] are able to improve the convergence rates by modifying the scheme given by (7.3) through the use of regularization and projection. Their fully discrete regularized scheme reads ^[5]: find $u_h^n \in V_h, \ w_h^n \in M_h$ such that

where ${ \beta_{\text{K}}}_\epsilon$ is given by (7.5), essentially a Yosida approximation to $\beta_{\text{K}}$,

for some $0 < \epsilon < \frac{k_l}{c_l}$.

The work of ^[44] uses a semi-implicit scheme for phase relaxation coupled with (2.6) given by $\epsilon \frac{\partial \chi}{\partial t} + { \mathcal{H}^{-1}}(\chi) \ni u,$ They seek ${\chi_h}^n \in M_h$ as an independent variable and solve

where $(u_h^n, \psi)_h = \int_{\Omega} I_h(u_h^n \psi)$, with $I_h : C^0(\overline{\Omega}) \rightarrow V_h$ being the linear interpolator. We see that (7.6b) is equivalent to the Chernoff formula (7.3b) with $\mu = \frac{\tau}{\epsilon}$. This shows the subtle difference in the scheme by ^[5] and ^[44]: in ^[44] numerical integration $(u_h^n, \psi)_h$ is employed whereas in ^[5] the projection operator is used to obtain $(P_h^0 u_h^n, \psi)$.

Remark 7.1. (7.6b) is obtained using the discretization

To account for $u_h^{n-1}$ in (7.7) instead of $u_h^n$, the stability condition $\tau \leq \epsilon$ must be enforced ^[31].

P1-P1 fully implicit approach in ^[3] A scheme of a different flavor is explored in ^[3]. Fully implicit in time formulation of (2.6) is approximated with $u_h^n \in V_h$

This discrete systems is, in practice, similar to (7.2) except it applies to (ST) and pays considerable attention to the identification and the role of $P_{h}^0$ in this last equation. While no regularization of $\alpha$ is needed, the results are not accompanied by numerical computations. Optimal convergence rates ^[3](Theorem 2.7) apply to all models (1.2)

where $0 \leq r < \infty$ is a constant such that

In particular, for (ST) and (2.8) we have $r = 1$. This corresponds to an order of convergence $\approx 1$ when $\tau = O(h)$. However, ^[3] do not include numerical implementation details or experiments.

Other P1-P1 schemes include those in relaxation models ^[31].

7.4.   Convergence studies of P1-based and P0-P0 algorithms.

We carry out convergence analyses when the true solution $\theta, w$ is known, or when only its proxy, a fine grid solution $\theta_{h_{fine}}, w_{h_{fine}}$ is available. For time dependent problems the use of $\theta_{h_{fine}}, w_{h_{fine}}$ renders convergence order verification in some norms impractical. Therefore in this paper we only use $L^p$ norms; we also confine ourselves only to the error in scalar unknowns, deferring the discussion of the error in the fluxes to future work.

7.4.1.   Error norms

As stated in Introduction, the notation $f \in L^{\infty}(L^p)$ means $f \in L^{\infty}(0, T;L^p(\Omega))$. We denote the norms appropriately, say as $||{f}||_{{\infty, p}}$; all these have to be approximated. In particular, we distinguish the grid norms

We also use a tighter approximation than the grid norm

7.4.2.   P1-based schemes

The theoretically estimated convergence error depends, as usual, on $h, \tau$ and $\epsilon$. Of the literature we have reviewed, ^[26,31,44] provide numerical results supporting their theoretically derived convergence rates. We set up additional experiments and convergence study as a prequel to the study of our P0-P0 schemes for (ST) problem: we use analytical solutions given in ^[26,44] for $d = 1$. The theoretical convergence orders as well as those we tested are tabulated in Table 13. We compare the [P1-P0] schemes given in ^[5,44] in Examples 3.1 and 3.2, respectively; see the plots shown in Figure 13. Additionally, we mention the work in ^[4] which provides a semi-discrete scheme which we further discretize in space following ^[5]. For this reason, along with using a small regularization parameter $\epsilon$ in (7.4), the numerical solution following the formulation as in ^[4] is virtually indistinguishable from ^[5] in Example 2 and hence is not shown in Figure 13.

All together, we observe that $\theta$ is approximated well, qualitatively and quantitatively, by all the schemes. However, $w$ appears to be "smeared" near the interface and features higher errors. Of all the schemes, that in ^[5] produces the best approximation and convergence rates. The examples we show are consistent with the rates proved in ^[44]; see Table 13.

7.5.   Auxiliary properties

We recall now one especially useful and well known feature of numerical implementation of (3.6) when numerical integration is used to get the entries of matrix $\mathcal{K}$. As discussed in ^[24,49], these follow from the use of trapezoidal (T) and midpoint (M) rules $(\int_{\Omega} k^{-1}(q_h)_1 \psi_{i+1/2, j})_{TM}$ which leads to an algebraic expression involving the so-called transmissivity or transmissibility edge factor $\mathcal{T}_{i+1/2, j} = h_{y, j}k_{i+1/2, j}$, where

is the weighted scaled harmonic average of $k_{ij}$ and $k_{i+1, j}$ so that (see, e.g., ^[24](eq.(15)))

We emphasize that the use of harmonic averages leads to conservative fluxes; this is in contrast with primal formulations in which arithmetic averages are used, and fluxes are not conservative.

Next, we integrate $\int_{\Omega} \nabla \cdot \psi_{i+1/2} \theta_h$ and obtain, for the total normal flux $h_{y, j}q_h \cdot\nu \vert_{\gamma_{i+1/2, j}} = h_{y, j}q_{i+1/2, j}$ across $\gamma_{i+1/2, j}$ $\omega_{i, j}$ and the first component $(q_h)_1$ of $q_h$

The right hand side explains how the entries of matrix $\mathcal{B}^T$ arise.

A similar expression is obtained for $(q_h)_2$ and $(q_{i, j+1/2})$ using $\mathcal{T}_{i, j+1/2}^{-1}$.

The use of factors $\mathcal{T}$ allows the interpretation of (7.12) as a finite difference analogue of $q = -k\nabla \theta$. It also explains why the matrix $\mathcal{K}$ is diagonal.

Last but not least, (7.11) is done also for the second component of flux $(q_h)_2$ across $\omega_{ij}$.

Handling Dirichlet boundary conditions. The expression (7.12) is valid for the interior edges away from external boundaries and interfaces. If the edge $\gamma_{i+1/2, j}$ is on a boundary on which Dirichlet condition $\theta\vert_{\gamma_{i+1/2, j}} = \theta_*$ is prescribed with some $\theta_*$, then the analogue of (7.12) reads

The portion of the expression associated with $\theta_*$ moves to the right hand side of (3.3), but the structure of the matrix does not change.

7.6.   Linear heat equation with a jump condition

We consider the special linear case with piecewise constant coefficients of (4.1) from Example 4

7.6.1.   Stationary solution

We also consider the stationary solution $q^{stat}(x) = q(x), \theta^{stat}(x) = \theta(x)$ to (7.14) which satisfy

It is not difficult to find its analytical solution, with $q = q^{(1)} = q^{(2)} = C$ and

In particular in the special case $k_1 = 1 = k_2$, and $a = 0, b = 1, \theta_0 = 1, \theta_1 = 0, x^* = \tfrac{1}{2}$ we get

From this we have the jump $[\theta]\vert_{ x^*} = \theta^{(2)}(x^*)-\theta^{(1)}(x^*) = -\tfrac{ \rho_{R}}{1+ \rho_{R}}$ scaling linearly with $\rho_{R}$ as $\rho_{R}\downarrow 0$, unlike $O(\sqrt{ \rho_{R}})$ predicted for the evolution problem in (4.3).

Acknowledgements

This work was partially supported by the National Science Foundation DMS-1912938 and DMS-1522734, and by the NSF IRD plan 2019-21 for M. Peszynska.

This material is based upon work supported by and while serving at the National Science Foundation. Any opinion, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.

The authors would like to thank the anonymous reviewers whose remarks helped to improve the paper.

Conflict of interest

The authors declare there is no conflicts of interest.