Non-intrusive load monitoring based on low frequency active power measurements

Chinthaka Dinesh; Pramuditha Perera; Roshan Indika Godaliyadda; Mervyn Parakrama B. Ekanayake; Janaka Ekanayake; Chinthaka Dinesh; Pramuditha Perera; Roshan Indika Godaliyadda; Mervyn Parakrama B. Ekanayake; Janaka Ekanayake

doi:10.3934/energy.2016.3.414

AIMS Energy

2016, Volume 4, Issue 3: 414-443. doi: 10.3934/energy.2016.3.414

Previous Article Next Article

Research article Topical Sections

Non-intrusive load monitoring based on low frequency active power measurements

1.
Department of Electrical and Electronic Engineering, Univesity of Peradeniya, Sri Lanka
2.
Department of Electrical and Computer Engineering, Rutgers University, USA
3.
Cardiff School of Engineering, Cardiff University, UK

Received: 12 December 2015 Accepted: 21 March 2016 Published: 25 March 2016

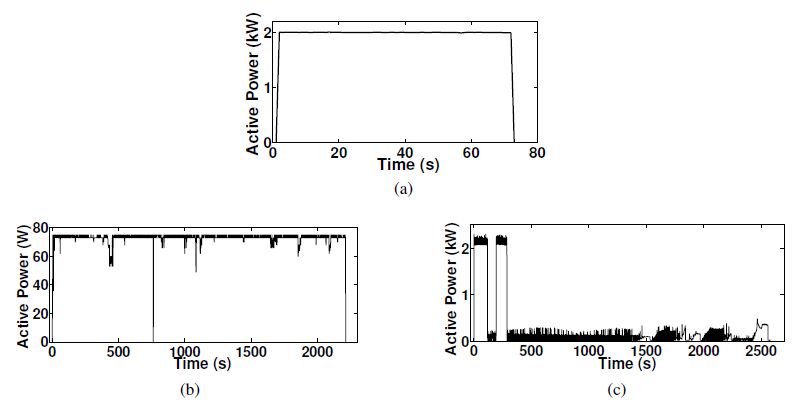
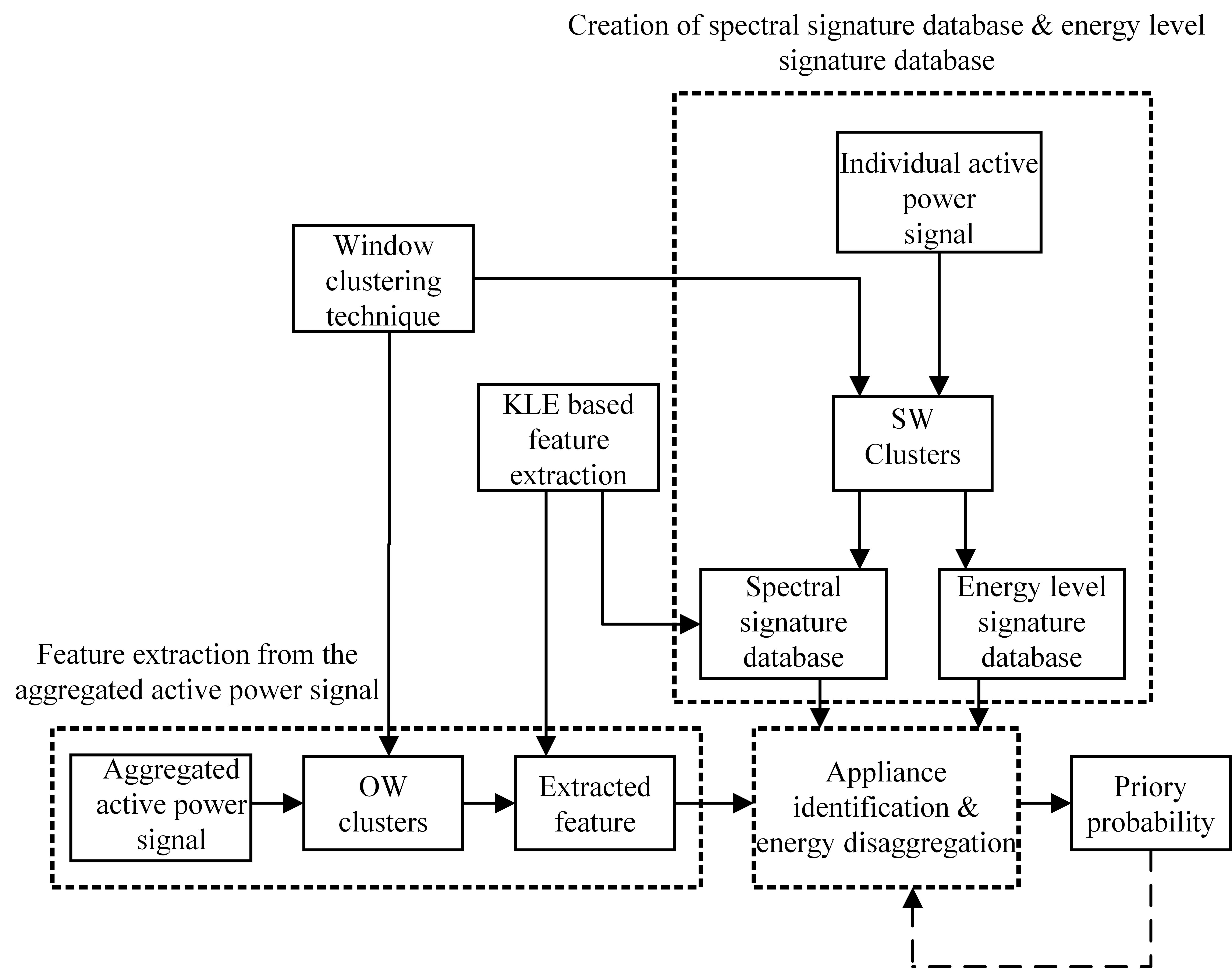
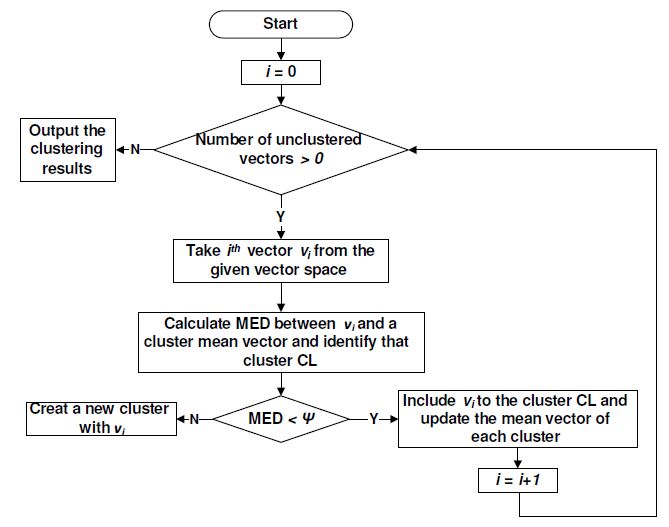
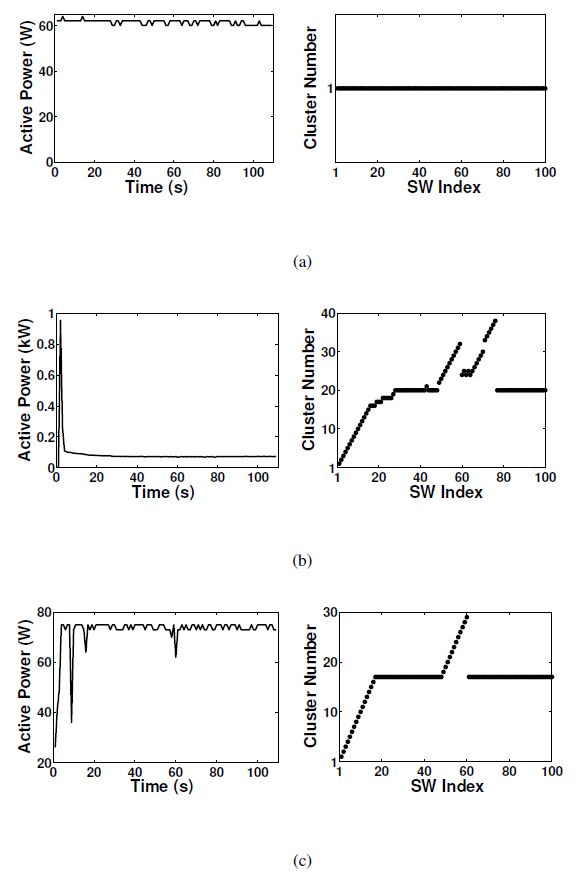
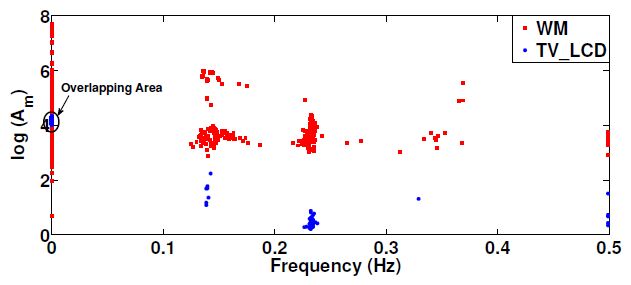
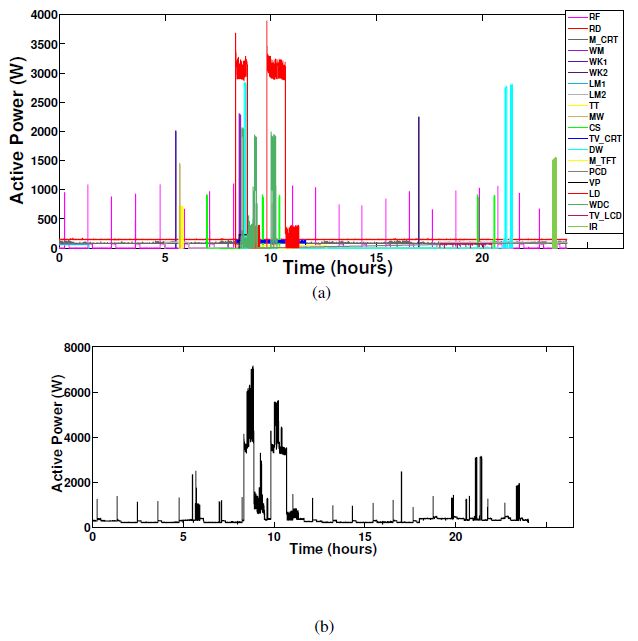
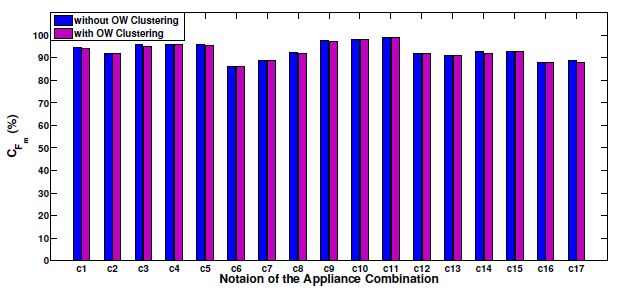
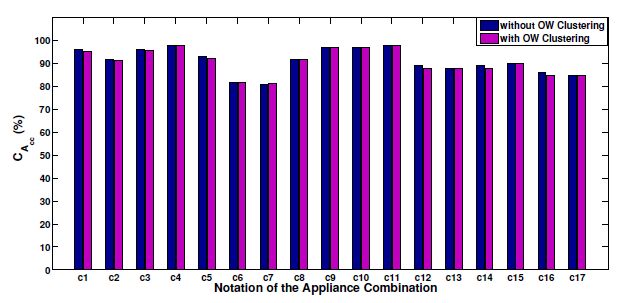
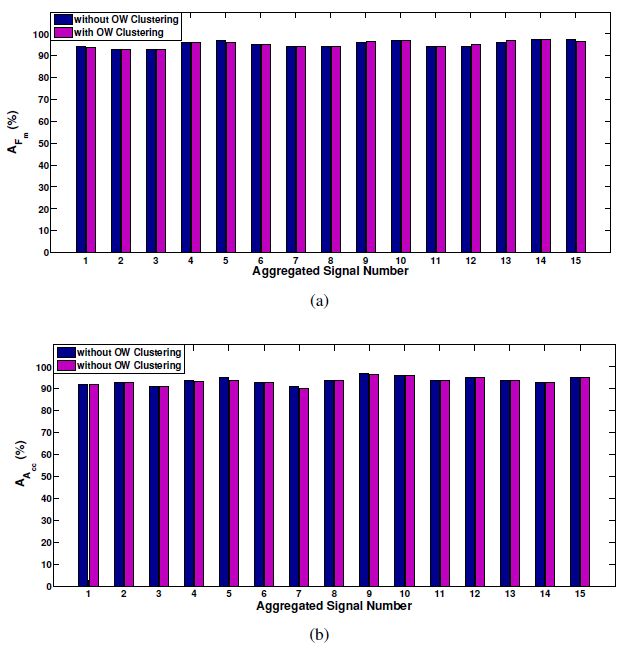
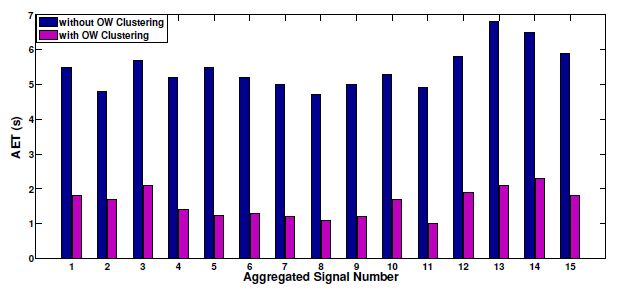
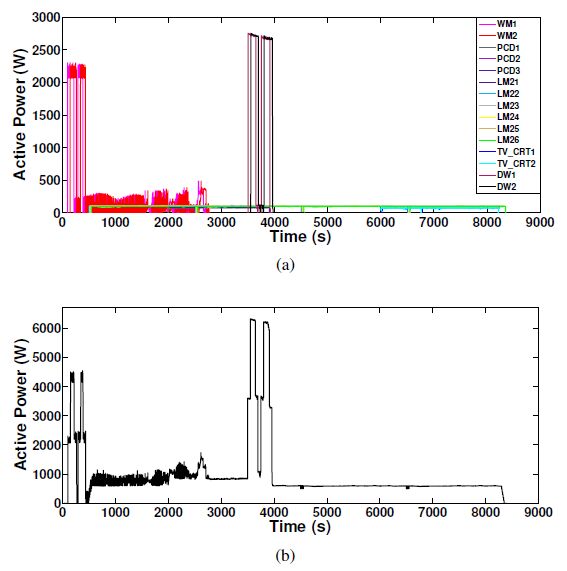
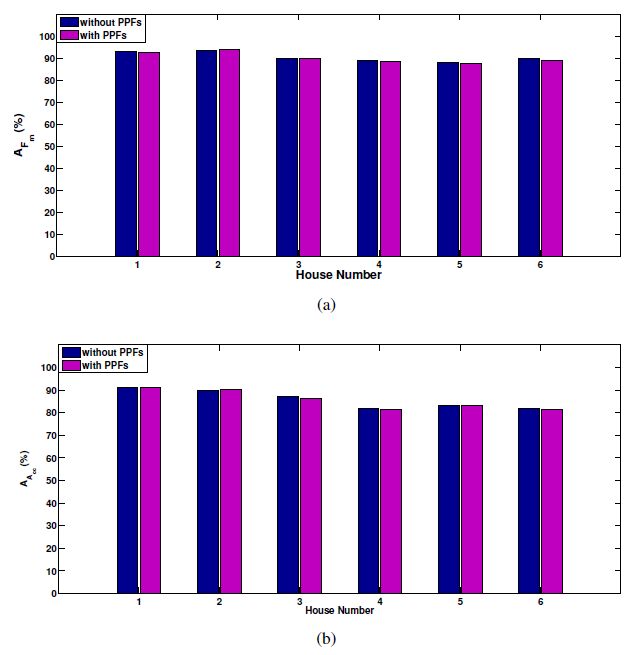
A Non-Intrusive Load Monitoring (NILM) method for residential appliances based on active power signal is presented. This method works effectively with a single active power measurement taken at a low sampling rate (1 s). The proposed method utilizes the Karhunen Loéve (KL) expansion to decompose windows of active power signals into subspace components in order to construct a unique set of features, referred to as signatures, from individual and aggregated active power signals. Similar signal windows were clustered in to one group prior to feature extraction. The clustering was performed using a modified mean shift algorithm. After the feature extraction, energy levels of signal windows and power levels of subspace components were utilized to reduce the number of possible appliance combinations and their energy level combinations. Then, the turned on appliance combination and the energy contribution from individual appliances were determined through the Maximum a Posteriori (MAP) estimation. Finally, the proposed method was modified to adaptively accommodate the usage patterns of appliances at each residence. The proposed NILM method was validated using data from two public databases: tracebase and reference energy disaggregation data set (REDD). The presented results demonstrate the ability of the proposed method to accurately identify and disaggregate individual energy contributions of turned on appliance combinations in real households. Furthermore, the results emphasise the importance of clustering and the integration of the usage behaviour pattern in the proposed NILM method for real households.

Keywords:

Citation: Chinthaka Dinesh, Pramuditha Perera, Roshan Indika Godaliyadda, Mervyn Parakrama B. Ekanayake, Janaka Ekanayake. Non-intrusive load monitoring based on low frequency active power measurements[J]. AIMS Energy, 2016, 4(3): 414-443. doi: 10.3934/energy.2016.3.414

Related Papers:

[1]	Wu Zeng, Zheng-ying Xiao . Few-shot learning based on deep learning: A survey. Mathematical Biosciences and Engineering, 2024, 21(1): 679-711. doi: 10.3934/mbe.2024029
[2]	Long Wen, Liang Gao, Yan Dong, Zheng Zhu . A negative correlation ensemble transfer learning method for fault diagnosis based on convolutional neural network. Mathematical Biosciences and Engineering, 2019, 16(5): 3311-3330. doi: 10.3934/mbe.2019165
[3]	Jinyi Tai, Chang Liu, Xing Wu, Jianwei Yang . Bearing fault diagnosis based on wavelet sparse convolutional network and acoustic emission compression signals. Mathematical Biosciences and Engineering, 2022, 19(8): 8057-8080. doi: 10.3934/mbe.2022377
[4]	Hao Chen, Shengjie Li, Xi Lu, Qiong Zhang, Jixining Zhu, Jiaxin Lu . Research on bearing fault diagnosis based on a multimodal method. Mathematical Biosciences and Engineering, 2024, 21(12): 7688-7706. doi: 10.3934/mbe.2024338
[5]	Guanghua Fu, Qingjuan Wei, Yongsheng Yang . Bearing fault diagnosis with parallel CNN and LSTM. Mathematical Biosciences and Engineering, 2024, 21(2): 2385-2406. doi: 10.3934/mbe.2024105
[6]	Yajing Zhou, Xinyu Long, Mingwei Sun, Zengqiang Chen . Bearing fault diagnosis based on Gramian angular field and DenseNet. Mathematical Biosciences and Engineering, 2022, 19(12): 14086-14101. doi: 10.3934/mbe.2022656
[7]	Qiushi Wang, Zhicheng Sun, Yueming Zhu, Chunhe Song, Dong Li . Intelligent fault diagnosis algorithm of rolling bearing based on optimization algorithm fusion convolutional neural network. Mathematical Biosciences and Engineering, 2023, 20(11): 19963-19982. doi: 10.3934/mbe.2023884
[8]	Cong Wang, Chang Liu, Mengliang Liao, Qi Yang . An enhanced diagnosis method for weak fault features of bearing acoustic emission signal based on compressed sensing. Mathematical Biosciences and Engineering, 2021, 18(2): 1670-1688. doi: 10.3934/mbe.2021086
[9]	Xuyang Xie, Zichun Yang, Lei Zhang, Guoqing Zeng, Xuefeng Wang, Peng Zhang, Guobing Chen . An improved Autogram and MOMEDA method to detect weak compound fault in rolling bearings. Mathematical Biosciences and Engineering, 2022, 19(10): 10424-10444. doi: 10.3934/mbe.2022488
[10]	Giuseppe Ciaburro . Machine fault detection methods based on machine learning algorithms: A review. Mathematical Biosciences and Engineering, 2022, 19(11): 11453-11490. doi: 10.3934/mbe.2022534

Abstract

1. Introduction

In industrial systems, bearings are important mechanical components, and their normal operation is crucial to ensure the stability and safety of the system ^[1]. As a key mechanical component, bearing failure can seriously affect the reliable operation of the system. Under long-time operation and harsh environments, bearings are prone to failure, leading to system performance degradation and even accidents. The bearing fault detection has been facing technical difficulties such as complex signals, diverse fault modes, and weak early fault characteristics, which is a hot spot in this research field. It has been found that the probability of bearing failure is the highest among other components ^[2], and more than 41% of machine failures are caused by bearings ^[3]. Therefore, bearing failure detection is important for industrial systems. Bearings in different operating conditions have different levels of vibration and noise, and these bearing vibration signals reflect the mechanical operation in real time ^[4]. In addition, the rapid development of sensor technology makes the acquisition of vibration signals more convenient. Therefore, the acquisition and analysis of vibration signals is a commonly used rolling bearing fault diagnosis method ^[5].

Traditionally, the research on bearing fault detection is mainly focused on the field of signal analysis, which is mainly to obtain the time-domain, frequency-domain and time-frequency characteristics of the vibration signals, and the commonly used methods are power spectrum analysis ^[6], cepstrum analysis ^[7], envelope spectral analysis ^[8], wavelet analysis ^[9], continuous wavelet transform (CWT) ^[10], and empirical modal decomposition (EMD) ^[11]. Although they have achieved some success, these methods rely on manually designed features and have weak generalization ability, making them difficult to apply to new scenarios. Deep learning is an effective solution for this issue. Deep learning allows for layer-by-layer feature extraction through multilayer neural networks, which can automatically learn to represent features in the data ^[12,13]. This enables deep learning for fault detection in vibration signals to better capture complex features in the signals. Currently, there are many deep learning based methods, such as recurrent neural networks (RNN) ^[14], long short-term memory networks (LSTM) ^[15], convolutional neural networks (CNN) ^[16], deep ensemble learning network ^[17], multi-attention fusion residual convolutional neural network ^[18], deep convolutional variational autoencoder ^[19], etc. Through ingeniously integrating multilayer network architectures and complex data representation capabilities, these methods have significantly propelled innovation and progress in the field of fault detection and feature extraction in deep learning.

However, most of the deep learning based methods rely on a large amount of sample data for training, but in practice, this poses a challenge for fault detection due to the variation of bearing vibration information under different operating conditions and the difficulty of obtaining a large amount of sample data. Therefore, how to achieve accurate fault detection using few samples has become a hot topic. At present, small sample learning methods mainly include data augmentation based methods, meta learning based methods, transfer learning based methods, metric learning based methods, etc. Data augmentation is a method of addressing insufficient sample size by directly increasing the diversity of sample size and distribution ^{[20,21,22,23]}. Data augmentation can be combined with other methods to improve detection performance under small samples. However, due to the insufficient number of annotated samples, simply enhancing the sample and feature space for small samples can only bring limited performance improvement, making it difficult to fundamentally solve the problem of small sample object detection. Meta learning is to transfer prior knowledge from annotated source domains to new domains with few data by simulating a series of similar small sample training tasks ^[24]. It can quickly update model parameters with a small number of support set samples with only a few iterations under specific tasks. However, meta learning requires manually constructing the support set in the task and can only perform pretraining and transfer on fixed tasks. Furthermore, it usually has high computational complexity and prunes to non-convergence issues during the learning iteration process. Metric learning maps the features of potential targets and basic data to the same embedding space, then classifies them through similarity measurement ^[25]. Metric learning generally needs to solve the following three problems: class prototype representation of base classes, measurement mechanism of bounding boxes, and loss function design. Metric learning is easy to implement incremental learning because after training the model on the base class dataset, it can be directly used to detect new classes. However, when the data volume is large and the feature dimension is high, metric learning has problems such as long computation time and high memory consumption, which reduces the real-time performance of the algorithm. Transfer learning is also to transfer prior knowledge from annotated source domains to new domains with little data. Typically, transfer learning methods include fine tuning, multitask learning, domain adverse training, zero shot learning, etc. Compared with meta learning, transfer learning based methods do not require designing small samples training tasks, making them widely used. Currently, some works ^{[26,27,28,29]} have attempted to use transfer learning to address the issue of small sample fault detection. However, transfer learning still faces some challenges and difficulties, such as establishing a correspondence between the source domain and the target domain and maintaining the performance of the source domain. These methods mentioned above do not begin from fully explore the hidden information of the data itself; therefore, this paper aims to solve the problem of fewer samples in bearing fault detection by using the characteristics of the finite original signal itself to improve the efficiency and performance of small-sample learning.

To overcome the above issues, this paper proposes a few shot bearing fault detection methods. The main contributions of this paper include:

1) A bearing fault detection model using multidimensional convolution and attention is proposed, which adapts to few-sample conditions via a tailored network structure.

2) A data conversion module is designed to form multichannels by combining various data preprocessing methods, which effectively retains key edge information and fully utilizes data information.

3) A feature extraction module is designed, which combines self-attention mechanism with multi-scale CNNs, enabling a more comprehensive capture of data features and an improved performance of the proposed method.

4) A sample similarity measurement module is designed, which maps features to a measurement space for similarity assessment and effectively distinguishes intrinsic data differences to enhance the network's ability to measure sample similarity.

The rest of the paper is as follows. Section 2 describes the related work, Section 3 describes the framework of the proposed method and the details of each modular part, Section 4 gives the experimental results, and Section 5 gives the conclusion.

2. Related work

Bearing fault detection is a typical classification and anomaly detection problem, often using the vibration signal to determine its operating state. The key problem of bearing fault detection is how to accurately extract features from the sensor data and design an effective model. Meanwhile, it also needs to consider the adaptability and robustness in the actual working conditions.

2.1. Bearing fault detection methods based on traditional methods

Traditional bearing fault detection methods mainly rely on characterizing the signal in the time, frequency, and time-frequency, domains to extract features, and using classifiers to discriminate different fault types. Li et al.^[30] effectively extracted the characteristic frequencies of inner and outer ring faults by proposing an adaptive morphological update to enhance the wavelet transform. Fu et al. ^[31] considered the nonlinear non-Gaussian non-smooth features of the signal, and used ensemble empirical mode decomposition (EEMD) for decomposition of the original signal. This method extracts the root mean square value and power spectrum center of mass features as inputs and uses the optimized Elman AdaBoost model for classification and identification of bearing faults. Zheng et al. ^[32] proposed an adaptive power spectrum Fourier decomposition method to solve the problems of too many components and cross-mixing in Fourier decomposition. This method works by automatically searching the intervals of each component in the power spectrum of the original signal and decomposing the signal into multiple single components. The fault feature contained in these single components can be used to diagnose bearing faults. Konar and Chattopadhyay ^[10] considered the unsuitability of Fourier analysis for analyzing nonstationary and transient signals and proposed the use of CWT for feature extraction, then input the features into support vector machines (SVMs) to detect the bearing faults in induction motors. These methods based on signal analysis have been widely used; however, they suffered from the limitations of relying on expertise and a prior experience, as well as the need to manually design the feature extraction.

2.2. Deep learning based bearing fault detection method

With the continuous development and improvement of deep learning technology, deep learning-based bearing fault detection methods play a more important role in future industrial applications. Deep learning-based methods can learn complex feature representations from large amounts of raw sensor data without relying on expertise and manual feature engineering to address bearing fault detection. Deep learning has been applied in emerging areas of industry such as state feature extraction methods using similarity to monitor the propagation process of gear surface wear ^[33] and using digital twins to solve the problem of monitoring and evaluating surface wear in industrial gear systems ^[34]; these studies provide more possibilities for deep learning in industrial applications. In addition, to address the needs of bearing fault detection, Ni et al. ^[35] proposed a deep learning network structure, pulse-Coupled integrated residual network (PIResNet), to solve the problem of fault diagnosis of rolling bearings under different operating conditions, using the method of deep learning of physical information. Peng et al. ^[36] proposed a deeper one-dimensional convolutional neural network (Der-1DCNN) deep convolutional neural network method based on 1D residual blocks to address the needs of high-speed train bearings for fault detection in strong noise environments and variable load conditions. The one-dimensional convolutional approach can capture local temporal features in the signals, but it is unable to capture long-term dependencies due to the limited coverage of convolutional kernels. Peng et al. ^[37] converted one-dimensional time series signals into two-dimensional image signals as inputs to a two-dimensional convolutional neural network (2D-CNN) model through a linear mapping for bearing fault identification and classification. However, this method does not take into account the problem of incoherent edge information in each row in the 2D convolution. 2D convolution can enable the model to capture the periodic changes on different time scales in the data at the same time, but its sensory field is fixed, which may not be able to flexibly adapt to the dependencies of different time spans. Yu et al. ^[15] proposed a hierarchical algorithm based on stacked LSTM networks for bearing fault diagnosis, which directly takes the raw timing signals as inputs and extracts the features automatically. LSTM can maintain and update the information in long sequences by the design of the gating structure and the memory cells to deal with the long-term temporal relationships. However, due to the fixed length of the memory cells, it is often only able to capture local dependencies rather than global dependencies of the entire sequence. Some works have proposed combining the above methods with each other. Combining the above methods can take advantage of their respective strengths to improve the performance of the model in feature extraction. For example, Wang et al. ^[38] automatically learned the features of the signal at different scales by combining two channels, 1D CNN and 2D CNN, and the network can learn the local correlation between neighboring and non-neighboring intervals of the periodic signal. Khorram et al. ^[39] proposed an end-to-end 1D CNN+LSTM network architecture that considers both local and global features of time series.

2.3. Solutions for few samples

Although deep learning based methods have achieved great success, most of these methods rely on a large amount of data for training and optimization. However, most of the data is normal with only a small proportion of faulty data, which is a typical few-sample problem. Therefore, some works have proposed solutions to the few-sample problem. Liu et al. ^[20] used a generative adversarial networks (GAN) to construct a generator to obtain reconstructed residuals and enhance the feature extraction capability of the recognizer through an adversarial mechanism. A LSTM based an Autoencode framework is established to reduce the dimensionality of the original sensing data and extract critical time fault features. Yang et al. ^[21] used a conditional generative adversarial network to learn the distribution of the original 1D data, generated new sample data to expand the sample size, and used 2D-CNN to extract image features and classify bearing fault types. Li et al. ^[29] used a transfer learning approach utilizing CNNs and multilayer perceptrons (MLPs) as base models, with some of the base models transferred to the target domain for fine-tuning. The above methods for a few samples provide some solutions, but they usually require a large amount of non-primitive data to train and optimize the model. GAN-based methods still require sufficient data to train a stable generator, with limitations such as the quality of generated samples being difficult to assess, and discrepancies between expanded and real data. Transferring-based methods require both source and target domains. As a result, lots of works are needed to ensure effective knowledge transfer between source and target domains. In the case of limited data volume, these methods may not achieve the expected performance.

3. The proposed method

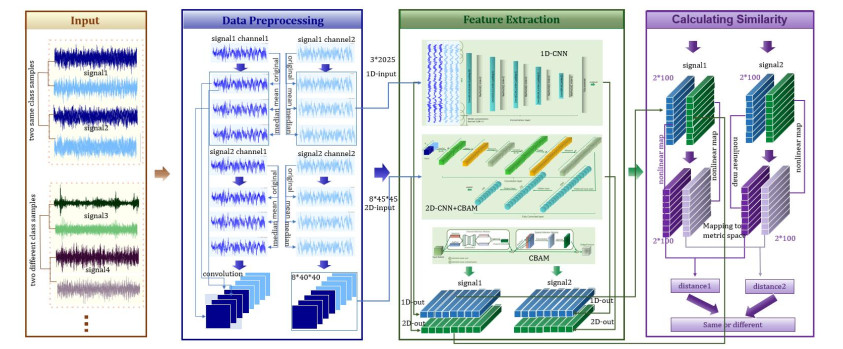
In this paper, a multichannel multidimensional bearing fault detection method is proposed, and the main architecture of the proposed model is shown in Figure 1, where multiple channels are generated by preprocessing the input data through the preprocessing block, then the processed data is input into the model. After the feature extraction block consisting of the multidimensional convolution and the attention mechanism, the extracted feature vectors are passed through the similarity measure block to measure the similarity between the two samples, then the probability that whether two samples belong to the same category is output. The data preprocessing block converts the data into multiple channels through median filtering, mean filtering, and convolution operations, which can retain key edge information and make full use of the information in the data. The feature extraction block captures the data features more comprehensively through multidimensional convolution with hybrid attention mechanism. The similarity metric block maps the extracted feature vectors to the space of the metric through a nonlinear method, then calculates the similarity between the samples. The ability to model the nonlinear relationship between two samples can be improved through the nonlinear mapping, which in turn improves the accuracy of measuring the similarity between samples. The rest of this section describes the data preprocessing, feature extraction, and similarity measure blocks in detail.

Figure 1. Overall model architecture.

DownLoad: Full-Size Img PowerPoint

3.1. Multichannel data preprocessing

For faulty bearings, abrupt changes in the bearing signal amplitude occur, as the rolling element passes over the faulty region of the bearing. These sudden changes would disturb the overall distribution of the signal and, therefore, can be used as important clues for detecting faulty bearings. In order to fully explore and utilize the information contained in the signal, additional channels processed by median filtering and mean filtering are introduced to the original signal. Adding multiple channels can provide more information to the CNN. In addition, we introduce using 1D convolution as a channel in the process of 2D data conversion. This multichannel fusion preprocessing strategy aims to enhance the model's ability to identify meaningful patterns in the signal while reducing the interference of noise on the analysis results, thus improving the accuracy and reliability of the subsequent analysis. The overall result of this section is shown in the Figure 2.

Figure 2. Visual results of multichannel data processing.

DownLoad: Full-Size Img PowerPoint

3.1.1. Preprocessing of 1D data

Median filtering aims to suppress extreme values and impulse noise, while mean filtering helps to smooth the signal and reduce random fluctuations. Considering the limitations of the subsequent 2D-CNN, the original signal is cropped to the size of $ N^2 $, the channels processed by median filtering and mean filtering are additionally introduced on top of the original signal, and the combination of the original data, and the filtered data can provide more information.

The input original signal is $ X_{i} $, and the output of the median filter with a window number of $ 2m+1 $ at the $ t $-th data is:

$\begin{equation} X_{\text {imedian }}(t) = \operatorname{Median}\left\{X_i(t-m), \ldots, X_i(t), \ldots X_i(t+m)\right\} \end{equation}$ $

(3.1)

where Median{} denotes the median of all samples taken within the window of processed data at this time. The input original signal is $ X_i $, and the output of the mean filter with a window of $ 2n+1 $ at the $ t $-th data is:

$\begin{equation} X_{\text {imean }}(t) = \operatorname{Mean}\left\{X_i(t-n), \ldots, X_i(t), \ldots X_i(t+n)\right\} \end{equation}$ $

(3.2)

where Med{} denotes the mean of all samples taken within the window of processed data at this time.

The output after data preprocessing is:

$\begin{equation} X_{i\_1{ }}{ }^{\prime} = \left[X_i, X_{\text {imean }}, X_{\text {imedian }}\right] \end{equation}$ $

(3.3)

3.1.2. Converting 1D data to 2D data

In order to make the edge information more coherent for the process of 2D data conversion, we introduced 1D convolution as another processing channel on the basis of the above processing method. To begin, the one-dimensional original data $ X_{i} $ is subjected to the convolution operation with kernel $ K $. The result after convolution is:

$\begin{equation} X_{\text {iconv }} = K \otimes X_i \end{equation}$ $

(3.4)

where $ \otimes $ is the convolution operation.

We map the signal from 0 to 255,

$\begin{equation} \left\{ \begin{aligned} & X_i{ }^{\prime} = g\left(\frac{X_i(c)-X_{i\_{ }min} (c)}{X_{i\_{ }max }(c)-X_{i \_{ }min }(c)}\right) \times 255 \\ & X_{\text {imean }}{ }^{\prime} = g\left(\frac{X_{\text {imean}}(c)-X_{\text {imean}\_{ }\text{min }}(c)}{X_{\text {imean}\_{ }\text{max}}(c)-X_{\text {imean}\_{ }\text{min }}(c)}\right) \times 255 \\ & X_{\text {imedian }}{ }^{\prime} = g\left(\frac{X_{\text {imedian }}(c)-X_{\text {imedian}\_{ }\text{min }}(c)}{X_{\text {imedian}\_{ }\text{max}}(c)-X_{\text {imedian}\_{ }\text{min }}(c)}\right) \times 255 \\ & X_{\text {iconv}}{ }^{\prime} = g\left(\frac{X_{\text {iconv}}(c)-X_{\text {iconv}\_{ }\text{min }}(c)}{X_{\text {iconv}\_{ }\text{max}}(c)-X_{\text {iconv}\_{ }\text{min }}(c)}\right) \times 255 \end{aligned} \right. \end{equation}$ $

(3.5)

where g() means rounding the normalized signal value.

The result of the convolution is added to $ X_{i\_1}{ }^{\prime} $ as the channel, which becomes $ X_{i\_2} $.

$\begin{equation} X_{i\_2{ }}{ }^{\prime} = \left[X_i{ }^{\prime}, X_{\text {imean }}{ }^{\prime}, X_{\text {imedian }}{ }^{\prime}, X_{\text {iconv }}{ }^{\prime}\right] \end{equation}$ $

(3.6)

Then the one-dimensional vector $ X_{i\_2} $ is converted into the desired $ 4\times N \times N $ matrix $ X_{i\_2}{}^{\prime} $, denoted as:

$\begin{equation} \left[\begin{array}{cccc} X_{i_{-} 2}{ }^{\prime}(c) & X_{i_2{ }^{\prime}}{ }^{\prime}(c+1) & \cdots & X_{i_{-} 2}{ }^{\prime}(c+N-1) \\ X_{i_{-} 2^{\prime}}{ }^{\prime}(c+N) & X_{i_{-} 2}{ }^{\prime}(c+N+1) & \cdots & X_{i_{-} 2}{ }^{\prime}(c+2 N-1) \\ \vdots & \vdots & \ddots & \vdots \\ X_{i_{-}{ }^{\prime}}{ }^{\prime}\left(c+N^2-N\right) & \cdots & \cdots & X_{i_2 2^{\prime}}\left(c+N^2-1\right) \end{array}\right] \end{equation}$ $

(3.7)

3.2. Multidimensional convolutional and attentions feature extraction block

In this study, a feature extraction block incorporating 1D-CNN, 2D-CNN, and a convolutional block attention module (CBAM) is proposed for bearing fault detection. The block aims to make full use of the feature information in the bearing vibration signals, which can capture the data features more comprehensively and improve the feature extraction capability and model performance.

3.2.1. 1D feature extraction

The 1D convolutional kernel moves along the time axis to capture the local temporal dependencies within the signal. The 1D-CNN utilizes the model in wavelet decomposition CNN (WDCNN) to extract 1D features from the input vibration signals. This model effectively captures the input vibration signals by employing wide convolutional layers and multistage convolutional layers. The use of multilayer convolutional kernels enables the network to delve deeper and extract a well-represented model structure. Through the multilayer convolutional kernels and pooling operations of the WDCNN model, the temporal features of the vibration signal can be extracted more deeply, resulting in a stronger feature representation. The structure of the WDCNN model is shown in Figure 3:

Figure 3. WDCNN structure.

DownLoad: Full-Size Img PowerPoint

3.2.2. 2D feature extraction

The main structure of 2D feature extraction is designed as shown in Figure 4, which consists of a series of convolutional layers, a CBAM module, and a fully connected layer. 2D-CNN enables the model to capture both spatial information and local features in the data with attention to periodic variations on different time scales. CBAM is introduced to operate channel attention and spatial attention on the features, which can selectively enhance or suppress the channel and spatial information in the feature map to extract more discriminative features, thus improving the feature extraction capability.

Figure 4. 2D feature extraction section.

DownLoad: Full-Size Img PowerPoint

Figure 5. CBAM module.

DownLoad: Full-Size Img PowerPoint

In this block, CBAM is an attention mechanism module that combines the channel attention module (CAM) and the spatial attention module (SAM). CAM enhances the network's representation in the channel dimension by adaptivly learning the weights of each channel and fusing the important ones with weights. SAM utilizes the correlation between any two point features to mutually enhance the representation of their respective features, and, therefore, focuses more on spatial location features. CBAM first calculates the importance of each channel through CAM, then applies the channel attention weights to the feature map. Subsequently, the importance of each location is calculated by SAM to obtain the feature map, which captures the global dependency of features. The CBAM module is introduced to improve the model representation by focusing on the important parts of the input feature map, capturing the important features in the data, and improving the feature extraction capability and model performance.

The entire network structure consists of two convolutional layers, two CBAM modules, two max-pooling layers, and two fully connected layers. Each convolutional layer is followed by a CBAM module, and a max-pooling layer is used after each CBAM, followed by two fully connected layers. The final length of the output sequences is kept as the same length of the outputs after 1D feature extraction.

3.3. Measuring sample similarity based on nonlinear mapping

Sample similarity measurement is the core issue of fault detection. As a typical few-shot method, siamese networks measure the similarity of two samples by calculating the $ L1 $ or $ L2 $ distance of the eigenvectors of them. However, because the bearing vibration signal has the characteristics of periodicity, multifrequency, nonlinearity and randomness, the direct $ L1 $ or $ L2 $ distance to the feature vector cannot effectively measure the similarity between samples. Metric learning is a solution for the above issue, which maps samples into the same embedding space and then calculates their similarity. Inspired by metric learning, this paper proposes a similarity measurement method mapping to the metric space and then calculates the $ L1 $ distance as shown in Eq (3.9).

$\begin{equation} f(x_{i}) = \frac{1}{1+e^{-x_{i}}} \end{equation}$ $

(3.8)

$\begin{equation} D\left(\mathrm{x}_{\mathrm{i}}, \mathrm{x}_{\mathrm{i}+1}\right) = \sum\left|f\left(\mathrm{x}_{\mathrm{i}}\right)-f\left(\mathrm{x}_{\mathrm{i}+1}\right)\right| \end{equation}$ $

(3.9)

First of all, the feature vector output after feature extraction is mapped nonlinearly. We use the sigmoid activation function, which restricts the range of values of the feature vector between 0 and 1, normalizes the range of values of the features, and makes the features more comparable. Compared with the direct $ L1 $ distance to the feature vectors, the method of using the sigmoid activation function mapping and $ L1 $ distance calculation can more accurately measure the similarity between the samples, which improves the accuracy and stability of the similarity calculation.

The output is obtained by Eq (3.10), which represents the probability that the two input samples are the same:

$\begin{equation} P\left(\mathrm{x}_{\mathrm{i}}, \mathrm{x}_{\mathrm{i}+1}\right) = f\left(\mathrm{FC}\left(\mathrm{D}\left(\mathrm{x}_{\mathrm{i}}, \mathrm{x}_{\mathrm{i}+1}\right)\right)\right) \end{equation}$ $

(3.10)

where FC is the fully connected layer.

4. Experiment

4.1. Experimental setup and data description

The code for the paper was implemented on a server equipped with two RTX4090Ti GPUs. The bearing failure dataset from Case Western Reserve University (CWRU) is used. The bearing failure dataset from CWRU contains different types of bearing failures in four states: normal operation, inner ring failure, outer ring failure, and rolling element failure. Each failure type simulates three single point failures of varying severity, with failure diameters of 0.07 inches, 0.14 inches, and 0.21 inches, for a total of 10 states ^[40]. The data contains the fan-side vibration data, the drive-side vibration data base vibration data, and the motor speed.

We compared the proposed method with SVM ^[10], WDCNN ^[40], 2DCNN ^[37], and a few-shot method ^[41]. The kernel function of SVM is a radial basis function that automatically adjusts the value of the kernel parameter according to the number of input features, with a penalty parameter of 1 and a "One-vs-One" decision function. The details of WDCNN ^[40] are shown in Table 1, and the details of the 2DCNN-based ^[37] approach are also given in Table 2. Both methods use a learning rate of 0.01, adopt cross-entropy loss as the loss function, and set epochs to 3000. The few-shot-based approach ^[41], which employs the WDCNN as the feature extraction portion of the twin network, uses the $ L1 $ distance to measure the similarity between samples. The learning rate of the method is set to 0.01, the loss function adopts the binary cross-entropy loss, and the epoch is set to 10,000. The learning rate and epoch of our method also refer to the few-shot-based approach, and we have carried out a number of experiments; we set the learning rate to 0.01, the loss function adopts the binary cross-entropy loss, and the epoch is set to 12,000.

Table 1. Parameters setting for WDCNN.

No.	Layer Type	Kernel Size/Stride	Kernel Number	Output Size (Width × Depth)
1	Convolution1	64 × 1/1 × 1	16	128 × 16
2	Pooling1	2 × 1/2 × 1	16	64 × 16
3	Convolution2	3 × 1/1 × 1	32	64 × 32
4	Pooling2	2 × 1/2 × 1	32	32 × 32
5	Convolution3	3 × 1/1 × 1	64	32 × 64
6	Pooling3	2 × 1/2 × 1	64	16 × 64
7	Convolution4	3 × 1/1 × 1	64	16 × 64
8	Pooling4	2 × 1/2 × 1	64	16 × 64
9	Convolution5	3 × 1/1 × 1	64	6 × 64
10	Pooling5	2 × 1/2 × 1	64	3 × 64
11	Fully-connected	100	1	100 × 1
12	Fully-connected	10	1	10 × 1

| Show Table

DownLoad: CSV

Table 2. Parameters setting for 2D-CNN.

No.	Layer Type	Kernel Size	Kernel Number	Output Size
1	Convolution1	7 × 7	64	44 × 44
2	Pooling1	2 × 2	64	21 × 21
3	Convolution2	5 × 5	32	18 × 18
4	Pooling2	2 × 2	32	8 × 8
5	Fully connected	10	1	10

| Show Table

DownLoad: CSV

4.2. Effect of number of training samples on performance

In the few-shot-based approach, the input is a sample pair coming from the same class or different classes, and the output is the probability of two input samples belonging to the same class. The test samples are then classified according to the most similar samples in the test set. Assuming that a test needs to be performed on $ x_{t} $, the template set $ T $ contains samples from each class:

$\begin{equation} T = \{(X_1, Y_1) \ldots \ldots(X_i, Y_i)\} \end{equation}$ $

(4.1)

$\begin{equation} M\left(x_t, \left(X_1, X_2, \ldots, X_i\right)\right) = argmax\left(P\left(x_t, x_m\right)\right), x_m\in T \end{equation}$ $

(4.2)

$\begin{equation} y_t = y_m \end{equation}$ $

(4.3)

where $ p() $ denotes the computation of similarity between two samples, and $ y_{m} $ is the label corresponding to the sample with the highest similarity.

In the training phase, all experiments were conducted ten times to ensure the fairness of the experiments. Our method is compared with four classical methods, and to illustrate the performance of the method for bearing fault detection with different sample sizes, the sample size of each group is set to 60, 90,120,200,300,480,720,900, 1200, 1500. The training convergence curves of the sample size 200 are shown in Figure 6, and accuracy of all methods are given in Figure 7. Meanwhile, multi-category receiver operating characteristic curve (ROC) curves are generated for each category by calculating the true and false positive rates, then micro-averaging and macro-averaging are performed to obtain the micro-averaged area under the ROC curve (AUC) and macro-averaged AUC as an evaluation metric for the overall performance of the classifiers. The ROC curves are shown in Figure 8, and the results of training time, testing time, and F1-score are shown in Table 3.

Figure 6. Training convergence curves.

DownLoad: Full-Size Img PowerPoint

Figure 7. Comparison of experimental results.

DownLoad: Full-Size Img PowerPoint

Figure 8. ROC with 200 samples.

DownLoad: Full-Size Img PowerPoint

Table 3. Time and F1-score.

	60-time-train	60-time-test	60-F1-score	200-time-train	200-time-test	200-F1-score
wdcnn^[40]	324.10 s	0.676 s	0.491	117.70 s	1.214 s	0.612
cnn^[37]	286.366 s	0.130 s	0.527	235.590 s	3.960 s	0.779
fewshot^[41]	431.295 s	7.777 s	0.684	460.762 s	9.507 s	0.891
ours	602.958 s	9.992 s	0.716	1021.204 s	15.901 s	0.899

| Show Table

DownLoad: CSV

Our model performs better with higher average accuracy when the training sample size is 60, 90,120,200,300,480,720,900, 1200, 1500. As the number of training samples continues to increase, the accuracy of the algorithms will actually get closer. These performance comparisons show that our model effectively improves the accuracy of bearing fault detection in a few sample situations.

It can be seen that the latter two methods, which determine whether they belong to the same class or different classes by measuring the similarity of the input signals and then classifying them, are much better than the other methods in terms of accuracy in the task under small sample conditions. Among them, our method works better than the other methods in the small sample condition of 20-1500, especially in the sample number of 300 with the baseline model than the improvement of 8.32%. This shows that our method is effective in the small sample condition and it can better capture the local features and implicit information in the small samples.

By looking at the ROC curve (in the classification task), it can be seen that our method has an ROC curve closer to the upper left corner compared to the other three methods. This trend suggests that our model is able to achieve a high true positive rate (TPR) while maintaining a low false positive rate (FPR) relative to the other methods, illustrating that our method is more accurate and effective in its ability to differentiate between different categories. In addition, the larger area under the ROC curve is also an important indicator for assessing the overall performance of the model, further emphasizing the superiority of our method. The analysis of the F1-score results shows that our method has a higher F1-score compared to the other three methods. This demonstrates that our method is more balanced and reliable in dealing with category imbalance or in scenarios with high requirements for both accuracy and coverage.

4.3. Comparative experiments in noisy environments

In this experiment, we discuss the performance in a noisy environment to simulate the variation of the operating conditions in the dataset. The signal-to-noise ratio is defined as in Equation 4.4. We train the model using the raw data provided by CWRU, with the number of samples set to 60, 90,120,200,300,480,720,900, 1200, 1500, and then test it with Gaussian white noise with an additive range of 2 dB to 10 dB.

$\begin{equation} SNR = 10{log}_{10}\left(\frac{P_s}{P_n}\right) \end{equation}$ $

(4.4)

where $ P_{s} $ is the power of the signal and $ P_{n} $ is the power of the noise.

Table 4 shows the performance comparison of three different models in various noise environments. The results show that in most cases, our models are able to identify and utilize the valid information in the data more accurately than the other models, especially when confronted with noise, and our models achieve better test scores. The negative impact of noise on model performance is highlighted by the fact that the performance of all models decreases as the noise level increases. However, our model shows a clear advantage in this challenge, especially when the sample size is increased, by being able to distinguish between signal and noise more efficiently, which improves the robustness of the model. In addition, the experimental data also shows that even in a small sample size and noisy environment, our method maintains good performance, exhibiting greater robustness and generalization ability than the other two methods.

Table 4. Test results under noise conditions.

model	num	SNR (dB)
model	num	2	4	6	8	10
	20	34.91	36.56	37.72	37.97	39.08
	40	61.49	65.97	68.30	69.44	70.39
	60	62.59	68.25	70.87	73.21	74.13
	90	71.19	76.79	80.13	81.57	82.44
	120	70.96	76.81	80.57	82.01	82.45
fewshot^[41]	200	67.02	77.09	80.12	82.84	83.93
fewshot^[41]	300	61.19	71.83	78.47	83.20	85.23
	480	70.61	80.35	85.05	88.19	89.92
	600	64.85	77.19	83.95	88.24	89.55
	720	63.31	77.61	85.45	89.91	91.89
	900	58.87	74.91	85.13	90.81	93.05
	1200	61.45	78.52	88.16	92.73	94.77
	1500	53.00	71.75	85.03	90.67	93.69
wdcnn^[40]	20	20.98	21.12	21.22	21.17	21.12
	40	32.38	37.29	41.62	44.30	44.84
	60	44.57	46.60	47.05	47.61	48.40
	90	45.31	48.44	50.48	51.23	51.71
	120	44.41	46.59	48.03	48.49	49.21
	200	62.11	67.00	69.64	71.36	72.16
	300	66.11	69.01	72.44	73.45	74.03
	480	63.88	68.03	70.10	71.50	72.40
	600	61.43	67.81	71.39	73.21	73.92
	720	63.89	69.39	71.73	72.99	73.49
	900	71.11	74.65	75.63	76.70	76.79
	1200	64.73	74.00	78.36	81.00	82.27
	1500	67.01	75.58	79.85	81.96	82.55
ours	20	39.00	39.92	40.22	40.00	41.02
	40	63.58	70.16	72.49	73.68	74.50
	60	62.76	73.36	76.85	78.17	78.74
	90	69.96	76.61	80.72	83.32	84.23
	120	63.33	73.48	80.68	84.20	85.88
	200	64.64	77.16	85.8	89.77	91.28
	300	64.99	79.41	87.49	91.89	93.52
	480	71.21	84.04	91.28	94.33	95.21
	600	61.45	79.47	88.61	92.37	94.01
	720	68.56	84.20	91.11	94.11	95.65
	900	65.87	83.05	91.01	94.96	96.41
	1200	68.60	82.20	92.09	96.23	97.95
	1500	67.21	83.59	91.57	95.94	97.23

| Show Table

DownLoad: CSV

4.4. Comparison experiment under new working conditions

In this experiment, we evaluated the test results of sample size for each training model at a sample size of 60, where the training set and the test set are different rotational speeds as shown in Table 5. Two of the working conditions are used for training, and the new working conditions are tested to evaluate the effectiveness of the detection of the emergence of the new conditions under the few sample conditions. In this experiment, we aim to evaluate the detection effectiveness of different training models in the face of new working conditions when dealing with less sample datasets.

Table 5. Dataset labels and their corresponding speeds.

Dataset	A	B	C	D
Speed	1730	1750	1772	1797

| Show Table

DownLoad: CSV

According to Figure 9, our method shows high average accuracy in all 12 different test cases. In particular, when the training sample size is 60, our method outperforms the best results of other methods by an average accuracy of 1.33%. This result emphasizes the effectiveness of our method in learning scenarios with few samples. With only 60 samples, the models are able to effectively learn and adapt to new working conditions, which demonstrates the learning efficiency and generalization ability of our method. The performance of all models improves as the sample size increases, but our method shows more significant performance gains. When the sample size is increased to 600, at this point, the average accuracy of our method is 5.48% higher than the best results of the other methods. These results indicate that our method has better performance when dealing with less sample datasets, especially when faced with new working conditions. The experimental results in this section show that our method has significant advantages in dealing with less sample datasets and in adapting to new working conditions.

Figure 9. Comparative experiment under new working conditions.

DownLoad: Full-Size Img PowerPoint

4.5. Ablation analysis of the proposed method

In Table 6, we show the results of model ablation for sample sizes of 60 and 600 to verify the contribution of each module.

Table 6. Ablation results of the proposed method.

Num	method	exp	SNR(dB)
Num	method	exp	2	4	6	8	10	None
0	Original model	60	62.76	73.36	76.85	78.17	78.74	79.29
0	Original model	600	61.45	79.47	88.61	92.37	94.01	94.95
1	No -preprocess	60	60.33	68.91	73.57	76.77	77.00	78.80
1	No -preprocess	600	60.27	75.69	83.64	87.03	88.59	90.25
2	No-1D-CNN	60	47.40	66.00	75.60	77.89	77.79	78.86
2	No-1D-CNN	600	46.45	67.68	82.26	88.41	90.02	92.33
3	No-2D-CNN+CBAM	60	62.36	68.67	70.87	73.24	75.21	76.74
3	No-2D-CNN+CBAM	600	54.65	78.35	83.95	88.24	90.34	91.84
4	No-Nonlinear mapping	60	49.13	61.17	69.27	72.11	73.51	73.99
4	No-Nonlinear mapping	600	42.57	61.77	78.47	89.21	92.56	94.49

| Show Table

DownLoad: CSV

(1) Item 1 demonstrates the effectiveness of the preprocessing block. We observe a decrease in accuracy of 0.49% and 4.7% in the noiseless condition compared to the full model, which suggests that by adding channels through our preprocessing method, more input information can be maintained in the convolution operation. This reduces information loss and provides a more comprehensive representation of features, which facilitates bearing fault detection.

(2) Items 2 and 3 demonstrate the partial effectiveness of feature extraction block. We observe that the accuracy without 1DCNN decreases by 0.43% and 2.62% compared to the full model under noiseless condition, and the accuracy without 1DCNN decreases by 2.53% and 3.11% compared to the full model, which shows that our approach of using a mixture of one-dimensional convolution and two-dimensional convolution, and the attentional mechanism is effective. We demonstrate the advantage of the multidimensional feature extraction method over single dimension.

(3) Item 4 demonstrates the results of using the $ L1 $ method to measure the similarity between samples decreased by 5.3% and 3.11% compared to the original in the noiseless condition. The method of using nonlinear mapping is more effective than directly calculating the $ L1 $ distance, which demonstrates that our method has a greater advantage over the measurement of similarity between samples.

5. Conclusions

The detection and diagnosis of rolling bearing fault is very important for the safe operation of rotating machinery. Bearing fault may cause great economic losses and even endanger the safety of personnel, so it is very important to find and diagnose it in time. However, it is difficult to collect enough bearing fault data under all working conditions. In order to solve this problem, this paper proposes a bearing fault diagnosis method based on the multidimensional convolution and attention mechanism, which uses median filtering, mean filtering, and convolution operation to preprocess the original data, and uses 1D-CNN and 2DCNN+CBAM to realize efficient feature extraction. At the same time, the similarity between samples is measured by nonlinear mapping of feature vectors into metric space. The experimental results verify the effectiveness of this method and have broad industrial application prospects.

In future work, we will focus on developing more lightweight and efficient models for deployment on mobile terminals and edge devices, making the models lighter and more efficient to handle the complexity and diversity of faults that may occur in real industrial scenarios. In addition, in the network feature extraction part, consideration can be given to structures such as lightweight network structures or deep separable convolutions to reduce the complexity and computational overhead of the model while maintaining the ability to efficiently extract bearing fault features. Furthermore, exploring other network structures suitable for small sample learning that can diagnose unknown types of bearing faults occurring in real industrial scenarios could be beneficial.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by National Natural Science Foundation of China (62273337) and Shenyang Youth Science and Technology Innovation Talent Support Program Project (RC210478).

Conflict of interest

The authors declare there is no conflict of interest.

References

[1]	Hart GW (1992) Nonintrusive appliance load monitoring. Proc IEEE 80: 1870-1891. doi: 10.1109/5.192069
[2]	Erol-Kantarci M, Mouftah HT (2011) Wireless Sensor Networks for Cost-Efficient Residential Energy Management in the Smart Grid. IEEE Trans Smart grid 2: 314-325. doi: 10.1109/TSG.2011.2114678
[3]	Yu-Hsiu Lin, Men-Shen Tsai (2014) Development of an Improved Time Frequency AnalysisBased Nonintrusive Load Monitor for Load Demand Identification. IEEE Trans Instrumentation and Measurement 63: 1470-1483. doi: 10.1109/TIM.2013.2289700
[4]	Dong M, Meira MCM, Xu W, et al (2012) An Event Window Based Load Monitoring Technique for Smart Meters. IEEE Trans Smart Grid 3: 782-796.
[5]	Figueiredo MB, Almeida AD, Ribeiro B (2011) An Experimental Study on Electrical Signature Identification of Non-Intrusive Load Monitoring System. Proc 10th Int Conf Adaptive and Natural Computer Algorithm (ICANNGA’11) 747-758.
[6]	Liang J, Ng S, Kendall G, et al (2010) Load Signature Study-Part I: Basic Concept, Structure, and Methodology. IEEE Trans Power Del 25: 551-560. doi: 10.1109/TPWRD.2009.2033799
[7]	Liang J, Ng S, Kendall G, et al (2010) Load Signature Study-Part II: Disaggregation Framework, Simulation and Applications, Structure, and Methodology. IEEE Trans Power Del 25: 561-569. doi: 10.1109/TPWRD.2009.2033800
[8]	Li J, Ng SKK, Kendall G, et al (2012) Power Decomposition Based on SVM Regression. 2012 Proc IEEE Int Conf Modelling, Identification and Control : 1195-1199.
[9]	Lam H, Fung G, Lee W (2007) A Novel Method to Construct Taxonomy Electrical Appliances Based on Load Signature. IEEE Trans Consumer Electronics 53: 653-660. doi: 10.1109/TCE.2007.381742
[10]	Wang Z, Zheng G (2012) Residential Appliances Identification and Monitoring by a Nonintrusive Method. IEEE Trans Smart Grid 3: 80-92. doi: 10.1109/TSG.2011.2163950
[11]	Zeifman M, Roth K (2011) Nonintrusive appliance load monitoring: Review and outlook. IEEE Trans Consumer Electronics 57: 76-84. doi: 10.1109/TCE.2011.5735484
[12]	Giusti A, Salani M, Gianni A, et al (2014) Restricted Neighbourhood Communication Improves Decentralized Demand-Side Load Management. IEEE Trans Smart grid 5: 92-101. doi: 10.1109/TSG.2013.2267396
[13]	Parson O, Ghosh S, Weal M, et al (2012) Non-intrusive load monitoring using prior models of general appliance types. Proc IEEE Int Conf Artificial Intelligence(AAAI-12) 356-362.
[14]	Zoha A, Glihak A, Imran MU, et al (2012) Non-intrusive load monitoring approaches for disaggregated energy sensing: A survey. Sensors 12: 16838-16866. doi: 10.3390/s121216838
[15]	Dinesh C, Nettasinhe BW, Godaliyadda RI, et al (2015) Residential Appliance Identification Based on Spectral Information of Low Frequency Smart Meter Measurements. IEEE Trans Smart Grids (In press).
[16]	Reinhardt A, Baumann P, Burgstahler D, et al (2012) On the Accuracy of Appliance Identification Based on Distributed Load Metering data. Proc IEEE Int Conf Sustainable Internet and ICT for Sustainability (SustainlT’2012) : 1-9.
[17]	Kolter J, Johnson M (2011) REDD: A public data set for energy disaggregation research. in Workshop on Data Mining Applications in Sustainability (SIGKDD) 1-6.
[18]	Maccone, Claudio (1994) Telecommunications, KLT and relativity. IPI Press.
[19]	Cheng TZ (1995) Mean Shift, Mode Seeking, and Clustering. IEEE Trans Pattern Anal Mach Intell 17: 790-799. doi: 10.1109/34.400568
[20]	Georgescu B, Shimshoni I, Meer P (2003) Mean Shift Based Clustering in High Dimensions: A Texture Classification Example. 2002 Proc IEEE Int Conf Computer Vision 1: 456-463.
[21]	Zoha A (2002) Statistical inference. Duxbury Pacific Grove, CA 2.
[22]	Olson DL , Delen D (2008) Advanced Data Mining Techniques. Springer, 1.

This article has been cited by:

Yue Yan, Hu Liu, Linfeng Gan, Runtong Zhu, A novel arc detection and identification method in pantograph-catenary system based on deep learning, 2025, 15, 2045-2322, 10.1038/s41598-025-88109-x

Reader Comments

Your name:*

Email:*
© 2016 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)