Figure 1.
Block diagram of the utilized DC-DC converter.
A photovoltaic (PV)-based generator is a crucial component of modern electricity grids. Most PV systems utilize various maximum power point tracking (MPPT) algorithms to inject the maximum available power into the utility. However, on sunny days, consistently obtaining maximum power can lead to increased thermal stress and a reduced reliability of the power electronic-based DC-DC converter. This paper presents a thermal model for the DC-DC converter that evaluates the accumulated temperature based on power losses and ambient temperature sensed by the thermal sensor. A thermal control strategy is suggested to maintain the temperature of the converter's main components within allowable limits. The thermal control includes two stages: a primary stage that adjusts the switching frequency of the IGBT switches to decrease the accumulated temperature and a secondary stage that adjusts the current-based MPPT algorithm to reduce the maximum current through the main switch. This approach aims to extend the lifespan of the utilized DC-DC converter and lower its operational cost. Furthermore, the allowable range for switching frequency variation is determined through a stability analysis of the frequency response, which is evaluated using a Bode plot for the closed-loop system. The proposed thermal control was implemented in a MATLAB/Simulink environment. The associated results demonstrate the effectiveness of the proposed control in maintaining temperature within acceptable limits and thereby improving the reliability of the system.
Citation: Rasool M. Imran, Kadhim Hamzah Chalok, Siraj A. M. Nasrallah. Innovative two-stage thermal control of DC-DC converter for hybrid PV-battery system[J]. AIMS Electronics and Electrical Engineering, 2025, 9(1): 26-45. doi: 10.3934/electreng.2025002
| [1] | I.E.S. Naidu, S. Srikanth, A. Siva sarapakara Rao, Adabala Venkatanarayana . A novel mine blast optimization algorithm (MBOA) based MPPT controlling for grid-PV systems. AIMS Electronics and Electrical Engineering, 2023, 7(2): 135-155. doi: 10.3934/electreng.2023008 |
| [2] | Said Oucheriah, Abul Azad . Current-sensorless robust sliding mode control for the DC-DC boost converter. AIMS Electronics and Electrical Engineering, 2025, 9(1): 46-59. doi: 10.3934/electreng.2025003 |
| [3] | Muamer M. Shebani, M. Tariq Iqbal, John E. Quaicoe . Comparison between alternative droop control strategy, modified droop method and control algorithm technique for parallel-connected converters. AIMS Electronics and Electrical Engineering, 2021, 5(1): 1-23. doi: 10.3934/electreng.2021001 |
| [4] | Mohamed M. Albarghot, Mohamed T. Iqbal, Kevin Pope, Luc Rolland . Dynamic modeling and simulation of the MUN Explorer autonomous underwater vehicle with a fuel cell system. AIMS Electronics and Electrical Engineering, 2020, 4(1): 114-131. doi: 10.3934/ElectrEng.2020.1.114 |
| [5] | José M. Campos-Salazar, Juan L. Aguayo-Lazcano, Roya Rafiezadeh . Non-ideal two-level battery charger—modeling and simulation. AIMS Electronics and Electrical Engineering, 2025, 9(1): 60-80. doi: 10.3934/electreng.2025004 |
| [6] | Suliana Ab-Ghani, Hamdan Daniyal, Abu Zaharin Ahmad, Norazila Jaalam, Norhafidzah Mohd Saad, Nur Huda Ramlan, Norhazilina Bahari . Adaptive online auto-tuning using Particle Swarm optimized PI controller with time-variant approach for high accuracy and speed in Dual Active Bridge converter. AIMS Electronics and Electrical Engineering, 2023, 7(2): 156-170. doi: 10.3934/electreng.2023009 |
| [7] | Jing Ou, Yingzhen Liu, Martin Doppelbauer . Torque analysis and slot regions assignment of a DC-excited flux-modulated machine with two stator windings. AIMS Electronics and Electrical Engineering, 2017, 1(1): 4-17. doi: 10.3934/ElectrEng.2017.1.4 |
| [8] | Efthymios N. Lallas . A survey on key roles of optical switching and labeling technologies on big data traffic of Data Centers and HPC environments. AIMS Electronics and Electrical Engineering, 2019, 3(3): 233-256. doi: 10.3934/ElectrEng.2019.3.233 |
| [9] | Desh Deepak Sharma, Ramesh C Bansal . LSTM-SAC reinforcement learning based resilient energy trading for networked microgrid system. AIMS Electronics and Electrical Engineering, 2025, 9(2): 165-191. doi: 10.3934/electreng.2025009 |
| [10] | Fayrouz Dkhichi . Improved MPPT algorithm: Artificial neural network trained by an enhanced Gauss-Newton method. AIMS Electronics and Electrical Engineering, 2023, 7(4): 380-405. doi: 10.3934/electreng.2023020 |
A photovoltaic (PV)-based generator is a crucial component of modern electricity grids. Most PV systems utilize various maximum power point tracking (MPPT) algorithms to inject the maximum available power into the utility. However, on sunny days, consistently obtaining maximum power can lead to increased thermal stress and a reduced reliability of the power electronic-based DC-DC converter. This paper presents a thermal model for the DC-DC converter that evaluates the accumulated temperature based on power losses and ambient temperature sensed by the thermal sensor. A thermal control strategy is suggested to maintain the temperature of the converter's main components within allowable limits. The thermal control includes two stages: a primary stage that adjusts the switching frequency of the IGBT switches to decrease the accumulated temperature and a secondary stage that adjusts the current-based MPPT algorithm to reduce the maximum current through the main switch. This approach aims to extend the lifespan of the utilized DC-DC converter and lower its operational cost. Furthermore, the allowable range for switching frequency variation is determined through a stability analysis of the frequency response, which is evaluated using a Bode plot for the closed-loop system. The proposed thermal control was implemented in a MATLAB/Simulink environment. The associated results demonstrate the effectiveness of the proposed control in maintaining temperature within acceptable limits and thereby improving the reliability of the system.
The environmental degradation due to industrial pollution makes it imperative to use clean energy solutions for generating electricity. The efficiency of various clean energy sources varies with the environmental conditions at the site of installation. In dry regions with clear skies, high solar radiation, and elevated temperatures, like in Iraq, both PV generators and solar concentrators are feasible options for energy production.
PV systems convert solar irradiation into electricity with the help of power electronic converters [1]. These converters can be configured in either a single stage of DC-DC or in two stages, DC-DC and DC-AC. In both configurations, the DC-DC stage is essential and requires vital control techniques. A DC-DC converter, built from power electronic components, converts the variable DC power delivered by the PV panel into stable DC power that can be stored or directly feed electrical loads [2]. The rated power of power electronic components, such as switches, is chosen in a way that keeps both system reliability and initial cost in consideration.
Reliability is the ability of a system to perform its required function without failure for a specified period of time. The most significant factor that influences the reliability of the power electronic switch is the operating temperature [3]. The cycles of heating up and cooling down cause mechanical stress on power electronic components due to the disparity of thermal expansion rates [4]. This decreases the reliability of the system and shortens its lifetime. Thus, operating temperature should be monitored, kept under control, and maintained within permitted limits. There are several techniques for monitoring the operating temperature of a power converter, including module-integrated sensors, open-loop estimators, and closed-loop observers [5,6,7].
Along with these monitoring methods, the thermal control and management techniques of various DC-DC power converters have also been developed by researchers [8,9,10,11,12,13]. In conventional thermal control methods, the operating temperatures are typically managed by thermal design through proper selection of the heat sink's thermal resistance [14]. However, this technique is passive and cannot actively regulate the thermal state of internal layers inside the power electronic components. In [15], researchers proposed regulating the temperature of converter components by adjusting the duty ratio. This method monitors the converter's temperature and adjusts the on-time of the converter's switch in accordance with output power regulation. While this method ensures that the temperature is limited within permissible limits, it raises concerns about steady-state stability and thus reduces its reliability. Temperature regulation of a converter using circulating current control was also presented in [16,17]. This technique seeks to keep the operating temperature stable by injecting and extracting circulating currents in order to limit thermal cycling.
While this is generally more related to AC circuits, which are not our focus, it may still interact with passive filters and reduce their effectiveness. The result could be more serious ripple and noise in the output voltage. The regulation of gate-driver parameters, such as gate voltage and gate resistance, is able to control a large fraction of both conduction and switching losses, thus lowering the amplitude of thermal cycles [18,19]. The technique has beneficial effects in terms of minimizing thermal stress and improving performance; it does not even affect the converter output ripple by the change in gate parameters. Yet, the effectiveness of this approach is limited by the capabilities of the gate-drive circuitry, which may have constraints on how much and how quickly it can be adjusted.
To realize effective thermal regulation, gate-driver parameters should be set with a sufficient margin beyond the maximum required levels, increasing initial costs probably. This method also requires an extra circuit which increases the complication of the system. The authors of [20] have proposed a methodology for determining the degraded lifetime of a number of paralleled DC-DC converters based on the number of thermal cycles. This gives updated information in order to set maximum margins of temperature and output power. However, this described method has limitations in accuracy and does not address the instantaneous causes of thermal stress.
Another method for thermal control involves managing the turn-off losses of an IGBT through a parallel-connected snubber circuit [21,22]. This circuit features variable resistance, variable capacitance, and an auxiliary switch, allowing for flexible operation tailored to specific system requirements. Depending on the chosen resistance and capacitance values, the IGBT can operate in either weak or strong absorption modes, effectively influencing turn-off losses. Snubber action is provided at the turn-off phase by adjusting the delay time of the auxiliary switch. Such technique reduces thermal cycling and improves the overall reliability of the system; however, it requires an additional switch per IGBT, increasing both cost and complexity.
Active thermal control by optimizing switching losses is presented in [23]. This technique regulates the temperature through the gate drive of the GaN-based switches. Techniques for limiting temperature by regulating switching frequency have been discussed in [24,25]. Even though these techniques are active and can be applied over a wide range of switching frequencies, the conversion efficiency decreases beyond this range.
A two-stage thermal control strategy for the DC-DC converter is proposed in this paper to address the limitations of the previous approaches. The temperature of the converter is continuously monitored during operation. The first stage is initiated when the temperature reaches a preset limit by adjusting the switching frequency of the converter's switches. If the temperature remains high and the switching frequency reaches its lower permissible limit, the second stage is triggered. In this stage, the reference current generated by the current-based MPPT is tuned to keep the operating temperature within the acceptable range. The upper and lower bounds of the switching frequency are obtained by performing a detailed analysis of the frequency response of the closed-loop system.
Setting these limits is of vital importance to avoid instability and ensure the best performance. The proposed two-stage thermal control strategy actively adjusts switching frequency and reference current for improved thermal regulation compared to traditional methods like adjusting heat sink thermal resistance and regulating duty ratio, which cannot respond in real-time. This thermal control also incorporates frequency limits determined through stability analysis, enhancing reliability over active methods like the baseline of regulating switching frequency and optimizing switching losses with GaN-based switches. The proposed thermal control maintains compatibility with system components, unlike circulating current control, which can interact with passive filters and increase ripple and noise. Finally, it remains simple and low-cost compared to both adjusting gate-driver parameters and managing turn-off losses with a snubber circuit.
The contributions of this paper can be summarized as follows:
• Developing an innovative thermal control mechanism that regulates the junction temperature of an IGBT-based DC-DC converter in a PV system by dynamically adjusting the switching frequency up to a predefined limit. Beyond this limit, temperature is managed by adjusting the current through a current-based MPPT strategy to maintain acceptable switching losses.
• Determining the optimal switching frequency limits for the DC-DC converter to ensure stable and reliable operation. This is achieved through a detailed stability analysis and examination of the Bode plot of the entire closed-loop system.
• Addressing the trade-off between maximizing available PV power and reducing the thermal cycle length of the DC-DC converter. This approach aims to reduce short-term PV energy loss while extending the converter's lifespan over the long term.
The remainder of this paper is structured as follows: Section 2 presents the electrical and thermal models of the DC-DC converter. The thermal control mechanism is described in Section 3. Section 4 details the determination of stable switching frequency limits. Section 5 provides the results and their associated discussions. Finally, Section 6 concludes the paper.
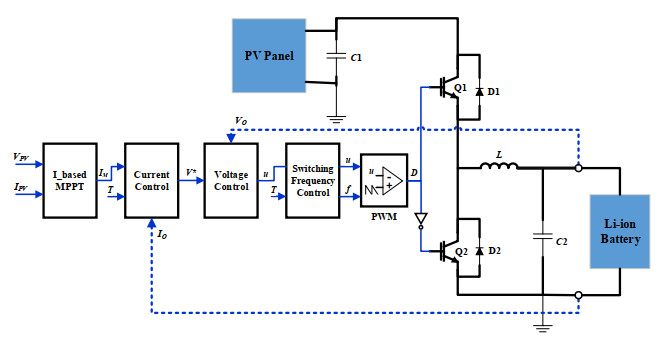
DC-DC converter is a device that steps up or steps down the voltage with an ability to control the output voltage, current, or both. The structure of the utilized DC-DC buck converter is depicted in Figure 1, where both switches in the Figure are IGBTs. The system under study features a PV panel as the power source and a Li-ion battery pack as the load. External loads were not considered in the study, as attaching such loads to the battery does not impact the control strategy. The values of both the inductor and the capacitor are set to cope with the variations in voltage, current, and switching frequency. Heat flow is evaluated based on ambient temperature, the attached heat sink, and the temperature profile of both switches. After heat is transferred to the attached heat sink, it spreads to the outside environment in the form of thermal radiation and thermal convection.
Identifying the junction temperature of an IGBT can be challenging. This difficulty arises from the large time constants and delayed response of the heat sink or cooling system compared to the temperature changes within the IGBT. As a result, direct measurement of the junction temperature from accessible points may lead to significant errors. To address this issue, the temperature of each IGBT switch is generated using a thermal model, which provides a more accurate representation of the junction temperature. The thermal model calculates the junction temperature by assessing the power losses during the switching and conduction states, incorporating the values of thermal resistance and capacitance. The first step in estimating the junction temperature involves calculating the power losses. In semiconductor switches, losses are generally classified into three categories: conduction losses, switching losses, and blocking losses. Blocking losses are very low and often negligible. Thus, the main losses in the switch are conduction and switching losses. The conduction losses (PCON) can be calculated by multiplying the instantaneous IGBT's collector current (IC) by the on-state collector-emitter voltage (VCE), as follows:
| PCON=IC×VCE(T,IC) | (1) |
It is important to note that VCE for the conduction state is a function of temperature (T) and IC, typically ranging between 1 and 3 V. Therefore, VCE can be obtained from a 2D lookup table based on these parameters.
On the other hand, the switching losses of an IGBT are the sum of the losses during the turn-on and turn-off states. The switching losses (PSW) of a single IGBT are obtained using the following equations, where EON and EOFF are energy losses during the turn-on and turn-off states, respectively [13].
| EON=tOFF∫tONIC×VCE(T,IC)dt | (2) |
| EOFF=tON′∫tOFFIC×VCE(T,IC)dt | (3) |
| PSW=(EON+EOFF)×fSW | (4) |
It is evident from Eq (4) that the switching frequency is directly proportional to power losses; therefore, increasing the frequency raises the IGBT's junction temperature. Consequently, managing the switching frequency is crucial for controlling junction temperature and ensuring the reliability of the IGBT. The junction temperature (TJ) can be approximated using the thermal impedance formula as follows [26]:
| TJ=Tamb+PZt | (5) |
where Tamb is the ambient temperature, P is the sum of PCON and PSW, and Ztis the thermal impedance, represented through the thermal model. Various models are available to emulate the thermal behavior inside an IGBT and estimate the junction temperature; however, the resistance-capacitance (RC) thermal model is the most common since it is straightforward and considerably accurate. Two types of RC thermal models exist, namely Cauer and Foster. The Cauer model utilizes a more intricate network of resistors and capacitors, allowing for a detailed and precise representation of thermal behavior, particularly where temperature gradients and non-uniform heat distribution are significant. In contrast, the Foster model is simpler and may not capture these complexities as effectively. This study employed the Cauer model for its precision in depicting the complex thermal dynamics of the IGBT, which is essential for accurate junction temperature estimation and reliable performance analysis. The Cauer model uses a ladder network of RC pairs to represent heat conduction and storage across the IGBT layers. The utilized Cauer model includes seven distinct layers as depicted in Figure 2 (a). The thermal resistance (Rti) and capacitance (Cti) for each layer are calculated as follows [27]:
| Rti=diKiAi | (6) |
| Cti=ρicpiAidi | (7) |
where di is the layer thickness, ki is the thermal conductivity, Ai is the cross-sectional area, ρi is the density, and cp i is the specific heat capacity. The time constant for each layer is τi = Rti Cti.
The repeated process of charging and discharging the model capacitance mimics the energy losses during on and off states of an IGBT. The heat transfer path starts from the IGBT junction and spreads to the outer environment through a heat sink. The parameters for modeling each of the seven layers in the Cauer thermal model are detailed in [28]. Switching losses in the presented thermal model can be considered as an ideal current source, as in Figure 2 (b).
The rising temperature of converter components leads to premature malfunction, solder melting, and other damages that reduce the lifespan of the converter. The heating up and cooling down of an electronic component deteriorates its condition due to the different thermal coefficients of its layers. It is therefore necessary to maintain the temperature of an electronic component within permissible limits. The MPPT feature works to inject the maximum available power into the load, and therefore the current passing through the electronic switches is high most of the time, especially in the summer due to high solar irradiance. This high current causes an increase in temperature, in addition to its rise in the surrounding environment during hot climates. To avoid high temperatures and maintain a low thermal variation for the electronic components in a DC-DC converter, two stages of thermal control were proposed.
Higher switching frequency offers several benefits such as faster response to load changes and transient conditions, lower output ripple, higher power density, and better filtering capability, potentially enhancing the overall efficiency. However, increasing the switching frequency also increases switching losses, which can raise the junction temperature of IGBT switches, as illustrated in Eq (4). Therefore, it is possible to control the operating temperature by adjusting the frequency of the PWM carrier signal. Abrupt changes in this frequency may lead to system instability or performance degradation, making smooth transitions crucial. Usually, frequency ramping or gradual adjustment methods have been used to smooth transitions by varying the PWM carrier frequency slowly, preventing sudden spikes in switching losses and ensuring stable power delivery. In this study, a PI compensator is employed to manage frequency adjustments more precisely. The PI compensator adjusts the PWM carrier frequency in real time based on the difference between the desired temperature limit (T1st) and the measured temperature (Treal). By tuning the PI gains, the compensator ensures a smooth and accurate transition to the desired frequency with minimal overshoot or oscillation. The temperature limit T1st serves as a reference and is compared to Treal to generate an error signal. This error signal is then multiplied by proportional and integral gains to produce the amount of frequency adjustment as described in Eq (8). It is noted that the response of the junction temperature is relatively slow compared to changes in the switching frequency, which can cause a lag in the control response and potentially lead to oscillations. To address this, a feedforward (FF) control loop is incorporated to provide predictive capability for future temperature changes. The predicted temperature, calculated as Treal + dT/dt, is used in the feedforward loop. The gain for this feedforward loop is the temperature error signal itself, ensuring that the feedforward effect is proportional to the error, as outlined in Eq (9).
| fSW=fMax−[(Treal−T1st)(KP_1+∫Ki_1dt)+FF]fMax−fMin0 | (8) |
| FF=(Treal−T1st)(Treal+dTdt) | (9) |
where fMax and fMin are the maximum and minimum limits of switching frequency, respectively. Kp_1 and Ki_1 are the proportional and integral gains of this thermal control stage, respectively. Adjusting the switching frequency has limits; beyond these limits, the system slows down, and the regulation efficiency of the output signal decreases. Therefore, when the frequency reaches its lower limit (fMin), another variable needs adjustment to keep the temperature within the limit.
To attain the maximum power provided by a PV panel, an MPPT algorithm is required. Different MPPT algorithms are available; however, perturb and observe (P&O) is the most popular due to its simplicity and fast response. The P&O algorithm usually starts with an initial value of power. Then, depending on the measured value of the PV power, the algorithm generates a dynamic perturbation in the measured value of voltage to sense the direction in which the power increases until it reaches the maximum value. This value is usually set by the voltage controller in terms of duty ratio to the interconnected DC-DC converter. If the controller of a converter is used to attain the maximum current, the dynamic perturbation can be applied for the measured value of current instead of voltage. In this case, the algorithm is called current-based MPPT, which is illustrated in the flowchart of Figure 3.
The generated maximum current (IMPPT) can be set as a reference for the current controller in order to realize the maximum available PV power. However, the maximum current may not be required when the temperature of the DC-DC converter is high. To keep the converter's switch temperature at its boundary when the switching frequency control reaches the limit, the maximum current generated by current-based MPPT can be adjusted. The desired limit of the temperature (T2nd), which is set slightly higher than T1st, is used as a reference for the current controller and compared to the measured temperature (Treal) to generate an error signal. The error signal is multiplied by proportional and integral gains to produce the amount of current adjustment as follows:
| I∗=IMPPT−[(Treal−T2nd)(KP_2+∫Ki_2dt)] | (10) |
where Kp_2 and Ki_2 are the proportional and integral gains of the maximum current adjustment stage, respectively.
The attained reference current (I*) is then compared with the measured value of current (IO) to generate an error signal for the current controller, which in turn produces the reference value of voltage (V*) as:
| V∗=(I∗−IO)(KP_i+∫Ki_idt) | (11) |
where Kp_i and Ki_i are the proportional and integral gains of the current controller, respectively.
Finally, V* is compared to the measured value of the output voltage (VO) to generate an error signal for the voltage controller as:
| u=(V∗−VO)(KP_v+∫Ki_vdt) | (12) |
where Kp_v and Ki_v are the proportional and integral gains of the voltage controller, respectively.
The two stages of thermal control are depicted in Figure 4.
While varying the switching frequency helps regulate the operating temperature, it also affects the steady-state stability of the DC-DC converter. To ensure that the switching frequency is adjusted within appropriate margins, a stability analysis is conducted in this section to determine the stable limits of the switching frequency. To clarify the steps involved in this stability analysis, a flowchart outlining the process is presented in Figure 5.
The switching state for IGBT1 and IGBT2 is formed by the duty cycle (D), where D = tON / (tON + tOFF). In both cases, when IGBT1 is on, IGBT2 is off, and vice versa; the dynamics of the system, including output capacitor voltage (vC) and inductor current (iL) can be characterized by observing the average behavior of the DC-DC converter as follows:
| diLdt=1L(Vin−vC)D−1LvC(1−D) | (13) |
| dvCdt=1C(iL−vCRT)D+1C(iL−vCRT)(1−D) | (14) |
Equations (13) and (14) can be rearranged and Laplace transformed as follows:
| siL=VinLD−1LvC | (15) |
| svC=1CiL−1RTCvC | (16) |
where RT denotes the load resistance, which is representative of the battery's typical internal resistance.
Since the output and input of the DC-DC converter are the capacitor voltage (vC) and the duty ratio (D), respectively, the transfer function of the system can be expressed as Eq (17) after applying appropriate mathematical transformations.
| GC=vCD=Vin(LCs2+LRTs+1) | (17) |
The transfer functions of both the voltage controller (GV) and current controller (GI) are represented as:
| GV=KP_vs+Ki_vs | (18) |
| GI=KP_is+Ki_is | (19) |
Figure 6 illustrates the block diagram of the overall system, where GPWM represents the transfer function of the PWM block, as described by Eq (20). For average behavior, GPWM is assumed to be equal to 1. Given that the output current (IO) is defined as IO = IL – IC, and IC is given by IC = ω C vC, IO can be calculated from Eq (16) and then expressed in Eq (21).
| GPWM=Du | (20) |
| IO=vC(Cs−ωC+1RT) | (21) |
The measured output current is fed back to the current controller after passing through a low-pass filter (LPF). Thus, the transfer function (GO) that generates IO can be expressed as:
| GO=Cs−ωC+1RTτs+1 | (22) |
where τ represents the time constant of the LPF and is related to the cutoff frequency (fC) by τ = 1 / 2πfC.
Equation (23) represents the transfer function of the entire system depicted in Figure 6.
| GT=GIGVGPWMGCGOGIGVGPWMGCGO+GVGPWMGC+1 | (23) |
To determine the upper and lower limits of the switching frequency, a Bode plot of the closed-loop system representing the frequency response between vC and V* was generated using MATLAB and is depicted in Figure 7 (a).
The Bode plot illustrates how the system's gain and phase shift vary with frequency, which is essential for assessing stability and performance in control systems. The crossover frequency (fx), where the gain crosses 0 dB, indicates the stability of the system. A higher gain margin and phase margin at the crossover frequency are critical for ensuring system robustness. The switching frequency should typically be above five times the crossover frequency, as indicated on the Bode plot, to prevent instability, and below ten times the crossover frequency to maintain adequate gain and performance [29]. Based on this analysis, the initial frequency limits are set to a minimum of 10 kHz and a maximum of 20 kHz. These frequency limits ensure a proper rise in the IGBT's junction temperature. However, incorporating the current control loop into the system modifies the crossover frequencies. Consequently, the lower limit of the switching frequency is increased to 20 kHz. The Bode plot for the overall system, which includes the current control loop, is presented in Figure 7 (b). The revised upper and lower limits of the switching frequency are summarized in Table 2.
In order to verify the proposed thermal control, a buck converter is designed in MATLAB/Simulink using Simscape tools, as shown in Figure 8. The system parameters, including the inductor and capacitors, were determined based on variations in voltage, current, and switching frequency [30] and are summarized in Table 1. The control parameters for the proposed method were established through a trial-and-error process and are presented in Table 2, along with the frequency limits achieved from Bode plot analysis. The input to the system is the variable irradiation, and the system load is a Li-ion battery pack.
| Parameter | Value |
| PV panel power | 2000 W |
| PV panel voltage | 60 V |
| Li-ion battery pack capacity | 30 Ah |
| Li-ion battery pack voltage | 38 V |
| Capacitor 1, capacitor 2 | 1200 µF, 22 µF |
| Filter inductor, resistor | 2 mH, 10 kΩ |
| Cutoff frequency of LPF (fC) | 1 kHz |
DownLoad:
CSV
| Parameter | Value |
| Kp_1, Ki_1, Kp_2, Ki_2 | 10000, 80, 57, 16 |
| Kp_i, Ki_i, Kp_v, Ki_v | 6,500, 2.4, 38 |
| Desired temperature limits (T1st, T2nd) | 340 K, 342 K |
| Switching frequency (fMax, fMin) | 40 kHz, 20 kHz |
DownLoad:
CSV
The PV panel is structured by connecting a number of PV cells to acquire the required supply current and open-circuit voltage. To verify the proposed theory of thermal control, the PV irradiation was set to vary in order to inject a variable current into the battery and accordingly experience different operating temperatures of the IGBTs. The switching state of both IGBTs is opposite, which means that only one IGBT is on at a time.
To verify the effectiveness of the proposed thermal control, the simulated system underwent three cases: without thermal control, with the first stage of thermal control, and with both stages of thermal control. The irradiance values are set to 800, 1100,600, 1000, and 450 (W/m2) for the periods (0‒2), (2‒4), (4‒6), (6‒8), and (8‒10), respectively. The current drawn by the battery for the first case is depicted in Figure 9 in red. Given that the switching frequency is set to 40 kHz, the resulting temperature in this case is shown in Figure 10 in red, which has the highest record among the other cases. For a similar irradiation posture, the first stage of thermal control is activated, which adjusts the switching frequency. The attitudes of both current and temperature for the second case are depicted in blue in Figure 9 and Figure 10, respectively. It can be seen from Figure 10 that the temperature has reduced for the second case in the periods (0‒4) and (6‒8). Figure 11 clarifies the adjustment of the switching frequency during the mentioned periods in red. The new temperature did not reach the desired value, which is set to 340 K, because frequency adjustment has limits, after which the conversion efficiency decreases.
Then, the third case, which operates with two stages of thermal control, is implemented for the same irradiance. The current, temperature, and switching frequency related to the third case are depicted in green in Figure 9, Figure 10, and Figure 11, respectively. The desired temperature in the second stage is set to 342 K, which is a bit higher than that of the first stage to avoid conflict between the two controllers. It is clear from Figure 10 that the second stage brought the temperature within its limit by adjusting the maximum reference current. Figure 9 illustrates the adjustment made to the output current in green.
To clarify the benefits of the frequency limitations established through stability analysis, the proposed two-stage thermal control is compared to the baseline method from the literature [24,25], which adjusts only the switching frequency to achieve the desired temperature. Both control methods are subjected to similar pulse currents to reach the same junction temperature. In addition to temperature, the comparison includes the average voltage ripple of both methods, measured every 0.005 seconds and expressed as a percentage of the output voltage. This analysis highlights the contribution of limiting the switching frequency on conversion efficiency and overall performance. Figure 12 illustrates that the baseline method, shown in blue, struggles to attain the desired temperature. Furthermore, by allowing frequency variations beyond the lower limits, this method results in greater fluctuations in inductor current, which increases voltage ripple. This, in turn, compromises voltage quality and contributes to higher losses.
To illustrate the reduction in thermal cycling and its impact on the lifespan of the DC-DC converter, the converter was subjected to an extended test scenario involving three groups of thermal cycles. During each group, the PV irradiation oscillated between high and low values, as depicted in Figure 13 (a). This oscillation directly influences the converter's output current, which in turn impacts the thermal cycling of the converter. Oscillating between the highest and lowest expected irradiance induces rapid changes in junction temperature, resulting in a severe thermal profile, depicted in red in Figure 13 (b). By applying the proposed two-stage thermal control method, the maximum temperature experienced during each cycle was reduced.
This reduction in temperature led to a decrease in the length of thermal cycles in the first, second, and third groups from 5 to 2.7 K, from 10 to 6 K, and from 15.5 to 8.7 K, respectively. The resulting thermal cycles are shown in blue in Figure 13 (b). The average thermal cycle length was reduced from 10.15 to 5.8 K, representing an overall reduction of approximately 43% using the proposed approach. To quantify the impact of this reduction on the lifespan of the DC-DC converter, we used the Coffin-Manson model. The lifespan enhancement can be estimated using the following equation [31]:
| NfN′f=(ΔTaΔTn)b | (24) |
where Nf / Nf' is the ratio of the estimated number of thermal cycles to failure with the thermal control method to the number of thermal cycles to failure before applying the method, and ΔTa and ΔTn are the average thermal cycle lengths before and after applying the method, which are 10.15 and 5.8 K, respectively. b is a positive exponent that characterizes the material-specific sensitivity of lifespan to changes in thermal cycle length, generally ranging from 1 to 3 for many electronic materials. For a conservative estimate, we assume b to be 1 to account for lower sensitivity. Accordingly, the estimated lifespan of the DC-DC converter is enhanced by a factor of approximately 1.75 due to the proposed thermal control method. This indicates that the lifespan is expected to be 75% longer compared to the original conditions. This significant improvement in lifespan underscores the effectiveness of the proposed thermal control method.
This paper proposes an innovative two-stage thermal control for the DC-DC buck converter. The first stage adjusts the switching frequency to regulate the operating temperature. This adjustment is restricted by performance limits, after which the conversion efficiency decreases. Thus, the second stage of the proposed thermal control ensures that the temperature is maintained within the required limit. The control system is designed to make maximum use of the current-based MPPT algorithm on the one hand and to control the converter's temperature on the other. The system was simulated in MATLAB using the Simscape toolbox, and a performance comparison was conducted among three scenarios: without thermal control, with first-stage thermal control, and with thermal control at both stages. The results demonstrated that the temperature of the DC-DC converter can be fully maintained through both stages of the proposed thermal control. Notably, the results indicate that with the proposed thermal control, the converter's lifespan is expected to be 75% longer compared to the original conditions. This estimate is based on the Coffin-Manson model, which relates thermal cycling to material fatigue, underscoring the reliability benefits of enhanced thermal control. The results also verify that setting appropriate limits for the switching frequency ensures stable operation and optimal performance. In addition to its effectiveness, the proposed thermal control is characterized by simplicity and computational ease. A limitation that may be associated with the second stage of thermal control is that the maximum PV power may not always be consumed. Future directions will include validating these findings through experimental testing, exploring optimizations to enhance converter performance, and adapting the thermal control approach to different power converters, particularly inverters.
Rasool M. Imran: Conceptualization, Methodology, Writing ‒ original draft; Kadhim Hamzah Chalok: Formal analysis, Investigation; Siraj A. M. Nasrallah: Validation, Writing ‒ review and editing. The paper was a collaborative effort between all authors. All authors have read and approved the final version of the manuscript.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
The authors declare no conflicts of interest in this paper.
| [1] |
Naidu IES, Srikanth S, Rao A, Venkatanarayana (2023) A novel mine blast optimization algorithm (MBOA) based MPPT controlling for grid-PV systems. AIMS Electron Electr Eng 7: 135‒155. https://doi.org/10.3934/electreng.2023008 doi: 10.3934/electreng.2023008
|
| [2] |
Moon SY, Chandrarathna SC, Shafique A, Lee JW (2024) A compact DC-DC converter with pulse-counting MPPT and fast one-path self-startup for thermal energy harvesting. IEEE Trans Circuits Syst I Reg Papers 71: 2457‒2470. https://doi.org/10.1109/TCSI.2024.3377003 doi: 10.1109/TCSI.2024.3377003
|
| [3] |
Gabriel OE, Huitink DR (2023) Failure mechanisms driven reliability models for power electronics: A review. J Electron Packag 145: 020801. https://doi.org/10.1115/1.4055774 doi: 10.1115/1.4055774
|
| [4] |
Shen J, Zhang J, Huang X, Qiu L, Fang Y (2023) Active thermal management method for output-parallel DAB DC–DC converters under parameter mismatches and asymmetrical modulation. IEEE Trans Power Electron 38: 8237‒8248. https://doi.org/10.1109/TPEL.2023.3266287 doi: 10.1109/TPEL.2023.3266287
|
| [5] |
Van der Broeck CH, De Doncker RW (2019) Thermal monitoring of power electronic modules with minimal sensing effort. IEEE Energy Conversion Congress and Exposition (ECCE), 5989‒5996. https://doi.org/10.1109/ECCE.2019.8912612 doi: 10.1109/ECCE.2019.8912612
|
| [6] | Li J, Hu G, Ma F, Qiu R, Chen J (2023) Research on IGBT junction temperature prediction method based on Extended Kalman Filtering. International Conference on Wireless Power Transfer, 181‒188. https://doi.org/10.1007/978-981-97-0869-7_19 |
| [7] |
Dou Y (2021) An improved prediction model of IGBT junction temperature based on backpropagation neural network and Kalman filter. Complexity 2021: 5542889. https://doi.org/10.1155/2021/5542889 doi: 10.1155/2021/5542889
|
| [8] | Marquez A, Leon JI, Vazquez S, Franquelo LG (2018) Closed-loop active thermal control via power routing of parallel DC-DC converters. IEEE 12th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG 2018), 1‒6. https://doi.org/10.1109/CPE.2018.8372586 |
| [9] |
Ozkan G, Papari B, Hoang PH, Deb N, Edrington CS (2019) An active thermal control method for AC-DC power converter with sequence-based control approach. IEEE Electric Ship Technologies Symposium (ESTS), 263‒267. https://doi.org/10.1109/ESTS.2019.8847886 doi: 10.1109/ESTS.2019.8847886
|
| [10] |
Vitale G, Lullo G, Scirè D (2020) Thermal stability of a DC/DC converter with inductor in partial saturation. IEEE Trans Ind Electron 68: 7985‒7995. https://doi.org/10.1109/TIE.2020.3014580 doi: 10.1109/TIE.2020.3014580
|
| [11] |
Prasobhu PK, Buticchi G, Brueske S, Liserre M (2016) Gate driver for the active thermal control of a DC/DC GaN-based converter. IEEE Energy Conversion Congress and Exposition (ECCE), 1‒8. https://doi.org/10.1109/ECCE.2016.7855131 doi: 10.1109/ECCE.2016.7855131
|
| [12] |
Imran RM, Chalok KH (2024) Innovative mode selective control and parameterization for charging Li-ion batteries in a PV system. AIMS Energy 12: 822‒839. https://doi.org/10.3934/energy.2024039 doi: 10.3934/energy.2024039
|
| [13] |
Alavi O, Rajabloo T, De Ceuninck W, Daenen M (2022) Non-isolated DC-DC converters in fuel cell applications: Thermal analysis and reliability comparison. Applied Sciences 12: 5026. https://doi.org/10.3390/app12105026 doi: 10.3390/app12105026
|
| [14] |
Kalker S, Ruppert LA, Van Der Broeck CH, Kuprat J, Andresen M, Polom TA, et al. (2021) Reviewing thermal-monitoring techniques for smart power modules. IEEE J Emerg Sel Topics Power Electron 10: 1326‒1341. https://doi.org/10.1109/JESTPE.2021.3063305 doi: 10.1109/JESTPE.2021.3063305
|
| [15] | Andresen M, Buticchi G, Liserre M (2016) Active thermal control of isolated soft switching DC/DC converters. IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, 6818‒6823. https://doi.org/10.1109/IECON.2016.7793676 |
| [16] |
Kadandani NB, Dahidah M, Ethni S, Muhammad M (2021) Lifetime and reliability improvements in modular multilevel converters using controlled circulating current. J Power Electron 21: 1611‒1620. https://doi.org/10.1007/s43236-021-00297-7 doi: 10.1007/s43236-021-00297-7
|
| [17] |
Wang Q, Liu J, Wu P, Qin X (2023) A lifetime improvement active thermal control strategy for wind turbine parallel converters based on reactive circulating current. Electronics 12: 3125. https://doi.org/10.3390/electronics12143125 doi: 10.3390/electronics12143125
|
| [18] |
Gonzalez JO, Alatise O (2017) Impact of the gate driver voltage on temperature sensitive electrical parameters for condition monitoring of SiC power MOSFETs. Microelectronics Reliability 76: 470‒474. https://doi.org/10.1016/j.microrel.2017.06.082 doi: 10.1016/j.microrel.2017.06.082
|
| [19] |
Andresen M, Ma K, Buticchi G, Falck J, Blaabjerg F, Liserre M (2018) Junction temperature control for more reliable power electronics. IEEE Trans Power Electron 33: 765‒776. http://dx.doi.org/10.1109/TPEL.2017.2665697 doi: 10.1109/TPEL.2017.2665697
|
| [20] | Peyghami S, Davari P, Blaabjerg F (2018) System-level lifetime-oriented power sharing control of paralleled DC/DC converters. IEEE Applied Power Electronics Conference and Exposition (APEC), 1890‒1895. https://doi.org/10.1109/APEC.2018.8341275 |
| [21] |
Wang R, Huang X, Li J (2021) Active thermal management for SiC MOSFETs based on equivalent adjustment of buffer capacitor. IEEE Trans Circuits Syst. Ⅱ Express Briefs 69: 1502‒1506. https://doi.org/10.1109/TCSⅡ.2021.3135273 doi: 10.1109/TCSⅡ.2021.3135273
|
| [22] |
Wang B, Zhou L, Zhang Y, Wang K, Du X, Sun P (2017) Active junction temperature control of IGBT based on adjusting the turn-off trajectory. IEEE Trans Power Electron 33: 5811‒5823. https://doi.org/10.1109/TPEL.2017.2749383 doi: 10.1109/TPEL.2017.2749383
|
| [23] |
Prasobhu PK, Raveendran V, Buticchi G, Liserre M (2018) Active thermal control of GaN-based DC/DC converter. IEEE Trans Ind Appl 54: 3529‒3540. http://dx.doi.org/10.1109/TIA.2018.2809543 doi: 10.1109/TIA.2018.2809543
|
| [24] | Falck J, Andresen M, Liserre M (2015) Active thermal control of IGBT power electronic converters. IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, 1‒6. http://dx.doi.org/10.1109/IECON.2015.7392925 |
| [25] | Ahsan S, Mughal A, Rapiz M (2022) Controlling temperature of DC-DC converter using switching frequency adjustment, Electrical Engineering Department at California Polytechnic State University. Available from: https://digitalcommons.calpoly.edu/eesp/554 |
| [26] |
Hanini W, Ayadi M (2021) Electrothermal modeling of the Insulated Gate Bipolar Transistor (IGBT) using PSpice: Application to DC–DC converter. J Control Autom Electr Syst 32: 507‒521. https://doi.org/10.1007/s40313-020-00672-y doi: 10.1007/s40313-020-00672-y
|
| [27] | Cao R, Li Y, Zhang Y, Liu X, Lv C, Zhang J (2020) Thermal modeling of power semiconductor devices with heat sink considering ambient temperature dynamics. IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), 290‒295. https://doi.org/10.1109/IPEMC-ECCEAsia48364.2020.9367773 |
| [28] |
Ma K, He N, Liserre M, Blaabjerg F (2015) Frequency-domain thermal modeling and characterization of power semiconductor devices. IEEE Trans Power Electron 31: 7183‒7193. http://dx.doi.org/10.1109/TPEL.2015.2509506 doi: 10.1109/TPEL.2015.2509506
|
| [29] | Erickson RW, Maksimovic D (2020) Fundamentals of power electronics, 3rd Ed., Cham, Switzerland. http://dx.doi.org/10.1007/978-3-030-43881-4 |
| [30] | Lee J (2015) Basic calculation of a buck converter's power stage. Richtek Technol Corp AN041: 1‒8. Available from: http://acots.info/pdf/an041_en.pdf |
| [31] | Ciappa M, Fichtner W (2000) Lifetime prediction of IGBT modules for traction applications. IEEE 38th Annual International Reliability Physics Symposium (Cat. No. 00CH37059), 210‒216. https://doi.org/10.1109/RELPHY.2000.843917 |
Figures(13) / Tables(2)
Rasool M. Imran, Kadhim Hamzah Chalok, Siraj A. M. Nasrallah. Innovative two-stage thermal control of DC-DC converter for hybrid PV-battery system[J]. AIMS Electronics and Electrical Engineering, 2025, 9(1): 26-45. doi: 10.3934/electreng.2025002
| Parameter | Value |
| PV panel power | 2000 W |
| PV panel voltage | 60 V |
| Li-ion battery pack capacity | 30 Ah |
| Li-ion battery pack voltage | 38 V |
| Capacitor 1, capacitor 2 | 1200 µF, 22 µF |
| Filter inductor, resistor | 2 mH, 10 kΩ |
| Cutoff frequency of LPF (fC) | 1 kHz |
DownLoad:
CSV
| Parameter | Value |
| Kp_1, Ki_1, Kp_2, Ki_2 | 10000, 80, 57, 16 |
| Kp_i, Ki_i, Kp_v, Ki_v | 6,500, 2.4, 38 |
| Desired temperature limits (T1st, T2nd) | 340 K, 342 K |
| Switching frequency (fMax, fMin) | 40 kHz, 20 kHz |
DownLoad:
CSV
| Parameter | Value |
| PV panel power | 2000 W |
| PV panel voltage | 60 V |
| Li-ion battery pack capacity | 30 Ah |
| Li-ion battery pack voltage | 38 V |
| Capacitor 1, capacitor 2 | 1200 µF, 22 µF |
| Filter inductor, resistor | 2 mH, 10 kΩ |
| Cutoff frequency of LPF (fC) | 1 kHz |
| Parameter | Value |
| Kp_1, Ki_1, Kp_2, Ki_2 | 10000, 80, 57, 16 |
| Kp_i, Ki_i, Kp_v, Ki_v | 6,500, 2.4, 38 |
| Desired temperature limits (T1st, T2nd) | 340 K, 342 K |
| Switching frequency (fMax, fMin) | 40 kHz, 20 kHz |
