1.
Introduction
The accelerating adoption of electric vehicles (EVs) is largely motivated by the global urgency to mitigate climate change, with fossil fuel–based transportation being a major contributor to greenhouse gas emissions [1,2]. Governments and the private sector are working together to advance EV technologies, aiming to make EVs as viable and accessible as conventional vehicles. A critical factor influencing EV efficiency and performance is the battery system, which governs key metrics like driving range, reliability, and lifespan. The battery is managed by a battery management system (BMS), which ensures safe operation by monitoring thermal and electrical parameters, balancing cell charge, and coordinating other auxiliary functions [3].
Apart from batteries, the efficiency of EVs relies heavily on power converters, specifically the traction inverter and the battery charger (BC). While the inverter controls power flow between the battery and motor, the BC regulates energy transfer from the grid (or alternative sources) to the battery, impacting attributes such as charging speed, range, and battery longevity [4]. BCs are classified based on factors like charging type (conductive vs. inductive), installation location (on-board vs. off-board), and power flow capability (unidirectional vs. bidirectional). Established standards such as IEC 61851-1 and SAE J1772 further distinguish BC types based on charging modes, levels, and safety protocols [1].
DC fast chargers and their associated power converter topologies, such as single-phase and three-phase isolated and non-isolated converters, are widely implemented in EV charging infrastructure. For instance, on-board battery chargers (OBCs) commonly integrate an EMI filter, an AC-DC converter with power factor correction (PFC), and a DC-DC converter. Variants of these topologies allow bidirectional power flow to support vehicle-to-grid interactions, enhancing grid flexibility [2]. However, while existing works cover a range of converter configurations and performance optimization methods [2,5,6], most omit the impact of non-idealities inherent in switching devices and energy storage components. These non-idealities, associated with parameters like switch resistance and inductor characteristics, significantly affect converter efficiency, dynamic response, and control accuracy.
In this study, we investigate a two-level DC-DC battery charger (2L-BC) with a focus on modeling and compensating for these non-idealities. Prior literature on DC-DC converters includes insightful contributions regarding fast-charging infrastructure and converter configurations [7,8,9,10]. Yet, few works address the non-ideal behavior of converters in EV battery charging contexts. For instance, research on general DC-DC converters has examined the impact of non-idealities in switch and inductor behavior, although without direct application to EV charging systems [11,12,13].
This article presents a comprehensive study of a 2L-BC model that includes the effects of non-idealities in switches and energy storage components, which is an area not commonly addressed in depth within the literature. The analysis focuses on how these non-ideal parameters influence essential operating points and performance metrics under both steady-state and dynamic conditions, offering critical insights for enhancing EV charger design and efficiency.
A key part of this study examines the equilibrium voltage VC and its sensitivity to series resistances rL and RDS(on), revealing that as these parasitic resistances increase, VC decreases significantly. This finding highlights the impact of non-idealities on output stability and efficiency. The analysis further investigates the inductance L and capacitance C under varying non-ideal conditions, showing that L decreases as both rL and RDS(on) decrease, establishing a direct relationship that influences energy transfer and response time in the converter. In contrast, the capacitance C remains nearly constant despite variations in rL and rC, confirming its stabilizing role in smoothing voltage ripples in the system.
Additionally, this study highlights the effects of non-idealities on charger efficiency (η). The analysis shows that efficiency peaks under ideal conditions, where parasitic resistances are minimized, while increased parasitic resistances cause a notable drop in performance. These findings emphasize the importance of accounting for non-ideal effects in charger design, providing essential considerations for optimizing both steady-state and transient behaviors in EV charging systems.
The paper is organized as follows: Sections 2 and 3 present the topology and mathematical model of the studied charger. Sections 4 and 5 explore the charger's efficiency and sensitivity to non-idealities incorporated in the model. Sections 6 and 7 focus on the dimensioning of energy storage components, such as the inductor and capacitor, and the synthesis of the linear output-feedback compensator. Finally, Sections 8 and 9 present the simulation results and conclusions of the study.
2.
Battery charger topology
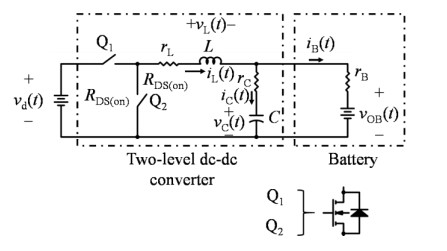
The proposed battery charger topology (2L-BC) is illustrated in Figure 1. It is based on a two-level DC-DC converter, with the load modeled as a standard battery [14]. The 2L-BC topology consists of two switches, labeled Q1 and Q2, which operate complementarily [15]. These switches are implemented using MOSFET devices, each incorporating its associated RDS(on) resistance and driving resistors.
In addition to the switches, the 2L-BC model includes the series resistances of the inductor (rL) and capacitor (rC), which reflect the non-idealities in these components. The battery is represented by its internal voltage, vOB(t), and its internal resistance, rB. The system variables include the input voltage, vd(t), the inductor voltage, vL(t), and the capacitor voltage, vC(t). The currents flowing through the inductor, capacitor, and battery are denoted as iL(t), iC(t), and iB(t), respectively.
It is assumed that the 2L-BC operates in continuous conduction mode, ensuring a stable operating regime for the converter under all conditions.
3.
Battery charger modeling
This section presents the modeling of the 2L-BC charger in both steady-state and dynamic regimes.
3.1. Modeling 2L-BC in steady state
As a preliminary step in the modeling process, it is essential to identify the switching strategy employed by the converter switches (Q1 and Q2). This enables the determination of the switching function of the system in a steady state, which is represented by the variable sf(t). The switching frequency of the 2L-BC is labeled as fs, and the switching period is defined as Ts = 1/fs. It is known that both switches operate in a complementary manner, and thus, the following strategy is derived and defined as follows: in the first half-cycle of the switching period, i.e., when 0 ≤ t < D∙Ts, switches Q1 and Q2 operate as closed and open, respectively. Subsequently, for the second half-cycle, that is, when D∙Ts ≤ t < Ts, Q1 and Q2 operate as open and closed, respectively. With this information, it is possible to define sf(t) as follows [17]:
It should be noted that D is the duty cycle under stationary conditions.
The governing equations for the voltage of L [vL(t)] and the current of C [iC(t)] are derived by applying Kirchhoff's laws of voltage and current. These equations are functions of the variation of the topology as the switching half-cycles occur. The topology in the first switching half-cycle is shown in Figure 2(a), and the expressions for vL(t) and iC(t) are given by:
where Rin = RDS(on) + rL. In contrast, the small ripple approximation (SRA) principle is applied to (2) and (3), assuming that the ripple of the voltages vd(t), vC(t), and vOB(t) and of the current iL(t) is sufficiently small to be neglected, a common assumption in practice [15,16]. The revised versions of (2) and (3) following the application of the SRA are presented in (4) and (5).
The topology of the system when operating in the second half-cycle is depicted in Figure 2(b), and the expressions of vL(t) and iC(t) are defined as follows:
Then, applying the SRA to (6) and (7), the new equations related to this switching half-cycle are given by:
In light of the fact that the 2L-BC operates in a state of steady-state, the principles of inductor volt-second balance and capacitor charge balance are applied to the system. With regard to the former, it is demonstrated that the average voltage of L over one switching period (Ts), i.e., < vL(t) > Ts, must be zero [15]. Consequently, the inductor volt-second balance is calculated from (4) and (8) and stated as follows:
Conversely, the capacitor charge balance principle is applied according to (5) and (9), resulting in the verification that equation < iC(t) > Ts = 0, as given by [15]:
It should be noted that (10) and (11) represent the model of the charger in equilibrium (steady state). For this system, the unknown variables are VC and IL, while the known variables are D and VOB. Solving for VC and IL yields the steady state variables given by:
From (11), it can be observed that the VC dynamics under steady-state conditions exhibit a slight dependence on the charger non-idealities, particularly with regard to RDS(on) and rL. This is due to the fact that, in practice, rB is significantly larger than Rin, resulting in rB || Rin ≈ rB. Therefore, the equilibrium state of the system may change if such resistances are not considered. The model of the charger in steady-state is illustrated in Figure 3.
3.2. Modeling 2L-BC in steady state
Figure 2 and (1)−(3), (8), and (9) provide the 2L-BC switching model defined by
Subsequently, the averaging operator ⟨x(t)⟩Ts=1Ts⋅∫tt−Tsx(τ)⋅dτ is applied to (13) over a Ts, resulting in the averaged model of the 2L-BC, defined as follows [15,17]:
Finally, the model in (14) is linearized using the Taylor series and the perturbation of the variables around the points of the charger [11,18] in steady-state. The equilibrium model of the charger, as represented in (12) [15,17], is used to calculate the steady-state values. It should be noted that in the switched model of the charger described in (13), the switching function is replaced by its averaged version, with the addition of a small disturbance in AC, i.e., d(t). The linearization of the charger results in the derivation of the small-signal state-space model, shown as follows:
It should be noted that the variables with hats are the small-signal variables, which are assumed to be much smaller than their steady-state variables [15]. The state vector, defined in (15) as x(t)=[ˆiL(t),ˆvC(t)]T, groups the state variables. The input vector, defined as u(t)=[ˆvd(t),ˆvOB(t),ˆd(t)]T, groups the input variables. Finally, the output vector, defined as y(t) = [x(t), ˆiB(t)]T, groups the input variables. In this charger, the outputs have been defined as the state variables plus the load current. Furthermore, x(t) ∈ {R2} and {u(t), y(t)} ∈ {R3}. Conversely, the matrices of the model in (15) are defined as follows:
From here, Am, Bm, Cm, and Dm are the state, input, output, and direct transmission matrices, respectively. Also, Am M2x2 ∈ {Κ}, Bm M2x3 ∈ {Κ}, Cm, M3x2 ∈ {Κ}, and Dm M3x3 ∈ {Κ}.
4.
Efficiency calculation
An interesting figure of merit to characterize the charger is the expression of the performance parameter (η) [15,19,20,21]. It is known that η = Po/Pi, where Pi and Po are the input and output power of the charger, respectively. According to Figure 3, Pi and Po are given by
From (17), Av1 and Av2 are defined as steady-state voltage gains, specifically Av1 = VC/Vd and Av2 = VC/VOB. Then, the expression of η is calculated and shown as follows:
It is interesting to note that this expression is of the nonlinear type, mainly due to the presence of Av1 and Av2. Furthermore, it can be seen that the efficiency is strongly dependent on the non-idealities RDS(on) and rL, and it can be confirmed from (18) that this dependence is of the hyperbolic type.
Some observations can be drawn from the latter:
● The efficiency is highly sensitive to the non-idealities of the charger, such as the resistance RDS(on) and the inductor resistance rL.
● The dependence on these resistances follows a hyperbolic type, emphasizing that as the losses increase (due to higher RDS(on) or rL), the efficiency decreases.
This section highlights the importance of these non-idealities in the performance of the charger and how they affect its overall efficiency. The equation provides a framework to optimize the design by minimizing these losses to maximize efficiency.
5.
Sensitivity analysis
The goal of the sensitivity analysis is to evaluate how variations in the non-ideal resistive parameters—specifically rL, rC, and RDS(on)—affect the efficiency η of the 2L-BC. By computing partial derivatives of the efficiency equation with respect to each of these parameters [22], insights are obtained into the individual and relative impacts of each non-ideality on system efficiency.
5.1. Sensitivity to rL
The analysis of sensitivity with respect to the inductor resistance rL reveals its significant influence on the overall efficiency η of the 2L-BC. As rL directly contributes to the input resistance Rin (where Rin = RDS(on) + rL), an increase in rL raises Rin, thereby affecting the voltage gain terms Av1 and Av2, both of which depend on Rin. The partial derivative of efficiency with respect to rL is given by:
Equation (19) indicates that the sensitivity of η to rL is inversely proportional to Rin2. This hyperbolic relationship implies that an increase in rL leads to a decrease in efficiency, highlighting rL as a critical parameter. Reducing rL by selecting low-resistance inductors or optimizing inductor design can mitigate resistive losses and enhance charger efficiency. Thus, managing inductor resistance is essential for optimizing overall system performance, particularly in high-efficiency applications
5.2. Sensitivity to rC
The capacitor resistance rC influences the voltage gain Av2, defined as the ratio of the capacitor voltage VC to the output voltage VOB. Changes in rC modify Av2, which in turn affects efficiency. The partial derivative of η with respect to rC is expressed as:
Expression (20) shows that the sensitivity of η to rC is influenced by rC's interactions with rB and Rin. This complex relationship implies that increasing rC can significantly affect efficiency due to its quadratic effect on the gain term, reducing η more strongly as rC rises. Consequently, minimizing rC through capacitor selection or design adjustments can enhance efficiency, especially in systems where resistive losses are critical. This emphasizes the importance of keeping rC low for optimal performance in high-efficiency charging applications.
5.3. Sensitivity to RDS(on)
The MOSFET on-resistance RDS(on) also contributes to Rin, thus influencing both voltage gains Av1 and Av2, which impact efficiency. The sensitivity of η to RDS(on) is derived by differentiating the efficiency equation with respect to RDS(on):
Expression (21) reveals that RDS(on) and rL produce identical sensitivity effects on η due to their combined role in Rin. The analysis indicates that increases in either RDS(on) or rL lead to efficiency reductions, as both raise Rin, which in turn lowers Av1 and Av2, thus decreasing η. This result underscores the importance of minimizing both RDS(on) and rL to improve efficiency, especially in high-performance charger designs where resistive losses need to be minimized.
6.
L and C sizing
In order to calculate the energy storage elements, L and C, the slopes (m) of iL(t) and vC(t) during the first switching half-cycle, i.e., in the time interval 0 ≤ t < D∙Ts, are considered. These slopes are obtained from (4) and (5), respectively. Additionally, the slopes of iL(t) and vC(t) are depicted in Figure 4(a) and (b), respectively. Based on Figure 4 and the aforementioned equations, the values of L and C are calculated and presented as follows:
From (22) and (23), the maximum allowable ripple percentages with respect to VC and IL, i.e., ΔVC and ΔIL respectively, can be calculated. It can also be seen that both ΔVC and ΔIL represent the constraints imposed on 2L-BC, which must be met. It is once again evident that the non-idealities of the charger affect the sizing of the energy storage elements, specifically at L and C. Nevertheless, as indicated by (22) and (23), the sizing of L is more significantly influenced by the variation of RDS(on) and rL than by the sizing of C.
7.
Compensator synthesis
The linear model in (15) is considered, and the Laplace transform (s) is applied to obtain the s-domain model shown as follows:
In (24), I is an identity matrix of dimension 2×2. From (24), it follows that Y(s) = [IL(s), VC(s), IB(s)]T and U(s) = [Vd(s), VOB(s), D(s)]T are the complex output and input vectors, respectively. These vectors are defined as {U(s), Y(s)} ∈ 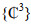 .
.
Figure 5 presents the proposed control diagram for the 2L-BC, structured with a standard output feedback configuration [18]. The primary control goal is to regulate iB(t) using a PI compensator, chosen for its simplicity and well-established performance in power electronics applications. The PI compensator, extensively studied in the literature, is widely recognized for its effectiveness in reducing steady-state errors and ensuring stable transient responses, making it highly suitable for systems like the 2L-BC.
In this configuration, the PI controller outputs the duty cycle d(t), which is then fed into the charger modulator. The modulator produces the switching function sf(t), which manages the states of switches Q1 and Q2 according to (1). This approach leverages the robustness of PI control to handle non-idealities in the 2L-BC, thereby enhancing system stability and performance across variable load conditions.
The transfer function of interest for this control system is obtained from (24), which corresponds to:
The steady-state gain (k), the zero (ωz), and the poles (ωp1 and ωp2) are defined as follows:
The controller described in Figure 5 is designed using the phase-margin test (PMT) [15]. As illustrated in Figure 5, and in accordance with the extensive literature on PI compensators, this compensator can be modeled as follows [15]:
where kp and τi are the proportional and integral constants, respectively. The block diagram associated with this loop is illustrated in Figure 6. On the other hand, the loop gain of the system is defined by:
On the other hand, the modulator is based on pulse-width modulation (PWM), and its design and operation are described in Figure 7 [15,16]. Its Laplace model is given by M(s) = 1/VM, where, in this case, VM = 1 V. The high-frequency carry function is represented by the following model:
According to the PMT, it is necessary to study the frequency behavior of the loop gain where the compensator Gc(s) is not involved, assuming that Gc(s) ≈ 1. This loop gain [Tu(s)] is given by:
Table 1 provides a list of the parameters associated with the charger under study [23]. Table 1 indicates that the frequency response of (30) can be obtained and illustrated in Figure 8. With regard to the PMT, the crossover frequency (fc) of the frequency response of Tu(s) can be considered to be equal to the switching frequency of the charger, that is, fc = fs = 27 kHz. Consequently, Figure 8 reveals that fc ≈ 13.2 kHz. Consequently, a compensator is necessary to bring the fc of the uncompensated system as close as possible to fs. As part of the procedure, the compensated loop gain of the system has been defined in (25). However, by making the change of variable s = j∙ω, assuming ω > > 1, defining that ωc = ωs, and considering (24):
valid for high frequencies. The PMT can be applied to yield the following [15]:
and, to ensure good stability, τi = 100/ωs is defined [15]. Consequently, the PI compensator has already been designed. In order to verify that the PI has been properly designed, (28) must be evaluated. Figure 9 illustrates the frequency response of the compensated loop gain.
From Figure 9, it can be established that the fc (≈ 29 kHz) is close to fs, which indicates that the design of the PI compensator is adequate.
8.
Simulation results
The simulation of the switched and averaged 2L-BC models defined in (13) and (14), respectively, is performed using MATLAB Simulink and Table 1. The control system proposed in Figure 5 is also implemented. The 2L-BC is supplied with a dc voltage Vd = 800 V and operates with an fs of 27 kHz.
The initial conditions of the 2L-BC are imposed on the battery and inductor currents, as well as on the capacitor voltage. This is indicated by the following values: iB0 = iL0 = 0 A and vC0 = 400 V. In contrast, the initial reference value of the load current is I*B = 30 A.
Figure 10 depicts the simulation results for the transient dynamic responses of iB(t), iL(t), vC(t), d(t), and vOB(t) in their switched version, i.e., iBsm(t), iLsm(t), vCsm(t), dsm(t), vOBsm(t), and in their averaged version, i.e., iBav(t), iLav(t), vCav(t), dav(t), and vOBav(t), respectively. Regarding the 2L-BC operation, at 60 ms, there is a step change in iB(t), reaching a new value of 40 A and subsequently entering a steady state. Additionally, at 90 ms, a change in the load is generated, resulting in a shift in the internal battery voltage, vOB(t), from 450 to 350 V. This disturbance in the system dynamics is observed at 90 ms.
Figure 10(a) illustrates that iB(t) behaves as if it were a first-order system, exhibiting no overshoot and zero steady-state errors. The settling times are notably brief, with iB(t) reaching its steady state after startup in just 30 ms. Following the step change in iB*(t), iB(t) reaches its final steady-state value in 4 ms. Furthermore, upon the occurrence of a change in load, a transient is generated in iB(t) of a very short duration (resembling a pulse, as described by [18]), with a duration of approximately 1.5 µs, after which it returns to its steady state value of 40 A. This situation serves to illustrate the optimal design of the PI compensator, while also demonstrating the adequate stability of the system.
Conversely, it can be demonstrated that the sizing of L and C is adequate and meets the ripple requirement. That is, the ripple of iL(t) and vC(t) is lower than ΔIL and ΔVC, respectively.
As illustrated in Figure 10(b) and (c), it can be observed that the values of ΔIL and ΔVC reach 0.16% and 2.4%, respectively.
In addition, the dynamics of iL(t) and vC(t) are observed to work correctly with a step change in iB*(t) and a change in load. After starting, vC(t) takes the value of 480 V and iL(t) takes the value of 30 A.
Then, for the step change in iB(t), a logical increase in both variables [in iL(t) and vC(t), respectively] is generated. Finally, when the disturbance is generated in the load, iL(t) takes its maximum value of 45.43 A and, after 13 ms, it returns to its value of 40 A. On the other hand, vC(t) suffers a significant decrease, taking a transient value of 395.4 V, and after 10 ms, it reaches its final steady state value of 390 V. Such a condition generated in both variables after the load disturbance can be verified by analyzing expressions (2), (3), (6), and (7).
In Figure 10(d), it is observed that after system startup, the duty ratio d(t) takes the value of 0.64. After the step change in iB(t), d(t) takes a new steady state value of 0.66 and finally, when the load change occurs, d(t) undergoes an impulse type of disturbance and reaches its minimum value of 0.01 for a time of 1.5 μs [similar to iB(t)]. It also assumes a new steady state value of 0.54. On the other hand, a stable and unsaturated behavior is observed at d(t), which implies a greater slack in the control of iB(t). In addition, a small overshoot in d(t) is observed in response to the step change in iB(t). It is also observed that the switching frequency fs is transferred to d(t) due to the operation of the switches according to the switching strategy described in (1).
Figure 11 presents a series of surface plots analyzing the effects of variations in non-ideal parameters on the equilibrium point VC and the values of inductance L and capacitance C. Specifically, Figure 11(a) shows the equilibrium voltage VC as a function of inductor resistance rL and MOSFET on-resistance RDS(on); Figure 11(b) illustrates the variation of L as a function of rL and RDS(on); and Figure 11(c) depicts the variation of C as a function of rL and capacitor resistance rC. The constant parameters and respective variables are listed in Table 2.
In Figure 11(a), the expression for VC follows (12), while the expressions for L and C in Figures 11(b) and 11(c) are given by (22) and (23), respectively. From Figure 11(a), it is evident that VC decreases significantly with increases in rL and RDS(on), indicating an inverse relationship. This finding aligns with the sensitivity analysis, which showed that higher rL and RDS(on) reduce efficiency due to increased input resistance Rin, impacting the voltage gain terms Av1 and Av2.
In Figure 11(b), the value of L decreases as both rL and RDS(on) decrease, demonstrating a direct relationship between L and these parameters. This relationship is consistent with the overall system's sensitivity to resistive elements, suggesting that minimizing rL and RDS(on) can mitigate resistive losses and positively influence system performance.
In contrast, Figure 11(c) indicates that the magnitude of C remains nearly constant despite variations in rL and rC, confirming the observations in Section 6. The value of C appears close to zero in the plot for scaling purposes, although it is approximately 100 nF.
Figure 12 illustrates the sensitivity of efficiency η as a function of rL and RDS(on), derived from (18). The surface plot reveals that charger performance is maximized under ideal conditions, where rL = RDS(on) = 0. As these non-ideal parameters increase, efficiency η declines sharply, consistent with the sensitivity analysis that showed an inverse relationship between η and both rL and RDS(on). This trend underscores the critical importance of minimizing these resistive losses when designing high-efficiency chargers. Table 3 lists the constant parameters and the variables relevant to this analysis.
These observations provide essential design insights, highlighting that reducing non-idealities rL, RDS(on), and rC is imperative for maintaining high efficiency in charger applications.
Figure 13 depicts the surfaces plotted in relation to the sensitivity expressions derived in (19)−(21). From this, it can be demonstrated that as rL and RDS(on) increase, the efficiency (η) decreases significantly until a saturated value is reached [see Figure 13(a)]. Additionally, Figure 13(b) illustrates that as rC increases, η also decreases significantly. This further verifies the strong dependence of these non-idealities on the behavior of η.
Figure 14 illustrates the step response of the loop gain in (25). From this figure, it can be observed that the dynamics under transient of (25) behave as a first-order system. Moreover, it can be identified that the system reaches a steady state at approximately 20 ms, demonstrating that the system responds rapidly to disturbances of this nature.
Finally, Figure 15 depicts the root locus diagram of (28). From this figure, it can be concluded that the loop gain exhibits a totally stable behavior, as all its poles are in the left half-plane of the s-plane. Furthermore, it is demonstrated that the system in question (28) has two zeros and two poles.
9.
Conclusions
This work presents a detailed analysis of the two-level battery charger (2L-BC) performance using both switched and averaged models, with simulations conducted to validate the proposed control system and its design. The simulation results demonstrate that the system performs effectively under a range of operating conditions, with robust transient responses and well-behaved dynamic characteristics. Specifically, the battery current, inductor current, and capacitor voltage exhibit first-order dynamics, with settling times of just 30 ms after startup and 4 ms following step changes in load. These results confirm the rapid response capabilities of the system, highlighting the efficient performance of the PI compensator in maintaining minimal steady-state errors and overshoot.
Ripple analysis further supports the adequacy of the system design, with the ripple in inductor current and capacitor voltage kept well below the specified limits, verifying that the inductance and capacitance values chosen meet the performance requirements. The duty cycle shows stable behavior even during load changes, further illustrating the control strategy's effectiveness in maintaining system stability under dynamic conditions. These findings underscore the importance of a well-designed control system that can manage real-time variations while minimizing ripple and ensuring efficient power conversion.
Sensitivity analyses on non-ideal parameters, including inductor resistance, MOSFET on-resistance, and capacitor resistance, reveal their significant impact on system performance, particularly efficiency and equilibrium voltage. As these resistive losses increase, efficiency declines due to higher losses in the power stages. The equilibrium voltage decreases with higher values of inductor resistance and MOSFET on-resistance, highlighting the importance of minimizing these resistances to maintain high efficiency. Additionally, the analysis confirms that the sizing of the inductor and capacitor is well-calibrated to meet ripple requirements without compromising performance.
The efficiency analysis indicates that maximum performance is achieved when resistive losses are minimized. As resistances such as inductor resistance, MOSFET on-resistance, and capacitor resistance increase, efficiency declines sharply, reinforcing the need for careful component selection to reduce these non-idealities. The results suggest that even small increases in these resistances can lead to significant efficiency losses, underscoring the importance of considering component tolerances and non-idealities during the design phase.
The loop gain analysis indicates that the system's dynamics behave as a first-order system, with fast transient responses and minimal overshoot. The system reaches steady-state conditions quickly, demonstrating its ability to respond efficiently to rapid disturbances. The root locus analysis confirms the stability of the control system, with all poles residing in the left half-plane of the s-plane, ensuring robust performance under various operating conditions.
Overall, the findings from this study offer valuable insights into the design and optimization of battery chargers, emphasizing the importance of selecting components with low resistances to maximize system efficiency. The proposed control system is shown to be effective in ensuring stable and efficient operation, providing an essential framework for future developments in high-efficiency power converters. Future research could explore further refinements in the control strategy and experimental validation, as well as the integration of more advanced control techniques, such as model predictive or sliding mode control, to enhance system robustness and transient response, especially in the presence of larger disturbances or component aging.
Author contributions
Conceptualization: JMCS; Formal analysis: JMCS, JLAL, and RF; Investigation: JMCS, JLAL, and RF; Methodology: JMCS and RF; Supervision: JMCS; Validation: JMCS, JLAL, and RF; Visualization: JLAL and RF; Writing − original draft: JMCS; Writing − review & editing: JLAL and RF.
Conflict of interest
The authors declare that there is no conflict of interest in this paper.









 DownLoad:
DownLoad:

 closed and Q2
closed and Q2 

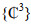 .
.