Quantum chemical calculations on calcium oxalate and dolichin A and their binding efficacy to lactoferrin: An in silico study using DFT, molecular docking, and molecular dynamics simulations

1.   Introduction

The last couple of decades have seen a large number of researchers emphasizing the integration of two or more models into a single one to coordinate the efforts of two or more functions in a firm. Indeed, as shown in many studies, decision making in an integrated model can lead to significant savings over decision making in the separate models. The integrated models we have in mind are the production planning model and the maintenance model. This integrated model has been largely studied, see for example the overviews of Ben-Daya and Rahim ^[1] and Van Horenbeek et al. ^[2]. The model of interest to us was introduced by Cho et al. ^[3]. The performance of the production process they considered worsens over time in the absence of maintenance. They measured the performance of the process in terms of the proportion of 'good' (non-defective) units produced.

Using the maximum principle, the authors obtained the necessary conditions for the controls (production rate and preventive maintenance rate) to be optimal in the case of a quadratic production cost function and linear maintenance cost function. They used a two-stage algorithm, tailored to this problem, to solve for the optimal controls.

This model has been further investigated by other researchers. Maurer et al. ^[4] studied the same model under different cost structures. They used a second order sufficiency test to prove optimality of the computed controls. The dynamics of the model were also studied by Bukhari ^[5] who used an adaptive control approach. Assuming a system of the tracking type, Bukhari and El-Gohary ^[6] substituted a tracking error objective function for the profit objective function of Cho et al. ^[3]. They also used the maximum principle to obtain the optimal production and maintenance rates. Besides production and maintenance, Li ^[7] incorporated emission tax and pollution R&D investment. Again, the maximum principle was used to derive the optimal production rate, the optimal maintenance rate, and the optimal pollution R&D investment rate.

Our intention in this paper is to further investigate the model of Cho et al. ^[3] in the following two ways: 1) By generalizing the model; and 2) by applying a different solution technique.

Concerning the model, first we introduce the deterioration of items while in stock. This is a very important topic in inventory theory as shown by the numerous survey papers that have been written on the subject. The field of deteriorating and perishable inventory models has undergone substantial evolution, as detailed in several comprehensive reviews. Bakker et al. ^[8] and Janssen et al. ^[9] analyze developments in inventory systems since the early 2000s, focusing on deterioration rates, demand variability, and supply chain coordination. These reviews highlight the importance of incorporating realistic assumptions and the potential for empirical studies to enhance model applicability. Goyal and Giri ^[10] and Raafat ^[11] provide foundational insights, mapping the trajectory of inventory models that address perishability and the economic implications of inventory deterioration.

In more recent analyses, Chaudhary et al. ^[12] and Kaushik ^[13] examine inventory models tailored for perishable products, emphasizing the role of time-dependent demand, shelf life, and pricing strategies. These reviews underscore the necessity of sophisticated models to reduce waste and optimize inventory levels, suggesting that integrating stochastic elements and customer behavior can further enhance model robustness. Li et al. ^[14] also contribute by reviewing the various replenishment policies and demand types, offering a comprehensive overview of the deteriorating inventory models and their applications.

Additionally, Karaesmen et al. ^[15] and Pahl and Vo$ß$ ^[16] delve into the management of perishable and aging inventories, discussing the integration of deterioration and lifetime constraints in production and supply chain planning. Their work emphasizes dynamic models that adapt to changing conditions and the potential of big data and machine learning to refine inventory management. Nahmias ^[17] provides a classic review of perishable inventory theory, setting a foundation for understanding early inventory policies. Sharan and Sayyed ^[18] conclude with a focus on mathematical approaches to deteriorating inventory models, advocating for optimization algorithms and simulation techniques to advance the field further.

Thus, not only does the process deteriorate over time, but the end product also deteriorates while it is on the shelves. Second, we use a more general cost function of which the objective function of Cho et al. ^[3] is a special case. Third, we assume that all the exogenous parameters involved (items deterioration rate, obsolescence rate of process performance in the absence of maintenance, and demand rate) are general functions of time.

Concerning the solution method, Cho et al. ^[3] used an algorithm that was adapted to their control problem. In contrast, we employ the nonlinear model predictive control (NMPC), which seems particularly well-suited to control a dynamic model with nonlinear constraints and an objective function.

We notice that our work treats the model introduced and studied in Cho et al. ^[3]. We tried to refer to all the relevant works studying the same model such as the ones cited in the introduction. Unfortunately, we found in the literature a small number of works on this subject and we are trying to expand the utility of their model in the hope that it will attract other researchers to work on the same topic.

2.   Model building

We will be following the notation of Cho et al. ^[3] as much as possible. Let $\theta(t)$, $\alpha(t)$, and $s(t)$ denote the items deterioration rate at time $t$, the obsolescence rate of process performance in the absence of maintenance (non-decreasing function of time), and demand rate at time $t$, respectively. The state of the system is described by the state variables $x(t)$ and $p(t)$ ($0 \le p(t) \le 1$), which denote the inventory level at time $t$ and the proportion of good units of end items produced at time $t$, respectively. Control over the system is achieved through the control variables $u(t)$ and $m(t)$, representing the scheduled production rate at time $t$ and maintenance rate applied at time $t$, respectively.

Next, we derive the equations that describe the dynamics of the inventory level and the proportion of good units produced over time in the production system in response to production rates, maintenance activities, demand, and deterioration. For the inventory dynamics, we note that the inventory increases at a rate proportional to the product of the proportion of good units produced, $p(t)$, and the scheduled production rate, $u(t)$; and the inventory decreases due to demand, $s(t)$, and the deterioration of items in stock at a rate of $\theta(t) x(t)$. Therefore, the change in the inventory level, $\dot{x}(t)$ is such that:

For the production quality dynamics, we note that the proportion of good units decreases at a rate dependent on the obsolescence of the production process, $\alpha(t)$, and the maintenance rate, $m(t),$ both of which reduce $p(t)$; and the maintenance efforts, $m(t)$, also contribute positively to the proportion of good units. Therefore, the change in the proportion of good units produced, $\dot{p}(t)$, is such that:

Here, the initial inventory level at time $t = 0$ is given by $x_0$ and the initial proportion of good units at time $t = 0$ is given by $p_0$.

To determine the optimal production and maintenance cost, we follow the same idea as in Cho et al. ^[3] and minimize the prediction horizon a cost function that is a combination of various cost elements, namely production, inventory, and maintenance. The forms of the cost elements are taken from Cho et al. ^[3] in nonlinear forms.

The first cost element penalizes the production of defective items, encouraging the system to maintain a high $p(t)$ (i.e., a high proportion of good units). Since $p(t)$ is the proportion of good units produced, $1 - p(t)$ is the proportion of defective units. Multiplying the production rate $u(t)$ by $1 - p(t)$ gives the rate at which defective items are produced. Letting $w$ represent a cost factor that quantifies the cost associated with producing defective items, the cost associated with the production of defective or substandard items during the time interval $[t_0, t_0 + T]$ is given by

The second cost element penalizes high inventory levels, encouraging the system to avoid excess inventory. Using a quadratic function to account for increasing costs due to higher levels of inventory (e.g., storage, spoilage, or insurance costs), the inventory holding cost during the time interval $[t_0, t_0 + T]$ is given by

where $h_1, h_2 > 0$.

The third cost element balances the cost of production, discouraging both excessive production (due to the quadratic term) and underproduction (which could lead to unmet demand). Using again a quadratic cost to reflect possible increasing marginal costs at higher production rates (e.g., overtime pay, wear and tear on machinery), the production cost during the time interval $[t_0, t_0 + T]$ is given by

where $r_1, r_2 > 0$.

The fourth cost element controls the maintenance activity, balancing the cost of maintenance against the need to maintain a high $p(t)$ by preventing obsolescence (managed by $m(t)$). Using again a quadratic cost to account for the fact that aggressive maintenance might incur higher costs (e.g., more frequent servicing, downtime), the production cost during the time interval $[t_0, t_0 + T]$ is given by

where $c_1, c_2 > 0$.

Combining these cost elements, we write our objective function as

where

By taking into account production quality, inventory costs, production costs, and maintenance costs, our objective is to find the optimal balance between production, inventory, and maintenance activities that minimizes the total cost over the time period of interest.

3.   Model solution

We are faced with the problem of minimizing the cost function (2.3) subject to the state equations (2.1) and (2.2). We proceed using the trapezoid formula to calculate the integral. For simplicity, we will be writing $t$ instead of $t_0$. Let $n$ be a positive integer and divide the interval $[t, t+T]$ into $n$ sub-intervals of equal length $h = \frac{T}{n}$. Then, by the trapezoid formula for $n$ intervals, the objective function (2.3) can be approximated as follows:

To calculate the summation in expression (3.1) above, we apply the first-order Taylor approximation to $x(t+ih)$ and $p(t+ih)$ to get:

where

Note that taking the square of $x(t+ih)$ yields:

where

Substituting in (2.4), we get:

Let

Then,

Hence, substituting this expression in (3.1) yields

Therefore, using a matrix notation, we can write:

where

with

Simple computations permit us to write

The unique global maximum of the objective function $J$ is reached at the couple $(U^*(t), M^*(t))$, which is the solution of the vectorial system of two equations:

From (3.2) we have

Inserting (3.4) into (3.3), we obtain

Substituting the value of $M^*(t)$ in (3.4), we obtain the value of $U^*(t)$ as follows

Based on the principal of Model Predictive Control (MPC), only the first components $m^*(t)$, $u^*(t)$ of $M^*(t)$, $U^*(t)$ are applied in the state equations (2.1) and (2.2), respectively. Then, by solving (2.1) and (2.2) we get the optimal state variables $x^*(t)$ and $p^*(t)$. Therefore, we obtain

and

with

Inserting the previous explicit forms of $m^*(t)$ and $u^*(t)$ in the system of differential equations (2.1) and (2.2) yields a system of nonlinear differential equations that can be solved numerically. We summarize, in the following steps of the solution procedure:

4.   Illustrative example

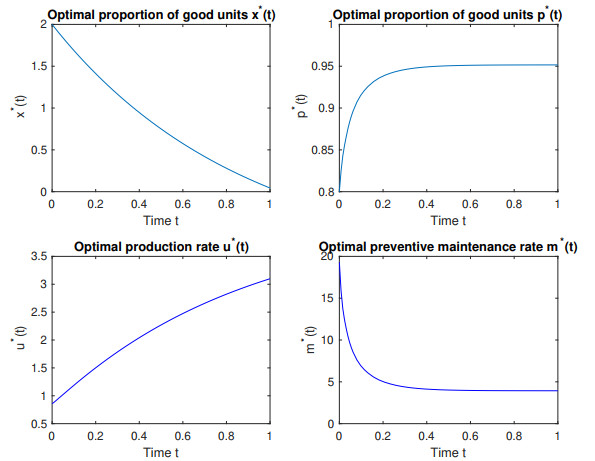
Let us take the same data as in reference ^[3]. Assume that $x_0 = 2$, $p_0 = 0.8$, $T = 1$, $c_1 = 0.025$, $c_2 = 0.1$, $w = 1$, $h_1 = 0.01$, $h_2 = 1$, $r_1 = 0.01$, $r_2 = 4$, and $n = 20$. In a first example, we assume that the three known functions $s$, $\alpha$, and $\theta$ are constant, that is, $s(t) = 4$, $\alpha(t) = 0.02$, and $\theta(t) = 0.01$. In this case, the optimal solutions $x^*$ and $p^*$ of the system of state differential equations are shown in Figure 1. Also shown in Figure 1 are the optimal control variables $u^*$ and $p^*$.

Figure 1.  Case $s(t) = 4$, $\alpha(t) = 0.2$, and $\theta(t) = 0.01$: Optimal inventory level $x^*(t)$ (top left) and optimal proportion of good units $p^*(t)$ (top right); optimal production rate $u^*(t)$ (bottom left) and optimal preventive maintenance rate $m^*(t)$ (bottom right).

DownLoad: Full-Size Img PowerPoint

The optimal inventory level $x^*(t)$ consistently diminishes as time progresses. Starting from an initial value of approximately 2, it gradually declines to 0 by the end of the prediction horizon. This indicates that the system exhausts its inventory during production, depending on the produced units to restock. The optimal proportion of good units $p^*(t)$ commences below 0.9 and swiftly rises, nearing a plateau around 0.95. This implies an enhancement in production quality over time, stabilizing close to an upper threshold. The optimal production rate $u^*(t)$ initiates slightly above 0.5 and steadily escalates throughout the prediction period, reaching about 3.5. This mirrors a gradual increase in production activity as the system advances. Finally, the optimal rate of preventive maintenance $m^*(t)$ commences at a notably high level (approximately 20) and swiftly diminishes over time, eventually stabilizing at a low level near 5. This indicates that intensive preventive maintenance is crucial at the beginning of the process to ensure production quality, but the necessity for maintenance decreases as the system stabilizes. The optimal objective function value in this example is $J^* = 58.1242$.

Assume now that the known functions $s$, $\alpha$, and $\theta$ are not constant and are such that $s(t) = 0.4t+2$, $\alpha(t) = \frac{0.1}{10+t}$, and $\theta(t) = 0.01+0.04\sin(t)$. We take the rest of the parameters as follows: $x_0 = 1.2$, $p_0 = 0.8$, $T = 1$, $c_1 = 0.025$, $c_2 = 0.1$, $w = 1$, $h_1 = 0.01$, $h_2 = 1$, $r_1 = 0.01$, $r_2 = 4$, and $n = 20$. In this non constant case, the optimal inventory level $x^*$, the optimal proportion of good units $p^*$, the optimal production rate $u^*$, and the optimal preventive maintenance rate $m^*$ are shown in Figure 2.

Figure 2.  Case $s(t) = 0.4t+2$, $\alpha(t) = \frac{0.1}{10+t}$, and $\theta(t) = 0.01+0.04\sin(t)$: Optimal inventory level $x^*(t)$ (top left) and optimal proportion of good units $p^*(t)$ (top right); and optimal production rate $u^*(t)$ (bottom left) and optimal preventive maintenance rate $m^*(t)$ (bottom right).

DownLoad: Full-Size Img PowerPoint

The optimal level of inventory $x^*(t)$ shows a consistent decline over time, starting at approximately 1.2 and reaching 0 by the end of the prediction horizon. This implies that as production progresses, the inventory is being used up, and the demand is met with the units produced. The optimal proportion of good units $p^*(t)$ initiates at around 0.8 and experiences a rapid increase, converging towards a value close to 1 by the end of the forecast horizon. This suggests a swift enhancement in production quality, stabilizing at almost perfect quality (nearly 100% good units). The optimal rate of production $u^*(t)$ commences at a relatively low level of about 0.5 and steadily rises over time, reaching approximately 2. This indicates a gradual escalation in production activity as the system progresses towards the optimum output. Finally, the optimal rate of preventive maintenance $m^*(t)$ starts at a high point (around 25) and diminishes rapidly, eventually stabilizing at a lower level close to 5. This signifies that initially, a substantial amount of preventive maintenance is necessary to enhance the production process's quality. However, the requirement for maintenance declines as the system stabilizes over time. The optimal objective function value is $J^* = 25.4288$.

5.   Sensitivity analysis and managerial implications

As is well known, conducting sensitivity analysis on system parameters provides valuable insights and aids in informed managerial decision-making. We choose some key parameters and assess their impact on the optimal solution and the optimal objective functional value. The sensitivity analysis is performed in the general case where the known functions $s$, $\alpha$, and $\theta$ are not constant.

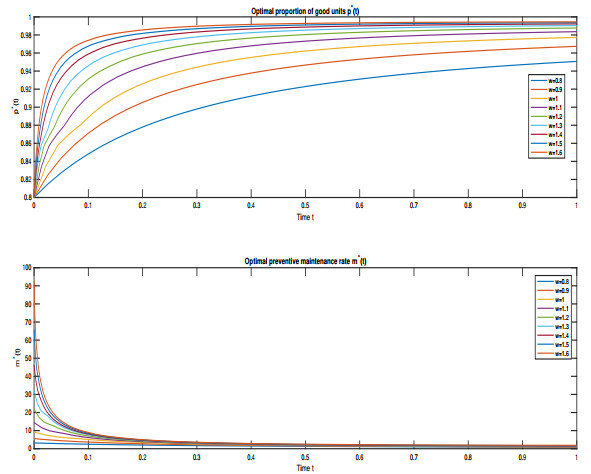
Sensitivity to $w$. This sensitivity analysis reflects the weight of production quality control (i.e., penalizing the proportion of defective units) on the total cost.

First, we note that the change in the values of $w$ does not affect the optimal inventory level and the optimal production rate. Looking at Figure 3 (top), we observe that the optimal proportion of good units $p^*(t)$ increases continuously as $w$ increases. This suggests that the system seeks to retain a higher proportion of good units to reduce the penalty associated with faulty goods when the cost of quality (expressed by w) is more significant. Also, Figure 3 (bottom) shows that for all values of $w$, the first preventive maintenance rate $m^*(t)$ spikes dramatically at the beginning, indicating an immediate attempt to increase or maintain the proportion of good units. On the other hand, $m^*(t)$ rapidly decays with time, suggesting that following an initial burst of maintenance actions, the system stabilizes and requires less work.

Figure 3.  Case $s(t) = 0.4t+2$, $\alpha(t) = \frac{0.1}{10+t}$, and $\theta(t) = 0.01+0.04\sin(t)$ and $w$ in the range $\{0.8;0.9;1;1.1;1.2;1.3;1.4;1.5;1.6\}$: Optimal proportion of good units $p^*(t)$ (top); and optimal preventive maintenance rate $m^*(t)$ (bottom).

DownLoad: Full-Size Img PowerPoint

Sensitivity analysis in Table 1 shows that the optimal objective function value $J^*$ rises dramatically with an increase in $w$. For example, with $w = 0.8$, the total cost is relatively low ($J^* = 18.25$), while it increases exponentially to 332.30 when $w = 1.6$. This rapid growth shows the substantial impact that increased focus on product quality has on the overall cost. The cost of maintaining higher-quality products becomes more expensive. This makes intuitive sense because ensuring a higher proportion of good units (through increased maintenance or production adjustments) requires more resources.

Table 1.  Sensitivity to $w$.

w	0.8	0.9	1	1.1	1.2	1.3	1.4	1.5	1.6
$J^*$	18.25	18.87	22.90	25.92	37.20	58.60	100.98	182.15	332.30

---

 | Show Table

DownLoad: CSV

Some important managerial insights can be gained from these experiments. First, in order to effectively manage the production process, quality and cost must be balanced. In proportion to the system's increased emphasis on quality (seen by rising $w$), overall expenses climb dramatically. Businesses that prioritize excellent quality will see significant cost increases; those that can tolerate a little lower proportion of good units can retain manageable expenses. Beyond a certain point, expenses start to grow sharply, indicating that more quality improvements might not always be worth the money. To prevent unjustified cost rises, managers must carefully consider how much to invest in reaching greater quality levels. Second, initial preventative maintenance is critical in every case, irrespective of the quality level selected. Early maintenance investments contribute to the establishment of a reliable and effective manufacturing process. As continuous maintenance rates level out over time, long-term cost benefits are realized. Thus, even if the initial expenses could be substantial, businesses gain from a proactive approach centered on preventive maintenance since it eventually lowers operating costs and effectively preserves output quality over time.

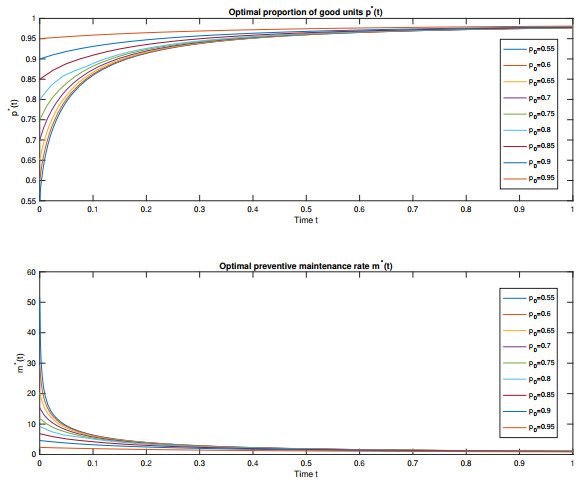
Sensitivity to $p_0$. This analysis reflects the impact of the initial proportion of favorable items on the optimal policy.

We also note that the change in the values of $p_0$ does not affect the optimal inventory level and the optimal production rate. Figure 4 (top) shows that the system attains a greater initial fraction of good units as $p_0$ rises. It follows that the higher the starting quality level $p_0$, the less work is required to maintain or increase this proportion during the production process. Also, Figure 4 (bottom) shows that the initial preventive maintenance rate $m^*(t)$ is larger as $p_0$ drops. This suggests that greater effort (in the form of maintenance) is needed early on to improve the manufacturing quality if the initial proportion of good units is low. Similarly, the initial maintenance rate is comparatively low for higher $p_0$ values (e.g., 0.95 or 0.9), indicating that fewer corrective actions are required when the system starts at a higher quality level.

Figure 4.  Case $s(t) = 0.4t+2$, $\alpha(t) = \frac{0.1}{10+t}$, and $\theta(t) = 0.01+0.04\sin(t)$ and $p_0$ in the range $\{0.55;0.6;0.65;0.7;0.75;0.8;0.85;0.9;0.95\}$: Optimal proportion of good units $p^*(t)$ (top); and optimal preventive maintenance rate $m^*(t)$ (bottom).

DownLoad: Full-Size Img PowerPoint

Sensitivity analysis in Table 2 demonstrates that when $p_0$ falls, the overall cost $J^*$ increases. For instance, the cost is $J^* = 17.07$ with $p_0 = 0.95$, but $J^* = 104.67$ with $p_0 = 0.55$. This is a notable rise that shows that, because of the greater requirement for corrective and preventive maintenance, starting with a lower initial proportion of good units leads to a significantly higher ultimate cost. A lower initial quality level results in higher maintenance costs as well as higher expenses over time due to manufacturing inefficiencies and errors, as shown by the increase in $J^*$ with decreasing $p_0$.

Table 2.  Sensitivity to $p_0$.

p0	0.95	0.9	0.85	0.8	0.75	0.7	0.65	0.6	0.55
$J^*$	17.07	18.10	19.12	22.89	24.16	30.27	39.71	54.23	104, 67

---

 | Show Table

DownLoad: CSV

Important managerial insights can be gained from these analyses. First, setting a high priority for early quality $p_0$ turns out to be essential for lowering production and maintenance expenses over the long run. Higher $p_0$ systems from the outset require less intervention and continuous maintenance, which reduces overall costs and maximizes resource efficiency. Managers should invest in quality control processes early in the production cycle to avoid costly corrective steps later, as indicated by the significant increase in costs when $p_0$ is low. Because of this, establishing a high-quality baseline before beginning manufacturing is a crucial tactic for cost effectiveness. Second, stabilizing production quality is mostly dependent on preventive maintenance, especially in cases where initial quality is poor. Early maintenance efforts are essential for maintaining stable, long-term operations, regardless of where you start. It is evident from the decrease of the preventive maintenance rate $m^*(t)$ with time that fewer resources are needed to maintain quality once it has stabilized. As a result, early maintenance investments not only raise quality levels right away but also lower the need for maintenance down the road, leading to long-term sustainable production methods. Managers can effectively manage the trade-off between quality and cost by striking a balance between long-term maintenance methods and initial investments in quality.

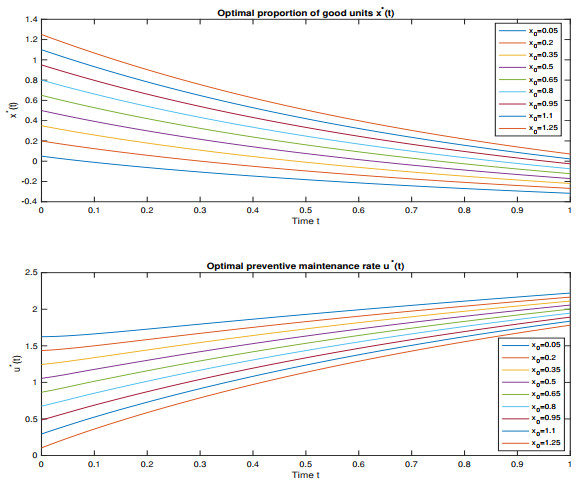
Sensitivity to $x_0$. This analysis shows how the initial inventory level affects the best strategy.

This time, we note that the change in the values of $x_0$ does not affect the optimal proportion of good units and the optimal maintenance rate. From Figure 5 (top), it can be seen that as production increases, inventory gradually depletes, as shown by the decreasing optimal inventory level $x^*(t)$ over time. Starting with a higher $x_0$, however, enables the system to rely on the initial stock instead of rapidly increasing production, which results in more cost-effective operations. Also, Figure 5 (bottom) shows that the optimal pace of production over time, $u^*(t)$ exhibits an increasing trend, indicating that preventative maintenance efforts are high at first but become less so as the system stabilizes. The stability across several $x_0$ values suggests that the proportion of good units rather than the initial inventory has a greater influence on the production rate.

Figure 5.  Case $s(t) = 0.4t+2$, $\alpha(t) = \frac{0.1}{10+t}$, and $\theta(t) = 0.01+0.04\sin(t)$ and $w$ in the range $\{0.05;0.2;0.35;0.5;0.65;0.8;0.95;1.1;1.25\}.$ Optimal proportion of good units $p^*(t)$ (top); and optimal preventive maintenance rate $m^*(t)$ (bottom).

DownLoad: Full-Size Img PowerPoint

Sensitivity analysis in Table 3 illustrates that the optimal objective function value $J^*$ experiences a decline as the initial inventory level $x_0$ rises. For instance, when $x_0$ is set at 0.05, the total cost is $J^* = 45.27$, which decreases to 19.80 when $x_0$ reaches 1.25. This trend indicates that higher initial inventory levels are associated with reduced total costs. The reduction in $J^*$ implies that commencing with a greater inventory level can lead to lower overall production and maintenance expenses. This phenomenon likely arises from the fact that a higher initial inventory minimizes the need for frequent adjustments in production and maintenance efforts. It is important to note that the decrease in $J^*$ is not linear in relation to variations in $x_0$. As $x_0$ increases, the incremental reductions in $J^*$ become progressively smaller. Although enhancing the initial inventory proves advantageous, the benefits tend to diminish as inventory levels rise. This observation suggests the existence of a threshold beyond which additional increases in initial inventory may not yield significant cost reductions, highlighting the importance of balancing inventory investments.

Table 3.  Sensitivity to $x_0$.

x0	0.05	0.2	0.35	0.5	0.65	0.8	0.95	1.1	1.25
$J^*$	45.27	36.95	33.71	30.91	28.26	25.81	23.59	21.59	19.80

---

 | Show Table

DownLoad: CSV

This analysis yields several conclusions and insights for managers. To begin, it underscores the crucial significance of maintaining a high initial inventory level $x_0$. Managers should give priority to accumulating a sufficient stock of high-quality units before production commences, as this leads to substantial cost savings over time. The inverse correlation between $x_0$ and total cost $J^*$ illustrates that early investments in quality inventory can lead to significant savings in both production and maintenance. By starting with a higher proportion of good units, the system requires fewer aggressive interventions, making the process more cost-effective and efficient. The second insight from this analysis is that as production advances, a gradual increase in maintenance efforts is crucial, especially for lower initial inventory levels. However, with a higher starting inventory, the system stabilizes more effectively, enabling managers to implement preventive maintenance more gradually, leading to improved long-term cost optimization. In terms of resource management, the key insight is that early investment in inventory quality, combined with a strategic, dynamically adjusted maintenance plan, enables better control over costs while ensuring production efficiency.

6.   Conclusions

We emphasize the crucial importance of optimal control in optimizing production and maintenance functions in manufacturing systems. We considered a very important model introduced in the work by Cho et al. ^[3] in which the authors used the maximum principal to solve the system, and we considered a completely different method called (NMPC) to solve a more general model as explained in Section 3. By conducting sensitivity analysis and providing numerical examples, we have illustrated that a larger initial inventory of good units substantially decreases total costs, underscoring the significance of early investments in quality management. The results indicated that preventive maintenance not only stabilizes production processes but also leads to cost efficiency over time, especially when combined with a robust inventory strategy. Furthermore, dynamically adjusting maintenance efforts based on initial inventory levels offers managers valuable insights into resource allocation and cost management. As systems stabilize, a gradual reduction in maintenance efforts can be strategically implemented, ensuring long-term operational efficiency.

Researchers can build upon this work by exploring several avenues. For example, extending the model to include stochastic elements could provide a more realistic representation of production and maintenance processes, enabling a deeper understanding of how these factors interact. Additionally, investigating the impact of external variables, such as technological advancements, could enhance the model's applicability and relevance in dynamic environments. Researchers could also examine the effects of different quality control methodologies, comparing traditional approaches with emerging techniques like machine learning and predictive analytics.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The first author extends his appreciation to Researchers Supporting Project number (RSPD2025R1001), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare there is no conflicts of interest.