Resistive and propulsive forces in wheelchair racing: a brief review

1.   Introduction

Paralympics play an important role in society's culture and sport practice [1]. Wheelchair racing is one of the biggest events in Paralympics [2]. Here, it is possible to identify four distinct classes (T51, T52, T53, and T54), in which the athletes' classification depends on the disability criteria (i.e. spinal cord injury) and is set according to their muscular strength [3],[4]. For an athlete to be eligible in one of these classes, he or she may be affected by one or more of these characteristics: limb deficiency (amputee), loss of range of motion, muscle weakness or paralysis (resulting from spinal injury or bifid spine) and different limbs' sizes [3]. The International Paralympic Committee defines the classification of these athletes as follows [3]: (1) T51–athletes who have a decrease on shoulders muscles strength and difficulty in elbows extension for the pushing action during the propulsive phase. The athletes do not have muscle activity and strength in the trunk muscles. Typically, athletes' propulsion is achieved by the elbow flexors and wrist extensors; (2) T52–the athletes use shoulders, elbow, and wrist muscles to propel the wheelchair. One can observe a possible weakness in the muscular strength of the fingers. The trunk muscles strength are typically absent; (3) T53–athletes may present full ability in the upper limbs; however, they may not have muscular activity in the abdominal or lower spine; and (4) T54–the participants preserve the upper limbs muscular strength and can have muscular activity in the entire trunk. T54 athletes may also have some leg capacity [3].

Wheelchair racing involves short (sprint events; 100 m, 200 m, and 400 m), middle (800 m and 1500 m), and long-distance races (5000 m and 10000 m). During the race, athletes must reach maximum speed as soon as possible and maintain it [5]. For that, higher power must be applied during the propulsive phase; and the stroke cycle is divided into the propulsive and the recovery phase [5]. The propulsive phase can be divided into: (1) the catch (the moment when the hand first touches the handrims, close to 12: 00); (2) the drive phase (pushing the handrims, between 12: 00 and 6: 00), and; (3) the release phase (the moment the hand breaks contact with the handrims, close to 6: 00) [2]. The recovery phase is the moment between the release phase and the catch, the beginning of a new stroke cycle. This moment is characterized by a backwards hyperextension of the athletes' upper limbs [2]. During the stroke cycle, the propulsive force results from the athlete's upper limbs strength applied on the handrims. Resistive forces are the drag force and the rolling resistance [5]. The athlete's ability to decrease resistance and increase propulsion can improve performance [5]. The movement phase is the moment of hand and wrist acceleration on the handrim, usually between 2: 00 and 5: 00. The release phase is when the contact between the hand and the rim breaks, close to 6: 00 [2]. The catch is the moment the hand touches the rim, it usually occurs around 1: 00 and 2: 00. [2]

To date, it is possible to find just a few studies assessing resistive forces in wheelchair racing [6],[7]. And to the best of our knowledge, only one study was found assessing the athletes' upper limbs strength [8]. Furthermore, most studies that have assessed propulsion in wheelchair racing have focused on the upper limbs' kinematics [8],[9]. As far as the authors know, there are no studies with protocols assessing both propulsive (based on upper limbs strength) and resistive forces. So, understanding and reporting the methods/tests available to assess such forces can allow and help to control and monitor the training sessions. This will help to identify the impact of impairments on athletes' performance and ensure that classification can be determined by injury type, training and fitness level, and assess the athletes' differences between categories. Therefore, this study seeks to present different methods and tests (laboratory and field) to evaluate the propulsive and resistive forces of wheelchair racing athletes.

2.   Resistive forces / propulsive forces

2.1.   Resistive forces

In wheelchair racing, the main resistive forces are drag and rolling resistance [7],[10]. For speeds above 4,5 m/s, the drag contribution is above 40% [7],[10]. During a Paralympic event (100 m), a T52 elite athlete may reach 5 m/s in the first 15 m [7]. Therefore, the rolling resistance is the main resistive force. During a 100 m race, the drag contribution is more than 40% during the last 75 m [5],[7],[10]. Wheelchair sprinters can use different strategies to minimize both rolling resistance and drag [10]. The drag is dependent on the subjects' anthropometric characteristics, speed and the athlete-wheelchair system [11], temperature [12], and position of the athletes side-by-side on the track [13]. For instance, athletes' posture and body position (i.e., surface area) in the wheelchair influence drag by about 30% [11]. However, other conditions such as temperature and position of the athletes side-by-side on the track have not been tested yet. Moreover, a reduction of the mass in the athlete-wheelchair system may improve performance [14], and it is expected that increasing tire pressure may also improve the athletes' performance [15]. Tire pressure and type influence wheelchair impulse and propulsion [15]. Therefore, the wheelchair properties should also be optimized in order to improve the athletes' performance [15].

Much of this knowledge gap derives from a lack of understanding of the relative contributions of the biomechanical effort of the wheelchair user and the cost of mechanical wheelchair propulsion to the resulting movement [16]. A primary metric of wheelchair mobility is called “effort”, which reflects the biomechanical effort of the wheelchair user while pushing the wheelchair. Studies on human propulsion effort, usually measure this variable as metabolic cost. These researches have investigated the impact of different wheelchairs types and configurations. However, these studies fail to provide information for clinical decision-making to modify the wheelchairs beyond their standard configuration [16], or use methods based on human subjects' dimensions, lacking sensitivity [17],[18] to adopt different wheelchair configurations [17],[18]. Given the enormous diversity of human users and their biomechanics of propulsion in different wheelchairs, the most efficient way is to first focus on developing standardized measures representative of the cost of mechanical wheelchair propulsion [17],[18].

2.1.1.   Drag

2.1.1.1.   Wind tunnel

Wind tunnel analyses are the gold standard method for aerodynamics assessment [2],[19]. However, it is considered expensive and time-consuming [2],[19]. The versatility and reality of a wind tunnel reinforce its importance for aerodynamic research, considered a gold standard technique [2],[20],[21]. The flow in a wind tunnel test section must meet high requirements to obtain accurate and reliable measurement data. A good flow quality requires a certain degree of spatial uniformity and temporal stability of speed and pressure [22]. Thus, changes in the environmental conditions in the wind tunnel room can affect the data [22]. However, in wind tunnel tests it is not possible to obtain detailed information about the fluid flow behavior [22]. Testing different conditions in a wind tunnel requires reality-based approaches [23], therefore it is not possible to make predictions and simulations, which can increase costs in this methodology [2],[19].

There are two types of wind tunnels, the open circuit and closed circuit. In the open circuit type, there is an inlet and an outlet field. This is the most simplistic and affordable type to build. In these tunnels, air is expelled directly into the laboratory and is normally re-entered after circulating through the laboratory [24],[25]. However, some tunnels use a source of compressed gas [24]. The open circuit wind tunnels are relatively immune to temperature fluctuations and major disturbances in the return flow. That is caused by laboratory volume that is much higher than the tunnel [24]. There are two types of open circuit wind tunnels, the suck down and blower. Blower tunnels are the most flexible because the fan is at the entrance to the tunnel, so the test section can easily be changed or modified, seriously interrupting the flow. These tunnels tolerate that the outlet diffusers can be completely omitted to allow easier access to samples and test instruments, although the omission often results in a noticeable loss of energy [24],[25]. The suck down type is also called suction tunnel, usually more susceptible to low frequency instability in the return flow. However, some claims have been made to minimize the inlet vorticity due to the fluid not passing through the fan before entering the test [24],[26].

In closed circuit wind tunnels, the flow outlet returns to the inlet portion of the tunnel (entrance); whereas, in closed circuits the amount of the air and its flow are constant, improving the efficiency of the tests. Typically, closed circuit wind tunnels are larger and designed to maintain as much fluid flow uniformity as possible [25]–[27]. Ventilators in the test section power the tunnels. Moreover, some include multi-stage compressors (required for transonic and supersonic air speeds) [25]–[27]. These closed circuit wind tunnels are characterized by air recirculation, lower air energy requirement, lower speeds and better control of test conditions. [24]–[27].

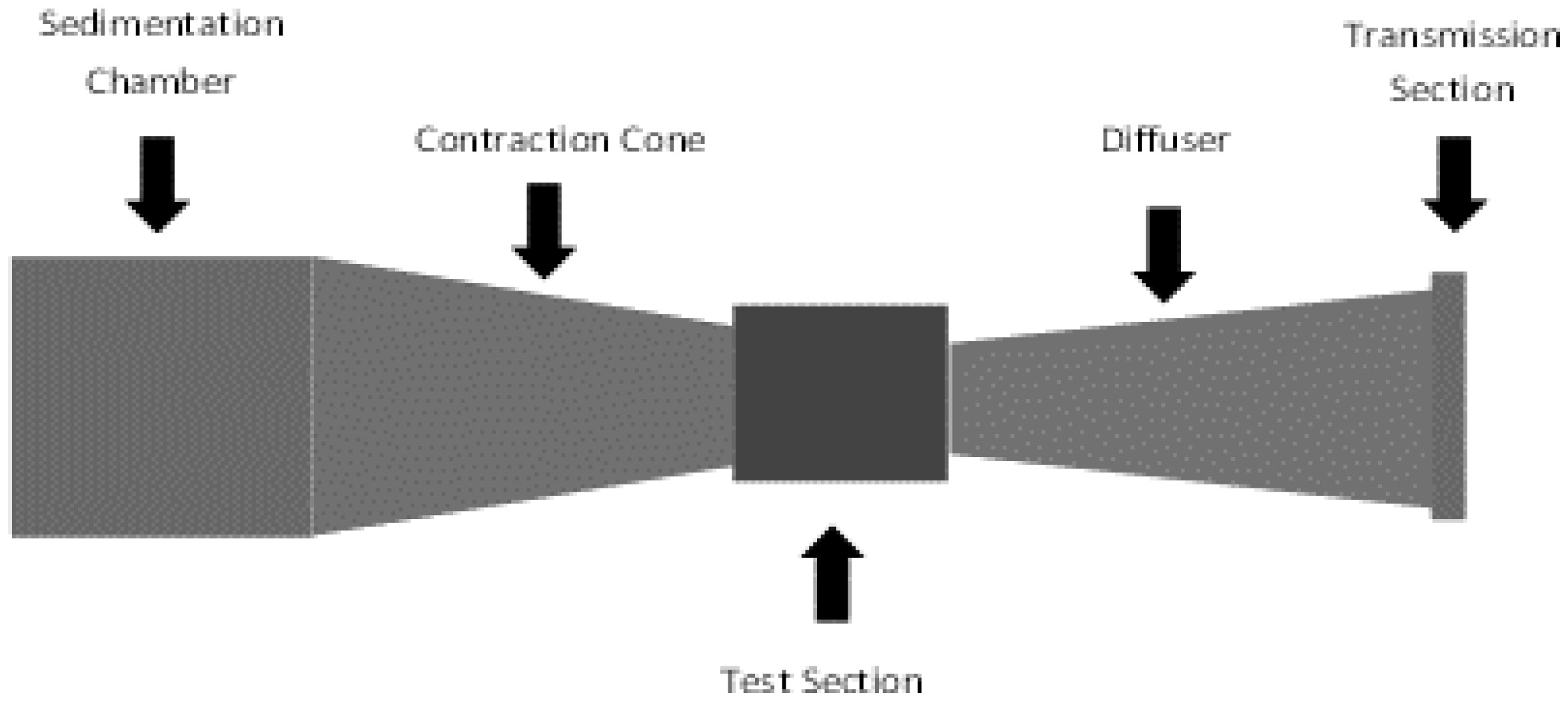
It is possible to identify five main components in wind tunnels (Figure 1). The components are the sedimentation chamber, the contraction cone, the test section, the diffuser, and the transmission section [24],[25]. In the sedimentation chamber, it is possible to find a honeycomb material to conduct and preserve the airflow uniformity. The rotating fan creates a movement in the air that has an undesirable effect on the test section. The honeycomb eliminates this uneven air flow [24],[26]. The contraction cone component is designed to increase the air speed in the test section without additional turbulence in the air flow [24]. The objects to be tested and analyzed are placed in the test section [24],[26]; where, in this chamber the evaluations and observations are made [24],[27]. The diffuser chambers are similar to cones, expanding as they move away from the test section. This allows an increase in the fluid pressure and a decrease in its velocity. The air flow is slowed down and minimizes the turbulence in the diffuser; here, the test section is connected to the fan [24],[27]. Finally, the transmission section allows choosing the wind speed in the test section. [21]. So far, no study assessing the aerodynamics of wheelchair racing athletes by wind tunnel was found. That said, there is a need to fill this research gap. Further research should compare drag through the gold standard method (wind tunnel) with numerical simulations, experimental testing, and analytical procedures. Comparing them can help to better understand the fluid flow behaviour and the drag variations between methods.

2.1.1.2.   Analytical procedures

Drag can be estimated by analytical procedures (equation 1). These provide information in real-time and on site and are more accessible compared to other available techniques such as the numerical simulations and experimental procedures [20]. However, analytical procedures require the use of assumptions and/or estimated values for specific variables. To date, no study compared analytical procedures with different drag assessment techniques in wheelchair racing. In cycling, it is possible to find studies comparing analytical procedures with numerical simulations and the results show high values of agreement between the methods [20],[28]. That said, it is necessary to minimize the research gap by assessing the effect of different temperatures, altitudes, equipment, and performance predictions based on analytical procedures.

In which, Fd is the drag force (in N), p is the air density (in kg/m³), v is the velocity (in m/s), A is the surface area (m²), and C_D represents the drag coefficient (dimensionless). The effective area (ACD) is computed by the product of C_D and A.

2.1.1.3.   Coasting deceleration techniques

Deceleration techniques do not allow to control environmental factors such as wind, humidity, temperature, and variations in the subjects' positions [2],[11]. However, aerodynamic and rolling resistance can be tested to provide realistic possibilities that cannot be achieved in laboratorial settings. Deceleration techniques found in the literature are: (1) rolling distance applying the ramp methods; (2) the timing gate method that measures the decrease in speed at different points between two brands (doors); and (3) the speed method that directly measures velocity at each time [2].

The method of rolling distance with the ramp consists in rolling a wheelchair from a ramp to the track. The wheelchair will be accelerated on the ramp, then the total distance covered will be measured [29]. The timing method is an alternative to rolling distance; in which the unit of measure will be the time that the wheelchair spends between two marks. In these procedures, the wheelchair may be accelerated before the marks [29]. Finally, in the speed method, the athlete can accelerate the wheelchair to maximum speed, then speeds are recorded in each instance [14],[29].

The friction force on a rolling object is not usually a topic discussed in introductory physics textbooks. Although the invention of the wheel is one of the essential world achievements, rolling friction is usually ignored [30].

2.1.1.4.   Numerical simulation

Computational fluid dynamics (CFD) is part of biomechanics and aims to analyze the fluid flow behavior. This methodology allows the discretization of Navier-Stokes equations by the finite volume method [31],[32]. These equations come from Newton's second law in fluid mechanics, assuming that the fluid stress is the sum of the diff [31],[33]. The solution to the equations determines the fluid speed at a given point in space and time. In CFD, space is divided into small cells to form a grid or mesh volume. Then an algorithm is applied to solve the equations of volume motion [31]. For data collection, a three-dimensional model of a wheelchair racing athlete is required. The three-dimensional model can be acquired by three dimensional scanners [11],[33]. Software such as Sense 3D (3D Systems, Inc., Rock Hill, SC, USA) and Geomagic Studio (3D Systems, Rock Hill, SC, USA) allow the image processing. The files can be saved in IGES format (* .igs) in order to be executable in the Ansys Mesh module (Ansys Fluent 16.0, Ansys Inc., Pennsylvania, USA); here, it is possible to generate the grid or mesh elements. The Mesh module (Ansys Mesh, Ansys Inc., Pennsylvania, USA) will allow building the graphic model representative of the volume subdivided into small cells or elements and define the boundary conditions [11],[33]. At solid borders and close to them, FLUENT (Fluent®) calculates the Reynolds and energy stresses [11],[32].

The Fluent® commercial code can be used in order to predict the behavior of physical phenomenon by numerical calculations. So far, this was the only software used to assess the aerodynamics of wheelchair racing athletes through numerical simulations [5],[11]. The numerical code allows the output of pressure, viscosity, total drag, and respective coefficients [20],[21]. The average Reynolds values that come from the Navier-Strokes equations (RANS) have been used in sports aerodynamics analysis [11],[20],[21]. These equations are solved by decomposing the instantaneous values into means. The fluid flow behavior is given by equation 2, Reynolds tension by equation 3, temperature by equation 4, and mass transfer by equation 5.

In the equations, the instantaneous velocity and the position are given by µi and xi respectively, the instantaneous pressure is given by p, t is the time, ρ the fluid density, the molecular kinematic viscosity is given by v, the cp is the heat capacity, the thermal conductivity is k, the S_ij is the strain-rate tensor, c is the instantaneous concentration, and D is the molecular diffusion coefficient. The Reynolds stresses component µj′µi′ ¯ is the turbulence of the mean flow, and the fluid flow parcels will create the exchange of momentum.

For aerodynamic analysis of wheelchair races, turbulent flows, characterized by fluctuating velocity fields as supported by the literature, can be used [5],[11]. Fluctuations can be small-scale and high-frequency, and computation time may be expensive. However, it is possible to calculate the mean of the instantaneous equations, manipulating them so that in small scale they are removed. This creates a set of less expensive equations by new unknown variables to be added. These unknown variables are determined by the turbulence models. The turbulence models are necessary for the fluids computational simulations. In Fluent® there are several models available [11],[32],[34]: (i) -Standard K-epsilon; (ii) -Standard K-ϵ; (iii) -Realizable K-ϵ; (iv) -Spalart-Allmoras; (v) -Reynolds Stress (RSM). The turbulence model used in past studies with a wheelchair racing athlete was the k-ϵ (Realizable k-ϵ) [11],[28],[35]. This model presents speed curves similar to the Standard K– ϵ model, which presents greater computing savings [11],[28].

Fluent® processes, solves, and outputs the results. When importing the created mesh, it allows defining the boundaries, fluid properties, materials and it executes the resolution operations using the SIMPLE © or PISO algorithm. Upon that, it is possible to study the fluid flow behavior, transmission of heat and/or mass, changes of phases, chemical reactions, and movements. In Fluent®, it is possible to obtain data such as viscosity, pressure and total drag, as well as the respective drag coefficients [11].

It is possible to find CFD studies on the aerodynamics of wheelchair racing [5],[7],[11]. To date, the literature presents works that used numerical simulations or analytical models to assess resistive forces with a single elite athlete [5],[7],[11],[35]. Comparing different methods to assess drag with CFD in wheelchair racing athletes is still unclear. Moreover, there is a lack of research assessing different athlete's positions, competitive categories, and temperature effects on drag.

2.1.2.   Rolling resistance

In wheelchair racing, rolling resistance results from the friction of the tires on the ground. Rolling resistance can be reduced by mass and/or equipment [2] and can be determined using equation 6.

In equation 6, F_R is the rolling resistance, µ_r is the coefficient of resistance, m is the mass of the athlete in the wheelchair, g is the acceleration of gravity and k_f is the coefficient of the influence of speed on the rolling resistance, and v² is the velocity.

2.1.2.1.   Equipment

Sawatzky et al. [36] conducted a study on tire pressure. The authors found no significant differences in rolling resistance until the pressure decreased to 50% of the recommended value. However, the performance with a solid tire was inferior compared to the pneumatic tire, even when inflated to 25% of the recommended pressure. Tires that were inflated to only 25% corresponded to an increase of almost 25% in energy expenditure. This study showed that when inflated at 50% of the recommended pressure, the pneumatic tires have less rolling resistance than solid tires. Wheelchair athletes who use solid tires may experience greater fatigue due to the added resistance [36]. In road cycling, tire pressure influences performance and comfort. A bicycle with high tire pressure is more efficient because it has less rolling resistance. However, it is not as comfortable as it increases the vibration from the road surface to the athlete [37]. It is possible to find studies on tire pressure and its effect on cyclists and wheelchair athletes [37]. However, no study was found on the influence of tire type and pressure levels on the performance of wheelchair racing sprinters.

2.1.2.2.   Mass reduction method

In wheelchair racing the wheelchair mass is an important parameter for rolling resistance. Diminishing the rolling resistance by the mass reduction allows an improvement in winning time [14]. The influence of mass on victory time is much higher comparing to the influence of the rolling friction coefficient (1.5x to 4x higher) and higher than the drag coefficient (4x to 5.5x higher) in sprinting events (15 > 30 s race) [14]. With small mass reductions, the arrival time can improve even in sprint events [14].

To assess rolling resistance in field tests, athletes may race in the same conditions (stroke frequency, similar environmental conditions, total power or maximum speed trials) with different masses. Thus, the rolling resistance can explain the differences between the two conditions (with and without additional mass). This method (trials comparison) can be used to compare different tires, wheelchairs, spokes diameters, and pressures. The athlete's bioenergetics may be controlled to fully recover between trials [14]. So, the effect of rolling resistance can be explained by the difference between copulated mass and no additional mass.

2.1.2.3.   Speed decay

Rolling resistance is usually ignored and the inability to explain or model the deceleration of a rotating rigid object on a rigid horizontal surface requires a mechanism for this phenomenon [30].

It is possible to find an equation for the relationship between the effective frictional force and the normal force on an object rolling freely along a horizontal or inclined track [29],[38]. Upon that, if the object is a standard laboratory cart, this ratio is equal to the rolling resistance coefficient for realistic inclined angles. The fundamental reason why rolling resistance overcomes static friction in this case is that the wheels, as rotating components, represent only a percentage of the total mass of the cart [30].

Rolling resistance results from the loss of mechanical energy when descending a ramp [30]. There are two contributions: the deformation of the wheels and/or track, and the torque that is opposing the rotation of the wheels [39],[38]. The deformation results from the flattening and/or depression of the track caused by the vehicle [40]. Static or kinetic friction mainly influences the torque that opposes the rotation of the wheels. Thus, rolling resistance acts at every moment on a moving object [40].

The partial contribution of rolling resistance and drag force shows a non-linear relationship with speed. There is a greater contribution of rolling resistance at slow speeds, while the role of drag force increases with speed. Therefore, customized solutions must be designed to reduce rolling resistance in Paralympic athletes, due to the decisive role in performance [6].

2.2.   Propulsion forces

The spinal cord injury makes the athletes dependent on the upper limbs' strength for mobility (wheelchair propulsion). The strength for these tasks is provided mainly by the musculature of the upper limbs [37]. During the propulsive phase, the wheelchair will be accelerated by the athlete's ability to transfer power and strength to the handrims. Therefore, performance (speed) depends on the athlete's strength and ability to generate mechanical power [5].

Propulsive forces in wheelchair racing may be assessed by quantifying the amount of force that is applied on the handrims. However, no study was found assessing propulsive force in wheelchair racing athletes. Most studies focus on athlete's upper limbs strength and kinematic analysis [8],[9]. Thus, the assessment of the athlete's upper limbs strength has been used alternatively to assess propulsive force. Some studies with disable-bodied subjects on wheelchair analyzed procedures such as dynamometer [8], one-repetition maximum [41], and medicine ball throw [42].

In the study by Miyazaki et al. [43] a force sensor system was used on the wheelchair wheel. The tangential force waveforms were measured and then the waveforms were classified as bimodal or unimodal depending on the athletes' propulsion style (technique). Thus, the ability to apply propulsive force during the push phase, which is difficult to estimate by kinematic analysis, could be estimated using the force sensor system [43]. However, the authors did not compare the differences between propulsive tangential force and upper limbs strength.

Altogether, the literature is scarce on the subject of propulsion and upper limbs strength assessment. So far, there are no standardized methods to assess propulsive force and upper limbs strength [8],[9]. Thus, it is important to present different tests to assess upper limbs strength. In the authors' understanding, the greater the strength of the upper limbs, the higher the probability of increased levels of propulsive tangential force.

2.2.1.   Dynamometry

One of the standard technologies capable of providing data reliability for muscular strength is the isokinetic dynamometry [44]. Vanlandewijck et al. [8] measured the upper limbs strength on elbows extension with and without backrest support in wheelchair athletes. In this test, the participants were seated in a fixed chair on the floor. In front of the participants there was a dynamometer fixed on the wall, adjustable in height and width and positioned in front of the chest.

The participant imposed maximum strength for 3 seconds, perpendicular to the plates and pushing against the wall with both hands. Three tests were performed with full recovery between tests. The authors presented values of mean maximal force of 52.02 kilograms of force (Kgf) with backrest; and 30.48 Kgf without backrest for the wheelchair basketball athlete. In the same study, a wheelchair tennis athlete produced a force of 54.72 Kgf with a backrest support; and 10.62 Kgf without the backrest support. It should be noted that the inclusion of abdominal muscles resulted in a strength loss of 41.41% for the basketball athlete and 80.59% for the tennis athlete. This procedure can probably be used to assess the propulsive forces (upper limbs strength) of the wheelchair runner. However, there may be some concerns to rule out abdominal muscles activity. The Figure 2 presents a representative dynamometry test to assess elbows extension strength levels.

2.2.2.   One-repetition maximum

As in most sports [44],[45], strength is a component of success in competition and so it is in wheelchair racing. Recommendations for exercises and training stimuli are based on coaches' experiences and, in particular, comprehensive research in sports science [46]. However, it is possible to identify a lack of research on wheelchair racing with precise guidelines for specific training protocols, especially in strength training [46].

Tørhaug et al. [47] assessed the effect of strength training on maximal bench press on work economy during wheelchair propulsion in men with spinal cord injury. The strength tests (one-repetition maximum test, 1RM) were performed using an adjustable bench press and a calibrated bar in the Eleiko Olympic version (Eleiko AB, Halmstad, Sweden) encoder (20 kg, 2,85 cm in diameter, 2,20 m in length) with weights. All participants were lying supine on a pedestal tied with a Velcro strap at the waist for stability and then stood up. Power, force, and speed were recorded using the MuscleLab 4000e (V.8.10; Ergotest Innovation A.S., Porsgrunn, Norway). The MuscleLab system's maximum measurement error is less than 0,3, 0,9 and 1,2% for strength, speed, and power, respectively. To determine the 1RM for each participant, loads were added (three to five times) with rest periods of 5 minutes until reaching the maximum value. The 1RM was accepted when the entire survey was completed in a controlled manner, without assistance [47]. This protocol allows assessing the maximum strength of the upper limbs of wheelchair racing athletes. However, a set of procedures are required to stabilize the trunk, avoiding falls or unbalance positions/postures. Moreover, medical recommendations might be taken in account about spinal cord injury severity and integrity during the exercise [48].

2.2.3.   Throwing the medicine ball

The use of medicine balls in sports has been used to assess upper limbs strength [48]–[50]. The combination of strength and speed usually has strength as a key element for the successful execution [50]. Given this, it is expected that strength training programs can improve the muscle power of athletes, helping them to accelerate as quickly as possible [5].

The medicine ball throw test is inexpensive and can provide the trainer with valuable information about the effectiveness of training programs [50]. This test has been used to assess propulsive strength [41]. Thus, the aforementioned test might be used to assess the upper limbs muscular power in wheelchair racing athletes (Figure 3). The athletes can be instructed to, in a seating position, keep both feet parallel and shoulder-width while throwing the medicine ball (mass of 1 kg and circumference of 0,72 m) [51]. The speed and distance that the ball hits on the field allow us to quantify muscular strength [41].

To date, no study has been found that assessed the upper limbs strength of wheelchair racing athletes by the medicine ball throw. Moreover, there is a need to compare the medicine ball throw with different methods (e.g., dynamometry and one-repetition maximum) [41].

3.   Conclusions and further research

This study presented a set of methodologies to assess propulsive and resistive forces. Additionally, recommendations were provided for different evaluations. The wheelchair racing resistive forces can be assessed by analytical procedures, experimental tests, and numerical simulations. This paper presented a set of tests to assess upper limbs strength to generate propulsion forces in wheelchair racing athletes. However, there is limited research about direct methods to assess propulsive tangential force. It is possible that the tests presented may be useful to predict the strength and resistance of the upper limbs of athletes.

To date, there is no study comparing the different methods. There is a lack of research about equipment testing and performance predictions in different environmental conditions in wheelchair racing. Furthermore, it is important to understand the effect of different environment temperatures on the athletes' performance and the effect of their track disposition during the race. That said, different competitive categories, postures, temperatures and athletes' disposition on the track influence the resistive and propulsive forces of the subjects and, consequently, their performance.

The community should be aware that by decreasing the mass of the athlete-wheelchair system, the performance will be improved if the athlete maintains full power (ability to generate force). Controversy, small adjustments in technique and changing the position in the chair, can reduce drag and, consequently, improve performance. Athletes must maintain proper body alignment and synchronization during stroke cycles, allowing them to reach and maintain maximum speed with less energy cost [5].

Coaches and analysts can use these methodologies to conduct evidence-based practice, helping athletes to improve their performance.