Modeling and computation for unsteady blood flow and solute concentration in a constricted porous artery

1.   Introduction

A main cause for the diseases in blood vessels and in the heart is formation of so-called stenosis, which, for example, as a result of fatty materials in the artery, reduces the cross sectional area of blood passage and hence can prevent enough blood supply to the distal bed [1]–[3]. There were studies of the blood flow in catheterized arteries [4]–[8] as well as those where the blood was represented by a two-phase model [9],[10]. Two-phase models were developed and studied in the past. In particular, a two-phase macroscopic blood flow and continuum approach was considered in [10]. In such approach fluid is composed of a suspension of the blood cells, which were referred to as particles, and plasma. So, plasma and blood cells were considered as a co-existing phase that spans the flow domain in the artery [9]. The author in [9] applied an experimentally based form [11] for the stenosis in the artery with elastic wall, where the blood was represented by a two-phase model. The author considered the case where the aspect ratio γ of the artery's radius to the axial extent of the stenosis was small. Other studies of the elastic aspect of the artery wall were done in [2],[12],[13].

There have been studies of solute, heat and mass transfer in arteries and tissues that were done in the last three decades or so [14]–[21], and very recent ones have gained significant attention [6],[7],[13],[22]–[26] since they have conducted investigations with the use of advanced technologies to model problems with nano-fluids [25],[26] and nano-tubes [7] inside the arteries. The authors in [15] developed a model for the heat transfer in combined artery blood and tissue, and they solved their model numerically. The authors in [9] investigated unsteady solute dispersion in a blood vessel by using a two-phase Casson model. They found that mean value of concentration of solute reduced with increasing radius of the vessel. The authors in [17] studied the steady case of transport of a drug in a catheterized arterial blood flow with atherosclerosis by using a simple model for drug equation that contained only convection and diffusion terms. They solved this equation numerically by an implicit finite difference method and found that convective drug transport is effective when the diffusivity coefficient is very small. The authors in [20] developed a two-fluid (micro-polar and Newtonian) blood flow model for transport of a reactive [16] and diffusive species in a rigid artery. They found that axial and transverse concentrations of species were enhanced with increasing reactive rate. The authors in [18] studied solute dispersion in a non-Newtonian blood flow in a circular tube that was based on an empirical modeling formula for the blood flow. They included the effect of chemical reaction [16] due to presence of solute in blood. They assumed uniform blood pressure gradient with blood velocity only a function of radial variable. They calculated solute dispersion coefficient and found that it decreases as reactive parameter increases.

There have also been laboratory experiments of solute transport across a material interface of porous media [27] as well as dispersive transport across interfaces [28]. The authors in [27] carried out experiments for solute transport as it crosses an interface of porous media. They found, in particular, that for low Reynolds number flow, solute transport across such an interface was mainly due to convective transport that dominated the diffusive process. Recent investigations [29] considered a fluid flow in a circular tube with an externally imposed electromagnetic field to study the dispersion mechanism of soluble materials. In [30], the authors considered a drug targeting problem to understand how drug micro-particles accumulate at the affected region. Other recent and relevant investigations related to fluid flow in porous medium with connection to drug delivery problems are reported in [20],[31],[32].

In the present study, we investigated unsteady blood flow and concentration of a reactive and diffusive solute, which is the main focus in the present study, in a porous artery that is constricted due to the presence of stenosis. As in [9], we assumed the aspect ratio γ to be small, as is consistent in the experiment [11]. However, in contrast to other unsteady investigations [9],[12],[33], where opposite to the realistic cases, their time-averaged blood flow quantities were zero, in the present case the time-averaged solutions for blood flow quantities and solute concentration are non-zero. Unlike the other work [3],[9],[12], we consider unsteady constricted porous arterial blood flow, where pressure force is determined from the governing momentum equation [34],[35].

In the present work, the considered physical system of the blood flow in the constricted porous artery carries solute concentration of a solute, such as, for example, oxygen, carbon dioxide, nutrients, etc. The main motivation of the present study was how solute transported by the blood flowing in the constricted porous artery behaves subjected to the combined roles played by hematocrit, stenosis height, chemical reaction, pulse oscillation, diffusion and convection. In addition, the results of such study that will be described physically later in section 4 will be useful for further understanding and insight into the nature of transportation of solute of the above examples or drug mechanism in the circulatory system for particular patients with specific blood flow regime.

2.   Governing system and modeling

We consider axisymmetric blood flow in a section of a constricted artery, whose medium is assumed to contain pores due to the presence of severely fatty materials and artery clogging blood-clots [14],[33],[36], in a partially constricted circular cylindrical tube with radius R₀ (radius of the artery), constricted due to the presence of stenosis. The length of the artery is assumed to be very large as compared with the artery radius, so that we can neglect the end effects.

The present physical problem is about blood flow inside the porous artery that carries also concentration of a general solute such as, in particular, oxygen and is based on the equations for the solute concentration, continuity and momentum [34],[35]. It should be noted that due to a very complex nature of the actual blood flow system, its circulatory motion in human artery and the presence of a solute, it would be a formidable task to be able to analyze the actual blood flow motion. Therefore, in the present study we make a number of assumptions that can be reasonably justified, as we will explain later in this section.

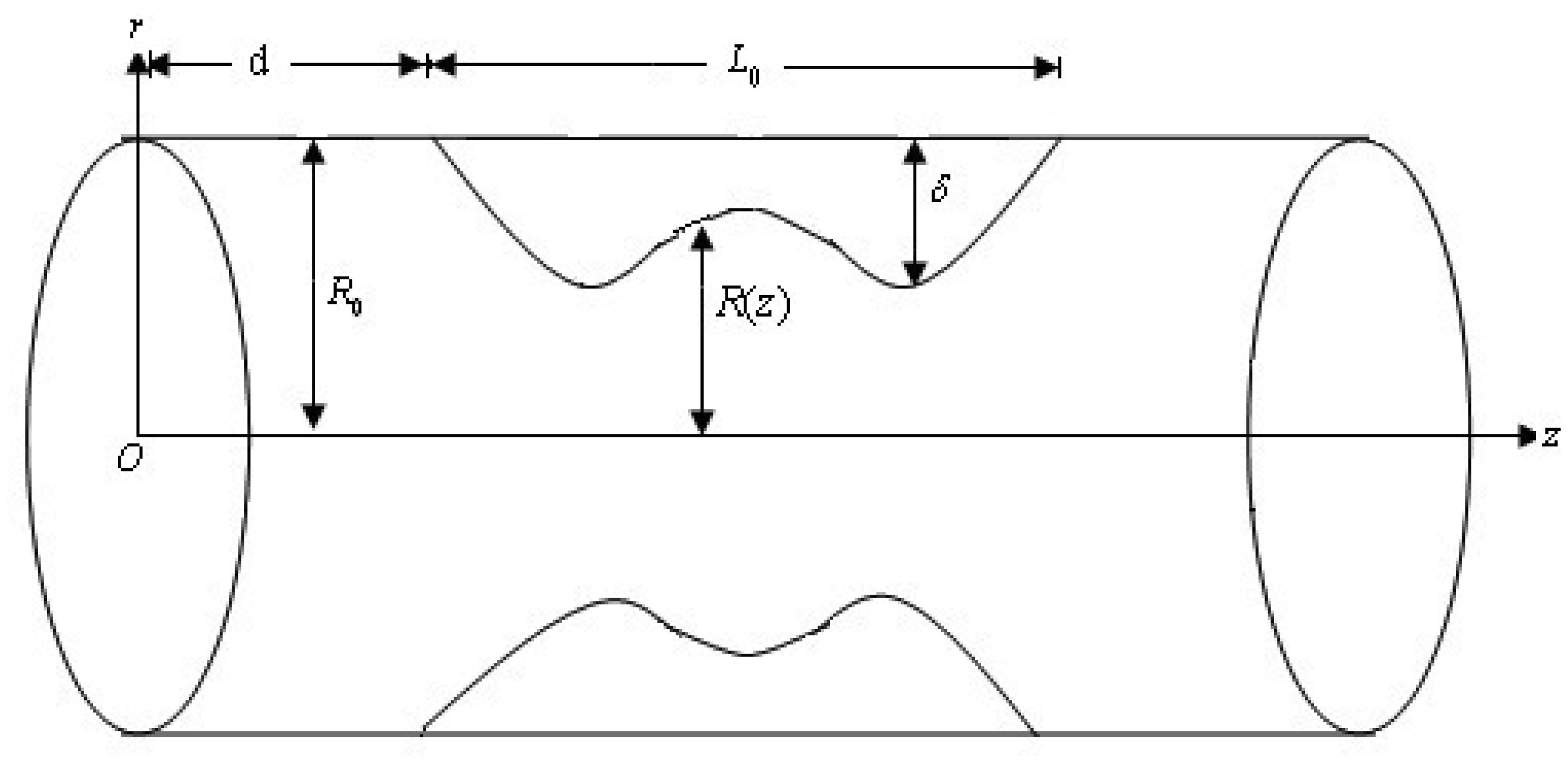
Figure 1 shows a diagram of the model geometry of the described artery, where the constriction is due to the presence of stenosis, with axial length L₀. R(z) is the function representing the artery's boundary, whose expression is given in section 2, and δ is maximum height of the stenosis.

We start by considering the governing system of equations for the blood flow and solute concentration in their axisymmetric form, and these equations are represented in the cylindrical coordinate system whose axial direction is taken to be the same along the axial direction of the porous artery. They are

where r and z are the radial and axial variables, respectively, in the cylindrical coordinates; t is the time variable; u and v are the components of the blood velocity vector along the axial and radial directions, respectively; u→ is the vector containing both u and v; C is the solute concentration; D₀ is the diffusivity coefficient of the solute, E₀ is the reaction constant of the solute, which is the coefficient of a considered linear model for a reaction term that is due to the presence of the solute in the blood; ρ is the actual density; P is the blood pressure; k is permeability of the porous medium; µ_s is variable blood viscosity formula due to the presence of red cells in plasma that are taken into account, where such formula was proposed first by Einstein [36]; µ is the dynamic viscosity of the plasma in the blood; λ is the maximum hematocrit at the center of cylindrical tube; and n (≥2) is the parameter that can determine the formula's constriction. We also make a note that the above equations will be subjected to modeling and simplifying assumptions. These simplified equations will be complemented with boundary conditions. The relevant boundary conditions for the above system are given by Eqs 2e,f and Eqs 5f,g.

We now first make the governing Eqs 1a,e dimensionless by using U, UR₀ /L₀, L₀, R₀, R₀/U and µU L₀/R₀² as scales for the axial velocity, radial velocity, axial length, radial length of the artery, time and pressure, respectively, where U = (L₀ µ/k) is the velocity scale for the blood flow. Next, we make these dimensionless forms of the equations for Eqs 1a–e as simple as possible under justifiable conditions for mild stenosis with (δ/R₀ << 1), unidirectional flow and convective assumption [35], where the axial velocity component and the axial property convection dominate over the radial velocity component and radial property convection term, and subjected to the assumptions that the inertial terms in the momentum Eqs 1a–c are small, which are reasonable since Reynolds number, which represents ratio of inertia to viscous forces, is generally small in comparison to unity. We also follow experimental evidence [11] and assume that the aspect ratio γ ≡ R₀/L₀ << 1 and shall treat γ as a small parameter to be used for power series expansions of dependent variables in a perturbation procedure to determine our unsteady solution to the blood flow and solute concentration. We then make use of our already described conditions and the assumptions [8]; in particular, the blood pressure is only a function of axial and time variables, which is reasonable since inertial terms as well as terms due to viscous effects are all small due to unidirectional blood flow for section of the artery that is axially straight (Figure 1). Furthermore, radial velocity is then small as compared to the axial velocity, and subsequently viscous and convective terms in (1c) and (1e) due to the radial velocity contribution are relatively small as compared to the viscous and convective terms due to the axial velocity contribution and are neglected. In addition, the axial derivative terms in the viscous and diffusion parts in (1c) and (1e) are relatively small as compared to the radial derivative terms in viscous and diffusion parts, respectively, which is due to the fact that the aspect ratio of the chosen artery section is very small. Thus, Eqs 1a–d led to relatively simpler ones, which are in dimensionless form; and for simplicity of notations, we provide them below by adopting the same symbols as those in their dimensional form:

where K=k/R₀² is permeability parameter, D = D₀ L₀/(U R₀²) is the diffusivity parameter, and E = E₀L₀/U is the reaction parameter due the presence of solute in the blood artery. Eqs 2a–c are subjected to the following boundary conditions to the zeroth order in γ:

where

where R(z) is the radial structure of the inside boundary of the tube in its dimensionless form, ϵ = [3δ/(2R₀)] is the size of the maximum stenosis height, referred to as the stenosis height, and b = d/L₀ is the dimensionless axial part of the artery section that is not constricted. The z variable ranges from 0 to 2, and damaged region is found on 0.4 < z < 1.6. Outside of this region the artery (healthy region) takes the form of a perfect cylinder or tube. Since the present focus of study is on solute concentration aspects and, as we referred to before in section 1, because of the nature of the particular dense porous medium of the considered artery, permeability parameter K of the porous artery is very small < O (0.1). Thus, in this paper we consider the limit of very small K, so that the term containing this parameter in (2a) is not taken into account. The boundary conditions for the solute concentration will be very much related to the method of calculation of the solution for the solute equation and will be given later in the next section after such method is described.

We now consider the resulting system (2a–h) for the arterial blood flow and the solute concentration, which is an unsteady system. We first apply a perturbation procedure and use the small aspect ratio parameter (γ << 1) as the perturbation parameter for the perturbation procedure by applying power series expansions in powers of γ for the dependent variables in the above system. We have

where the quantities with subscripts 0 and 1 can be at most functions of t, z and r.

We shall carry out both analytical and numerical procedures to calculate various expressions that are described in the next section for several different values of the hematocrit parameter λ, diffusivity parameter D, aspect ratio γ, reaction parameter E, frequency of the blood pulsation and over a range of values, in general, in time, axial and radial variables. For all the calculations, we set b = 0.4, L₀ = 1.0, ϵ = 0.1, γ = 0.06 [2], constant n = 2, volume flow rates Q₀ and Q₁, whose expressions will be given in the next section, and are set initially equal to 1 in most of the calculations, but we also determine their effects on different quantities by choosing different values for them. For other constants and parameters, we also choose different values in order to find their effects.

3.   Analysis and solutions

3.1.   Leading order modeling system

For the system to the lowest order in γ, we set

Using (3)-(4) in (2a–f) and keeping terms only to the zeroth order in γ, we find that there is no time-derivative term in the resulting system. This system has only a solution which is independent of time. Thus, to this zeroth order in γ this system can have solution that is at most a function of r and z. Using this result in (2a)-(2b), we find

Since u₀ is given in terms of the unknown pressure gradient (dP₀/dz), we obtain an expression for the pressure gradient by assuming a prescribed volume flow rate in the tube at this order given by

Using (5a) in (5b) and solving for the pressure gradient, we find

Next, using and (5a) in (2c) and carrying out integration in the radial direction, we find

where it should be noted that, using the simple L'Hopital's rule of calculus, it can be shown that there is no singularity at r=0 for v₀, and it satisfies the given boundary condition (2e).

Next, to solve solute concentration (2d) at the zeroth order in γ and based on the already obtained result that at this order C₀ does depend only on radial and axial variables, we use the method of separation of variables by setting

Using (5a) and (5e) in (2d), we solve for the functions H₀ and Z₀, subjected to the conditions that the solute washes away at the internal boundary of the artery and

where the constants g_i (i = 0, 1, 2) are prescribed values 2.0 for i = 0, −1.0 for i = 2 and −1.0 for i = −1.0. Our repeated calculations for different values of these constants turn out to not change the qualitative aspects of our results. Using (5a) and (5e) in (2d) and dividing each term that contains Z₀ by Z₀, we find a second ordinary differential equation for H₀ only if

is a constant. Then, the second order differential equation for H₀ is in the form

We evaluate the constant a₁ in (5h) at z=0 using (5f) and then apply integration for the differential Eq 5h to find that

The integral in the power of the exponential function in (2j) is solved by a Simpson rule [1]. We solve the second order differential Eq 5i for H₀ subjected to the conditions (5g) as an initial value problem by an efficient Runge-Kutta (RK4) scheme of fourth order [37]. The initial condition begins at r = R for given z, and then by using a simple transformation type change of independent variable, the integration proceeds until it reaches very close to r = 0.001, since we avoid singularity point at r = 0 of (5i). The expression for the flow resistance that also refers to as impedance F₀, is given by

where Δp₀ is the pressure drop across the axial length 1+2b of the artery section and is given by

where b=d/L₀. Using (5a), we can calculate the wall shear stress τ_w0 to the zeroth order in γ. It is given by

3.2.   Next order modeling system

Using (3) in (2a–f) and retaining only terms that are in the order γ, we find that the system for the blood flow and solute concentration can admit oscillatory solutions in time. The blood flow variables can admit the following form:

provided the value of volume flow rate at O(γ), which is designated by Q₁, is chosen to be the same as Q₀ that we assume in this paper. Here, ω is the frequency of the blood flow oscillation. Using the method of separation of variables, we find that the expression for solute concentration at this order can be admitted by such method in the following form:

where H₁ satisfies the second order differential equation

and the boundary conditions are set to be of the same form as those in (5f,g).

This second order differential equation is solved numerically, similar to that explained before for H₀. Basically, we convert the second order differential equation into a system of two ordinary differential equations of first order. This system is non-homogeneous with non-homogeneity due to presence of H₀ which is calculated from (5i) and (5g) and is known as a set of collected data at this stage. Next, the values of the initial conditions for H₁ at the inner boundary of the artery is chosen to be the same as those given in (5g) since H₁ has to be zero due to the assumption that solute is washed away at r = R(z), and the value of the initial condition for dH₁/dr to be any value other than that for dH₀/dr was found to make very minor and negligible quantitative difference in the value of the solution for the solute concentration. We then solve this system of two linear differential equations and such initial conditions by a similar Runge-Kutta (RK4) scheme to that described before. In both computations for (5i) and (7e) we choose right grid spacing that leads to the most accurate results. We also carried out a validation test for our stated computation for the functions H₀ and H₁ by combining and converting both equations (6i) and (7e) into a system of four first order ordinary differential equations and solving the resulting initial value problem with four initial conditions these two functions and their radial derivatives using a similar Runge-Kutta scheme of fourth order [37]. The calculated results for this test indicated basically the same results that we found based on separate systems for these two functions.

Following results (7a)–(7c) at first order in γ, we determine the flow resistance F₁ and the wall shear stress τ_w1 at this order, which are given below:

The results that are described in the next section are for the total solutions up to order γ ² for the blood flow velocity u, blood pressure force (-dP/dz), flow resistance F, wall shear stress τ_w = τ_w0, solute concentration C and their rates of changes with respect to independent variables, along with the dependence of these quantities with respect to the parameters, frequency of the blood pulsation, stenosis height effects and independent variables in time and space.

4.   Results and discussions

The problem under present study is for a physical system of unsteady blood flow and solute concentration in a section of constricted porous artery, and we constructed its model in section 2 and carried out analysis and solutions of the resulting modeling system in section 3. We computed the solutions over a range of values of the parameters, which includes those from experimental studies in [11] and [19], for this system. Values of dimensional quantities in the SI system of units that are involved in the range of values of the parameters are R₀ = 1.5 mm, L₀ = 26 mm, δ = 0.4 mm, D₀ = 0.001 (mm)²/sec, E₀ = 0.003 per sec and U = 8 mm/sec. The ranges of values of the parameters that we study here are hematocrit 0.1 ≤ λ ≤ 1.0, pulse frequency 3.0 ≤ ω ≤ 7.0, diffusion 0.001 ≤ D ≤ 0.05, reactive rate 0.0001 ≤ E ≤ 0.3, stenosis height 0.05 ≤ ϵ ≤ 0.25 and artery aspect ratio 0.05 ≤ γ ≤ 0.15.

In this section, we present and discuss the results for the solutions of the blood flow quantities and solute concentration that were described in the last section. We generated calculated data for these quantities at different values of the parameters, constants, spatial and time variables.

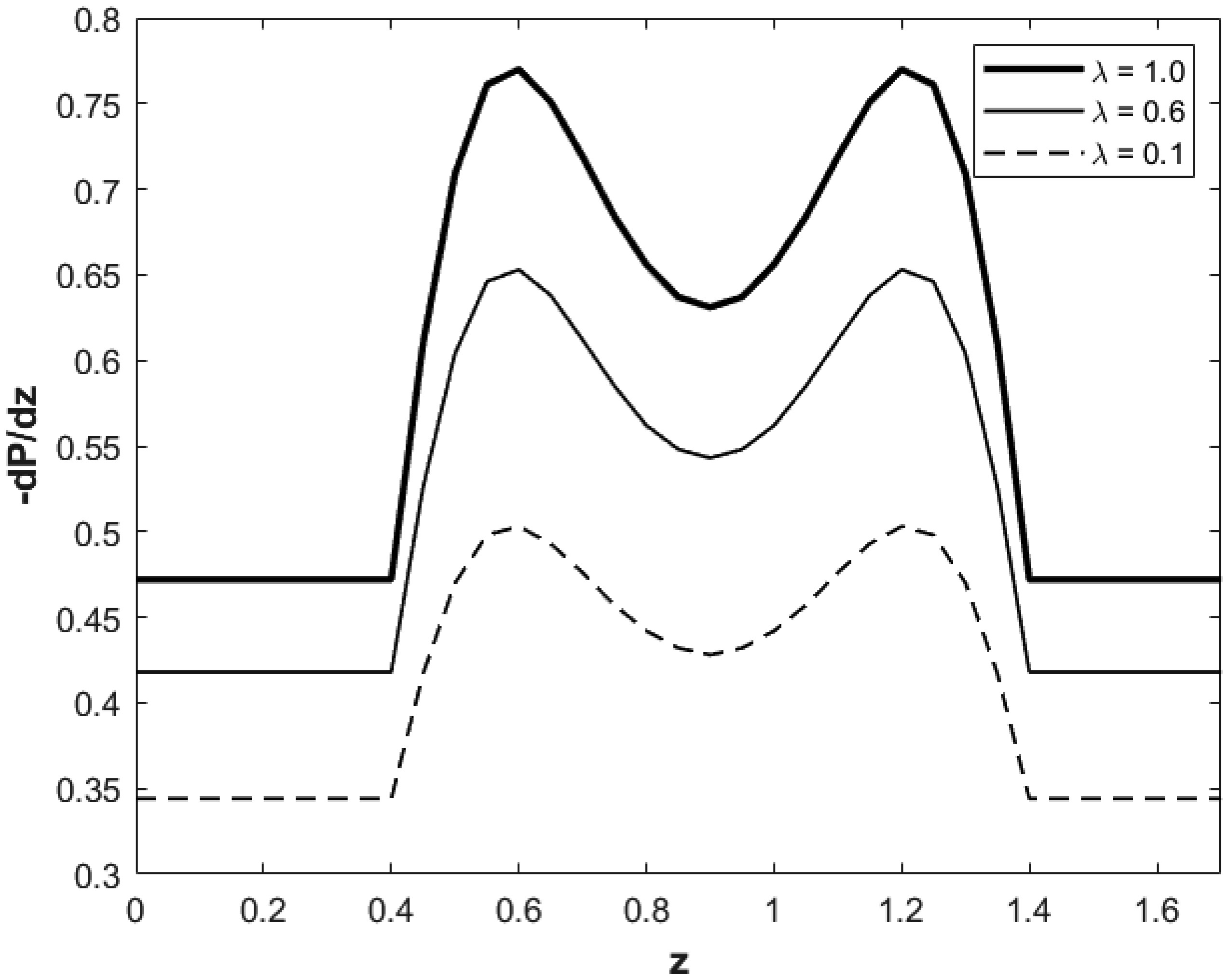
Figure 2 presents blood pressure gradient force versus z, for a given instant in time, ω = 5.0, and for several values of the hematocrit. Stenosis region is given on 0.4 < z < 1.4, and outside this range of z values the artery is modeled as a perfect cylinder or thin tube of constant thickness. For the non-stenosis region, blood pressure gradient is constant and has smaller value compared to the stenosis region. It can be seen from this figure that the value of the blood pressure gradient force increases with increasing the hematocrit and is also increased significantly by the peaks of stenosis, which are at axial level close to 0.6 and 1.2. These results are physically reasonable since higher amount of hematocrit implies higher percentage of the blood red cells amount in the plasma that can intensify the blood pressure force in the arterial blood flow. The presence of stenosis in the artery section makes the cross sectional area of the blood flow smaller relative to the case without presence of stenosis, and, thus, in the present case of assumed constant volume blow flow rate, axial blood flow speeds up, leading to higher blood pressure force in the artery. Our additional generated data for higher stenosis height ϵ indicated that blood pressure force increases with increasing ϵ, which is in accordance with our above physical and bio-fluid dynamics interpretation.

Figure 3 presents blood pressure gradient force versus time for given z, ω and different values of the hematocrit. It shows that the blood pressure force oscillates in time, and the oscillations grow with increasing hematocrit. Such oscillations grow significantly in the stenosis zone. Our additional generated data for different values of the volume flow rates indicate that the pressure gradient force increases with increasing the value of the volume flow rate. From physical and bio-fluid dynamical point of view, these results indicate that growing pulse oscillations of blood pressure force with higher percentage of red cells in the blood as well as with increasing the blood flow through the section of the artery under the stenosis presence are the results of narrowing down the blood flow path in the artery. Higher value of the volume flow rate also speeds up blood flow and intensifies blood pressure force.

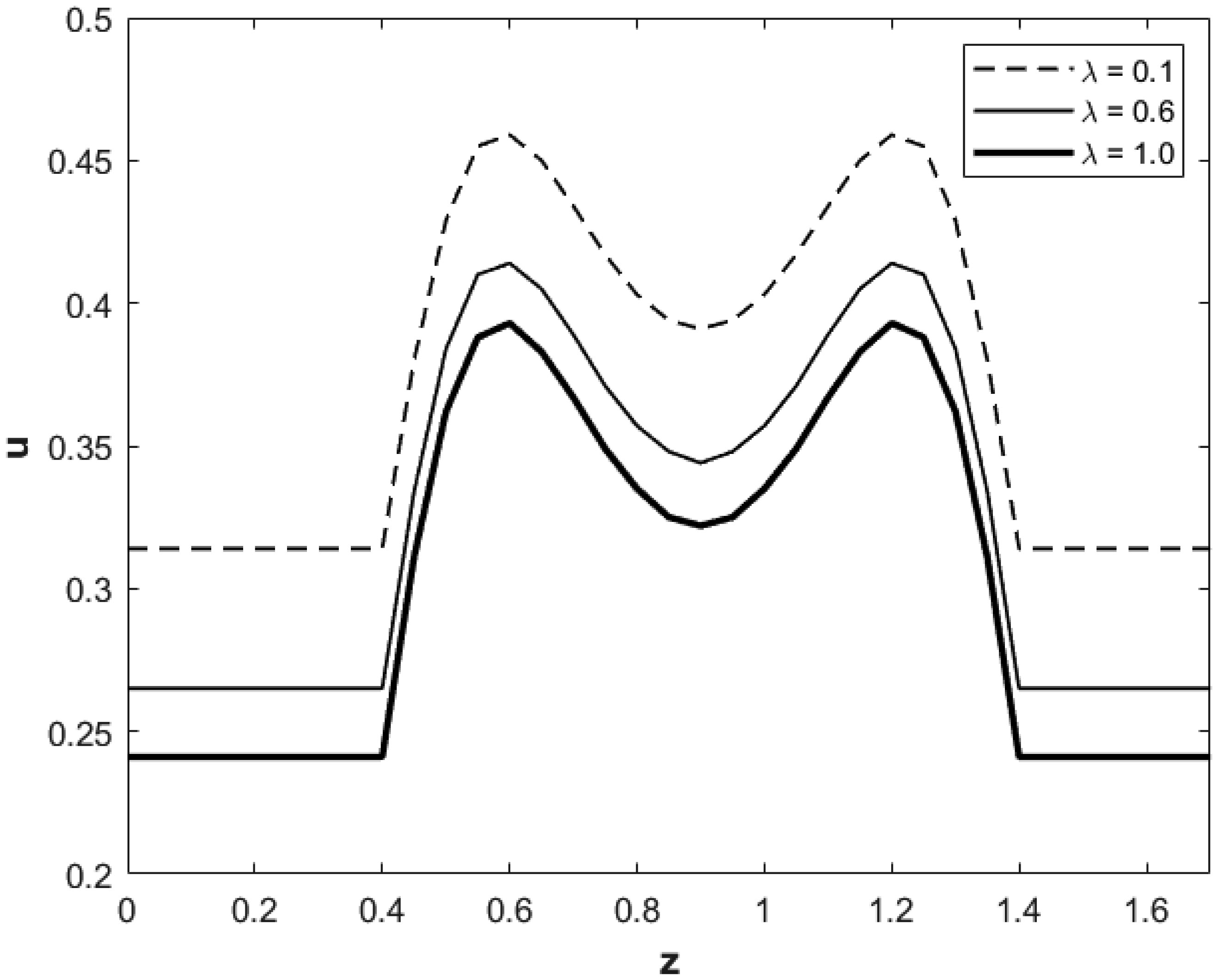
Figure 4 presents axial velocity of the blood flow versus z for r = 0.2, t = 1.0, ω = 5.0 and different values of hematocrit. The flow characteristics are influenced as blood passes through the stenosis region, which is found on 0.4 < z < 1.4. The constant velocity in the blood increases as it enters the narrow stenosis region at z > 0.4 and goes back to its initial state as it exists the stenosis region at z > 1.4. It can be seen from this figure that in contrast to the blood pressure gradient force, the axial velocity of the blood deceases with increasing the hematocrit, which is reasonable, from a physical point of view, since higher amount of red cells in the plasma makes it harder for the blood velocity to move forward. However, similar to the case of blood pressure force, the value of the blood velocity is notably higher at axial levels very close to the peaks of the stenosis. Our additional calculations for higher value of stenosis height indicated that blood speed increases with ϵ as well as with strong blood pressure force. Thus, presence of stenosis and its height can increase blood speed, and such speed gets higher with higher height of the stenosis.

We also generated data for blood speed versus radial or time variable. The blood speed increases with r and oscillates in time. The oscillations grow significantly in the stenosis zone. For given instant in time, we find that similar to the case of blood pressure force the blood speed is constant outside the stenosis zone, while it is variable, and its magnitude increases with the stenosis effect. These results agree physically since blood speed is enhanced for blood flow closer to the internal boundary of the porous artery, and blood pressure and blood speed pulse oscillations are basic nature of circulatory flow system.

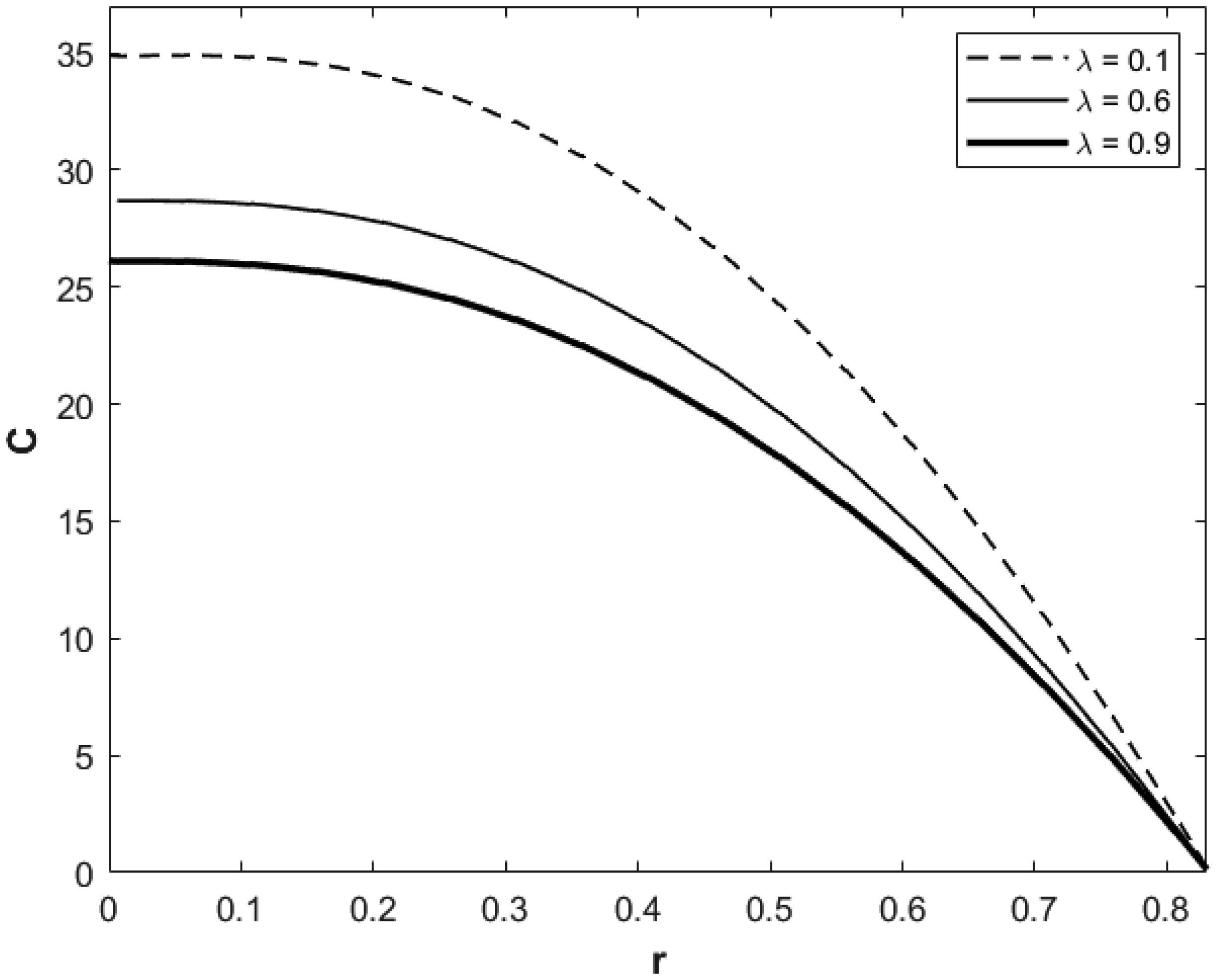
We calculated flow resistance F versus hematocrit parameter and for given values of time and the pulsation frequency. We found that the magnitude of the flow resistance increases with increasing hematocrit, which is especially notable for small λ < 0.2 or moderately large λ > 0.4. The physical interpretation of growing impedance with hematocrit is consistent with similar physical properties of the blood pressure force, as the former is an overall integration of the latter. Our results for F versus time and for different values of hematocrit and the pulsation frequency indicate that the flow resistance oscillates in time, its oscillations grow with increasing the hematocrit, and the pulsation period is smaller with larger ω. We also calculated wall shear stress versus axial variable for given t and ω and different values of λ. The results indicated that wall shear stress increases with hematocrit, and stenosis height locations appear to make the shear stress higher. Our result for wall shear stress versus time variable and for given values of the parameters and axial variable indicated that shear stress oscillates in time. The oscillations grow significantly in the stenosis zone. Since presence of stenosis in the artery is basically a cardiovascular disease, it leads to high blood flow and higher wall shear stress and with other physical properties that were presented above for the blood flow and its speed in the artery.

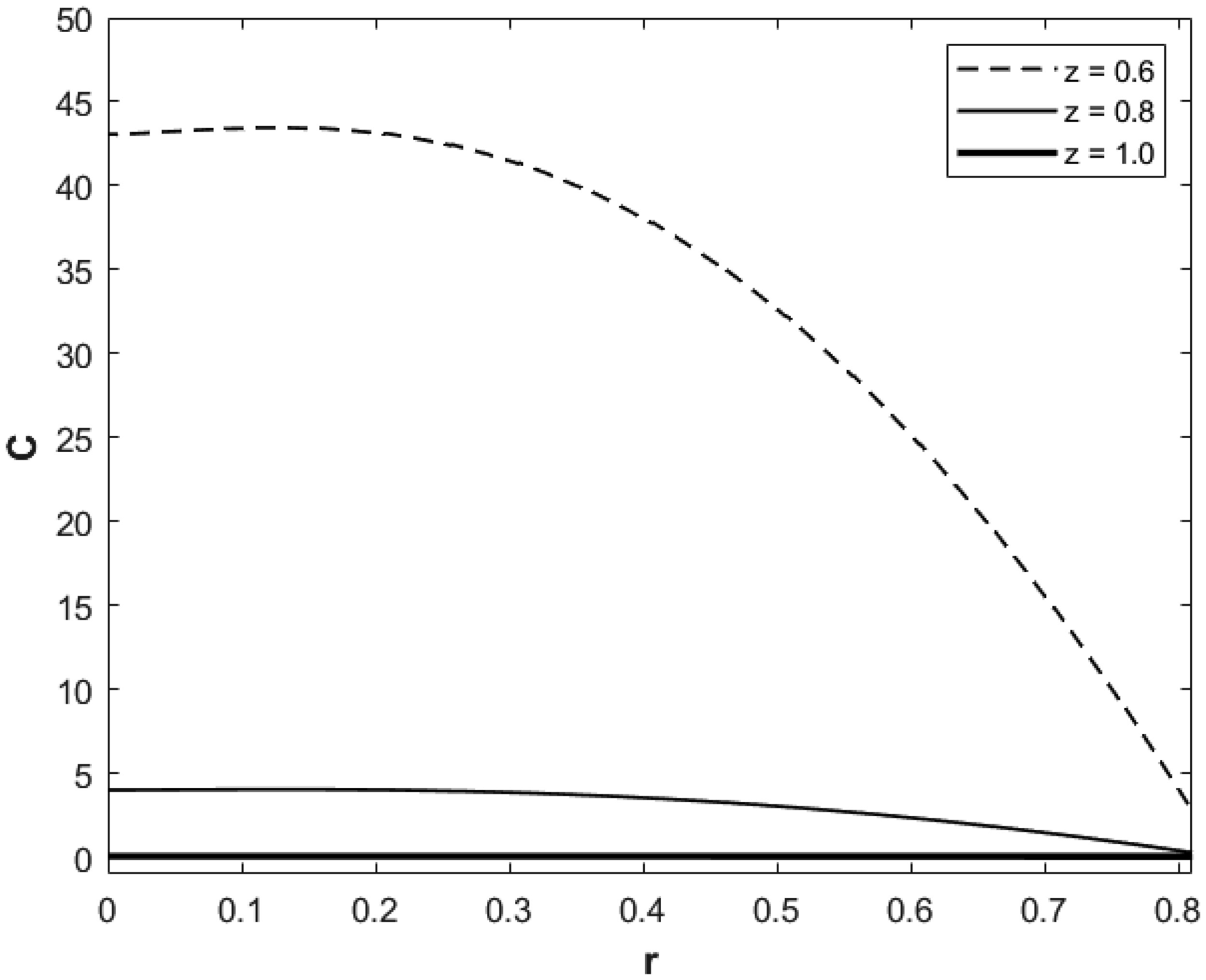
Figure 5 presents solute concentration versus radial variable for E = 0.002, D = 0.01, t = 1, ω = 5.0, λ = 0.6 and different values of the axial variable: 0.6 (dashed line), 0.8 (solid line) and 1.0 (dotted line). It can be seen from this figure that larger value of the solute concentration is closer to the region with higher peak of stenosis effect (z~0.6), which also raises the blood pressure force and make it possible for the solute concentration to be transported at faster rate. Physically and from fluid dynamic branches in chemical engineering and thermodynamic principles, the solute is carried by the blood flow and gains higher values near the region of the stenosis and more so close to the peak of the stenosis, where the blood flow intensifies and, thus, more amount of solute concentration can be located. At z=0.8, which is at the vertical level close to the region of weak stenosis (z~0.9), blood pressure force is also less effective, and solute is transported at lower rate, so that solute concentration is small but not as small as the location corresponding to z=1.0, where the blood pressure is already more reduced as blood flow passes z=0.9 level. From Figure 5, we also observe that radial rate of decrease of the solute concentration increases with increasing radial variable notably for r above some small value, and such rate of decrease is higher at the axial levels close to the stenosis peak. Our additional calculations for higher value of the stenosis height indicated that solute concentration is higher for higher ϵ, and axial rate of change of C increases for solute concentration near axial levels close to the maximum stenosis height level. Figure 5 also shows that solute concentration decreases with increasing axial or radial distance. Physically and from a chemical engineering point of view as solute is carried by the blood flow the presence of the chemical reaction, which is also known as protein binding, and its effect on the solute becomes noticeable by reducing the solute molecules. Thus, it leads to reduction in the solute concentration as blood flow moves further in the axial direction. Solute is also expected to be washed away very close to the internal surface of the artery in this model, and, thus, solute decreases as blood flow approaches such surface.

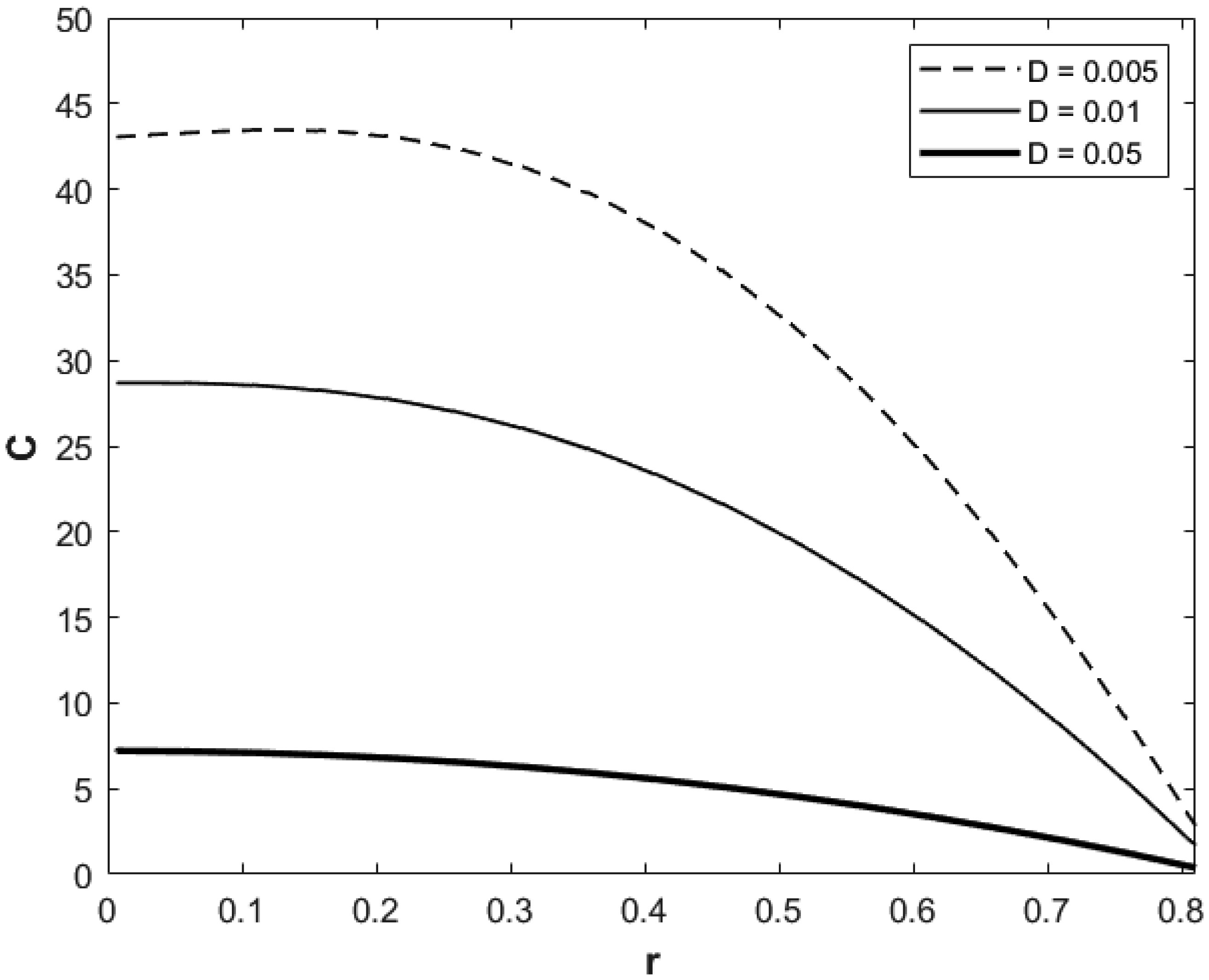
Figure 6 presents solute concentration versus radial variable for given values of t, z, E, ω and λ but different values of the diffusivity parameters. From physical and bio-fluid dynamical point of view it can be indicated from this figure that for relatively small diffusivity effect of solute, convective concentration of the solute is dominant and transporting solute at higher value, while large diffusivity dominates over convection, and solute is transported much less strongly by the diffusion of the solute. From this figure we also observe that radial rate of change of C decreases at a faster rate for r slightly bigger than 0.2 and is more notable for the case where convective transport of solute is more dominant than the conductive one. Our additional calculated results for higher ϵ indicated that it leads to higher values of the solute concentration, and axial rate of change of C increases for very low diffusivity of the solute. Physically and bio-fluid dynamically it is interesting to see that for higher value of the height of mild stenosis blood flow near such height carries larger amount of solute concentration.

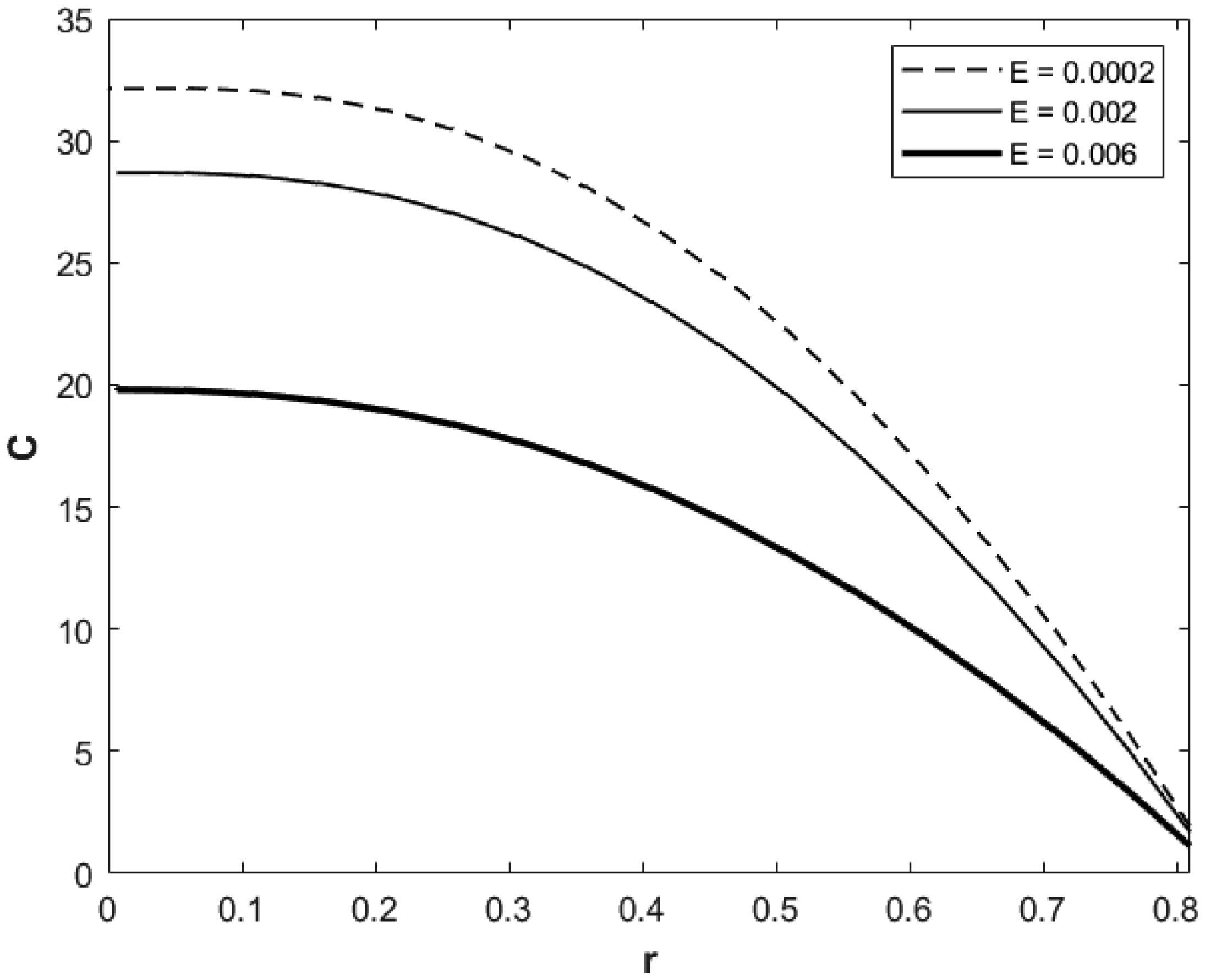
Figure 7 presents solute concentration versus r for t = 1.0, z = 0.6, D = 0.01, ω = 5.0, λ = 0.6 and different values of chemical reaction parameter. From physical and chemical engineering aspects, it can be seen from this figure that higher value of chemical reaction due to the presence of solute leads to higher amount of solute that is lost in the blood flow system. Similar to results observed from Figure 6, we can also see from Figure 7 that the radial rate of change of solute concentration decreases, which is in the presence of protein binding, at a faster rate for r beyond some small value and more notably for the case of larger value of reaction parameter. Our additional calculations indicated that axial rate of change of solute concentration increases for very weak operation of chemical reaction. Our additional calculation for the parameter values as in Figure 7 but for several different values of hematocrit indicated that for values of hematocrit larger than 0.6, solute concentration is enhanced, while for hematocrit less than 0.6 solute concentration increases above those shown in Figure 7. In Figure 8, we find that the solute concentration C is smaller in the non-stenosis region compared to the stenosis region (see Figure 7). Solute concentration C in the non-stenosis region decreases with increasing values of E. Thus, from chemical engineering and thermodynamic aspects and for solute such as drug or nutrients, the loss of such solute by the presence of chemical reaction is higher for case of very high red cell percentage in the blood, while the opposite holds for very small such percentage.

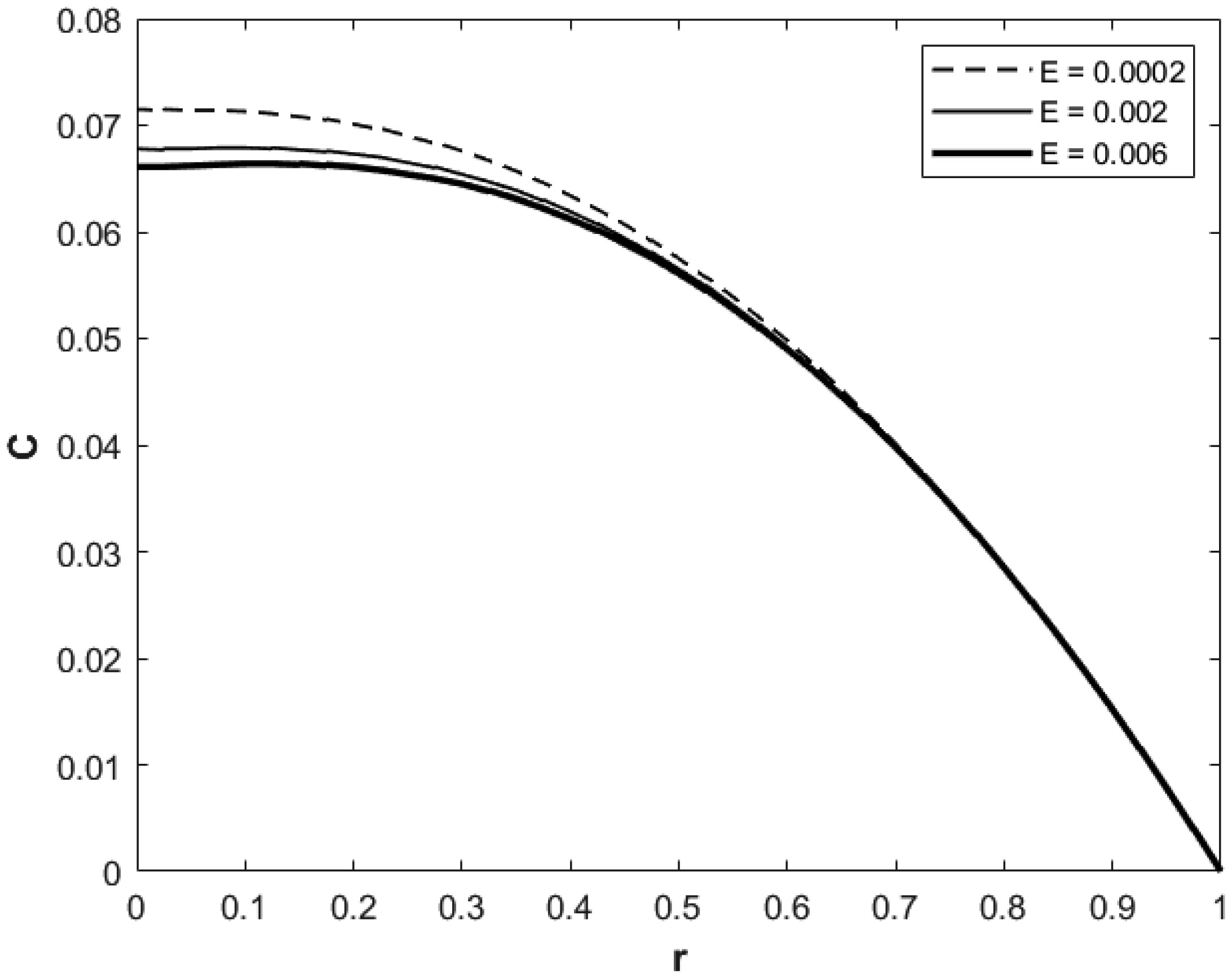
Figure 9 presents solute concentration versus r for t = 1.0, z = 0.6, D = 0.01, E = 0.002, ω = 5.0 and different values of hematocrit. Physically and from biomedical aspects this figure shows that higher percentage of red cells in the blood reduces solute concentration. Similar to Figures 6-7, we can observe from this figure that radial rate of decrease of solute concentration is at a higher value for r above some small value. Our additional calculations indicated that the axial rate of change of solute concentration appears to increase for very low hematocrit as in case of patient with anemia.

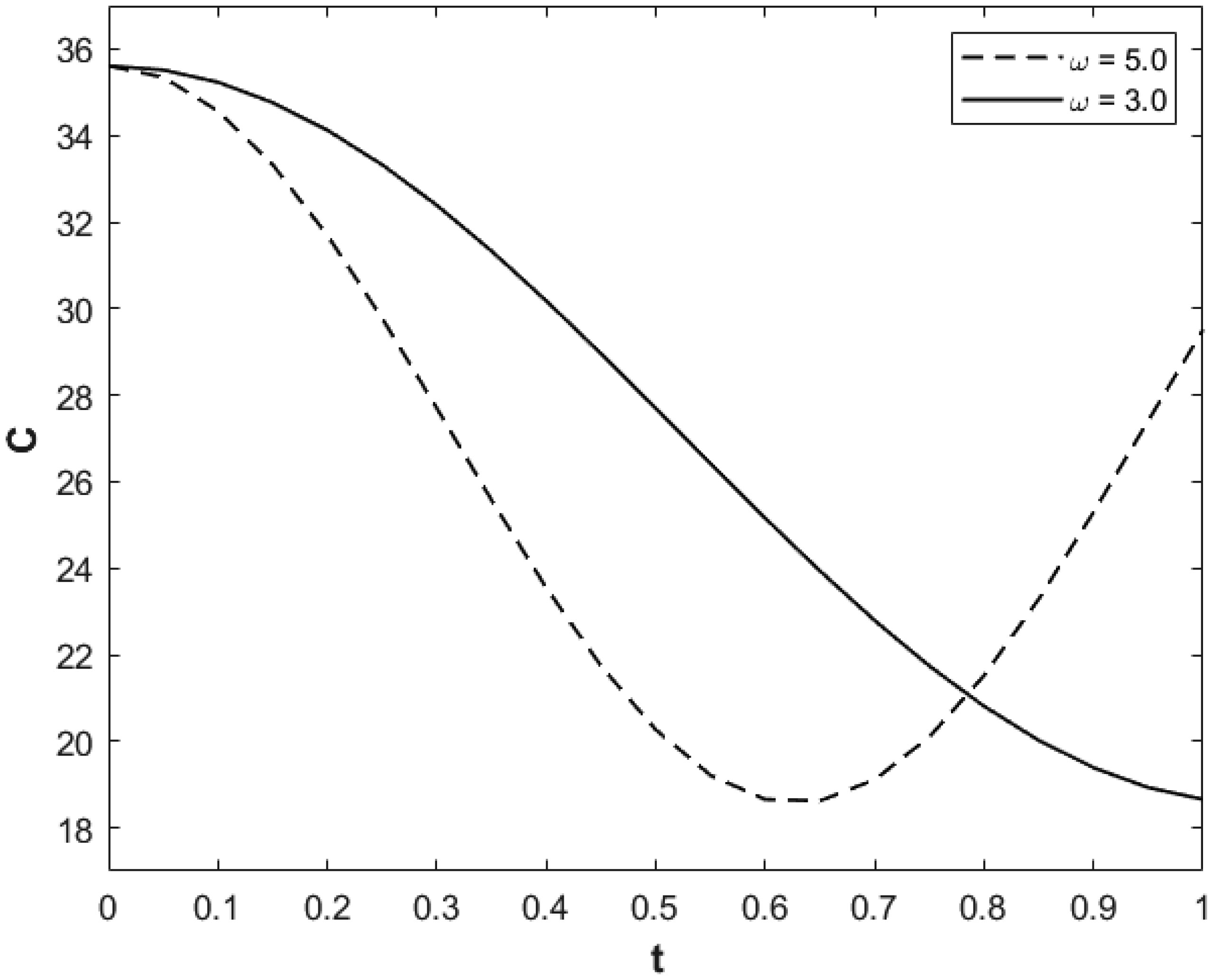
Figure 10 presents solute concentration versus time for given values of the parameters and spatial variables but for different pulsation frequency. It can be seen from this figure as well as from the results based on our additional calculations generated that higher blood pulsation period appears to increase solute concentration. Physically, this result indicates that blood flow with lower pulsation frequency tends to oscillate the blood flow at a faster rate that consequently makes the solute concentration to be transported at a smaller rate. We also did additional calculations for C versus t with the same vales of the parameters and spatial variables as in the case ω = 5.0 and D = 0.01 in Figure 9 but for higher values of diffusivity parameter D ≥ 1.0. We found that the value of solute concentration becomes very small (C << 1). The results clearly indicate physically that convective transport of the solute becomes very weak when diffusion process is notably significant.

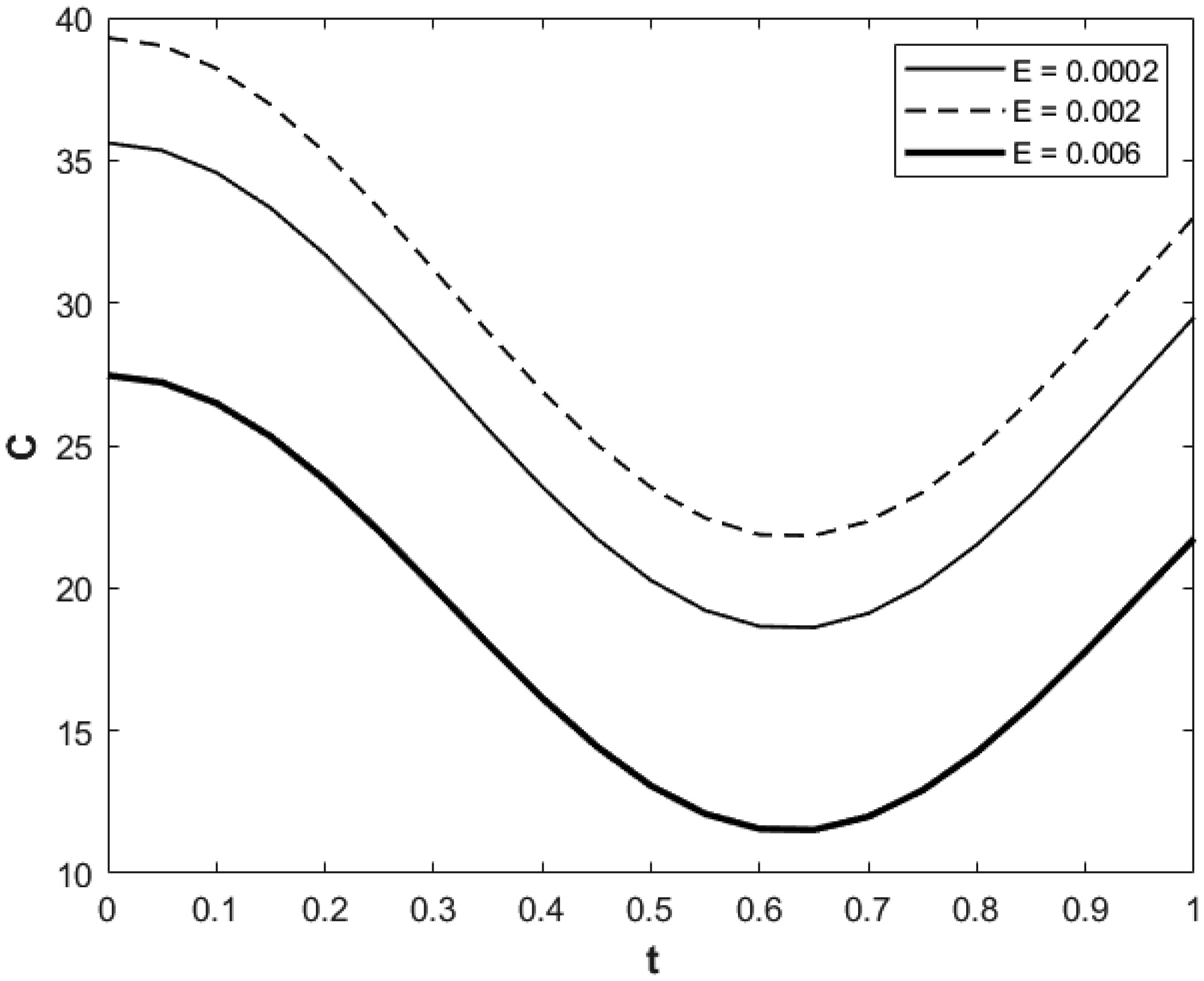
Figure 11 presents solute concentration for given values of the parameters and spatial variables but for different values of chemical reaction parameter. Physically and from chemical engineering aspects, we can observe, consistent with the results to be inferred from this figure and based on the results of our additional calculations, that higher chemical reaction makes solute concentration be lost at higher value. Our additional calculations also indicated that pulse oscillations magnify for cases of low amount of hematocrit or very small chemical reaction as well as for the case where convective transport of solute is significant.

5.   Conclusions

We investigated unsteady blood flow and concentration of a diffusive and reactive solute in a constricted porous artery, where a variable viscosity formula for the blood was used that took into account the presence of red cells in the plasma. For the case of small ratio of the artery radius to the axial extent of the stenosis, we carried out both theoretical and computational methods for a model of prescribed physical system to determine important time-dependent quantities of the blood flow and solute concentration in the porous artery for different values of time and space variables as well as for different values of the parameters that represent combined effects due to the presence of pulsation period, convection/diffusion, chemical reaction, stenosis and hematocrit.

We found that chemical reaction resulted in some amount of solute concentration loss in the arterial blood flow. Higher blood pulsation period increased solute concentration, while higher amount of hematocrit in the blood reduced solute concentration. In the local axial levels in the artery, close to the axial values of maximum stenosis height solute concentration was notably higher. Strong blood pressure force or impedance increased solute transport. Convective solute transport was notable for very low solute diffusivity. Solute concentration decreased with increasing either axial or radial distance. Various quantities oscillated with pulse frequency and magnified for high values of the volume flow rate, convective solute transport and stenosis height. High value of the frequency of the pulsation decreased solute concentration. Higher amount of hematocrit increased the blood pressure force and the wall shear stress, but it decreased the blood speed and solute concentration. Higher values of the volume flow rate increased blood pressure force, blood speed and convective solute transport. Solute concentration was higher more in the core region of the porous artery. Radial rate of change of solute concentration decreased notably for radial distance above some small value, and such rate of decrease was higher for very low diffusivity, hematocrit or chemical reactive response. Axial rate of change of solute concentration increased close to the location of the maximum stenosis height.

Some important physical conclusions that can be drawn from the present study of the already described physical system are given as follows. The loss of solute concentration by the chemical reaction becomes more severe for very high value of red cell percentage in the blood. High blood pulsation frequency weakens solute transport. Very low hematocrit makes solute transport more effective. Blood flow carries less solute concentration at higher axial or radial level. Close to the maximum stenosis height, solute transport and its axial rate of increases more effectively. Convective solute transport is more effective with high impedance or blood pressure force. Very high hematocrit reduces solute transport, and increases the wall shear stress. These conclusions indicate that from chemical engineering and thermodynamic aspects, taking into account an understanding of a combination of the effects due to the chemical reaction, stenosis height, blood flow pulsation period and hematocrit can give better prediction to be able to provide sufficient transport of solute in the blood as in the examples of relevant amount and doses of drug or sufficient amount of nutrients transport in the blood that may be needed to improve health conditions of some patients.

Comparing present results in our already described modeling system of a physical system with two related investigations in the past that we described briefly in section 1, we found the result on chemical reaction effect on the solute dispersion carried out in [18] with no presence of stenosis and no consideration of hematocrit, which were under more sever approximations such as uniform pressure gradient and zero-dependence of axial velocity with respect to axial variable, agrees with the corresponding result in the present study that solute concentration decreases with increasing reaction rate. The work described in [17], under a simple drug transport model, where no effects of reaction and hematocrit were taken into account, provided a result that convective drug transport is dominant for sufficiently small diffusion effect and agrees with the corresponding results in the present study.

In the present investigation we considered blood flow and solute concentration in a porous artery, where present results were all about important and notable features of various blood flow quantities and solute concentration that can provide useful information to biomedical areas in the cardiovascular system. In addition, the present results needed to be uncovered in order to have some understanding when more specific cases for the solute can be considered, such as oxygen, carbon dioxide, etc. in a patient's arterial blood flow system that may have other medical deficiencies like very low hematocrit, etc. Such particular cases can make chemical reaction of such solute more interrelated to the patient's body metabolic system and may also stimulate experimental studies for specific kinds of patients with cases that could lead to medically and experimentally generated data in order to identify components of the patients' arterial blood flow and tissues diseases, which subsequently may facilitate diagnostic treatment and better health for such patient. The results of our present investigation were an outcome of our original motivation to pursue such study and investigation. Our overall results can give more understanding and open new avenues in technological and engineering areas in medical and chemical branches.

Our present results are for a more physically complete model than other models investigated by others in past in the sense that we have included many important physical effects that can exist in blood flow in constricted porous artery, such as those by stenosis, pulsation in time, hematocrit, chemical reaction, diffusion and convection. We uncovered many new results, where all such effects present jointly and provide information about changes and rate changes of quantities such as solute transport as those stated effects acted upon such quantity. We believe that our results can be useful not just for understanding and insight but also for design and development new technological areas in chemical and biomedical engineering and in artificial bioprocesses.

6.   Future work

Further work will include a study in which not only a single artery is considered but a network of arteries to resemble a model that is closer to the one found in the human body. We will also conduct further studies in the area of drug delivery in restricted arteries to understand how a drug or treatment can benefit a patient. The ultimate goal is to collaborate with medical and pharmaceutical industries to generate patient specific models along with treatments that will benefit patients with atherosclerosis and other related diseases in the blood and heart.