Stock returns and inflation expectations: Evidence from 20 major countries

Structural Abstract

Purpose: We present an uncertainty hypothesis, which provides evidence for examining the relation between stock returns and (expected) inflation based on the data of 20 major global stock markets.

Design/methodology/approach: The GED-APARCH model is used to estimate the relation between stock market returns and inflation while controlling for extreme shocks arising from the 2008–2009 global financial crisis (GFC) and 2019–2020 COVID-19 pandemic.

Findings: Based on the testing sample period from January 1990 to June 2023 in 20 major countries, we found strong evidence to support a negative correlation between market returns and (expected) inflation in 18 out of the 20 countries, thereby confirming studies by Fama (1981), Geske and Roll (1983). Further evidence reveals that EMV is positively associated with inflation. This evidence shows that EMV produces a negative effect on U.S. as well as global stock returns supporting the uncertainty hypothesis (Chiang, 2023) and the U.S. volatility spillover hypothesis. We conclude that both domestic inflation and U.S. equity market volatility (EMV) have harmful effects on stock returns. Ignoring the significance of U.S. EMV inevitably produces a biased estimator in the test equation. The current study is robust across different specifications of inflation and stock market returns.

Research limitations/implications: A different model such as a VAR approach can be used to examine the null hypothesis. The variables included in the VAR may include (real) stock market returns, expected inflation, expected real output and monetary growth. However, this extension is more appropriately explored in another paper.

Practical implications: This study has contributed to the practical implications for portfolio management. Essentially, this study identifies two major risk variables, EMV due to inflation and EMV associated with interest rate changes. The former captures investors' sentiment, whereas the latter highlights the Fed's policy stance. Both variables exhibit a negative effect on stock returns.

Originality/value: This study develops a new model to explain the negative relation between stock market returns and (expected) inflation. The link is through the U.S. EMV, which is positively associated with heightened inflation or an upward shift in the Fed's policy but negatively affects stock returns. In addition to providing an empirical estimation, this study employs an asymmetric power GARCH model, which is rich in modeling various properties of heteroskedasticity and long memory.

1.   Introduction

For the past four decades, the Fed has been able to keep the inflation rate around its 2% target level largely because of its effective management of its monetary policy. These decades of rate stability ended as a consequence of the massive quantitative easing implemented as part of the rescue plans aimed at relieving the COVID-19 pandemic. In fact, the inflation rate surged, reaching 8.2% as reported by the U.S. Bureau of Labor Statistics on September 13, 2022. In an effort to combat the rampant inflation, the Fed started to raise interest rates in mid-March 2022 and has hiked interest rates at 11 consecutive meetings up to the FOMC meeting on July 25–26 2023, when the fed funds rate was in the range of 5.25–5.50%, the highest level in more than 22 years. The need for further rate hikes and policy uncertainty depend on the prevailing future inflation rate. In retrospect, the Fed's determination to fight inflation caused a significant selloff in stocks, a result of investors' fears and ongoing pessimistic economic outlook, which could further depress the economy as it results in a recession. Viewed from this perspective, there exists a prospect that stock market returns are negatively associated with inflation expectations, without even accounting for the effects of a rise in geopolitical risks (Chiang, 2021; Caldara and Iacoviello, 2022) resulting from the Russian-Ukraine conflicts and its impact on inflation in 2022–2023.

Evidence of the negative relation between stock market returns and inflation expectation was documented by Fama (1981). In his penetrating 1981 article, Fama proposes a "proxy hypothesis" and maintains that a rise in stock returns signals an increase in output; however, output increase is negatively associated with a rise in inflation. Gallagher and Taylor (2002) test U.S. data and find results to support the proxy hypothesis. Yet, Kaul (1987) finds evidence that the negative relation between stock market returns and inflation expectation in the U.S. data can be explained only in times of a counter-cyclical monetary policy. In addition, Liu et al. (1993) report that there is no significant connection between real stock market returns and expected real economic activity. Yet, the finding of a negative correlation between real stock market returns and real economic performance by Majid (2010) further casts some doubt on Fama's underlying connections.

Geske and Roll (1983) propose a reverse causation relation, arguing that a drop in stock market prices reveals a decline in economic performance and potential tax revenue; this decline in tax revenue will cause larger government budget deficits financed by monetization that result in higher inflation expectations. James et al. (1985) examine the relation among different macroeconomic variables, including stock market returns, real economic activity, inflation and monetary growth, using a multivariate time series model and find sound evidence to back up Geske and Roll's (1983) hypothesis.

Neither Fama's proxy hypothesis that presumes a negative relation between stock market returns and inflation expectations nor Geske and Roll's (1983) causal hypothesis, which starts with changes in real activity that induces monetary/fiscal policy response and in turn a change in inflation, can be used to fully illustrate the negative stock market and inflation relation. To stomp out the recent surge in inflation, the Fed committee has actively raised interest rates. The uncertainty of future rate hikes, however, has created fears that have increased EMV and, in turn, jeopardized stock market performance. We propose an uncertainty hypothesis that links the relation of inflation-equity market volatility and stock returns. The evidence thus provides insights into the uncertainty approach to validate investors' sentiment as well as the spillover effect from the Fed's actions to U.S. and subsequently international stock market performances.

In conducting empirical estimations, we use a sample of 20 major countries to examine the relation between stock returns and inflation. This broad sample of countries helps not only to reduce the biasedness from using a small set of countries but also provides better information with respect to different countries' behavior.

This paper makes several contributions. First, this study employs an asymmetrical power GARCCH model (APARCH), which covers the various features of heteroskedasticity, including asymmetry, variance clustering and long-memory process. In addition, the model includes dummy variables to control for capturing impacts arising from 2008–2009 global financial crisis and 2020–2021 COVID-19 pandemic. Second, this study shows that stock market returns move positively with conditional variance and confirms the risk-return trade-off hypothesis (Bali and Engle, 2010). Third, there are strong negative correlations between stock returns and (expected) inflation for 18 out of 20 major markets; the exceptions are Brazil and Russia, which are positively correlated due to higher prevailing inflation. Fourth, evidence shows that inflation in U.S. and EMV (both inflation and monetary policy induced) are significantly and positively correlated, and EMV has a significant negative effect on U.S. and global stock returns. This volatility-stock return effect adds an additional channel that explains stock returns. Fifth, besides domestic inflation, the news of changes in EMV has an incremental power to explain stock return equations. Thus, the U.S. stock market risk should be explicitly priced into stocks for each country's investments.

The remainder of this paper is organized as follows. Section 2 contains a literature review. Section 3 outlines an econometric model, which features a GED-APGARCH model. Section 4 provides a description of the data for empirical estimations. Section 5 presents empirical results for the stock market return equation. Section 6 reports robustness tests for the real stock return equation. Section 7 discusses conclusions for the empirical findings.

2.   Literature review

The Fisher hypothesis (1930) posits that the stock market returns are positively related to the expected inflation. The rationale for this behavior stems from the notion that compensation is required to offset a loss from inflation. To test the Fisher hypothesis, Boudoukh and Richardson (1993) use long historical data to investigate markets in the U.S. and U.K. and find sound evidence to support the Fisher hypothesis. In a subsequent study using multi-country panel data, Solnik and Solnik (1997) reach comparable results that are in line with the early results obtained by Boudoukh and Richardson (1993) and conclude that the Fisher hypothesis is valid in the long run. Wong and Wu (2003) examine data for G7 and eight Asian countries and find a positive relationship for the Fisher hypothesis in a long horizon. Hasan (2008) examines the Fisher hypothesis using U.K. data. Toyoshima and Hamori (2011) investigate this issue by adding data for the U.S. and Japan, and their testing results agree with the Fisher hypothesis and the existence of a positive relation between stock market returns and inflation. This evidence implies that stocks can be viewed as a good instrument for hedging against inflation.

However, a number of studies reject the Fisher hypothesis. For instance, Nelson (1976) investigates U.S. data and finds evidence that fails to support the Fisher hypothesis. His results reveal a negative relation between stock returns and an expected change in the inflation rate. By the same token, Gultekin (1983) estimates the data for 26 countries and fails to find consistent support for the Fisher hypothesis in most countries. Davis and Kutan (2003) and Spyrou (2004) examine the Fisher effect on international markets; however, they find very little evidence to support the Fisher hypothesis.

Several studies have shown mixed outcomes depending on the sources of shocks, sample periods and monetary regimes used in their analyses. For instance, Marshall (1992) finds that stock market returns are negatively correlated with expected inflation when inflation is generated by fluctuations in real economic activity. Cifter (2015) examines data for Mexico and South Africa and reports that the coefficient of real stock return-inflation relation is negative during periods of recession. Narayan and Zheng (2010), who investigate the U.K. stock market, report that stocks lack the ability to hedge against inflation in the short horizon. Tiwari et al. (2022) use long historical, annual U.S. data to investigate the relation between stock market returns and inflation. The research using wavelet techniques shows evidence of a weak co-movement between stock returns and inflation in the short run and a stronger co-movement toward the long run.

Al-khazali (2003) investigates data for a group of emerging markets and finds a negative relation between stock market prices and inflation in all countries, except Malaysia. Graham (1996) tests the stock return in relation to inflation under different monetary policy regimes. His results indicate the presence of a negative relation in times when monetary policy is implemented during a counter-cyclical or neutral period; a positive relation occurs when the policy is conducted in a procyclical phase.¹

¹The intention of this section is to provide a review of major studies rather than an exhaustive review of literature. Madadpour and Asgari (2019) provide a more detailed literature review of early studies.

In their earlier study, Modigliani and Cohn (1979) suggest a money illusion hypothesis and contend a rational investor should anticipate that cash flows would move with the inflation rate, rising in proportion to the discount rate. However, if investors fail to adjust equity cash flows upward in the same proportion as the upward shift in the discount rate during higher expected inflation, the undervaluation in stocks will lead to a drop in the stock price. Testing of NYSE, AMEX and NASDAQ stocks, evidence from Cohen et al. (2005) supports the model with money illusion.

Fama's (1981) proxy hypothesis is pertinent to explain the negative relation between real stock returns and inflation. Fama's idea is consistent with the studies by Nelson (1976), Fama and Schwert (1977). Fama (1981) contends that there is a positive relation between real stock returns and real economic activity and a negative relation between real economic activity and expected inflation, which results in a negative relation between real stock returns and expected inflation. Gallagher and Taylor (2002) conduct an empirical analysis that confirms the proxy hypothesis. In testing the data for the U.S., U.K., Germany and Canada, Liu et al. (1993) demonstrate that expected inflation is negatively correlated with expected real production; however, they found no significant evidence to support the relation between real stock returns and expected real production, which leads to a rejection of the proxy hypothesis. In his study of Indonesian data, Majid (2010) fails to find evidence to support the inverse relation between real stock market returns and inflation based on Fama's explanation. His results show a positive relation between real output production and inflation as predicted by the Phillips curve (Kryzanowski and Rahman, 2009). Their findings are in contrast to the premise of the proxy hypothesis.

Geske and Roll (1983) offer an alternative hypothesis. Their interpretation is that a decline in stock prices indicates a slowdown in economic activity, which puts a strain on government revenue and heralds budget deficits. The anticipated government borrowing to fund debts may be financed by monetization. As a result, a rise in money supply triggers an upward shift in inflation expectations. This process explains the negative relation between stock market returns and expected inflation. Solnik (1983) examines the data for nine countries and fails to find a significant connection between real returns and inflationary expectations. This finding results in a rejection of the relation between stock returns and inflationary expectations for each major stock market. Using a VARMA model to examine the relation among stock returns, real activity, inflation and money supply change, James et al. (1985) find evidence in line with Geske and Roll's hypothesis. Kaul (1987) provides a different explanation for the relation between stock market returns and expected inflation. It can be argued that a decline in the stock market signals weaker economic activities, which can induce a central bank to generate a quantity easing, that in turn, gives rise to a higher inflation expectation. Due to the fact that the U.S. mainly adopted a counter-cyclical approach to its monetary policy for most of the post-war era, Kaul (1987) finds evidence to support a negative correlation between stock market returns and expected inflation using this time period.

The causality of economic variables is rather complicated depending on the sources of shocks or initial condition. Geske and Roll's (1983) model starts with a decline in real activity that causes government deficits, which are financed by monetization and in turn result in inflation. This scenario is inconsistent with the current market condition that we face. In order to stomp out inflation, the Fed adopted an aggressive monetary policy stance with multiple rate hikes, causing significant stock market volatility that led the stock market to plunge. This inflation-stock volatility-stock return channel has not been comprehensively studied although the issue was mentioned in the literature. For instance, Saryal (2007) examines the data in two countries, Turkey and Canada, with vastly different rates of inflation. Her study finds that the rate of inflation is highly predictive of stock market volatility in Turkey, whereas it has a weaker but still significant impact on the Canadian market. Chiang (2023) also incorporates the equity market volatility into the real stock return-inflation specification and finds a significant negative relation between real stock index returns and expected inflation for 12 major economies. Recently, Batten et al. (2021) finds that during the GFC, investors reduced their stock positions and conclude that implied volatility shocks adversely affect the portfolio returns of stock oil hedges. In a follow up study, Batten et al. (2023) report evidence that VIX has a significant impact on European bank returns. Moreover, in a study using the bibliometric analysis to examine the stock market returns-inflation relation, Hoong et al. (2023) argue that it is vital to integrate theoretical implications in light of the volatile market conditions and rising inflation rate in the empirical analysis.

Despite the significant insight that can be gained from using market volatility to explain the relation between real stock market returns and inflation expectations, very little research has explored this market volatility channel and the potential resulting relations. Our aim of this paper is to present evidence to validate the links between (real) stock market returns and inflation expectations via an EMV channel. These linkages can be described by the following two paths. First, heightened inflation in the U.S. leads to a rise in EMV (Saryal, 2007; Baker et al., 2022; Chiang, 2023; Chiang and Tang, 2023); second, heightened market volatility in the U.S. causes decline stock returns in the U.S., which has a spillover effect to global markets through financial contagion.²

²There are studies focusing on sectoral investigation. For instance, Bouri et al. (2023) find energy and materials have the capacity to hedge against inflation risk. Kilian and Zhou (2021) find a significant short-run impact of rising oil prices on U.S. inflation.

3.   Econometric model

The above discussions lead us to specify a regression model expressed as:

where ${\beta }_{1} < 0$, ${\beta }_{2} < 0$, ${\beta }_{3} < 0,$ The error term, ${\varepsilon }_{t}$│${\mathrm{\Omega }}_{t-1}\backsim \mathrm{G}\mathrm{E}\mathrm{D}(0, {\sigma }_{t-1}^{2}, \nu)$.

Equation (1) is a mean equation expressing the stock market return, ${R}_{t}$, is related to inflation, ${\pi }_{t}$ (or expected inflation, ${\pi }_{t}^{e}$) (Fama, 1981) while controlling for the extreme observations captured by indicator variables, ${I}_{Crisis}\;\mathrm{a}\mathrm{n}\mathrm{d}\;{I}_{COVID-19}$ for the 2008–2009 global financial crisis (GFC) and 2019–2020 COVID-19 pandemic (Cheema et al., 2020; Terry et al., 2002). The variance equation follows the specification of Ding et al. (1993) and features an asymmetric power GARCH (APARCH) model, which is given by:

The model contains a power transformation ($\delta$) of the conditional standard deviation process, which deviates from absolute residuals; where $\delta$ > 0, |$\gamma_{{i}}$|$\leq 1$ for i = 1, 2, ..., r; $\gamma_{{i}}$ = 0 for all i > r, and r$\leq p$ If the null hypothesis $\gamma_{{i}}$ = 0 for all i is rejected, the result suggests an asymmetric effect. It should be noted that ARCH, GARCH and GJR-GARCH models are all nested in this specification.

To simplify the process, it is convenient to impose j = i = 1 in (2). The specification for APARCH (1, 1) model can be expressed as:

The parameters to be estimated involve calculations of $\omega$, $\alpha, \mathrm{\gamma }$, $\beta$ and $\delta$. The specification of (3) is appealing since it is simple yet captures different properties of heteroscedasticity of variance and allows the data to determine an optimal $\delta$ value.

We follow Nelson (1991) and Li et al. (2005), who assume that ${\varepsilon }_{t}$ obeys GED distribution, which is expressed as:

The use of GED distribution allows us to deal with leptokurtotic property (fat tails), which is often embodied in asset series as noted by Li et al. (2005) and Chiang (2020).

4.   Data

The data in this study cover the sample period from December 1989 through June 2022 (and extended to May 2023 for robustness test) for 20 countries; some countries such as China and Indonesia have later started points for the data. The data contain aggregate stock indices, including the United States (US), Canada (CA) United Kingdom (UK), France (FR), Germany (GM), Italy (IT), Japan (JP), Brazil (BR), Russia (RU), India (IN), China (CN), South Africa (SA), Spain (ES), the Netherlands (NE), Sweden (SD), Switzerland (SW), Turkey (TK)), Indonesia (ID), South Korea (KO) and Mexico (MX). The same countries are selected for consumer price index (CPI). The selection of these countries is built around the G20 or top 20 GDP. Argentina, Australia and Iran are not included among these countries due to a lack of monthly CPI data available in the source of data base of the Federal Reserve Bank of St. Louis. The stock return or inflation is derived by taking the natural log-difference of the price index times 100. The monthly inflation rates in Table 1 range from 0.04% (Japan) to 4.29% (Brazil), whereas the rate for the U.S. is 0.21%, which is close to the 0.22% for both the U.K. and Italy.

The monthly stock market returns in Table 2 range from −0.06% (Japan) to 5.88% (Brazil). Evidence shows that Brazil has a higher stock return along with high inflation. The standard deviations of stock returns indicate that the U.S. (3.66) has the lowest risk compared with Brazil (25.94), which has the highest risk and is about 7 times higher than that of U.S. The Jarque-Bera statistics (JB) in stock market returns for examining normality are significantly large relative to the critical point (5.991) at the 5% level with 2 degrees of freedom, which supports a rejection of the null of normality for real stock return series. The data confirm the relevancy of using GED-APARCH procedure.

We also utilize the variable of EMV calibrated to inflation or the interest rate as proposed by Baker et al. (2022), who construct a newspaper-based Equity Market Volatility (EMV) tracker that moves with the CBOE Volatility Index (VIX) (see Table 3) and with realized S & P 500 volatility of returns. EMV refers to three-words that contains: E: {economic}, M: {stock market, equity}, V: {volatility} and their variants, and $\mathrm{\Pi }$:{cpi, inflation, and the likes}. To construct an Inflation EMV tracker, ${EMV}_{\pi, t}$, Baker et al. (2022) use the following formula:

where # denotes the count of newspaper articles in the indicated set, and ${EMV}_{t}$ is the value of the overall EMV tracker in month t. By using the same procedure, Baker et al. (2022) derive ${EMV}_{i, t}$.³

³By the same token, Baker et al. (2022) calculate the share of EMV articles in the category of interest rates and multiply it by the EMV tracker value to obtain category-specific trackers. The measure changes in interest rates that affect EMV during month t is given by ${EMV}_{i, t}$, which is simply used to replace ${EMV}_{\pi, t}$ in equation (5). The terms for Interest Rates: {interest rates, yield curve, fed funds rate, overnight rate, repo rate, T-bill rate, bond rate, bond yield} and Monetary Policy: {monetary policy, money supply, open market operations, fed funds rate, discount window, quantitative easing, forward guidance, interest on reserves, Fed chair, the fed}. See (Baker et al., 2022) and the link Policy News and Equity Market Volatility for the details.

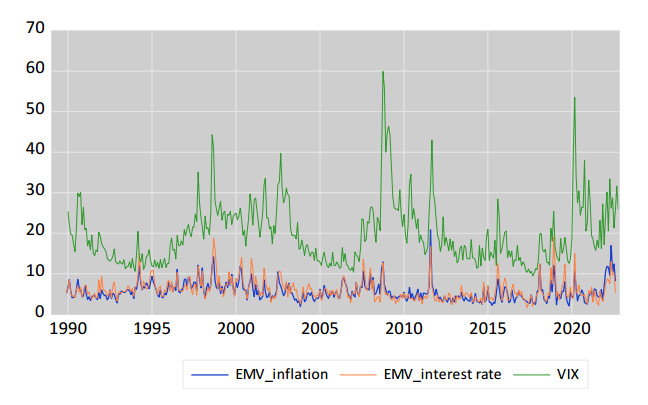
A demonstration of the time series paths of different volatility measures can be seen in Figure 1 that reveals both ${EMV}_{\pi, t}$ and ${EMV}_{i, t}$ are positively correlated with ${VIX}_{t}$. Thus, both ${EMV}_{\pi, t}$ and ${EMV}_{i, t}$ can be viewed as variants of U.S.${VIX}_{t}.$ Moreover, an estimate obtained by regressing ${emv}_{\pi, t}$ (ln${EMV}_{\pi, t}$) and ${emv}_{i, t}$ (ln${EMV}_{i, t}$), respectively, on inflation (${\pi }_{t}$) shows a positive relation, which is statistically significant. The evidence is reported in Table 4, where ${emv}_{\pi, t}$ and ${emv}_{i, t}$ are positively correlated with inflation and are statistically significant.

5.   Empirical evidence

5.1.   Evidence of stock returns and inflation

Estimates of Equations (1) with (3) and (4) are shown in Table 5. Several empirical findings merit comments. First, the correlations between stock market returns and inflation are mainly negative and statistically significant at the conventional level. These results are consistent with Fama's "proxy hypothesis" (1981). Exceptions are the estimates for Brazil and Russia, which display higher inflation than the other countries under investigation. Yet, the positive sign results for these two countries are consistent with the findings by Solnik and Solnik (1997) and Hasan (2008).

Second, the evidence indicates that the indicator variables for both the 2008–2009 GFC and 2020–2021 COVID-19 present negative signs and are statistically significant. The testing results are consistent with the findings provided by Cheema et al. (2020) and Chiang (2022). Note that these indicator variables were excluded in the previous tests of stock returns-inflation equation. The inclusion of these extreme observations is necessary since those influential observations can produce biased estimators (Tsay, 1988).

Third, evidence shows that most coefficients of ${\varepsilon }_{t-1}$ are negative and significant. These results are consistent with the leverage effect (Glosten et al., 1993). In addition to the coefficient of ${\sigma }_{t-1}^{\delta }$ which is positive and whose values of $\delta$ are not exactly equal to 2, indicating that the return volatility series presents a clustering phenomenon and an evolution of variance with a long memory (Chen et al., 2018). Taken together, the evidence supports the specification of using an APARCH model.

5.2.   Evidence from expected inflation

Researchers (Kaul, 1990; Chiang, 2023) propose expected inflation can be an alternative variable, which can be used in the test equation. Numerous methods were used to form this expectation. In this study, we extend the adaptive expectation process (Geske and Roll, 1983; Beladi et al., 1993; Kolluri and Wahab, 2008) by adding a seasonal factor. This process is in the spirit of partial adjustment, which is a time series model in the form of an ARIMA(0, 1, 1) process. It is expressed by adding a seasonal factor yield:

where ${\pi }_{t}$ is actual inflation; ${\pi }_{t}^{e}$ is expected inflation at time t; ${(\pi }_{t-1}-{\pi }_{t-1}^{e})$ is the forecasting error of inflation; $\alpha$ and $\gamma$ are parameters following the restrictions of 1≥ $\alpha$ ≥ 0 and 1≥ $\gamma$ ≥ 0, respectively; ${\pi }_{t-12}$ is a seasonal factor. Estimates of expected inflation are reported in Table 6. All the estimated parameters are consistent with the restrictions and satisfy the range of 1 > $\alpha$ > 0. Among the 20 countries, five are absent of seasonal patterns.

Estimates of adaptive expectation $\left({\pi }_{t}^{e}\right)$ using Equation (6), as reported in Table 7, show that the coefficients of ${\pi }_{t}^{e}$ are negative and statistically significant, indicating that stock market returns are negatively related to expected inflation. The evidence is in line with the findings by Solnik (1983) and James et al. (1985). The exceptions again are Brazil and Russia where the coefficients exhibit positive signs. The findings appear to be consistent with the evidence that these two countries present higher than average inflation rates as shown in Table 2. The evidence of positive signs is consistent with the findings by Saryal (2007), Choudhry (2001) and Kumari (2011) in their studies of high inflation countries. The evidence is also in line with Chaudhary and Marrow (2022), who measure investors' expectations using traded inflation-indexed contracts and find that in the post-2000 period, stocks provide positive returns in response to higher expected inflation.

5.3.   Robustness test by using instrumental variable

It is useful to conduct a robustness test using a different measure of inflation expectations. To this end, the lagged inflation was used as an instrument to predict inflation as denoted by ${\pi }_{IV, t}^{e}$. This is equivalent to imposing the restriction of $\alpha$ = $\gamma$ = 0 in Equation (6). The estimated results, which are reported in Table 8, show that the estimated coefficients and the related statistical results are comparable. These results include the positive coefficients for Brazil and Russia, two countries that have higher inflation rates and comparable higher stock returns; these market forces drive stock returns and expected inflation, which are positively correlated. With respect to the other variables, statistical performances are maintained as demonstrated by similar qualitative results. The evidence shows the model is robust whether the expectations are formed by an adaptive fashion or using the lagged value to serve as an instrumental variable.

5.4.   Effect of U.S. Inflation induced equity market volatility

This section introduces a new variable, $\Delta {EMV}_{\pi, t}$, which is the change in EMV calibrated to U.S. inflation. This variable reflects the change of forward-looking stock market volatility as reported in economic news (Terry et al., 2020; Baker et al., 2022). Incorporating the argument of $\Delta {emv}_{\pi, t}$ into the model, the mean equation becomes:

where $\Delta {emv}_{\pi, t}$ is a change in EMV calibrated to the U.S. inflation rate. The lower case ${emv}_{\pi, t}$ denotes ln (${EMV}_{\pi, t})$. The restriction ${\beta }_{3} < 0$ suggests that as ${emv}_{\pi, t}$ intensifies, investors' fears will increase and lead to a selloff that causes stocks to plunge. Note that the term of ${EMV}_{\pi, t}$ differs from the risk term of Cieslak and Pflueger (2023), who specify an inflation risk term as the covariance between consumption and expected inflation in their model.

Table 9 reports the estimates of stock market returns in response to expected inflation with an addition of a $\Delta {emv}_{\pi, t}$ term utilizing the GED-APARCH(1, 1) procedure. The explanatory power for the estimated equations, interestingly, is improved as reflected in higher or at least equal adjusted R-squared. In reviewing results for Brazil and Russia, the coefficients of expected inflation for both countries continue to show positive signs, but only Brazil's coefficient is positive and statistically significant. This result is similar to that of Tripathi and Kumar (2015), who find that only Brazil demonstrates a positive relation among the BRICS countries. The evidence shows that Brazil has been experiencing a monthly high inflation rate (4.29%) and high stock returns (5.88%). Importantly, evidence for 18 out of 20 countries is negative and statistically significant, supporting the inflation-stock return relation as proposed by Fama (1981) or Geske and Roll (1983).

A most noticeable result in Table 9 is the estimated coefficients of $\Delta {emv}_{\pi, t}$, which present negative signs and are strongly significant for all countries. This outcome is consistent with the phenomenon that as inflation rises in U.S., the input costs of production increases which cuts profits as well as future cash flows; as a result, investors' fears grow, heightening stock market volatility in U.S. market. This heightened volatility further spills over to the rest of world through the contagion effect (Koutmos and Booth, 1995; Karolyi, 1995; Chiang et al., 2007; Chen et al., 2018; Wang et al., 2018; Chiang, 2020). This spillover explains the negative correlations between global stock market returns and U.S. equity market volatility. In addition, the latter is also positively correlated with U.S. inflation as reported in Table 4. Thus, the evidence supports the uncertainty hypothesis, which runs from ${\pi }_{t}^{US}$→ $\Delta {emv}_{\pi, t}$ → ${R}_{t}^{i}$. This link differs from Fama's proxy hypothesis, which relies on a connection with real activity (${q}_{t}$), that is, ${\pi }_{t}^{US}$ → $\Delta {q}_{t}\to {R}_{t}^{i}$.⁴ Our testing result is consistent with the studies by Bessler and Yang (2003) and Rapach et al. (2013) as they show that the U.S. stock market plays a significant role in the price movements of global stock returns. Yet, this study provides a new channel for understanding the negative effect that US $\Delta {emv}_{\pi, t}$ has on global stock returns rather than via a channel of purchasing power parity observed by Yang et al. (2006). Note that the negative coefficient of $\Delta {emv}_{\pi, t}$ implies that a risk premium will be awarded to investors for taking the excessive risk when they buy stocks at time t-1.⁵ Yet, this finding differs from Sarte (1998), who finds the inflation risk is not significant due to the fact that inflation surprises and unexpected movements in consumption growth exhibit little covariation in U.S. data.

⁴The relation of output growth ($\Delta {q}_{t}$) in relation to inflation (${\pi }_{t}$) in the U.S. is as follows. The correlation is positive and highly significant. This evidence is in contrast to Fama's assertion (1981).

⁵Using U.K. in Table 9 as an example, the coefficient of $\Delta {emv}_{\pi, t}$ in ${R}_{t}^{UK} =$-0.021$\cdot \Delta {emv}_{\pi, t}$ = -0.021${emv}_{\pi, t}$ + 0.021${emv}_{\pi, t-1}$, predicts a positive relation between ${R}_{t}^{UK}$ and ${emv}_{\pi, t-1}$, which is consistent with mean-variance analysis.

Comparable results are produced for the rest of the other explanatory variables as shown in Table 9. However, the coefficients of risk variable (ln${\sigma }_{t}^{2}$) become less significant or even change sign due to the dominance of $\Delta {emv}_{\pi, t}.$ It appears that the $\Delta {emv}_{\pi, t}$ has more information content as compared with that of ln${\sigma }_{t}^{2}$ due to the fact that the former contains more explanatory power from news sources. It is interesting to compare the test results in Table 9 against the conventional models of Balduzzi (1995) and Li et al. (2010). Specifically, this study appears to have more information content, which is attributable to its improved model specifications related to the expected inflation variable, its ability to capture the risk factor, $\Delta {emv}_{\pi, t}$ and the power $\delta$ of the heteroskedasticity equation.

6.   Robust test for real stock market returns and market volatility spillovers

6.1.   Effects of expected inflation and inflation induced stock volatility

In the Fisher apparatus, inflation is viewed as a monetary phenomenon, which implies no real effect on economic activities. However, during highly volatile market conditions, the change in expected inflation can have an impact on real stock market returns since adjustments in the stock market and commodity prices do not move at the same pace as the release of news about inflation. By recognizing this possibility, this section estimates the real stock returns in relation to expected inflation and changes in EMV. The estimates using two different measures of expected inflation are shown in Tables 10 and 11.

Several findings emerge from our tests. First, Fisher's hypothesis that the real stock market returns are independent of expected inflation is mainly rejected. The evidence confirms that a negative relation between real stock market returns and expected inflation is valid and significant. The results are in line with the evidence reported by Lin (2009) and Chiang (2023). This, however, is not the case in the Japanese market where the estimated result is insignificant as low inflation and low stock return coexist (see Tables 1 and 2). On the other hand, both Brazil and Russia exhibit positive signs as these two countries experience high inflation and stock returns.

Second, the coefficients of $\Delta {emv}_{\pi, t}$ are negative and highly significant, indicating U.S. equity market volatility has a noticeable effect on the domestic market as well as a spillover effect to global markets. This effect appears to have a more profound effect than the countries' own conditional variance as denoted by ln${\sigma }_{t}^{2}$. Third, for all the other estimates, the results are comparable. Therefore, the propositions are robust across different measures of stock market returns, whether it is real or nominal.

6.2.   Effect of expected inflation and U.S. interest rate induced stock volatility

The above analysis is based on $\Delta {emv}_{\pi, t}$ in the estimated model, highlighting the influence of inflation on investors' sentiment that can lead to stock volatility and in turn affect stock returns. Likewise, we observe that the Fed's active attitude toward rate hikes also generates fears that cause stock market volatility. This section tests the uncertainty hypothesis via the effect of the Fed's interest rate changes on EMV (denoted by ${emv}_{i, t}$), which could also cause the stock market to plunge (Baker et al., 2022). Table 11 reports the estimates by replacing $\Delta {emv}_{\pi, t}$ with $\Delta {emv}_{i, t}$. The statistical results are remarkable, and the qualitative directions are comparable to those using $\Delta {emv}_{\pi, t}$.

Focusing on two key variables, we turn to ${\pi }_{t}^{e}$ and $\Delta {emv}_{i, t}$ in this table. First, the evidence suggests that with the exceptions of Brazil and Russia, the relation between real stock market returns and expected inflation continues to be negative and significant. This finding is consistent with the study observed by Lin (2009). Second, the coefficients of $\Delta {emv}_{i, t}$ are negative, and all the parameters are decidedly significant. The test results are consistent with the U.S. monetary policy stance throughout 2022–2023 when the Fed aggressively raised interest rates to stomp out inflation, causing market volatility and stock market returns to plunge. This negative effect then spread to global stock markets. This process together with the evidence that ${emv}_{i, t}$ is positively correlated with ${\pi }_{t}^{US}$ as shown in Table 4 supports the uncertainty hypothesis that runs through the channel from ${\pi }_{t}^{US}$→ $\Delta {emv}_{i, t}$ → ${R}_{t}^{i}$. It is clear that Table 11 provides solid evidence to back up the uncertainty hypothesis that postulates real stock market returns negatively respond to expected inflation.

6.3.   A robust test for sample sensitivity

It is generally recognized that regression models are sensitive to sample size. When the paper was revised, more observations were available that allowed this study to extend the sample period to May 2023, which includes the later period of COVID-19 and covers more observations of the Fed's ongoing rate hikes. Due to additional observations, it is anticipated that the patten of inflation expectations might alter. For this reason, Table 12 reports the estimated coefficients for $\alpha$ and $\text{γ}$ based on an adaptive expectation model. Those values were identified by the Box-Jenkins procedure. The figures reported in Table 12 are comparable, except for some minor variations for the U.S., which finds a seasonal factor. In this later case, the $\alpha$ values become insignificant for France and Germany. As shown in Table 6, the values of root mean square errors (RMSE) for Russia, Brazil and Turkey are relatively higher as compared with other countries, suggesting the inflation expectations are more diverse and harder to predict for these three markets.

Having generated the expected inflation, the models presented in Table 11 are re-estimated and the results using a sample period of December 1989 through May 2023 are reported in Table 13. The estimated statistics presented in Table 13 are qualitatively comparable. For instance, the coefficients for both ${\pi }_{t}^{e}$ and $\Delta {emv}_{i, t}$ are negative, and only Brazil remains positive for the coefficient of expected inflation. However, the significance level for the coefficients of $\Delta {emv}_{i, t}$ are higher as well as the adjusted R squares. It appears that 13 out of 20 cases for the z-statistics of $\Delta {emv}_{i, t}$ as well as ${\overline R }^{2}$ improved. It can be concluded that the model is robust even when the additional observations for the extended Fed's rate hikes were included.

6.4.   Effects of domestic and U.S. expected inflations

Since the evidence in Table 4 shows that equity market volatilities, whether calibrated to inflation or change in interest rates, are positively correlated with the implied volatility and inflation, they have an effect on the real stock market returns. In addition, Yang et al. (2006) note that U.S. inflation has a direct effect on inflation in global markets. It is, therefore, of interest to conduct a direct test that links real stock returns to domestic and U.S. expected inflation. The statistical results are provided in Table 14.

The evidence indicates that the model is robust across different sources of expected inflation. Specifically, domestic expected inflation produces very comparable estimated results as the previous tables indicate, the exceptions are Brazil and Russia, which have positive coefficients. In particular, the coefficients of ${\pi }_{t}^{e}$ for the other 18 countries show significantly negative signs and are consistent with previous findings (Fama, 1981; James et al., 1985; Kolluri and Wahab, 2008). Even more remarkable is the result that all coefficients of ${\pi }_{t}^{e, US}$ are negative and significant at the conventional level, including the coefficients for Brazil and Russia. Moreover, the magnitude of coefficients for the absolute value is much larger in each country, indicating the profound impact of U.S. inflation on global stock returns.

7.   Conclusions and summary

Fama's (1981) proxy hypothesis provides the basis for testing the relation between stock market returns and inflation. His interpretation (1981) is based on the premise there is a negative relation between inflation and real activity and a positive correlation between real activity and stock market returns. Geske and Roll (1983) observe that there is a negative effect from a rise in expected inflation on stock market returns, which can be achieved from reversed money growth/tax revenues, which shifts inflation downward. While both hypotheses (Fama, 1981 and Geske and Roll, 1983) are valid in a regime of low or moderate inflationary environment when inflation expectations do not impinge on economic agents' sentiment. We provide an alternative explanation that focuses on the premise that inflation could trigger investors' fears, causing increased equity market volatility and stock returns to plummet.

Testing of major stock markets using monthly data shows that the stock returns of 18 out of 20 examined countries (the exceptions being Brazil and Russia) are negatively correlated to (expected) inflation. The evidence of a negative correlation is consistent with the hypotheses of Modigliani and Cohn (1979), Fama (1981), Geske and Roll (1983) and McCarthy et al. (1990). However, we found that the evidence consistently supports a negative relation between (real) stock market returns and (expected) inflation, which passes through two different channels: (a) The U.S. EMV has a negative impact on U.S. stock returns as well as a spillover effect to global markets and (b) EMV is positively related to U.S. inflation or interest rate changes. Thus, these two connections provide evidence to substantiate the uncertainty hypothesis that holds a negative relation between stock market returns and inflation. The finding is consistent with the result reported by Chiang (2023).

The results are robust utilizing different measures of different sample periods, inflation expectations, domestic and U.S. expected inflations, real stock returns vs. the nominal stock returns and equity market volatility induced by inflation, which causes a change in investors' sentiments or is driven by monetary policy uncertainty as reflected by the Fed's behavior.

Finally, while conducting the empirical estimations, the extreme observations during the periods of the 2008-2009 global financial crisis and the 2020–2021 pandemic are found to have significant downturn effects. Using dummy variables to control these two extreme time periods helps to mitigate the estimated biases. Further, using the GED-APARCH(1, 1) procedure in this study is appealing, since the model is able to address the volatility clustering, fat-tail, asymmetric shock and long memory property for the stock return series.

This study has significant implications as it draws particular attention to the impact of inflation induced equity market volatility, which can change investors' sentiment and affect stock returns. In addition, this study indicates that the Fed's monetary policy uncertainty on interest rates can cause equity market volatility that causes the stock market to plunge. All these uncertainty factors should be priced into the stock investments.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

All authors declare no conflicts of interest in this paper.