Stochastic invariance for hybrid stochastic differential equation with non-Lipschitz coefficients

1.   Introduction

In the paper, we consider the stochastic invariance for the following hybrid stochastic differential equations (HSDEs)

where $r(t)$ is a Markov chain taking values in $\mathcal{M} = \{1, 2, 3, \cdots, N\}$ with generator $\Gamma = (\gamma_{ij})_{N\times N}$ (see ^[1]). This equation can be regarded as the result of the following equation

switching from one to the others according to the movement of the Markov chain, and the initial condition

where $f :\mathbb{R}^{d}\times\mathcal{M}\rightarrow \mathbb{R}^{d}$ and $g :\mathbb{R}^{d}\times\mathcal{M}\rightarrow \mathbb{R}^{d\times d}$.

Jump system is a hybrid system with state vector that has two components $X(t)$ and $r(t)$. The first one is in general referred to as the state, and the second one is regarded as the mode. In its operation, the jump system will switch from one mode to another in a random way, and the switching between the modes is governed by a Markov process with discrete and finite state space. Due to the increasing demands from real systems and phenomena in which both continuous dynamics and discrete events are involved, hybrid models have been increasing considered for decades and have received a lot of attention, for example: existence and uniqueness of solutions, approximate solutions(see ^[1,2]); stability theory (see ^[3,4,5,6,7]); almost sure stability (see ^[8,9,10]). As, for stochastic invariance, to the best of our knowledge, there is no paper which investigates the stochastic invariance theory for hybrid stochastic differential equations. Thus, we will make the first attempt to study the problem on the non-Lipschitz coefficients condition. Our results are inspired by the one ^[11] where stochastic invariance theory for Eq 1.2 with $r(t)\equiv1$ has been studied.

Stochastic invariance is a method to study the space state of solutions which people usually consider it from the view of attractor, for example (see ^[12,13]). The first stochastic invariance result can be found in ^[14]. After then, there exist already a lot of literatures concerning invariance as well as the connected notion of viability; characterizations of both have been expressed through stochastic tangent cones (see ^[11,15]), distance function (see ^[16]), martingale decomposition theory (see ^[17]) or other approaches. Although these approaches were different, they had at least one thing in common: they had to make a choice between the assumptions on smoothness of the domain and the regularity of the coefficients, which was a restriction for these existing results to apply in practice. To overcome this difficulty and to analyze the stochastic invariance of solutions for the hybrid stochastic differential equations with non-Lipschitz coefficients, we adopt the method developed by Jaber and Bouchard ^[11]. The method is based on the properties of $It\hat{o}$ integral and the compactness of solution space, and which require neither smoothness of the domain nor Lipschitz coefficients condition. In the following Theorem 3.1, we first check that the solution space of Eq 1.2 is also locally compact (see, Remark 1.3), then we prove the sufficiency of Theorem 3.1 by the maximum principle, this is the same as Theorem 2.3 in ^[11]. Under some additional constraint (martingale measure $\widetilde{u}(dt, dy) = v(dt, dy)-u(dy)$ is independent of Brownian motion $W$) on the jump system, we prove the necessary by twice $It\hat{o}$ integral, it is the same process as one in ^[11] except for extra $\sum_{j = 1}^{N}\gamma_{ij}\phi(x, j)$ term.

The rest of this paper is organized as follows. In Section 2, we give some definitions and preliminaries. In Section 3, we state the main results and their proof. In Section 4, we compare the stochastic invariance with robustness respect to hybrid systems. In Section 5, we provide a numerical simulation and the most probable phase portrait to illustrate our main results.

2.   Preliminaries

Let $\mathbb{R}^{d}$ be a d-dimensional Euclidean space endowed with the inner product $\langle u, v\rangle: = \sum\limits_{i = 1}^{d}u^{i}v^{i}$ for $u, v\in \mathbb{R}^{d}$ and the Euclidean norm $|u|: = \langle u, u\rangle^{\frac{1}{2}}$, for $u\in \mathbb{R}^{d}$. Let $\mathbb{M}^{d}$ denote the collect of all $d\times d$ matrices with real entries and $A_{ij}$ means the entry of the $i$-$th$ row and the $j$-$th$ column. $\mathbb{S}^{d}$ stands for the cone of symmetric $d\times d$ matrices. We use the standard notion $I_{d}$ to denote the $d\times d$ identity matrix. Given $x = (x^{1}, \cdots, x^{d}) \in \mathbb{R}^{d}$, $diag [x]$ denotes the diagonal matrix whose $i$-$th$ diagonal component is $x^{i}$. If $A$ is a symmetric positive semi-definite matrix, then $A^{\frac{1}{2}}$ denotes its symmetric square-root. By a filtered probability space, we mean a quadruple $(\Omega, \mathcal{F}, \{\mathcal{F}_{t} \}_{t\geqslant 0}, P)$, where $\{\mathcal{F}_{t} \}_{t\geqslant 0}$ is a $\sigma$-$algebra$ of $\mathcal{F}$ and satisfies the usual conditions, i.e., $(\Omega, \mathcal{F}, P)$ is a complete probability space, and $\mathcal{F}_{0}$ contains all P-null sets of $\mathcal{F}$, for each $t\geqslant 0, \mathcal{F}_{t_{+}} : = \bigcap_{s > t}\mathcal{F}_{s} = \mathcal{F}_{t}$. Let $\{W_{t}\}_{t \geqslant 0}$ be an m-dimensional Brownian motion defined on the filtered probability space $(\Omega, \mathcal{F}, \{\mathcal{F}_{t} \}_{t\geqslant 0}, P)$. Let ${r(t), t\geqslant t_{0}}$ be a right continuous Markov chain on the same probability space taking values in a finite state space $\mathcal{M} = \{1, 2, \cdots, N\}$ with generator $\Gamma = (\gamma_{ij})_{m\times m}$ given by

in which $\delta > 0$ and $\lim_{\delta \rightarrow 0^{+}}\frac{o(\delta)}{\delta} = 0$. Here $\gamma_{ij}\geqslant 0$ is the transition rate from $i$ to $j$, if $i\neq j$, while

We always assume that $r(t)$ is independent of $w(t)$. It is known that almost all sample paths of $r(t)$ are right-continuous step functions with a finite number of simple jumps in any finite subinterval of $\mathbb{R}_{0}^{+}$. We stress that the Markov chain $r(t)$ can be represented as a stochastic integral with respect to a Poisson random measure. Indeed, let $\Delta_{ij}$, $i\neq j$, be consecutive (with respect to the lexicographic ordering on $\mathcal{M}\times \mathcal{M}$), left closed and right open intervals of the real line each having length $\lambda_{ij}$. Define a function

by

Then

where $v(dt, dy)$ is a Poission random measure with intensity $dt\times\mu(dy), \; \mu(\cdot)$ is the Lebesgue measure on $\mathbb{R}$.

Let us consider the following assumptions:

$\rm(H1)$ $f$ and $g$ satisfy the linear growth condition. That is, there exists a constant $K > 0$ such that

for all $x\in \mathbb{R}^{d}$ and $i\in\mathcal{ M}$;

$\rm(H2)$ $C$ can be extended to a $\mathcal{C}_{loc}^{1.1}(\mathbb{R}^{d}, \mathbb{S}^{d})$ function that $C = gg^{T}$ on $\mathcal{D}$;

$\rm(H3)$ Equation 1.2 has an equilibrium at $X(t) = 0, \; i.e. \; f(0, i) = 0$ and $g(0, i) = 0,$ for all $i\in \mathcal{M}$.

The first two conditions are the same thing as (H1) and (H2) of Theorem 2.3 in ^[11]. Because of the characteristics of the jump system, we increased the condition (H3) to ensure the continuity of the sample paths of solutions for Eq 1.2.

Definition 2.1. A closed subset $\mathcal{D}\subset \mathbb{R}^{d}$ is said to be stochastically invariant with respect to Eq 1.2 if, for all $x\in \mathcal{D}$, there exists a weak solution (X, W) of Eq 1.2 starting at $X(0) = x$ such that $X(t)\in \mathcal{D}$ almost surely for all $t\geqslant 0$.

Let $\mathcal{C}_{0}^{\infty}(\mathbb{R}^{d})$ denote the space of the real-valued, infinitesimal differentiable functions on $\mathbb{R}^{d}$ with compact support. For any $\phi\in\mathcal{C}_{0}^{\infty}(\mathbb{R}^{d})$, we define an operator $\mathcal{L}$:

Definition 2.2. Let $\mathcal{L}$ be a semi-elliptic differential operator of the form(see ^[18], Definition 8.3.2)

Where $i\in \mathcal{M}$ and the coefficients $[f_{j}(X(t), i)] = f(X(t), i), [g_{jk}(X(t), i)] = \frac{1}{2}gg^{T}((X(t), i))$ are locally bounded Borel measurable functions on $\mathbb{R}^{n}$. Then we say that a probability measure $\tilde{P}^{x} on ((R^{n})^{[0, \infty)}, \mathcal{B})$ solves the martingale problem for $\mathcal{L}$ (starting at x) if the process

is a martingale w.r.t.${\mathcal{M}_{t}}$.

Then

We assume that $\widetilde{u}$ is independent of $B$ while $\widetilde{\mu}(dt, dy) = v(dt, dy)-\mu(dy)$ is a martingale measure (see ^[19]).

Remark 2.1. $\mathcal{L}$ is a semi-elliptic differential operator, not a generator of an It$\hat{o}$ diffusion X(t) given by Eq 1.2 (see ^[18], P145).

Definition 2.3. A probability measure $Q_{\xi}$ on $(\Omega, M)$ solves the martingale problem associated with $f$ and $C = gg^{T}$ with initial data $\xi$ if

1. $Q_{\xi} (X^{\circ}(0) = \xi) = 1.$

2. $\phi(X^{\circ}(t))- \int_{0}^{t}(\mathcal{L}\phi)(X^{\circ}(0))ds, \; t\geqslant 0$ is a $(M_{t}, Q_{\xi})$-$martingale$ for all $\phi \in C_{0}^{\infty} (\mathbb{R}^{d})$.

Now we shall state the relation between the martingale problem of Definition 2.3 and its weak solutions. Firstly, assume that there exists a weak solution of Eq 1.2 with initial data $\xi$, then there exists a sextuple $(\Omega, \; \mathcal{F}, \; \mathcal{F}_{t}, \; P, \; B, \; X\; )$ such that

holds a.s, or equivalently

Define the probability measure

Then, $Q_{\xi}$ solves the martingale problem of Definition 2.3 for the coefficients $f$ and $C = gg^{T}$, where $T$ denotes the transpose. For $\phi\in\mathcal{C}_{0}^{\infty} (\mathbb{R}^{d}\times \mathcal{M})$, applying It$\hat{o}$ formula, we have

Then, we obtain that

is a $(\mathcal{F}_{t}^{B}, P)$-$martingale$ (Let $(\mathcal{F}^{B}_{t})_{t\geqslant 0}$ be a complete filtration generated by Brownian motion $B$). Since It$\hat{o}$ integrals are martingales, and $\widetilde{\mu}(ds, dy)$ is martingale measure and which is independent of $B$. Then by transformation of measures, we get

is a $(M_{t}, Q_{\xi})$-$martingale$ on the canonical space $\Omega = \mathcal{C}(\mathcal{M}\times \mathbb{R}; \mathbb{R}^{d})$. This shows that $Q_{\xi}$ (which is a distribution of the solution process) solves the martingale problem.

Definition 2.4. Let $\mathcal{N}_{\mathcal{D}}^{1}$, $\mathcal{N}_{\mathcal{D}}^{2}$ and $\mathcal{N}_{\mathcal{D}}^{1, prox}$ be respectively the first order normal cone, the second order normal cone and proximal cone at the point $x$

in which $d_{\mathcal D}$ is the distance function to $\mathcal{D}$.

Remark 2.2. (see ^[8], Theorem 3.23) Let $p\geqslant 2$ and $x_{0}\in L_{\mathcal{F}_{t_{0}}}^{p}(\Omega, \mathbb{R}^{d})$, Assume that the linear growth condition (H1) and (H3) hold. Then

where $C^{*} = 2^{p-2}(1+\mathbb{E}|X(0)|^{p})e^{p\alpha(T-t_{0})}(|2(T-t_{0})|^{\frac{p}{2}}+|p(p-1)|^{\frac{p}{2}})$ and $\alpha = \sqrt{K}+\frac{K(p-1)}{2}$.

Hence, Kolmogorov's continuity criterion ensures that the sample paths of $X$ are (locally) $\epsilon$-Hölder continuous for any $\epsilon \in (0, \frac{1}{2}).$

Remark 2.3. (see ^[20], Theorem 2.1) When the diffusion coefficient $g$ is independent of the past history, we show that the trajectory field has a version whose sample functions are almost all compact.

3.   Main results

In this section, we shall give the main results of this paper. First of all, we need to prepare several lemmas for the latter stochastic invariance analysis.

Lemma 3.1. Assume that $C\in \mathcal{C}_{loc}^{1.1}(\mathbb{R}^{d}, S^{d})$. Let $X(0) = x\in\mathcal{D}$ and $i\in\mathcal{M}$ such that the spectral decomposition of $C(x, i)$ is given by

where $\lambda_{1}(x, i) > \lambda_{2}(x, i) > \cdots > \lambda_{r}(x, i) > 0$ and $Q(x, i)Q^{T}(x, i) = I_{d}, \; r\leqslant d$.

Then there exists an open (bounded) neighborhood $N(x)$ of $x$ and two $\mathbb{M}^{d}-$valued measurable functions on $\mathbb{R}^{d}$

and

such that

(i) $C(y, i) = Q(y, i)\Lambda (y, i)Q^{T}(y, i)\; and\; Q(y, i)Q^{T}(y, i) = I_{d}$, for all $y \in \mathbb{R}^{d};$

(ii) $\lambda_{1}(y, i) > \lambda_{2}(y, i) > \cdots > \lambda_{r}(y, i) > max\{\lambda_{j}(x, i), \; r+1\leqslant j\leqslant d\}\bigvee 0$, for all $y\in N (x, i);$

(iii) $\bar{g} :y\longrightarrow \bar{Q}(y, i)\bar{\Lambda}(y, i)^{\frac{1}{2}}$ and $\bar{g}\in\mathcal{C}^{1, 1}(N(x, i), \mathbb{M}^{d})$, in which $\bar{Q} = [q_{1}, \cdots, q_{r}, 0, \cdots, 0]$ and $\bar{\Lambda} = diag[\lambda_{1}, \cdots, \lambda_{r}, 0, \cdots, 0]$.

Moreover, we have

Proof. Since $u\in\ker C(x, i)$ satisfies

Since $C\in\mathcal{C}_{loc}^{1, 1}$, we can get $\overline{C} = \overline{g}\overline{g}^{T}$ is differentiable at $(x, i)$, combing with Definition 7.4 and 7.6, and the fact that $\overline{g}\overline{g}^{T} = C\overline{Q}\overline{Q}^{T}$ and $\overline{Q}(x, i)\overline{Q}^{T}(x, i) = C(x, i)C(x, i)^{+}$, we have

Lemma 3.2. Given $g\in \mathcal{C}_{b}^{1, 1}(\mathbb{R}^{d}, \mathbb{S}^{d})$(i.e. $g$ is differentiable with a bounded and a globally Lipchitz derivative). Then

Proof. Fix $(x, i)\in \mathcal{D}$ and $u\in\ker g(x, i)$. Since

we have

Combining with the above equality, we get

Lemma 3.3. Let $\{W_{t}\}_{t\geqslant0}$ be a d-dimensional Brownian motion on a filtered probability space $(\Omega, \mathcal{F}, \{\mathcal{F}_{t}\}_{t\geqslant0}, \mathbb{P})$. Let $\alpha\in \mathbb{R}^{d}$, $\{\beta_{t}\}_{t\geqslant0}\in\mathbb{R}^{d}, \{\delta_{t}\}_{t\geqslant0}\in\mathbb{M}^{d}$ and $\{\theta_{t}\}_{t\geqslant0}\in\mathbb{R}$ satisfy

(1) $\beta$ is bounded;

(2) $\int_{0}^{t}\|\delta_{s}\|^{2}ds < \infty$ for all $t\geqslant 0;$

(3) there exists a random variable $\eta > 0$, such that

$\int_{0}^{t}\|\delta_{s}-\delta_{0}\|^{2}ds = \circ(t^{1+\eta});$

(4) $\theta$ is continuous at $0$ a.s..

Suppose that for all $t\geqslant 0$,

Then,

(a) $\alpha = 0;$

(b) $-\delta_{0}\in S_{+}^{d};$

(c) $\theta_{0}-\frac{1}{2}Tr(\delta_{0})\leqslant 0.$

Proof. Observe that the conditions of Lemma 3.3 are different from the one (^[21], Lemma 2.1), but both results are the same. So our main aim is to reduce the case (^[21], Lemma 2.1) which holds under (e.g. $R_{t} = o\, (t)$). Since $w^{i}(t) = 2\int_{0}^{t}w^{i}(s)dw^{i}(s)+t$ and inequality (3.2), we have

where

Since $\theta$ is continuous at 0, we get $R_{t}^{1} = \circ(t) \; a.s.$. Moreover, in view of (^[22], Proposition 3.9), we have $R_{t}^{2} = \circ(t) \; a.s.,$ as $\beta$ is bounded. Define $M^{ij} = \delta^{ij}-\delta_{0}^{ij}$ and $M^{i} = \int_{0}^{\cdot}\sum_{j = 1}^{d}M^{ij}_{r}dw^{j}(r)$ for $i, j\in\{1, 2, \cdots, d\}$. We can deduce that $(s^{1+\eta}) = \circ \langle M^{i}\rangle\; a.s.$. By using the Dambis-Dubins-Schwarz theorem, we know that $M_{s}^{i}$ is a time changed Brownian motion, By the law of iterated logarithm for Brownian motion $(s^{1+\frac{\eta}{2}}) = \circ(M_{s}^{i})^{2}\; a.s.$. We have $(t^{2+\frac{\eta}{2}}) = \circ \langle R_{t}^{3}\rangle\; a.s.$. By applying the Dambis-Dubins-Schwarz theorem and law of iterated logarithm for Brownian motion again, we get that $R_{t}^{3} = \circ(t) \; a.s..$

Theorem 3.1. (Invariance characterization) Let $\mathcal{D}$ be closed. Assume that $f$, $g$ and C are continuous and satisfy assumptions (H1)$-$(H3). Then, the set $\mathcal{D}$ is stochastically invariant with respect to the Eq 1.2 if and only if

for any initial data $X(0) = x\in \mathcal{D}$ and all $u\in \mathcal{N}_\mathcal{D}^{1}(x, i)$, $i\in \mathcal{M}$.

3.1.   Necessary condition

In this subsection, we prove that the conditions of Theorem 3.1 are necessary for $\mathcal{D}$. Our general strategy is similar to ^[11]. The main idea consists of using the spectral decomposition of C in the form $Q\Lambda Q^{T}$ in which $Q$ is an orthogonal matrix and $\Lambda$ is diagonal positive semi-definite. Then divide the proof into 3 cases (Ⅰ, Ⅱ, Ⅲ).

Ⅰ. The case of distinct and $non$-$zero$ eigenvalues

Since $C\in \mathcal{C}_{loc}^{1, 1}(\mathbb{R}^{d}, \mathbb{S}^{d})$, $C(x)$ has distinct and non-zero eigenvalues, we can reduce to the case where $Q$ and $\Lambda^{\frac{1}{2}}$ are smooth enough and $\Lambda$ has strictly positive entries. The dynamics of $X$ can be written as

where $B = \int_{0} Q(X(s), i) ^{T} dw(s)$ is a Brownian motion. We consider a smooth function $\phi :\mathbb{R}^{d}\rightarrow \mathbb{R}$ such that $\max_{\mathcal{D}}\phi = \phi(x, i)$ for $x = X(0)$ and there exists a constant $M_{1} > 0$, such that $D^{2}\phi(X(t), i)\leqslant M_{1}$ for all $t > 0.$ Since $\mathcal{D}$ is stochastically invariant, $\phi(X(t), i)\leqslant\phi(x, i)$, for all $t\geqslant0$. Further, by using It$\hat{o}$ formula, we get

Let $(\mathcal{F}^{B}_{t})_{t\geqslant 0}$ be a complete filtration generated by Brownian motion $B$, since $B$ and $\widetilde{u}(dt, dy)$ is independent, we get

Applying It$\hat{o}$ formula to $D\phi g (X(s), i)$, we have

First note that $\mathbb{E}_{\mathcal{F}^{B}}[\mathcal{L}(D\phi)g(X(s), i)]$ is bounded, the condition

holds and $\mathcal{L}\phi(X(s), i)$ is continuous at $0$, all these follow from (H3) and the fact that smoothness of $Q$ and $\Lambda$, and $\phi$ has compact support. Moreover,

is Lipschitz's.

Combining these with Remark 2.2 and (H1), we can find constants $L' > 0$ and $M_{1} > 0$ such that

Thus, by using Lemma 3.3, we have

and

Under appropriate regularity conditions, we can choose a suitable test function $\phi$ such that $D\phi(x, i) = u^{T}.$ Further, by using Lemma 3.2 we get (3.3) and (3.4).

Ⅱ. The case of distinct eigenvalues

Assume that $\mathcal{D}$ is stochastically invariant with respect to the Eq 1.2. Let $X(0) = x\in \mathcal{D}$ and $C$ has distinct eigenvalues, then (3.3) and (3.4) hold at point $x$, for all $u\in \mathcal{N}_{\mathcal{D}}^{1}(x, i)$. Proof. Let $(X, W)$ denote a weak solution of Eq 1.2 with the initial data $X(0) = x$ such that $X(t)\in \mathcal{D}$, for all $t\geqslant 0$. If $x$ is in the interior of $\mathcal{D}$, then $\mathcal{N}_\mathcal{D}^{1, prox}(x) = \{0\}$ and (3.3) and (3.4) clearly hold. Therefore, from now on, we assume that $x\in\partial \mathcal{D}$ and $u\in \mathcal{N}_{\mathcal{D}}^{1, prox}(x, i)$.

Next, divide the rest proof into 4 Steps.

Step 1. There exists a function $\phi\in C_{b}^{\infty}(\mathbb{R}^{d}, \mathbb{R})$ with compact support in $N(x)$ such that $\max_{\mathcal{D}}\phi = \phi(x) = 0$ and $D\phi(x) = u^{T}$ (see ^[23], Chapter 6. E).

Step 2. Since $\mathcal{D}$ is invariant under the point $x$, $\phi(X(t), i)\leqslant\phi(x, i),$ for all $t\geqslant0$. Applying $It\hat{o}$ formula to $\phi(X(t), i)$, we have

Define a Brownian motion $\overline{B} = \int_{0}^{.}Q(X(s), i)^{T}dw(s)$. Recall that $Q$ is orthogonal together with

Since $Q\overline{\Lambda}^{\frac{1}{2}} = \overline{Q}\overline{\Lambda}^{\frac{1}{2}}$, the left-hand side of inequality (3.5) can be written in the form

Let $(\mathcal{F}^{\overline{B}}_{t})_{t\geqslant 0}$ be a complete filtration generated by $\overline{B}$, combining with (^[24], Lemma 14.2) and the fact that the martingale $\overline{B}$ is independent of $\overline{B}^{\perp}$ and $\widetilde{u}$. Then, we have

Applying $It\hat{o}$ formula to $D\phi\overline{g}(X(s), i)$, we get

Step 3. Now we check that we can apply Lemma 3.3. First note that all the above processes are bounded, because of Lemma 3.1, (H1) and the fact that $\phi$ has compact support. In addition, given $T > 0$, (H3) and the independence of the increments of $\overline{B}$ imply that $\theta_{s} = \mathbb{E}_{\mathcal{F}_{s}^{\overline{B}}}[\mathcal{L}\phi(X(s), i)]$ for all $s\leqslant T$, due to that $\theta$ is continuous at 0 a.s. Similarly, $\delta_{s} = \mathbb{E}_{\mathcal{F}_{s}^{\overline{B}}}D(D\phi\overline{g})\overline{g}(X(s), i)$ on [0, T]. Moreover, assume that

since $D^{2}\phi(X(s), i)$ and $D\phi(X(s), i)$ are bounded, by using Jensen's inequality, Remark 2.2 and (H1), we can derive

for all $s, r\in[0, 1],$ where $L'$ is a positive constant. By Kolmogorov's continuity criterion, $r$ has $\epsilon$-Hölder sample paths for $0 < \epsilon < \frac{1}{4}$. In particular $\int_{0}^{t}\|\delta_{s}-\delta_{0}\|^{2}ds = \circ(t^{1+\epsilon})$ for $0 < \epsilon < \frac{1}{2}$.

Step 4. In view of Step 3, by using Lemma 3.3, we have

and

Applying (3.7), we get

or equality (3.7) implies that

owing to the symmetry of $C(x)$. In terms of inequality (3.8), $D\phi(x, i) = u^{T}$ and Definition 7.6, we have

which is equivalent to (3.4) by using equality (3.1) and Lemma 3.2.

Ⅲ. The case of the same eigenvalues.

Proposition 3.1. Assume that $\mathcal{D}$ is stochastically invariant with respect to the Eq 1.2 and $C$ has the same eigenvalues. Then conditions (3.3) and (3.4) hold for all $x = X(0)\in \mathcal{D}$ and $u\in N_{\mathcal{D}} ^{1}(x, i),$ $i\in\mathcal{M}.$

Proof. Since $C$ has the same eigenvalues, let $\lambda_{1}(x, i)\geqslant\cdots\geqslant\lambda_{d}(x, i)$, we can perform a change of variable such that $\lambda_{i}(x, i)$ satisfies the conditions of the case Ⅰ or Ⅱ. First, we assume that

for $0 < \varepsilon < 1.$ Since $\mathcal{D}$ is invariant with respect to $X$, hence, $\mathcal{D}^{\varepsilon} = A^{\varepsilon}\mathcal{D}$ is invariant with respect to $X^{\varepsilon}: = A^{\varepsilon}X_{.}.$

Note that

where $f_{\varepsilon} = A^{\varepsilon}f((A^{\varepsilon})^{-1})$ and $C_{\varepsilon}: = A^{\varepsilon}C((A^{\varepsilon})^{-1})(A^{\varepsilon})^{T}$ have the same regularity and growth as $f$ and $C$. On the one hand, $C$ has nonzero eigenvalue, the positive eigenvalues of $C_{\varepsilon}$ are all distinct at $x^{\varepsilon} = A^{\varepsilon}x$, as $C_{\varepsilon}(x^{\varepsilon}, i) = Q(x, i)diag\left[(1-\varepsilon){\lambda_{1}(x, i)}, \cdots, (1-\varepsilon)^{d}\lambda_{d}(x, i)\right]Q(x, i)^{T}$. Therefore, we can apply the case Ⅰ to $((X^{\varepsilon}, i), \mathcal{D}^{\varepsilon})$, then we get

on the other hand, $C$ has zero eigenvalues, the positive eigenvalues of $C_{\varepsilon}$ are all distinct at $x^{\varepsilon} = A^{\varepsilon}x$. Therefore, we can apply the case Ⅱ to $((X^{\varepsilon}, i), \mathcal{D}^{\varepsilon})$, then we have (3.10). By the Definition 2.3 and continuity of $\varepsilon$, set $\varepsilon\rightarrow 0$ on $(3.10)$, we derive

for all $u\in N_{\mathcal{D}}^{1}(x, i)$, $i\in \mathcal{M}$.

3.2.   Sufficient condition

In this section, we prove that the necessary conditions of Theorem 3.1 are also sufficient.

We will show that (3.3) and (3.4) imply that the generator $\mathcal{L}$ of $X$ satisfies the positive maximum principle (see ^[25], P165): If $\phi\in \mathcal{C}^{2}(\mathbb{R}^{d}, \mathbb{R})$, $x\in\mathcal{D}$, and $max_{\mathcal{D}}\phi = \phi(x)\geqslant 0$, we have $\mathcal{L}\phi(x)\leqslant 0$.

Proposition 3.2. Assume that (3.3) and (3.4) hold for all $X(0) = x\in \mathcal{D}$, and $u\in N_{\mathcal{D}}^{1}(x, i).$ Then the generator $\mathcal{L}$ satisfies the positive maximum principle.

Proof. It is similar to the proof of the Proposition 4.1 in ^[11]

for any smooth function $\phi$ such that $\max_{\mathcal{D}}\phi = \phi(x, i)\geqslant 0$.

Utilizing (3.4), We have

Remark 3.1. The linear operator $\mathcal{L}$ satisfying the positive maximum principle is dissipative, therefore theory of dissipative structure can be used to prove Theorem 3.1.

Proposition 3.3. Under the assumptions of Theorem 3.1, assume that condition (3.3) and (3.4) hold for all $x\in \mathcal{D}$ and $u\in N_{\mathcal{D}}^{1}(x)$. Then $\mathcal{D}$ is stochastically invariant with respect to the Eq 1.2.

Proof. We know that $\mathcal{L}$ satisfies the positive maximum principle and the trajectory field of Eq 1.2 has a version whose sample functions are almost all compact (see Remark 2.3), then there exists a compact subset of $\mathcal{D}_{E}[0, \infty)$, where $(E, r)$ denotes a metric space (see^[25], p122). Then, (^[25], Theorem 4.5.4) yields the existence of a solution to the martingale problem associated with $\mathcal{L}$ with sample paths in the space of $c\grave{a} dl\grave{a}g$ functions with values in $\mathcal{D}^{\Delta} = \mathcal{D}\bigcup{\Delta}$ which is the one-point compactification of $\mathcal{D}$. Recall Remark 2.2 and (^[25], Proposition 5.3.5), then we get that the solution has a modification with continuous sample paths in $\mathcal{D}$. Finally, (^[25], Theorem 5.3.3) implies the existence of weak solution $(X, W)$ such that $X(t)\in \mathcal{D}$ almost surely for all $t > 0$.

Remark 3.2. The Theorem 3.1 doesn't hold if $r(t)$ is dependent of w(t). Since It$\hat{o}$ formula doesn't hold if $r(t)$ is dependent of w(t).

Remark 3.3. When $r(t)\equiv1,$ Theorem 3.1 is equivalent to the Theorem 2.3 in ^[11]. When $r(t)\equiv1$, $\tau = 0$ and $G(X_{t}) = 0$ hold, Theorem 3.1 is equivalent to the Theorem 3.1 in ^[26].

4.   Robustness

Equation (1.2) can be regarded as a stochastically perturbed system of the determined hybrid differential equation,

We know that Eq 4.1 is asymptotically stable under the conditions of (H1)$-$(H2). Then there is a natural problem: if the system (1.2) is asymptotically stable, how much stochastic perturbation can this system tolerate without losing the property of asymptotic stability? Such a kind of problems are known as the problem of robust stability, which has received a great deal of attention, for example ^{[27,28,29,30]}. Robustness of the $\psi$-type stability requires that the solution of this Eq 1.2 is almost surely $\psi$-type stable: $\limsup_{t\rightarrow\infty}\frac{\ln|x(t)|}{\ln\psi} < 0$. It is obvious that this $\psi$-type stability implies the almost surely exponential stability when $\psi(t) = e^{\alpha t}$ for any $\alpha$. The almost surely exponential stability for Eq 1.2 requires that $\mathbb{E}[2(X(t), i)^{T}f(X(t), i)+|g(X(t), i)|^{2}]\leqslant -\lambda \mathbb{E}|X(t)|^{2}$, for any $\lambda > 0$. Which implies that

when $\phi(x) = x^{2}$. Therefore, the generator $\mathcal{L}$ satisfies the positive maximum principle, then there exists a weak solution $X(t)$ of Eq 1.2 such that $X(t)\in \mathcal{D}$, where $D$ is stochastically invariant with respect to the Eq 1.2. So robustness can derive stochastic invariance. On the contrary, it is not true, for example below Eq 5.1.

5.   Application

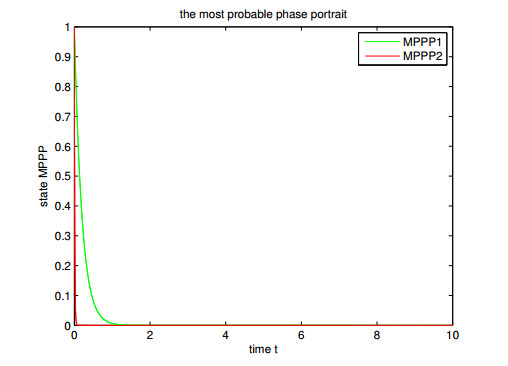
In this section, we will give an example of stochastic invariance which does not support robustness. Moreover, we give the numerical solution of the example and its most probable phase portraits to illustrate the contours of the paths of solution. We restrict to a one-dimensional setting for ease of computation and notation.

Example 5.1. Let $w(t)$ be a scalar Brownian motion. Let $r(t)$ be a right-continuous Markov chain taking values in $\mathcal{M} = \{1, 2\}$ with generator $\Gamma = \left(\begin{array}{cc} -1 & 1 \\ 3 & -3 \\ \end{array} \right).$

Assume that $w(t)$ and $r(t)$ are independent. Consider a one-dimensional linear stochastic differential equation with Markovian switching of the form

here $\alpha(i) = \alpha(r(t))$ and $\sigma(i) = \sigma(r(t))$ $(i = 1, 2)$. Let us put

We can regard Eq 5.1 as the result of the following two equations

and

switching to each other according to the movement of the Markov chain $r(t)$ with the initial data $x = X(0).$ Then, with the previous notations, $\mathcal{D}\subset\mathbb{R}$, define $\phi:\mathbb{R}\times \mathcal{M}\rightarrow \mathbb{R}_{+}$ by

with $\beta_{1} = 1$ and $\beta_{2} = \frac{1}{2}$. Therefore, the first order normal cone given by Definition 2.4 reads

Then, the set $\mathcal{D}\subset \mathbb{R}$ is stochastically invariant with respect to the Eq 5.1 if and only if

Proof.

5.1.   Sufficient condition

Since

hence, condition (H1) is satisfied. We can derive from (5.4)

Choose

we have

and

Hence, the generator $\mathcal{L}$ satisfies the positive maximum principle, by using of (^[25], Theorem 5.3.3), we get that there exists a weak solution $(X, W)$ such that $X(t)\in \mathcal{D}$ almost surely for all $t > 0$.

5.2.   Necessary condition

Assume that $X(0) = x$ and $\phi (x, i) = \beta _{i}x^{\frac{1}{4}}$. Since the set $\mathcal{D}$ is stochastically invariant with respect to (5.1), there exist

Applying It$\hat{o}$ formula twice to (5.6), we have

where

Combing with Lemma 3.3, we can derive

5.3.   Robustness

Since

By using almost surely asymptotic estimates theory (^[8], Theorem 3.26), for any given initial data $X(0)$, there exists a solution $X(t, \xi)$ to Eq.5.1 and this solution has the property

However, we can not derive

Hence, solution of (5.1) is not robust stability (see ^[28]).

Remark 5.1. For the system (5.1), robustness is a sufficient condition for stochastic invariance, not a necessary condition.

Remark 5.2. In robustness theory one can get how much perturbation the equation can tolerate; in stochastic invariance theory one can get the coverage area of all weak solutions to the equation. This is a balance. In addition, one can still obtain specific initial value in stochastic invariance theory, but one can not get it in robustness theory.

5.4.   Numerical simulation of HSDEs-Euler-Maruyama method

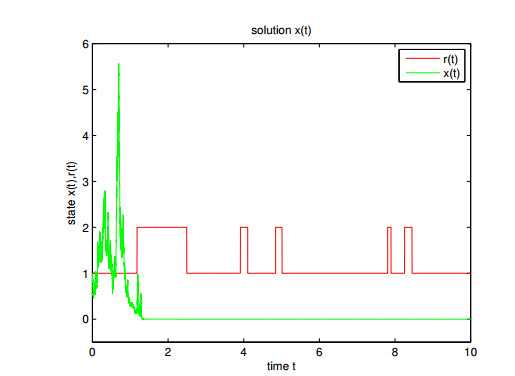
In order to further visualize the solution trajectory of the equation, we will give its numerical solution and the most probable phase portrait of (5.1). We will apply Euler-Maruyama (EM) method to the linear HSDE in Eq 5.1 on [0, 10] and get $10^4$ discrete paths of X(t), just as Figure 1 shows

The red line notes Markovian switching and the green line notes sample paths of Eq 5.1, we see that all solutions approach stable as $t > 2$. We conclude the maximizer at time $t$ respectively from Eqs 5.2 and 5.3 that

for every $x_{0}\in\mathbb{ R}$. Then, the most probable dynamical system is

this is the same as the corresponding deterministic dynamical system $\dot{x} = \alpha x, \; \; \alpha < 0$. The most probable phase portraits ^[31] provide geometric pictures of most probable or maximal likely orbits of stochastic dynamical systems, the most probable phase portrait for Eq 5.1 is displayed in Figure 2, the red line notes solutions of (5.2) and the green line notes solutions of (5.3). Analogously to the deterministic differential equations setting, all solutions tend to the origin, in this case the equilibrium point is called a sink.

6.   Conclusions

In this paper, stochastic invariance theory for HSDEs has been studied. The necessary and sufficient conditions for the Theorem 3.1 have been established. This obtained result improved and generalized the result in ^[11]. Moreover, an example is given to illustrate our Theorem.

7.   Appendix

For convenience, we collect some definitions and properties of matrix tools intensively used in the proofs throughout the article in this Appendix.

Definition 7.1. Fix $A\in \mathbb{M}^{m, n}$. The Moore-Penrose pseudoin-verse of $A$ is the unique $n\times m$ matrix $A^{+}$ satisfying: $AA^{+}A = A$, $A^{+}AA^{+} = A^{+}$, $AA^{+}$ and $A^{+}A$ are Hermitian.

Definition 7.2. (the decomposition theorem of Hermitian Matrix) If $A\in \mathbb{M}^{d}$ is a real Hermitian Matrix, if and only if there exists a real orthogonal matrix $Q\in \mathbb{M}^{d}$ and a real diagonal matrix $\Lambda = diag[(\lambda_{i})_{i\leqslant d}]\in \mathbb{M}^{d}$ such that $A = Q\Lambda Q^{T}$.

Proposition 7.1. If $A\in \mathbb{M}^{d}$ has the spectral decomposition $Q\Lambda Q^{T}$ for some orthogonal matrix $Q\in \mathbb{M}^{d}$ and a diagonal matrix $\Lambda = diag[(\lambda_{i})_{i\leqslant d}]\in \mathbb{M}^{d}$. Then, $A^{+} = Q\Lambda^{+} Q^{T}$ in which $\Lambda^{+} = diag[(\lambda_{i}^{-1}\mathbb{I}_{\lambda_{i}\neq0})_{i\leqslant d}]$ and $AA^{+} = Q diag[(\mathbb{I}_{\lambda_{i}\neq0})_{i\leqslant d}] Q^{T}$. Moreover, if $A$ is positive semi-definite and $B^{\frac{1}{2}}$, then $B^{+} = Q(\Lambda^{+})^{\frac{1}{2}}Q^{T}$.

Definition 7.3. Let $A = (a_{ij})\in \mathbb{M}^{m_{1}, n_{1}}$ and $B\in \mathbb{M}^{m_{2}, n_{2}}$. The Kronecker product $(A\otimes B)$ is defined as the $m_{1}m_{1}\times n_{1}n_{2}$ matrix

Definition 7.4. (see ^[32], Chapter 9) Let $A$ and $B$ be as in Definition 7.3, $C\in \mathbb{M}^{n_{1}, n_{3}}$ and $D\in \mathbb{M}^{n_{2}, n_{4}}$. Then,

Definition 7.5. (Jacobian matrix) Let $F$ be a differential map from $\mathbb{M}^{n, q}$ to $\mathbb{M}^{m, p}$. The Jacobian matrix $DF(X)$ of $F$ at $X$ is defined as the following $mp\times nq$ matrix:

Definition 7.6. Let $F$ be a differentiable map from $\mathbb{M}^{n, q}$ to $\mathbb{M}^{m, p}$ and $H$ be a differentiable map from $\mathbb{M}^{n, q}$ to $\mathbb{M}^{p, l}$. Then, $D(GH) = (H^{T}\otimes I_{m})DG+(I_{l}\otimes G)DH$.

Acknowledgments

The authors gratefully acknowledge the financial supports by Young innovative talents project of general colleges and universities in Guangdong Province under Grant numbers 2018KQNCX238, as well as the Doctoral Scientific Research Foundation of Jiaying University.

Conflict of interest

The authors declared that they have no conflicts of interest to this work.