Variation of the electronic properties of the silicene nanosheet passivated by hydrogen atoms: A DFT investigation

1.   Introduction

Recently, much more attention has been attracted on the graphene nanosheet due to its extraordinary interesting properties, including great mechanical, electronic, and transport properties ^[1,2,3,4]. This has led to its potential applications in different field such as electric/photonics integrated circuits (ICs), medical sensors, and hydrogen storage applications ^{[5,6,7,8,9,10]}. Graphene, which is a two-dimensional structure, is a semi-metallic structure with the Dirac-like electronic structure and zero-band-gap characteristics ^[11]. Using the theoretical and experimental approaches, the properties of the graphene adsorbed by different atoms and molecules are evaluated. The adsorbed graphene has found different potential applications in several fields such as charge carrier doping ^[12], catalysts ^[13], gas sensor ^[14,15], hydrogen separation ^[16] and band-gap engineering ^[17].

Considering the mentioned great properties of the graphene, the new structures such as 2D nano-structures from group Ⅳ of the periodic table (including silicene ^[18], germanene ^[19,20] and stanene ^[21]) have been considered. Some reports were published since 2004 on the production of the single layered nanosheet made by the Si atoms, which is called silicene ^[22]. It was shown that the silicene is the thinnest possible silicon layer which possess great physical properties ^[19] and has variety of applications ^[23]. Furthermore, due to the Dirac cone, quantum spin Hall Effect, ultra-high mobility and easy integration with the silicon-based microelectronics ^[24,25,26], silicene can be considered as a more suitable choose to be used in the non-electronic devices. To realize the potential application of the silicene, it is important to understand its electronic transport properties in order to achieve high efficient devices ^{[26,27,28,29,30]}.

The first principles calculations along with the Monte Carlo method was used by Li et al. ^[27] to study the electron-phonon interaction as well as the electronic transport properties of a monolayer silicene. The orbital degree of freedom, the orbital magnetization and the orbital magnetic momentum contributes significantly to the electronic transport (tunneling) properties of silicene ^[31]. Charge transport mechanisms in post-graphene materials were studied by Sangwan et al. ^[32]. They directed a comprehensive investigation on the intricacies of electronic transport of the silicene including band structure control with thickness and external fields, scattering mechanisms, electrical contacts, and doping. Shakouri et al. ^[33], investigated the electronic charge transport through a zigzag silicene nanoribbon subjected to an external electric field. The valley-dependent energy band as well as charge transport property of silicene nanosheet under a periodic potential were investigated by Lu et al. ^[34]. It was found that the band gap and Dirac point of the silicene are clearly dependent on the valley index. Moreover, they obtained a remarkable valley polarization by effective tuning of the silicene structural parameters. Sahin and Peeters ^[35] performed estimated the spin-orbit band gap of the silicene as 1.5 meV.

Some researches show that the atomic and molecule adsorption can lead to effective tuning of the silicene electronic properties ^{[36,37,38,39,40,41,42,43,44]}. In terms of experimental achievement, it has been shown that a single layer silicene has the capacity to be completely hydrogenated and transformed into H-silicene ^[40,41]. After atomic hydrogenation, the hybridization of the silicene atoms is changed from sp² (or mixed sp²-sp³) into the sp³ state. This lead to significant variation in the electronic properties of the resulted structure compared to the previous one ^[40,42]. Using first principle calculations, Pulci et al. ^[42] investigated the electronic properties of hydrogenated monolayer siliene and germanene nanosheet. They obtained the density of state (DOS) and macroscopic polarizability of the mentioned nanosheets upon hydrogenation. Moreover, they compared the physical properties of the hydrogenated nanostructures with the pristine ones.

The predicted intrinsic mobility of the monolayer silicene was abated as almost 1200 cm²/Vs at room temperature. Nagarajan et al. ^[43] investigated the influence of the NH₃ adsorption on the electronic properties of the armchair silicene. They showed that the adsorbing the NH₃ on the silicene nanosheet results in the variation of the Ⅰ-Ⅴ characteristics. The influence of the P and Al adsorption on the structural, electronic and magnetic properties of the armchair silicene nanoribbons were evaluated by Zhang et al. ^[44]. A large band gap around was obtained around the Fermi level of the Al and P doped silicene.

In this paper DFT method is used to evaluate the electrical properties of the silicene and H-silicene nanosheets. Then, the Ⅰ-Ⅴ characterizes, the density of states (DOS) and the structure of the H-silicene band are evaluated and comparted with those of the pure silicene nanosheet counterparts. Simulation results reveals two separate spectrum areas in the DOS and a Gaussian shape Ⅰ-Ⅴ characteristic in a broad range from 0 to 5 V.

2.   Computational details

To compute the corresponding electronic structure and electronic properties in a 2D-Si nanosheet molecular device, the first-principles calculation with the help of DFT is fully investigated. To obtain more accurate results, energy of system is converged with respect to effective parameters of self-consistent calculations, such as the cut-off energy and the number of K-points. The DFT method with the aim of SIESTA package ^[45] is used here for all of the simulations.

The Landauer-Büttiker formula ^[46] is used to obtain the current in the central scattering region. This formula is expressed as Eq 1,

where e and h denote the electron charge and the Planck constant, respectively. Moreover, f represents the Fermi-Dirac distribution function (refer to ^[47] to know more about these functions and their properties) and $\mu_{L(R)}$ shows the electrochemical potential for the left or right electrode. Finally, $T(E, V)$ is defined as the electronic transmission constant obtained under bias voltage V and is expressed as Eq 2,

in which ${\Gamma _{L(R)}} = i\left[{\mathit{\Sigma }_{L(R)}^r - \mathit{\Sigma }_{L(R)}^a} \right]$ represents the coupling matrix between the central scattering region and the left or right electrode. Moreover, $G_{M}^{r(a)}$ is advanced Green's function in the central scattering region.

A vacuum unit cell with the dimensions of 10 Å along with y and z axes is used to study the electronic properties of silicene nanosheet. By using this padding, interactions between the silicene atoms and its periodic images are prevented. The convergence force is considered as 0.05 eV/Å and when the system is reached to this value, it is said that the structure is optimized.

3.   Details of DFT simulation

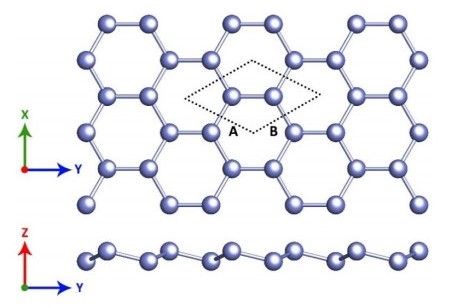
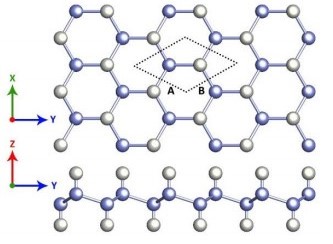
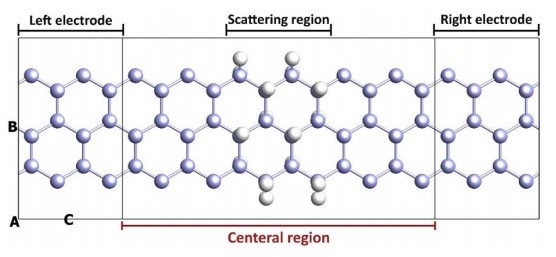
Evaluation of the structural and electronic properties of the silicene and H-silicene nanosheets are performed by using the first principles calculations. For this purpose, the SIESTA package ^[48] is utilized. During the entire calculations, the density mesh cutoff is set as 300 Ry and the energy shift parameter is selected as 100 meV. The Monkhorst–Pack scheme was used to sample the Brillouin zone with a 21 × 21 × 1 K-points sampling. For the exchange-correlation functional the generalized gradient approximation (GGA) in the form of PBE is applied. Furthermore, a vacuum distance of 20 Å is selected to avoid the interactions between the nearest unit cells in the periodic boundry condition. Optimizing the geometry has been performed by minimizing the force and stress tolerance down to 0.001 eV/Å and 0.0001 GPa, respectively. To calculate the Ⅰ-Ⅴ curve a supercell with the lateral distance of about 10 Å from the edge is used. The silicene nanosheet is composed of 60 Si atoms in total which 24 of atoms are the quota of the electrodes. In H-silicene nanosheet, 16 H atoms are added in the middle of the nanosheet as shown in Figure 1. In should be mentioned that the hydrogenation of the silicene leads to transforming the hybridization state from mixed sp² to sp^{3 [45]}.

Figure 1.  Top view of the 50% H-silicene device.

DownLoad: Full-Size Img PowerPoint

4.   Results and discussion

In Figures 2 and 3 the top and side view of silicene and fully hydrogenated silicene (H-silicene) nanosheets have been presented. Upon the calculations, the lattice constants for the silicene and H-silicene nanosheets are obtained as 3.84 Å and 3.87 Å, respectively which are in a very good agreement with previous results ^[49]. Also, the buckling height of the silicene and H-silicene (δ) are gained as 0.54 Å and 0.73 Å, respectively. Therefore, it can be concluded that the buckling height of the silicene increases by hydrogenation. Similarly, the bond length of the H-silicene (2.35 Å) is also larger than the associated value for the pure silicene (2.28 Å) which are in agreement with results in the ref ^[50].

Figure 2.  Top and side view of pure silicene monolayer. The unit cell has been specified by dotted rhombus.

DownLoad: Full-Size Img PowerPoint

Figure 3.  Top and side view of fully H-silicene monolayer. The unit cell has been specified by dotted rhombus.

DownLoad: Full-Size Img PowerPoint

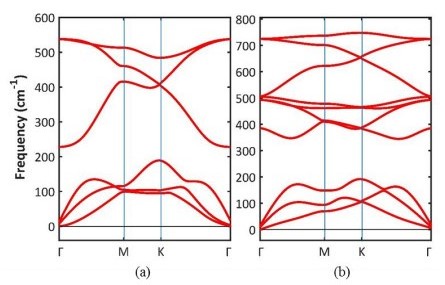
To check the dynamical stability of the system after the passivation by hydrogen atoms, we have calculated the phonon dispersion of the monolayer (see Figure 4). As can be seen, no imaginary mode is seen before and after the passivation and the material is kinetically and dynamically stable. Our results are in good agreements with the previous studies ^{[27,51,52,53]}. Moreover, the maximum of vibration frequency for this monolayer is increased after the passivation which means the bonds have become stronger. On the other hand, the chemical stability of the system is also improved, because, the dangling bonds are saturated after the passivation.

Figure 4.  The phonon band dispersion of the (a) pure and (b) hydrogenated silicene monolayer along the high symmetry points Γ, M, and K. There is no mode with imaginary frequency.

DownLoad: Full-Size Img PowerPoint

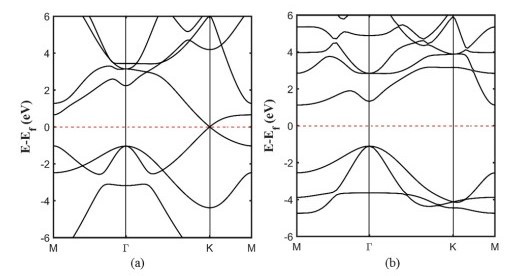
The electrical properties of the pure silicene and H-silicene nanosheets have also been computed. The calculated band structures in the absence or presence of hydrogen atoms have been plotted in the Figure 5. As simply can be seen, the silicene nanosheet is a semi-metal because of the zero band gap and Dirac cone at the Fermi level in the K point. The energy spectrum is not linear around Fermi level. It is observed from Figure 5b, that the band structure of H-silicene in GGA level suggests the indirect band gap as 2.23 eV so that the valence band maximum (VBM) occurs at the Γ-point and the conduction band minimum (CBM) occurs at the M-point. In fact, after the fully hydrogenation, the band gap of silicene are opened and the location of VBM and CBM are modified from K-point to the Γ and M points, respectively. These are while the hydrogenation has no effect on the energy degeneracy of the VBM at Γ-point in the electronic band structure. These features will be very promising for manufacturing of the 2D flexible nanosheets in the nanoelectronics and optoelectronics ^[54].

Figure 5.  Band structures of (a) pure silicene and (b) fully H-silicene monolayers in the GGA level. The Fermi level has been set on zero.

DownLoad: Full-Size Img PowerPoint

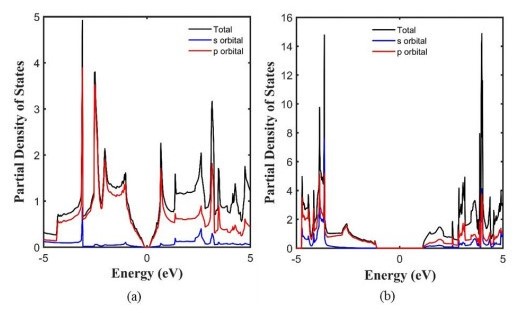
To observe the contribution of different orbitals around the Fermi level, the partial density of states (PDOS) of the pure silicene and H-silicene nanosheets have also been calculated and shown in Figure 6. It is obvious that in both nanosheets PDOS, the portion of p orbital is quite dominant than s orbital in the VBM and CBM. These are completely in agreement with this fact that in nanosheets with hexagonal lattice such as graphene and germanene the contribution of p orbital is dominant than the other orbitals.

Figure 6.  Partial density of state of (a) pure silicene and (b) fully H-silicene monolayers in the GGA levels. The Fermi level has been set on zero.

DownLoad: Full-Size Img PowerPoint

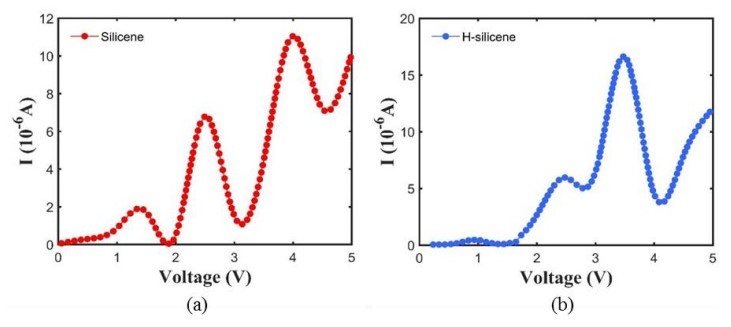
In this part, the current-voltage (Ⅰ-Ⅴ) curves of both nanosheets are obtained and plotted in Figure 7. It should be noted that the hydrogenation is not fully in here because of the large band gap (2.33 eV) that it produces. Such a band gap will never be favorable for high conductivity. In fact, the hydrogenation is about 50% (see Figure 3) that creates no band gap and indicates metallic behavior as in the ref ^[50]. The difference between pure silicene and 50% H-silicene is higher density of states around the Fermi level for 50% H-silicene in comparison to pure silicene which is desirable for a high conductivity. From Figure 7, it is clear that in the pure silicene nanosheet, the level of current has two peaks around 2.5 and 4 V with a maximum magnitude of 11 μA. However, in the H-silicene nanosheet, the current is found to be narrower with just one peak around 3.5 V where its peak increases up to 17.4 μA. In addition, for the applied voltage of 0 to 5 V, the average current is 4.8 and 8.1 for pure silicene and 50% H-silicene, respectively. In other words, the resistivity of the silicene decreases by the 50% hydrogenation, which is opposite proportional to the electrical conductivity and transport properties. This is due to the higher density of states around the Fermi level in H-silicene than the pure one. Therefore, hydrogenating of the silicene nanosheet can make it a good candidate to be applied as a gas sensor in which the sensitivity is an important factor for the detection of the gas atoms.

Figure 7.  I-V curves of (a) pure silicene and (b) 50% H-silicene nanosheets.

DownLoad: Full-Size Img PowerPoint

5.   Conclusions

In summary, the electronic properties of the silicene and H-silicene nanosheets are investigated using the DFT approach. The simulation results show that the hydrogen functionalized silicene nanosheet possess a promising Ⅰ-Ⅴ characteristic rather than the pure silicene nanosheet. Besides, the Ⅰ-Ⅴ characteristic curve for the H-silicene have a Gaussian shape with one peak which covers the voltage range from 0 to 5 V. On the other hand, investigating the influence of the hydrogenation on the bandgap properties of the silicene, it was observed that the H-silicene has an indirect band gap, with the value of 2.33 eV. However, the silicene nanosheet possesses a semi-metallic behavior with a zero band gap.

Conflict of interests

The authors declare no conflict of interest.